In-Process Monitoring of Temperature Evolution during Fused Filament Fabrication: A Journey from Numerical to Experimental Approaches
Abstract
:1. Introduction
2. FFF Parameters and Their Impact on Part Quality
- An overview performed on the influence of process parameters through the part quality fabricated by the FFF process appears to have conflict in their obtained results. For example, a study in 2002 concluded that the layer thickness has a less significant influence on the tensile strength. After 3 years, other researchers found that the tensile strength of an FFF part first decreased and then increased as the layer thickness increased. A few years later, in 2010, another research proposed that the layer thickness has a low impact on the tensile strength. These consequences call for a comprehensive investigation through the FFF parameters;
- FFF parameters not only affect the part quality but also greatly influence the build time involved. However, studies on the influence of process parameters on the build time were found to be in the development stage;
- Almost all research has focused on investigating one material at a time, or even one parameter. In contrast, there are a number of parameters in reality that play an essential role during production. Furthermore, based on the various research in literature, investigating the simultaneous effect of important parameters is required in order to better understand the FFF parameters;
- A thorough investigation of the combined effect of FFF parameters is required, which helps in further understanding the influence of each parameter with their interaction on the bond quality. This point of view helps to optimize the FFF process in order to reach the final goal, which is the improvement of bond quality.
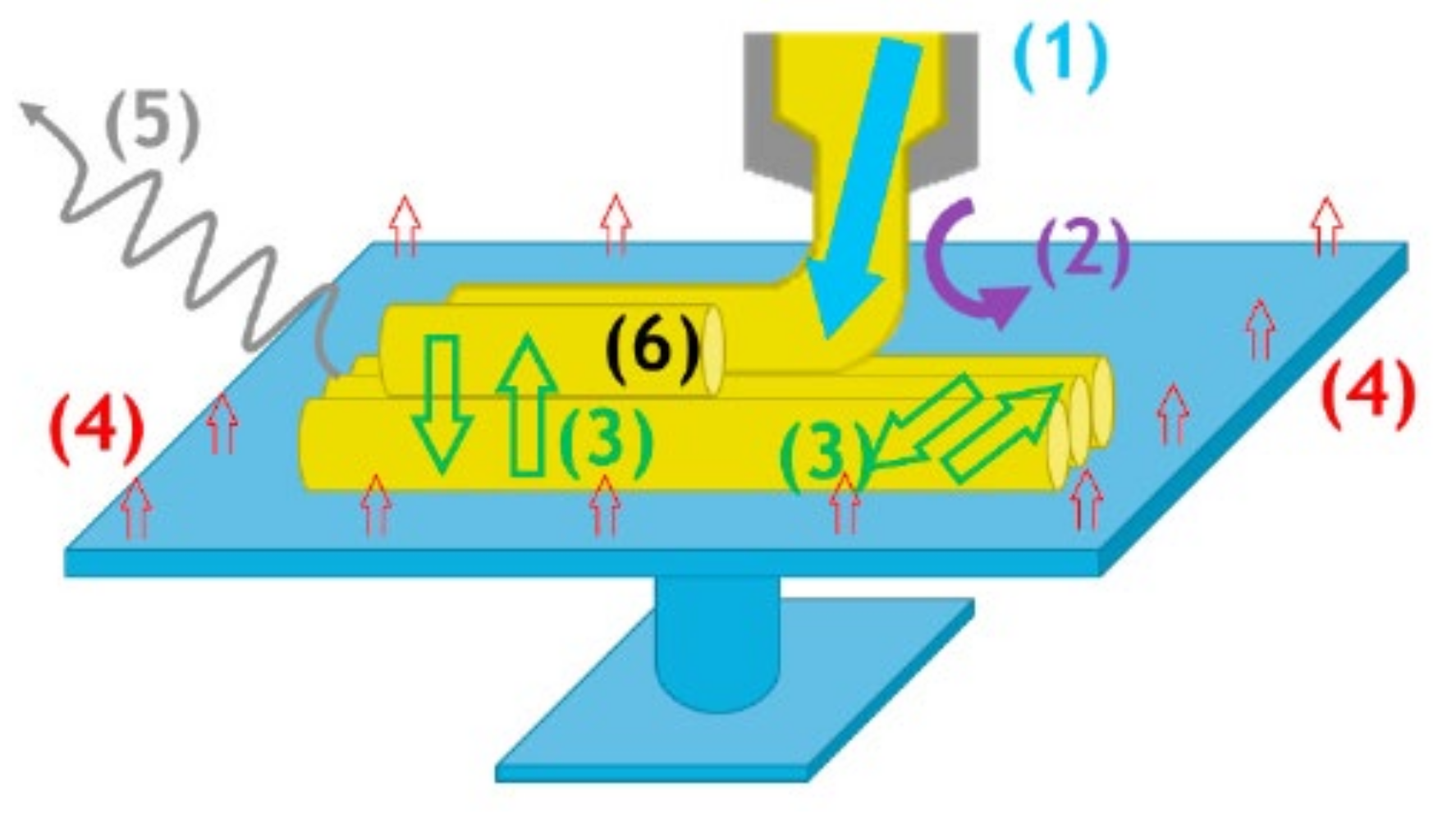
3. Role of Heat Transfer in FFF
- (1)
- Heat induced by the liquefier;
- (2)
- Convective cooling of the filaments with the air: the effect of heat transfer coefficient (hconv) is inevitable [54];
- (3)
- Heat exchanges between the adjacent filaments: the conductance and deposition sequences control the interaction intensity;
- (4)
- Heat brought by the support plate: this is defined as the conduction controlled by the thermal contact conductance and contact area;
- (5)
- Radiative losses: This consists of radiation between the filament and surroundings and radiation between adjacent filaments;
- (6)
- Heat source from the exothermal crystallization for semi-crystalline polymers.
3.1. Influence of Process Parameters on Cooling Stage and Quality Part
3.1.1. Liquefier Temperature
3.1.2. Platform Temperature
3.1.3. Print Speed
- The interaction of parameters and their influences on the temperature evolution of filaments must be included;
- The temperature profile of filaments is an important matter and influences the bonding;
- The temperature dependence viscosity must be included.
3.2. Influence of Heat Transfer on Rheological Characteristics
4. Temperature Evolution of Filaments in FFF
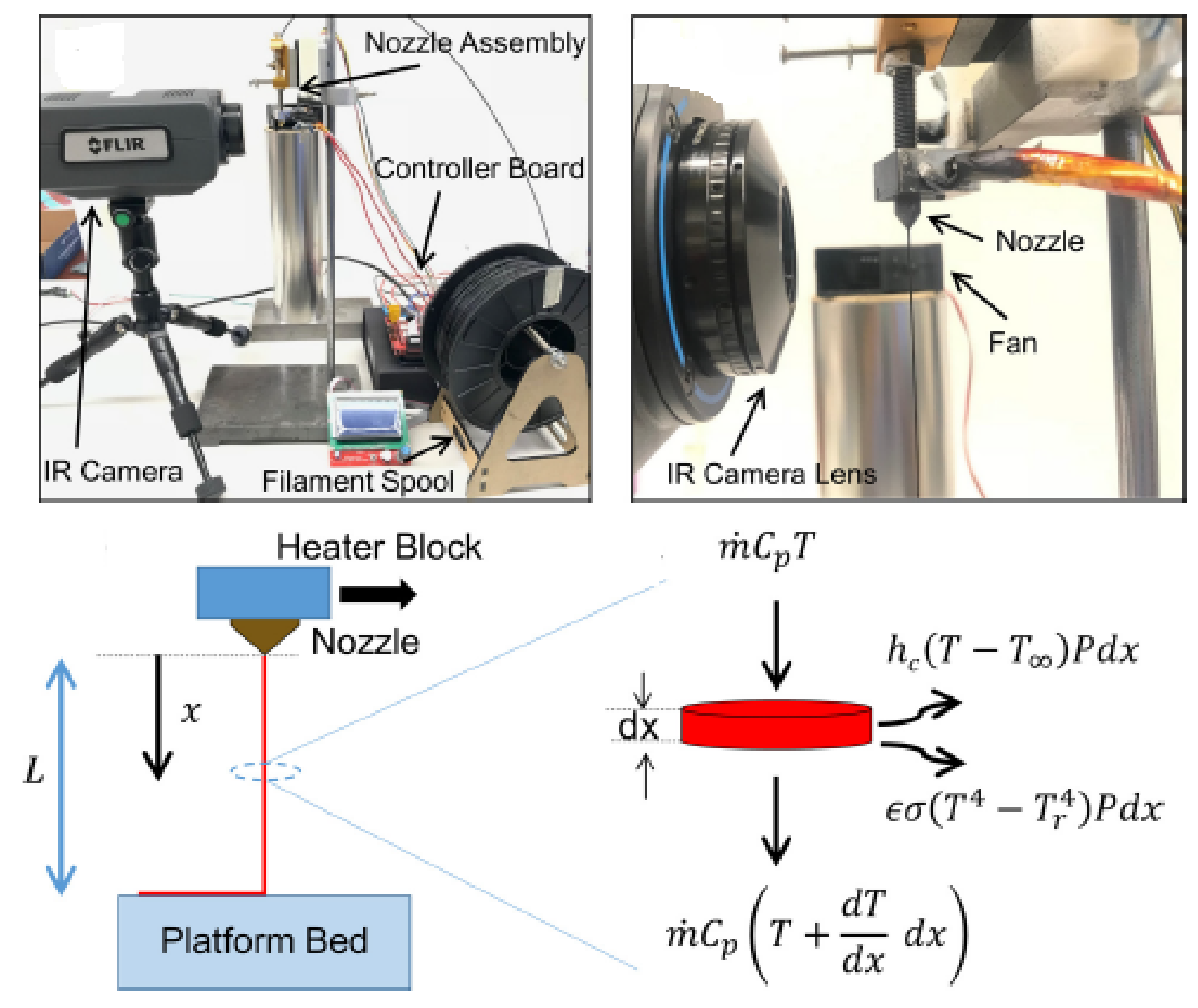
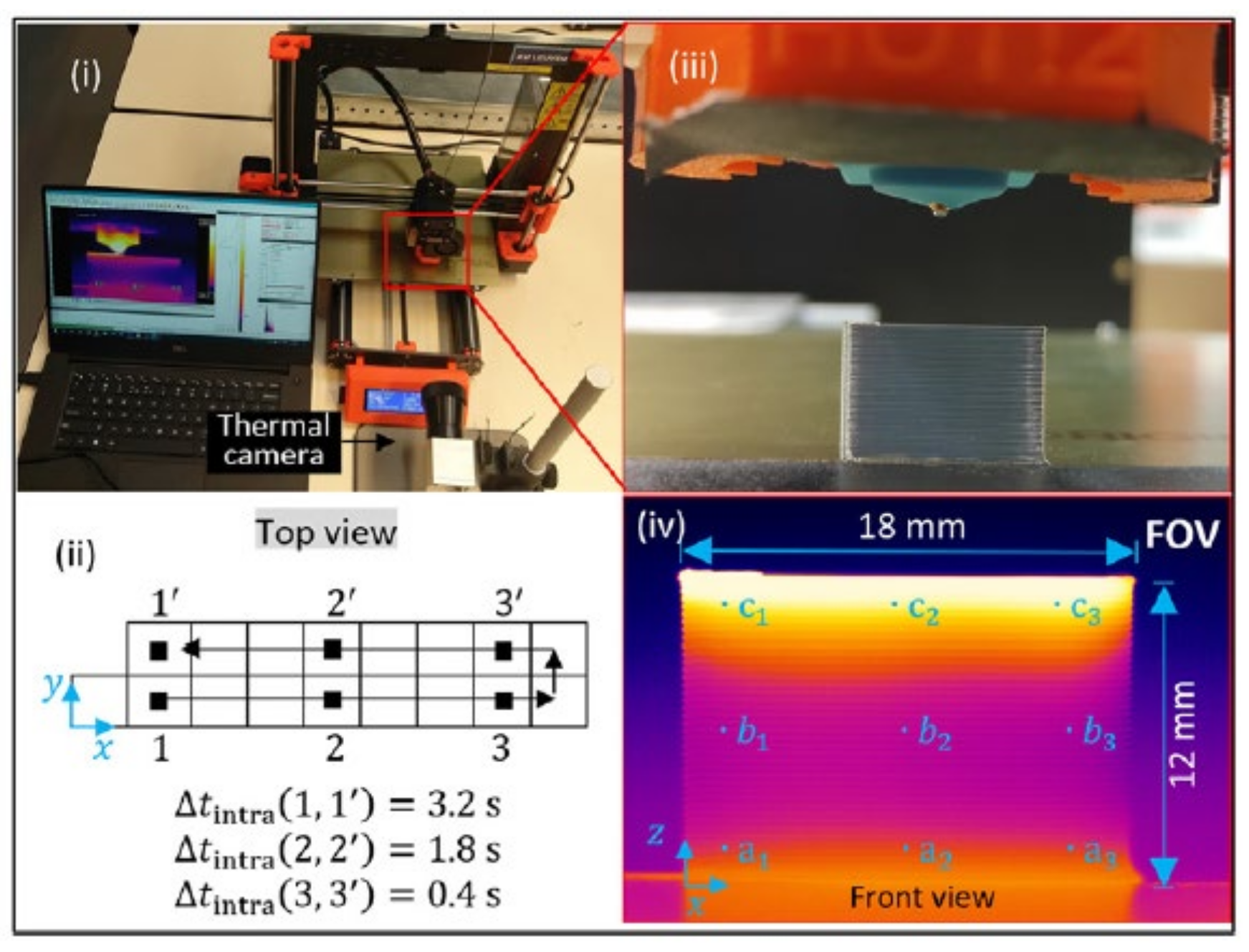
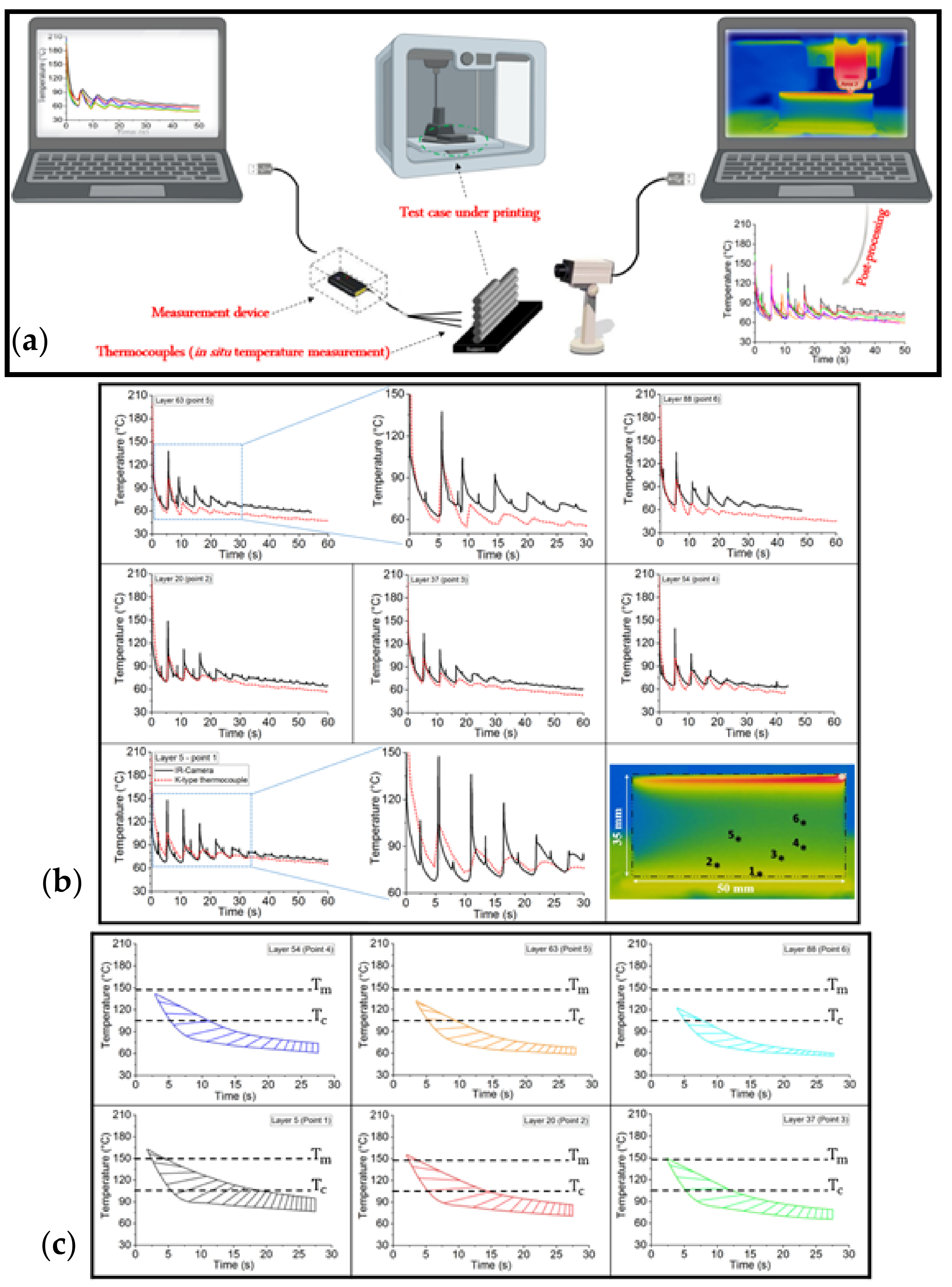
4.1. In-Process Monitoring of Temperature Profile
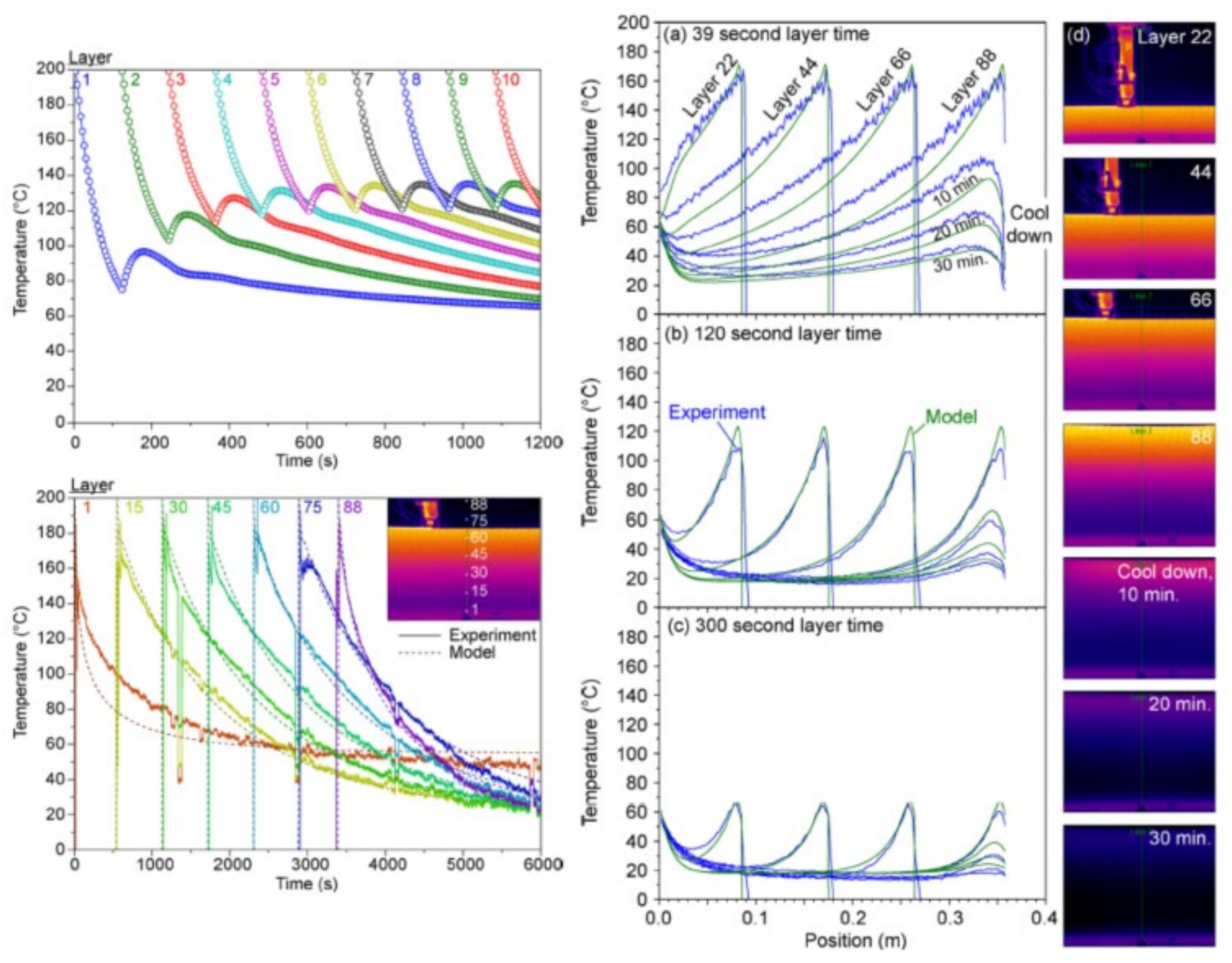
4.1.1. Global Temperature Recording on the External Surface of Deposited Layers
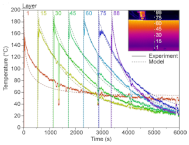
- The lower the distance from the platform, the lower the cooling rate;
- The difference between the onset of the peaks from the obtained results by the IR camera and the developed code shows the limitation of the infrared thermography.
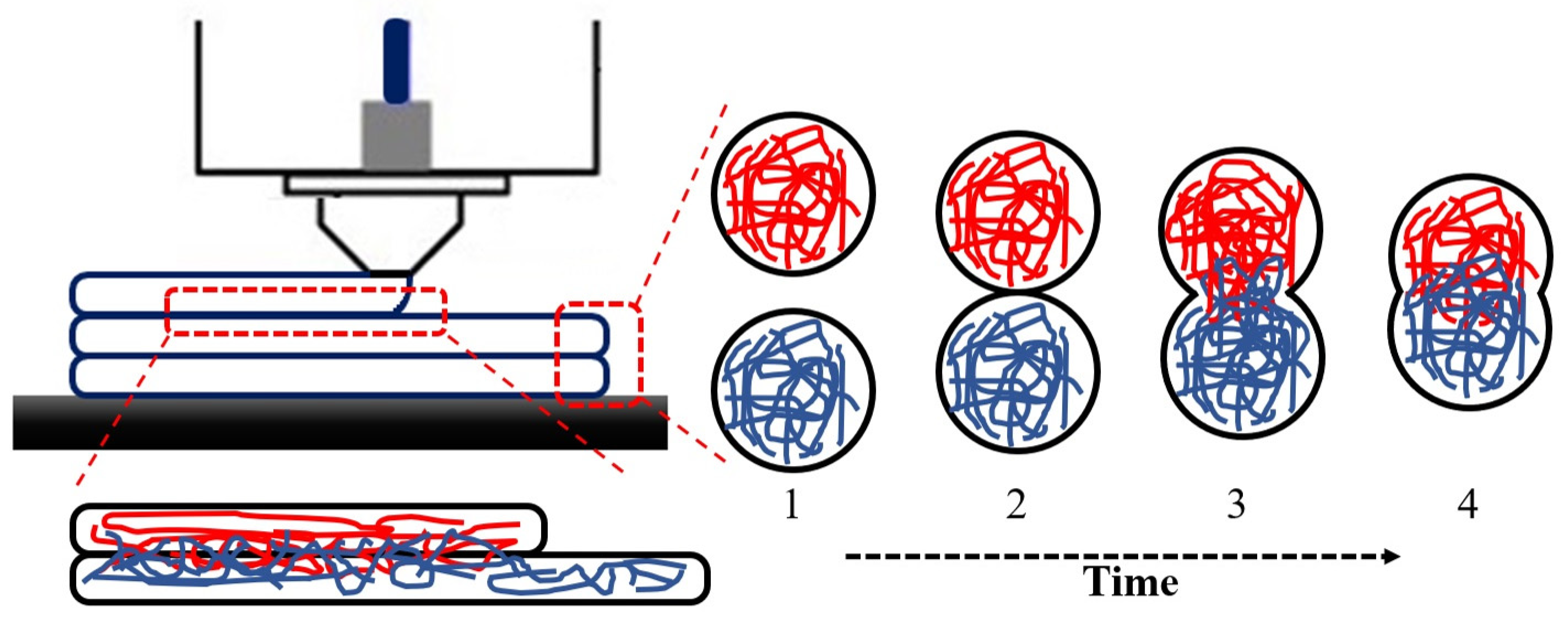
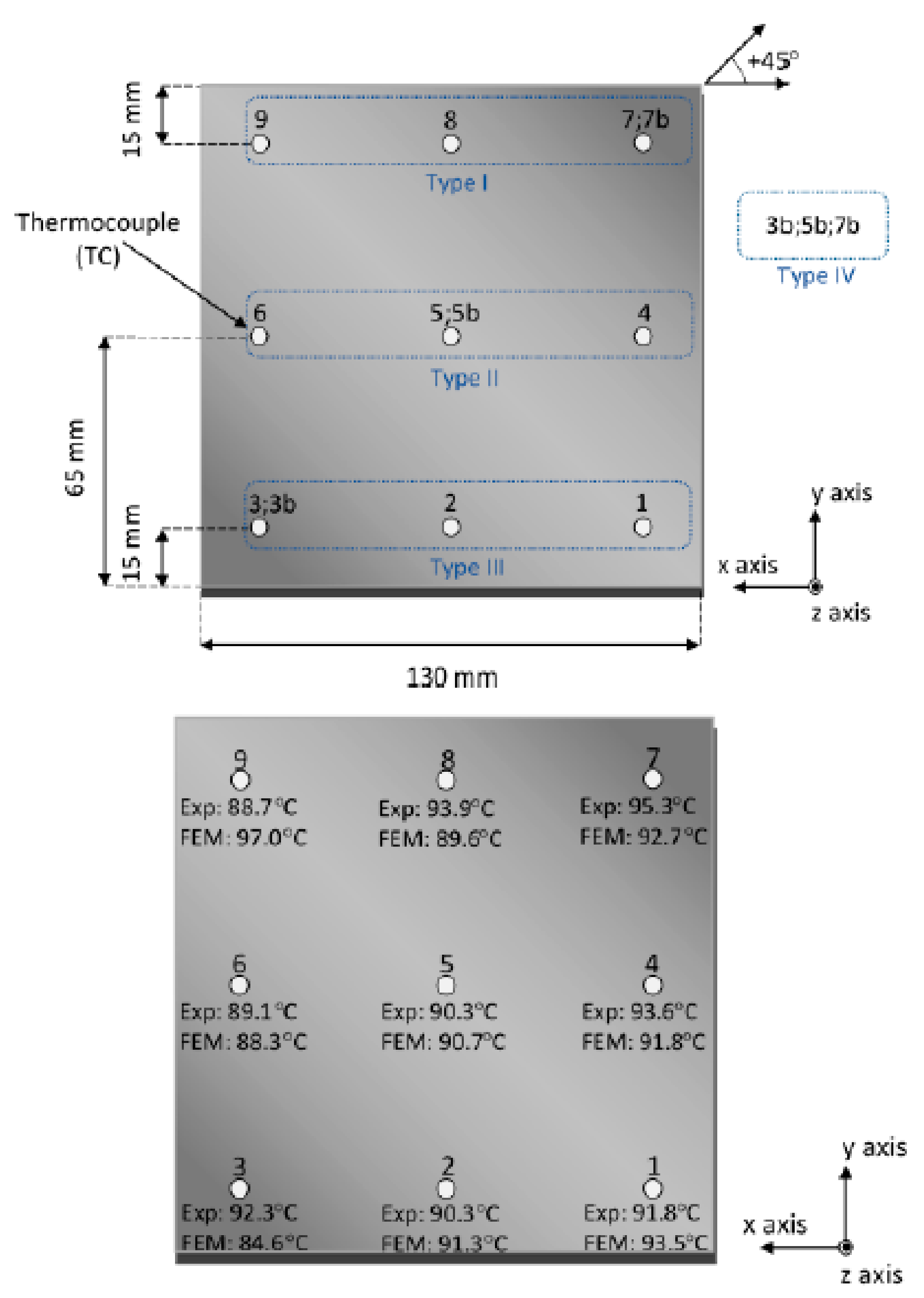
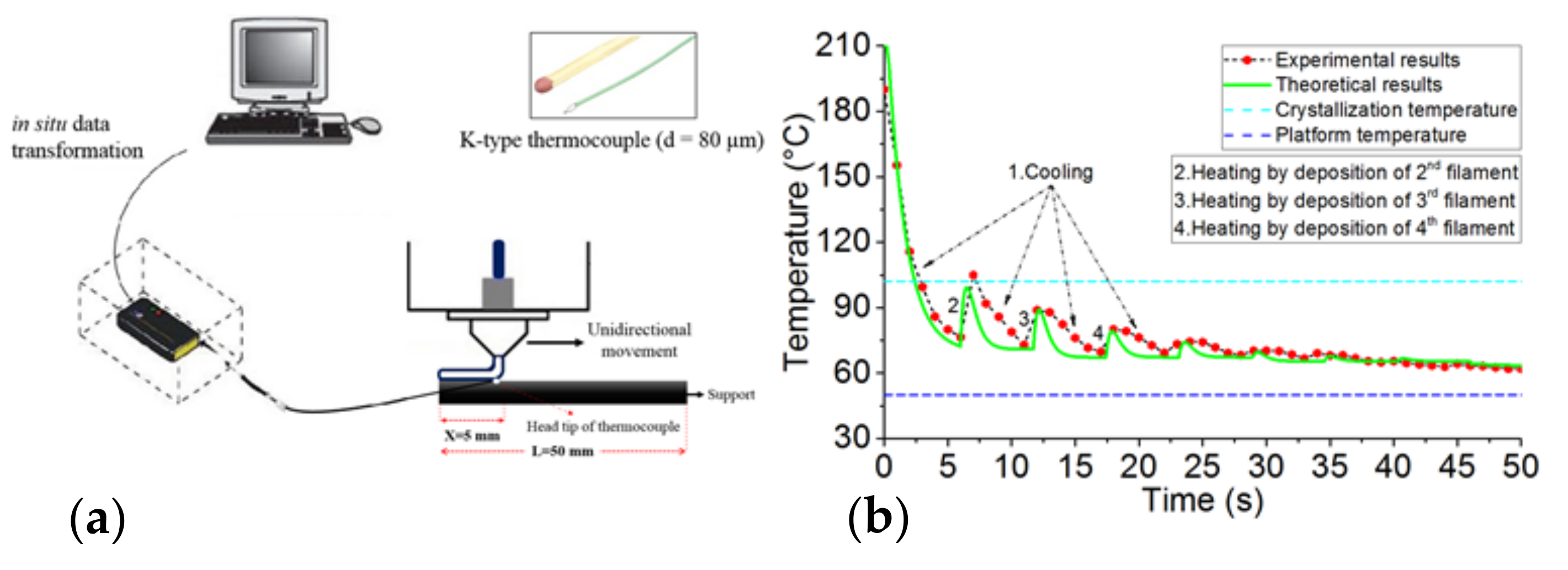
4.1.2. Local Temperature Recording at the Interfaces of Adjacent Layers
4.2. Advantages and Limitations of Implemented Approaches
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hiemenz, J. 3D Printing with FDM: How It Works; Stratasys: Rehovot, Israel, 2011; Volume 1, pp. 1–5. [Google Scholar]
- Ashley, S. Rapid prototyping systems. Mech. Eng. 1991, 113, 34. [Google Scholar]
- Flowers, J. Rapid Prototyping in Technology. Technol. Teacher 2002, 62, 7–11. [Google Scholar]
- Chua, C.K.; Siaw, M.C.; Lin, S.C.; Eu, K.H.; Lew, K.F. Rapid prototyping assisted surgery planning. Int. J. Adv. Manuf. Technol. 1998, 14, 624–630. [Google Scholar] [CrossRef]
- Vaezi, M.; Seitz, H.; Yang, S. A review on 3D micro-additive manufacturing technologies. Int. J. Adv. Manuf. Technol. 2013, 67, 1721–1754. [Google Scholar] [CrossRef]
- Vanaei, S.; Parizi, M.; Salemizadehparizi, F.; Vanaei, H.R. An overview on materials and techniques in 3d bioprinting toward biomedical application. Eng. Regen. 2021, 2, 1–18. [Google Scholar]
- El Magri, A.; Vanaei, S.; Vaudreuil, S. An overview on the influence of process parameters through the characteristic of 3D-printed PEEK and PEI parts. High Perform. Polym. 2021, 33, 862–880. [Google Scholar] [CrossRef]
- Sohrabian, M.; Vaseghi, M.; Khaleghi, H.; Dehrooyeh, S.; Kohan, M.S.A. Structural Investigation of Delicate-Geometry Fused Deposition Modeling Additive Manufacturing Scaffolds: Experiment and Analytics. J. Mater. Eng. Perform. 2021, 30, 6529–6541. [Google Scholar] [CrossRef]
- Lee, J.-Y.; An, J.; Chua, C.K. Fundamentals and applications of 3D printing for novel materials. Appl. Mater. Today 2017, 7, 120–133. [Google Scholar] [CrossRef]
- Kruth, J. Material Incress Manufacturing by Rapid Prototyping Techniques. CIRP Ann. 1991, 40, 603–614. [Google Scholar] [CrossRef]
- Chennakesava, P.; Narayan, Y.S. Fused deposition modeling-insights. In Proceedings of the International Conference on Advances in Design and Manufacturing ICAD&M, Tiruchirappalli, Tamil Nadu, India, 5–7 December 2014. [Google Scholar]
- de Leon, A.C.; Chen, Q.; Palaganas, N.B.; Palaganas, J.O.; Manapat, J.; Advincula, R.C. High performance polymer nanocomposites for additive manufacturing applications. React. Funct. Polym. 2016, 103, 141–155. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, M.; Zhou, Z.; Gou, J.; Hui, D. 3D printing of polymer matrix composites: A review and prospective. Compos. Part B Eng. 2017, 110, 442–458. [Google Scholar] [CrossRef]
- Wohlers, T.; Gornet, T. History of additive manufacturing. Wohlers Rep. 2014, 24, 118. [Google Scholar]
- El Magri, A.; Mabrouk, K.E.; Vaudreuil, S. Preparation and characterization of poly (ether ether ketone)/poly (ether imide)[PEEK/PEI] blends for fused filament fabrication. J. Mater. Sci. 2021, 56, 14348–14367. [Google Scholar] [CrossRef]
- Dakshinamurthy, D.; Gupta, S. A Study on the Influence of Process Parameters on the Viscoelastic Properties of ABS Components Manufactured by FDM Process. J. Inst. Eng. (India) Ser. C 2018, 99, 133–138. [Google Scholar] [CrossRef]
- El Magri, A.; Vanaei, S.; Shirinbayan, M.; Vaudreuil, S.; Tcharkhtchi, A. An Investigation to Study the Effect of Process Parameters on the Strength and Fatigue Behavior of 3D-Printed PLA-Graphene. Polymers 2021, 13, 3218. [Google Scholar] [CrossRef]
- Crump, S.S. Fast, precise, safe prototypes with FDM. ASME PED 1991, 50, 53–60. [Google Scholar]
- Magri, A.E.; Mabrouk, K.E.; Vaudreuil, S.; Touhami, M.E. Mechanical properties of CF-reinforced PLA parts manufactured by fused deposition modeling. J. Thermoplast. Compos. Mater. 2021, 34, 581–595. [Google Scholar]
- EL Magri, A.; El Mabrouk, K.; Vaudreuil, S.; Touhami, M.E. Experimental investigation and optimization of printing parameters of 3D printed polyphenylene sulfide through response surface methodology. J. Appl. Polym. Sci. 2021, 138, 49625. [Google Scholar] [CrossRef]
- De Pieri, A.; Byerley, A.M.; Musumeci, C.R.; Salemizadehparizi, F.; Vanderhorst, M.A.; Wuertz-Kozak, K. Electrospinning and 3D bioprinting for intervertebral disc tissue engineering. JOR Spine 2020, 3, 1117. [Google Scholar] [CrossRef]
- Vanaei, H.R.; Raissi, K.; Deligant, M.; Shirinbayan, M.; Fitoussi, J.; Khelladi, S.; Tcharkhtchi, A. Toward the understanding of temperature effect on bonding strength, dimensions and geometry of 3D-printed parts. J. Mater. Sci. 2020, 55, 14677–14689. [Google Scholar] [CrossRef]
- El Magri, A.; Vaudreuil, S.; El Mabrouk, K.; Touhami, M.E. Printing temperature effects on the structural and mechanical performances of 3D printed Poly-(phenylene sulfide) material. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020; Volume 783, p. 012001. [Google Scholar] [CrossRef]
- Vanaei, H.R.; Shirinbayan, M.; Vanaei, S.; Fitoussi, J.; Khelladi, S.; Tcharkhtchi, A. Multi-scale damage analysis and fatigue behavior of PLA manufactured by fused deposition modeling (FDM). Rapid Prototyp. J. 2021, 27, 371–378. [Google Scholar] [CrossRef]
- Vanaei, H.; Shirinbayan, M.; Deligant, M.; Raissi, K.; Fitoussi, J.; Khelladi, S.; Tcharkhtchi, A. Influence of process parameters on thermal and mechanical properties of polylactic acid fabricated by fused filament fabrication. Polym. Eng. Sci. 2020, 60, 1822–1831. [Google Scholar] [CrossRef]
- Dizon, J.R.C.; Espera, A.H.; Chen, Q.; Advincula, R.C. Mechanical characterization of 3D-printed polymers. Addit. Manuf. 2018, 20, 44–67. [Google Scholar] [CrossRef]
- Turner, B.N.; Strong, R.; Gold, S.A. A review of melt extrusion additive manufacturing processes: I. Process Design Modeling Rapid Prototyp. J. 2014, 20, 192–204. [Google Scholar] [CrossRef]
- Turner, B.N.; A Gold, S. A review of melt extrusion additive manufacturing processes: II. Materials, dimensional accuracy, and surface roughness. Rapid Prototyp. J. 2015, 21, 250–261. [Google Scholar] [CrossRef]
- Parandoush, P.; Lin, D. A review on additive manufacturing of polymer-fiber composites. Compos. Struct. 2017, 182, 36–53. [Google Scholar] [CrossRef]
- Das, A.; McIlroy, C.; Bortner, M.J. Advances in modeling transport phenomena in material-extrusion additive manufacturing: Coupling momentum, heat, and mass transfer. Prog. Addit. Manuf. 2021, 6, 3–17. [Google Scholar] [CrossRef]
- Ahn, S.; Montero, M.; Odell, D.; Roundy, S.; Wright, P.K. Anisotropic material properties of fused deposition modeling ABS. Rapid Prototyp. J. 2002, 8, 248–257. [Google Scholar] [CrossRef] [Green Version]
- Caminero, M.Á.; Chacón, J.M.; García-Plaza, E.; Núñez, P.J.; Reverte, J.M.; Becar, J.P. Additive Manufacturing of PLA-Based Composites Using Fused Filament Fabrication: Effect of Graphene Nanoplatelet Reinforcement on Mechanical Properties, Dimensional Accuracy and Texture. Polymers 2019, 11, 799. [Google Scholar] [CrossRef] [Green Version]
- Buj-Corral, I.; Bagheri, A.; Sivatte-Adroer, M. Effect of Printing Parameters on Dimensional Error, Surface Roughness and Porosity of FFF Printed Parts with Grid Structure. Polymers 2021, 13, 1213. [Google Scholar] [CrossRef] [PubMed]
- Pennington, R.C.; Hoekstra, N.L.; Newcomer, J.L. Significant factors in the dimensional accuracy of fused deposition modelling. Proc. Inst. Mech. Eng. Part E J. Process. Mech. Eng. 2005, 219, 89–92. [Google Scholar] [CrossRef]
- Chaidas, D.; Kitsakis, K.; Kechagias, J.; Maropoulos, S. The impact of temperature changing on surface roughness of FFF process. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2016; Volume 161, p. 012033. [Google Scholar] [CrossRef] [Green Version]
- Aslani, K.-E.; Chaidas, D.; Kechagias, J.; Kyratsis, P.; Salonitis, K. Quality Performance Evaluation of Thin Walled PLA 3D Printed Parts Using the Taguchi Method and Grey Relational Analysis. J. Manuf. Mater. Process. 2020, 4, 47. [Google Scholar] [CrossRef]
- Katti, D.; Sharma, A.; Katti, K. Predictive Methodologies for Design of Bone Tissue Engineering Scaffolds. In Materials for Bone Disorders; Elsevier BV: Amsterdam, The Netherlands, 2017; pp. 453–492. [Google Scholar]
- Górski, F.; Wichniarek, R.; Kuczko, W.; Zawadzki, P.; Buń, P. Strength of abs parts produced by fused deposition modelling technology—A critical orientation problem. Adv. Sci. Technol. Res. J. 2015, 9, 12–19. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Kim, S.; Kim, H.; Ahn, S. Measurement of anisotropic compressive strength of rapid prototyping parts. J. Mater. Process. Technol. 2007, 187–188, 627–630. [Google Scholar] [CrossRef]
- Es-Said, O.S.; Foyos, J.; Noorani, R.; Mendelson, M.; Marloth, R.; Pregger, B.A. Effect of Layer Orientation on Mechanical Properties of Rapid Prototyped Samples. Mater. Manuf. Process. 2000, 15, 107–122. [Google Scholar] [CrossRef]
- Smith, W.C.; Dean, R.W. Structural characteristics of fused deposition modeling polycarbonate material. Polym. Test. 2013, 32, 1306–1312. [Google Scholar] [CrossRef]
- Schöppner, V.; Ktp, K.P. Mechanical properties of fused deposition modeling parts manufactured with Ultem * 9085. In Proceedings of the 69th Annual Technical Conference of the Society of Plastics Engineers (ANTEC’11), Boston, MA, USA, 1–5 May 2011. [Google Scholar]
- EL Magri, A.; El Mabrouk, K.; Vaudreuil, S.; Chibane, H.; Touhami, M.E. Optimization of printing parameters for improvement of mechanical and thermal performances of 3D printed poly(ether ether ketone) parts. J. Appl. Polym. Sci. 2020, 137, 49087. [Google Scholar] [CrossRef]
- Wang, P.; Zou, B.; Xiao, H.; Ding, S.; Huang, C. Effects of printing parameters of fused deposition modeling on mechanical properties, surface quality, and microstructure of PEEK. J. Mater. Process. Technol. 2019, 271, 62–74. [Google Scholar] [CrossRef]
- Wu, W.; Geng, P.; Li, G.; Zhao, D.; Zhang, H.; Zhao, J. Influence of Layer Thickness and Raster Angle on the Mechanical Properties of 3D-Printed PEEK and a Comparative Mechanical Study between PEEK and ABS. Materials 2015, 8, 5834–5846. [Google Scholar] [CrossRef]
- Rahman, K.M.; Letcher, T.; Reese, R. Mechanical properties of additively manufactured PEEK components using fused filament fabrication. In ASME International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
- Byberg, K.I.; Gebisa, A.W.; Lemu, H.G. Mechanical properties of ULTEM 9085 material processed by fused deposition modeling. Polym. Test. 2018, 72, 335–347. [Google Scholar] [CrossRef]
- Forés-Garriga, A.; Pérez, M.A.; Gómez-Gras, G.; Pozo, G.R. Role of infill parameters on the mechanical performance and weight reduction of PEI Ultem processed by FFF. Mater. Des. 2020, 193, 108810. [Google Scholar] [CrossRef]
- Masood, S.; Mau, K.; Song, W. Tensile Properties of Processed FDM Polycarbonate Material. Mater. Sci. Forum 2010, 654-656, 2556–2559. [Google Scholar] [CrossRef]
- Motaparti, K.P.; Taylor, G.; Leu, M.; Chandrashekhara, K.; Castle, J.; Matlack, M. Effects of build parameters on compression properties for ULTEM 9085 parts by fused deposition modeling. In Proceedings of the 27th Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 8–10 August 2016. [Google Scholar]
- Lee, B.; Abdullah, J.; Khan, Z. Optimization of rapid prototyping parameters for production of flexible ABS object. J. Mater. Process. Technol. 2005, 169, 54–61. [Google Scholar] [CrossRef]
- Casavola, C.; Cazzato, A.; Moramarco, V.; Pappalettere, C. Orthotropic mechanical properties of fused deposition modelling parts described by classical laminate theory. Mater. Design 2016, 90, 453–458. [Google Scholar] [CrossRef]
- Rathee, S.; Srivastava, M.; Maheshwari, S.; Siddiquee, A. Effect of varying spatial orientations on build time requirements for FDM process: A case study. Def. Technol. 2017, 13, 92–100. [Google Scholar] [CrossRef]
- Rodriguez, J.F.; Thomas, J.P.; Renaud, J.E. Characterization of the mesostructure of fused-deposition acrylonitrile-butadiene-styrene materials. Rapid Prototyp. J. 2000, 6, 175–186. [Google Scholar] [CrossRef]
- Bellehumeur, C.; Li, L.; Sun, Q.; Gu, P. Modeling of Bond Formation Between Polymer Filaments in the Fused Deposition Modeling Process. J. Manuf. Process. 2004, 6, 170–178. [Google Scholar] [CrossRef]
- Lepoivre, A.; Boyard, N.; Levy, A.; Sobotka, V. Heat Transfer and Adhesion Study for the FFF Additive Manufacturing Process. Procedia Manuf. 2020, 47, 948–955. [Google Scholar] [CrossRef]
- Costa, S.F.; Duarte, F.; Covas, J. Towards modelling of Free Form Extrusion: Analytical solution of transient heat transfer. Int. J. Mater. Form. 2008, 1, 703–706. [Google Scholar] [CrossRef]
- Costa, S.; Duarte, F.; Covas, J. Thermal conditions affecting heat transfer in FDM/FFE: A contribution towards the numerical modelling of the process: This paper investigates convection, conduction and radiation phenomena in the filament deposition process. Virtual Phys. Prototyp. 2015, 10, 35–46. [Google Scholar] [CrossRef]
- Thomas, J.; Rodríguez, J. Modeling the fracture strength between fused-deposition extruded roads 16. In Proceedings of the 2000 International Solid Freeform Fabrication Symposium, Austin, TX, USA, 7–9 August 2000. [Google Scholar]
- Yardimci, M.A.; Güçeri, S. Conceptual framework for the thermal process modelling of fused deposition. Rapid Prototyp. J. 1996, 2, 26–31. [Google Scholar] [CrossRef]
- AtifYardimci, M.; Hattori, T.; Guceri, S.I.; Danforth, S.C. Thermal analysis of fused deposition. In Proceedings of the 1997 International Solid Freeform Fabrication Symposium, Austin, TX, USA, 11–13 August 1997. [Google Scholar]
- Zhang, Y.; Chou, Y.K. Three-dimensional finite element analysis simulations of the fused deposition modelling process. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2006, 220, 1663–1671. [Google Scholar] [CrossRef]
- Ji, L.B.; Zhou, T.R. Finite Element Simulation of Temperature Field in Fused Deposition Modeling. Adv. Mater. Res. 2010, 97–101, 2585–2588. [Google Scholar] [CrossRef]
- Crump, S.S. Modeling Apparatus for Three-Dimensional Objects. U.S. Patent 5340433A, 23 August 1994. [Google Scholar]
- Peng, F.; Vogt, B.D.; Cakmak, M. Complex flow and temperature history during melt extrusion in material extrusion additive manufacturing. Addit. Manuf. 2018, 22, 197–206. [Google Scholar] [CrossRef]
- Serdeczny, M.P.; Comminal, R.; Pedersen, D.B.; Spangenberg, J. Experimental and analytical study of the polymer melt flow through the hot-end in material extrusion additive manufacturing. Addit. Manuf. 2020, 32, 100997. [Google Scholar] [CrossRef]
- Vaes, D.; Coppens, M.; Goderis, B.; Zoetelief, W.; Van Puyvelde, P. Assessment of Crystallinity Development during Fused Filament Fabrication through Fast Scanning Chip Calorimetry. Appl. Sci. 2019, 9, 2676. [Google Scholar] [CrossRef] [Green Version]
- Cattenone, A.; Morganti, S.; Alaimo, G.; Auricchio, F. Finite Element Analysis of Additive Manufacturing Based on Fused Deposition Modeling: Distortions Prediction and Comparison With Experimental Data. J. Manuf. Sci. Eng. 2018, 141, 011010. [Google Scholar] [CrossRef]
- Seppala, J.E.; Migler, K.D. Infrared thermography of welding zones produced by polymer extrusion additive manufacturing. Addit. Manuf. 2016, 12, 71–76. [Google Scholar] [CrossRef] [Green Version]
- D’Amico, A.; Peterson, A.M. An adaptable FEA simulation of material extrusion additive manufacturing heat transfer in 3D. Addit. Manuf. 2018, 21, 422–430. [Google Scholar] [CrossRef]
- Costa, S.; Duarte, F.; Covas, J. Estimation of filament temperature and adhesion development in fused deposition techniques. J. Mater. Process. Technol. 2017, 245, 167–179. [Google Scholar] [CrossRef]
- Chacón, J.M.; Caminero, M.A.; García-Plaza, E.; Núñez, P.J. Additive manufacturing of PLA structures using fused deposition modelling: Effect of process parameters on mechanical properties and their optimal selection. Mater. Des. 2017, 124, 143–157. [Google Scholar] [CrossRef]
- Coogan, T.J.; Kazmer, D.O. Bond and part strength in fused deposition modeling. Rapid Prototyp. J. 2017, 23, 414–422. [Google Scholar] [CrossRef]
- Jatti, V.S.; Jatti, S.V.; Patel, A.P.; Jatti, V.S. A Study on Effect of Fused Deposition Modeling Process Parameters on Mechanical Properties. Int. J. Sci. Technol. Res. 2019, 8, 689–693. [Google Scholar]
- Ning, F.; Cong, W.; Hu, Y.; Wang, H. Additive manufacturing of carbon fiber-reinforced plastic composites using fused deposition modeling: Effects of process parameters on tensile properties. J. Compos. Mater. 2017, 51, 451–462. [Google Scholar] [CrossRef]
- Guessasma, S.; Belhabib, S.; Nouri, H. Thermal cycling, microstructure and tensile performance of PLA-PHA polymer printed using fused deposition modelling technique. Rapid Prototyp. J. 2020, 26, 122–133. [Google Scholar] [CrossRef]
- Jiang, S.; Liao, G.; Xu, D.; Liu, F.; Li, W.; Cheng, Y.; Li, Z.; Xu, G. Mechanical properties analysis of polyetherimide parts fabricated by fused deposition modeling. High Perform. Polym. 2019, 31, 97–106. [Google Scholar] [CrossRef]
- Yang, C.; Tian, X.; Li, D.; Cao, Y.; Zhao, F.; Shi, C. Influence of thermal processing conditions in 3D printing on the crystallinity and mechanical properties of PEEK material. J. Mater. Process. Technol. 2017, 248, 1–7. [Google Scholar] [CrossRef]
- Ding, S.; Zou, B.; Wang, P.; Ding, H. Effects of nozzle temperature and building orientation on mechanical properties and microstructure of PEEK and PEI printed by 3D-FDM. Polym. Test. 2019, 78, 105948. [Google Scholar] [CrossRef]
- Berretta, S.; Davies, R.; Shyng, Y.; Wang, Y.; Ghita, O. Fused Deposition Modelling of high temperature polymers: Exploring CNT PEEK composites. Polym. Test. 2017, 63, 251–262. [Google Scholar] [CrossRef]
- Monzón, M.D.; Gibson, I.; Benítez, A.N.; Lorenzo, L.; Hernández, P.M.; Marrero, M.D. Process and material behavior modeling for a new design of micro-additive fused deposition. Int. J. Adv. Manuf. Technol. 2013, 67, 2717–2726. [Google Scholar] [CrossRef]
- Xiaoyong, S.; LiangCheng, C.; Honglin, M.; Peng, G.; Zhanwei, B.; Cheng, L. Experimental Analysis of High Temperature PEEK Materials on 3D Printing Test. In Proceedings of the 2017 9th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Changsha, China, 14–15 January 2017; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2017; pp. 13–16. [Google Scholar]
- Aliheidari, N.; Tripuraneni, R.; Ameli, A.; Nadimpalli, S. Fracture resistance measurement of fused deposition modeling 3D printed polymers. Polym. Test. 2017, 60, 94–101. [Google Scholar] [CrossRef]
- Sun, Q.; Rizvi, G.M.; Bellehumeur, C.T.; Gu, P. Effect of processing conditions on the bonding quality of FDM polymer filaments. Rapid Prototyp. J. 2008, 14, 72–80. [Google Scholar] [CrossRef]
- Christiyan, K.G.J.; Chandrasekhar, U.; Venkateswarlu, K. A study on the influence of process parameters on the Mechanical Properties of 3D printed ABS composite. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK; p. 012109.
- Abeykoon, C.; Sri-Amphorn, P.; Fernando, A. Optimization of fused deposition modeling parameters for improved PLA and ABS 3D printed structures. Int. J. Lightweight Mater. Manuf. 2020, 3, 284–297. [Google Scholar] [CrossRef]
- Geng, P.; Zhao, J.; Wu, W.; Ye, W.; Wang, Y.; Wang, S.; Zhang, S. Effects of extrusion speed and printing speed on the 3D printing stability of extruded PEEK filament. J. Manuf. Process. 2019, 37, 266–273. [Google Scholar] [CrossRef]
- Jiang, Z.; Diggle, B.; Tan, M.L.; Viktorova, J.; Bennett, C.W.; Connal, L.A. Extrusion 3D Printing of Polymeric Materials with Advanced Properties. Adv. Sci. 2020, 7, 2001379. [Google Scholar] [CrossRef]
- Scheithauer, U.; Schwarzer, E.; Richter, H.-J.; Moritz, T. Thermoplastic 3D Printing-An Additive Manufacturing Method for Producing Dense Ceramics. Int. J. Appl. Ceram. Technol. 2014, 12, 26–31. [Google Scholar] [CrossRef]
- Comminal, R.; Pimenta, F.; Hattel, J.; Alves, M.; Spangenberg, J. Numerical simulation of the planar extrudate swell of pseudoplastic and viscoelastic fluids with the streamfunction and the VOF methods. J. Non-Newtonian Fluid Mech. 2018, 252, 1–18. [Google Scholar] [CrossRef]
- Xia, H.; Lu, J.; Tryggvason, G. A numerical study of the effect of viscoelastic stresses in fused filament fabrication. Comput. Methods Appl. Mech. Eng. 2019, 346, 242–259. [Google Scholar] [CrossRef]
- Du, J.; Wei, Z.; Wang, X.; Wang, J.; Chen, Z. An improved fused deposition modeling process for forming large-size thin-walled parts. J. Mater. Process. Technol. 2016, 234, 332–341. [Google Scholar] [CrossRef]
- Liu, J.; Anderson, K.L.; Sridhar, N. Direct Simulation of Polymer Fused Deposition Modeling (FDM)—An Implementation of the Multi-Phase Viscoelastic Solver in OpenFOAM. Int. J. Comput. Methods 2020, 17, 1844002. [Google Scholar] [CrossRef] [Green Version]
- Duty, C.; Ajinjeru, C.; Kishore, V.; Compton, B.; Hmeidat, N.; Chen, X.; Liu, P.; Hassen, A.A.; Lindahl, J.; Kunc, V. What makes a material printable? A viscoelastic model for extrusion-based 3D printing of polymers. J. Manuf. Process. 2018, 35, 526–537. [Google Scholar] [CrossRef]
- Fitzpatrick, J.; Descamps, N.; O’Meara, K.; Jones, C.; Walsh, D.; Spitere, M. Comparing the caking behaviours of skim milk powder, amorphous maltodextrin and crystalline common salt. Powder Technol. 2010, 204, 131–137. [Google Scholar] [CrossRef]
- Kasmaee, M.; Varaminian, F.; Khadiv-Parsi, P.; Saien, J. Effects of different surfactants and physical properties on the coalescence of dimethyl disulfide drops with mother phase at the interface of sodium hydroxide aqueous solutions. J. Mol. Liq. 2018, 263, 31–39. [Google Scholar] [CrossRef]
- Gross, M.; Steinbach, I.; Raabe, D.; Varnik, F. Viscous coalescence of droplets: A lattice Boltzmann study. Phys. Fluids 2013, 25, 052101. [Google Scholar] [CrossRef] [Green Version]
- Kamyabi, M.; Sotudeh-Gharebagh, R.; Zarghami, R.; Saleh, K. Principles of viscous sintering in amorphous powders: A critical review. Chem. Eng. Res. Des. 2017, 125, 328–347. [Google Scholar] [CrossRef]
- Frenkel, J. Viscous flow of crystalline bodies under the action of surface tension. J. Phys. 1945, 9, 385. [Google Scholar]
- Pokluda, O.; Bellehumeur, C.T.; Vlachopoulos, J. Modification of Frenkel’s model for sintering. AIChE J. 1997, 43, 3253–3256. [Google Scholar] [CrossRef]
- Bellehumeur, C.T.; Bisaria, M.K.; Vlachopoulos, J. An experimental study and model assessment of polymer sintering. Polym. Eng. Sci. 1996, 36, 2198–2207. [Google Scholar] [CrossRef]
- Hopper, R.W. Coalescence of Two Equal Cylinders: Exact Results for Creeping Viscous Plane Flow Driven by Capillarity. J. Am. Ceram. Soc. 1984, 67, C-262. [Google Scholar] [CrossRef]
- Tarafdar, R.M.; Bergman, T.L. Detailed Numerical and Experimental Investigation of Non-Isothermal Sintering of Amorphous Polymer Material. J. Heat Transf. 2002, 124, 553–563. [Google Scholar] [CrossRef]
- Wadsworth, F.B.; Vasseur, J.; Von Aulock, F.W.; Hess, K.-U.; Scheu, B.; Lavallée, Y.; Dingwell, D.B. Nonisothermal viscous sintering of volcanic ash. J. Geophys. Res. Solid Earth 2014, 119, 8792–8804. [Google Scholar] [CrossRef]
- Bhalodi, D.; Zalavadiya, K.; Gurrala, P.K. Influence of temperature on polymer parts manufactured by fused deposition modeling process. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 113. [Google Scholar] [CrossRef]
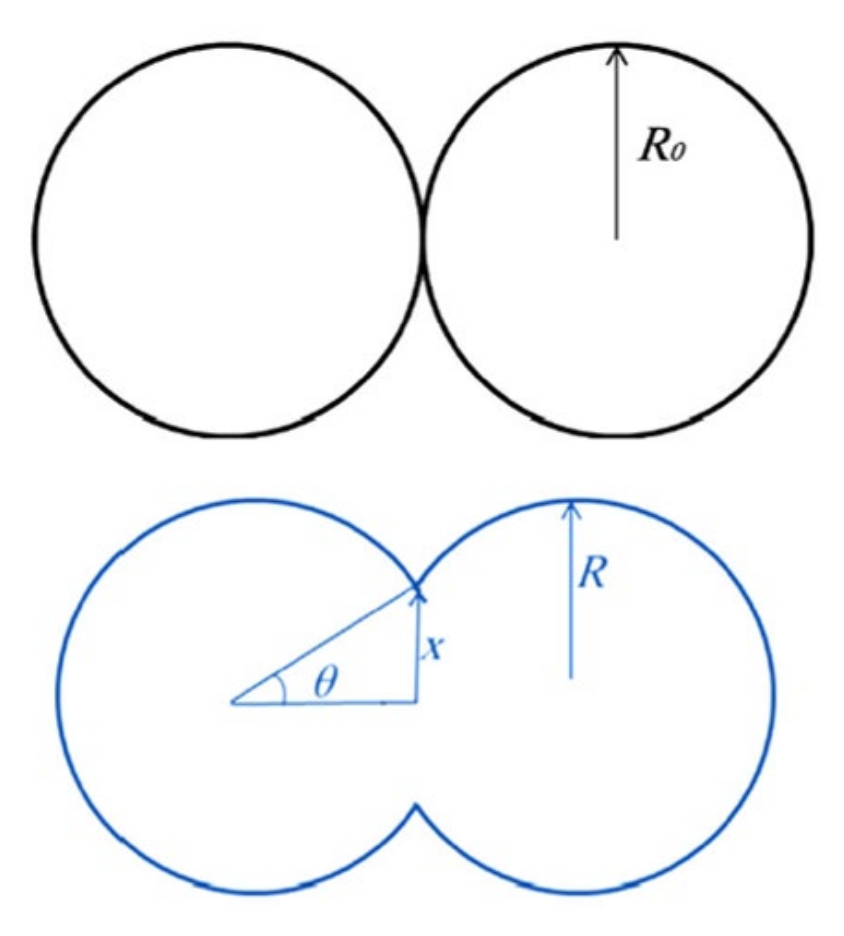
- Polychronopoulos, N.D.; Vlachopoulos, J. The role of heating and cooling in viscous sintering of pairs of spheres and pairs of cylinders. Rapid Prototyp. J. 2020, 26, 719–726. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.; Yu, W.; Deng, Y. Numerical investigation of the influence of process conditions on the temperature variation in fused deposition modeling. Mater. Design 2017, 130, 59–68. [Google Scholar] [CrossRef]
- Zhang, Y.; Shapiro, V. Linear time thermal simulation of fdm process. In International Design Engineering Technical Conferences and Computers and Information in Engineering Conference; American Society of Mechanical Engineers: New York, NY, USA, 2017. [Google Scholar]
- Pourali, M.; Peterson, A.M. Thermal modeling of material extrusion additive manufacturing. In Polymer-Based Additive Manufacturing: Recent Developments; American Chemical Society (ACS): Washington, DC, USA, 2019; pp. 115–130. [Google Scholar]
- Zhou, X.; Hsieh, S.-J. Thermal analysis of fused deposition modeling process using infrared thermography imaging and finite element modeling. In Thermosense: Thermal Infrared Applications XXXIX; SPIE: Washington, DC, USA, 2017; p. 1021409. [Google Scholar]
- Seppala, J.E.; Han, S.H.; Hillgartner, K.E.; Davis, C.S.; Migler, K.B. Weld formation during material extrusion additive manufacturing. Soft Matter 2017, 13, 6761–6769. [Google Scholar] [CrossRef]
- Compton, B.G.; Post, B.K.; Duty, C.E.; Love, L.; Kunc, V. Thermal analysis of additive manufacturing of large-scale thermoplastic polymer composites. Addit. Manuf. 2017, 17, 77–86. [Google Scholar] [CrossRef]
- Prajapati, H.; Ravoori, D.; Jain, A. Measurement and modeling of filament temperature distribution in the standoff gap between nozzle and bed in polymer-based additive manufacturing. Addit. Manuf. 2018, 24, 224–231. [Google Scholar] [CrossRef]
- Rudolph, N.; Chen, J.; Dick, T. Understanding the temperature field in fused filament fabrication for enhanced mechanical part performance. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2019. [Google Scholar]
- El Moumen, A.; Tarfaoui, M.; Lafdi, K. Modelling of the temperature and residual stress fields during 3D printing of polymer composites. Int. J. Adv. Manuf. Technol. 2019, 104, 1661–1676. [Google Scholar] [CrossRef]
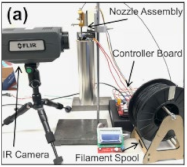
- Ferraris, E.; Zhang, J.; Van Hooreweder, B. Thermography based in-process monitoring of Fused Filament Fabrication of polymeric parts. CIRP Ann. 2019, 68, 213–216. [Google Scholar] [CrossRef]
- Kuznetsov, V.E.; Solonin, A.N.; Tavitov, A.; Urzhumtsev, O.; Vakulik, A. Increasing strength of FFF three-dimensional printed parts by influencing on temperature-related parameters of the process. Rapid Prototyp. J. 2020, 26, 107–121. [Google Scholar] [CrossRef]
- Basgul, C.; Thieringer, F.M.; Kurtz, S.M. Heat transfer-based non-isothermal healing model for the interfacial bonding strength of fused filament fabricated polyetheretherketone. Addit. Manuf. 2021, 46, 102097. [Google Scholar]
- Eom, R.-I.; Lee, H.; Lee, Y. Evaluation of Thermal Properties of 3D Spacer Technical Materials in Cold Environments using 3D Printing Technology. Polymers 2019, 11, 1438. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, C.-Y.; Liu, C.-Y. The influence of forced-air cooling on a 3D printed PLA part manufactured by fused filament fabrication. Addit. Manuf. 2019, 25, 196–203. [Google Scholar] [CrossRef]
- Kousiatza, C.; Karalekas, D. In-situ monitoring of strain and temperature distributions during fused deposition modeling process. Mater. Design 2016, 97, 400–406. [Google Scholar] [CrossRef]
- Kousiatza, C.; Chatzidai, N.; Karalekas, D. Temperature Mapping of 3D Printed Polymer Plates: Experimental and Numerical Study. Sensors 2017, 17, 456. [Google Scholar] [CrossRef] [Green Version]
- Yin, J.; Lu, C.; Fu, J.; Huang, Y.; Zheng, Y. Interfacial bonding during multi-material fused deposition modeling (FDM) process due to inter-molecular diffusion. Mater. Design 2018, 150, 104–112. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, Y.; Pigeonneau, F. Thermal analysis of the fused filament fabrication printing process: Experimental and numerical investigations. Int. J. Mater. Form. 2021, 14, 763–776. [Google Scholar] [CrossRef]
- Zhang, Y.; Guillemot, G.; Bernacki, M.; Bellet, M. Macroscopic thermal finite element modeling of additive metal manufacturing by selective laser melting process. Comput. Methods Appl. Mech. Eng. 2018, 331, 514–535. [Google Scholar] [CrossRef]
- Vanaei, H.R.; Shirinbayan, M.; Costa, S.F.; Duarte, F.M.; Covas, J.A.; Deligant, M.; Khelladi, S.; Tcharkhtchi, A. Experimental study of PLA thermal behavior during fused filament fabrication. J. Appl. Polym. Sci. 2021, 138, 49747. [Google Scholar] [CrossRef]
- Fang, T. Online Image Processing and Defect Detection in Layered Manufacturing Using Process Signature. Ph.D. Thesis, Rutgers University, New Brunswick, NJ, USA, 2000. [Google Scholar]
- Vanaei, H.; Deligant, M.; Shirinbayan, M.; Raissi, K.; Fitoussi, J.; Khelladi, S.; Tcharkhtchi, A. A comparative in-process monitoring of temperature profile in fused filament fabrication. Polym. Eng. Sci. 2021, 61, 68–76. [Google Scholar] [CrossRef]





| Modeling Approach | Description | Results | Ref |
|---|---|---|---|
| Finite volume method |
|
| [60] |
| Finite element method |
|
| [61] |
| Analytical heat transfer modeling |
|
| [59] |
| Finite element method using ANSYS |
|
| [62] |
| Finite element method using ABAQUS |
|
| [58] |
| Finite difference method |
|
| [107] |
| Explicit finite difference method |
|
| [108] |
| Research | Results | Illustration | Ref |
|---|---|---|---|
| Infrared thermography of welding zone, in-process monitoring of temperature profile |
|  | [69] |
| Infrared thermography of filaments’ temperature history at their interfaces |
|  | [110] |
| Thermal analysis of large-scale thermoplastic polymer composites |
|  | [112] |
| Weld formation during FFF |
|  | [111] |
| Filament temperature distribution in the stand-off gap between liquefier and platform |
|  | [113] |
| Effect of temperature field on mechanical strength |
|  | [114] |
| Evaluation of thermal properties of 3D spacer |
|  | [119] |
| Temperature and residual stress modeling |
|  | [115] |
| Influence of forced-air cooling |
| 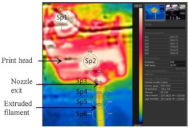 | [120] |
| Thermography-based in-process monitoring of temperature profile |
| 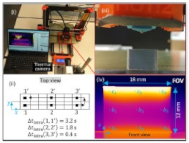 | [116] |
| Influence of temperature-related parameters on strength of 3D-printed parts |
| 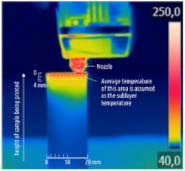 | [117] |
| Heat transfer and adhesion study |
|  | [56] |
| Heat transfer and interfacial bonding strength |
| 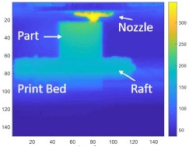 | [118] |
| Material | Description | Results | Ref |
|---|---|---|---|
| ABS | Simultaneous monitoring of temperature and strain using fiber Bragg grating sensor | Process optimization by correlation of temperature and residual stress | [121] |
| ABS | Obtaining weld temperatures using the temperature profile of printed layers | Correlation of recorded temperature profile to relaxation time and viscosity | [69] |
| PLA | Measuring the temperature profile of deposited layers | High difference between the model and recorded results | [110] |
| CF-ABS | Measuring the thermal evolution of composite | Evaluation of thermal stress evolution, warping, and fracture initiation | [112] |
| ABS | Using K-type thermocouples | Good agreement with the developed model | [122] |
| ABS | Using thermal history in rheology | Optimization of inter-layer strength and development of new materials | [111] |
| TPU-ABS | Using K-type thermocouples for implementation on interfacial bonding | Understanding of interfacial bonding mechanism to improve the mechanical properties | [123] |
| PLA | Using IR-camera for temperature recording | Different cooling rates in different sections correspond to its mechanical properties | [114] |
| TPU | Using IR-camera for temperature recording | Evaluation of thermal properties of 3D spacer technical material | [119] |
| PA12 | Using IR-camera as a part of thermo-mechanical analysis of printed parts | Modeling of temperature variation and residual stress (5%) | [115] |
| PLA | Infrared-based setup (IR-camera) | Correlation of temperature profile with bond length | [116] |
| PLA | Measuring surface temperature of the printed samples | Temperature recording permits the strength approximation of the interlayer bonding of the material | [117] |
| ABS-PEEK | Prediction of adhesion using the recorded temperature profile of deposited layers using IR-camera | Implementing the obtained results in rheological characteristics | [56] |
| ABS | Using T-type thermocouples for temperature recordings | Developing a model using the obtained results for prediction of bonding quality | [124] |
| PEEK | Using IR-camera for temperature recording in non-isothermal healing model for interfacial bonding | Liquefier temperature has high impact on layer healing, with 100% healing at high platform temperature | [118] |
| Approach | Advantages | Limitations |
|---|---|---|
| Global approach |
|
|
| Local approach |
|
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vanaei, H.R.; Shirinbayan, M.; Deligant, M.; Khelladi, S.; Tcharkhtchi, A. In-Process Monitoring of Temperature Evolution during Fused Filament Fabrication: A Journey from Numerical to Experimental Approaches. Thermo 2021, 1, 332-360. https://doi.org/10.3390/thermo1030021
Vanaei HR, Shirinbayan M, Deligant M, Khelladi S, Tcharkhtchi A. In-Process Monitoring of Temperature Evolution during Fused Filament Fabrication: A Journey from Numerical to Experimental Approaches. Thermo. 2021; 1(3):332-360. https://doi.org/10.3390/thermo1030021
Chicago/Turabian StyleVanaei, Hamid Reza, Mohammadali Shirinbayan, Michael Deligant, Sofiane Khelladi, and Abbas Tcharkhtchi. 2021. "In-Process Monitoring of Temperature Evolution during Fused Filament Fabrication: A Journey from Numerical to Experimental Approaches" Thermo 1, no. 3: 332-360. https://doi.org/10.3390/thermo1030021
APA StyleVanaei, H. R., Shirinbayan, M., Deligant, M., Khelladi, S., & Tcharkhtchi, A. (2021). In-Process Monitoring of Temperature Evolution during Fused Filament Fabrication: A Journey from Numerical to Experimental Approaches. Thermo, 1(3), 332-360. https://doi.org/10.3390/thermo1030021










