Revisiting the Clausius/Clapeyron Equation and the Cause of Linearity

Abstract

In general, for an organic compound a plot of the log vapor pressure versus inverse temperature is linear over a wide temperature range. This however can lead to a point of confusion in an undergraduate thermodynamics course. This linear behavior is typically explained using the Clausius/Clapeyron equation. That is, starting with the Clapeyron equation one first assumes (1) that the change in compressibility upon vaporization is approximately 1, or equivalently that the vapor phase may be treated as an ideal gas where the molar volume of the vapor is much greater than that of the liquid, which may be assumed negligible. And second (2), that the enthalpy of vaporization is constant. While the resulting linear behavior is captured, the underlying assumptions are not applicable over the wide range of temperatures of interest. Here we discuss the shortcomings of the conventional explanation of the Clausius/Clapeyron equation. We further demonstrate that a simple solution is to instead assume that the enthalpy of vaporization relative to the change in compressibility upon vaporization is constant. We provide a series of examples and MATLAB code that can be used in an undergraduate thermodynamics course.

1. Introduction

The knowledge and understanding, in addition to the ability to predict, phase equilibrium is of central importance for the design of a wide range of chemical processes. As such, phase equilibrium thermodynamics is a keystone in the undergraduate chemical engineering curriculum. Early in this discussion students are typically introduced to the Clapeyron equation.

In general, for an organic compound, a plot of the log vapor pressure versus inverse temperature is linear over a wide temperature range. The Clapeyron equation relates the log vapor pressure to the the inverse temperature, and is derived using our fundamental equation, thermodynamic definitions, and our criteria of phase equilibrium. It is common in the undergraduate curriculum to make a series of two assumptions to go from the Clapeyron to the Clausius/Clapeyron equation. First, it is common to assume (1) that the change in compressibility upon vaporization is approximately 1, or equivalently that the vapor phase may be treated as an ideal gas where the molar volume of the vapor is much greater than that of the liquid, which may be assumed negligible. And second (2), that the enthalpy of vaporization is constant. The resulting expression predicts that the log vapor pressure versus inverse temperature is linear, in apparent agreement with reference data [1,2,3,4,5,6].

Unfortunately, this may be misleading and cause confusion to some students. Namely, it is known that the enthalpy of vaporization is a positive, temperature-dependent quantity that goes to zero at the critical point. Likewise, the change in compressibility upon vaporization is approximately one at low temperatures, but goes to zero at the critical point. In the present manuscript we encourage use of a single assumption that the enthalpy of vaporization relative to the change in compressibility upon vaporization is constant. This is motivated by use of the freely available reference data from “Thermophysical Properties of Fluid Systems” by NIST [7] and with MATLAB code (or MS Excel template) accompanying the electronic version of this manuscript which may be integrated into the undergraduate course. We have shown that this is superior to the conventional explanation, in addition to being simpler.

Given its importance, several articles related to the Clausius/Clapeyron equation have appeared in the Journal of Chemical Education over the past 70 years. In 1951, Brown [8] motivated the inclusion of compressibility as carried out here in the present study. Likewise, the article “Putting Clapeyron’s Equation into Practical Use with No Help from Clausius” by Waldenstrøm et al. [9], points out the limitation of the conventional form of the Clausius/Clapeyron equation which assumes that the change in compressibility upon vaporization is taken to be 1. The authors subsequently provide an excellent discussion on the modeling of the log vapor pressure as a function of temperature. Unfortunately, the material is likely too advanced for most undergraduate thermodynamics courses where students are exposed to the Clapeyron equation for the first time. This is similar to the more recent article “On the Clausius/Clapeyron vapor pressure equation” by Velasco et al. [10] who likewise point out the limitation of the conventional form of the Clausius/Clapeyron equation which assumes change in compressibility upon vaporization is taken to be 1. In the introduction, they further mention that for some substances the ratio of the enthalpy of vaporization relative to the change in compressibility upon vaporization is constant, as we will show in the present manuscript. The authors used this to model the phase behavior of a range of fluids wherein the critical point was adopted as the reference state, which facilitates the use of reduced units. Furthermore, the authors developed an analytic correction to the Clausius/Clapeyron equation. While this work mentions that for some substances the ratio of the enthalpy of vaporization relative to the change in compressibility upon vaporization is constant, they do not provide further explanation or examples.

In the work of Pollnow [11] the author discussed how to regress the constants A and B in the integrated Clausius/Clapeyron equation of the form ${log}_{10}{P}^{\mathrm{sat}}=A-B/T$ using reference data. However, the constant B is related to the enthalpy of vaporization divided by the molar gas constant, suggesting that the change in compressibility upon vaporization is taken to be 1. In the work of Discoll [12] the author describes an apparatus to measure the enthalpy of vaporization via the Clausius/Clapeyron equation. The form of the Clausius/Clapeyron equation employed neglects (and makes no mention of) the change in compressibility upon vaporization. Fortunately, the author is dealing with low pressures where it is reasonable to assume the change in compressibility upon vaporization is 1. Likewise, Galleano et al. [13] describes modifications that can be made to a commercially available pressure cooker to allow student to measure the enthalpy of vaporization via the Clausius/Clapeyron equation, where the employed form likewise neglects (and makes no mention of) the change in compressibility upon vaporization.

In the present study our intention is to provide resources to help introduce the Clapeyron equation in an undergraduate thermodynamics course. We provide MATLAB code and an MS Excel template that works with freely available reference data from “Thermophysical Properties of Fluid Systems” by NIST [7] to improve student understanding. Using the available reference data, we demonstrate that assuming the ratio of the enthalpy of vaporization relative to the change in compressibility upon vaporization is constant is often a reasonable assumption, and is far superior to the conventional approach. We further demonstrate the ability of the resulting expression to model the reference vapor pressure data. In directly modeling and working with actual reference data, we believe student engagement and understanding are enhanced.

2. Clapeyron Equation

While there are multiple, common approaches to drive the Clapeyron equation, here we will make use the dimensionless (molar) Gibbs free energy, $G/\left(RT\right)$, as a generating function [1]. Starting with our definitions of G:

$$G=H-TS$$

(1)

and

$$dG=-SdT+VdP$$

(2)

we next work out the corresponding differential for the dimensionless (molar) Gibbs free energy:

$$\begin{array}{cc}\hfill d\left(\frac{G}{RT}\right)& =\frac{1}{R}\left[\frac{TdG-GdT}{T^2}\right]=\frac{dG}{RT}-\frac{G}{R{T}^2}dT\hfill \\ \hfill & =\frac{1}{RT}[-SdT+VdP]-\frac{(H-TS)}{R{T}^2}dT\hfill \\ \hfill & =-\frac{S}{RT}dT+\frac{V}{RT}dP-\frac{H}{R{T}^2}dT+\frac{S}{RT}dT\hfill \end{array}$$

(3)

which leads to the final expression:

$$d\left(\frac{G}{RT}\right)=-\frac{H}{R{T}^2}dT+\frac{V}{RT}dP$$

(4)

Next, two simplifications are made. Starting with the first differential:

$$d\left(\frac{1}{T}\right)=-\frac{1}{T^2}dT$$

(5)

and then the second:

$$\frac{V}{RT}=\frac{Z}{P}$$

(6)

where:

$$d\left(\ln P\right)=\frac{1}{P}dP$$

(7)

Therefore:

$$d\left(\frac{G}{RT}\right)=\frac{H}{R}d\left(\frac{1}{T}\right)+Zd\left(\ln P\right)$$

(8)

Considering the general case of equilibrium between phases I and $II$, at coexistence:

$$\begin{array}{cc}\hfill & T^I=T^{II}=T\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & P^I=P^{II}=P^{\mathrm{sat}}\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & G^I=G^{II}=G\hfill \end{array}$$

(11)

If the system were to remain in a state of equilibrium for a change in T and P, we have:

$$\begin{array}{cc}\hfill d\left(\frac{G^I}{RT}\right)& =d\left(\frac{G^{II}}{RT}\right)\hfill \\ \hfill \frac{H^I}{R}d\left(\frac{1}{T}\right)+Z^{I}d\left(\ln P^{\mathrm{sat}}\right)& =\frac{H^{II}}{R}d\left(\frac{1}{T}\right)+Z^{II}d\left(\ln P^{\mathrm{sat}}\right)\hfill \end{array}$$

(12)

Collecting terms:

$$\begin{array}{cc}\hfill -\frac{(H^{II}-H^I)}{R}d\left(\frac{1}{T}\right)& =(Z^{II}-Z^I)d\left(\ln P^{\mathrm{sat}}\right)\hfill \\ \hfill -\frac{(H^{II}-H^I)}{R(Z^{II}-Z^I)}& =\frac{d\left(\ln P^{\mathrm{sat}}\right)}{d(1/T)}\hfill \end{array}$$

(13)

For the case of vapor–liquid equilibrium, let phase $II$ be vapor and phase I be liquid. This results in (one of several forms of) the Clapeyron equation:

$$\frac{d\left(\ln P^{\mathrm{sat}}\right)}{d(1/T)}=-\frac{\Delta H^{\mathrm{vap}}}{R\Delta Z^{\mathrm{vap}}}$$

(14)

2.1. Clausius/Clapeyron Equation

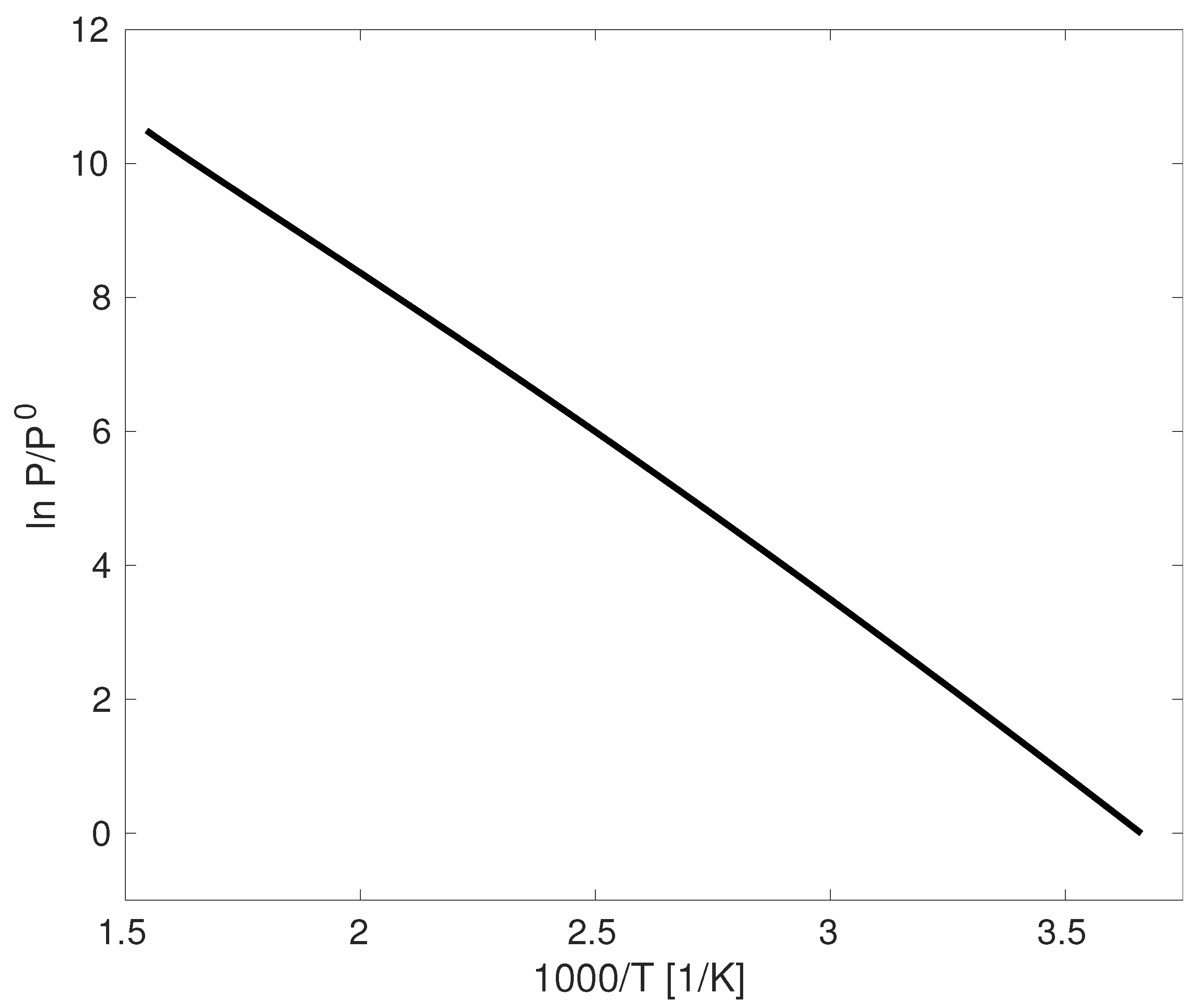
While the Clapeyron Equation (Equation (14)) is rigorously correct, we next make a series of assumptions that will ultimately lead to the Clausius/Clapeyron equation commonly introduced in the undergraduate curriculum. This is motivated by Figure 1, wherein a plot of $\ln P^{\mathrm{sat}}$ versus $1/T$ appears linear from the triple point to the critical point [1,2,3,4,5,6], considering the case of water as an example [7,14]. We note that all of the figures included in this manuscript were prepared with MATLAB code available in the supporting information accompanying the electronic version of this manuscript. While in this manuscript we only consider the case of water and hexane as examples, additional systems are provided as an example in the supporting information.

On the right hand side, first we consider $\Delta Z^{\mathrm{vap}}$. At low temperatures well removed from the critical point, it can be assumed the vapor phase is an ideal gas. For this case we take:

$$\begin{array}{cc}& \Delta Z^{\mathrm{vap}}=Z^V-Z^L=\frac{P{V}^{\mathrm{ig}}}{RT}-\frac{P{V}^L}{RT}=\frac{P}{RT}(V^{\mathrm{ig}}-V^L)\end{array}$$

(15)

Further assuming that $V^{\mathrm{ig}}$ is much greater than $V^L$ such that $V^L$ can be assumed negligible:

$$\Delta Z^{\mathrm{vap}}\approx \frac{P{V}^{\mathrm{ig}}}{RT}=1$$

(16)

This is equivalent to assuming that $Z^V=1$ and the $Z^L$ is negligible. This results in the expression:

$$\frac{d\left(\ln P^{\mathrm{sat}}\right)}{d(1/T)}=-\frac{\Delta H^{\mathrm{vap}}}{R}$$

(17)

In general, undergraduate students are told that the assumptions are reasonable so long as we are well removed from the critical point [1,2,3,4,5,6].

Next, in order to integrate Equation (17), the temperature dependence of $\Delta H^{\mathrm{vap}}$ must be known. If we assume that $\Delta H^{\mathrm{vap}}$ is constant over a temperature range of interest, we obtain the expression:

$$\ln P^{\mathrm{sat}}=A-\frac{B}{T}$$

(18)

where A and B are positive constants, where:

$$A=\ln P_0^{\mathrm{sat}}+\frac{\Delta H^{\mathrm{vap}}}{R{T}_0}$$

(19)

where $T_0$ is the reference temperature and $P_0^{\mathrm{sat}}$ the reference saturation pressure at $T_0$, and:

$$B=\frac{\Delta H^{\mathrm{vap}}}{R}$$

(20)

Equation (18) suggests that a plot of $\ln P^{\mathrm{sat}}$ versus $1/T$ should be linear with a negative slope. This well explains the observation of Figure 1. While most undergraduate textbooks acknowledge that the assumption that $Z^V\approx 1$ and that $Z^L$ is negligible is only reasonable at low pressures well removed from the critical point, Equations (18)–(20) are typically the end point for discussion [1,2,3,4].

While this provides justification of the linear trend in Figure 1, it is misleading and can cause confusion to the undergraduate student learning the material for the first time. At low pressures well removed from the critical point, it is reasonable to assume $\Delta Z^{\mathrm{vap}}\approx 1$. However, at the critical point where the two phases cease to exist, $\Delta Z^{\mathrm{vap}}\to 0$. Therefore, $\Delta Z^{\mathrm{vap}}$ decreases with increasing temperature. Likewise, $\Delta H^{\mathrm{vap}}$ is not constant as evident by the Watson equation typically introduced in the undergraduate curriculum [15,16,17]. Below the critical point $\Delta H^{\mathrm{vap}}>0$, and at the critical point $\Delta H^{\mathrm{vap}}\to 0$. We therefore find also that $\Delta H^{\mathrm{vap}}$ decreases with increasing temperature. Knowing this, the previous approach used to arrive at Equation (18) is less than satisfying, even though it appears to agree with Figure 1.

This shortcoming is acknowledged by two of the common undergraduate textbooks which we reviewed. Koretsky [6] arrives at Equation (18) using the assumptions listed earlier. However, he acknowledges that the error introduced by assuming $\Delta H^{\mathrm{vap}}$ is constant (assumption 3) is approximately offset by the error introduced by assuming $Z^L$ is negligible and $Z^V=1$ (assumptions 1 and 2).

A further discussion is provided by Elliott and Lira [5]. In that work the authors arrive at Equation (18) using the assumptions listed earlier. However, this is followed in their textbook by Section 9.3 “Shortcut Estimation of Saturation Properties”. Here the authors mention that one may alternatively arrive at Equation (18) by instead assuming that $\Delta H^{\mathrm{vap}}/\Delta Z^{\mathrm{vap}}$ is constant. Further, this assumption is reasonable over the range $0.5<T_r<1$, where $T_r=T/T_c$ is the reduced temperature, where $T_c$ is the critical temperature. The authors then use the critical point ($T_r=1$) and acentric factor ($T_r=0.7$) as reference points to solve for the constants A and B, to develop a predictive vapor pressure expression. We note also that the suggestion of assuming $\Delta H^{\mathrm{vap}}/\Delta Z^{\mathrm{vap}}$ is constant is also made in references [17,18]; however, these are references not typically used in undergraduate courses.

2.2. Updated Clausius/Clapeyron Equation Discussion

Here our motivation is to build upon the work of Elliott and Lira [5], and present an alternative discussion and motivation for Equation (18) to explain the linearity of $\ln P^{\mathrm{sat}}$ versus $1/T$. Within our discussion here we will consider the case of water and hexane, using reference data readily available from the “Thermophysical Properties of Fluid Systems” by NIST [7]. MATLAB code used for all of the analysis and figures is provided in the supporting information accompanying the electronic version of this manuscript, along with additional systems that may be used as an example. The goal of the MATLAB code is to provide a useful resource for undergraduate thermodynamics students.

It is our recommendation that one should start with the rigorously correct Clapeyron equation (Equation (14)). From there, one need only introduce the single assumption that the ratio $\Delta H^{\mathrm{vap}}/\Delta Z^{\mathrm{vap}}$ is constant which allows one to obtain the integrated Clausius/Clapeyron equation (Equation (18)), where now:

$$A=\ln P_0^{\mathrm{sat}}+\frac{\Delta H^{\mathrm{vap}}}{R\Delta Z^{\mathrm{vap}}{T}_0}$$

(21)

where $T_0$ is the reference temperature and $P_0^{\mathrm{sat}}$ the reference saturation pressure at $T_0$, and:

$$B=\frac{\Delta H^{\mathrm{vap}}}{R\Delta Z^{\mathrm{vap}}}$$

(22)

This is a simple update to the conventional instruction. This is motivated and reinforced to students in a series of simple plots.

First, in Figure 2 and Figure 3 we consider plots of $\Delta H^{\mathrm{vap}}/R$ and $\Delta Z^{\mathrm{vap}}$ versus T, and a plot of $\Delta H^{\mathrm{vap}}/R$ versus $\Delta Z^{\mathrm{vap}}$. The plots span the temperature range from the triple point to the critical point. As expected, $\Delta H^{\mathrm{vap}}/R$ is positive, decreasing to a value of 0 at the critical point. Likewise, $\Delta Z^{\mathrm{vap}}\approx 1$ at low temperatures, decreasing to a value of 0 at the critical point. We therefore see that it is not reasonable to assume $\Delta Z^{\mathrm{vap}}=1$ over the entire temperature range, nor is it reasonable to assume $\Delta H^{\mathrm{vap}}$ is constant over the entire temperature range. However, the functional dependence of $\Delta H^{\mathrm{vap}}/R$ and $\Delta Z^{\mathrm{vap}}$ versus T are similar. Furthermore, the plot of $\Delta H^{\mathrm{vap}}/R$ versus $\Delta Z^{\mathrm{vap}}$ appears to be linear, except near the triple point. Near the triple point, the rate of decrease in $\Delta H^{\mathrm{vap}}$ is greater than $\Delta Z^{\mathrm{vap}}$.

Next, in Figure 4 and Figure 5 we plot $\Delta H^{\mathrm{vap}}/\left(R\Delta Z^{\mathrm{vap}}\right)$ versus T and $1/T$ from the triple point to the critical point. We compare the case where $\Delta Z^{\mathrm{vap}}=1$, corresponding to the case of $\Delta H^{\mathrm{vap}}/\left(R\Delta Z^{\mathrm{vap}}\right)=\Delta H^{\mathrm{vap}}/R$, to the case where we account for the temperature dependence of $\Delta Z^{\mathrm{vap}}$. We find that the range of values for $\Delta H^{\mathrm{vap}}/\left(R\Delta Z^{\mathrm{vap}}\right)$ is significantly smaller than for $\Delta H^{\mathrm{vap}}/R$. While both $\Delta H^{\mathrm{vap}}$ and $\Delta Z^{\mathrm{vap}}$ decrease with increasing temperature, the effect in $\Delta H^{\mathrm{vap}}/\left(R\Delta Z^{\mathrm{vap}}\right)$ appears to cancel. We see that it is more reasonable to assume $\Delta H^{\mathrm{vap}}/\left(R\Delta Z^{\mathrm{vap}}\right)$ is constant as compared to assuming $\Delta H^{\mathrm{vap}}$ is constant.

This is further emphasized by the Watson plot in Figure 6 and Figure 7. In a Watson plot, we find that $\ln \Delta H^{\mathrm{vap}}/R$ versus $\ln \left(1-T_r\right)$ yields a straight line [15,16,17]. In Figure 6 we consider the case of $\ln \Delta H^{\mathrm{vap}}/\left(R\Delta Z^{\mathrm{vap}}\right)$ and $\ln \Delta H^{\mathrm{vap}}/R$ (where $\Delta Z^{\mathrm{vap}}=1$) versus $\ln \left(1-T_r\right)$. While $\ln \Delta H^{\mathrm{vap}}/R$ versus $\ln \left(1-T_r\right)$ yields a straight line as expected, we find that $\ln \Delta H^{\mathrm{vap}}/\left(R\Delta Z^{\mathrm{vap}}\right)$ versus $\ln \left(1-T_r\right)$ appears nearly constant. We do observe curvature near the triple point, but in general $\ln \Delta H^{\mathrm{vap}}/\left(R\Delta Z^{\mathrm{vap}}\right)$ appears constant over a wide range of temperatures.

As our final example, we return to our starting point of the Clapeyron equation (Equation (14)), then separate and numerically integrate the resulting expression. Integrating from a reference temperature ($T_0$) and corresponding reference pressure ($P_0^{\mathrm{sat}}$):

$$\begin{array}{c}\hfill {\int }_{\ln P_0^{\mathrm{sat}}}^{\ln P^{\mathrm{sat}}}d\left(\ln P^{\mathrm{sat}}\right)=-{\int }_{1/T_0}^{1/T}\frac{\Delta H^{\mathrm{vap}}}{R\Delta Z^{\mathrm{vap}}}d(1/T)\\ \hfill \ln \frac{P^{\mathrm{sat}}}{P_0^{\mathrm{sat}}}=-{\int }_{1/T_0}^{1/T}\frac{\Delta H^{\mathrm{vap}}}{R\Delta Z^{\mathrm{vap}}}d(1/T)\end{array}$$

(23)

In order to evaluate this expression, one must know the temperature dependence of $\Delta H^{\mathrm{vap}}/\Delta Z^{\mathrm{vap}}$. Fortunately, tabulated data are readily available from the “Thermophysical Properties of Fluid Systems” by NIST which can be numerically integrated and compared to the reference vapor pressure data. In the top pane of Figure 8 and Figure 9, we numerically integrate two sets of temperature-dependent data and compare to reference vapor pressure data, taking our reference state to be the triple point. In the first case, we set $\Delta Z^{\mathrm{vap}}=1$, which corresponds to numerically integrating $\Delta H^{\mathrm{vap}}/R$. The predicted data match the reference vapor pressure at the triple point by construction, but diverge at the critical point due to propagation of errors and the assumption of $\Delta Z^{\mathrm{vap}}=1$ breaks down with increasing temperature. Clearly then, $\Delta Z^{\mathrm{vap}}$ is important for accurate calculations. In the second case we numerically integrate $\Delta H^{\mathrm{vap}}/\left(R\Delta Z^{\mathrm{vap}}\right)$. The resulting predictions match the reference data as expected.

Following this, in the middle pane we consider the case of assuming $\Delta H^{\mathrm{vap}}/\left(R\Delta Z^{\mathrm{vap}}\right)$ is constant. For the value of $\Delta H^{\mathrm{vap}}/\left(R\Delta Z^{\mathrm{vap}}\right)$ we compare the use of the value at the lowest temperature (the triple point, min), the average value (avg) and the average (natural) log value (Lavg), and the value at the highest temperature (just below the critical point, max). We find that the use of the average and average log value result in excellent predictions that appear to overlap the reference data. The use of the value at the highest temperature also performs exceptionally well. The performance with the minimum temperature is the worst; nonetheless, the predictions are still very good considering they require only knowledge of $\Delta H^{\mathrm{vap}}/\left(R\Delta Z^{\mathrm{vap}}\right)$ at the triple point.

Lastly, in the bottom pane, we consider the case of assuming $\Delta Z^{\mathrm{vap}}=1$ and assuming $\Delta H^{\mathrm{vap}}/R$ is constant. For the value of $\Delta H^{\mathrm{vap}}/R$ we again use the value at the lowest temperature (the triple point, min), the average value (avg) and the average (natural) log value (Lavg), and the value at the highest temperature (just below the critical point, max). Interestingly, the best set of predictions is made using the value at the triple point. At the triple point, the assumption that $\Delta Z^{\mathrm{vap}}=1$ is reasonable, and we find that the predictions using a constant value of $\Delta H^{\mathrm{vap}}/\left(R\Delta Z^{\mathrm{vap}}\right)$ and $\Delta H^{\mathrm{vap}}/R$ at the triple point are indistinguishable from each other. The other predictions noticeably diverge from the reference data, with the predictions worst using the value of $\Delta H^{\mathrm{vap}}/R$ at the highest temperature where the assumption that $\Delta Z^{\mathrm{vap}}=1$ is least appropriate.

3. Summary and Conclusions

The knowledge and understanding of fluid phase equilibrium is indispensable for the design of a wide range of chemical processes, and as such is a cornerstone of the undergraduate chemical engineering curriculum. In the study of phase equilibrium, early attention is often devoted to the use of the Clapeyron equation. Starting with our fundamental thermodynamic relationships and criteria for phase equilibrium, the Clapeyron equation presents the opportunity to make reasonable assumptions to obtain a simple expression capable of explaining the linearity of a plot of the log vapor pressure versus inverse temperature. Unfortunately, the assumptions made are often not appropriate and may cause confusion among students.

Here we encourage use of a single assumption that $\Delta H^{\mathrm{vap}}/\left(R\Delta Z^{\mathrm{vap}}\right)$ is constant. This is motivated by use of NIST reference data and MATLAB code (or MS Excel template) accompanying the electronic version of this manuscript. We have shown that this is superior to the conventional approach of assuming first (1) that the change in compressibility upon vaporization ($\Delta Z^{\mathrm{vap}}$) is approximately 1, or equivalently that the vapor phase may be treated as an ideal gas where the molar volume of the vapor is much greater than that of the liquid, which may be assumed negligible. And second (2), that the enthalpy of vaporization ($\Delta H^{\mathrm{vap}}$) is constant. While the conventional approach is able to explain linearity, it can be misleading as both $\Delta H^{\mathrm{vap}}$ and $\Delta Z^{\mathrm{vap}}$ are known to go to zero at the critical point.

While this may appear a minor detail, we believe this is important as most students are introduced to the thermodynamics of phase equilibrium for the first time. The beauty of the Clapeyron equation is that we are able to derive an expression to interpret real phase equilibrium data using our fundamental equations. The student should not be confused or misled, as this is an important skill we wish to encourage students to develop and apply in the future.

The MATLAB code accompanying the electronic version of this manuscript may serve as a valuable resource in an undergraduate thermodynamics course. Included with it is an instructional document on how to operate the MATLAB code itself as well as “Thermophysical Properties of Fluid Systems” by NIST [7] reference data for thirty-four chemical species. An MS Excel template is also provided. Instructions are additionally provided for downloading and updating the analysis for additional systems. The use of MATLAB code or MS Excel presents opportunities for undergraduates to explore the characterization of phase equilibrium, to compare/contrast different chemical species, and to fully understand and appreciate the underlying assumptions of the Clausius/Clapeyron equation.