The Effect of Temperature on the London Dispersive and Lewis Acid-Base Surface Energies of Polymethyl Methacrylate Adsorbed on Silica by Inverse Gas Chromatography
Abstract
1. Introduction
2. IGC Methods and Materials
3. Experimental Results
3.1. London Dispersive Surface Energy of Silica Particles
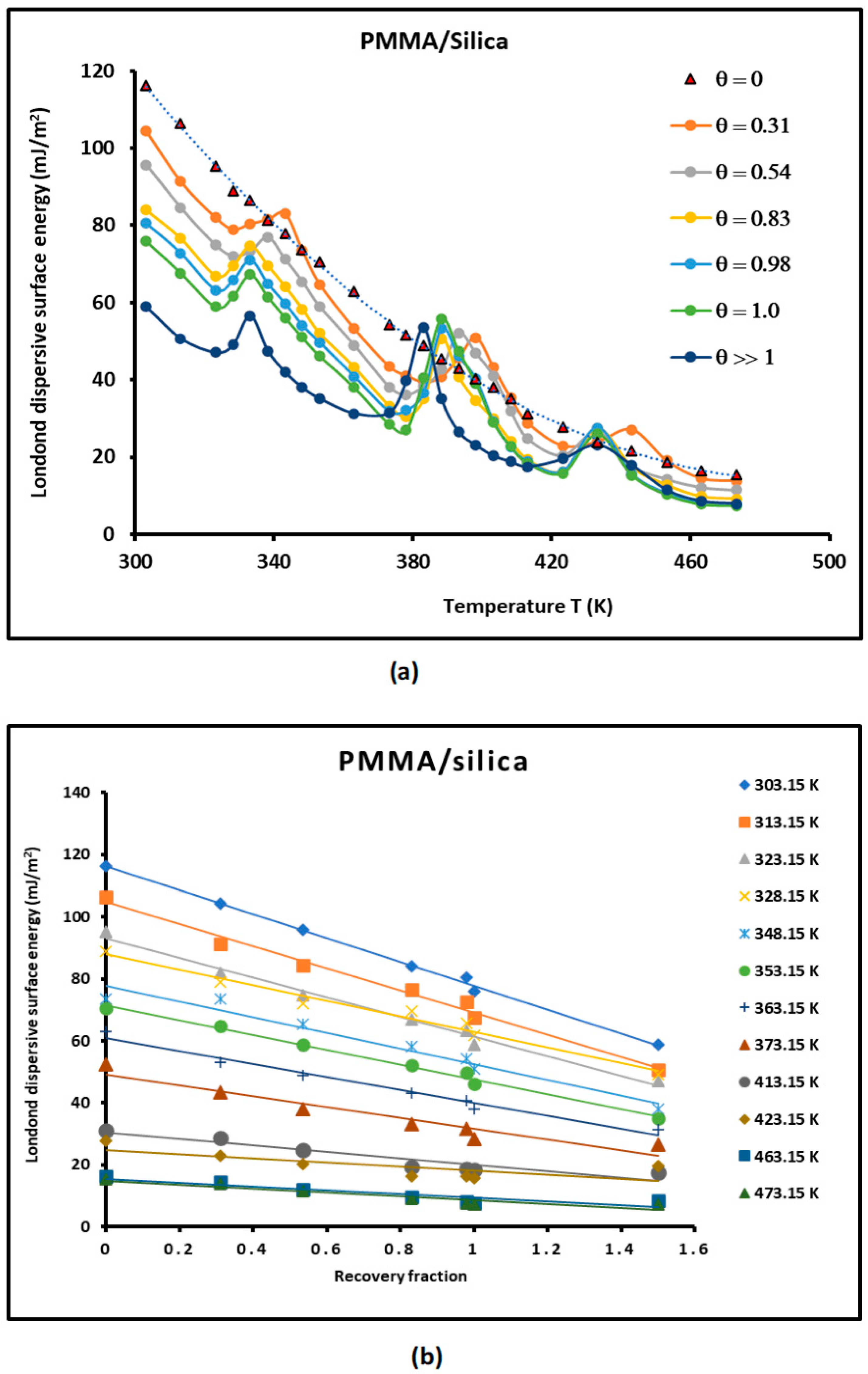
3.2. Study of of PMMA and PMMA/Silica Composites
- -
- The London dispersive surface energy decreases when the recovery fraction fractions of PMMA adsorbed on silica increases whatever the used molecular model;
- -
- The adsorption of PMMA on silica strongly affects the physicochemical properties of PMMA relative to its bulk phase. The transition temperatures observed in PMMA alone change with the recovery fraction;
- -
- When approaching the monolayer of adsorption of PMMA on silica particles, there is a spontaneous decreasing evolution of the London dispersive surface energy from silica particles (Table 1) to PMMA in the bulk phase (Table 2), and when passing through the different recovery fractions from to (Table 3 and Figure 5), the behavior of the PMMA monolayer becomes closer to PMMA in its bulk phase.
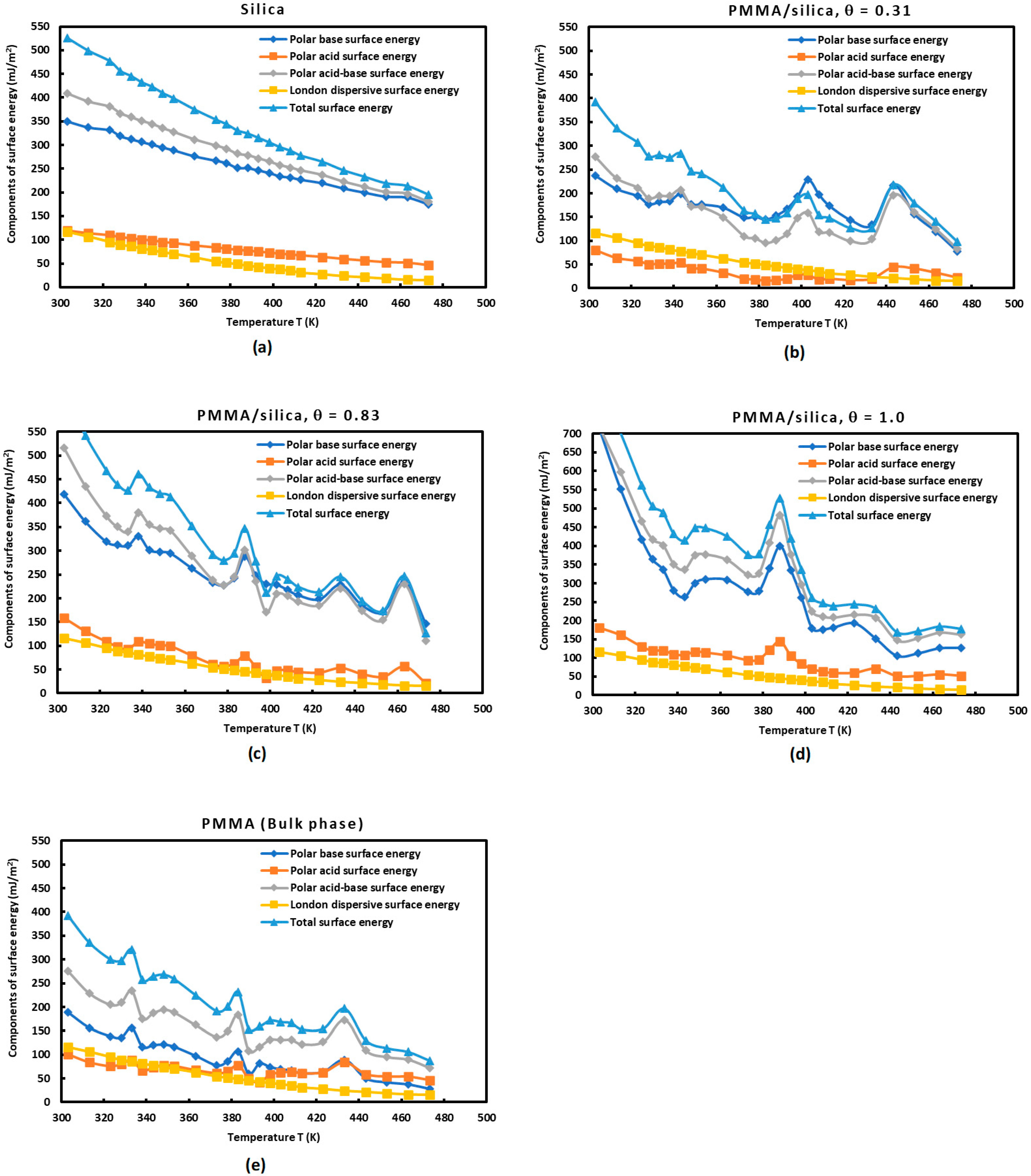
3.3. Lewis’s Acid-Base Polar Surface Energies of PMMA/Silica
- -
- All curves of the acid-base polar surface energies decreased against the temperature, except at the transition temperature where higher values of these parameters were observed for the different recovery fractions.
- -
- The acid polar surface energy of silica did not present any appreciated variation when the recovery fraction of PMMA increased. Globally, the acidity of silica particles is not very affected by the adsorbed amount of PMMA.
- -
- An important change in the value of the base polar surface energy was observed when the recovery fraction of PMMA varied. It seems that a maximum of was obtained in the case of a monolayer ( of PMMA adsorbed on silica particles, and the acid-base polar surface energy was the highest in this later case. For this value of , a maximum of was also observed. In the case of the monolayer of adsorption of PMMA on silica, it can be deduced that the polar surface energy was higher than those of silica and PMMA taken separately, and it approximately approached the summation of these two extreme cases of and PMMA in the bulk phase.
- -
- Figure 8 shows all curves of the Lewis acid-base surface energies as a function of the temperature and gave similar variations as those of . The behavior of these Lewis surface parameters showed an increase before every transition temperature until reaching their maximum values at the transition temperature directly followed by a decrease in the Lewis surface energies. These variations of neighboring transition temperatures are due to the fluctuations and relaxation of the chain groups of PMMA as a function of the temperature.
4. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Papadopoulou, S.K.; Panayiotou, C. Assessment of the thermodynamic properties of poly(2,2,2-trifluoroethyl methacrylate) by inverse gas chromatography. J. Chromatogr. A 2014, 1324, 207–214. [Google Scholar] [CrossRef] [PubMed]
- Voelkel, A.; Strzemiecka, B.; Adamska, K.; Milczewska, K. Inverse gas chromatography as a source of physiochemical data. J. Chromatogr. A 2009, 1216, 1551. [Google Scholar] [CrossRef] [PubMed]
- Al-Saigh, Z.Y.; Munk, P. Study of polymer-polymer interaction coefficients in polymer blends using inverse gas chromatography. Macromolecules 1984, 17, 803. [Google Scholar] [CrossRef]
- Dritsas, G.S.; Karatasos, K.; Panayiotou, C. Investigation of thermodynamic properties of hyperbranched aliphatic polyesters by inverse gas chromatography. J. Chromatogr. A 2009, 1216, 8979. [Google Scholar] [CrossRef]
- Papadopoulou, S.K.; Karapanagiotis, I.; Zuburtikudis, I.; Panayiotou, C. Thermodynamic characterization of poly(2,2,3,3,3-pentafluoropropyl methacrylate). J. Polym. Sci. B Polym. Phys. 2010, 48, 1826. [Google Scholar] [CrossRef]
- Papadopoulou, S.K.; Panayiotou, C. Thermodynamic characterization of poly(1,1,1,3,3,3-hexafluoroisopropyl methacrylate) by inverse gas chromatography. J. Chromatogr. A 2012, 1229, 230. [Google Scholar] [CrossRef]
- Coimbra, P.; Coelho, M.S.N.; Gamelas, J.A.F. Surface characterization of polysaccharide scaffolds by inverse gas chromatography regarding application in tissue engineering. Surf. Interface Anal. 2019, 51, 1070–1077. [Google Scholar] [CrossRef]
- Kołodziejek, J.; Voelkel, A.; Heberger, K. Characterization of hybrid materials by means of inverse gas chromatography and chemometrics. J. Pharm. Sci. 2013, 102, 1524. [Google Scholar] [CrossRef][Green Version]
- Heydar, K.; Nazifi, M.; Sharifi, A.; Mirzaei, M.; Gharavi, H.; Ahmadi, S. Determination of Activity Coefficients at Infinite Dilution of Solutes in New Dicationic Ionic Liquids Based on Morpholine Using Gas–Liquid Chromatography. Chromatographia 2013, 76, 165. [Google Scholar] [CrossRef]
- Doman’ska, U.; Lukoshko, E.V. Measurements of activity coefficients at infinite dilution for organic solutes and water in the ionic liquid 1-butyl-1-methylpyrrolidinium tricyanomethanide. J. Chem. Therm. 2013, 66, 144. [Google Scholar] [CrossRef]
- Yoo, B.; Afzal, W.; Prausnitz, J.M. Solubility parameters for nine ionic liquids. Ind. Eng. Chem. Res. 2012, 51, 9913. [Google Scholar] [CrossRef]
- Lazar, P.; Karlický, F.; Jurečka, P.; Kocman, M.; Otyepková, E.; Šafářová, K.; Otyepka, M. Adsorption of small organic molecules on graphene. J. Am. Chem. Soc. 2013, 135, 6372–6377. [Google Scholar] [CrossRef] [PubMed]
- Belgacem, M.N.; Czeremuszkin, G.; Sapieha, S.; Gandini, A. Surface by XPS characterization and inverse gas of cellulose fibres chromatography. Cellulose 1995, 2, 145–157. [Google Scholar] [CrossRef]
- Papadopoulou, S.K.; Tsioptsias, C.; Pavlou, A.; Kaderides, K.; Sotiriou, S.; Panayiotou, C. Superhydrophobic surfaces from hydrophobic or hydrophilic polymers via nanophase separation or electrospinning/electrospraying. Colloids Surf. A 2011, 387, 71–78. [Google Scholar] [CrossRef]
- Ryan, H.M.; Douglas, J.G.; Rupert, W. Inverse Gas Chromatography for Determining the Dispersive Surface Free Energy and Acid-Base Interactions of Sheet Molding Compound-Part II 14 Ligno-Cellulosic Fiber Types for Possible Composite Reinforcement. J. Appl. Polym. Sci. 2008, 110, 3880–3888. [Google Scholar]
- Jacob, P.N.; Berg, J.C. Acid-base surface energy characterization of microcrystalline cellulose and two wood pulp fiber types using inverse gas chromatography. Langmuir 1994, 10, 3086–3093. [Google Scholar] [CrossRef]
- Carvalho, M.G.; Santos, J.M.R.C.A.; Martins, A.A.; Figueiredo, M.M. The Effects of Beating, Web Forming and Sizing on the Surface Energy of Eucalyptus globulus Kraft Fibres Evaluated by Inverse Gas Chromatography. Cellulose 2005, 12, 371–383. [Google Scholar] [CrossRef]
- Chtourou, H.; Riedl, B.; Kokta, B.V. Surface characterizations of modified polyethylene pulp and wood pulps fibers using XPS and inverse gas chromatography. J. Adhesion Sci. Technol. 1995, 9, 551–574. [Google Scholar] [CrossRef]
- Dorris, G.M.; Gray, D.G. Adsorption of n-alkanes at zero surface coverage on cellulose paper and wood fibers. J. Colloid Interface Sci. 1980, 77, 353–362. [Google Scholar] [CrossRef]
- Donnet, J.B.; Park, S.J.; Balard, H. Evaluation of specific interactions of solid surfaces by inverse gas chromatography. Chromatographia 1991, 31, 434–440. [Google Scholar] [CrossRef]
- Donnet, J.B.; Custodéro, E.; Wang, T.K.; Hennebert, G. Energy site distribution of carbon black surfaces by inverse gas chromatography at finite concentration conditions. Carbon 2002, 40, 163–167. [Google Scholar] [CrossRef]
- Gamble, J.F.; Davé, R.N.; Kiang, S.; Leane, M.M.; Tobyn, M.; Wang, S.S.Y. Investigating the applicability of inverse gas chromatography to binary powdered systems: An application of surface heterogeneity profiles to understanding preferential probe-surface interactions. Int. J. Pharm. 2013, 445, 39–46. [Google Scholar] [CrossRef] [PubMed]
- Balard, H.; Maafa, D.; Santini, A.; Donnet, J.B. Study by inverse gas chromatography of the surface properties of milled graphites. J. Chromatogr. A 2008, 1198–1199, 173–180. [Google Scholar] [CrossRef]
- Bogillo, V.I.; Shkilev, V.P.; Voelkel, A. Determination of surface free energy components for heterogeneous solids by means of inverse gas chromatography at finite concentrations. J. Mater. Chem. 1998, 8, 1953–1961. [Google Scholar] [CrossRef]
- Das, S.C.; Zhou, Q.; Morton, D.A.V.; Larson, I.; Stewart, P.J. Use of surface energy distributions by inverse gas chromatography to understand mechanofusion processing and functionality of lactose coated with magnesium stearate. Eur. J. Pharm. Sci. 2011, 43, 325–333. [Google Scholar] [CrossRef]
- Das, S.C.; Stewart, P.J. Characterising surface energy of pharmaceutical powders by inverse gas chromatography at finite dilution. J. Pharm. Pharmacol. 2012, 64, 1337–1348. [Google Scholar] [CrossRef]
- Bai, W.; Pakdel, E.; Li, Q.; Wang, J.; Tang, W.; Tang, B.; Wang, X. Inverse gas chromatography (IGC) for studying the cellulosic materials surface characteristics: A mini review. Cellulose 2023, 30, 3379–3396. [Google Scholar] [CrossRef]
- Dong, S.; Brendlé, M.; Donnet, J.B. Study of solid surface polarity by inverse gas chromatography at infinite dilution. Chromatographia 1989, 28, 469–472. [Google Scholar] [CrossRef]
- Feeley, J.C.; York, P.; Sumby, B.S.; Dicks, H. Determination of surface properties and flow characteristics of salbutamol sulphate, before and after micronisation. Int. J. Pharm. 1998, 172, 89–96. [Google Scholar] [CrossRef]
- Gamble, J.F.; Leane, M.; Olusanmi, D.; Tobyn, M.; Supuk, E.; Khoo, J.; Naderi, M. Surface energy analysis as a tool to probe the surface energy characteristics of micronized materials—A comparison with inverse gas chromatography. Int. J. Pharm. 2012, 422, 238–244. [Google Scholar] [CrossRef]
- Newell, H.E.; Buckton, G.; Butler, D.A.; Thielmann, F.; Williams, D.R. The use of inverse gas chromatography to measure the surface energy of crystalline, amorphous, and recently milled lactose. Pharm. Res. 2001, 18, 662–666. [Google Scholar] [CrossRef] [PubMed]
- Newell, H.E.; Buckton, G. Inverse gas chromatography: Investigating whether the technique preferentially probes high energy sites for mixtures of crystalline and amorphous lactose. Pharm. Res. 2004, 21, 1440–1444. [Google Scholar] [CrossRef]
- Kołodziejek, J.; Głowka, E.; Hyla, K.; Voelkel, A.; Lulek, J.; Milczewska, K. Relationship between surface properties determined by inverse gas chromatography and ibuprofen release from hybrid materials based on fumed silica. Int. J. Pharm. 2013, 441, 441–448. [Google Scholar] [CrossRef] [PubMed]
- Ho, R.; Wilson, D.A.; Heng, J.Y.Y. Crystal habits and the variation in surface energy heterogeneity. Cryst. Growth Des. 2009, 9, 4907–4911. [Google Scholar] [CrossRef]
- Ho, R.; Hinder, S.J.; Watts, J.F.; Dilworth, S.E.; Williams, D.R.; Heng, J.Y.Y. Determination of surface heterogeneity of D-mannitol by sessile drop contact angle and finite concentration inverse gas chromatography. Int. J. Pharm. 2010, 387, 79–86. [Google Scholar] [CrossRef]
- Ho, R.; Naderi, M.; Heng, J.Y.Y.; Williams, D.R.; Thielmann, F.; Bouza, P.; Keith, A.R.; Thiele, G.; Burnett, D.J. Effect of milling on particle shape and surface energy heterogeneity of needle-shaped crystals. Pharm. Res. 2012, 29, 2806–2816. [Google Scholar] [CrossRef] [PubMed]
- Sesigur, F.; Sakar, D.; Yazici, O.; Cakar, F.; Cankurtaran, O.; Karaman, F. Dispersive Surface Energy and Acid-Base Parameters of Tosylate Functionalized Poly(ethylene glycol) via Inverse Gas Chromatography. J. Chem. 2014, 2014, 402325. [Google Scholar] [CrossRef]
- Calvet, R.; Del Confetto, S.; Balard, H.; Brendlé, E.; Donnet, J.B. Study of the interaction polybutadiene/fillers using inverse gas chromatography. J. Chromatogr. A 2012, 1253, 164–170. [Google Scholar] [CrossRef][Green Version]
- Papadopoulou, S.K.; Dritsas, G.; Karapanagiotis, I.; Zuburtikudis, I.; Panayiotou, C. Surface characterization of poly(2,2,3,3,3-pentafluoropropyl methacrylate) by inverse gas chromatography and contact angle measurements. Eur. Polym. J. 2010, 46, 202–208. [Google Scholar] [CrossRef]
- Dritsas, G.S.; Karatasos, K.; Panayiotou, C. Investigation of thermodynamic properties of hyperbranched poly(ester amide) by inverse gas chromatography. J. Polym. Sci. Polym. Phys. 2008, 46, 2166–2172. [Google Scholar] [CrossRef]
- Ishihara, M.; Watanabe, T.; Hirata, T.; Sasaki, T. Melt adsorption of poly(tert-butyl methacrylate) and poly(ethyl methacrylate) on silica studied with chip nanocalorimetry. Polym. J. 2024, 276, 517–527. [Google Scholar] [CrossRef]
- Napolitano, S. Irreversible adsorption of polymer melts and nanoconfinement effects. Soft Matter 2020, 16, 5348–5365. [Google Scholar] [CrossRef]
- Gawek, M.; Omar, H.; Szymoniak, P.; Schönhals, A. Growth kinetics of the adsorbed layer of poly(2-vinylpyridine)—An indirect observation of desorption of polymers from substrates. Soft Matter 2023, 19, 3975–3982. [Google Scholar] [CrossRef]
- Zuo, B.; Zhou, H.; Davis, M.J.; Wang, X.; Priestley, R.D. Effect of local chain conformation in adsorbed nanolayers on confined polymer molecular mobility. Phys. Rev. Lett. 2019, 122, 217801. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Zhou, J.; Liu, M. Interphase in polymer nanocomposites. ACS Au 2022, 2, 280–291. [Google Scholar] [CrossRef]
- Tian, H.; Bi, C.; Li, Z.; Wang, C.; Zuo, B. Metastable polymer adsorption dictates the dynamical gradients at interfaces. Macromolecules 2023, 56, 4346–4353. [Google Scholar] [CrossRef]
- Wang, N.; Wu, X.; Liu, C.S. Opposite Effects of SiO2 Nanoparticles on the Local α and Larger-Scale α’ Segmental Relaxation Dynamics of PMMA Nanocomposites. Polymers 2019, 11, 979. [Google Scholar] [CrossRef] [PubMed]
- Ma, M.; Cui, W.; Guo, Y.; Yu, W. Adsorption-desorption effect on physical aging in PMMA-silica nanocomposites. Polymer 2022, 255, 125124. [Google Scholar] [CrossRef]
- Cui, W.; You, W.; Sun, Z.; Yu, W. Decoupled polymer dynamics in weakly attractive poly(methyl methacrylate)/silica nanocomposites. Macromolecules 2021, 54, 5484–5497. [Google Scholar] [CrossRef]
- Boucher, V.M.; Cangialosi, D.; Alegría, A.; Colmenero, J. Enthalpy recovery of PMMA/silica nanocomposites. Macromolecules 2010, 43, 7594–7603. [Google Scholar] [CrossRef]
- Huang, C.-C.; Liu, C.-Y. Peculiar α-β relaxations of Syndiotactic-Poly(methyl methacrylate). Polymer 2021, 225, 123760. [Google Scholar] [CrossRef]
- Kawaguchi, D.; Sasahara, K.; Inutsuka, M.; Abe, T.; Yamamoto, S.; Tanaka, K. Absolute local conformation of poly(methyl methacrylate) chains adsorbed on a quartz surface. J. Chem. Phys. 2023, 159, 244902. [Google Scholar] [CrossRef] [PubMed]
- Hamieh, T.; Rezzaki, M.; Schultz, J. Study of the transition temperatures and acid-base properties of poly (methyl methacrylate) adsorbed on alumina and silica, by using inverse gas chromatography technique. Colloids Surf. A Physicochem. Eng. Asp. 2001, 189, 279–291. [Google Scholar] [CrossRef]
- Hamieh, T.; Schultz, J. New approach to characterise physicochemical properties of solid substrates by inverse gas chromatography at infinite dilution. I. II. And III. J. Chromatogr. A 2002, 969, 17–47. [Google Scholar] [CrossRef] [PubMed]
- Hamieh, T. Temperature Dependence of the Polar and Lewis Acid-Base Properties of Poly Methyl Methacrylate Adsorbed on Silica via Inverse Gas Chromatography. Molecules 2024, 29, 1688. [Google Scholar] [CrossRef]
- Fowkes, F.M. Attractive forces at interfaces. Ind. Eng. Chem. 1964, 56, 40–52. [Google Scholar] [CrossRef]
- Fowkes, F.M. Determination of interfacial tensions, contact angles, and dispersion forces in surfaces by assuming additivity of intermolecular interactions in surfaces. J. Phys. Chem. 1962, 66, 382. [Google Scholar] [CrossRef]
- Fowkes, F.M. Additivity of intermolecular forces at interfaces. J. Phys. Chem. 1963, 67, 2538–2541. [Google Scholar] [CrossRef]
- Hamieh, T. Study of the temperature effect on the surface area of model organic molecules, the dispersive surface energy and the surface properties of solids by inverse gas chromatography. J. Chromatogr. A 2020, 1627, 461372. [Google Scholar] [CrossRef]
- Hamieh, T.; Ahmad, A.A.; Roques-Carmes, T.; Toufaily, J. New approach to determine the surface and interface thermodynamic properties of H-β-zeolite/rhodium catalysts by inverse gas chromatography at infinite dilution. Sci. Rep. 2020, 10, 20894. [Google Scholar] [CrossRef]
- Hamieh, T. New methodology to study the dispersive component of the surface energy and acid-base properties of silica particles by inverse gas chromatography at infinite dilution. J. Chromatogr. Sci. 2022, 60, 126–142. [Google Scholar] [CrossRef] [PubMed]
- Papirer, E.; Brendlé, E.; Ozil, F.; Balard, H. Comparison of the surface properties of graphite, carbon black and fullerene samples, measured by inverse gas chromatography. Carbon 1999, 37, 1265–1274. [Google Scholar] [CrossRef]
- Chung, D.L. Carbon Fiber Composites; Butterworth-Heinemann: Boston, MA, USA, 1994; pp. 3–65. [Google Scholar] [CrossRef]
- Donnet, J.B.; Bansal, R.C. Carbon Fibers, 2nd ed.; Marcel Dekker: New York, NY, USA, 1990; 584p. [Google Scholar] [CrossRef]
- Friedlander, H.N.; Peebles, L.H., Jr.; Brandrup, J.; Kirby, J.R. On the chromophore of polyacrylonitrile. VI. Mechanism of color formation in polyacrylonitrile. Macromolecules 1968, 1, 79–86. [Google Scholar] [CrossRef]
- Huang, X. Fabrication and Properties of Carbon Fibers. Materials 2009, 2, 2369–2403. [Google Scholar] [CrossRef]
- Qiao, Z.; Ding, C. Recent progress in carbon fibers for boosting electrocatalytic energy conversion. Ionics 2022, 28, 5259–5273. [Google Scholar] [CrossRef]
- Hamieh, T. Surface acid-base properties of carbon fibres. Adv. Powder Technol. 1997, 8, 279–289. [Google Scholar] [CrossRef]
- Le Vu, H.; Nguyen, S.H.; Dang, K.Q.; Pham, C.V.; Le, H.T. The Effect of Oxidation Temperature on Activating Commercial Viscose Rayon-Based Carbon Fibers to Make the Activated Carbon Fibers (ACFs). Mater. Sci. Forum 2020, 985, 171–176. [Google Scholar] [CrossRef]
- Liu, Y.; Gu, Y.; Wang, S.; Li, M. Optimization for testing conditions of inverse gas chromatography and surface energies of various carbon fiber bundles. Carbon Lett. 2023, 33, 909–920. [Google Scholar] [CrossRef]
- Pal, A.; Kondor, A.; Mitra, S.; Thua, K.; Harish, S.; Saha, B.B. On surface energy and acid-base properties of highly porous parent and surface treated activated carbons using inverse gas chromatography. J. Ind. Eng. Chem. 2019, 69, 432–443. [Google Scholar] [CrossRef]
- Hamieh, T. New Physicochemical Methodology for the Determination of the Surface Thermodynamic Properties of Solid Particles. AppliedChem 2023, 3, 229–255. [Google Scholar] [CrossRef]
- Sawyer, D.T.; Brookman, D.J. Thermodynamically based gas chromatographic retention index for organic molecules using salt-modified aluminas and porous silica beads. Anal. Chem. 1968, 40, 1847–1850. [Google Scholar] [CrossRef]
- Saint-Flour, C.; Papirer, E. Gas-solid chromatography. A method of measuring surface free energy characteristics of short carbon fibers. 1. Through adsorption isotherms. Ind. Eng. Chem. Prod. Res. Dev. 1982, 21, 337–341. [Google Scholar] [CrossRef]
- Saint-Flour, C.; Papirer, E. Gas-solid chromatography: Method of measuring surface free energy characteristics of short fibers. 2. Through retention volumes measured near zero surface coverage. Ind. Eng. Chem. Prod. Res. Dev. 1982, 21, 666–669. [Google Scholar] [CrossRef]
- Seulbee, L.; Lee, J.-H.; Kim, Y.-H.; Mahajan, R.L.; Park, S.-J. Surface energetics of graphene oxide and reduced graphene oxide determined by inverse gas chromatographic technique at infinite dilution at room temperature. J. Colloid Interface Sci. 2022, 628, 758–768. [Google Scholar]
- Brendlé, E.; Papirer, E. A new topological index for molecular probes used in inverse gas chromatography for the surface nanorugosity evaluation, 2. Application for the Evaluation of the Solid Surface Specific Interaction Potential. J. Colloid Interface Sci. 1997, 194, 217–224. [Google Scholar] [CrossRef] [PubMed]
- Brendlé, E.; Papirer, E. A new topological index for molecular probes used in inverse gas chromatography for the surface nanorugosity evaluation, 1. Method of Evaluation. J. Colloid Interface Sci. 1997, 194, 207–216. [Google Scholar] [CrossRef]
- Hamieh, T. Some Irregularities in the Evaluation of Surface Parameters of Solid Materials by Inverse Gas Chromatography. Langmuir 2023, 39, 17059–17070. [Google Scholar] [CrossRef] [PubMed]
- Gutmann, V. The Donor-Acceptor Approach to Molecular Interactions; Plenum: New York, NY, USA, 1978; 279p. [Google Scholar]
- Hamieh, T. The Effect of Temperature on the Surface Energetic Properties of Carbon Fibers Using Inverse Gas Chromatography. Crystals 2024, 14, 28. [Google Scholar] [CrossRef]
- Hamieh, T. New Progress on London Dispersive Energy, Polar Surface Interactions, and Lewis’s Acid-Base Properties of Solid Surfaces. Molecules 2024, 29, 949. [Google Scholar] [CrossRef]
- Hamieh, T. London Dispersive and Lewis Acid-Base Surface Energy of 2D Single-Crystalline and Polycrystalline Covalent Organic Frameworks. Crystals 2024, 14, 148. [Google Scholar] [CrossRef]
- Hamieh, T. Inverse Gas Chromatography to Characterize the Surface Properties of Solid Materials. Chem. Mater. 2024, 36, 2231–2244. [Google Scholar] [CrossRef]
- Van Oss, C.J.; Good, R.J.; Chaudhury, M.K. Additive and nonadditive surface tension components and the interpretation of contact angles. Langmuir 1988, 4, 884. [Google Scholar] [CrossRef]
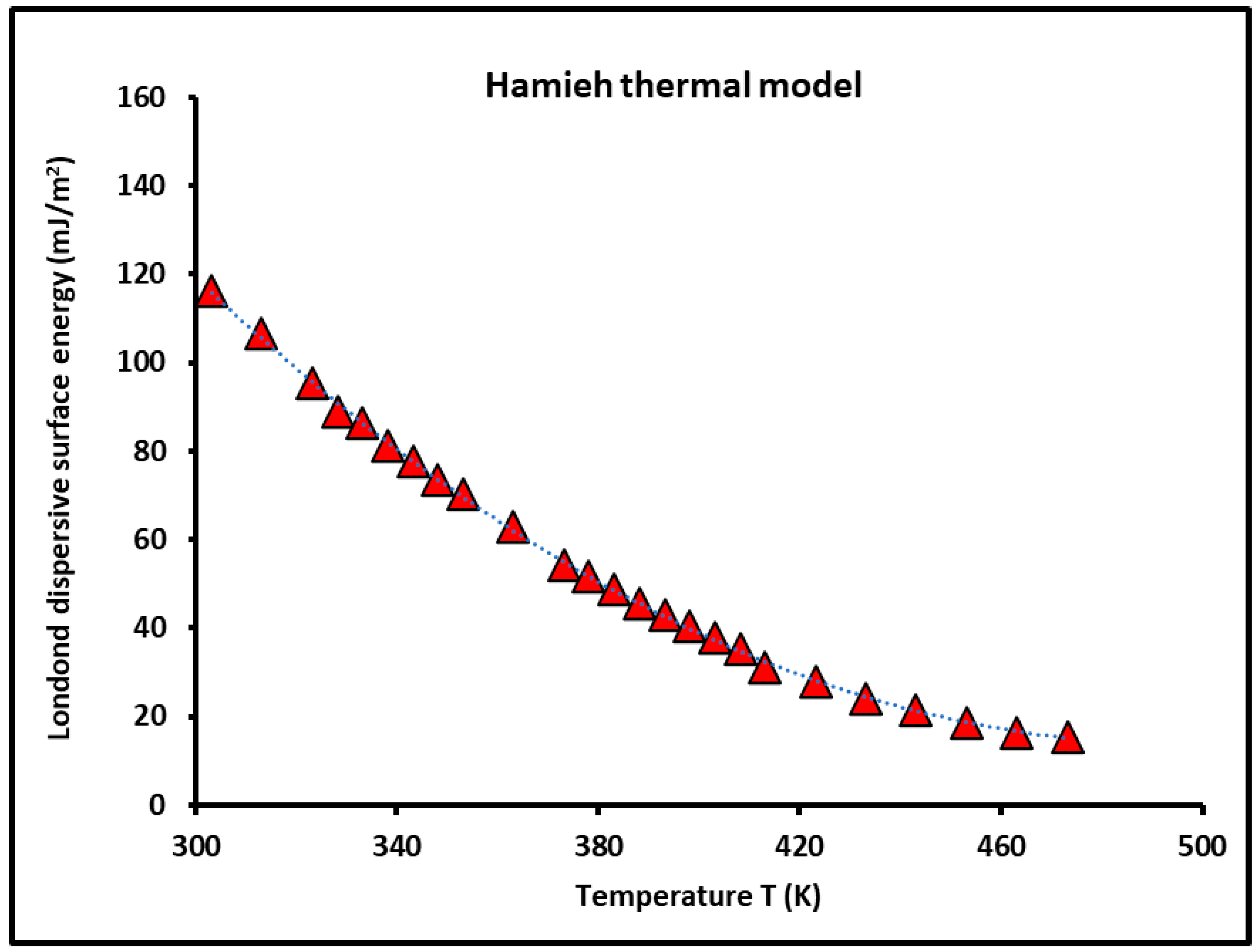
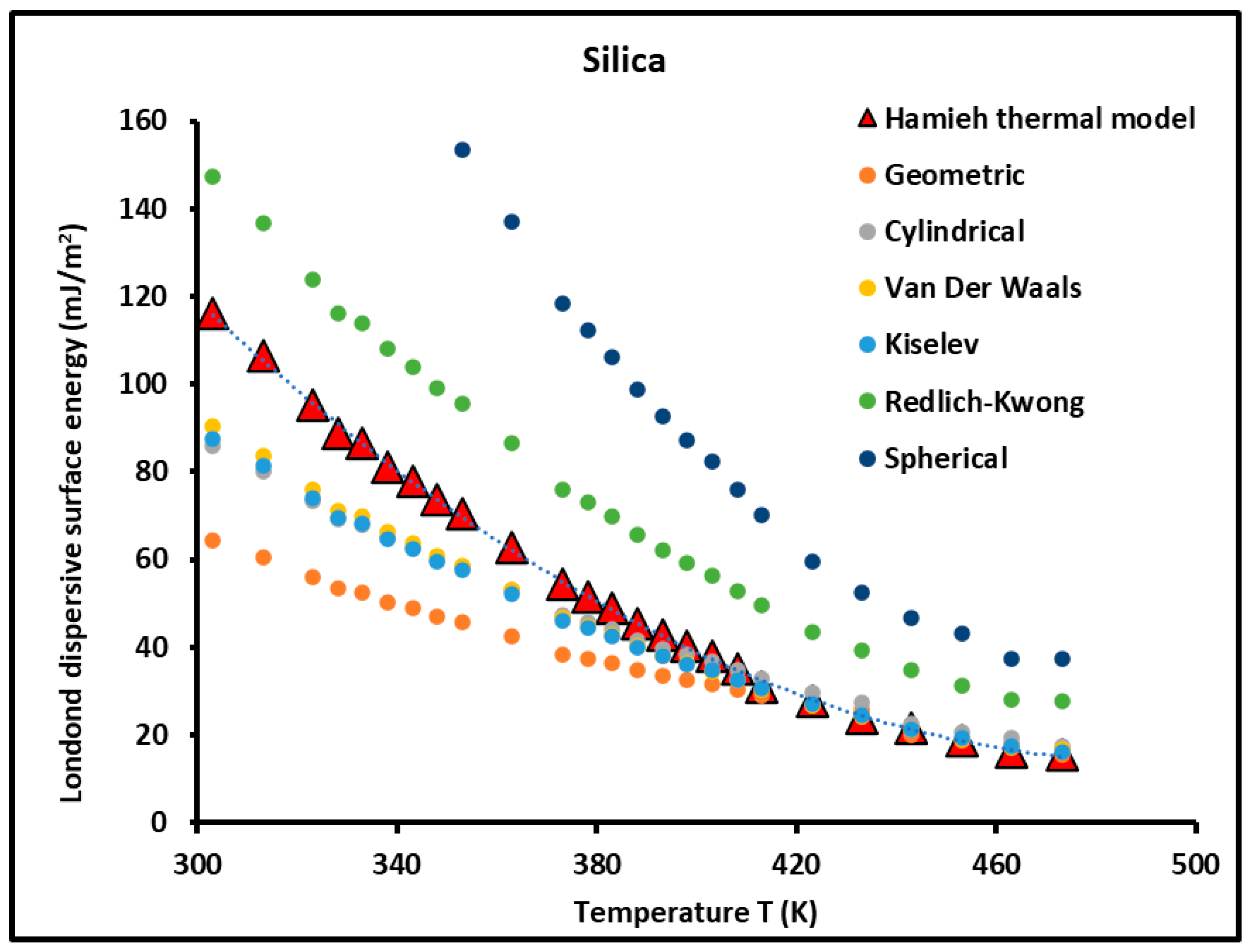
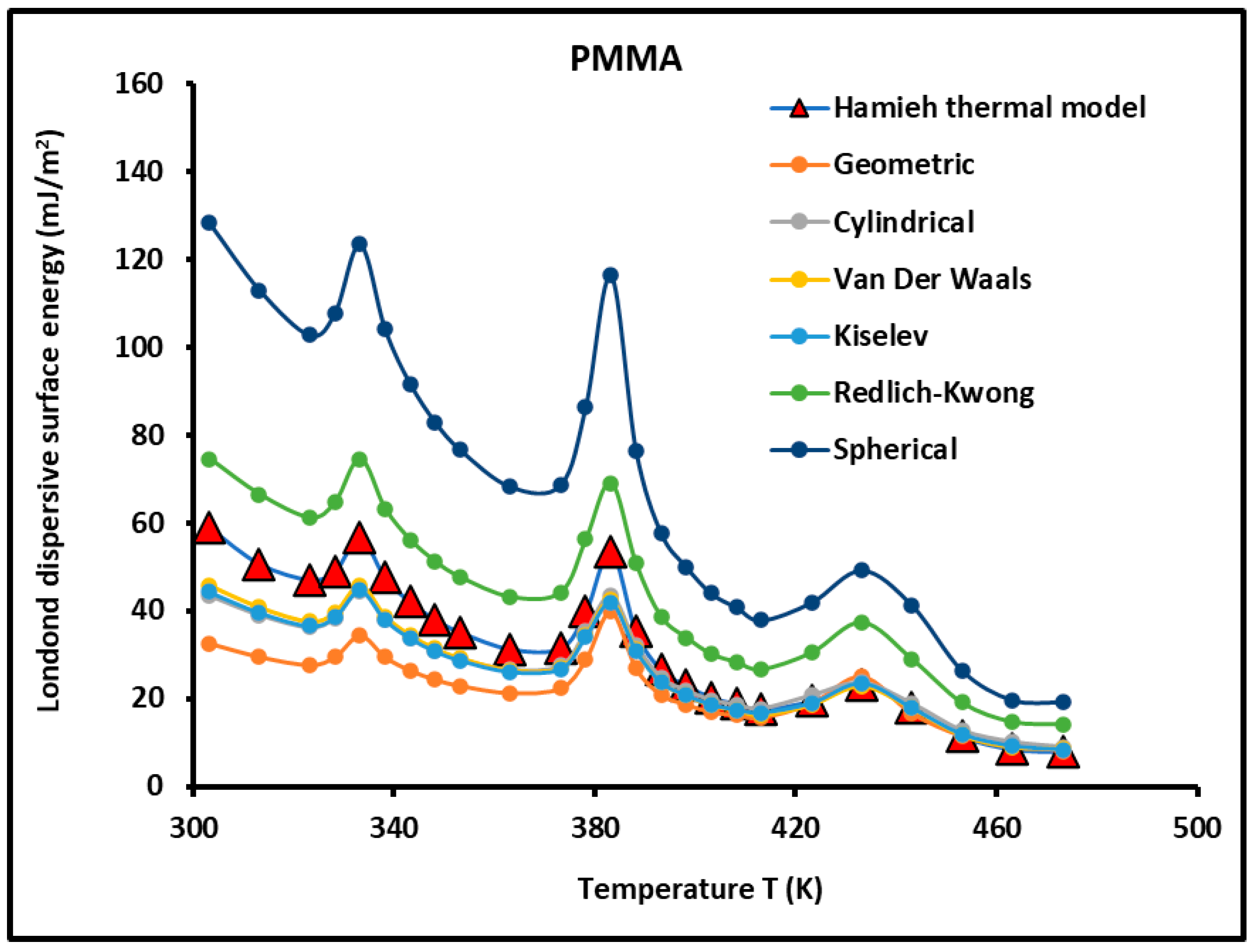
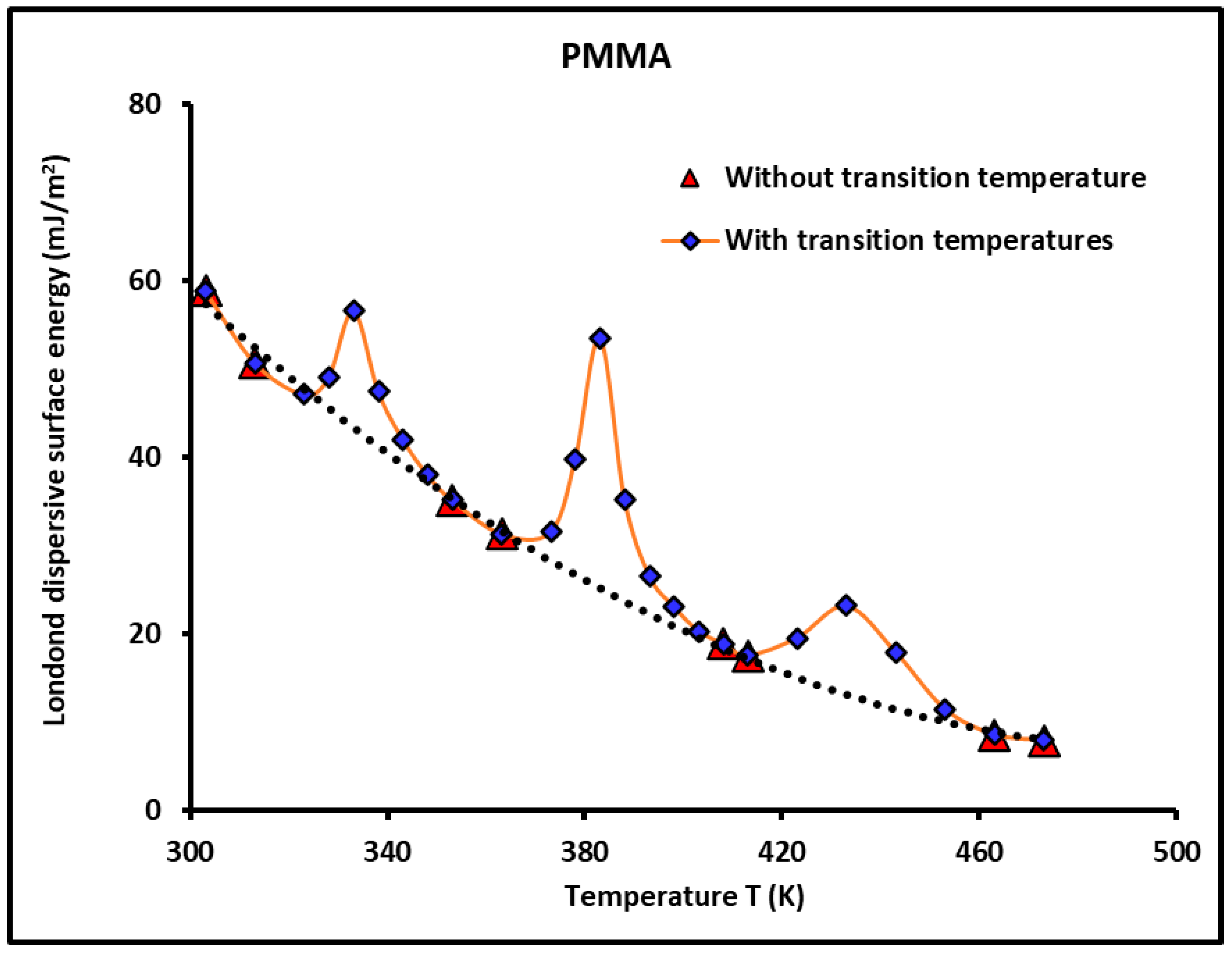


| T (K) | Hamieh Thermal Model | Geometric | Cylindrical | Van Der Waals | Kiselev | Redlich–Kwong | Spherical |
|---|---|---|---|---|---|---|---|
| 303.15 | 116.29 | 64.36 | 85.89 | 90.32 | 87.55 | 147.35 | 253.33 |
| 313.15 | 106.48 | 60.64 | 80.22 | 83.74 | 81.35 | 136.6 | 232.09 |
| 323.15 | 95.37 | 55.98 | 73.36 | 75.97 | 73.97 | 123.92 | 207.92 |
| 328.15 | 88.87 | 53.59 | 69.12 | 71.26 | 69.48 | 116.24 | 193.73 |
| 333.15 | 86.42 | 52.4 | 67.96 | 69.78 | 68.13 | 113.83 | 188.45 |
| 338.15 | 81.23 | 50.33 | 64.91 | 66.22 | 64.86 | 108.02 | 177.77 |
| 343.15 | 77.81 | 48.84 | 62.64 | 63.73 | 62.39 | 103.95 | 169.66 |
| 348.15 | 73.68 | 47.11 | 60.05 | 60.79 | 59.6 | 99.16 | 160.63 |
| 353.15 | 70.45 | 45.91 | 58.16 | 58.57 | 57.51 | 95.54 | 153.56 |
| 363.15 | 62.86 | 42.65 | 53.3 | 53.1 | 52.31 | 86.61 | 136.95 |
| 373.15 | 54.33 | 38.5 | 47.41 | 46.68 | 46.14 | 76.13 | 118.24 |
| 378.15 | 51.68 | 37.5 | 45.8 | 44.8 | 44.37 | 73.06 | 112.41 |
| 383.15 | 48.93 | 36.39 | 44.05 | 42.8 | 42.48 | 69.8 | 106.33 |
| 388.15 | 45.55 | 34.78 | 41.72 | 40.22 | 40.01 | 65.6 | 98.87 |
| 393.15 | 43.01 | 33.48 | 39.78 | 38.08 | 37.96 | 62.11 | 92.62 |
| 398.15 | 40.28 | 32.5 | 38.22 | 36.29 | 36.27 | 59.19 | 87.27 |
| 403.15 | 38.02 | 31.63 | 36.78 | 34.62 | 34.69 | 56.47 | 82.25 |
| 408.15 | 35.25 | 30.3 | 34.81 | 32.47 | 32.62 | 52.95 | 76.13 |
| 413.15 | 31.13 | 29.07 | 32.93 | 30.41 | 30.64 | 49.59 | 70.32 |
| 423.15 | 27.85 | 26.93 | 29.55 | 26.65 | 27.04 | 43.46 | 59.71 |
| 433.15 | 23.93 | 25.9 | 27.45 | 24.21 | 24.7 | 39.48 | 52.37 |
| 443.15 | 21.53 | 19.93 | 22.67 | 21.38 | 21.41 | 34.88 | 46.62 |
| 453.15 | 18.74 | 18.79 | 20.75 | 19.11 | 19.26 | 31.17 | 43.1 |
| 463.15 | 16.34 | 18.13 | 19.28 | 17.23 | 17.49 | 28.11 | 37.52 |
| 473.15 | 15.47 | 15.65 | 17.5 | 16.96 | 16.16 | 27.66 | 37.41 |
| T(K) | Hamieh Thermal Model | Geometric | Cylindrical | Van Der Waals | Kiselev | Redlich–Kwong | Spherical |
|---|---|---|---|---|---|---|---|
| 303.15 | 58.87 | 32.58 | 43.48 | 45.73 | 44.32 | 74.61 | 128.26 |
| 313.15 | 50.68 | 29.5 | 39.03 | 40.75 | 39.58 | 66.47 | 112.94 |
| 323.15 | 47.11 | 27.65 | 36.23 | 37.53 | 36.54 | 61.23 | 102.73 |
| 328.15 | 49.08 | 29.49 | 38.44 | 39.65 | 38.66 | 64.69 | 107.82 |
| 333.15 | 56.62 | 34.33 | 44.52 | 45.72 | 44.63 | 74.58 | 123.47 |
| 338.15 | 47.53 | 29.45 | 37.98 | 38.76 | 37.96 | 63.22 | 104.05 |
| 343.15 | 42.03 | 26.38 | 33.83 | 34.43 | 33.7 | 56.16 | 91.65 |
| 348.15 | 38.03 | 24.31 | 30.99 | 31.38 | 30.76 | 51.19 | 82.93 |
| 353.15 | 35.14 | 22.89 | 29 | 29.22 | 28.68 | 47.66 | 76.6 |
| 363.15 | 31.31 | 21.23 | 26.54 | 26.45 | 26.05 | 43.14 | 68.21 |
| 373.15 | 31.53 | 22.34 | 27.51 | 27.09 | 26.78 | 44.18 | 68.63 |
| 378.15 | 39.80 | 28.87 | 35.26 | 34.49 | 34.17 | 56.26 | 86.57 |
| 383.15 | 53.54 | 39.82 | 43.41 | 42.36 | 41.9 | 69.1 | 116.35 |
| 388.15 | 35.24 | 26.89 | 32.26 | 31.12 | 30.95 | 50.75 | 76.52 |
| 393.15 | 26.59 | 20.85 | 24.77 | 23.72 | 23.64 | 38.68 | 57.69 |
| 398.15 | 23.08 | 18.62 | 21.89 | 20.79 | 20.78 | 33.91 | 50.01 |
| 403.15 | 20.31 | 16.9 | 19.65 | 18.51 | 18.53 | 30.18 | 43.96 |
| 408.15 | 18.87 | 16.22 | 18.63 | 17.38 | 17.46 | 28.35 | 40.77 |
| 413.15 | 17.54 | 15.63 | 17.71 | 16.35 | 16.74 | 26.67 | 37.83 |
| 423.15 | 19.53 | 18.88 | 20.72 | 18.69 | 18.96 | 30.48 | 41.87 |
| 433.15 | 23.16 | 25.01 | 23.62 | 22.91 | 23.47 | 37.37 | 49.22 |
| 443.15 | 17.91 | 16.58 | 18.85 | 17.79 | 17.81 | 29.01 | 41.27 |
| 453.15 | 11.48 | 11.5 | 12.71 | 11.71 | 11.79 | 19.1 | 26.4 |
| 463.15 | 8.58 | 9.51 | 10.12 | 9.05 | 9.18 | 14.76 | 19.71 |
| 473.15 | 7.93 | 8.04 | 8.98 | 8.68 | 8.29 | 14.16 | 19.16 |
| T (K) | Hamieh Thermal Model | Geometric | Cylindrical | Van Der Waals | Kiselev | Redlich–Kwong | Spherical |
|---|---|---|---|---|---|---|---|
| 303.15 | 104.37 | 57.76 | 77.09 | 81.07 | 78.57 | 132.24 | 227.37 |
| 313.15 | 91.30 | 51.99 | 68.78 | 71.80 | 69.75 | 117.13 | 199.00 |
| 323.15 | 81.98 | 48.12 | 63.06 | 65.31 | 63.59 | 106.54 | 178.75 |
| 328.15 | 78.95 | 47.09 | 61.39 | 63.31 | 61.73 | 103.28 | 172.15 |
| 333.15 | 80.44 | 48.78 | 63.26 | 64.95 | 63.41 | 105.95 | 175.41 |
| 338.15 | 81.52 | 50.51 | 65.15 | 66.46 | 65.09 | 108.41 | 178.40 |
| 343.15 | 83.10 | 52.17 | 66.90 | 68.05 | 66.63 | 111.01 | 181.19 |
| 348.15 | 73.51 | 47.00 | 59.91 | 60.65 | 59.46 | 98.93 | 160.25 |
| 353.15 | 64.73 | 42.18 | 53.43 | 53.82 | 52.84 | 87.78 | 141.09 |
| 363.15 | 53.21 | 36.09 | 45.11 | 44.94 | 44.27 | 73.31 | 115.91 |
| 373.15 | 43.45 | 30.79 | 37.91 | 37.33 | 36.90 | 60.88 | 94.56 |
| 378.15 | 41.08 | 29.80 | 36.40 | 35.60 | 35.27 | 58.07 | 89.35 |
| 383.15 | 39.48 | 29.35 | 35.54 | 34.53 | 34.27 | 56.33 | 85.81 |
| 388.15 | 40.75 | 31.10 | 37.30 | 35.98 | 35.79 | 58.69 | 88.48 |
| 393.15 | 45.69 | 35.85 | 42.56 | 40.74 | 40.62 | 66.45 | 99.10 |
| 398.15 | 50.97 | 41.15 | 48.37 | 46.28 | 45.89 | 74.90 | 110.42 |
| 403.15 | 43.24 | 36.00 | 41.84 | 39.38 | 39.46 | 64.23 | 93.55 |
| 408.15 | 35.25 | 30.10 | 34.52 | 32.17 | 32.33 | 52.47 | 75.41 |
| 413.15 | 28.80 | 25.66 | 29.07 | 26.84 | 27.04 | 43.78 | 62.08 |
| 423.15 | 22.94 | 22.18 | 24.34 | 21.95 | 22.27 | 35.80 | 49.18 |
| 433.15 | 23.99 | 21.38 | 22.44 | 19.60 | 20.07 | 31.96 | 42.09 |
| 443.15 | 27.13 | 25.13 | 28.57 | 29.95 | 26.99 | 43.95 | 62.52 |
| 453.15 | 19.05 | 19.10 | 21.09 | 19.42 | 19.57 | 31.68 | 43.80 |
| 463.15 | 14.48 | 16.06 | 17.08 | 15.27 | 15.50 | 24.91 | 33.25 |
| 473.15 | 13.85 | 14.04 | 13.03 | 10.36 | 11.03 | 16.89 | 20.69 |
| Adsorption of PMMA on Silica for | |||||||
| T (K) | Hamieh Thermal Model | Geometric | Cylindrical | Van Der Waals | Kiselev | Redlich–Kwong | Spherical |
| 303.15 | 95.71 | 53.22 | 70.69 | 74.34 | 72.05 | 121.26 | 208.47 |
| 313.15 | 84.53 | 48.13 | 63.67 | 66.47 | 64.57 | 108.43 | 184.23 |
| 323.15 | 74.85 | 43.93 | 57.57 | 59.62 | 58.06 | 97.26 | 163.19 |
| 328.15 | 72.05 | 42.97 | 56.03 | 57.78 | 56.34 | 94.26 | 157.12 |
| 333.15 | 73.29 | 44.44 | 57.63 | 59.17 | 57.77 | 96.53 | 159.81 |
| 338.15 | 76.92 | 47.65 | 61.43 | 62.71 | 61.42 | 102.29 | 168.35 |
| 343.15 | 71.19 | 44.68 | 57.31 | 58.31 | 57.08 | 95.12 | 155.23 |
| 348.15 | 65.49 | 41.87 | 53.37 | 54.03 | 52.97 | 88.14 | 142.77 |
| 353.15 | 58.91 | 38.09 | 48.43 | 49.22 | 48.08 | 80.29 | 129.15 |
| 363.15 | 48.96 | 33.21 | 41.51 | 41.36 | 40.74 | 67.46 | 106.65 |
| 373.15 | 38.16 | 27.04 | 33.3 | 32.78 | 32.41 | 53.47 | 83.06 |
| 378.15 | 36.12 | 26.2 | 32 | 31.31 | 31.01 | 51.06 | 78.57 |
| 383.15 | 38.33 | 28.5 | 34.51 | 33.53 | 33.28 | 54.69 | 83.32 |
| 388.15 | 42.68 | 32.58 | 39.08 | 37.7 | 37.5 | 61.49 | 92.7 |
| 393.15 | 52.06 | 40.83 | 48.5 | 46.42 | 46.28 | 75.72 | 112.92 |
| 398.15 | 46.88 | 37.86 | 44.5 | 42.24 | 42.22 | 68.89 | 101.55 |
| 403.15 | 40.96 | 34.09 | 39.63 | 37.3 | 37.37 | 60.84 | 88.61 |
| 408.15 | 31.95 | 27.28 | 31.29 | 29.16 | 29.31 | 47.56 | 68.36 |
| 413.15 | 24.69 | 22.04 | 24.95 | 23.01 | 23.19 | 37.52 | 53.18 |
| 423.15 | 20.39 | 19.71 | 21.63 | 19.51 | 19.79 | 31.82 | 43.71 |
| 433.15 | 26.55 | 23.63 | 24.79 | 21.66 | 22.18 | 35.31 | 46.51 |
| 443.15 | 17.74 | 16.42 | 18.67 | 17.61 | 17.64 | 28.73 | 40.87 |
| 453.15 | 14.20 | 14.35 | 15.85 | 14.61 | 14.71 | 23.82 | 32.94 |
| 463.15 | 12.12 | 13.44 | 14.29 | 12.78 | 12.97 | 20.84 | 27.82 |
| 473.15 | 11.41 | 11.57 | 12.92 | 12.85 | 11.93 | 20.38 | 27.57 |
| Adsorption of PMMA on Silica for | |||||||
| T (K) | Hamieh Thermal Model | Geometric | Cylindrical | Van Der Waals | Kiselev | Redlich–Kwong | Spherical |
| 303.15 | 83.96 | 46.46 | 62.01 | 65.21 | 63.21 | 106.39 | 182.9 |
| 313.15 | 76.57 | 43.6 | 57.67 | 60.22 | 58.49 | 98.23 | 166.91 |
| 323.15 | 66.94 | 39.29 | 51.49 | 53.33 | 51.93 | 87 | 145.96 |
| 328.15 | 69.57 | 41.49 | 54.1 | 55.79 | 54.4 | 91.02 | 151.71 |
| 333.15 | 74.62 | 45.24 | 58.68 | 60.25 | 58.82 | 98.29 | 162.72 |
| 338.15 | 69.65 | 43.16 | 55.67 | 56.79 | 55.62 | 92.64 | 152.46 |
| 343.15 | 64.16 | 40.28 | 51.65 | 52.55 | 51.44 | 85.72 | 139.91 |
| 348.15 | 58.34 | 37.3 | 47.55 | 48.14 | 47.19 | 78.53 | 127.2 |
| 353.15 | 52.02 | 33.95 | 42.98 | 43.21 | 42.47 | 70.48 | 113.27 |
| 363.15 | 43.21 | 29.31 | 36.63 | 36.5 | 35.96 | 59.54 | 94.14 |
| 373.15 | 33.20 | 23.52 | 28.97 | 28.52 | 28.19 | 46.52 | 72.26 |
| 378.15 | 30.44 | 22.08 | 26.97 | 26.38 | 26.13 | 43.04 | 66.22 |
| 383.15 | 35.11 | 26.1 | 31.61 | 30.71 | 30.48 | 50.09 | 76.31 |
| 388.15 | 50.63 | 38.41 | 46.07 | 44.44 | 44.2 | 72.48 | 109.28 |
| 393.15 | 40.82 | 32.01 | 38.03 | 36.4 | 36.29 | 59.37 | 88.54 |
| 398.15 | 34.59 | 27.92 | 32.83 | 31.17 | 31.15 | 50.84 | 74.96 |
| 403.15 | 29.88 | 24.86 | 28.9 | 27.21 | 27.26 | 44.38 | 64.64 |
| 408.15 | 24.15 | 20.61 | 23.64 | 22.04 | 22.15 | 35.94 | 51.66 |
| 413.15 | 19.32 | 17.21 | 19.5 | 18.01 | 18.14 | 29.37 | 41.65 |
| 423.15 | 16.27 | 15.72 | 17.26 | 15.57 | 15.8 | 25.39 | 34.89 |
| 433.15 | 27.30 | 24.3 | 25.49 | 22.26 | 22.8 | 36.31 | 47.82 |
| 443.15 | 17.37 | 16.08 | 18.28 | 17.25 | 17.27 | 28.14 | 40.03 |
| 453.15 | 12.73 | 12.76 | 14.1 | 12.99 | 13.08 | 21.19 | 29.29 |
| 463.15 | 9.74 | 10.79 | 11.48 | 10.27 | 10.42 | 16.75 | 22.36 |
| 473.15 | 9.17 | 9.30 | 10.39 | 10.04 | 9.59 | 16.38 | 22.16 |
| Adsorption of PMMA on Silica for | |||||||
| T (K) | Hamieh Thermal Model | Geometric | Cylindrical | Van Der Waals | Kiselev | Redlich–Kwong | Spherical |
| 303.15 | 80.49 | 44.54 | 59.44 | 62.52 | 60.6 | 101.99 | 175.35 |
| 313.15 | 72.76 | 41.43 | 54.81 | 57.22 | 55.58 | 93.35 | 158.6 |
| 323.15 | 63.27 | 37.13 | 48.66 | 50.4 | 49.07 | 82.22 | 137.94 |
| 328.15 | 65.85 | 39.28 | 51.21 | 52.81 | 51.49 | 86.15 | 143.6 |
| 333.15 | 70.99 | 43.04 | 55.83 | 57.32 | 55.96 | 93.51 | 154.82 |
| 338.15 | 64.89 | 40.21 | 51.86 | 52.91 | 51.82 | 86.31 | 142.04 |
| 343.15 | 59.74 | 37.5 | 48.09 | 48.93 | 47.9 | 79.81 | 130.25 |
| 348.15 | 54.14 | 34.5 | 44.12 | 44.68 | 43.79 | 72.87 | 117.65 |
| 353.15 | 49.63 | 32.34 | 40.97 | 41.27 | 40.52 | 67.32 | 108.2 |
| 363.15 | 40.84 | 27.7 | 34.62 | 34.5 | 33.98 | 56.27 | 88.97 |
| 373.15 | 31.81 | 22.54 | 27.76 | 27.33 | 27.02 | 44.58 | 69.25 |
| 378.15 | 32.08 | 23.19 | 28.37 | 27.82 | 27.54 | 45.38 | 69.63 |
| 383.15 | 36.69 | 27.28 | 33.04 | 32.1 | 31.86 | 52.36 | 79.76 |
| 388.15 | 53.25 | 40.64 | 48.75 | 47.02 | 46.77 | 76.68 | 115.61 |
| 393.15 | 46.15 | 39.19 | 43.00 | 41.16 | 41.03 | 67.13 | 100.11 |
| 398.15 | 40.22 | 32.46 | 38.16 | 36.24 | 36.21 | 59.1 | 87.13 |
| 403.15 | 29.26 | 24.35 | 28.31 | 26.65 | 26.7 | 43.47 | 63.32 |
| 408.15 | 22.52 | 19.22 | 22.05 | 20.55 | 20.66 | 33.52 | 48.18 |
| 413.15 | 18.87 | 16.79 | 19.04 | 17.59 | 17.72 | 28.7 | 40.63 |
| 423.15 | 16.30 | 15.75 | 17.29 | 15.6 | 15.82 | 25.44 | 34.96 |
| 433.15 | 27.59 | 24.55 | 25.75 | 22.49 | 23.04 | 36.68 | 48.31 |
| 443.15 | 15.59 | 14.42 | 16.41 | 15.48 | 15.5 | 25.25 | 35.92 |
| 453.15 | 10.59 | 10.61 | 11.72 | 10.8 | 10.88 | 17.62 | 24.36 |
| 463.15 | 8.16 | 9.04 | 9.62 | 8.6 | 8.73 | 14.03 | 18.74 |
| 473.15 | 7.66 | 7.77 | 8.68 | 8.39 | 8.01 | 13.68 | 18.51 |
| Adsorption of PMMA on Silica for | |||||||
| T(K) | Hamieh Thermal Model | Geometric | Cylindrical | Van Der Waals | Kiselev | Redlich–Kwong | Spherical |
| 303.15 | 75.92 | 42.01 | 56.07 | 58.97 | 57.16 | 96.2 | 165.4 |
| 313.15 | 67.65 | 38.52 | 50.96 | 53.21 | 51.68 | 86.8 | 147.47 |
| 323.15 | 58.85 | 34.54 | 45.27 | 46.89 | 45.65 | 76.4 | 128.33 |
| 328.15 | 61.70 | 36.8 | 47.98 | 49.48 | 48.24 | 80.71 | 134.54 |
| 333.15 | 67.28 | 40.79 | 52.91 | 54.33 | 53.04 | 88.62 | 146.73 |
| 338.15 | 61.50 | 38.11 | 49.15 | 50.15 | 49.12 | 81.8 | 134.63 |
| 343.15 | 56.07 | 35.19 | 45.14 | 45.93 | 44.96 | 74.92 | 122.27 |
| 348.15 | 50.99 | 32.6 | 41.56 | 42.08 | 41.25 | 68.64 | 111.18 |
| 353.15 | 46.12 | 30.05 | 38.07 | 38.35 | 37.65 | 62.55 | 100.54 |
| 363.15 | 37.96 | 25.75 | 32.18 | 32.07 | 31.59 | 52.31 | 82.71 |
| 373.15 | 28.47 | 20.17 | 24.84 | 24.46 | 24.18 | 39.9 | 61.97 |
| 378.15 | 26.94 | 19.54 | 23.87 | 23.36 | 23.13 | 38.09 | 58.61 |
| 383.15 | 40.51 | 30.1 | 36.45 | 35.41 | 35.15 | 57.76 | 87.99 |
| 388.15 | 55.89 | 42.66 | 51.17 | 49.35 | 49.09 | 80.5 | 121.36 |
| 393.15 | 47.51 | 37.26 | 44.26 | 42.37 | 42.24 | 69.1 | 103.05 |
| 398.15 | 39.16 | 31.61 | 37.16 | 35.29 | 35.26 | 57.55 | 84.85 |
| 403.15 | 28.98 | 24.11 | 28.03 | 18.92 | 26.44 | 43.04 | 62.69 |
| 408.15 | 22.77 | 19.43 | 22.29 | 20.78 | 20.88 | 33.88 | 48.71 |
| 413.15 | 18.42 | 16.41 | 18.59 | 17.17 | 17.3 | 28 | 39.71 |
| 423.15 | 15.79 | 15.26 | 16.75 | 15.11 | 15.33 | 24.65 | 33.87 |
| 433.15 | 25.97 | 24.38 | 25.61 | 22.38 | 22.93 | 36.5 | 48.15 |
| 443.15 | 15.28 | 14.14 | 16.09 | 15.18 | 15.2 | 24.76 | 35.23 |
| 453.15 | 10.19 | 10.21 | 11.28 | 10.4 | 10.47 | 16.96 | 23.44 |
| 463.15 | 7.71 | 8.58 | 9.11 | 8.13 | 8.26 | 13.26 | 17.7 |
| 473.15 | 7.39 | 7.49 | 8.37 | 8.09 | 7.72 | 13.19 | 17.85 |
| Beta-Relaxation | Glass Transition | Liquid–Liquid | |
|---|---|---|---|
| 0.31 | 83.10 | 50.97 | 27.13 |
| 0.54 | 76.92 | 52.06 | 26.55 |
| 0.83 | 74.62 | 50.63 | 17.37 |
| 0.98 | 70.99 | 53.26 | 15.59 |
| 1.0 | 67.28 | 55.89 | 25.97 |
| PMMA | 56.62 | 53.54 | 23.16 |
| T (K) | R2 | |||
|---|---|---|---|---|
| 303.15 | = −38.63 + 116.32 | 0.994 | 38.63 | 116.32 |
| 313.15 | = −34.92 + 104.49 | 0.9779 | 34.92 | 104.49 |
| 323.15 | = −33.44 + 93.92 | 0.985 | 33.44 | 93.92 |
| 328.15 | = −23.85 + 87.36 | 0.9569 | 23.85 | 87.36 |
| 348.15 | = −23.40 + 76.95 | 0.9293 | 23.40 | 76.95 |
| 353.15 | = −23.26 + 71.15 | 0.9865 | 23.26 | 71.15 |
| 363.15 | = −22.75 + 61.70 | 0.9836 | 22.75 | 61.70 |
| 373.15 | = −23.19 + 52.36 | 0.9658 | 23.19 | 52.36 |
| 413.15 | = −13.59 + 31.82 | 0.9765 | 13.59 | 31.82 |
| 423.15 | = −11.84 + 27.13 | 0.9751 | 11.84 | 27.13 |
| 463.15 | = −8.69 + 16.72 | 0.9918 | 8.69 | 16.72 |
| 473.15 | = −8.27 + 15.87 | 0.9904 | 8.27 | 15.87 |
| T (K) | |||
|---|---|---|---|
| 303.15 | = −40.37 + 116.29 | 40.37 | 116.29 |
| 363.15 | = −37.96 + 62.86 | 37.96 | 62.86 |
| 473.15 | = −8.08 + 15.47 | 8.08 | 15.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamieh, T. The Effect of Temperature on the London Dispersive and Lewis Acid-Base Surface Energies of Polymethyl Methacrylate Adsorbed on Silica by Inverse Gas Chromatography. Thermo 2024, 4, 202-221. https://doi.org/10.3390/thermo4020012
Hamieh T. The Effect of Temperature on the London Dispersive and Lewis Acid-Base Surface Energies of Polymethyl Methacrylate Adsorbed on Silica by Inverse Gas Chromatography. Thermo. 2024; 4(2):202-221. https://doi.org/10.3390/thermo4020012
Chicago/Turabian StyleHamieh, Tayssir. 2024. "The Effect of Temperature on the London Dispersive and Lewis Acid-Base Surface Energies of Polymethyl Methacrylate Adsorbed on Silica by Inverse Gas Chromatography" Thermo 4, no. 2: 202-221. https://doi.org/10.3390/thermo4020012
APA StyleHamieh, T. (2024). The Effect of Temperature on the London Dispersive and Lewis Acid-Base Surface Energies of Polymethyl Methacrylate Adsorbed on Silica by Inverse Gas Chromatography. Thermo, 4(2), 202-221. https://doi.org/10.3390/thermo4020012








