Optimizing of Traffic-Signal Timing Based on the FCIC-PI—A Surrogate Measure for Fuel Consumption
Abstract
:1. Introduction
2. Literature Review
- Evaluating a surrogate objective function (the FCIC-PI) that balances mobility and sustainability metrics using high-resolution traffic and sustainability data. Previous studies did not use this objective function for optimization purposes. Additionally, very few signal-timing optimizations were carried out with microscopic simulation models that were calibrated and validated with the same level of detail and rigor.
- That the deployed objective function can account for any operational conditions (e.g., percentage of heavy vehicles) that impact sustainability metrics. This is a nontrivial contribution that has not been seen before, considering the significance of those various operational conditions on sustainability metrics.
- Assessing the impact of the profound presence of heavy vehicles on side streets on the optimization results. This is a critical contribution because current signal-timing optimization practices aim at providing signal priority to major-road traffic to minimize mobility metrics. Such a practice may ignore the significant sustainability footprint of side streets with high heavy-vehicle traffic.
3. Overview of FCIC-PI
- Di—is an average delay in pcus-hours per hour on the ith link (or movement) of the network;
- Ci—is an average number of pcus stops per second on the ith link (or movement) of the network;
- n—is the number of links or movements included in the optimization;
- K—is the weighting factor, which was defined, for a stopping event, by Stevanovic et al. [12] as
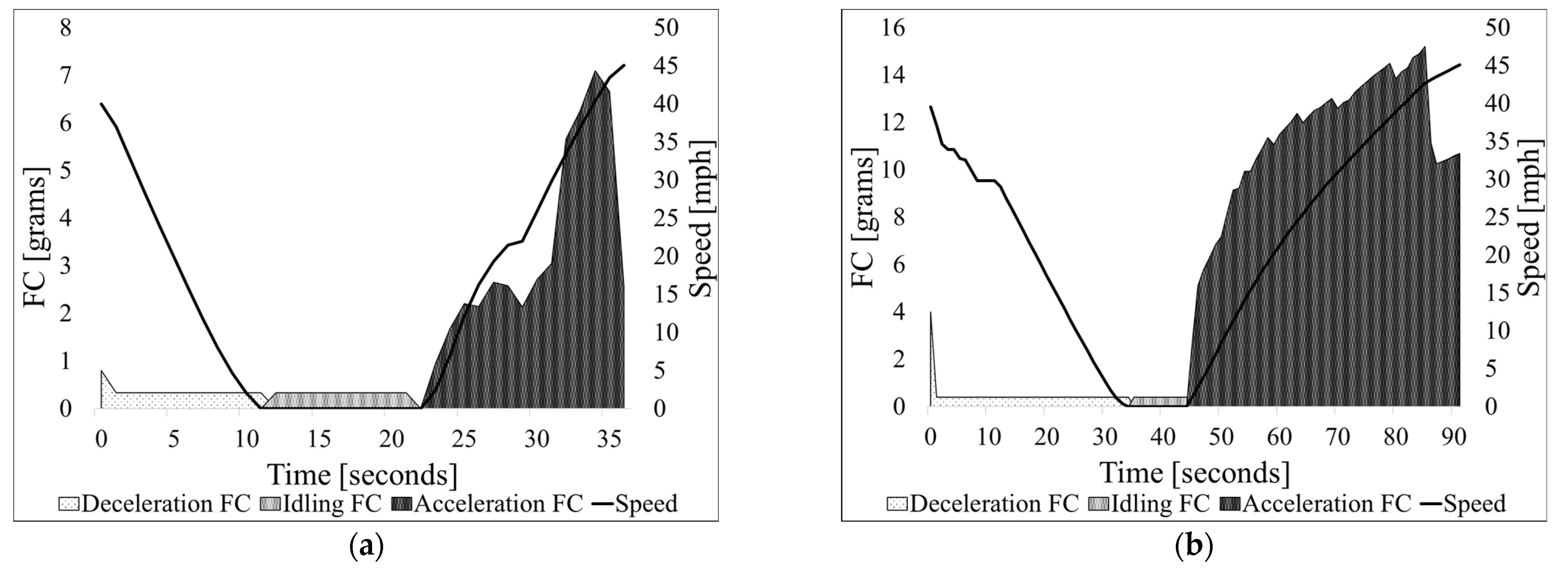
- FCD—fuel consumed during the deceleration phase (grams);
- FCI—fuel consumed during the idling phase (grams);
- FCA—fuel consumed during the acceleration phase (grams);
- TI—total idling time (seconds).
- Di—is the total stop delay at movement i;
- Si—is the total number of stops at movement i.
4. Methodology
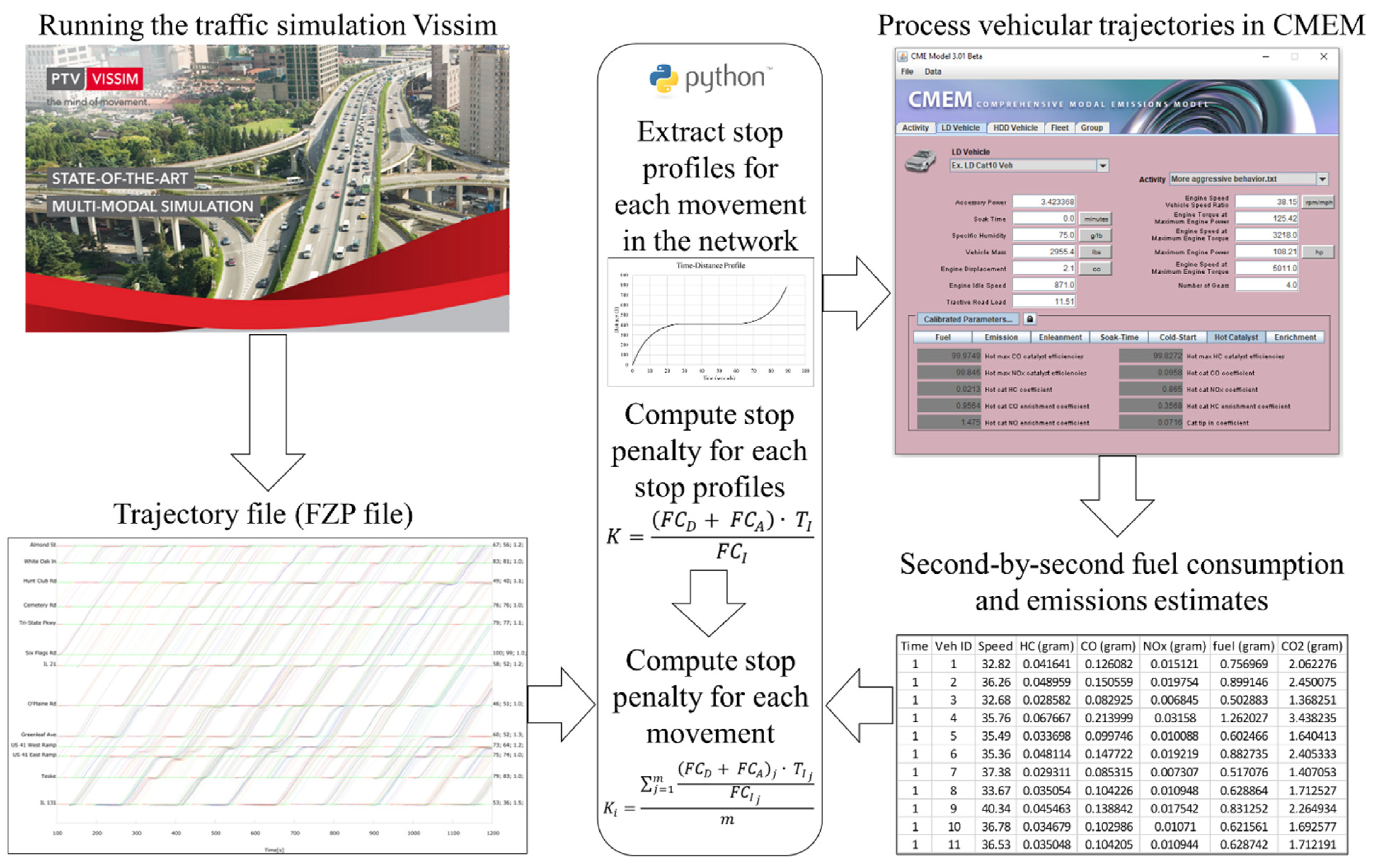
4.1. Vissim
4.2. CMEM
4.3. Computation of Stop Penalty
4.4. Retime Optimization Tool
| Algorithm 1: Description of the genetic algorithm optimization coded in the Retime optimization tool. |
| Step 0: Initializing G, total number of generations T, total number of timing plans per generation i, current number of population i = 0 Generation of initial population p of timing plans tp, k ∈ [1, …, T]
Evaluation of tp p, k [1, …, T]
fitness = max(fitness, …, fitness) IF (i = G) Stop and RETURN tpp ELSE GO TO Step 3 Step 3: Generating New Population i = i + 1 Generation of new population p
|
4.5. Retime Stochastic Optimizations
- Scenario 1 represented moderate operational conditions, which were the actual conditions from the case-study site (discussed later). This scenario optimized all four signal-timing parameters (cycle length, offsets, splits, and phase sequence). The cycle-length search range was 40–200 s. Scenarios 2 and 3 also represented moderate operational conditions where the differences were in the parameters optimized, the cycle-length search range, and the movements included, as briefly described below.
- Scenario 2 aimed to fix the phase sequence as it was in the field and narrow the cycle-length search range to 40–160 s. In addition to its importance in revealing the impact of not optimizing the phase sequence and having a narrower cycle-length search range, this scenario was needed because the government agency operating the case-study corridor prefers to have leading left-turns on all signals.
- Scenario 3 followed the settings of scenario 2 to optimize through-traffic movements only on major and minor streets. This scenario added significant importance to through-traffic movements, especially on minor streets, compared to the case where left-turn movements on a major street were optimized. That aligns with most transportation agencies’ standard practices, prioritizing through-traffic movements to provide good signal coordination.
- Scenario 4 assumed an increased percentage of heavy vehicles (from 0% to 15%), but only in the vehicular distribution of the side streets. This increase was applied only for four-leg intersections, and only through-traffic movements saw increased heavy-vehicle traffic. It was intended that this scenario would give higher weight to side-street traffic and open side-street greens more to reduce the FC of such heavily loaded truck movements. For example, a standard PI (which consists only of delays and stops) would not pick up such a change, as delays and stops do not contain information about heavy trucks producing extra FC. At the same time, the FCIC-PI is “equipped” to do so through additional “knowledge” embedded in specific K factors (of heavy-traffic side-street movements).
- Scenario 5 also increased the percentage of heavy vehicles in the vehicular distribution, but this time, it was carried out for the westbound direction of the major road. Similarly to the second scenario, the percentage of heavy vehicles was set to 15%. We note that those 15% of heavy vehicles traveled across the entire corridor in the westbound direction, thus representing a heavy traffic route.
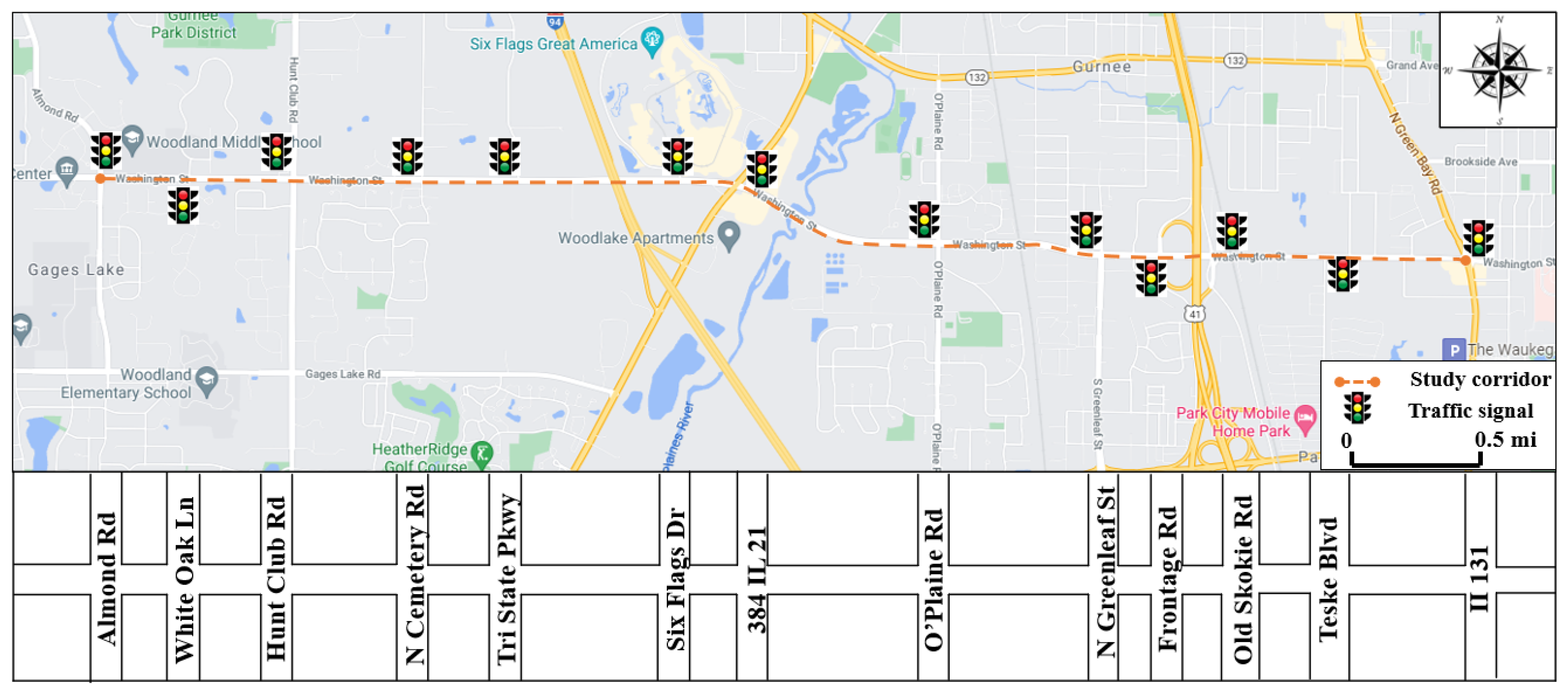
5. Case Study
6. Results and Discussion
- In most cases, current studies used an isolated hypothetical intersection with a simple phasing design to assess new methodologies for optimizing traffic signals. The outcomes of such methodologies can be considered unreliable because their testbeds did not represent coordination designed in most urban areas. Hence, our study evaluated the proposed optimization methodology by modeling and optimizing a corridor with a realistic scale to what is typically found in the field.
- This study has shown that most emissions do not correlate linearly with FC. The exception was CO2, as discussed earlier in this paper. Such a finding has not been reached by any of the previous relevant optimization studies. It is important to note that the optimization goal may not need to minimize all sustainability metrics simultaneously. Instead, various urban areas or corridors can have different optimization objectives depending on the major detrimental sustainability metric in each area.
- Most of the previous notable studies were time-consuming and required intensive computational loads. Hence, this study evaluated deploying the FCIC-PI, which can be utilized simply by modifying the stop penalties in commonly used optimization programs (e.g., Vistro and Synchro). Such programs are known for their practicality and user-friendly interfaces. It is crucial to note that a few optimization methods were proposed to reduce computational optimization load. Nevertheless, those methods still consume more time and processing loads than what might be practical to implement in the field.
- Many previous articles optimized one or two signal parameters (e.g., cycle length and offset). Such a practice can be partially attributed to operating agencies’ policies, which restrict what signal parameters can be modified and by how much. An example is the LCDOT, the operating agency of the testbed (Washington Street) in this study. The LCDOT does not allow changing of phase sequencing in optimizing signal parameters. For evaluation purposes, however, this study performed a scenario (#1) that optimized all four signal parameters and showed that optimizing the phase sequence resulted in an additional ~3% savings in FC. Such findings might encourage agencies to seriously consider optimizing all signal parameters.
- Although there has been a consensus in the literature on the significant impacts of various operating conditions (e.g., heavy vehicles) on sustainability measures, none of the previous studies has investigated the impacts of such operating conditions on FC-saving results. Hence, one of the significant findings in this study is that including the impact of heavy vehicles on FC in the optimization process results in ~2–4% additional FC savings compared to cases where all vehicles are treated equally in terms of FC footprint. Future research should investigate the impacts of other conditions (e.g., driving behavior, road gradient, etc.).
- Online optimizations have deployed and demonstrated their power in many transportation applications. However, most of the current signal-timing optimization to improve sustainability in the literature cannot be connected to online data sources (e.g., an automated traffic signal performance measure or “ATSPM”). Unlike those studies, our study can simulate large networks with real-time data, as detailed in the following subsection.
6.1. Integration of FCIC-PI Methodology in ATSPMs
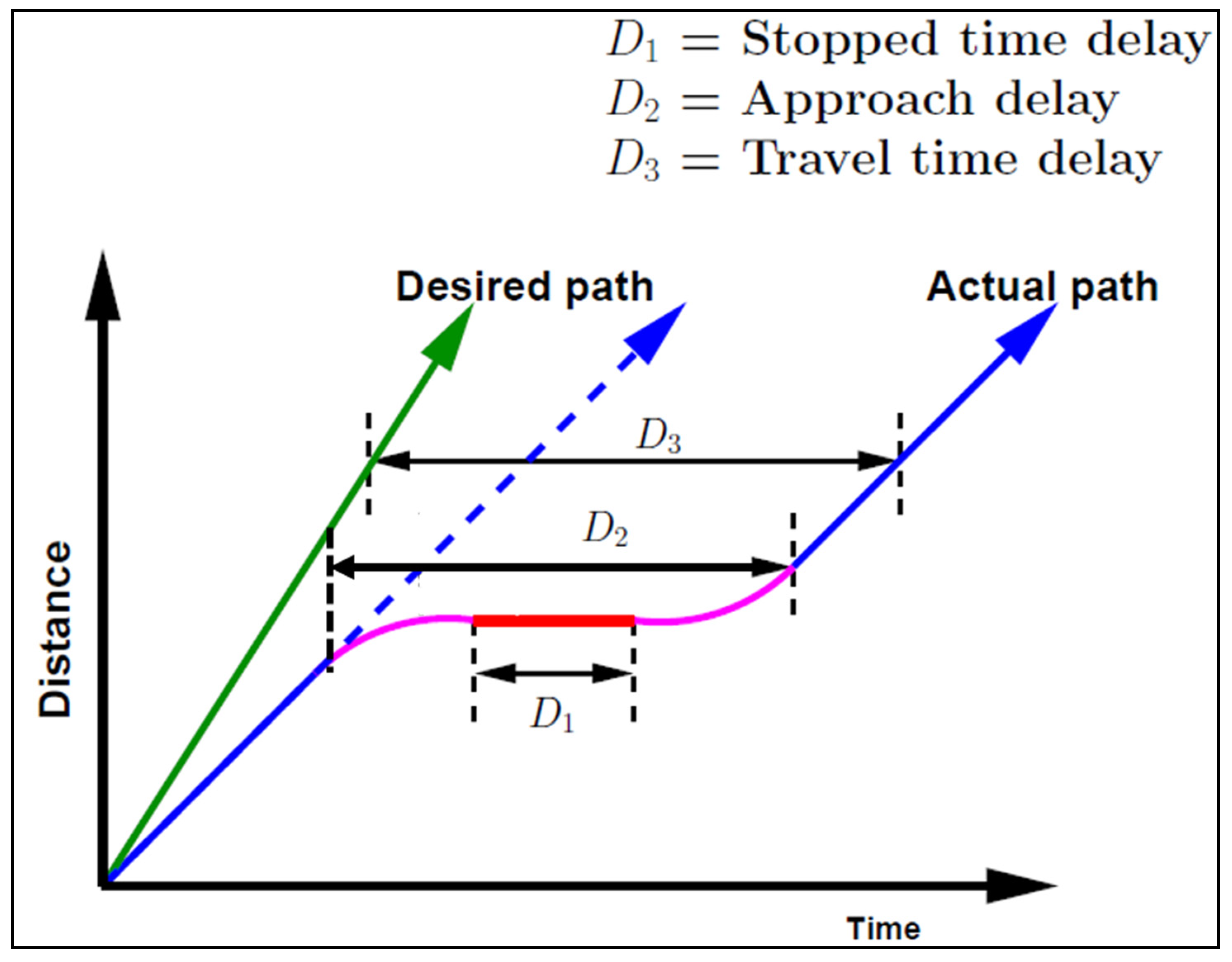
6.1.1. Retrieving Stop Delay
6.1.2. Calculating Stop Penalties
6.1.3. Retrieving Number of Stops
- i: eligible movement in the network with the estimated approach delay and percentage of arrivals on red;
- n: total number of eligible movements;
- D2: approach delay (s);
- FC: fuel consumption (grams or gallons);
- D: deceleration (s or hr);
- I: idling (s or hr);
- A: acceleration (s or hr);
- TI: idling duration (s or hr);
- V: traffic volume (veh/hr);
- AOR: percentage of arrivals on red (%/100).
7. Conclusions and Future Research
- The FCIC-PI seems to be a reliable surrogate objective function for fuel consumption when used to optimize traffic-signal timing. This novel PI combines conventional traffic-performance measures (stop delay and number of stops) with a set of factors representing each stop’s fuel-consumption weight.
- Using the FCIC-PI saves significant computation time that other approaches must endure because it does not require fuel-consumption estimates from postprocessing vehicular trajectories when optimizing signal timing. Hence, the FCIC-PI can be practical for regular optimizations of signal timing.
- The surrogate objective function used in the optimization resulted in a minimum savings of 8% in fuel consumption. Such savings were significantly increased to 14% (accompanied by significant improvements in the mobility measures) when the impact of a high percentage of heavy vehicles in the fleet was considered in the optimization.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Koonce, P.; Rodegerdts, L. Traffic Signal Timing Manual; No. FHWA-HOP-08-024; United States Federal Highway Administration: Washington, DC, USA, 2008. [Google Scholar]
- Cai, M.; Yin, Y.; Xie, M. Prediction of hourly air pollutant concentrations near urban arterials using artificial neural network approach. Transp. Res. Part D Transp. Environ. 2009, 14, 32–41. [Google Scholar] [CrossRef]
- Rakha, H.; Ding, Y. Impact of stops on vehicle fuel consumption and emissions. J. Transp. Eng. 2003, 129, 23–32. [Google Scholar] [CrossRef]
- Alshayeb, S.; Stevanovic, A.; Effinger, J.R. Investigating Impacts of Various Operational Conditions on Fuel Consumption and Stop Penalty at Signalized Intersections. Int. J. Transp. Sci. Technol. 2021, 11, 690–710. [Google Scholar] [CrossRef]
- Park, B.; Messer, C.J.; Urbanik, T. Traffic signal optimization program for oversaturated conditions: Genetic algorithm approach. Transp. Res. Rec. 1999, 1683, 133–142. [Google Scholar] [CrossRef]
- Robertson, D.I.; Bretherton, R.D. Optimizing networks of traffic signals in real time-the SCOOT method. IEEE Trans. Veh. Technol. 1991, 40, 11–15. [Google Scholar] [CrossRef]
- Park, B.; Yun, I.; Ahn, K. Stochastic optimization for sustainable traffic signal control. Int. J. Sustain. Transp. 2009, 3, 263–284. [Google Scholar] [CrossRef]
- Liao, T.Y. A fuel-based signal optimization model. Transp. Res. Part D Transp. Environ. 2013, 23, 1–8. [Google Scholar] [CrossRef]
- Bauer, C.S. Some energy considerations in traffic signal timing. Traffic Eng. 1975, 45, 19–25. [Google Scholar]
- Stevanovic, A.; Stevanovic, J.; Zhang, K.; Batterman, S. Optimizing traffic control to reduce fuel consumption and vehicular emissions: Integrated approach with VISSIM, CMEM, and VISGAOST. Transp. Res. Rec. 2009, 2128, 105–113. [Google Scholar] [CrossRef]
- Osorio, C.; Nanduri, K. Urban transportation emissions mitigation: Coupling high-resolution vehicular emissions and traffic models for traffic signal optimization. Transp. Res. Part B Methodol. 2015, 81, 520–538. [Google Scholar] [CrossRef]
- Stevanovic, A.; Shayeb, S.A.; Patra, S.S. Fuel Consumption Intersection Control Performance Index. Transp. Res. Rec. 2021, 03611981211004181. [Google Scholar] [CrossRef]
- Stevanovic, A.; Martin, P.T.; Stevanovic, J. VisSim-based genetic algorithm optimization of signal timings. Transp. Res. Rec. 2007, 2035, 59–68. [Google Scholar] [CrossRef]
- PTV. VISSIM 2020 User Manual; PTV AG, Planung Transport Verkehr AG Stumpfstraße 1; PTV: Karlsruhe, Germany, 2020. [Google Scholar]
- Al-Khalili, A.; El-Hakeem, A.K. A computer control system for minimization of fuel consumption in urban traffic network. In Proceedings of the IEEE Real Time Systems Symposium, Austin, TX, USA, 1 June 1984; pp. 249–254. [Google Scholar]
- Liao, T.Y.; Machemehl, R.B. Development of an aggregate fuel consumption model for signalized intersections. Transp. Res. Rec. 1998, 1641, 9–18. [Google Scholar] [CrossRef]
- Khalighi, F.; Christofa, E. Emission-based signal timing optimization for isolated intersections. Transp. Res. Rec. 2015, 2487, 1–14. [Google Scholar] [CrossRef]
- Han, K.; Liu, H.; Gayah, V.V.; Friesz, T.L.; Yao, T. A robust optimization approach for dynamic traffic signal control with emission considerations. Transp. Res. Part C Emerg. Technol. 2016, 70, 3–26. [Google Scholar] [CrossRef]
- Ma, X.; Jin, J.; Lei, W. Multi-criteria analysis of optimal signal plans using microscopic traffic models. Transp. Res. Part D Transp. Environ. 2014, 32, 1–14. [Google Scholar] [CrossRef]
- Ma, D.; Nakamura, H. Cycle length optimization at isolated signalized intersections from the viewpoint of emission. In Traffic and Transportation Studies; American Society of Civil Engineers: Reston, VA, USA, 2010; pp. 275–284. [Google Scholar]
- Kwak, J.; Park, B.; Lee, J. Evaluating the impacts of urban corridor traffic signal optimization on vehicle emissions and fuel consumption. Transp. Plan. Technol. 2012, 35, 145–160. [Google Scholar] [CrossRef]
- Lv, J.; Zhang, Y.; Zietsman, J. Investigating emission reduction benefit from intersection signal optimization. J. Intell. Transp. Syst. 2013, 17, 200–209. [Google Scholar] [CrossRef]
- Boriboonsomsin, K.; Barth, M. Impacts of road grade on fuel consumption and carbon dioxide emissions evidenced by use of advanced navigation systems. Transp. Res. Rec. 2009, 2139, 21. [Google Scholar] [CrossRef]
- Gallus, J.; Kirchner, U.; Vogt, R.; Benter, T. Impact of driving style and road grade on gaseous exhaust emissions of passenger vehicles measured by a Portable Emission Measurement System (PEMS). Transp. Res. Part D Transp. Environ. 2017, 52, 215–226. [Google Scholar] [CrossRef]
- Zhu, F.; Aziz, H.A.; Qian, X.; Ukkusuri, S.V. A junction-tree based learning algorithm to optimize network wide traffic control: A coordinated multi-agent framework. Transp. Res. Part C Emerg. Technol. 2015, 58, 487–501. [Google Scholar] [CrossRef]
- Yoon, J.; Ahn, K.; Park, J.; Yeo, H. Transferable traffic signal control: Reinforcement learning with graph centric state representation. Transp. Res. Part C Emerg. Technol. 2021, 130, 103321. [Google Scholar] [CrossRef]
- Scora, G.; Barth, M. Comprehensive Modal Emission Model (cmem) Version 3.01 User’s Guide; University of California: Riverside, CA, USA, 2006; Volume 836, p. 7. [Google Scholar]
- Robertson, D.I.; Lucas, C.F.; Baker, R.T. Coordinating Traffic Signals to Reduce Fuel Consumption. Proc. R. Soc. Lond. 1981, 387, 11–19. [Google Scholar]
- Barth, M.; Malcolm, C.; Younglove, T.; Hill, N. Recent validation efforts for a comprehensive modal emissions model. Transp. Res. Rec. 2001, 1750, 13–23. [Google Scholar] [CrossRef]
- Rakha, H.; Ahn, K.; Trani, A. Comparison of MOBILE5a, MOBILE6, VT-MICRO, and CMEM models for estimating hot-stabilized light-duty gasoline vehicle emissions. Can. J. Civ. Eng. 2003, 30, 1010–1021. [Google Scholar] [CrossRef]
- Alshayeb, S.; Stevanovic, A.; Park, B.B. Field-Based Prediction Models for Stop Penalty in Traffic Signal Timing Optimization. Energies 2021, 14, 7431. [Google Scholar] [CrossRef]
- Wilmink, I.R.; Viti, F.; Baalen, J.V.; Li, M. Emission modelling at signalised intersections using microscopic models. In Proceedings of the 16th ITS World Congress and Exhibition on Intelligent Transport Systems and Services, Stockholm, Sweden, 21–25 September 2009. [Google Scholar]
- Jie, L.; Van Zuylen, H.; Chen, Y.; Viti, F.; Wilmink, I. Calibration of a microscopic simulation model for emission calculation. Transp. Res. Part C Emerg. Technol. 2013, 31, 172–184. [Google Scholar] [CrossRef]
- Alshayeb, S.; Stevanovic, A.; Dobrota, N. Impact of Various Operating Conditions on Simulated Emissions-Based Stop Penalty at Signalized Intersections. Sustainability 2021, 13, 10037. [Google Scholar] [CrossRef]
- Mathew, T.V. Signalized Intersection Delay Models. Available online: https://www.civil.iitb.ac.in/tvm/nptel/572_Delay_A/web/web.html#x1-30002 (accessed on 14 February 2023).




| Performance Measure | Statistics | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | Scenario 5 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Base Case | Optimized | Mean Difference % | Base Case | Optimized | Mean Difference % | Base Case | Optimized | Mean Difference % | Base Case | Optimized | Mean Difference % | Base Case | Optimized | Mean Difference % | ||
| Total Delay (hr) | Mean | 245.89 | 233.37 | −5.1 | 245.89 | 242.07 | −1.55 | 245.89 | 241 | −1.99 | 307.7 | 274.3 | −10.85 | 358 | 313.5 | −12.43 |
| SD | 13.25 | 13.78 | 13.25 | 13.32 | 13.25 | 13.24 | 17.1 | 15.3 | 17.6 | 17.4 | ||||||
| Stops | Mean | 22,566 | 21,379 | −5.26 | 22,566 | 22,217 | −1.55 | 22,566 | 21,450 | −4.95 | 27,011 | 25,821 | −4.41 | 31,858 | 28,124 | −11.72 |
| SD | 1941 | 2169 | 1941 | 2025 | 1941 | 1952 | 2358 | 2390 | 1778 | 2377 | ||||||
| Stopped Total Delay (hr) | Mean | 132.13 | 125.14 | −5.29 | 132.13 | 128.49 | −2.76 | 132.13 | 131.7 | −0.32 | 166.5 | 148.9 | −10.57 | 218.1 | 167.4 | −23.25 |
| SD | 8.66 | 8.72 | 8.66 | 8.65 | 8.66 | 8.69 | 11.6 | 10.2 | 13.5 | 11.7 | ||||||
| Throughput (veh) | Mean | 11,384 | 11,407 | 0.2 | 11,384 | 11,409 | 0.22 | 11,384 | 11,396 | 0.11 | 12,187 | 12,185 | 0 | 11,850 | 12,163 | 2.64 |
| SD | 41 | 45 | 41 | 44 | 41 | 43 | 60 | 55 | 59 | 61 | ||||||
| Excess FC (g) | Mean | 1,793,948 | 1,604,469 | −10.6 | 1,793,948 | 1,651,540 | −7.9 | 1,793,948 | 1,672,606 | −11.8 | 3,008,700 | 2,590,648 | −13.9 | 2,950,549 | 2,605,509 | −11.7 |
| SD | 19,821.14 | 17,228.12 | 19,821.14 | 17,733.55 | 19,821.14 | 17,959.74 | 33,242.8 | 27,817.3 | 32,600.3 | 27,976.87 | ||||||
| Excess HC (g) | Mean | 125,237.2 | 115,021.6 | −8.2 | 125,237.2 | 117,897 | −5.9 | 125,237.2 | 118,602.2 | −9.4 | 151,916 | 137,478 | −9.5 | 166,758 | 158,412 | −5 |
| SD | 780.35 | 639.94 | 780.35 | 655.94 | 780.35 | 659.86 | 946.59 | 764.87 | 1039.01 | 881.35 | ||||||
| Excess CO (g) | Mean | 691,580 | 622,150.6 | −10 | 691,580 | 638,202 | −7.7 | 691,580 | 643,881.1 | −11.7 | 892,159 | 778,169 | −12.8 | 942,624 | 884,591 | −6.2 |
| SD | 7090.06 | 5958.98 | 7090.06 | 6112.72 | 7090.06 | 6167.11 | 9146.39 | 7453.33 | 9663.76 | 8472.64 | ||||||
| Excess NOx (g) | Mean | 14,258.3 | 13,095.34 | −8.2 | 14,258.3 | 13,348.6 | −6.4 | 14,258.3 | 13,042.13 | −10.9 | 33,597.1 | 28,841.6 | −14.2 | 29,276.5 | 23,946.5 | −18.2 |
| SD | 155.94 | 139.58 | 155.94 | 142.27 | 155.94 | 139 | 367.45 | 307.41 | 320.19 | 255.23 | ||||||
| Excess CO2 (g) | Mean | 4,180,735 | 3,723,337 | −10.9 | 4,180,735 | 3,837,664 | −8.2 | 4,180,735 | 3,893,212 | −12.1 | 7,686,980 | 6,574,926 | −14.5 | 7,342,063 | 6,356,867 | −3.4 |
| SD | 47,702.69 | 41,090.83 | 47,702.69 | 42,352.55 | 47,702.69 | 42,965.57 | 87,709.37 | 72,561.03 | 83,773.83 | 70,154.53 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshayeb, S.; Stevanovic, A.; Stevanovic, J.; Dobrota, N. Optimizing of Traffic-Signal Timing Based on the FCIC-PI—A Surrogate Measure for Fuel Consumption. Future Transp. 2023, 3, 663-683. https://doi.org/10.3390/futuretransp3020039
Alshayeb S, Stevanovic A, Stevanovic J, Dobrota N. Optimizing of Traffic-Signal Timing Based on the FCIC-PI—A Surrogate Measure for Fuel Consumption. Future Transportation. 2023; 3(2):663-683. https://doi.org/10.3390/futuretransp3020039
Chicago/Turabian StyleAlshayeb, Suhaib, Aleksandar Stevanovic, Jelka Stevanovic, and Nemanja Dobrota. 2023. "Optimizing of Traffic-Signal Timing Based on the FCIC-PI—A Surrogate Measure for Fuel Consumption" Future Transportation 3, no. 2: 663-683. https://doi.org/10.3390/futuretransp3020039
APA StyleAlshayeb, S., Stevanovic, A., Stevanovic, J., & Dobrota, N. (2023). Optimizing of Traffic-Signal Timing Based on the FCIC-PI—A Surrogate Measure for Fuel Consumption. Future Transportation, 3(2), 663-683. https://doi.org/10.3390/futuretransp3020039







