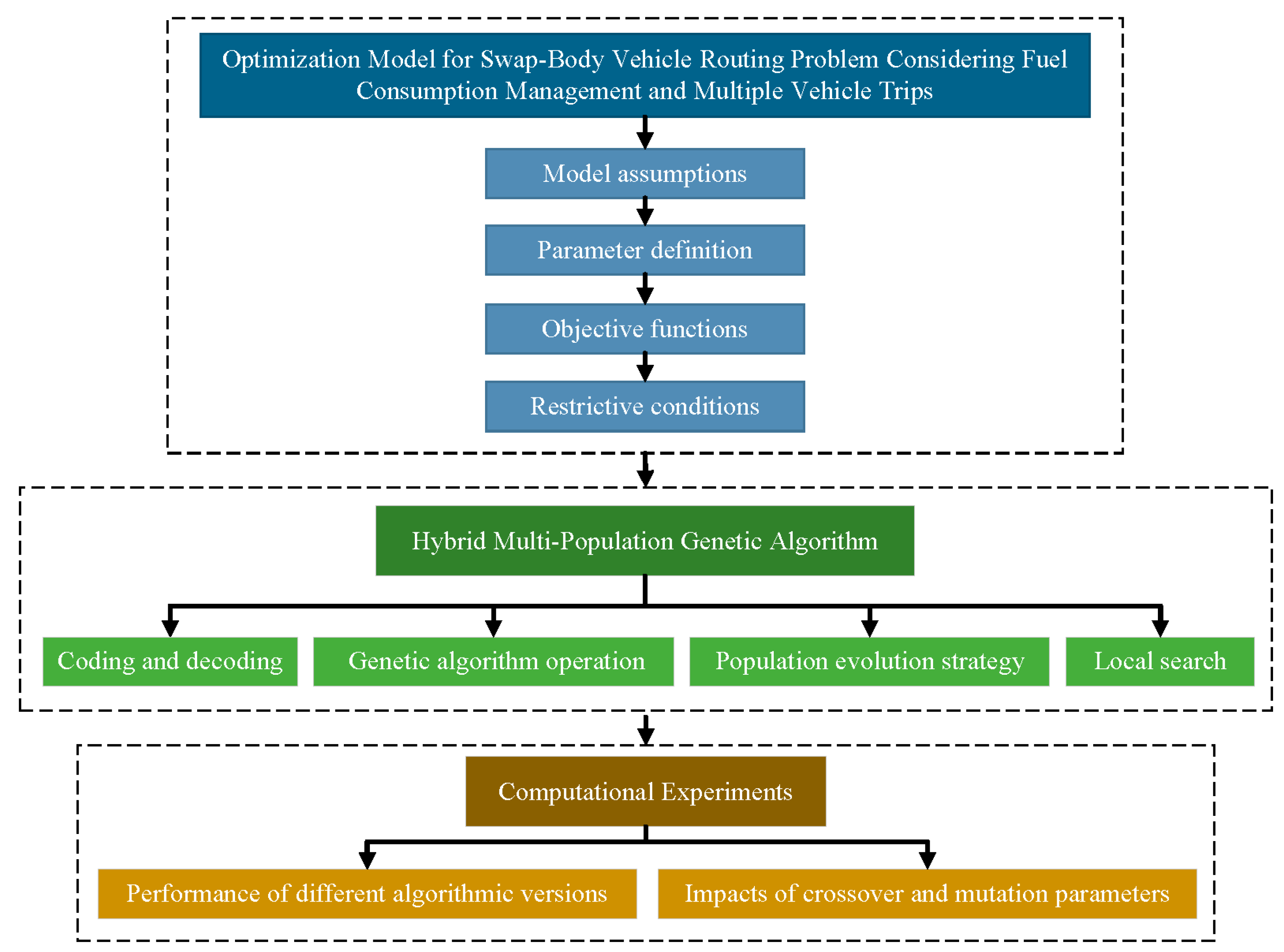
A Swap-Body Vehicle Routing Problem Considering Fuel Consumption Management and Multiple Vehicle Trips
Abstract
:1. Introduction
- Fuel consumption costs have not been considered.
- The possibility of vehicles conducting multiple distribution trips in the SBVRP has not been explored.
2. Optimization Model
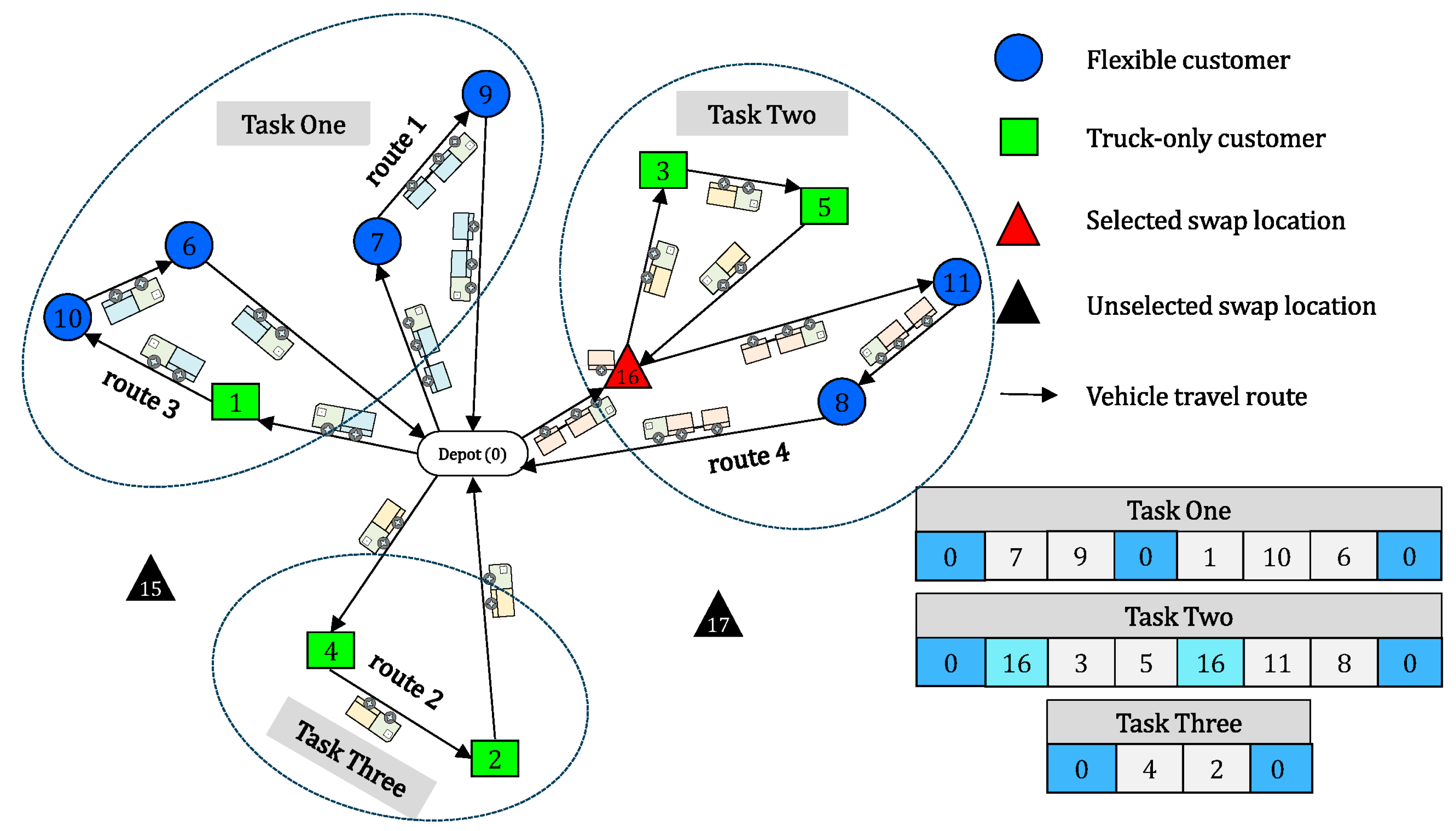
2.1. Problem Description
- Each vehicle trip departs from the depot and then returns to the depot.
- Truck-only customers can only be served by trucks, while flexible customers can be served by either trucks or trailers.
- Each customer has an associated demand , which must be met exactly once.
- Truck-only customers’ demands are bounded by , and the demands of flexible customers are limited by .
- Total demand for each truck route must be within the vehicle’s load capacity.
- The vehicle is allowed to serve multiple trips (routes) no more than the maximum distance .
- Road congestion and time-varying conditions are not considered; therefore, the average speeds of all vehicles are assumed to be the same.
2.2. Model Formulation
3. Hybrid Multi-Population Genetic Algorithm
3.1. Coding and Decoding
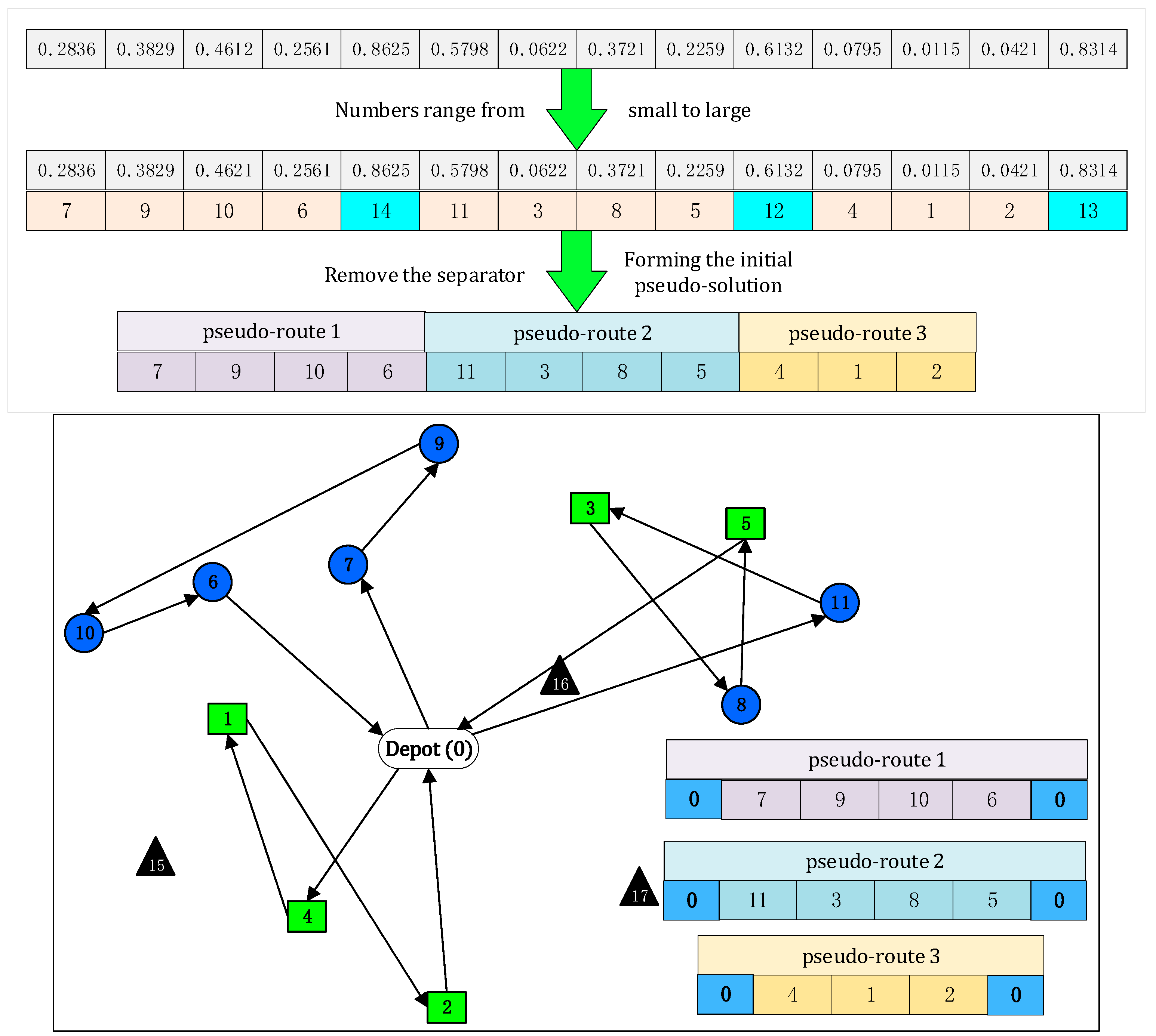
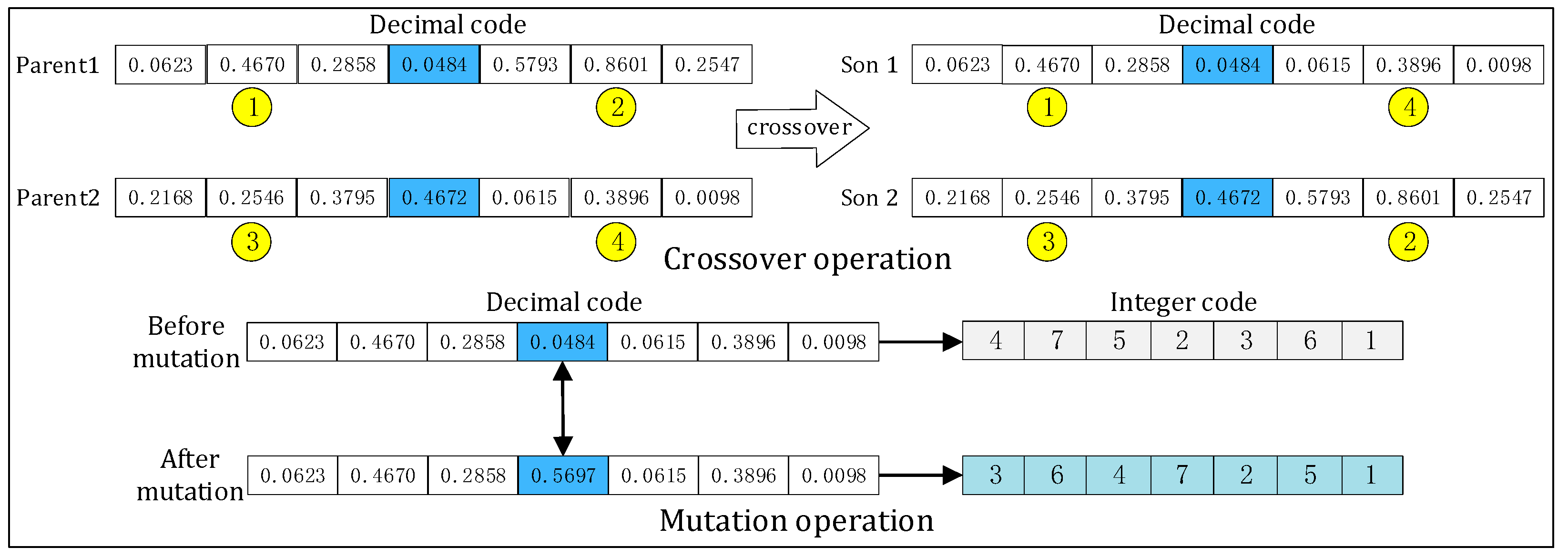
3.1.1. Coding
3.1.2. Decoding
- Step 1: Separating individuals into pseudo routes
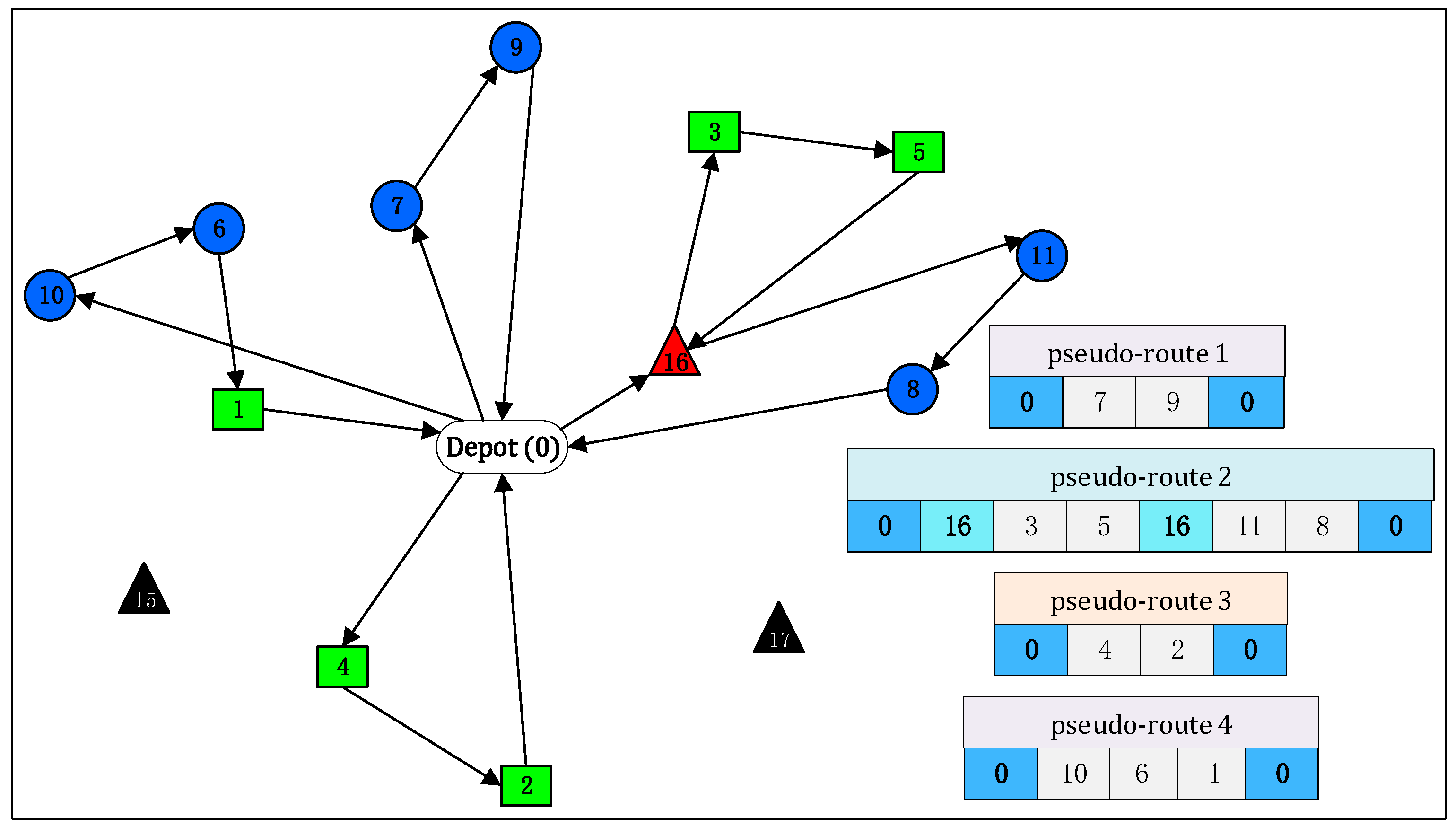
- Step 2: Feasible vehicle loading
| Algorithm 1: Feasible Vehicle Loading |
| Input: Solution , customer demand , truck loading capacity , empty set , route with no customers. Output: |
| //Removal operation |
| for each route |
| Differentiating truck-only customer set and flexible customer set from |
| while |
| Remove one customer from set to set and delete it from |
| end |
| while |
| Remove one customer in set to set and delete it from |
| end |
| end |
| //Playback operation |
| for each customer |
| if |
| for each |
| if |
| ; break end end |
| if |
| ; |
| end |
| else for each |
| if |
| ; break end end |
| if |
| ; |
| end |
| end |
| end |
- Step 3: Adding swap locations
- Step 4: Assigning delivery tasks (trips)
| Algorithm 2: Task Assignment |
| Input: Solution , number of routes , total distance of , number of vehicles , empty set ) and ). Output: , . |
| for
each route |
| while |
| end |
| if |
|
|
| end |
| end |
3.2. Genetic Algorithm Operation
3.3. Population Evolution Strategy
3.4. Local Search
4. Computational Experiments
4.1. Performance of Different Algorithmic Versions
4.2. Impacts of Crossover and Mutation Parameters
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lehmann, J.; Winkenbach, M. A matheuristic for the two-echelon multi-trip vehicle routing problem with mixed pickup and delivery demand and time windows. Transp. Res. Part C Emerg. Technol. 2024, 160, 104522. [Google Scholar] [CrossRef]
- Yaiprasert, C.; Hidayanto, A.N. AI-powered ensemble machine learning to optimize cost strategies in logistics business. Int. J. Inf. Manag. Data Insights 2024, 4, 100209. [Google Scholar] [CrossRef]
- Luo, R.; Ji, S.; Ji, T. An effective chaos-driven differential evolution for multi-objective unbalanced transportation problem considering fuel consumption. Appl. Soft Comput. 2021, 101, 107058. [Google Scholar] [CrossRef]
- Gkyrtis, K. Theoretical considerations from the modelling of the interaction between road design and fuel consumption on urban and suburban roadways. Modelling 2024, 5, 737–751. [Google Scholar] [CrossRef]
- Liu, J.; Feng, L.; Li, Z. The Optimal Road Grade Design for Minimizing Ground Vehicle Energy Consumption. Energies 2017, 10, 700. [Google Scholar] [CrossRef]
- Heid, W.; Hasle, G.; Vigo, D. Verolog solver challenge 2014–VSC2014 problem description. In VeRoLog; (EURO Working Group on Vehicle Routing and Logistics Optimization) and PTV Group, 2014; pp. 1–6. Available online: https://verolog.euro-online.org/wp-content/uploads/2021/09/CallVeRoLogChallenge2014.wh_-2.pdf (accessed on 18 May 2024).
- Cordeau, J.F.; Laporte, G.; Savelsbergh, M.W.; Vigo, D. Vehicle routing. In Handbooks in Operations Research and Management Science; Elsevier: Amsterdam, The Netherlands, 2007; Volume 14, pp. 367–428. [Google Scholar]
- Huber, S.; Geiger, M.J. Swap body vehicle routing problem: A heuristic solution approach. In Proceedings of the Computational Logistics: 5th International Conference, ICCL 2014, Valparaiso, Chile, 24–26 September 2014; Springer International Publishing: Cham, Switzerland, 2014; pp. 16–30. [Google Scholar]
- Huber, S.; Geiger, M.J. Order matters–a variable neighborhood search for the swap-body vehicle routing problem. Eur. J. Oper. Res. 2017, 263, 419–445. [Google Scholar] [CrossRef]
- Lum, O.; Chen, P.; Wang, X.; Golden, B.; Wasil, E. A heuristic approach for the swap-body vehicle routing problem. In Proceedings of the 14th INFORMS Computing Society Conference, Richmond, VA, USA, 11–13 January 2015; Volume 11, pp. 172–187. [Google Scholar]
- Miranda-Bront, J.J.; Curcio, B.; Méndez-Díaz, I.; Montero, A.; Pousa, F.; Zabala, P. A cluster-first route-second approach for the swap body vehicle routing problem. Ann. Oper. Res. 2017, 253, 935–956. [Google Scholar] [CrossRef]
- Absi, N.; Cattaruzza, D.; Feillet, D.; Housseman, S. A relax-and-repair heuristic for the Swap-Body Vehicle Routing Problem. Ann. Oper. Res. 2017, 253, 957–978. [Google Scholar] [CrossRef]
- Todosijević, R.; Hanafi, S.; Urošević, D.; Jarboui, B.; Gendron, B. A general variable neighborhood search for the swap-body vehicle routing problem. Comput. Oper. Res. 2017, 78, 468–479. [Google Scholar] [CrossRef]
- Toffolo, T.A.; Christiaens, J.; Van Malderen, S.; Wauters, T.; Berghe, G.V. Stochastic local search with learning automaton for the swap-body vehicle routing problem. Comput. Oper. Res. 2018, 89, 68–81. [Google Scholar] [CrossRef]
- Huber, S.; Cordeau, J.F.; Geiger, M.J. A matheuristic for the swap body vehicle routing problem. OR Spectr. 2020, 42, 111–160. [Google Scholar] [CrossRef]
- Karnaukhov, O.; Karnaukhova, I.; Karnaukhov, V.; Ryndina, O. Reducing fuel consumption by using correcting parameters system for heavy duty vehicles. Transp. Res. Procedia 2022, 63, 2820–2828. [Google Scholar] [CrossRef]
- Kuo, Y. Using simulated annealing to minimize fuel consumption for the time-dependent vehicle routing problem. Comput. Ind. Eng. 2010, 59, 157–165. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhao, Q.; Kaku, I.; Xu, Y. Development of a fuel consumption optimization model for the capacitated vehicle routing problem. Comput. Oper. Res. 2012, 39, 1419–1431. [Google Scholar] [CrossRef]
- Pradenas, L.; Oportus, B.; Parada, V. Mitigation of greenhouse gas emissions in vehicle routing problems with backhauling. Expert Syst. Appl. 2013, 40, 2985–2991. [Google Scholar] [CrossRef]
- Lin, C.; Choy, K.L.; Ho, G.T.; Chung, S.H.; Lam, H.Y. Survey of green vehicle routing problem: Past and future trends. Expert Syst. Appl. 2014, 41, 1118–1138. [Google Scholar] [CrossRef]
- Alinaghian, M.; Naderipour, M. A novel comprehensive macroscopic model for time-dependent vehicle routing problem with multi-alternative graph to reduce fuel consumption: A case study. Comput. Ind. Eng. 2016, 99, 210–222. [Google Scholar] [CrossRef]
- Liu, C.; Kou, G.; Zhou, X.; Peng, Y.; Sheng, H.; Alsaadi, F.E. Time-dependent vehicle routing problem with time windows of city logistics with a congestion avoidance approach. Knowl. -Based Syst. 2020, 188, 104813. [Google Scholar] [CrossRef]
- Utama, D.M.; Yurifah, A.; Garside, A.K. A novel hybrid spotted hyena optimizer: An algorithm for fuel consumption capacitated vehicle routing problem. Int. J. Technol. 2023, 14, 1049–1059. [Google Scholar] [CrossRef]
- Rahul, J.K.; Chakraborty, S.; Khayer, N.; Uddin, M.F.; Haque, M.R. Designing an Energy-Efficient Transportation Network to Transport Perishable Crops: An Aggregated VRP and X-means Clustering Approach. Heliyon 2023, 9, e19692. [Google Scholar] [CrossRef]
- Fernando, W.M.; Thibbotuwawa, A.; Perera, H.N.; Nielsen, P.; Kilic, D.K. An integrated vehicle routing model to optimize agricultural products distribution in retail chains. Clean. Logist. Supply Chain. 2024, 10, 100137. [Google Scholar] [CrossRef]
- Pak, Y.J.; Mun, K.H. A practical vehicle routing problem in small and medium cities for fuel consumption minimization. Clean. Logist. Supply Chain. 2024, 100164. [Google Scholar] [CrossRef]
- Brandão, J.C.S.; Mercer, A. The multi-trip vehicle routing problem. J. Oper. Res. Soc. 1998, 49, 799–805. [Google Scholar] [CrossRef]
- Fleischmann, B. The Vehicle Routing Problem with Multiple Use of Vehicles; Fachbereich Wirtschaftswissenschaften, Universität Hamburg: Hamburg, Germany, 1990. [Google Scholar]
- Tirkolaee, E.B.; Hosseinabadi, A.A.R.; Soltani, M.; Sangaiah, A.K.; Wang, J. A hybrid genetic algorithm for multi-trip green capacitated arc routing problem in the scope of urban services. Sustainability 2018, 10, 1366. [Google Scholar] [CrossRef]
- Pan, B.; Zhang, Z.; Lim, A. Multi-trip time-dependent vehicle routing problem with time windows. Eur. J. Oper. Res. 2021, 291, 218–231. [Google Scholar] [CrossRef]
- Şahin, M.K.; Yaman, H. A branch and price algorithm for the heterogeneous fleet multi-depot multi-trip vehicle routing problem with time windows. Transp. Sci. 2022, 56, 1636–1657. [Google Scholar] [CrossRef]
- Pham, Q.D.; Nguyen, T.H.; Bui, Q.T. Modeling and solving a multi-trip multi-distribution center vehicle routing problem with lower-bound capacity constraints. Comput. Ind. Eng. 2022, 172, 108597. [Google Scholar]
- Sugianto, W.C.; Kim, B.S. Iterated variable neighborhood search for integrated scheduling of additive manufacturing and multi-trip vehicle routing problem. Comput. Oper. Res. 2024, 167, 106659. [Google Scholar] [CrossRef]
- Calamoneri, T.; Corò, F.; Mancini, S. Management of a post-disaster emergency scenario through unmanned aerial vehicles: Multi-Depot Multi-Trip Vehicle Routing with Total Completion Time Minimization. Expert Syst. Appl. 2024, 251, 123766. [Google Scholar] [CrossRef]
- Zhao, J.; Poon, M.; Tan, V.Y.; Zhang, Z. A hybrid genetic search and dynamic programming-based split algorithm for the multi-trip time-dependent vehicle routing problem. Eur. J. Oper. Res. 2024, 317, 921–935. [Google Scholar] [CrossRef]
- Boriboonsomsin, K.; Barth, M. Impacts of road grade on fuel consumption and carbon dioxide emissions evidenced by use of advanced navigation systems. Transp. Res. Rec. 2009, 2139, 21–30. [Google Scholar] [CrossRef]
- Rahman, S.A.; Masjuki, H.H.; Kalam, M.A.; Abedin, M.J.; Sanjid, A.; Sajjad, H.J.E.C. Impact of idling on fuel consumption and exhaust emissions and available idle-reduction technologies for diesel vehicles—A review. Energy Convers. Manag. 2013, 74, 171–182. [Google Scholar] [CrossRef]
- Boriboonsomsin, K.; Durbin, T.; Scora, G.; Johnson, K.; Sandez, D.; Vu, A.; Jiang, Y.; Burnette, A.; Yoon, S.; Collins, J.; et al. Real-world exhaust temperature profiles of on-road heavy-duty diesel vehicles equipped with selective catalytic reduction. Sci. Total Environ. 2018, 634, 909–921. [Google Scholar] [CrossRef]
- Zhou, M.; Jin, H.; Wang, W. A review of vehicle fuel consumption models to evaluate eco-driving and eco-routing. Transp. Res. Part D Transp. Environ. 2016, 49, 203–218. [Google Scholar] [CrossRef]
- Fan, P.; Yin, H.; Lu, H.; Wu, Y.; Zhai, Z.; Yu, L.; Song, G. Which factor contributes more to the fuel consumption gap between in-laboratory vs. real-world driving conditions? An independent component analysis. Energy Policy 2023, 182, 113739. [Google Scholar] [CrossRef]
- Barth, M.; Younglove, T.; Scora, G. Development of a Heavy-Duty Diesel Modal Emissions and Fuel Consumption Model; Institute of Transportation Studies, UC Berkeley: Berkeley, CA, USA, 2005. [Google Scholar]
- Derbel, H.; Jarboui, B.; Hanafi, S.; Chabchoub, H. Genetic algorithm with iterated local search for solving a location-routing problem. Expert Syst. Appl. 2012, 39, 2865–2871. [Google Scholar] [CrossRef]









| Symbol | Definition |
|---|---|
| Sets | |
| Set of customers delivered by truck only, | |
| Set of customers that can be delivered by truck or trailer, | |
| Set of swap locations, | |
| Set of all nodes, | |
| Set of trucks, | |
| Set of trailers, | |
| Set of trips, | |
| Set of all arcs, | |
| Parameters | |
| Distance traveled by the truck from node to node | |
| Demand for node | |
| Use costs of swap location | |
| Salary of driver | |
| Fixed cost of renting a truck or trailer | |
| Driving cost per distance of truck or trailer | |
| Variable fuel cost per ton-kilometer | |
| Maximum distance allowed for drivers to work per day | |
| Rated load capacity of trucks or trailer | |
| Decision Variables | |
| The value is 1 if there is a direct route through arc and it belongs to the -th trip of truck , otherwise 0, | |
| The value is 1 if there is a direct route through arc and it belongs to the -th trip of trailer , otherwise 0, | |
| The value is 1 if truck is selected, otherwise 0 | |
| The value is 1 if trailer is selected, otherwise 0 | |
| The load of truck when it travels arc at its -th trip | |
| The load of trailer when it travels at its -th trip |
| Algorithmic Versions | Total Costs | Fuel Consumption | Proportion of Total Cost Reduction | Percentage of Fuel Cost Reduction |
|---|---|---|---|---|
| GA | 6661 | 3565 | — | — |
| HGA | 5356 | 2648 | 19.59% | 25.72% |
| MGA | 6217 | 3182 | 6.67% | 10.74% |
| HMGA | 5248 | 2584 | 21.21% | 27.52% |
| pc–pm | GA | HGA | MGA (PC = 0.9, PM = 0.1) | HMGA (PC = 0.9, PM = 0.1) | PC-PM | MGA (pc = 0.9, pm = 0.1) | HMGA (pc = 0.9, pm = 0.1) |
|---|---|---|---|---|---|---|---|
| 0.5–0.1 | 6500 | 5352 | 6484 | 5303 | 0.5–0.1 | 6005 | 5195 |
| 0.5–0.2 | 6511 | 5498 | 6671 | 5414 | 0.5–0.2 | 6702 | 5796 |
| 0.5–0.3 | 6686 | 5467 | 6565 | 5236 | 0.5–0.3 | 6530 | 5499 |
| 0.5–0.4 | 6602 | 5338 | 6555 | 5305 | 0.5–0.4 | 6334 | 5291 |
| 0.5–0.5 | 6463 | 5141 | 6276 | 5121 | 0.5–0.5 | 6352 | 5218 |
| 0.6–0.1 | 6997 | 5712 | 6711 | 5442 | 0.6–0.1 | 6721 | 5589 |
| 0.6–0.2 | 6593 | 5304 | 6898 | 5225 | 0.6–0.2 | 6211 | 5303 |
| 0.6–0.3 | 6962 | 5670 | 6529 | 5262 | 0.6–0.3 | 6654 | 5926 |
| 0.6–0.4 | 6834 | 5792 | 6807 | 5677 | 0.6–0.4 | 6340 | 5313 |
| 0.6–0.5 | 6826 | 5483 | 6630 | 5365 | 0.6–0.5 | 6436 | 5530 |
| 0.7–0.1 | 6638 | 5380 | 6768 | 5376 | 0.7–0.1 | 6378 | 5053 |
| 0.7–0.2 | 6905 | 5442 | 6797 | 5279 | 0.7–0.2 | 6405 | 5427 |
| 0.7–0.3 | 6563 | 5375 | 6568 | 5142 | 0.7–0.3 | 6778 | 5497 |
| 0.7–0.4 | 6877 | 5885 | 7070 | 5579 | 0.7–0.4 | 6744 | 5596 |
| 0.7–0.5 | 6967 | 5775 | 6406 | 5155 | 0.7–0.5 | 6407 | 5405 |
| 0.8–0.1 | 6629 | 5579 | 6536 | 5051 | 0.8–0.1 | 6537 | 5543 |
| 0.8–0.2 | 6854 | 5168 | 6148 | 4992 | 0.8–0.2 | 6623 | 5536 |
| 0.8–0.3 | 6867 | 5613 | 6816 | 5358 | 0.8–0.3 | 6613 | 5360 |
| 0.8–0.4 | 6632 | 5547 | 6332 | 5439 | 0.8–0.4 | 6355 | 5238 |
| 0.8–0.5 | 6678 | 5708 | 6992 | 6085 | 0.8–0.5 | 6579 | 5533 |
| 0.9–0.1 | 6836 | 5059 | 6493 | 5069 | 0.9–0.1 | 6305 | 5194 |
| 0.9–0.2 | 6530 | 5324 | 6845 | 5192 | 0.9–0.2 | 5878 | 5128 |
| 0.9–0.3 | 6572 | 5407 | 6802 | 5188 | 0.9–0.3 | 6279 | 5222 |
| 0.9–0.4 | 6423 | 5555 | 6604 | 5478 | 0.9–0.4 | 6527 | 5520 |
| 0.9–0.5 | 6818 | 5475 | 6700 | 5320 | 0.9–0.5 | 6531 | 5671 |
| pc–pm | PC–PM | MGA | HMGA | ||||
|---|---|---|---|---|---|---|---|
| B | A | B | A | %B | %A | ||
| 0.5–0.1 | 0.9–0.1 | 6258 | 6548 | 5297 | 5471 | −15.36 | −16.45 |
| 0.9–0.1 | 0.5–0.1 | 6524 | 6812 | 5243 | 5492 | −19.64 | −19.38 |
| 0.5–0.2 | 0.9–0.1 | 6518 | 6645 | 5140 | 5409 | −21.14 | −18.6 |
| 0.9–0.1 | 0.5–0.2 | 6415 | 6799 | 5414 | 5618 | −15.6 | −17.37 |
| 0.5–0.3 | 0.9–0.1 | 6160 | 6515 | 5092 | 5338 | −17.34 | −18.07 |
| 0.9–0.1 | 0.5–0.3 | 6345 | 6733 | 4867 | 5467 | −23.29 | −18.8 |
| 0.5–0.4 | 0.9–0.1 | 6609 | 6665 | 4998 | 5428 | −24.38 | −18.56 |
| 0.9–0.1 | 0.5–0.4 | 6157 | 6414 | 4847 | 5207 | −21.28 | −18.82 |
| 0.5–0.5 | 0.9–0.1 | 6277 | 6422 | 4959 | 5134 | −21 | −20.06 |
| 0.9–0.1 | 0.5–0.5 | 6179 | 6382 | 4929 | 5381 | −20.23 | −15.68 |
| 0.6–0.1 | 0.9–0.1 | 5914 | 6595 | 4969 | 5480 | −15.98 | −16.91 |
| 0.9–0.1 | 0.6–0.1 | 6597 | 6817 | 5320 | 5573 | −19.36 | −18.25 |
| 0.6–0.2 | 0.9–0.1 | 6718 | 6985 | 5448 | 5774 | −18.9 | −17.34 |
| 0.9–0.1 | 0.6–0.2 | 6228 | 6645 | 5116 | 5492 | −17.85 | −17.35 |
| 0.6–0.3 | 0.9–0.1 | 6538 | 6740 | 4924 | 5415 | −24.69 | −19.66 |
| 0.9–0.1 | 0.6–0.3 | 6666 | 6817 | 5321 | 5504 | −20.18 | −19.26 |
| 0.6–0.4 | 0.9–0.1 | 6495 | 6735 | 5096 | 5472 | −21.54 | −18.75 |
| 0.9–0.1 | 0.6–0.4 | 6286 | 6495 | 5356 | 5520 | −14.79 | −15.01 |
| 0.6–0.5 | 0.9–0.1 | 6352 | 6764 | 5199 | 5368 | −18.15 | −20.64 |
| 0.9–0.1 | 0.6–0.5 | 6552 | 6777 | 5065 | 5605 | −22.7 | −17.29 |
| 0.7–0.1 | 0.9–0.1 | 6562 | 6839 | 5127 | 5397 | −21.87 | −21.08 |
| 0.9–0.1 | 0.7–0.1 | 6381 | 6655 | 5148 | 5499 | −19.32 | −17.37 |
| 0.7–0.2 | 0.9–0.1 | 6431 | 6665 | 5168 | 5325 | −19.64 | −20.11 |
| 0.9–0.1 | 0.7–0.2 | 6499 | 6591 | 5127 | 5325 | −21.11 | −19.21 |
| 0.7–0.3 | 0.9–0.1 | 6263 | 6653 | 5014 | 5298 | −19.94 | −20.37 |
| 0.9–0.1 | 0.7–0.3 | 6396 | 6457 | 5471 | 5641 | −14.46 | −12.64 |
| 0.7–0.4 | 0.9–0.1 | 6469 | 6833 | 5113 | 5365 | −20.96 | −21.48 |
| 0.9–0.1 | 0.7–0.4 | 6152 | 6751 | 5165 | 5422 | −16.04 | −19.69 |
| 0.7–0.5 | 0.9–0.1 | 6202 | 6514 | 5197 | 5330 | −16.2 | −18.18 |
| 0.9–0.1 | 0.7–0.5 | 6284 | 6505 | 5466 | 5740 | −13.02 | −11.76 |
| 0.8–0.1 | 0.9–0.1 | 6393 | 6490 | 5019 | 5174 | −21.49 | −20.28 |
| 0.9–0.1 | 0.8–0.1 | 6370 | 6573 | 5282 | 5477 | −17.08 | −16.67 |
| 0.8–0.2 | 0.9–0.1 | 5920 | 6305 | 5013 | 5296 | −15.32 | −16 |
| 0.9–0.1 | 0.8–0.2 | 6471 | 6602 | 5103 | 5320 | −21.14 | −19.42 |
| 0.8–0.3 | 0.9–0.1 | 6358 | 6536 | 5126 | 5463 | −19.38 | −16.42 |
| 0.9–0.1 | 0.8–0.3 | 6208 | 6439 | 5132 | 5555 | −17.33 | −13.73 |
| 0.8–0.4 | 0.9–0.1 | 6173 | 6675 | 4953 | 5338 | −19.76 | −20.03 |
| 0.9–0.1 | 0.8–0.4 | 6526 | 6819 | 5286 | 5595 | −19 | −17.95 |
| 0.8–0.5 | 0.9–0.1 | 6371 | 6758 | 4981 | 5591 | −21.82 | −17.27 |
| 0.9–0.1 | 0.8–0.5 | 6391 | 6767 | 5293 | 5506 | −17.18 | −18.63 |
| 0.9–0.1 | 0.9–0.1 | 6194 | 6604 | 4730 | 5084 | −23.64 | −23.02 |
| 0.9–0.1 | 0.9–0.1 | 6306 | 6544 | 4914 | 5294 | −22.07 | −19.1 |
| 0.9–0.2 | 0.9–0.1 | 6187 | 6789 | 4806 | 5117 | −22.32 | −24.63 |
| 0.9–0.1 | 0.9–0.2 | 6413 | 6636 | 4713 | 5103 | −26.51 | −23.1 |
| 0.9–0.3 | 0.9–0.1 | 6759 | 6975 | 5067 | 5171 | −25.03 | −25.86 |
| 0.9–0.1 | 0.9–0.3 | 6587 | 6823 | 4802 | 5229 | −27.1 | −23.36 |
| 0.9–0.4 | 0.9–0.1 | 6195 | 6626 | 4829 | 5380 | −22.05 | −18.8 |
| 0.9–0.1 | 0.9–0.4 | 6353 | 6816 | 5057 | 5354 | −20.4 | −21.45 |
| 0.9–0.5 | 0.9–0.1 | 6114 | 6826 | 4937 | 5226 | −19.25 | −23.44 |
| 0.9–0.1 | 0.9–0.5 | 6341 | 6614 | 5073 | 5452 | −20 | −17.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Y.; Zhang, Y.; Yu, D.Z.; Liu, S.; Li, Y.; Shi, Y. A Swap-Body Vehicle Routing Problem Considering Fuel Consumption Management and Multiple Vehicle Trips. Future Transp. 2024, 4, 1000-1021. https://doi.org/10.3390/futuretransp4030048
Peng Y, Zhang Y, Yu DZ, Liu S, Li Y, Shi Y. A Swap-Body Vehicle Routing Problem Considering Fuel Consumption Management and Multiple Vehicle Trips. Future Transportation. 2024; 4(3):1000-1021. https://doi.org/10.3390/futuretransp4030048
Chicago/Turabian StylePeng, Yong, Yali Zhang, Dennis Z. Yu, Song Liu, Yuanjun Li, and Yangyan Shi. 2024. "A Swap-Body Vehicle Routing Problem Considering Fuel Consumption Management and Multiple Vehicle Trips" Future Transportation 4, no. 3: 1000-1021. https://doi.org/10.3390/futuretransp4030048
APA StylePeng, Y., Zhang, Y., Yu, D. Z., Liu, S., Li, Y., & Shi, Y. (2024). A Swap-Body Vehicle Routing Problem Considering Fuel Consumption Management and Multiple Vehicle Trips. Future Transportation, 4(3), 1000-1021. https://doi.org/10.3390/futuretransp4030048






