Dynamic Approach to Update Utility and Choice by Emerging Technologies to Reduce Risk in Urban Road Transportation Systems
Abstract
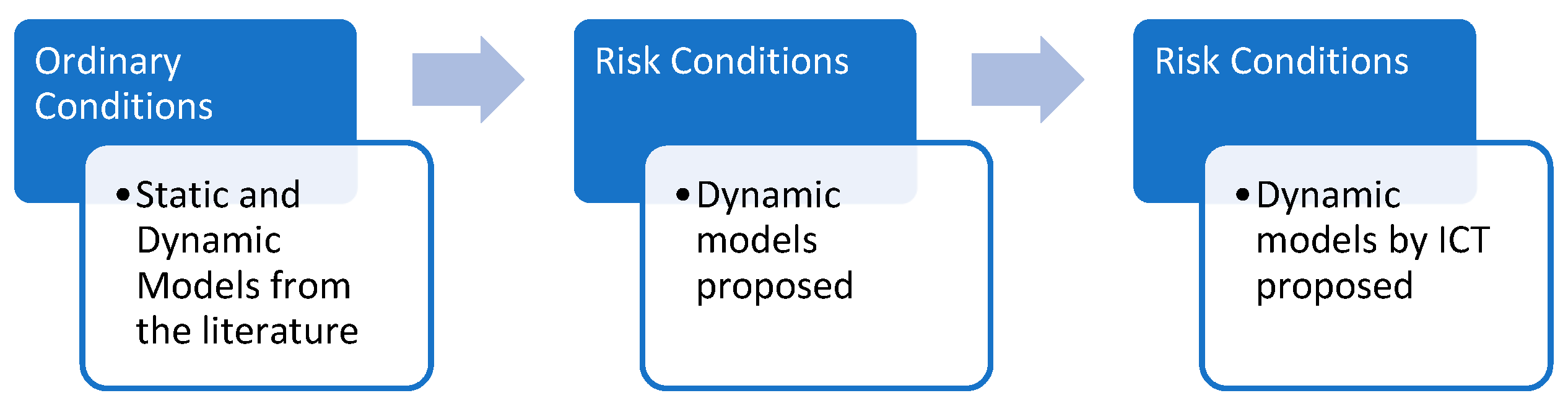
1. Introduction
2. The State of the Art
3. Summary of Demand Analysis in Different Time Evolutions of Risk and under Dynamic Ordinary Conditions
3.1. Temporal Evolution of Risk Conditions
- d0, the public authority decides to plan to reduce the risk;
- d1, the public authority decides to start training and exercises;
- d2, an event occurs, the effects on the population begin, and the procedures for reducing the exposure are activated;
- d3, a maximum effect related to the event is considered, and the exposure can no longer be reduced;
- d4, the event no longer produces direct effects on the population;
- Δx, the differences between dx and dx−1.
- mitigation, involves the modeling, planning, and programming activities developed in relation to a hypothesized event;
- preparedness, involves the activities carried out to prepare the population to respond to the effects of the event; in this way, the main actions are linked to the training and exercises on which specific models can be calibrated;
- response, involves all the activities that allow the effects to be reduced during the event, following the indications of the plan if there exists one and of the exercises if performed;
- recovery (community), involves all the stages of infrastructure reconstruction after the realization of the maximum effect.
- pre-impact phase, which occurs in [d0, d2), divided into two subphases as follows
- ○
- threat subphase, corresponding to interval [d0, d1), in which the decision-maker prepares the plan;
- ○
- warning subphase, corresponding to interval [d1, d2), in which the training and exercises can increase the knowledge of the user;
- impact phase, which occurs in [d2, d3], in which the user has the last time and the last possibilities to evacuate.
- post-impact phase, which occurs from d3 and is divided into two subphases:
- ○
- recoil subphase and rescue, which correspond to interval (d3, d4], where the condition of the user depends on the public safety effort;
- ○
- post-traumatic subphase, corresponding to interval (d4, dn), with dn as the final time of the post event.
- meteorological (weather-related) hazards such as the following,
- ○
- thunderstorm,
- ○
- flood,
- ○
- tornado,
- ○
- hurricane,
- ○
- winter storm,
- ○
- drought,
- ○
- wildfire;
- geological hazards such as the following,
- ○
- landslides and mudflows,
- ○
- earthquakes,
- ○
- tsunamis,
- ○
- volcanoes;
- transportation;
- disease;
- contamination.
3.2. Dynamic Demand Models under Ordinary Conditions
- 0 if kt−1 = kt in time t,
- 1 otherwise.
4. The Proposed Dynamic Model
4.1. The Dynamic Structure with the Two Updating Models
4.2. Utility Updating Process Considering the IoT
- is the value of attribute h of path k planned for day y;
- is the value of attribute h of path k experienced/tested on day y − 1;
- is the weight given to the experienced/tested value.
- is the value of Xhk at t of y; this information is made available via the IoT and shows how the network performance is evolving at the moment. For instance, it can show the travel time (Xhk) that other vehicles are testing out on day y in order to travel at time t on the same path k. Note that this information is updated for each time t across the entire network;
- is the value of Xhk, provided by EP_BD at t of y, as derived from Equation (5);
- ξ(∈]0,1]) is the weight assigned to the value without real-time information provided by EP_BD at time t of day y; in Equation (8), the value of ξ is considered fixed but it can also be viewed more broadly as a variable with t, shifting to 0 for the link where the vehicle is traveling (i.e., user is experimenting with a real-time value).
4.3. Choice Updating Process Considering Sequential Analysis
- to verify whether the transitions from an earlier state to a later state are significant, that is, if they differ from the possibility that the two states are independent;
- assuming that the transitions are significant, to determine how much is the lag of the process.
- by time interval, then fixed interval and free number of events in the interval;
- per event, and therefore, a fixed number of events and free time interval width.
- significance, which refers to the statistical significance of the sequences obtained related to lag 1 to be evaluated;
- stationarity, which refers to the sequential structure of the data, verifying if it is the same regardless of the start interval to be evaluated;
- homogeneity, which allows for whether the sequential structure of the data is identical among all the subjects belonging to the study set to be evaluated.
prob(Un,t−1[jt−1] > Un,t−1[it−1]∀jt−1,it−1 ∈ S,jt−1 ≠ it−1)
- a physical alternative can modify the value of the attributes/parameters from t − 1 to t, and then jt can be equal, or not, to jt−1 with jt, jt−1 ∈ St;
- St is equal to St−1 (St ≡ St−1 ≡ S), with the condition that both contain the same identical alternatives, permitting the alternatives to change attributes and/or parameters from t − 1 to t; if St ≠ St−1, a strong modification happens in the system because there is a new alternative born from t − 1 to t; this discontinuity cannot be represented as a sequence.
5. Proposed Dynamic Sequential Inter-Period Model: Comparisons with Existing Methodologies and Case Study
- all available paths have the same probability of being chosen (no real-time information for users);
- users receive real-time information on a link disruption when at nodes 1 and 2;
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alexander, D. Natural Disasters; UCL Press: London, UK, 1993; ISBN 978-1-85728-094-4. [Google Scholar]
- Alexander, D. Principles of Emergency Planning and Management; Oxford University Press: Oxford, UK, 2002; ISBN 978-0-19-521838-1. [Google Scholar]
- Kelman, I. Climate Change and the Sendai Framework for Disaster Risk Reduction. Int. J. Disaster Risk Sci. 2015, 6, 117–127. [Google Scholar] [CrossRef]
- UN Transforming Our World: The 2030 Agenda for Sustainable Development 2015. Available online: https://sdgs.un.org/2030agenda (accessed on 1 August 2024).
- Train, K. Discrete Choice Methods with Simulation, 2nd ed.; Cambridge University Press: Cambridge, UK, 2009; ISBN 978-0-521-76655-5. [Google Scholar]
- Domencich, T.A.; McFadden, D. Urban Travel Demand: A Behavioral Analysis: A Charles River Associates Research Study; Contributions to economic analysis; North-Holland Pub. Co.: Amsterdam, The Netherlands; American Elsevier: Amsterdam, The Netherlands, 1975; ISBN 978-0-444-10830-2. [Google Scholar]
- Cascetta, E. Transportation Systems Analysis; Springer Optimization and Its Applications; Springer US: Boston, MA, USA, 2009; Volume 29, ISBN 978-0-387-75856-5. [Google Scholar]
- Russo, F.; Chilà, G. Safety of Users in Road Evacuation: Modelling and DSS for Demand. In Proceedings of the WIT Transactions on Ecology and the Environment, Seville, Spain, 23–25 September 2024; WIT Press: Southampton, UK, 2009; Volume 120, pp. 465–474. [Google Scholar]
- Di Gangi, M.; Polimeni, A. Path Choice Models in Stochastic Assignment: Implementation and Comparative Analysis. Front. Future Transp. 2022, 3, 885967. [Google Scholar] [CrossRef]
- Baker, E.J. Hurricane Evacuation Behavior. Int. J. Mass Emergencies Disasters 1991, 9, 287–310. [Google Scholar] [CrossRef]
- Dow, K.; Cutter, S.L. Emerging Hurricane Evacuation Issues: Hurricane Floyd and South Carolina. Nat. Hazards Rev. 2002, 3, 12–18. [Google Scholar] [CrossRef]
- Solis, D.; Thomas, M.H.; Letson, D.; Solis, D.; Thomas, M.H.; Letson, D. Determinants of Household Hurricane Evacuation Choice in Florida. In Proceedings of the 2009 Annual Meeting, Atlanta, Georgia, 31 January–3 February 2009. [Google Scholar] [CrossRef]
- Rockloff, S.F.; Anderson, C.C.; Burton, L.P.; Terry, V.R.; Jensen, S.K.; Nolan, A.; Terry, P.C. Individual Resilience and Disaster-Specific Adaptation and Resilience Following a Bushfire Event in Regional Queensland. Sustainability 2024, 16, 7011. [Google Scholar] [CrossRef]
- Tesoriere, G.; Russo, A.; De Cet, G.; Vianello, C.; Campisi, T. The Centrality of Italian Airports before and after the COVID-19 Period: What Happened? Eur. Transp./Trasp. Eur. 2023, 93, 1–16. [Google Scholar] [CrossRef]
- Russo, A.; Campisi, T.; Bouhouras, E.; Basbas, S.; Tesoriere, G. Sustainable Maritime Passenger Transport: A Network Analysis Approach on a National Basis. In Computational Science and Its Applications—ICCSA 2023 Workshops; Gervasi, O., Murgante, B., Rocha, A.M.A.C., Garau, C., Scorza, F., Karaca, Y., Torre, C.M., Eds.; Lecture Notes in Computer Science; Springer Nature: Cham, Switzerland, 2023; Volume 14109, pp. 195–207. ISBN 978-3-031-37119-6. [Google Scholar]
- Rindone, C.; Russo, A. A Network Analysis for HSR Services in the South of Italy. In Computational Science and Its Applications—ICCSA 2024 Workshops; Gervasi, O., Murgante, B., Garau, C., Taniar, D.C., Rocha, A.M.A., Faginas Lago, M.N., Eds.; Lecture Notes in Computer Science; Springer Nature: Cham, Switzerland, 2024; Volume 14822, pp. 217–232. ISBN 978-3-031-65317-9. [Google Scholar]
- Henke, I.; Troiani, G.; Pagliara, F. An Analysis of the Vulnerability of Road Networks in Response to Disruption Events through Accessibility Indicators Specification. Transp. Plan. Technol. 2024, 47, 628–655. [Google Scholar] [CrossRef]
- Cheng, G.; Wilmot, C.G.; Baker, E.J. Destination Choice Model for Hurricane Evacuation. In Proceedings of the Transportation Research Board 87th Annual Meeting, Washington, DC, USA, 13–17 January 2008; Transportation Research Board: Washington, DC, USA, 2008. [Google Scholar]
- Dixit, V. Hurricane Evacuation: Origin, Route and Destination. In Electronic Theses and Dissertations; Routledge: London, UK, 2008; p. 3484. [Google Scholar]
- Chen, Y.; Xiao, D. Emergency Evacuation Model and Algorithms. J. Transp. Syst. Eng. Inf. Technol. 2008, 8, 96–100. [Google Scholar] [CrossRef]
- Pel, A.J.; Hoogendoorn, S.P.; Bliemer, M.C. Evacuation Modeling Including Traveler Information and Compliance Behavior. Procedia Eng. 2010, 3, 101–111. [Google Scholar] [CrossRef]
- Sheffi, Y.; Mahmassani, H.S.; Powell, W.B. A Transportation Network Evacuation Model. Transp. Res. Part A Policy Pract. 1982, 16A, 209–218. [Google Scholar] [CrossRef]
- Russo, F.; Vitetta, A. Urban Road Transportation Analysis in Emergency Conditions: Models and Algorithms. In Proceedings of the WIT Transactions on The Built Environment, Cambridge, UK, 26–28 July 2000; WIT Press: Southampton, UK, 2000; Volume 49. [Google Scholar]
- Musolino, G. Risk reduction in transport system in emergency conditions: A framework for decision support systems. In Proceedings of the Risk Reduction in Transport System in Emergency Conditions: A Framework for Supply Analysis, Rome, Italy, 7 December 2021; pp. 275–284. [Google Scholar]
- Musolino, G. Methods for Risk Reduction: Modelling Users’ Updating Utilities in Urban Transport Networks. Sustainability 2024, 16, 2468. [Google Scholar] [CrossRef]
- Musolino, G.; Vitetta, A. Short-Term Forecasting in Road Evacuation: Calibration of a Travel Time Function. WIT Trans. Built Environ. 2024, 116, 615–626. [Google Scholar]
- Vitetta, A. Risk Reduction in Transport System in Emergency Conditions: A Framework for Network Design Problems. In Safety and Security Engineering IX; WIT Press: Southampton, UK, 2021; pp. 267–274. [Google Scholar]
- Vitetta, A. Network Design Pro Blem for Risk Reduction in Transport System: A Models Specification. Int. J. TDI 2022, 6, 283–297. [Google Scholar] [CrossRef]
- Vitetta, A.; Quattrone, A.; Polimeni, A. Safety of Users in Road Evacuation: Modelling and DSS for Paths Design of Emergency Vehicles; WIT Press: Southampton, UK, 2009; pp. 485–495. [Google Scholar]
- Marcianò, F.A.; Musolino, G.; Vitetta, A. Signal Setting Optimization on Urban Road Transport Networks: The Case of Emergency Evacuation. Saf. Sci. 2015, 72, 209–220. [Google Scholar] [CrossRef]
- Marcianò, F.A.; Musolino, G.; Vitetta, A. A System of Models for Signal Setting Design of a Signalized Road Network in Evacuation Conditions; WIT Press: Southampton, UK, 2010; pp. 313–323. [Google Scholar]
- Rindone, C.; Panuccio, P. Planning for Risk Reduction in the Transport System at Urban Level. IJTDI 2023, 7, 27–34. [Google Scholar] [CrossRef]
- Rindone, C.; Panuccio, P. Risk Reduction in Transport System in Emergency Conditions: A Framework for Evacuation Planning. In Safety and Security Engineering IX; WIT Press: Southampton, UK, 2021; pp. 285–297. [Google Scholar]
- Russo, F.; Rindone, C. Methods for Risk Reduction: Training and Exercises to Pursue the Planned Evacuation. Sustainability 2024, 16, 1474. [Google Scholar] [CrossRef]
- Jiang, C.; Lu, L.; He, J.; Tan, C. A Two-Class Stochastic Network Equilibrium Model under Adverse Weather Conditions. J. Adv. Transp. 2020, 2020, 1–14. [Google Scholar] [CrossRef]
- Renn, O. Concepts of Risk: A Classification; Semantic Scholar: Westport, CT, USA, 1992. [Google Scholar]
- Cantarella, G.E.; Velonà, P. Assegnazione a Reti Di Trasporto: Modelli Di Processo Deterministico; FrancoAngeli: Milano, Italy, 2019; ISBN 978-88-917-8881-8. [Google Scholar]
- Cantarella, G.E. Dynamics and Stochasticity in Transportation Systems: Tools for Transportation Network Modelling; Elsevier: Amsterdam, The Netherlands, 2020; ISBN 978-0-12-814353-7. [Google Scholar]
- EC. European Civil Protection and Humanitarian Aid Operations; European Commission: Brussels, Belgium, 2023. [Google Scholar]
- UNDRR. United Nations Office for Disaster Risk Reduction; UNDRR: Geneva, Switzerland, 2023; Available online: https://www.undrr.org/ (accessed on 1 August 2024).
- NEMA. Australia Governments, Emergency Management Approaches; NEMA: Arlington, VA, USA, 2023. Available online: https://nema.gov.au/ (accessed on 1 August 2024).
- Blaser, L.; Ohrnberger, M.; Riggelsen, C.; Babeyko, A.; Scherbaum, F. Bayesian Networks for Tsunami Early Warning: Bayesian Networks for Tsunami Early Warning. Geophys. J. Int. 2011, 185, 1431–1443. [Google Scholar] [CrossRef]
- Cremen, G.; Galasso, C. Earthquake Early Warning: Recent Advances and Perspectives. Earth-Sci. Rev. 2020, 205, 103184. [Google Scholar] [CrossRef]
- UN. Global Survey of Early Warning Systems: An Assessment of Capacities, Gaps and Opportunities toward Building a Comprehensive Global Early Warning System for All Natural Hazards; UN: San Francisco, CA, USA, 2006. [Google Scholar]
- FEMA. Livestock in Disasters Course; FEMA: Washington, DC, USA, 2024. Available online: https://emilms.fema.gov/is_0111a/curriculum/1.html (accessed on 1 August 2024).
- FEMA. Emergencies and Disasters Classifications; FEMA: Washington, DC, USA, 2024. Available online: https://emilms.fema.gov/is_0111a/content/264.html (accessed on 1 August 2024).
- Vorst, H.C.M. Evacuation Models and Disaster Psychology. Procedia Eng. 2010, 3, 15–21. [Google Scholar] [CrossRef]
- Sun, Y.; Yamori, K. Risk Management and Technology: Case Studies of Tsunami Evacuation Drills in Japan. Sustainability 2018, 10, 2982. [Google Scholar] [CrossRef]
- Kim, B.-H.; Song, M.-J.; Cho, Y.-S. Safety Analysis of a Nuclear Power Plant against Unexpected Tsunamis. Sustainability 2022, 14, 13540. [Google Scholar] [CrossRef]
- Strahan, K.W.; Gilbert, J. Protective Decision-Making in Bushfire Part 2: A Rapid Systematic Review of the ‘Leave Early’ Literature. Fire 2021, 4, 42. [Google Scholar] [CrossRef]
- Costin, G.P. Bushfire: Retrofitting Rural and Urban Fringe Structures—Implications of Current Engineering Data. Energies 2021, 14, 3526. [Google Scholar] [CrossRef]
- Dube, K.; Chapungu, L.; Fitchett, J.M. Meteorological and Climatic Aspects of Cyclone Idai and Kenneth. In Cyclones in Southern Africa; Nhamo, G., Dube, K., Eds.; Sustainable Development Goals Series; Springer International Publishing: Cham, Switzerland, 2021; pp. 19–36. ISBN 978-3-030-74261-4. [Google Scholar]
- Nhamo, G.; Chikodzi, D. The Catastrophic Impact of Tropical Cyclone Idai in Southern Africa. In Cyclones in Southern Africa; Sustainable Development Goals Series; Springer International Publishing: Cham, Switzerland, 2021; pp. 3–29. ISBN 978-3-030-72392-7. [Google Scholar]
- Manski, C.F.; Sherman, L. An Empirical Analysis of Household Choice among Motor Vehicles. Transp. Res. Part A Gen. 1980, 14, 349–366. [Google Scholar] [CrossRef]
- Nielsen, O.A.; Sorensen, M.V. MSL for Mixed Logit Model Estimation—On Shape of Distribution; Association for European Transport (AET): Strasbourg, France, 2003. [Google Scholar]
- Chila, G.; Musolino, G.; Polimeni, A.; Rindone, C.; Russo, F.; Vitetta, A. Transport Models and Intelligent Transportation System to Support Urban Evacuation Planning Process. IET Intell. Transp. Syst. 2016, 10, 279–286. [Google Scholar] [CrossRef]
- Hensher, D.A.; Le Plastrier, V. Towards a Dynamic Discrete-Choice Model of Household Automobile Fleet Size and Composition. Transp. Res. Part B Methodol. 1985, 19, 481–495. [Google Scholar] [CrossRef]
- Johnson, L.; Hensher, D. Application of Multinomial Probit to a Two-Period Panel Data Set. Transp. Res. Part A Gen. 1982, 16, 457–464. [Google Scholar] [CrossRef]
- Comi, A.; Russo, F. Emerging Information and Communication Technologies: The Challenges for the Dynamic Freight Management in City Logistics. Front. Future Transp. 2022, 3, 887307. [Google Scholar] [CrossRef]
- Atzori, L.; Iera, A.; Morabito, G. The Internet of Things: A Survey. Comput. Netw. 2010, 54, 2787–2805. [Google Scholar] [CrossRef]
- DHL. Internet of Things in Logistics; DHL Trend Research: Troisdorf, Germany, 2015. [Google Scholar]
- Comi, A.; Rossolov, A.; Polimeni, A.; Nuzzolo, A. Private Car O-D Flow Estimation Based on Automated Vehicle Monitoring Data: Theoretical Issues and Empirical Evidence. Information 2021, 12, 493. [Google Scholar] [CrossRef]
- Nuzzolo, A.; Comi, A. Dynamic Optimal Travel Strategies in Intelligent Stochastic Transit Networks. Information 2021, 12, 281. [Google Scholar] [CrossRef]
- Bakeman, R.; Gottman, J.M. Observing Interaction: An Introduction to Sequential Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997; ISBN 978-0-521-45008-9. [Google Scholar]
- Gottman, J.M.; Roy, A.K. Sequential Analysis: A Guide for Behavioral Researchers; Cambridge University Press: Cambridge, UK, 1990; ISBN 978-0-521-34665-8. [Google Scholar]
- Di Gangi, M.; Watling, D.; Salvo, R.D. Modeling Evacuation Risk Using a Stochastic Process Formulation of Mesoscopic Dynamic Network Loading. IEEE Trans. Intell. Transport. Syst. 2022, 23, 3613–3625. [Google Scholar] [CrossRef]




| y | Current day |
| t | Time of the day |
| Ck[t,y] | Generalized travel cost of path k on day y at time t |
| Vector of path cost whose entry is Ck[t,y] | |
| Xhk[t,y] | The h-th attribute of the k-th path on day y at time t |
| Vector of path attributes whose entry is Xhk[t,y] | |
| Value of the h-th attribute of the k-th path on day y at time t | |
| Value of the h-th attribute of k-th path on day y | |
| Value of the h-th attribute of the k-th path experienced/tested on day y − 1 | |
| (∈]0,1]) | Weight given to the experienced/tested value |
| Value of the h-th attribute of the k-th path on day y at time t obtained through the IoT | |
| Value of the h-th attribute of the k-th path on day y at time t forecasted using previous experiences (i.e., without information from the IoT) | |
| Value of the h-th attribute of the k-th path on day y − 1 experienced/tested using previous experiences (i.e., without information from the IoT) | |
| ξ (∈]0,1]) | Weight given to the forecasted value |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Russo, F.; Comi, A.; Chilà, G. Dynamic Approach to Update Utility and Choice by Emerging Technologies to Reduce Risk in Urban Road Transportation Systems. Future Transp. 2024, 4, 1078-1099. https://doi.org/10.3390/futuretransp4030052
Russo F, Comi A, Chilà G. Dynamic Approach to Update Utility and Choice by Emerging Technologies to Reduce Risk in Urban Road Transportation Systems. Future Transportation. 2024; 4(3):1078-1099. https://doi.org/10.3390/futuretransp4030052
Chicago/Turabian StyleRusso, Francesco, Antonio Comi, and Giovanna Chilà. 2024. "Dynamic Approach to Update Utility and Choice by Emerging Technologies to Reduce Risk in Urban Road Transportation Systems" Future Transportation 4, no. 3: 1078-1099. https://doi.org/10.3390/futuretransp4030052
APA StyleRusso, F., Comi, A., & Chilà, G. (2024). Dynamic Approach to Update Utility and Choice by Emerging Technologies to Reduce Risk in Urban Road Transportation Systems. Future Transportation, 4(3), 1078-1099. https://doi.org/10.3390/futuretransp4030052








