Exact Solutions of Nonlinear Second-Order Autonomous Ordinary Differential Equations: Application to Mechanical Systems
Abstract
:1. Introduction
- •
- Exact solution of general second-order nonlinear autonomous undamped differential equations;
- •
- Identification of the system class from the initial conditions;
- •
- Identification of the system’s general properties (e.g., period, time to reach extremes, long term behavior) before computing the solution.
2. Exact Solutions
2.1. Parameter Mapping
2.2. Qualitative Behavior of the Solution
2.2.1. Case 1
2.2.2. Case 2
2.2.3. Case 3
2.2.4. Case 4
2.2.5. Case 5
2.2.6. Case 6
2.2.7. Case 7
2.2.8. Case 8
2.2.9. Case 9
3. Algorithm
4. Examples and Validation
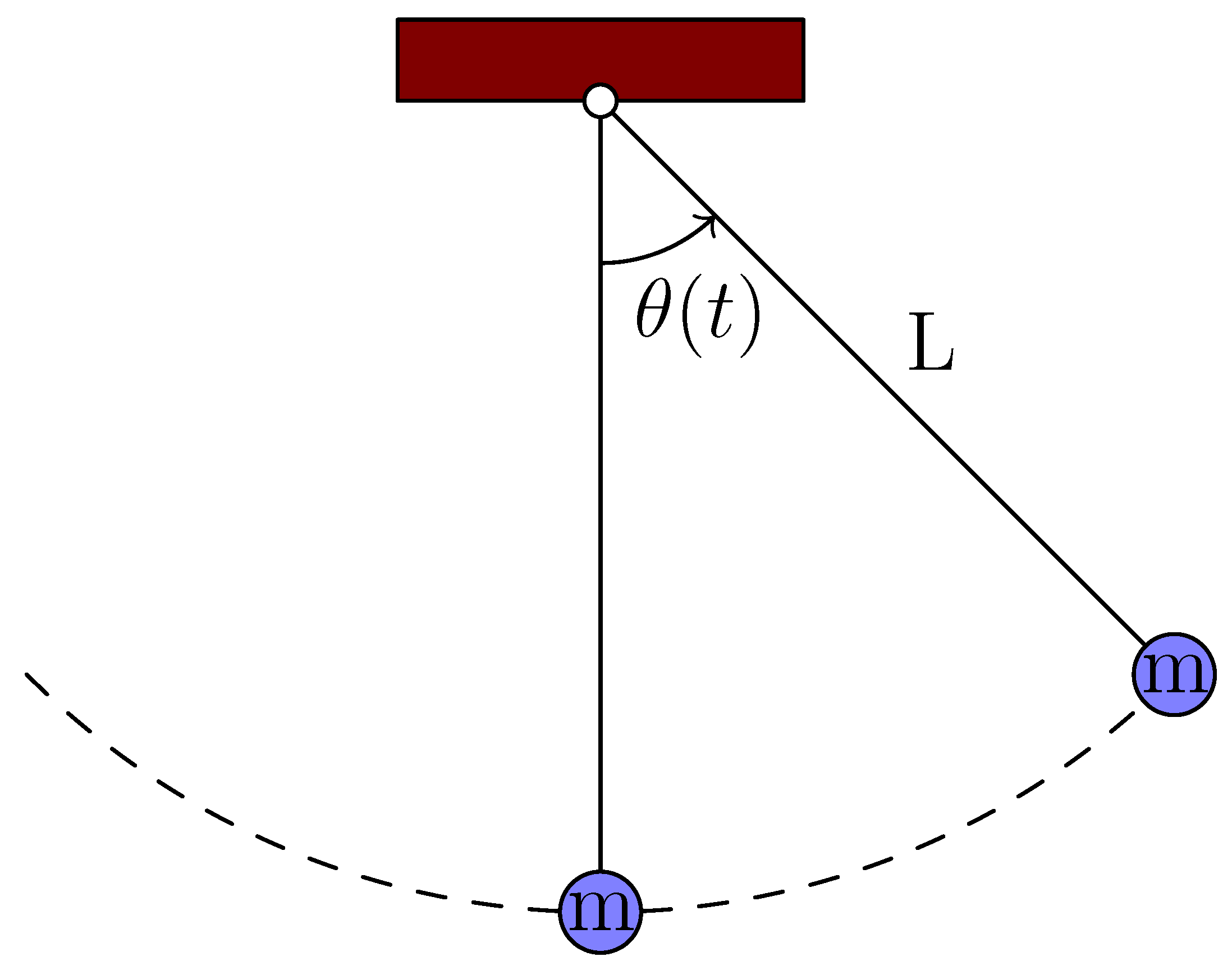
4.1. Nonlinear Pendulum
4.2. Nonlinear Pyramidal Truss
4.3. Spike System
5. Discussion and Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| IVP | initial value problem |
| ODE | ordinary differential equation |
References
- Lenci, S. Exact solutions for coupled Duffing oscillators. Mech. Syst. Signal Process. 2022, 165, 108299. [Google Scholar] [CrossRef]
- Nuttall, A.K.; Hartree, D.R.; Porter, A. The Response of a Non-Linear Electric Circuit to an Impulse. Math. Proc. Camb. Philos. Soc. 1936, 32, 304–320. [Google Scholar] [CrossRef]
- Goldstein, H.; Poole, C.P.; Safko, J.L. Classical Mechanics, 3rd ed.; Pearson: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Zhang, Y.Z. Exact polynomial solutions of second order differential equations and their applications. J. Phys. A Math. Theor. 2012, 45, 065206. [Google Scholar] [CrossRef]
- Ghaemi, M.B.; Gordji, M.E.; Alizadeh, B.; Park, C. Hyers-ulam stability of exact second-order linear differential equations. Adv. Differ. Equ. 2012, 2012, 36. [Google Scholar] [CrossRef] [Green Version]
- Liao, S.; Tan, Y. A General Approach to Obtain Series Solutions of Nonlinear Differential Equations. Stud. Appl. Math. 2007, 119, 297–354. [Google Scholar] [CrossRef]
- Bartha, F.A.; Krisztin, T.; Vígh, A. Stable periodic orbits for the Mackey-Glass equation. J. Differ. Equ. 2021, 296, 15–49. [Google Scholar] [CrossRef]
- Burmasheva, N.; Prosviryakov, E. Exact Solutions to Navier–Stokes Equations Describing a Gradient Nonuniform Unidirectional Vertical Vortex Fluid Flow. Dynamics 2022, 2, 175–186. [Google Scholar] [CrossRef]
- Carravetta, F. On the solution calculation of nonlinear ordinary differential equations via exact quadratization. J. Differ. Equ. 2020, 269, 11328–11365. [Google Scholar] [CrossRef]
- Liu, H.; Geng, Y. Symmetry reductions and exact solutions to the systems of carbon nanotubes conveying fluid. J. Differ. Equ. 2013, 254, 2289–2303. [Google Scholar] [CrossRef]
- Korman, P.; Li, Y. Exact multiplicity of positive solutions for concave–convex and convex–concave nonlinearities. J. Differ. Equ. 2014, 257, 3730–3737. [Google Scholar] [CrossRef]
- Cheviakov, A.F. Exact closed-form solutions of a fully nonlinear asymptotic two-fluid model. Phys. D Nonlinear Phenom. 2018, 370, 14–28. [Google Scholar] [CrossRef]
- Tur, A.; Yanovsky, V.; Kulik, K. Vortex structures with complex points singularities in two-dimensional Euler equations. New exact solutions. Phys. D Nonlinear Phenom. 2011, 240, 1069–1079. [Google Scholar] [CrossRef]
- Volpert, V.; Nec, Y.; Nepomnyashchy, A. Exact solutions in front propagation problems with superdiffusion. Phys. D Nonlinear Phenom. 2010, 239, 134–144. [Google Scholar] [CrossRef]
- MacNeil, J.M.L.; Smyth, N.F.; Assanto, G. Exact and approximate solutions for optical solitary waves in nematic liquid crystals. Phys. D Nonlinear Phenom. 2014, 284, 1–15. [Google Scholar] [CrossRef]
- Zubarev, N.; Zubareva, O. Exact solutions for the shape of a two-dimensional conducting liquid drop in a non-uniform electric field. Phys. D Nonlinear Phenom. 2012, 241, 921–928. [Google Scholar] [CrossRef]
- Santana, M.V.B.; Gonçalves, P.B.; Silveira, R.A.M. Closed-form solutions for the symmetric nonlinear free oscillations of pyramidal trusses. Phys. D Nonlinear Phenom. 2021, 417, 132814. [Google Scholar] [CrossRef]
- Newmark, N.M. A Method of Computation for Structural Dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar] [CrossRef]
- Runge, C. Ueber die numerische Auflösung von Differentialgleichungen. Math. Ann. 1895, 46, 167–178. [Google Scholar] [CrossRef] [Green Version]
- Tenenbaum, M.; Pollard, H. Ordinary Differential Equations; Dover Publications Inc.: Mineola, NY, USA, 1985. [Google Scholar]
- Beléndez, A.; Pascual, C.; Méndez, D.I.; Beléndez, T.; Neipp, C. Exact solution for the nonlinear pendulum. Rev. Bras. Ensino Física 2007, 29, 645–648. [Google Scholar] [CrossRef] [Green Version]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes 3rd Edition: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Beléndez, A.; Hernández, A.; Márquez, A.; Beléndez, T.; Neipp, C. Analytical approximations for the period of a nonlinear pendulum. Eur. J. Phys. 2006, 27, 539–551. [Google Scholar] [CrossRef] [Green Version]
- Lima, F.M.S. Simple ‘log formulae’ for pendulum motion valid for any amplitude. Eur. J. Phys. 2008, 29, 1091–1098. [Google Scholar] [CrossRef]
- Grimshaw, R. Nonlinear Ordinary Differential Equations; Taylor and Francis: Boca Raton, FL, USA, 1993. [Google Scholar]
- Jordan, D.; Smith, P. Nonlinear Ordinary Differential Equations: An Introduction for Scientists and Engineers; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Hermann, M.; Saravi, M. Nonlinear Ordinary Differential Equations: Analytical Approximation and Numerical Methods; Springer Link: Berlin/Heidelberg, Germany, 2016. [Google Scholar]














| Case | Lower Bound | Upper Bound |
|---|---|---|
| 1 | ||
| 2 | and | |
| 3 | and | |
| 4 | and | and |
| 5 | and | |
| 6 | and | |
| 7 | and | and |
| 8 | and | and |
| 9 | and | and |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santana, M.V.B. Exact Solutions of Nonlinear Second-Order Autonomous Ordinary Differential Equations: Application to Mechanical Systems. Dynamics 2023, 3, 444-467. https://doi.org/10.3390/dynamics3030024
Santana MVB. Exact Solutions of Nonlinear Second-Order Autonomous Ordinary Differential Equations: Application to Mechanical Systems. Dynamics. 2023; 3(3):444-467. https://doi.org/10.3390/dynamics3030024
Chicago/Turabian StyleSantana, Murillo V. B. 2023. "Exact Solutions of Nonlinear Second-Order Autonomous Ordinary Differential Equations: Application to Mechanical Systems" Dynamics 3, no. 3: 444-467. https://doi.org/10.3390/dynamics3030024
APA StyleSantana, M. V. B. (2023). Exact Solutions of Nonlinear Second-Order Autonomous Ordinary Differential Equations: Application to Mechanical Systems. Dynamics, 3(3), 444-467. https://doi.org/10.3390/dynamics3030024







