The In Silico Optimization of a Fed-Batch Reactor Used for the Enzymatic Hydrolysis of Chicory Inulin to Fructose by Employing a Dynamic Approach
Abstract
1. Introduction
| Characteristics | Glucose Isomerization [a,d] | Two-Step Cetus Process [b] | Inulin Hydrolysis [c] |
|---|---|---|---|
| Number of steps | 1 | 2 | 1 |
| Conversion (%) | 50 (limited by the equilibrium) [d] | 99 | 99.5 |
| Raw-material availability | Glucose from the starch of crops, molasses, cellulose, and food processing by-products [84] | Genetically modified chicory crop; cultures of Aspergillus sp. | |
| Impurities in the product | Yes | Traces | Negligible |
| Reaction type | Enzymatic isomerization | Enzymatic oxidation (step 1), followed by enzymatic reduction (step 2) | Enzymatic hydrolysis |
| Enzyme mobility | Immobilized [d] | Free (suspended) | Immobilized |
| Enzyme stability, and other additives | Intracellular glucose-isomerase (e.g., Streptomyces murinus) of low stability; metal (Al) salts | Pyranose 2-oxidase (P2Ox) and catalase (step 1); aldose reductase and NAD(P)H (step 2); enzymes are very costly | Inulinase |
| Temperature | 50–60 °C | 25–30 °C (50–60 °C)/ 30 °C | 55 °C (40–60 °C) |
| Reaction time | 7 h | 3–20 h (step 1); 25 h (step 2) | 13 h |
| pH | 7–8.5 | 6.5–7(−8.5); 7–8.5 | 5.5 |
| Number of reaction steps | 1 isomerization | 2 oxidation (step 1), reduction (step 2) | 1 hydrolysis |
| Coenzyme necessary? | No | Yes Catalase for step 1 to prevent P2Ox quick inactivation; NAD(P)H for step 2. NAD(P)H is continuously regenerated in situ | No |
| Product purification | Difficult [d] | Simple (due to high selectivity) | Simple (due to high selectivity) |
| Product purity | 2–5% impurities [d] | High (99.9%) | High (99.9%) |
| Operating Conditions | Value | Remarks |
|---|---|---|
| Reactor liquid volume | 1 L (initial) | Up to 10 L capacity |
| Temperature/pressure/pH (buffer solution) | 50–55 °C/normal/4.5–5 | Batch time (tf) = 780 min. |
| Initial concentrations of Ricca et al. [64] | [S]o = 40 (g/L) [E]o = 97 (U/L) [W]o = 988.4 (g/L) [F]o = 0; [G]o = 0 | To be optimized within imposed limits (this paper) |
| Optimization limits of control variables (initial BR, or in the FBR feeding) [63] [b,c,d] | [S]o; [S]in ∈ [40–200] g/L [E]o; [E]in ∈ [97–5500] (U/L) [W]o ∈ [98–4000] (g) FL ∈ [5 × 10−4–0.01] (L/min) | For FBR optimization, the W amount depends on the inlet feed flow rate (FL) of aqueous solution |
| Fructose polimerization degree in the inulin (m) | 29 (adopted) | 27–29 Inulin from chicory |
| Number of time-arcs for the optimized FBR (Ndiv) | 5 | FBR with variable feeding |
| Imposed inulin (S) conversion | Min. 90% | |
| Inulin solubility [b] | 60 g/L (10 °C) 160–400 g/L (50 °C), 330 g/L (90 °C) | [62,65,67] |
| Inulin solution viscosity, density [a] | Comparable to those of water | For [S] < 100 g/L [68,69] |
| Fructose solubility | 4000 g/L (ca., 22.2 M) (25 °C) | https://en.wikipedia.org/wiki/Fructose (last accessing 5 May 2025) |
| Glucose solution solubility | 5–7M (25–30 °C) | [90] |
| Glucose/fructose solution viscosity | Ca., 1–3 cps (for up to 0.3 M) and 1000 cps (4.5M, 30 °C) | [91] |
2. The Experimental Enzymatic Reactor
3. Process Kinetics and Reactor Dynamic Model
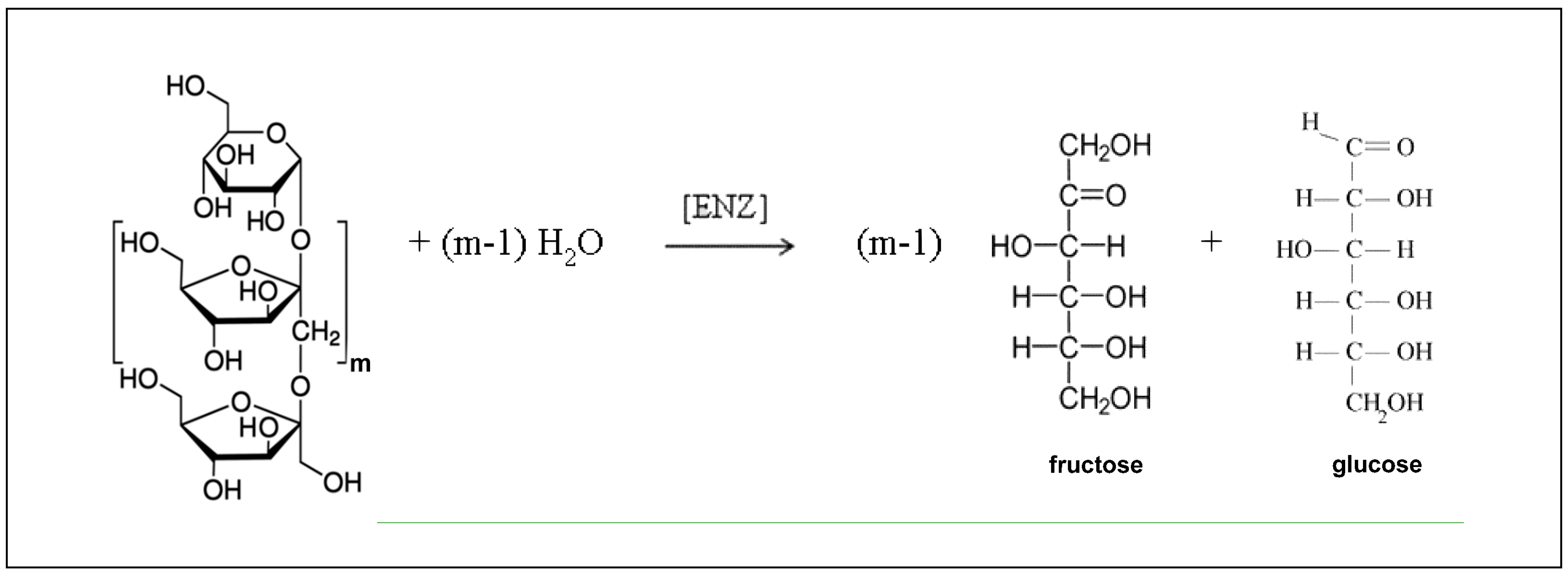
| Reaction Pathway (Figure 2): | |
| ; ; ; ; The above consecutive scheme is approximated by the overall reaction: | |
| Rate expressions:[a] | Rate constants: |
| ; = ; = ; Or, equivalently, one can write ; = ; = | m = 29; = 18 g/mol = = 180 g/mol = , g/U·min [b] = , g/L |
| T is better to keep it. Enzyme deactivation model: | |
| - Adopted first-order model: , ⇒ Or, equivalently, one can write | = , 1/h (experimental, free enzyme) |
| - Other data from the literature: Free enzyme [75] Immobilized enzyme [75] | , 1/min , 1/min |
| - Other rate expressions (pseudo-second-order, not tested here): , ⇒ Free enzyme [76] Immobilized enzyme [76] | , 1/h , 1/h |
| Species | Remarks |
|---|---|
| Species mass balances: ; ‘j’ = species index (S, F, W, G, E), With the initial conditions of , where ‘i’ = (S, E, W) are to be optimized; = 0, for j = (F, G). | The species reaction rate () expressions, the rate constants, and the stoichiometry (νij) are given in Table 3. Enzyme (E) deactivation is included in this dynamic balance. The optimal initial load of the BR (Table 6) is determined offline by solving in silico the associated NLP optimization problem (this paper). C = species concentration vector; k = rate constants vector. |
| Species | Remarks |
|---|---|
| Species mass balances: ; , for species ‘’' = S, F, G, E; , for ‘’' = S, E; , = control variables. ‘’' = S,E; ‘j’ = 1,.., ; unknown time-stepwise values to be determined from the FBR optimization. For species W, the mass balance is [b] [W]o = 988 g/L; = 0, for ‘j’ = (F, G). | For the optimal FBR with the adopted Ndiv = 5, the feeding policy is (Footnote [a]) |
| Liquid volume in the reactor (footnote [c]): ; = control variable; ‘j’ = 1, ..., ; unknown time-stepwise values to be determined from the FBR optimization. The unknown = (t = 0) = is determined together with all the values. | For the optimal FBR with the adopted Ndiv =10, the feeding policy is (Footnote [a]) |
4. Optimization Problem for BR and FBR
4.1. Selection of Control Variables
4.2. NLP Optimization with a Single Objective Function (Ω)
find control variables [S]o, [E]o, and [W]o such that
Max Ω(C, Co, k), where Ω = [F(t)]
CS,inlet,j, CE,inlet,j, and FL,j, B
for j = 1, …, Ndiv, with the adopted Ndiv = 5 time-arcs, and the initial FBR condition of Table 5, to obtain
Max Ω(C, Co, k), where Ω = [F(t)]
4.3. Optimization Problem Constraints
- (a)
- (b)
- (c)
- To limit the excessive consumption of raw materials, feasible searching ranges are imposed on the control/decision variable, as stipulated in Table 2.
Table 4 for the BR case.
Table 5 for the FBR case.
cj(t) ≥ 0, in Table 4 and Table 5, for all the species of index ‘j’ and for all t ∈ [0-tf]
[S]o; [S]in ∈ [40–400] g/L
[E]o; [E]in ∈ [97–5500] (U/L)
[W]o ∈ [988–4000] (g)
FL ∈ [5 × 10−4–0.01] (L/min)
4.4. Pareto-Optimal Front Optimization with Opposite Objective Functions
Minimum constant feed flow rate for various maximum F produced.
Maximum F production vs. minimum enzyme (E) consumption.
4.5. The Used Solvers
5. Optimization Results and Their Discussion
- (a)
- (b)
- A comparison of all BR operating alternatives in terms of fructose (F) production and raw-material consumption is in Table 6. In the BR case, this consumption is based only on the initial load. In the FBR case, the raw-material consumption (mass) is computed with the following formula:
- (c)
- (d)
- (1)
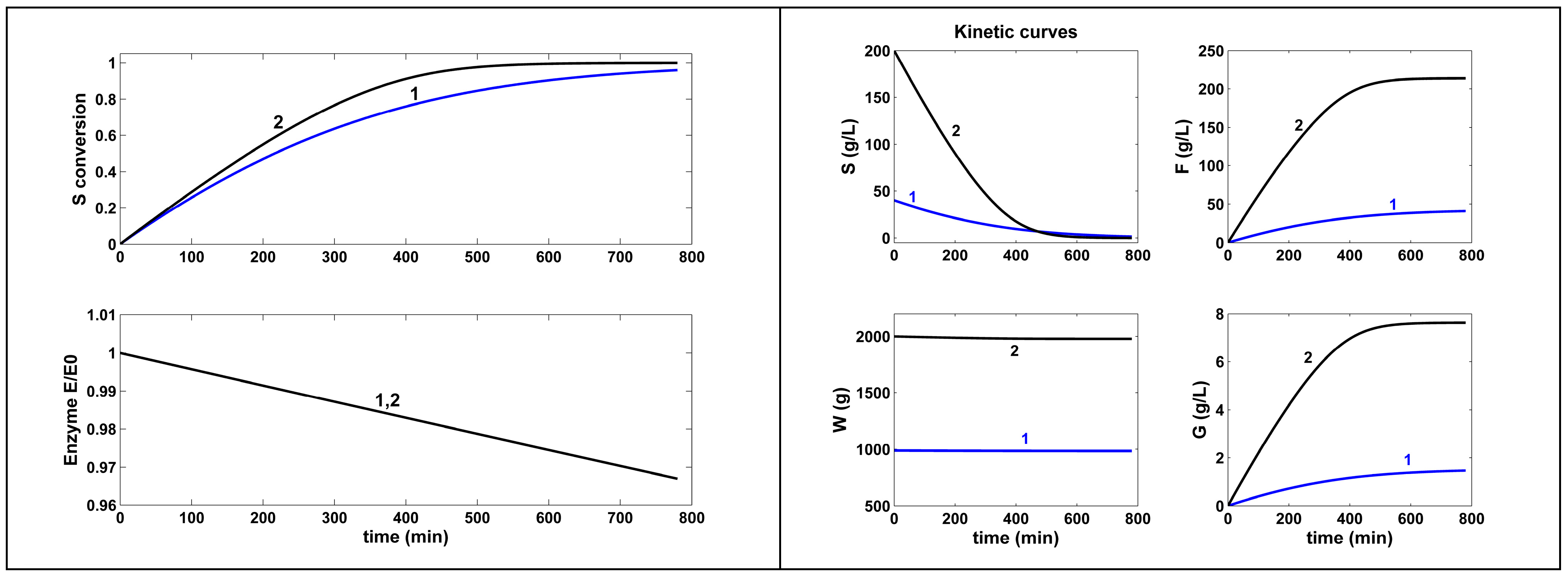
- The optimal NLP-operated BR, according to Equation (1A), under the constraints of Equation (2i–iv) for the control variables, reported incomparably better performances (5× in terms of more F produced, at the expense of consuming 5× more substrates and 30× more enzymes) compared to the experimental non-optimal BR trial of Ricca et al. [64] (in Table 6 and Figure 3).
- (2)
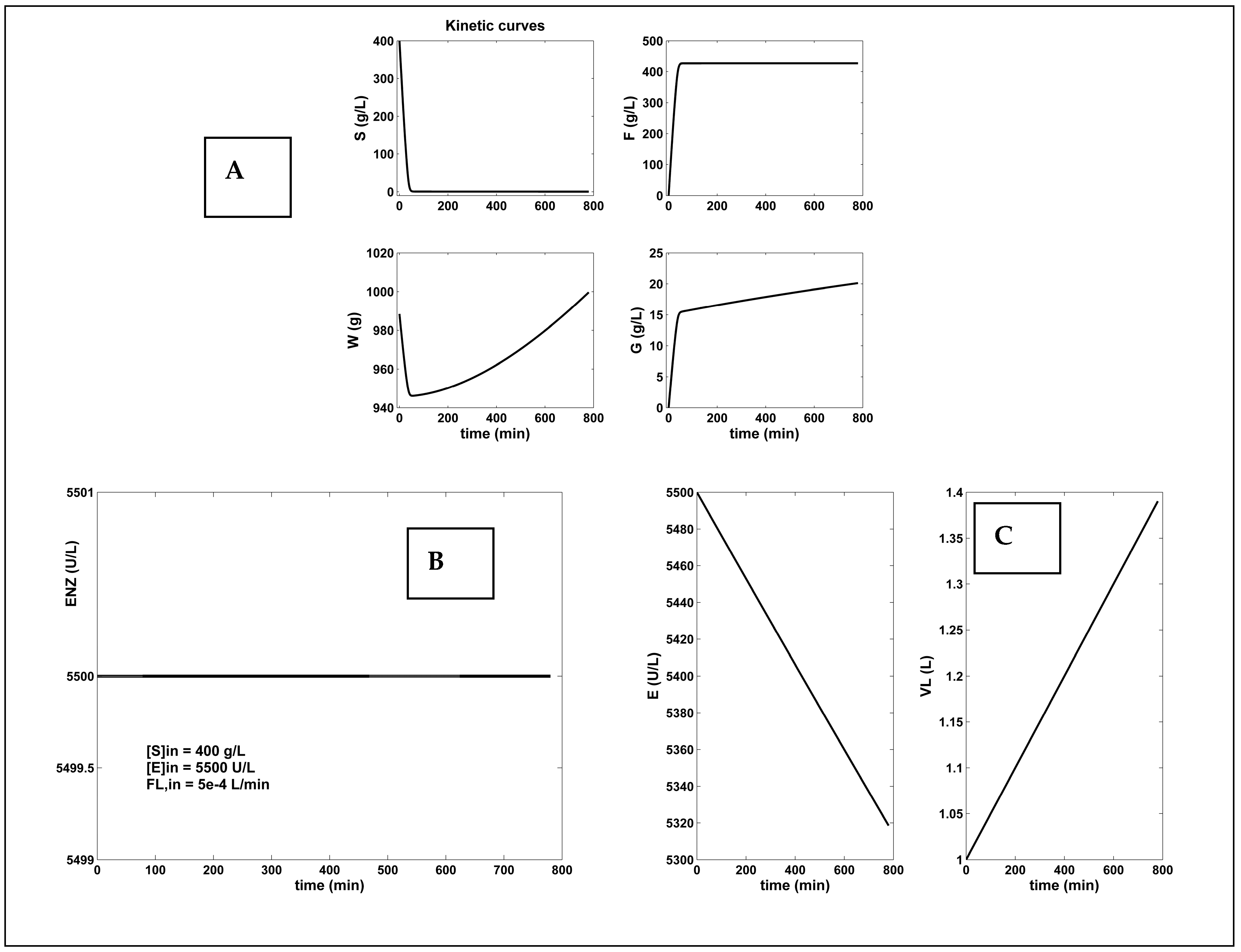
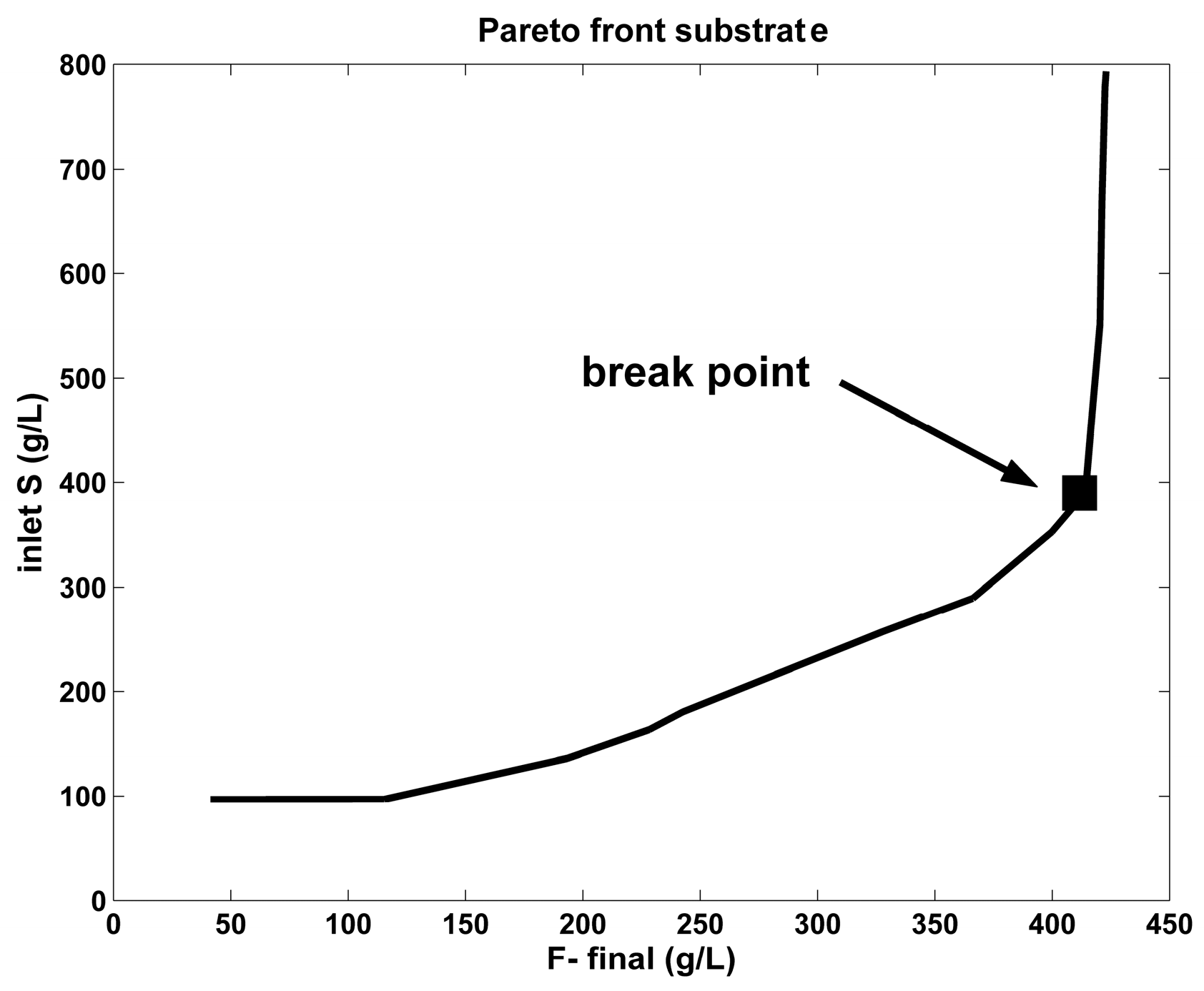
- By far, the best alternative is the FBR operated with a constant but optimal NLP feeding (Equation (1A)), or operated using the set-point (break-point) given by the Pareto-optimal front, Equation (3). Even if the F-production is similar to those of the optimal NLP-operated BR, the substrate consumption is 13×–15× lower, by consuming 15×–92× less enzymes (Table 6 and Figure 4). As revealed by the results of Table 6, the FBR operated with a constant, but using the set-point (break-point) given by the Pareto-optimal front (Equation (3)), under the constraints of Equation (2i–iv) for the control variables, reported the best performances, regarding all the objectives mentioned above.
- (3)
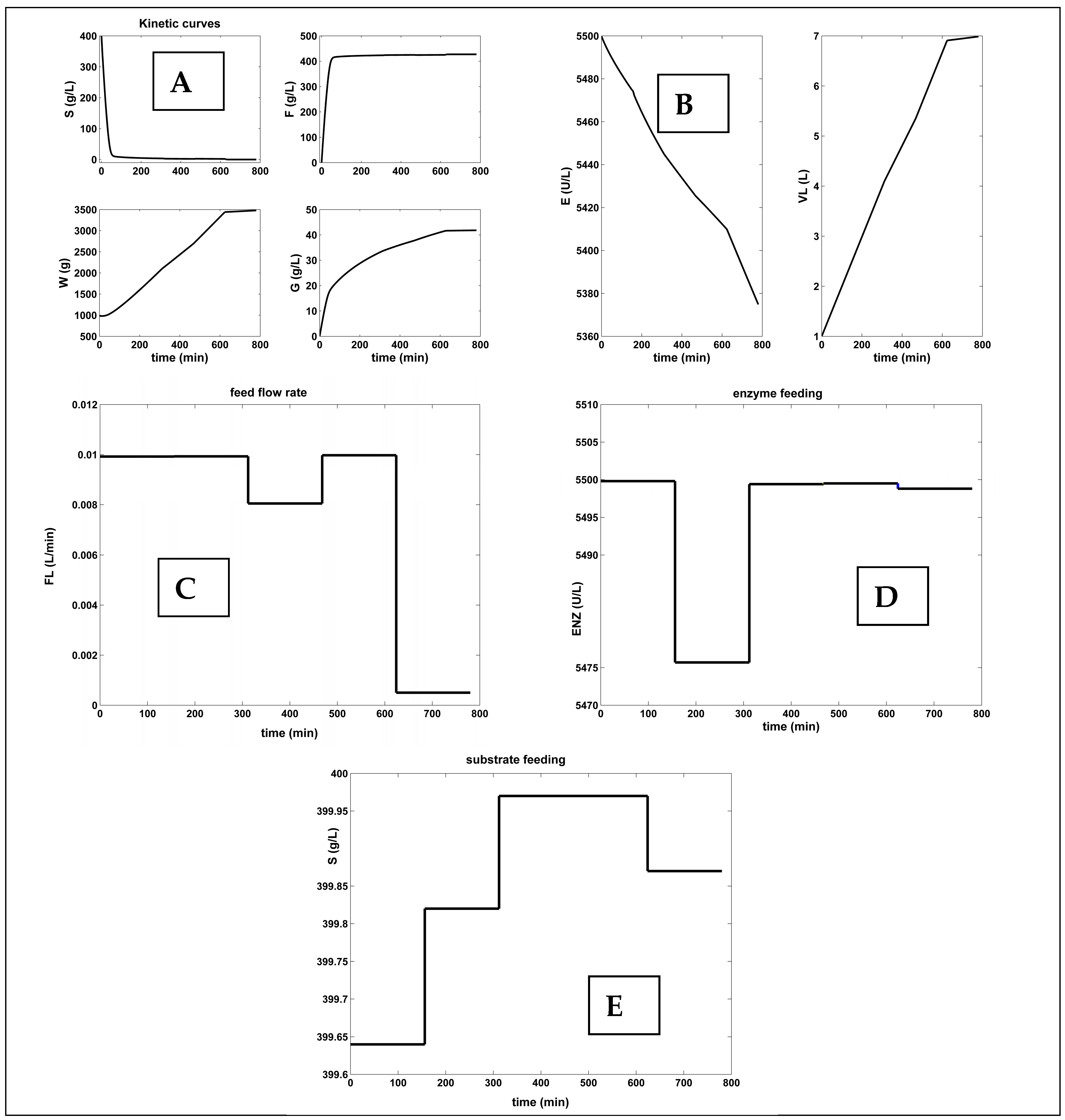
- By analyzing the FBR with an optimal NLP variable feeding, the results are quite modest. In spite of the realized good F-production, compared to the FBR operated with constant but Pareto-optimal feeding, the FBR with an optimal NLP variable feeding reported higher raw-material consumption (90× more enzymes and 13× more substrates).
- (4)
- Of course, enzyme stabilization by immobilization is expected to improve the process performances, as reviewed in the Introduction section [101].
- (5)
- The optimal FBR control strategy is very adaptable, which is because the employed process kinetic model of moderate complexity is flexible enough due to a fairly large number of rate constants. Thus, if significant inconsistencies are observed between the model-predicted bioreactor dynamics and the recorded data, then an intermediate numerical analysis step will be applied to improve the model adequacy (i.e., a ‘model updating’ step), and the bioreactor optimization is applied again with the novel model. This evolutionary adaptation of the enzymatic process model is the so-called ‘tendency modeling’ [34].
| Reactor Operation | Raw-Material Consumption [b] | Max F (Fructose), (g) [b] | Final VL (L) | ||||
|---|---|---|---|---|---|---|---|
| Type | Ndiv | Control Variables | S (Inulin), (g) (Equation (4)) | E (Enzyme) (U) (Equation (4)) | [a] | ||
| BR Non-optimal, Ricca et al. [64] | 1 | Nominal load [c,f] (Figure 4) | 40 | 9.7 (poor) | 41.05 | 1 | |
| [S]o | 40 | ||||||
| [E]o | 9.7 | ||||||
| Wo | 988.4 | ||||||
| BR Optimal load NLP (this paper) [h] | 1 | Initial load [f,b,h] (Figure 3) | 200 | 302 (fairly good) | 213.7 | 2 [g] | |
| [S]o | 200 | ||||||
| [E]o | 301.87 | ||||||
| Wo | 2000 | ||||||
| FBR Constant but optimal NLP feeding (this paper) [d] | 1 | Optimal feeding [f,j] (Figure 4) | 156 | 2145.9 (almost best) | 426.9 | 1.4 | |
| [S]in | 400 | ||||||
| [E]in | 5500 | ||||||
| FL,in | 5 × 10−4 | ||||||
| FBR Constant but Pareto-optimal feeding (this paper) [d] | 1 | Optimal feeding [f,j] | 180.4 | 357.9 (best) | 422.9 | 1.4 | |
| [S]in | 399.88 | ||||||
| [E]in | 793.19 | ||||||
| FL,in | 5.78 × 10−4 | ||||||
| FBR Variable optimal NLP feeding (this paper) [e] | 5 | Optimal feeding [f,j] (Figure 5) | 2393.7 | 3.29 × 104 (high consumptions and dilution) | 428 | 6.98 | |
| [S]in [40–400] | variable Figure 5E | ||||||
| [E]in [97–5500] | variable Figure 5D | ||||||
| FL,in [5 × 10−4–0.01] | variable Figure 5C | ||||||
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations and Notations
| - | species j concentration | |
| , , | - | kinetic model constants |
| k | - | rate constant vector |
| - | molecular weight | |
| - | mass | |
| - | fructose degree of polymerization in the inulin | |
| - | number of time arcs, that is, the number of equal divisions of the batch time for an FBR with variable feeding | |
| - | reaction rate of species j | |
| - | temperature | |
| - | time | |
| - | time interval | |
| - | batch time | |
| VL, VL | - | liquid volume |
| Greeks | ||
| , , , , | - | kinetic model constants |
| - | finite difference | |
| νij | - | the stoichiometric coefficient of species j in reaction i |
| Ω | - | optimization objective function |
| - | density | |
| Index | ||
| In, inlet | - | inlet |
| 0,o | - | initial |
| S, F, W, E, G | - | substrate, fructose, water, enzyme, and glucose, respectively |
| Abbreviations | ||
| BR | - | batch reactor |
| BRP | - | BR with intermittent addition of enzyme solution |
| E, ENZ | - | enzyme |
| F | - | fructose |
| FBR | - | Fed-batch reactor |
| G | - | glucose |
| HFCS | - | high fructose-glucose syrup |
| HFS | - | high fructose syrup |
| kDG | - | keto D-glucose (D-glucosone) |
| Max | - | maximum |
| NLP | - | nonlinear programming |
| P2Ox | - | pyranose 2-oxidase |
| P2Oxox | - | inactive form of P2Ox |
| S | - | substrate (inulin) |
| SBR | - | semi-batch reactor |
| W | - | water |
References
- Moulijn, J.A.; Makkee, M.; van Diepen, A. Chemical Process Technology; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Wang, P. Multi-scale features in recent development of enzymic biocatalyst systems. Appl. Biochem. Biotechnol. 2009, 152, 343–352. [Google Scholar] [CrossRef] [PubMed]
- Vasić-Rački, D.; Findrik, Z.; Presečki, A.V. Modelling as a tool of enzyme reaction engineering for enzyme reactor development. Appl. Microbiol. Biotechnol. 2011, 91, 845–856. [Google Scholar] [CrossRef] [PubMed]
- Maria, G. A review of algorithms and trends in kinetic model identification for chemical and biochemical systems. Chem. Biochem. Eng. Q. 2004, 18, 195–222. [Google Scholar]
- Gernaey, K.V.; Lantz, A.E.; Tufvesson, P.; Woodley, J.M.; Sin, G. Application of mechanistic models to fermentation and biocatalysis for next-generation processes. Trends Biotechnol. 2010, 28, 346–354. [Google Scholar] [CrossRef] [PubMed]
- Bonvin, D.; Srinivasan, B.; Hunkeler, D. Control and optimization of batch processes. IEEE Control. Syst. Mag. Dec. 2006, 34–45. Available online: https://www.researchgate.net/publication/37426142_Control_and_Optimization_of_Batch_Processes_Improvement_of_Process_Operation_in_the_Production_of_Specialty_Chemicals (accessed on 3 March 2025).
- Srinivasan, B.; Primus, C.J.; Bonvin, D.; Ricker, N.L. Run-to-run optimization via control of generalized constraints. Control. Eng. Pract. 2001, 9, 911–919.ec. [Google Scholar] [CrossRef]
- Dewasme, L.; Amribt, Z.; Santos, L.O.; Hantson, A.L.; Bogaerts, P.; Wouwer, A.V. Hybridoma cell culture optimization using nonlinear model predictive control. Int. Fed. Autom. Control. 2013, 46, 60–65. [Google Scholar] [CrossRef]
- Dewasme, L.; Cote, F.; Filee, P.; Hantson, A.L.; Wouwer, A.V. Macroscopic dynamic modeling of sequential batch cultures of hybridoma cells: An experimental validation. Bioengineering 2017, 4, 17. [Google Scholar] [CrossRef]
- Mendes, R.; Rocha, I.; Pinto, J.P.; Ferreira, E.C.; Rocha, M. Differential evolution for the offline and online optimization of fed-batch fermentation processes. In Advances in Differential Evolution; Studies in Computational Intelligence; Chakraborty, U.K., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 299–317. [Google Scholar]
- Liu, Y.; Gunawan, R. Bioprocess optimization under uncertainty using ensemble modeling. J. Biotechnol. 2017, 244, 34–44. [Google Scholar] [CrossRef]
- Hartig, F.; Keil, F.J.; Luus, R. Comparison of optimization methods for a fed-batch reactor. Hung. J. Ind. Chem. 1996, 23, 81–160. [Google Scholar]
- Amribt, Z.; Dewasme, L.; Wouwer, A.V.; Bogaerts, P. Optimization and robustness analysis of hybridoma cell fed-batch cultures using the overflow metabolism model. Bioprocess Biosyst. Eng. 2014, 37, 1637–1652. [Google Scholar] [CrossRef] [PubMed]
- Bonvin, D. Optimal operation of batch reactors—A personal view. J. Process Control. 1998, 8, 355–368. [Google Scholar] [CrossRef]
- Bonvin, D. Real-Time Optimization; MDPI: Basel, Switzerland, 2017. [Google Scholar]
- DiBiasio, D. Introduction to the control of biological reactors. In Chemical Engineering Problems in Biotechnology; Shuler, M.L., Ed.; American Institute of Chemical Engineers: New York, NY, USA, 1989; pp. 351–391. [Google Scholar]
- Abel, O.; Marquardt, W. Scenario-integrated on-line optimisation of batch reactors. J. Process Control. 2003, 13, 703–715. [Google Scholar] [CrossRef]
- Lee, J.; Lee, K.S.; Lee, J.H.; Park, S. An on-line batch span minimization and quality control strategy for batch and semi-batch processes. Control Eng. Pract. 2001, 9, 901–909. [Google Scholar] [CrossRef]
- Ruppen, D.; Bonvin, D.; Rippin, D.W.T. Implementation of adaptive optimal operation for a semi-batch reaction system. Comput. Chem. Eng. 1998, 22, 185–199. [Google Scholar] [CrossRef]
- Loeblein, C.; Perkins, J.; Srinivasan, B.; Bonvin, D. Performance analysis of on-line batch optimization systems. Comput. Chem. Eng. 1997, 21, S867–S872. [Google Scholar] [CrossRef]
- Rao, M.; Qiu, H. Process Control Engineering: A Textbook for Chemical, Mechanical and Electrical Engineers; Gordon and Breach Science: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Maria, G. Enzymatic reactor selection and derivation of the optimal operation policy, by using a model-based modular simulation platform. Comput. Chem. Eng. 2012, 36, 325–341. [Google Scholar] [CrossRef]
- Maria, G. Model-based optimization of a fed-batch bioreactor for mAb production using a hybridoma cell culture. Molecules 2020, 25, 5648–5674. [Google Scholar] [CrossRef]
- Koutinas, M.; Kiparissides, A.; Pistikopoulos, E.N.; Mantalaris, A. Bioprocess systems engineering: Transferring traditional process engineering principles to industrial biotechnology. Comput. Struct. Biotechnol. J. 2012, 3, e201210022. [Google Scholar] [CrossRef]
- Maria, G. Model-based optimisation of a batch reactor with a coupled bi-enzymatic process for mannitol production. Comput. Chem. Eng. 2020, 133, 106628–106635. [Google Scholar] [CrossRef]
- Wang, C.; Quan, H.; Xu, X. Optimal design of multiproduct batch chemical process using genetic algorithms. Ind. Eng. Chem. Res. 1996, 35, 3560–3566. [Google Scholar] [CrossRef]
- Srinivasan, B.; Bonvin, D.; Visser, E.; Palanki, S. Dynamic optimization of batch processes: II. Role of measurements in handling uncertainty. Comput. Chem. Eng. 2003, 27, 27–44. [Google Scholar] [CrossRef]
- Ozturk, S.S.; Palsson, B.O. Effect of initial cell density on hybridoma growth, metabolism, and monoclonal antibody production. J. Biotechnol. 1990, 16, 259–278. [Google Scholar] [CrossRef] [PubMed]
- Martinez, E. Batch-to-batch optimization of batch processes using the STATSIMPLEX search method. In Proceedings of the 2nd Mercosur Congress on Chemical Engineering, Rio de Janeiro, Costa Verde, Brasil, 14–18 August 2005. paper #20. [Google Scholar]
- Engasser, J.M. Bioreactor engineering: The design and optimization of reactors with living cells. Chem. Eng. Sci. 1988, 43, 1739–1748. [Google Scholar] [CrossRef]
- Lübbert, A.; Jørgensen, S.B. Bioreactor performance: A more scientific approach for practice. J. Biotechnol. 2001, 85, 187–212. [Google Scholar] [CrossRef]
- Binette, J.C.; Srinivasan, B. On the use of nonlinear model predictive control without parameter adaptation for batch processes. Processes 2016, 4, 27. [Google Scholar] [CrossRef]
- Maria, G.; Peptanaru, I.M. Model-based optimization of mannitol production by using a sequence of batch reactors for a coupled bi-enzymatic process—A dynamic approach. Dynamics 2021, 1, 134–154. [Google Scholar] [CrossRef]
- Fotopoulos, J.; Georgakis, C.; Stenger, H.G., Jr. Uncertainty Issues in the Modeling and Optimization of Batch Reactors with Tendency Models. Chem. Eng. Sci. 1994, 49, 5533–5547. [Google Scholar] [CrossRef]
- Smets, I.Y.; Claes, J.E.; November, E.J.; Bastin, G.P.; van Impe, J.F. Optimal adaptive control of (bio)chemical reactors: Past, present and future. J. Process Control. 2004, 14, 795–805. [Google Scholar] [CrossRef]
- Maria, G.; Crisan, M. Evaluation of optimal operation alternatives of reactors used for D-glucose oxidation in a bi-enzymatic system with a complex deactivation kinetics. Asia-Pac. J Chem Eng. 2014, 10, 22–44. [Google Scholar] [CrossRef]
- Franco-Lara, E.; Weuster-Botz, D. Estimation of optimal feeding strategies for fed-batch bioprocesses, Estimation of optimal feeding strategies for fed-batch bioprocesses. Bioprocess Biosyst. Eng. 2005, 28, 71–77. [Google Scholar] [CrossRef][Green Version]
- Maria, G.; Renea, L. Tryptophan production maximization in a fed-batch bioreactor with modified E. coli cells, by optimizing its operating policy based on an extended structured cell kinetic model. Bioengineering 2021, 8, 210–247. [Google Scholar] [CrossRef] [PubMed]
- Dan, A.; Maria, G. Pareto Optimal Operating Solutions for a Semibatch Reactor Based on Failure Probability Indices. Chem. Eng. Technol. 2012, 35, 1098–1103. [Google Scholar] [CrossRef]
- Avili, M.G.; Fazaelipoor, M.H.; Jafari, S.A.; Ataei, S.A. Comparison between batch and fed-batch production of rhamnolipid by Pseudomonas aeruginosai. Iran. J. Biotechnol. 2012, 10, 263–269. [Google Scholar]
- Koller, M. A review on established and emerging fermentation schemes for microbial production of polyhydroxyalkanoate (PHA) biopolyesters. Fermentation 2018, 4, 30. [Google Scholar] [CrossRef]
- Akinterinwa, O.; Khankal, R.; Cirino, P.C. Metabolic engineering for bioproduction of sugar alcohols. Curr. Opin. Biotechnol. 2008, 19, 461–467. [Google Scholar] [CrossRef]
- Fu, Y.; Ding, L.; Singleton, M.L.; Idrissi, H.; Hermans, S. Synergistic effects altering reaction pathways: The case of glucose hydrogenation over Fe-Ni catalysts. Appl. Catal. B Environ. 2021, 288, 119997. [Google Scholar] [CrossRef]
- Ahmed, M.J.; Hameed, B.H. Hydrogenation of glucose and fructose into hexitols over heterogeneous catalysts, A review. J. Taiwan Inst. Chem. Eng. 2019, 96, 341–352. [Google Scholar] [CrossRef]
- Liese, A.; Seelbach, K.; Wandrey, C. (Eds.) Industrial Biotransformations; Wiley-VCH: Weinheim, Germany, 2006. [Google Scholar]
- Myande Comp. Fructose Syrup Production, China. 2024. Available online: https://www.myandegroup.com/starch-sugar-technology?ad_account_id=755-012-8242&gad_source=1 (accessed on 3 March 2025).
- Marianou, A.A.; Michailof, C.M.; Pineda, A.; Iliopoulou, E.F.; Triantafyllidis, K.S.; Lappas, A.A. Glucose to fructose isomerization in aqueous media over homogeneous and heterogeneous catalysts. ChemCatChem 2016, 8, 1100–1110. [Google Scholar] [CrossRef]
- Hanover, L.M.; White, J.S. Manufacturing, composition, and applications of fructose. Am. J. Clin. Nutr. 1993, 58, 724S–732S. [Google Scholar] [CrossRef]
- Leitner, C.; Neuhauser, W.; Volc, J.; Kulbe, K.D.; Nidetzky, B.; Haltrich, D. The Cetus process revisited: A novel enzymatic alternative for the production of aldose-free D-fructose. Biocatal. Biotransform. 1998, 16, 365–382. [Google Scholar] [CrossRef]
- Shaked, Z.; Wolfe, S. Stabilization of pyranose 2-oxidase and catalase by chemical modification. Methods Enz. 1988, 137, 599–615. Available online: http://www.eng.tau.ac.il/~brauner/Workshop08Participant/Example-7/Prob-14-13.pdf (accessed on 3 March 2025).
- Maria, G.; Ene, M.D.; Jipa, I. Modelling enzymatic oxidation of D-glucose with pyranose 2-oxidase in the presence of catalase. J. Mol. Catal. B Enzym. 2012, 74, 209–218. [Google Scholar] [CrossRef]
- Bannwarth, M.; Heckmann-Pohl, D.; Bastian, S.; Giffhorn, F.; Schulz, G.E. Reaction geometry and thermostable variant of pyranose 2-oxidase from the white-rot fungus Peniophora sp. Biochemistry 2006, 45, 6587–6595. [Google Scholar] [CrossRef]
- Maria, G.; Ene, M.D. Modelling enzymatic reduction of 2-keto-D-glucose by suspended aldose reductase. Chem. Biochem. Eng. Q. 2013, 27, 385–395. [Google Scholar]
- Chenault, H.K.; Whitesides, G.M. Regeneration of nicotinamide cofactors for use in organic synthesis. Appl. Biochem. Biotechnol. 1987, 14, 147–197. [Google Scholar] [CrossRef]
- Parmentier, S.; Arnaut, F.; Soetaert, W.; Vandamme, E.J. Enzymatic production of D-mannitol with the Leuconostoc pseudomesenteroides mannitol dehydrogenase coupled to a coenzyme regeneration system. Biocatal. Biotransform. 2005, 23, 1–7. [Google Scholar] [CrossRef]
- Gijiu, C.L.; Maria, G.; Renea, L. Pareto optimal operating policies of a batch bi-enzymatic reactor for mannitol production. Chem. Eng. Technol. 2024, 48, e202300555. [Google Scholar] [CrossRef]
- Leonida, M.D. Redox enzymes used in chiral syntheses coupled to coenzyme regeneration. Curr. Med. Chem. 2001, 8, 345–369. [Google Scholar] [CrossRef]
- Liu, W.; Wang, P. Cofactor regeneration for sustainable enzymatic biosynthesis. Biotechnol. Adv. 2007, 25, 369–384. [Google Scholar] [CrossRef]
- Berenguer-Murcia, A.; Fernandez-Lafuente, R. New trends in the recycling of NAD(P)H for the design of sustainable asymmetric reductions catalyzed by dehydrogenases. Curr. Org. Chem. 2010, 14, 1000–1021. [Google Scholar] [CrossRef]
- Ghoreishi, S.M.; Shahrestani, R.G. Innovative strategies for engineering mannitol production. Trends Food Sci. Technol. 2009, 20, 263–270. [Google Scholar] [CrossRef]
- Roberfroid, M. Inulin-Type Fructans; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Ricca, E.; Calabro, V.; Curcio, S.; Iorio, G. The state of the art in the production of fructose from inulin enzymatic hydrolysis. Crit. Rev. Biotechnol. 2007, 27, 129–145. [Google Scholar] [CrossRef]
- Ricca, E.; Calabro, V.; Curcio, S.; Iorio, G. Fructose production by chicory inulin enzymatic hydrolysis: A kinetic study and reaction mechanism. Process Biochem. 2009, 44, 466–470. [Google Scholar] [CrossRef]
- Ricca, E.; Calabrò, V.; Curcio, S.; Iorio, G. Optimization of inulin hydrolysis by inulinase accounting for enzyme time- and temperature-dependent deactivation. Biochem. Eng. J. 2009, 48, 81–86. [Google Scholar] [CrossRef]
- Dıaz, E.G.; Catana, R.; Ferreira, B.S.; Luque, S.; Fernandes, P.; Cabral, J.M.S. Towards the development of a membrane reactor for enzymatic inulin hydrolysis. J. Membr. Sci. 2006, 273, 152–158. [Google Scholar] [CrossRef]
- Rocha, J.R.; Catana, R.; Ferreira, B.S.; Cabral, J.M.S.; Fernandes, P. Design and characterisation of an enzyme system for inulin hydrolysis. Food Chem. 2006, 95, 77–82. [Google Scholar] [CrossRef]
- Phelps, C.F. The physical properties of inulin solutions. Biochem. J. 1965, 95, 41–47. [Google Scholar] [CrossRef]
- Toneli, J.T.C.L.; Park, K.J.; Murr, F.E.X.; Martinelli, P.O. Rheological bahavior of concentrated inulin solution: Influence of soluble solids concentration and temperature. J. Texture Stud. 2008, 39, 369–392. [Google Scholar] [CrossRef]
- Bot, A.; Erle, U.; Vreeker, R.; Agterof, W.G.M. Influence of crystallisation conditions on the large deformation rheology of inulin gels. Food Hydrocoll. 2004, 18, 547–556. [Google Scholar] [CrossRef]
- Bendayan, M.; Rasio, E.A. Transport of insulin and albumin by the microvascular endothelium of the rete mirabile. J. Cell Sci. 1996, 109, 1857–1864. [Google Scholar] [CrossRef] [PubMed]
- Silva, A.T.C.R. Fructose solubility in water and ethanol/water. In Proceedings of the AIChE Meeting, Tampa, FL, USA, 8–13 November 2009; p. 1543. [Google Scholar]
- Chen, J.C.P.; Chou, G.C. Chen-Chou Cane Sugar Handbook; Wiley: New York, NY, USA, 1993; p. 24. [Google Scholar]
- Okutomi, T.; Nemoto, M.; Mishiba, E.; Goto, F. Viscosity of diluent and sensory -level of subarachnoid anaesthesia achieved with tetracaine. Can. J. Anesth. 1998, 45, 84–86. [Google Scholar] [CrossRef]
- Giordano, R.L.C.; Giordano, R.C.; Cooney, C.L. A study on intra-particle diffusion effects in enzymatic reactions: Glucose-fructose isomerisation. Bioprocess Eng. 2000, 23, 159–166. [Google Scholar] [CrossRef]
- Santos, A.M.P.; Oliveira, M.G.; Maugeri, F. Modelling thermal stability and activity of free and immobilized enzymes as a novel tool for enzyme reactor design. Bioresour. Technol. 2007, 98, 3142–3148. [Google Scholar] [CrossRef] [PubMed]
- Catana, R.; Eloy, M.; Rocha, J.R.; Ferreira, B.S.; Cabral, J.M.S.; Fernandes, P. Stability evaluation of an immobilized enzyme system for inulin hydrolysis. Food Chem. 2007, 101, 260–266. [Google Scholar] [CrossRef]
- Kim, W.Y.; Byun, S.M.; Uhm, T.B. Hydrolysis of inulin from Jerusalem artichoke by inulinase immobilized on aminoethylcellulose. Enzym. Microb. Technol. 1982, 4, 239–244. [Google Scholar] [CrossRef]
- Kim, C.H.; Rhee, S.K. Fructose production from Jerusalem artichoke by inulinase immobilized on chitin. Biotechnol. Lett. 1989, 11, 201–206. [Google Scholar] [CrossRef]
- Nakamura, T.; Ogata, Y.; Shitara, A.; Nakamura, A.; Ohta, K. Continuous Production of Fructose Syrups from Inulin by Immobilized Inulinase from Aspergillus niger Mutant 817. Jl. Ferment. Bioeng. 1995, 80, 164–169. [Google Scholar] [CrossRef]
- Yun, J.W.; Kim, D.H.; Kim, B.W.; Song, S.K. Production of inulo-oligosaccharides from inulin by immobilized endoinulinase from Pseudomonas sp. J. Ferment. Bioeng. 1997, 84, 369–371. [Google Scholar] [CrossRef]
- Gupta, A.K.; Singh, D.P.; Kaur, N.; Singh, R. Production, purification and immobilisation of inulinase from Kluyveromyces fragilis. J. Chem. Tech. Biotechnol. 1994, 59, 377–385. [Google Scholar] [CrossRef]
- Wenling, W.; Huiying, W.W.L.; Shiyuan, W. Continuous preparation of fructose syrups from Jerusalem artichoke tuber using immobilized intracellular inulinase from Kluyveromyces sp. Y-85. Process Biochem. 1999, 34, 643–646. [Google Scholar] [CrossRef]
- Workman, W.E.; Day, D.F. Enzymatic hydrolysis of inulin to fructose by glutaraldehyde fixed yeast cells. Biotechnol. Bioeng. 1984, 26, 905–910. [Google Scholar] [CrossRef]
- Akbas, M.Y.; Stark, B.C. Recent trends in bioethanol production from food processing byproducts. J. Ind. Microbiol. Biotechnol. 2016, 43, 1593–1609. [Google Scholar] [CrossRef] [PubMed]
- Tewari, Y.B.; Goldberg, R.N. Thermodynamics of the conversion of aqueous glucose to fructose. Appl. Biochem. Biotechnol. 1985, 11, 17–24. [Google Scholar] [CrossRef]
- Illanes, A.; Zúñiga, M.E.; Contreras, S.; Guerrero, A. Reactor design for the enzymatic isomerization of glucose to fructose. Bioprocess Biosyst. Eng. 1992, 7, 199–204. [Google Scholar] [CrossRef]
- Lee, H.S.; Hong, J. Kinetics of glucose isomerization to fructose by immobilized glucose isomerase: Anomeric reactivity of D-glucose in kinetic model. J. Biotechnol. 2000, 84, 145–153. [Google Scholar] [CrossRef]
- Straathof, A.J.J.; Adlercreutz, P. Applied Biocatalysis; Harwood Academic Publisher: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Dehkordi, A.M.; Safari, I.; Karima, M.M. Experimental and modeling study of catalytic reaction of glucose isomerization: Kinetics and packed-bed dynamic modelling. AIChE J. 2008, 54, 1333–1343. [Google Scholar] [CrossRef]
- Bishop, M. An Introduction to Chemistry; Chiral Publisher: Raleigh, NC, USA, 2013; Available online: https://preparatorychemistry.com/Bishop_contact.html (accessed on 3 March 2025).
- Laos, K.; Harak, M. The viscosity of supersaturated aqueous glucose, fructose and glucose-fructose solutions. J. Food Phys. 2014, 27, 27–30. [Google Scholar]
- Viet Bui, A.; Nguyen, M.H. Prediction of viscosity of glucose and calcium chloride solutions. J. Food Eng. 2004, 62, 345–349. [Google Scholar]
- Maria, G.; Renea, L.; Gheorghe, D. In-Silico optimization of a FBR for ethanol production by using several algorithms and operating alternatives. Rev. Roum. Chim. 2024, 70. in press. [Google Scholar]
- Moser, A. Bioprocess Technology—Kinetics and Reactors; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Dutta, R. Fundamentals of Biochemical Engineering; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Maria, G.; Renea, L.; Maria, C. Multi-objective optimization of the fed-batch bi-enzymatic reactor for mannitol production. Dynamics 2022, 2, 270–294. [Google Scholar] [CrossRef]
- Rao, S.S. Engineering Optimization—Theory and Practice; Wiley: New York, NY, USA, 2009; Chapter 14.10. [Google Scholar]
- Dan, A.; Maria, G. Pareto optimal operating solutions for a catalytic reactor for butane oxidation based on safety indices. U.P.B. Sci. Bull. Series B—Chemie 2014, 76, 35–48. Available online: http://www.scientificbulletin.upb.ro/ (accessed on 3 March 2025).
- Maria, G. Adaptive Random Search and Short-Cut Techniques for Process Model Identification and Monitoring. AIChE Symp. Ser. 1998, 94, 351–359. [Google Scholar]
- Maria, G. ARS combination with an evolutionary algorithm for solving MINLP optimization problems. In Modelling, Identification and Control; Hamza, M.H., Ed.; IASTED/ACTA Press: Anaheim, CA, USA, 2003; pp. 112–118. [Google Scholar]
- Bickerstaff, G.F. (Ed.) Immobilization of Enzymeas and Cells; Humana Press Inc.: Totowa, NJ, USA, 1997. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gheorghe, D.; Maria, G.; Renea, L.; Muscalu, C. The In Silico Optimization of a Fed-Batch Reactor Used for the Enzymatic Hydrolysis of Chicory Inulin to Fructose by Employing a Dynamic Approach. Dynamics 2025, 5, 10. https://doi.org/10.3390/dynamics5010010
Gheorghe D, Maria G, Renea L, Muscalu C. The In Silico Optimization of a Fed-Batch Reactor Used for the Enzymatic Hydrolysis of Chicory Inulin to Fructose by Employing a Dynamic Approach. Dynamics. 2025; 5(1):10. https://doi.org/10.3390/dynamics5010010
Chicago/Turabian StyleGheorghe, Daniela, Gheorghe Maria, Laura Renea, and Crina Muscalu. 2025. "The In Silico Optimization of a Fed-Batch Reactor Used for the Enzymatic Hydrolysis of Chicory Inulin to Fructose by Employing a Dynamic Approach" Dynamics 5, no. 1: 10. https://doi.org/10.3390/dynamics5010010
APA StyleGheorghe, D., Maria, G., Renea, L., & Muscalu, C. (2025). The In Silico Optimization of a Fed-Batch Reactor Used for the Enzymatic Hydrolysis of Chicory Inulin to Fructose by Employing a Dynamic Approach. Dynamics, 5(1), 10. https://doi.org/10.3390/dynamics5010010








