An Innovative Technique for Energy Assessment of a Highly Efficient Photovoltaic Module
Abstract
:1. Introduction
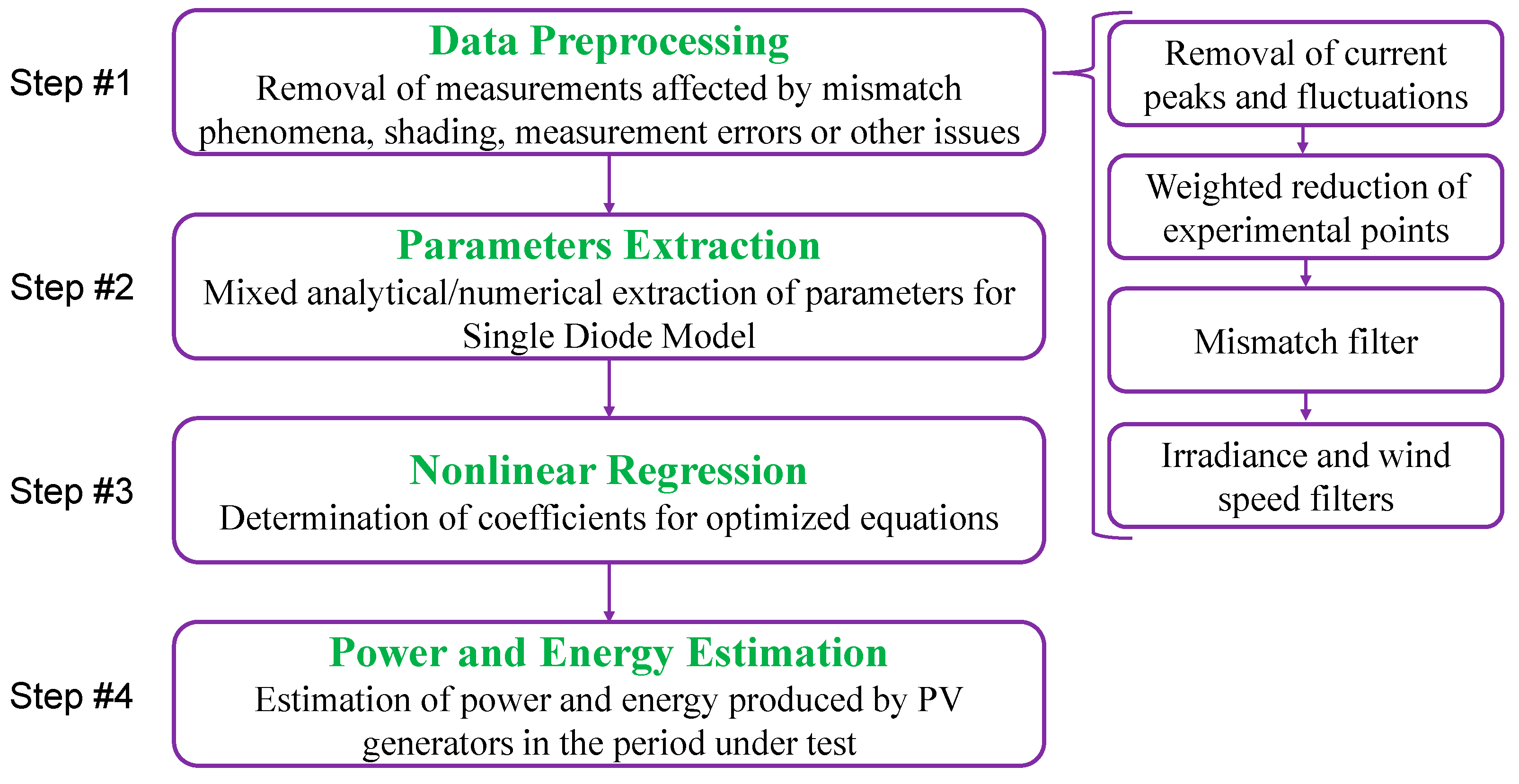
2. Innovative Methodology
2.1. Step #1—Data Preprocessing
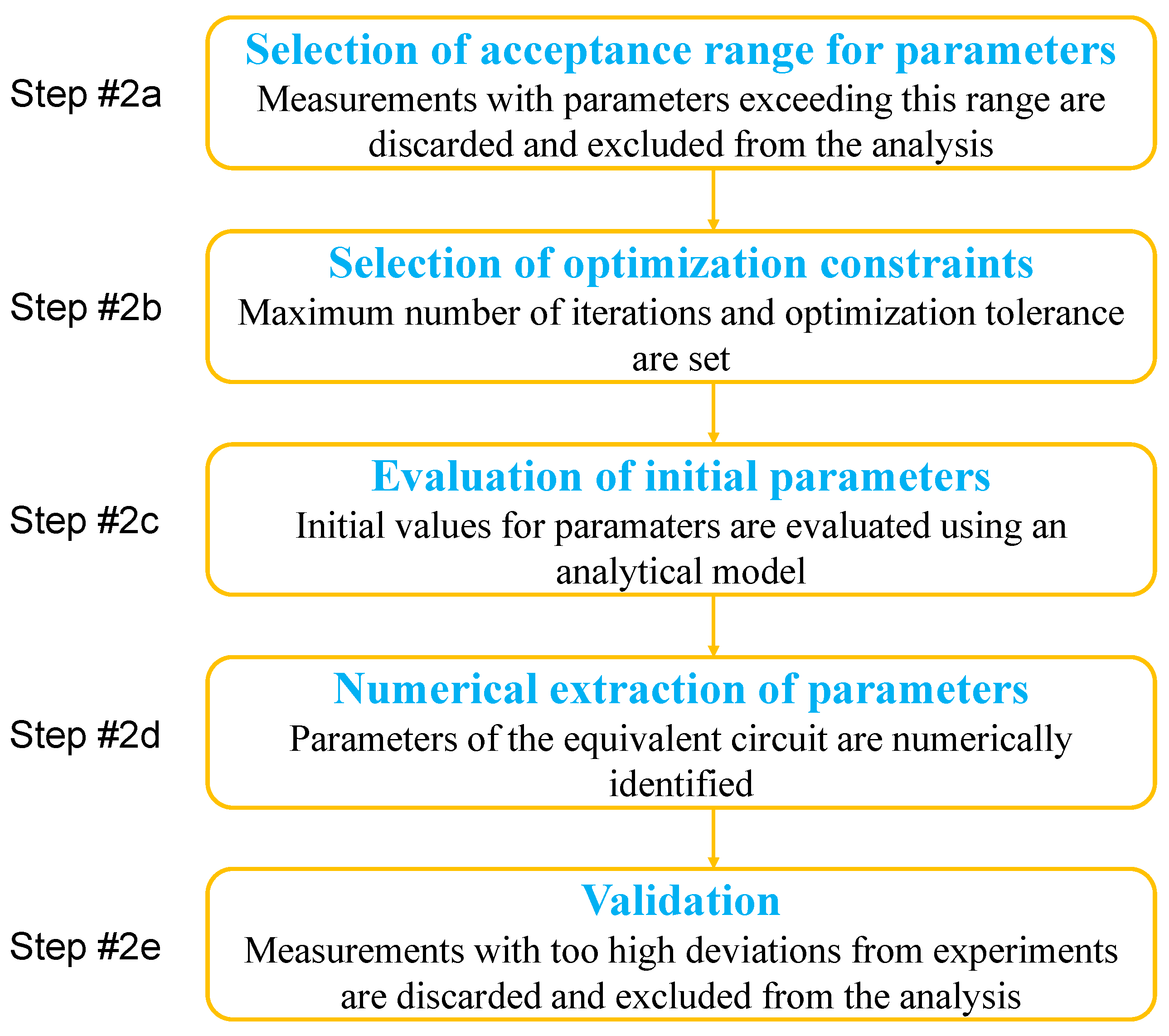
2.2. Step #2—Parameters Extraction
2.3. Step #3—Nonlinear Regression
2.4. Step #4—Power and energy estimation
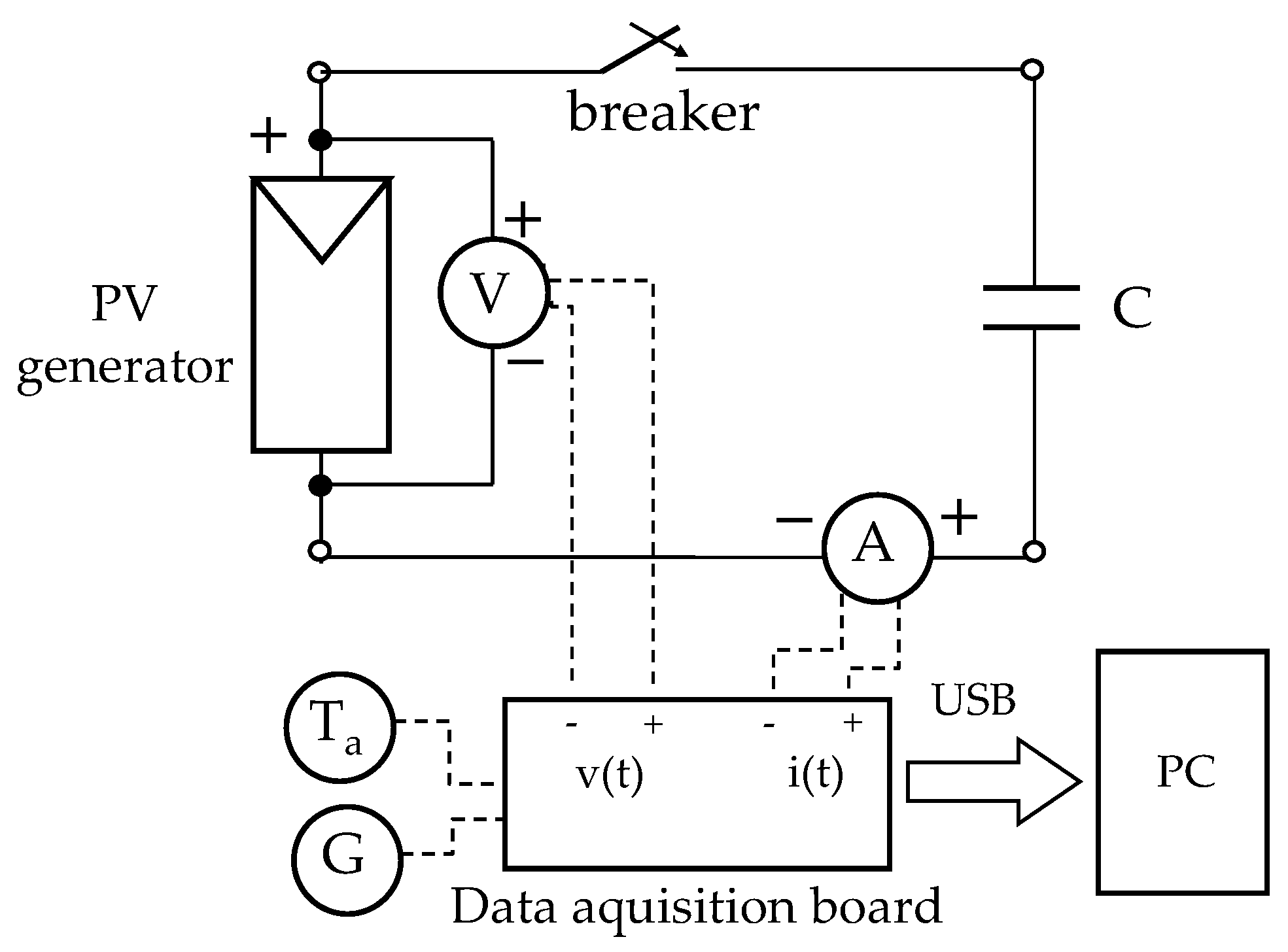
3. Measurement System
- A notebook PC with a LabVIEW software to emulate a digital storage oscilloscope.
- A multifunction data acquisition board with one A/D converter (successive approximation technology, 16 bit-resolution, sampling rate up to 1.25 MSa/s, maximum input of ±10 V, internal amplifier gains for lower ranges) and multiplexer.
- A differential voltage probe with two attenuation ratios 20:1 and 200:1 for voltage levels up to 140 V and 1400 V, respectively.
- Two current probes (Hall effect) with an output sensitivity of 100 mV/A for current values up to ±30 A, one for current measurement and the other one for trigger source.
- A pyranometer to acquire irradiance with uncertainty < 2%.
- A thermometer to acquire ambient temperature.
- A temperature probe to acquire the temperature on the rear side of the module.
- A capacitive load with capacitance equal to 10 mF.
4. PV Module under Test
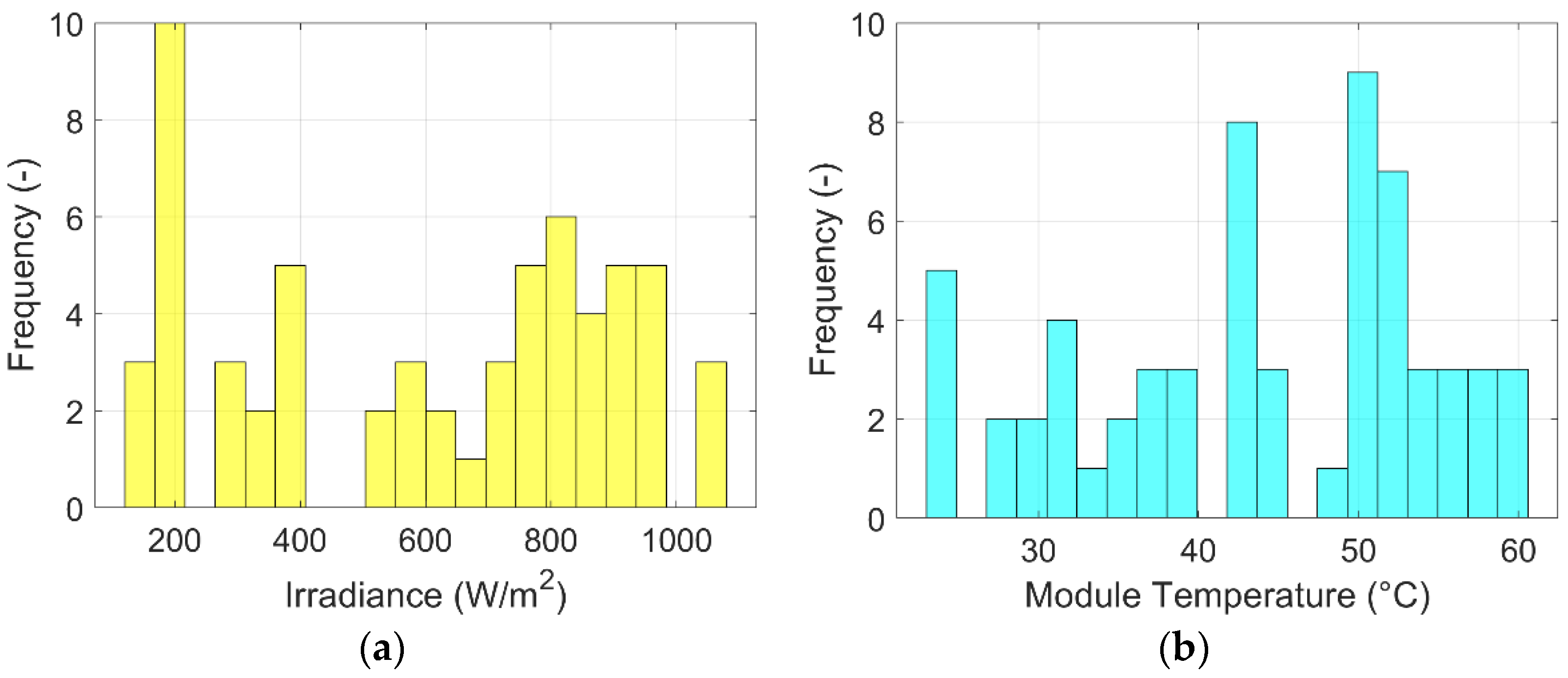
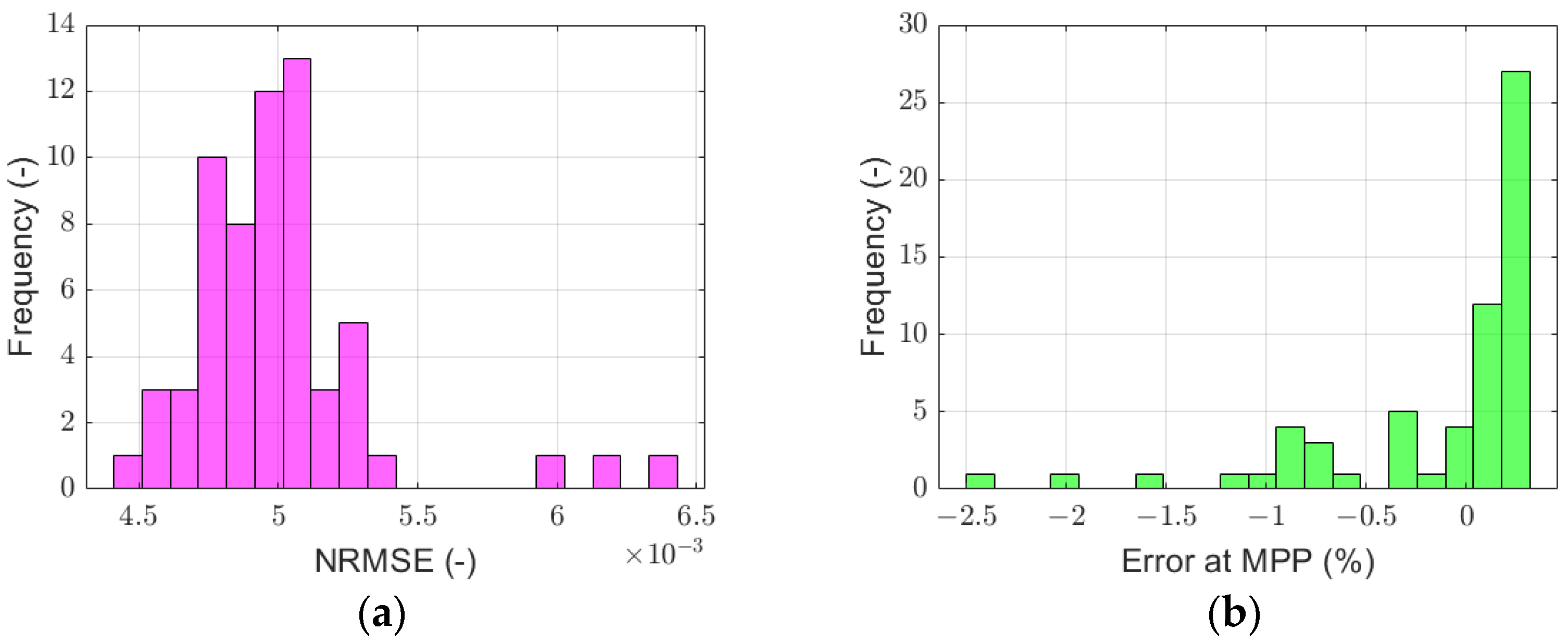
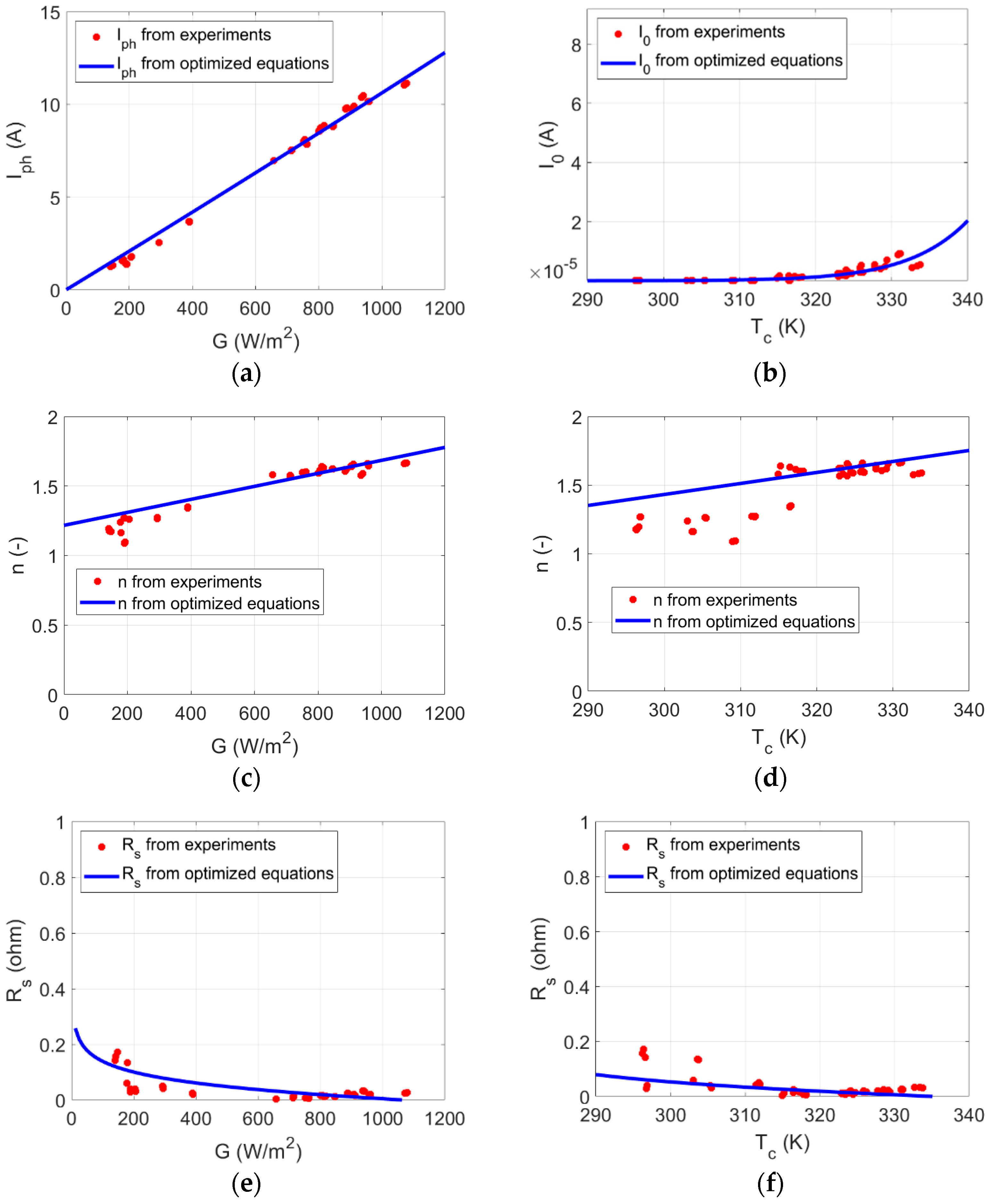
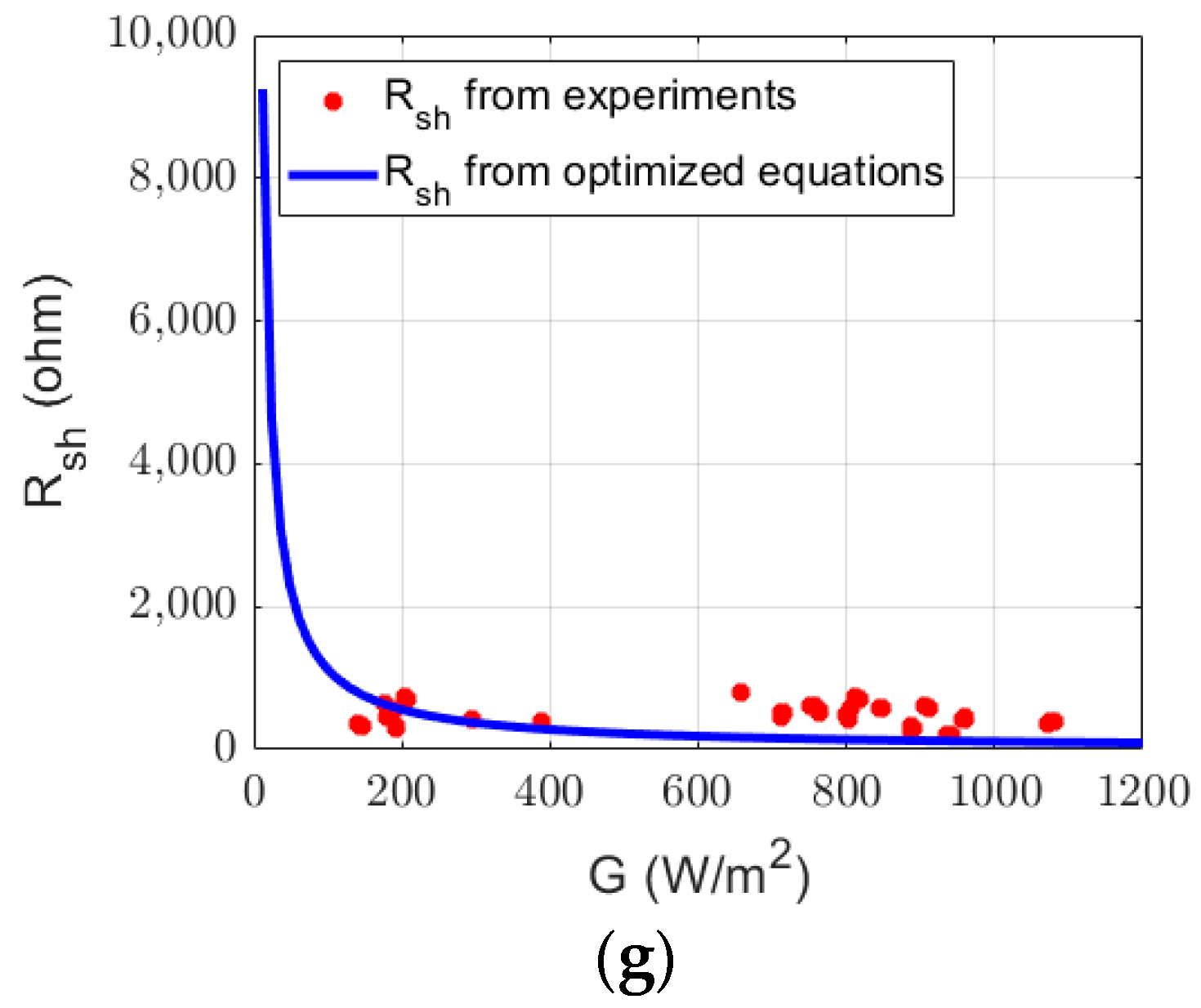
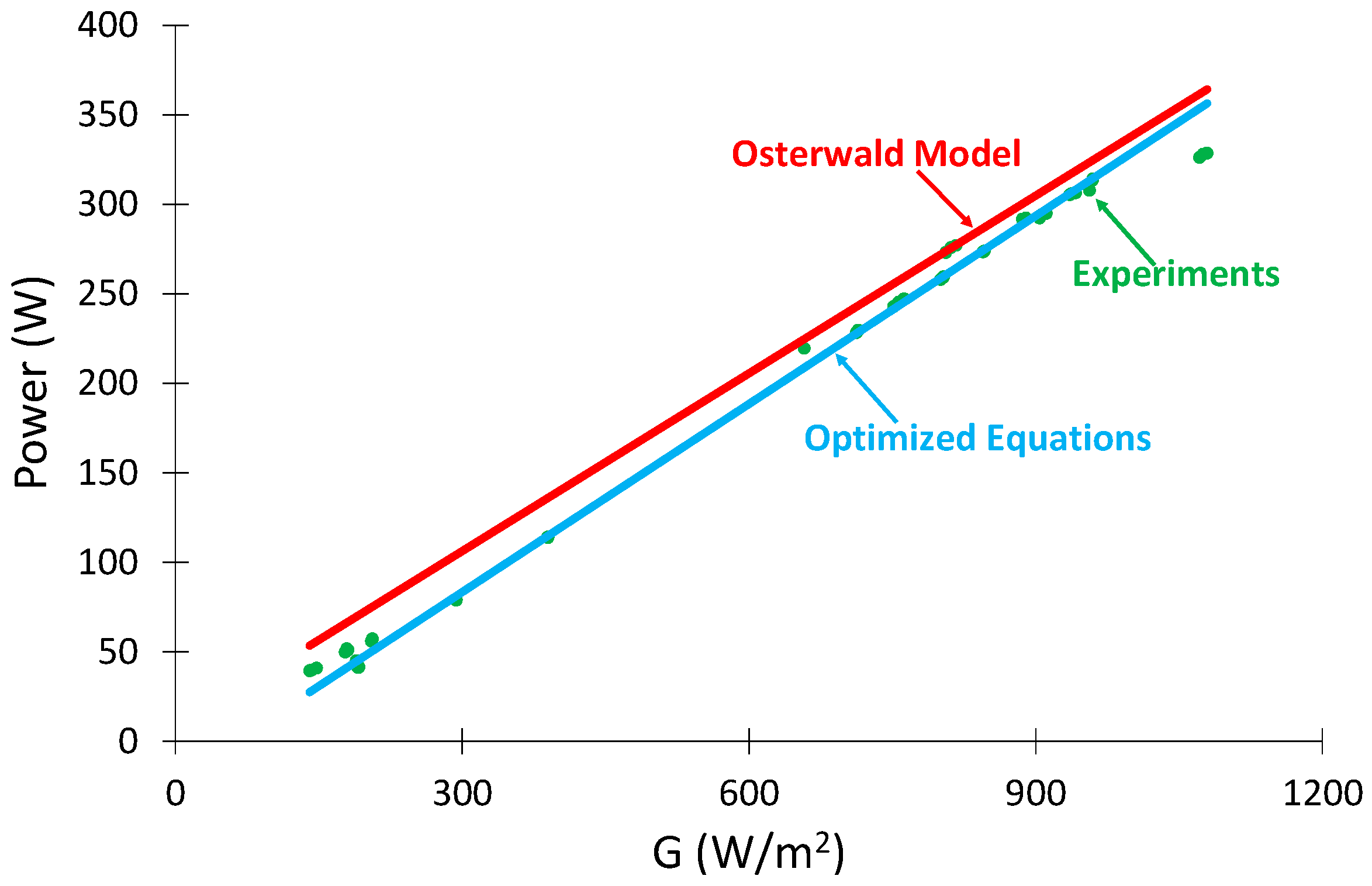
5. Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Di Leo, P.; Spertino, F.; Fichera, S.; Malgaroli, G.; Ratclif, A. Improvement of Self-Sufficiency for an Innovative Nearly Zero Energy Building by Photovoltaic Generators. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019. [Google Scholar]
- Ciocia, A.; Amato, A.; Di Leo, P.; Fichera, S.; Malgaroli, G.; Spertino, F.; Tzanova, S. Self-Consumption and Self-Sufficiency in Photovoltaic Systems: Effect of Grid Limitation and Storage Installation. Energies 2021, 14, 1591. [Google Scholar] [CrossRef]
- Spertino, F.; Fichera, S.; Ciocia, A.; Malgaroli, G.; Di Leo, P.; Ratclif, A. Toward the Complete Self-Sufficiency of an NZEBS Microgrid by Photovoltaic Generators and Heat Pumps: Methods and Applications. IEEE Trans. Ind. Appl. 2019, 55, 7028–7040. [Google Scholar] [CrossRef]
- Bahrami, M.; Gavagsaz-Ghoachani, R.; Zandi, M.; Phattanasak, M.; Maranzana, G.; Nahid-Mobarakeh, B.; Pierfederici, S.; Meibody-Tabar, F. Hybrid Maximum Power Point Tracking Algorithm with Improved Dynamic Performance. Renew. Energy 2019, 130, 982–991. [Google Scholar] [CrossRef]
- Harrag, A.; Messalti, S. Extraction of Solar Cell Parameters Using Genetic Algorithm. In Proceedings of the 2015 4th International Conference on Electrical Engineering (ICEE), Boumerdes, Algeria, 13–15 December 2015. [Google Scholar]
- Spertino, F.; Ciocia, A.; Di Leo, P.; Tommasini, R.; Berardone, I.; Corrado, M.; Infuso, A.; Paggi, M. A Power and Energy Procedure in Operating Photovoltaic Systems to Quantify the Losses According to the Causes. Sol. Energy 2015, 118, 313–326. [Google Scholar] [CrossRef] [Green Version]
- Lappalainen, K.; Valkealahti, S. Effects of PV Array Layout, Electrical Configuration and Geographic Orientation on Mismatch Losses Caused by Moving Clouds. Sol. Energy 2017, 144, 548–555. [Google Scholar] [CrossRef]
- Mohapatra, A.; Nayak, B.; Das, P.; Mohanty, K.B. A Review on MPPT Techniques of PV System under Partial Shading Condition. Renew. Sustain. Energy Rev. 2017, 80, 854–867. [Google Scholar] [CrossRef]
- Ahmad, J.; Spertino, F.; Ciocia, A.; Di Leo, P. A Maximum Power Point Tracker for Module Integrated PV Systems under Rapidly Changing Irradiance Conditions. In Proceedings of the 2015 International Conference on Smart Grid and Clean Energy Technologies (ICSGCE), Offenburg, Germany, 20–23 October 2015. [Google Scholar]
- Bizzarri, F.; Nitti, S.; Malgaroli, G. The Use of Drones in the Maintenance of Photovoltaic Fields. In Proceedings of the E3S Web of Conferences, Torino, Italy, 12–16 November 2018; Volume 119. [Google Scholar] [CrossRef]
- Kebir, S.T.; Haddadi, M.; Ait-Cheikh, M.S. An Overview of Solar Cells Parameters Extraction Methods. In Proceedings of the 3rd International Conference on Control, Engineering and Information Technology (CEIT), Tlemcen, Algeria, 25–27 May 2015. [Google Scholar]
- Nassar-Eddine, I.; Obbadi, A.; Errami, Y.; el Fajri, A.; Agunaou, M. Parameter Estimation of Photovoltaic Modules Using Iterative Method and the Lambert W Function: A Comparative Study. Energy Convers. Manag. 2016, 119, 37–48. [Google Scholar] [CrossRef]
- Awadallah, M.A.; Venkatesh, B. Estimation of PV Module Parameters from Datasheet Information Using Optimization Techniques. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015. [Google Scholar]
- Rhouma, M.B.H.; Gastli, A. An Extraction Method for the Parameters of the Solar Cell Single-Diode-Model. In Proceedings of the 2018 2nd European Conference on Electrical Engineering and Computer Science (EECS), Bern, Switzerland, 20–22 December 2018. [Google Scholar]
- Ishaque, K.; Salam, Z.; Taheri, H.; Shamsudin, A. Parameter Extraction of Photovoltaic Cell Using Differential Evolution Method. In Proceedings of the 2011 IEEE Applied Power Electronics Colloquium (IAPEC), Johor Bahru, Malaysia, 18–19 April 2011. [Google Scholar]
- Muhsen, D.H.; Ghazali, A.B.; Khatib, T.; Abed, I.A. A Comparative Study of Evolutionary Algorithms and Adapting Control Parameters for Estimating the Parameters of a Single-Diode Photovoltaic Module’s Model. Renew. Energy 2016, 96, 377–389. [Google Scholar] [CrossRef]
- Khare, A.; Rangnekar, S. A Review of Particle Swarm Optimization and Its Applications in Solar Photovoltaic System. Appl. Soft Comput. J. 2013, 13, 2997–3006. [Google Scholar] [CrossRef]
- Tossa, A.K.; Soro, Y.M.; Azoumah, Y.; Yamegueu, D. A New Approach to Estimate the Performance and Energy Productivity of Photovoltaic Modules in Real Operating Conditions. Sol. Energy 2014, 110, 543–560. [Google Scholar] [CrossRef]
- Jadli, U.; Thakur, P.; Shukla, R.D. A New Parameter Estimation Method of Solar Photovoltaic. IEEE J. Photovolt. 2018, 8, 239–247. [Google Scholar] [CrossRef]
- Oudira, H.; Mezache, A.; Chouder, A. Solar Cell Parameters Extraction of Photovoltaic Module Using NeIder-Mead Optimization. In Proceedings of the 2018 IEEE 5th International Congress on Information Science and Technology (CiSt), Marrakech, Morocco, 21–27 October 2018. [Google Scholar]
- Reza, M.N.; Mominuzzaman, S.M. Extraction of Equivalent Circuit Parameters for CNT Incorporated Perovskite Solar Cells Using Newton-Raphson Method. In Proceedings of the 2018 10th International Conference on Electrical and Computer Engineering (ICECE), Dhaka, Bangladesh, 20–22 December 2018. [Google Scholar]
- Kumar, M.; Shiva Krishna Rao, K.D. Modelling and Parameter Estimation of Solar Cell Using Genetic Algorithm. In Proceedings of the 2019 International Conference on Intelligent Computing and Control Systems (ICCS), Madurai, India, 15–17 May 2019. [Google Scholar]
- Merchaoui, M.; Sakly, A.; Mimouni, M.F. Particle Swarm Optimisation with Adaptive Mutation Strategy for Photovoltaic Solar Cell/Module Parameter Extraction. Energy Convers. Manag. 2018, 175, 151–163. [Google Scholar] [CrossRef]
- Campanelli, M.B.; Osterwald, C.R. Effective Irradiance Ratios to Improve I-V Curve Measurements and Diode Modeling over a Range of Temperature and Spectral and Total Irradiance. IEEE J. Photovolt. 2016, 6, 48–55. [Google Scholar] [CrossRef]
- Humada, A.M.; Hojabri, M.; Mekhilef, S.; Hamada, H.M. Solar Cell Parameters Extraction Based on Single and Double-Diode Models: A Review. Renew. Sustain. Energy Rev. 2016, 56, 494–509. [Google Scholar] [CrossRef] [Green Version]
- Majdoul, R.; Abdelmounim, E.; Aboulfatah, M.; Touati, A.W.; Moutabir, A.; Abouloifa, A. Combined Analytical and Numerical Approach to Determine the Four Parameters of the Photovoltaic Cells Models. In Proceedings of the 2015 International Conference on Electrical and Information Technologies (ICEIT), Marrakech, Morocco, 25–27 March 2015. [Google Scholar]
- Duran, E.; Piliougine, M.; Sidrach-De-Cardona, M.; Galan, J.; Andujar, J.M. Different Methods to Obtain the I-V Curve of PV Modules: A Review. In Proceedings of the Conference Record of the IEEE Photovoltaic Specialists Conference, San Diego, CA, USA, 11–16 May 2008. [Google Scholar]
- Spertino, F.; Ahmad, J.; Ciocia, A.; Di Leo, P.; Murtaza, A.F.; Chiaberge, M. Capacitor Charging Method for I–V Curve Tracer and MPPT in Photovoltaic Systems. Sol. Energy 2015, 119, 461–473. [Google Scholar] [CrossRef] [Green Version]
- Ciocia, A.; Di Leo, P.; Fichera, S.; Giordano, F.; Malgaroli, G.; Spertino, F. A Novel Procedure to Adjust the Equivalent Circuit Parameters of Photovoltaic Modules under Shading. In Proceedings of the 2020 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Sorrento, Italy,, 24–26 June 2020. [Google Scholar]
- Ciocia, A.; Carullo, A.; Di Leo, P.; Malgaroli, G.; Spertino, F. Realization and Use of an IR Camera for Laboratory and On-Field Electroluminescence Inspections of Silicon Photovoltaic Modules. In Proceedings of the 2019 IEEE 46th Photovoltaic Specialists Conference (PVSC), Chicago, IL, USA, 16–21 June 2019. [Google Scholar]


| Parameter | Range |
|---|---|
| Iph | 0–15 A |
| I0 | 0–10−3 A |
| n | 0–4 |
| Rs | 0–1 Ω |
| Rsh | 0–20,000 Ω |
| Tolerance | 10−30 |
| Maximum number of iterations | 10,000 |
| Rated power PPV | 370 W |
| Short-circuit current Isc | 10.82 A |
| Open-circuit voltage Voc | 42.8 V |
| Current temperature coefficient α | 0.04%/°C |
| Voltage temperature coefficient β | −0.24%/°C |
| Power temperature coefficient γ | −0.3%/°C |
| Nominal Operating Cell Temperature NOCT | 44 °C |
| Number of cells in series Nc | 60 |
| a | 10.47 A |
| b | 4.17∙10−8 A |
| c | 2.48 |
| d | 7.37∙10−4 m2/W |
| e | −4.62∙10−3 1/K |
| f | 0.0037 Ω |
| g | 17.19 |
| h | 112.1 Ω |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spertino, F.; Malgaroli, G.; Amato, A.; Qureshi, M.A.E.; Ciocia, A.; Siddiqi, H. An Innovative Technique for Energy Assessment of a Highly Efficient Photovoltaic Module. Solar 2022, 2, 321-333. https://doi.org/10.3390/solar2020018
Spertino F, Malgaroli G, Amato A, Qureshi MAE, Ciocia A, Siddiqi H. An Innovative Technique for Energy Assessment of a Highly Efficient Photovoltaic Module. Solar. 2022; 2(2):321-333. https://doi.org/10.3390/solar2020018
Chicago/Turabian StyleSpertino, Filippo, Gabriele Malgaroli, Angela Amato, Muhammad Aoun Ejaz Qureshi, Alessandro Ciocia, and Hafsa Siddiqi. 2022. "An Innovative Technique for Energy Assessment of a Highly Efficient Photovoltaic Module" Solar 2, no. 2: 321-333. https://doi.org/10.3390/solar2020018
APA StyleSpertino, F., Malgaroli, G., Amato, A., Qureshi, M. A. E., Ciocia, A., & Siddiqi, H. (2022). An Innovative Technique for Energy Assessment of a Highly Efficient Photovoltaic Module. Solar, 2(2), 321-333. https://doi.org/10.3390/solar2020018









