Computational Fluid Dynamics–Discrete Element Method Numerical Simulation of Hydrothermal Liquefaction of Sewage Sludge in a Tube Reactor as a Linear Fresnel Solar Collector

Abstract

This paper discusses the thermal and exergy efficiency analysis of the hydrothermal liquefaction (HTL) process, which converts sewage sludge into biocrude oil in a continuous plug–flow reactor using a linear Fresnel solar collector. The investigation focuses on the influence of key operational parameters, including slurry flow rate, temperature, pressure, residence time, and the external heat transfer coefficient, on the overall efficiency of biocrude oil production. A detailed thermodynamic evaluation was conducted using process simulation principles and a kinetic model to assess mass and energy balances within the HTL reaction, considering heat and mass momentum exchange in a multiphase system using UDF. The reactor’s receiver, a copper absorber tube, has a total length of 20 m and is designed in a coiled configuration from the base to enhance heat absorption efficiency. To optimize the thermal performance of biomass conversion in the HTL process, a Computational Fluid Dynamics–Discrete Element Method (CFD-DEM) coupling numerical method approach was employed to investigate improved thermal performance by obtaining a heat source solely through solar energy. This numerical modeling approach allows for an in-depth assessment of heat transfer mechanisms and fluid-particle interactions, ensuring efficient energy utilization and sustainable process development. The findings contribute to advancing solar-driven HTL technologies by maximizing thermal efficiency and minimizing external energy requirements.

1. Introduction

The growing amount of sewage sludge and the rising prices of electricity are driving the search for new, innovative forms of sewage sludge processing technology for biofuels. The production of sewage sludge worldwide, especially from municipal sewage treatment plants, is increasing year by year. It is estimated that between 0.5 and 30 kg of sludge/RLM is produced annually (in the USA, 23 kg/year of sludge is produced per person) [1]. In Poland, approx. 1 million tons of dry matter from sewage sludge is produced annually. According to the Central Statistical Office data, in 2003, 447 thousand tons of dry mass of municipal sewage sludge were produced in Poland, while in 2018 this amount had increased to 583 thousand tons, and in 2022, it was 1012 thousand tons [2,3]. The amount of sewage sludge produced shows a growing trend. In Poland, the amount of sewage sludge is increasing on average by about 1.8–3.7% per year, mainly due to the increase in the amount of municipal sewage transferred to treatment plants. The rate of growth depends on the region, degree of urbanization, and the development of sewage treatment systems. However, the general trend indicates a continuous increase in the amount of generated sludge along with the development of cities and industry [4].

One of the promising methods is the thermochemical processing of sewage sludge to biocrude oil in the HTL process. The obtained results indicate the potential for using proven devices for the thermal management of industrial sludge. Hydrothermal liquefaction (HTL) has been identified as a suitable thermochemical technique for converting biomass to biocrude oil at relatively high temperatures (473–673 K) and pressures (5–20 MPa) in the presence of water [4]. The four product fractions that are formed during the HTL process are organic liquid, aqueous phase fraction, gas, and solid residue. Its main limitation is the energy consumption of the process [5].

An alternative solution is to use solar energy. This energy is used to produce heat in many technologies, such as solar stills for evaporating water [6,7], solar cookers for preparing meals [8], solar dryers for preserving fruits and vegetables [9], air collectors for heating buildings [10,11], and various types of solar collectors for heating water [12,13,14]. A particularly promising solution is the linear Fresnel reflector, also known as a linear Fresnel solar collector or linear Fresnel concentrator. It consists of a series of mirror rows mounted on a metal structure at precisely calculated angles, which allows for the reflection of direct solar radiation towards the absorber tube, which placed in the collector’s focal line. The concentrated solar energy is transferred to the working fluid flowing through the absorber tube, which causes its temperature to increase and generates useful thermal power. In recent years, various designs of secondary reflectors have been presented, including parabolic, involute, butterfly, trapezoidal, triangular, and other reflectors with complex geometries. However, it should be noted that not all solar radiation reflected by mirrors is directed along the longitudinal axis to reach the absorber tube [15]. This phenomenon leads to final losses [16]. Some of the solar radiation does not reach the absorber tube, and these losses are influenced by the geographical latitude of the location, the time of day, and the geometry of the mirror field [17]. When using linear Fresnel mirrors to heat the HTL reactor, significant heat losses occur, which can reduce the efficiency of the biomass conversion process. Radiation losses result from the thermal emission of the heated reactor, especially at high temperatures, where the intensity of infrared emission increases according to the Stefan-Boltzmann law. Convective losses occur as a result of the contact between the heated reactor surface and the surrounding air, leading to the release of heat into the atmosphere, which is intensified by air flows and weather conditions. Reflection and absorption losses result from the limited efficiency of Fresnel mirrors, where part of the solar radiation is reflected in undesirable directions or absorbed by the optical elements themselves, reducing the amount of energy reaching the reactor. Additionally, thermal conduction losses occur through the reactor material, where heat escapes along the walls of the structure, especially if appropriate thermal insulation is not used. In large linear Fresnel reflectors, the mirror rows and the absorber are set at an angle of 0° to the horizontal plane. Moreover, due to their size, the absorber and the mirror rows do not move along the longitudinal axis. The use of linear Fresnel mirrors for heating the HTL reactor is associated with significant heat losses that can reduce the efficiency of the biomass conversion process.

Radiation losses result from the thermal emission of the heated reactor, especially at high temperatures, at which the intensity of infrared radiation emission increases according to the Stefan–Boltzmann law. Convective losses are caused by the contact of the heated reactor surface with the surrounding air, which leads to the release of heat into the atmosphere. This process is intensified by air flows and atmospheric conditions. Reflection and absorption losses are caused by the limited efficiency of Fresnel mirrors, where part of the solar radiation is reflected in undesirable directions or absorbed by optical elements, which reduces the amount of energy reaching the reactor. Additionally, heat conduction losses occur through the reactor material, where heat escapes along the walls of the structure, especially in the absence of appropriate thermal insulation [18,19,20,21].

Computational fluid dynamics (CFD) is an effective tool for simulating convective heat transfer, mass transfer, and chemical conversion of biomass in continuous flow reactors. Flores et al. [22] studied the thermal behavior of a prototype of a Friesler reflector heat pipe acting as an absorber using the CFD and Energy Plus v5.0 software package and concluded that the major part of the heat loss occurs by radiation from the bottom surface of the tube. Facao [23] analyzed and optimized a trapezoidal cavity receiver of a linear Fresnel solar collector concentrator using solar tracing, along with mass and heat transfer hydrodynamics in CFD software. In order to evaluate the overall heat transfer coefficient of the collector, CFD simulations were performed considering natural convection inside the reaction medium tube. Singh et al. [24] experimentally investigated the absorber performance of circular and rectangular tubes. The influence of the tube geometry significantly affected the process efficiency and effectiveness. They concluded that the efficiency of the circular tube (multitube) absorber was 28% higher compared to the rectangular tube absorber. Also, the efficiency of the rectangular tube absorber ranged from 24% to 63% for the selectively surface-coated absorber, compared to 53% for the plain black-coated absorber. Jance et al. [25] demonstrated through heat loss measurements that convective heat transfer in a trapezoidal cavity is minimal, and heat loss from the cavity occurs mainly through radiation. Natarajan et al. [26] presented a computational study of the heat loss characteristics using non-Boussinesq numerical simulation in the CFD package with FLUENT version 6.3. A trapezoidal cavity absorber with an aspect ratio (depth to width of the cavity) and a temperature ratio greater than 2.5 and 0.6 can be used to minimize internal heat loss in a tubular absorber. Water and oil were considered as the working fluids. Their results showed that this solar collector is capable of producing about 8.5 kW of usable power in summer, 5.3 kW in spring, and 2.9 kW in winter. Cucumo et al. [27] developed a mathematical law to analytically determine the position that each reflector should occupy during the day to reduce energy losses (final losses) in linear Fresnel solar concentration systems. Their study showed that the reflector must be independently moved in each direction. They also studied a configuration in which the reflectors are moved around the axis by the same motor to reduce operational costs.

The integration of linear Fresnel mirrors into an HTL reactor for processing sewage sludge into biocrude oil is a novel approach that significantly increases the energy efficiency of the HTL process. The use of concentrated solar energy as the main heat source reduces dependence on conventional energy sources, minimizing operating costs and carbon dioxide emissions. Unlike standard HTL systems that use electric or fuel heating, this technology improves the energy balance of the process by supplying renewable energy during solar hours. Previous studies have not considered such synergy, making this approach unique and opening new perspectives for the sustainable production of biofuels from organic waste. The current gap in the literature involves the lack of integrated, high-fidelity numerical modeling that incorporates both solar radiation dynamics and the complex rheology of sewage sludge in a multiphase environment. The proposed work aims to address this gap through a CFD-DEM coupling approach that simulates the real-time behavior of solar-heated tubular reactors under dynamic conditions.

This paper presents a CFD-DEM multiphase numerical simulation of hydrothermal liquefaction of sewage sludge to biocrude oil in a continuous plug-flow reactor, using a linear Fresnel solar collector to improve process thermal efficiency. Heat loss is also analyzed and estimated numerically by using ANSYS-Fluent 15 software. This numerical study is conducted on three-dimensional CFD-DEM coupling transient flow with high pressure and temperature to evaluate thermal performance. It combines laminar natural convection and surface radiation heat transfer in a plug flow reactor for the HTL process using renewable solar energy sources. This is of particular importance in the energy recovery of tubular reactors operating in continuous mode, which allows for savings in economic costs, as well as reductions in CO₂ emissions to the environment in the long run. Additionally, variations in sludge composition, weather fluctuations, and long-term operational stability were not considered, which may affect the scalability and implementation of the system.

2. Materials and Methods

A numerical study investigates the stable laminar flow of a compressible gas phase and an incompressible aqueous solution of sewage sludge with phase change through a plug flow reactor for the HTL process of biocrude oil production. Solar energy was used to heat the sewage sludge suspension, where the effect of radiation was modeled using the Discrete Ordinate (DO) method. The following equations are used for multiphase flow calculations:

The continuity equation for the compressible gas phase is as follows (1):

$${\displaystyle \frac{\partial ({\alpha }_q{\rho }_q)}{\partial t}}+\nabla \cdot \left({\alpha }_q{\rho }_q{\overline{v}}_q\right)={\stackrel{•}{m}}_g$$

(1)

The momentum equation for the fluid phase is as follows (2):

$${\displaystyle \frac{\partial }{\partial t}}\left(\rho \overline{v}\right)+\nabla \cdot \left(\rho \overline{v}\overline{v}\right)=-\nabla P+\nabla \cdot \left(\overline{\tau }\right)+\rho \overline{g}$$

(2)

The total energy equation is as follows (3):

$${\displaystyle \frac{\partial }{\partial t}}\left(\rho E\right)+\nabla \cdot \left(\overline{v}\left(\rho E+\rho \right)\right)=\nabla \cdot \left(k\nabla T-h\overline{J}+\left(\overline{\tau }\cdot \overline{v}\right)\right)$$

(3)

The energy balance equation describing heat transfer performed on a differential volume element is shown as follows (4):

$${\displaystyle \underset{V}{\int }\rho C_p\frac{\partial T}{\partial t}}dV={\displaystyle \underset{A_t}{\int }qd{A}_t+}{\displaystyle \underset{V}{\int }{q}_{P}dV}$$

(4)

where $V$ is a volume of the volume element, $\rho$ is the material density, $C_p$ is the heat capacity at constant pressure, $q$ is the heat flux, $A_t$ is the heat transfer area, $q_P$ is the power density derived from a volumetric source in the element.

The transient state of heat transfer in the fluid, described by one-dimensional energy balance in a fluid volume element, is as follows (5):

$${\displaystyle \underset{V}{\int }{\rho }_f\frac{\partial h}{\partial t}}dV+V{\displaystyle \underset{A_t}{\int }G\frac{\partial h}{\partial z}dV}={\displaystyle \underset{A_t}{\int }q{A}_t+{\displaystyle \underset{V}{\int }\frac{G}{{\rho }_f}}}\left({\displaystyle \frac{\partial P}{\partial z}}+f{\displaystyle \frac{G}{2D_h{\rho }_f}}\right)dV$$

(5)

where ${\rho }_f$ is the fluid density of element, $h$ is the specific enthalpy, $G$ is the mass flux, $P$ is the pressure, and f is the fricition coefficient.

The Nusselt number is calculated based on natural convection, as shown in Equation (6), as follows:

$$N{u}_{Dc}=\left\{0.6+{\displaystyle \frac{0.387R{a}_{D_c^{1/6}}}{{\left[1+{\left(\frac{0.559}{{\mathrm{Pr}}_{ca}}\right)}^{9/16}\right]}^{8/27}}}\right\}forR{a}_{Dc}\le {10}^{12}$$

(6)

The Rayleigh number is expressed as follows (7):

$$Ra={\displaystyle \frac{g\beta (T_c-T_a)D_c^3}{{\nu }^2}}{\mathrm{Pr}}_{ca}$$

(7)

The Herschel–Bulkley equation was used to calculate the slurry viscosity. The Herschel–Bulkley model is a non-Newtonian model that describes the viscous behavior of sludge suspensions. This model takes into account the minimum shear stress required to initiate flow (as in the Bingham model) and the non-linear relationship between shear stress and shear rate.

2.1. Radiation Model

The energy flux leaving each surface consists of directly emitted and reflected energy, where the reflected energy is expressed in terms of the energy flux leaving other surfaces, as follows (8):

$$q_{out,k}={\epsilon }_k\sigma T_k^4+{\rho }_k{q}_{in,k}$$

(8)

Taking into account the total number of surfaces, N, and direct function of the view factor (F_kj), the fraction of energy leaving surface k that is incident on surface j is expressed as follows (9):

$$q_{out,k}={\epsilon }_k\sigma T_k^4+{\rho }_k{\displaystyle \sum _{j=1}^N{q}_{out,j}{F}_{kj}}$$

(9)

The Discrete Ordinate (DO) radiation model was used for radiation exchange from the Friesler mirror to the HTL reactor heating. The DO model allows for tracking solar rays in various directions and takes into account scattering and absorption in a gaseous medium. It also supports direct and diffuse radiation. The DO model enables the precise tracking of solar radiation reflected from the Friesler mirror at various angles, which is crucial for concentrating heat on the reactor tube surface through multiple reflections. The emissivity and absorbency are 0.91 and 0.94, respectively. The linear Fresnel sensor, shown in the figure, reflects the angles of reflection of solar radiation. Each mirror is characterized by its position (Q_n), tilt angle (θ_n), and spacing. The individual formulas describing the angle of reflection to the reactor are provided as follows:

$$S_n=W_0\sin {\theta }_{n-1}\tan \left(2{\theta }_n+{\xi }_0\right)$$

(10)

$$Q_n=Q_{n-1}+W_0\cos {\theta }_{n-1}+S_n$$

(11)

$${\theta }_n={\displaystyle \frac{1}{2}}\left[{\tan }^{-1}\left({\displaystyle \frac{Q_n+\frac{w_0}{2}\cos {\theta }_{n-1}}{F-\frac{w_0}{2}\sin {\theta }_{n-1}}}\right)\right]$$

(12)

where n varies from 1 to k, where k is the number of mirrors, $\xi$ is the angular distance from the sun to any point on the earth, and each mirror strip is characterized by $Q_n$, which is the position, ${\theta }_n$, which is the tilt angle, and $S_n$, which is the spacing.

The useful exergy rate of a linear Fresnel solar collector, using sewage sludge water suspension as the working fluid, is expressed as follows (13):

$$E_u=Q_u-m_w{C}_w{T}_a\ln {\displaystyle \frac{T_{wo}}{T_{wi}}}$$

(13)

The exergy rate of available solar energy can be calculated using the Petela model, as follows:

$$E_s=Q_s\left[1-{\displaystyle \frac{4}{3}}\left({\displaystyle \frac{T_a}{T_s}}\right)+{\displaystyle \frac{4}{3}}{\left({\displaystyle \frac{T_a}{T_s}}\right)}^4\right]$$

(14)

2.2. HTL Kinetics and Reaction Conditions

The kinetic model for calculating the biocrude yield in the hydrothermal liquefaction (HTL) process from sewage sludge, based on reaction paths, was taken from the literature [28] and is presented in Figure 1. This model takes into account the biochemical content of proteins, carbohydrates, and lipids, which constitute the biofuel, gas, and water phases. The detailed conditions and mechanisms of the HTL reaction are described in the article [28]. The Peng–Robinson equation of state was used to calculate the gas volume as a function of pressure and temperature, and the thermodynamic properties were based on the NIST table for the supercritical phase of water. The hydrothermal liquefaction (HTL) process takes place at temperatures ranging from 240 to 375 °C, where the lower limit (approx. 250 °C) is the minimum temperature at which effective reactions for the decomposition of organic matter in sewage sludge begin. The upper limit is the critical temperature of water, above which water becomes supercritical. Within this range, intense reactions occur, but process control becomes more difficult. The HTL process is carried out at pressures between 75 and 200 bar, and heating is carried out using a Friesler mirror. In this context, the optimal choice of numerical model in ANSYS Fluent is a combination of several advanced models (multiphysics) that takes into account, among other factors, heat transfer by radiation concentrated in the sludge suspension.

2.3. Geometry and Meshing

The geometry of the tubular HTL reactor, heated by linear Friesler mirrors, is shown in Figure 1a. As seen in Figure 1b, T-flex cad 15 software was used to determine the angles of the strips based on their distance from the longitudinal center of the mirror strip. An axiometric view of the reactor is presented in Figure 1c, allowing for a better understanding of the structural layout and orientation relative to the solar path. This visualization is essential for analyzing the alignment of the collector with the dual-axis tracking system and optimizing its energy capture efficiency. The length of the reactor to the bend is 5 m, while the total length of the reactor is 25 m. The straight section of the reactor leading up to the first bend measures 5 m in length. This portion allows for the initial heating and flow stabilization of the sewage sludge suspension. The total length of the reactor is 25 m, which includes multiple straight sections and bends. The remaining 20 m accommodate further heating zones and reaction progression, with bends contributing to pressure drop and flow disturbance.

The simulation uses a computational hexahedral mesh set to “normal”. A mesh quality sensitivity analysis was performed by employing 3D meshes with the number of elements ranging between 225,687 and 578,955 and the number of nodes ranging between 904,748 and 1,905,820. A higher number of elements generates better calculation accuracy. A number of mesh elements of 312,841 was sufficient to provide independent results for the simulations. Compliance with the grid quality criteria was achieved, in which the skewness was 0.32, the orthogonal quality was 0.74, and the aspect ratio was 4.45. The radical thickness of the first boundary layer was 0.015 mm, while the increase ratio of thickness between layers was 0.2. A mesh was generated, taking into account refinements near critical zones, such as the HTL reactor and enclosure boundaries, to resolve the boundary layer [y + <=1].

2.4. Initial and Boundary Conditions

The model implements a set of boundary and initial conditions. The initial temperature of the HTL reactor is 24 °C. The non-slip condition is applied to the solid surfaces, while atmospheric pressure and zero velocity are assumed at the domain boundaries. The thermo-physical parameters of the water are presented in

Table 1. Thermo-physical parameters of the water.

Parameter	Value
Dynamic viscosity of water, µ	0.0001587 Pa·s
Thermal conductivity of water, λ	0.6845 W·m−1·K−1
Specific thermal capacity of water, Cp	4325 J·kg−1·K−1
Density of water, ρ	901.7 kg·m−3

. The reactor is covered with a black coating, and the emissivity coefficient and other parameters are shown in

Table 2. Parameters used for modeling [12,21,23,25].

Parameter	Value
Emissivity of reactor HTL tube, εr	0.098
Diameter of reactor tube, Dr, mm	20
Refractive index for glass cover	1.5
Transmissivity of glass cover	0.97

. The emissivity values for different surfaces are 0.93 for the pipes, 0.88 for the glass cover, and 1 for the remaining elements. The liquid flow varies in the range of 5–120 mL/min, and all the energy comes from the Fresnel mirror. The main calculation assumptions are as follows: the process takes place between 10:00 and 16:00, when the solar radiation is highest, a dual-axis solar tracking system was used to maximize energy yield, and insulation was modeled as an adiabatic zone, which allows for a significant reduction in computational costs with minimal impact on heat losses.

2.5. Numerical Procedure

The computational setup implemented in ANSYS Fluent for this analysis utilizes a three-dimensional, steady and transient state, pressure-based solver operating in double precision. To enhance accuracy, the Pressure-Implicit with Splitting of Operators (PISO) scheme is employed for pressure–velocity coupling, which incorporates additional corrections for neighboring cells and skewness to optimize computational efficiency. The equations are solved by applying the Pressure–Velocity Coupling–Pressure-Implicit with Splitting of Operators (PISO) scheme to discretized momentum equations. PISO is best suited for unsteady and multiphase flows, where there are variable interactions between the phases (e.g., liquid–gas–solid particles). It also provides stability for large pressure and velocity gradients, variable volume fractions of individual phases, and dynamic interfaces. Body Force Weighted is a pressure discretization scheme used in ANSYS Fluent within the Pressure-Based Solver. It is used to calculate pressure gradients where significant volumetric forces act on the fluid. The under-relaxation parameters are defined as follows: pressure (0.2) and momentum (0.6). Other relaxation coefficients remain at their default value of 1.0. The convergence criteria are determined by monitoring the residual values for each governing equation. The residual for the energy equation and other variables is set at 10⁻⁶. The thermodynamic modeling of the absorption machine allows us to solve the systems of algebraic equations, optimize the system parameters, and obtain the thermodynamic description. Engineering Equation Solver (EES) version 10.834, a software package for solving systems of algebraic equations, differential equations, and complex variable equations, is used for modeling the water sewage sludge heat absorption. Next, a UDF was written in C++17.

2.6. CFD-DEM Coupling Model for HTL Process

The coupling of the CFD-DEM algorithm is illustrated in Figure 2. In this work, an advanced numerical coupling method, CFD-DEM, was used, which enables the simulation of complex multiphase systems. This hybrid technique combines continuous fluid modeling (using average Navier–Stokes equations) with discrete solid particle modeling (discrete element method, DEM). CFD-DEM allows for tracking the motion and interactions of individual particles in fluid flow. Particles are treated as discrete objects with specific physical properties, such as mass, shape, or friction coefficient. Their mutual interactions, as well as interactions with the fluid, are modeled at the molecular level. Therefore, it is possible to thoroughly study phenomena such as sedimentation, mixing, particle transport, and their effects on flow properties. The CFD-DEM Eulerian–Lagrangian coupling is achieved over a volumetric mesh. Sludge slurries were determined to be non-Newtonian fluids with shear-thickening characteristics using Herschel–Bulkley rheological model. The thermophysical properties of the slurry consist of water and sewage sludge, with fluid parameters such as density, viscosity, thermal conductivity, and specific heat capacity, which are used as functions of temperature and pressure. The inter-particle interactions are resolved explicitly through the DEM method, coupled with fluid dynamics (CFD), and interphase interactions, which are addressed by solving the Navier–Stokes equations for each particle.

3. Results and Discussion

Figure 3a shows the distribution of the biocrude oil fraction in the external view of the reactor and the pressure drop along the reactor length (Figure 3b). The biocrude fraction is observed to be distributed along the reactor, with the highest intensity in the range from 14 to 25 m. In the hydrothermal liquefaction process, progressive heating of biomass, such as sewage sludge, initiates the conversion of sewage sludge to biocrude oil. In the initial reactor section, the temperature is suboptimal, limiting the efficiency of the conversion of sludge to biocrude oil. The maximum conversion (>0.014) occurs in the final section, where the highest residence times are reached. In the initial phase, these conditions are insufficient for the decomposition of organic compounds. Increased medium reactivity in the final section, resulting from optimal thermal conditions, intensifies biocrude oil production.

HTL reactions leading to the synthesis of biocrude oil are stepwise and depend on the retention time. In the initial phase, decomposition reactions dominate, leading to intermediate products. In the final phase, extended retention time favors condensation reactions, leading to biocrude oil formation. At the very beginning of the reactor, the average concentration of biocrude oil is 0.0023, which then increases to 0.0092 at 15 m in the reactor. This process is characterized by a dynamic equilibrium of decomposition, polymerization, and condensation reactions, with decomposition processes dominating at the beginning and condensation occurring in the final reaction stage. Especially in the range of 320–400 °C, repolymerization reactions become dominant in the formation of biocrude oil. However, in the final phase, due to the longer residence time in the reactor, the desired products are formed. The pressure drop along the reactor is a key process parameter. In long reactors, the flow resistance resulting from friction and turbulence leads to a significant pressure drop. According to the Darcy equation, the pressure drop is proportional to the reactor length. The pressure drop across a 25 m reactor is approximately 54 bar. Energy losses associated with flow resistance and turbulence also increase with the reactor length. Changes in flow velocity, resulting from the nature of the laminar sewage sludge flow, are influenced by changes in temperature and density of the medium. In the case of gas or vapor generation, their expansion along the reactor contributes to further pressure reduction.

Figure 4a below shows the solid mass fraction (char) in the external view of the reactor and the liquid mass fraction for Figure 3b for a 40 min process, at a suspension flow rate of F = 30 mL/min and a solar radiation intensity of I = 1000 W/m². In tubular reactors, especially those used in HTL processes, char deposition occurs intensively at pipe bends due to several factors related to flow dynamics and solid-state physics. At bends, the flowing fluid changes direction, which leads to an uneven distribution of flow velocity. As a result, solid particles (e.g., sewage sludge particles or other suspended particles) are subjected to centrifugal forces that change their trajectories, causing them to separate from the flowing medium and settle on the pipe walls. On the reactor bends, the solid mass fraction totals 0.011. Due to reduced flow velocity, particles can become trapped in dead zones where the flow is significantly slowed. In the long term, the accumulation of these particles leads to an increase in the local density of the deposits, which can result in clogging of the pipe, particularly affecting the stability of the flow process. Such phenomena can negatively affect the efficiency of the reaction processes in the reactor and the heat exchange, leading to increased flow resistance and a decrease in process efficiency. In the context of the design and operation of reactors, it is necessary to account for such risks by using appropriate cleaning methods, flow monitoring, and pipe geometry optimization. In Figure 4b, at higher temperatures in the final parts of the reactor, the liquid can evaporate and transition into the gas phase. Higher temperatures favor the evaporation of the liquid, especially in the case of substances with lower boiling points. This evaporation can contribute to a decrease in the liquid fraction because part of the liquid is converted into vapor, which can then enter the gas phase. Reduced viscosity can cause changes in flow, making heavier liquid fractions (e.g., biocrude oil) more prone to precipitate and settle out, which reduces the liquid fraction in the system.

Figure 5 illustrates the transient state of temperature distribution within the cross-section of a hydrothermal liquefaction (HTL) plug flow reactor operating at a flow rate (F) of 30 mL/min under solar irradiation of 800 W/m². This figure also depicts the transient heating rate across the reactor’s cross-section under the same operational conditions. Initially, during the first 40 min, the temperature profile exhibits a symmetrical characteristic. Beyond 40 min, a noticeable increase in the slurry heating temperature within the reactor is observed. The intensified thermal interaction induced by the configuration enhances fluid mixing, leading to more effective mixing near the tube walls. This results in a faster and more uniform temperature distribution and an increased temperature gradient, which weakens the boundary layer and improves heat transfer efficiency across the reactor’s cross-section. After 45 min, the fluid reaches its highest temperature near the reactor wall. By 60 min, the temperature gradients across the entire tube cross-section become more uniform.

Figure 6 shows the temperature obtained in the reactor heated by a Fresnel mirror, depending on the solar radiation intensity (DNI). The highest temperatures in the reactor were recorded between 11:00 and 14:00, when they reached about 200 °C for a flow rate of 0.3 L/min of sewage sludge, which corresponds to a Reynolds number (Re) of 637, indicating laminar flow. Figure 5 shows the reactor wall temperature as a function of the reaction medium flow rate and the conversion rate in the HTL process, which is strongly correlated with the temperature on the reactor walls. As the flow rate increases, the temperature on the reactor walls decreases, which is due to the increased heat transfer coefficient. A higher flow velocity causes a reduction in the thickness of the boundary layer, thereby decreasing thermal resistance and intensifying forced convection. As a result, heat is removed more quickly from the reactor wall and transported deeper into the fluid stream, which leads to a local decrease in wall temperature compared to lower-flow rate conditions. This phenomenon is described by the Nusselt number (Nu), which increases with the Reynolds number (Re), indicating improved heat transfer efficiency in turbulent flow conditions. In practice, this means that at higher flow rates, more heat energy must be supplied to maintain the set HTL process temperature. Temperature control in the reactor is crucial for optimizing the hydrothermal liquefaction reaction. This relationship is consistent with the Arrhenius equation, according to which the reaction rate decreases exponentially with decreasing temperature. In the HTL process, this results in a lower yield of the oil fraction and an increased share of the solid residue. The HTL process involves the conversion of biomass to bio-oil, and its efficiency strongly depends on the reaction temperature. Higher temperatures promote the depolymerization, hydrolysis, and decarboxylation of organic compounds. The heat transfer coefficient (h) plays a key role; a reduction in this coefficient limits the efficiency of energy supply to the reaction medium, which can lead to underheating and, consequently, a decrease in HTL efficiency.

The dependence of the residence time for the HTL tubular reactor on the inlet slurry flow rate is presented in Figure 7a. It can be seen that as the inlet flow rate increases, the residence time of the reactor decreases, and its temperature also decreases. A shorter residence time limits the duration the medium is exposed to the heated reactor walls, resulting in lower heat absorption. Additionally, rapid flow reduces the thermal contact between the fluid and the surface, weakening convective heat transfer. Figure 7b shows the effect of reducing the reactor diameter from 10 mm to 6.4 mm on the residence time of the medium and the temperature drop. It was observed that reducing the pipe diameter leads to a decrease in heat exchange efficiency due to the shorter contact time of the medium with the reactor walls, which results in a greater temperature drop. At smaller diameters and higher flow rates, the medium has a limited ability to absorb heat, which further increases the temperature difference between the reactor inlet and outlet.

Although a higher flow rate promotes intensified mixing, in the case of laminar flow, the heat exchange efficiency remains limited. A smaller reactor diameter also results in a shorter residence time of the medium, which leads to insufficient heating and lower conversion of sewage sludge to biocrude oil. Conversely, in the case of a larger pipe diameter, a smaller temperature drop is observed along the reactor. A longer residence time of the medium and improved heat exchange allow for more efficient transfer of heat energy. Although a larger diameter reactor may require more energy to heat a larger volume of the medium, more efficient heat absorption from the walls helps maintain a higher temperature during the HTL process. In addition, at reduced flow velocity, the boundary layer at the reactor walls becomes thinner, which improves heat exchange efficiency. In laminar flow, when flow velocities are low, a longer contact time of the medium with the pipe wall promotes more efficient transfer of heat energy. Increasing the reactor diameter, while maintaining the flow velocity, leads to a smaller temperature drop on the reactor walls because the larger heat exchange surface increases the energy absorption capacity. However, lower mixing intensity may limit the efficiency of heat transfer to the entire volume of the medium, especially in laminar flow. As a result, the temperature in the reactor will be more uniform, but there may be a slight decrease in heat exchange efficiency in areas with lower flow velocity. When the reactor diameter increases and the flow rate remains constant, the temperature drop is influenced by two opposing effects. On the one hand, a larger diameter improves heat exchange due to the larger contact surface of the medium with the reactor wall. On the other hand, a decrease in mixing intensity may limit heat transfer throughout the volume of the medium. At higher flow rates and larger pipe diameters, the temperature drop in the reactor is more pronounced. This is because the increased volume of the medium requires more thermal energy, and the shorter contact time of the medium with the wall further limits heat transfer.

The analysis of thermal and exergy efficiency for the four sludge slurry flow rates, shown in Figure 8a,b, which is a key element in the evaluation of the performance of a linear Fresnel solar collector. Thermal efficiency measures how well the collector uses the available solar radiation over a given time period, taking into account both optical and thermal losses. A clear correlation is observed between thermal efficiency and the quantity of heat energy effectively converted from solar input. Unlike simple instantaneous measures, the thermal efficiency curve provides a broader perspective, as it reflects the variation in solar irradiance throughout the measurement period. The calculations were carried out for a latitude of 37.0755° N. As the slurry flow rate increases in the HTL reactor, both thermal efficiency and exergy decrease. This reduction occurs due to a decrease in the contact time of the medium with the hot walls of the reactor, which reduces the efficiency of heat exchange. The boundary layer at the reactor wall becomes thinner, which can improve the heat exchange coefficient, but at the same time, it limits the ability of the medium to absorb energy per unit of time. The figure shows the exergy efficiency for four flow rates. This parameter depends on thermal efficiency, the temperature of the medium and the environment, and the level of solar radiation. In general, the exergy values in May are higher than those in April, which results from more favorable radiation conditions. It is important to highlight that energy efficiency tends to show greater fluctuations than thermal efficiency. This is mainly caused by nonlinear variations in fluid temperature, solar input, and collector performance. Additionally, as flow rates increase, the central regions of the reactor experience insufficient heating, limiting the overall conversion to biocrude oil due to incomplete reaction conditions. Increasing the exergy efficiency allows for the reduction of irreversibility losses and entropy generation. Additionally, a solar radiation tracking system was included, enabling the real-time optimization of energy use. The highest thermal efficiency values (0.4–0.48) and exergy (up to 0.26) were achieved between 11:00 and 14:00, which correlates with the maximum solar radiation intensity. These values were particularly high at low flow rates, suggesting that optimizing the medium flow can significantly improve the process efficiency. The presented results correspond well with the literature [23,29]. Compared to previous studies, the present work introduces a novel integration of solar-driven heating using Fresnel collectors with a plug flow reactor design. Earlier works have typically focused on trapezoidal heating system configurations [24,26]. Previous studies have not sufficiently explored spatial effects such as pressure drop, char deposition at bends, and transient thermal distribution across the reactor wall, which this work addresses in detail through numerical modeling [21,27].

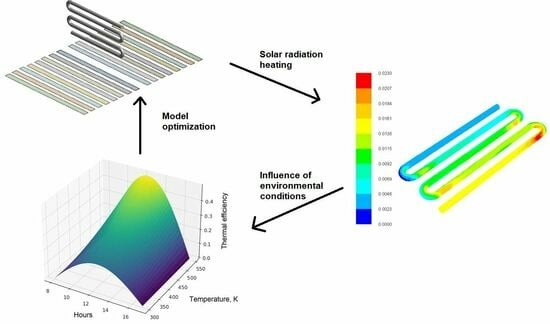
The results shown in the graph presented in Figure 9 indicate a clear dependence of thermal efficiency on temperature and hours of sunlight. The efficiency increases with temperature, reaching a maximum during a specific hourly interval between 11:02 a.m. and 2:17 p.m., suggesting a significant effect of solar irradiance on the efficiency of the system. The achieved temperature of 550 K during these hours is a promising result, capable of achieving a thermal efficiency of >0.4. It is observed that the efficiency is lower during the morning and late afternoon hours, which is due to the lower amount of available radiant energy and higher thermal losses. In the high-temperature range (>350 K), thermal efficiency increases and yields the stated efficiency. These results underscore the key role of dynamic optimization of operating parameters, including working fluid flow control strategies and reactor geometry. It is worth emphasizing that the thermal efficiency achieved in this study is notably higher than in earlier research [30], which can be attributed to the implementation of a solar tracking system.

The use of a Friesler mirror to heat a process reactor with solar energy for 6 h per day (10:00–16:00) can significantly reduce the demand for electrical energy, thereby lowering operating costs. Assuming that the mirror concentrates solar radiation with an efficiency of 70% and that the solar radiation during peak hours averages 800 W/m², it is possible to deliver about 3.36 kW/m² of usable thermal power. If the mirror system covers a collector area of 3 m², 10.08 kW of heat can be obtained, which meets the full thermal power demand of the reactor during system operation. Heating with electrical energy alone would require 9.45 kW for 6 h, which corresponds to a daily consumption of 56.7 kWh. The use of the Friesler mirror would save 92.8% of electricity during daytime operations, reducing consumption by 56.7 kWh per day and 20.7 MWh per year (for 365 days of operation). At an average electricity price of EUR 0.2/kWh, the average annual financial saving would be EUR 4140. On an operational scale, this represents a reduction in energy costs of ~47.8%, assuming that night-time reheating of the reactor requires the same amount of energy as daytime operations. An additional benefit is the reduction of CO₂ emissions; assuming that the electricity comes from a grid with a carbon footprint of 0.4 kg CO₂/kWh, the annual emission reduction is 8.28 t CO₂. The implementation of concentrated solar power (CSP) technology in thermochemical processes can be a key step toward the sustainable production of fuels from sewage sludge, minimizing environmental impact and reducing dependence on conventional energy sources. It is important to note that the efficiency of the system will vary depending on the season and weather conditions. The greatest savings will be achieved during the summer period when the sky is clear.

4. Conclusions

This paper presents a numerical model of hydrothermal liquefaction (HTL) of sewage sludge in a 25 m long, 20 mm diameter tubular reactor heated using a linear Fresnel mirror. Key parameters such as temperature, pressure, and residence time of the medium in the reactor had a significant impact on the efficiency of converting sewage sludge to biocrude oil. The highest fraction of biocrude was observed at a distance of 11–25 m from the beginning of the reactor, where thermal conditions were most favorable. As temperature and pressure increased, the depolymerization, pyrolysis, and condensation processes intensified, leading to an increase in the amount of final products. The pressure loss analysis showed that longer reactors generate higher flow resistance, which results in a reactor outlet pressure drop. Special attention was paid to the deposition of solid particles in the bends of the tube, which can cause flow clogging and reduce heat transfer efficiency. Studies have also shown that the pipe diameter affects heat exchange efficiency, with smaller diameters leading to greater temperature losses due to shorter contact time between the medium and the reactor wall. Larger diameters improve solar energy absorption but may lead to greater heat losses to the environment. Flow rate optimization has shown that higher flow rates reduce the reactor wall temperature, which affects the conversion of sewage sludge. An increase in the Reynolds number improves heat exchange but requires more energy. The thermal efficiency of the reactor reached its maximum between 11:00 and 14:00, when the highest radiation intensity from a Fresnel mirror allowed for a reduction in electricity costs by 47.8% per year, which translates into significant financial savings and a reduction in CO₂ emissions by 8.28 t per year. Further studies should focus on optimizing the reactor geometry, reducing heat losses, and examining the impact of atmospheric conditions on overall system efficiency.

Further research should focus on modeling the reduction of heat losses and the impact of atmospheric variables on the overall efficiency of the system. The implementation of concentrated solar power (CSP) in HTL processes can significantly increase the sustainable production of biofuels by minimizing the impact of energy demand and pollution on the environment.