Timescales for Detecting Magnetized White Dwarfs in Gravitational Wave Astronomy †
Abstract
:1. Introduction
2. Structure of Rotating Magnetized White Dwarfs
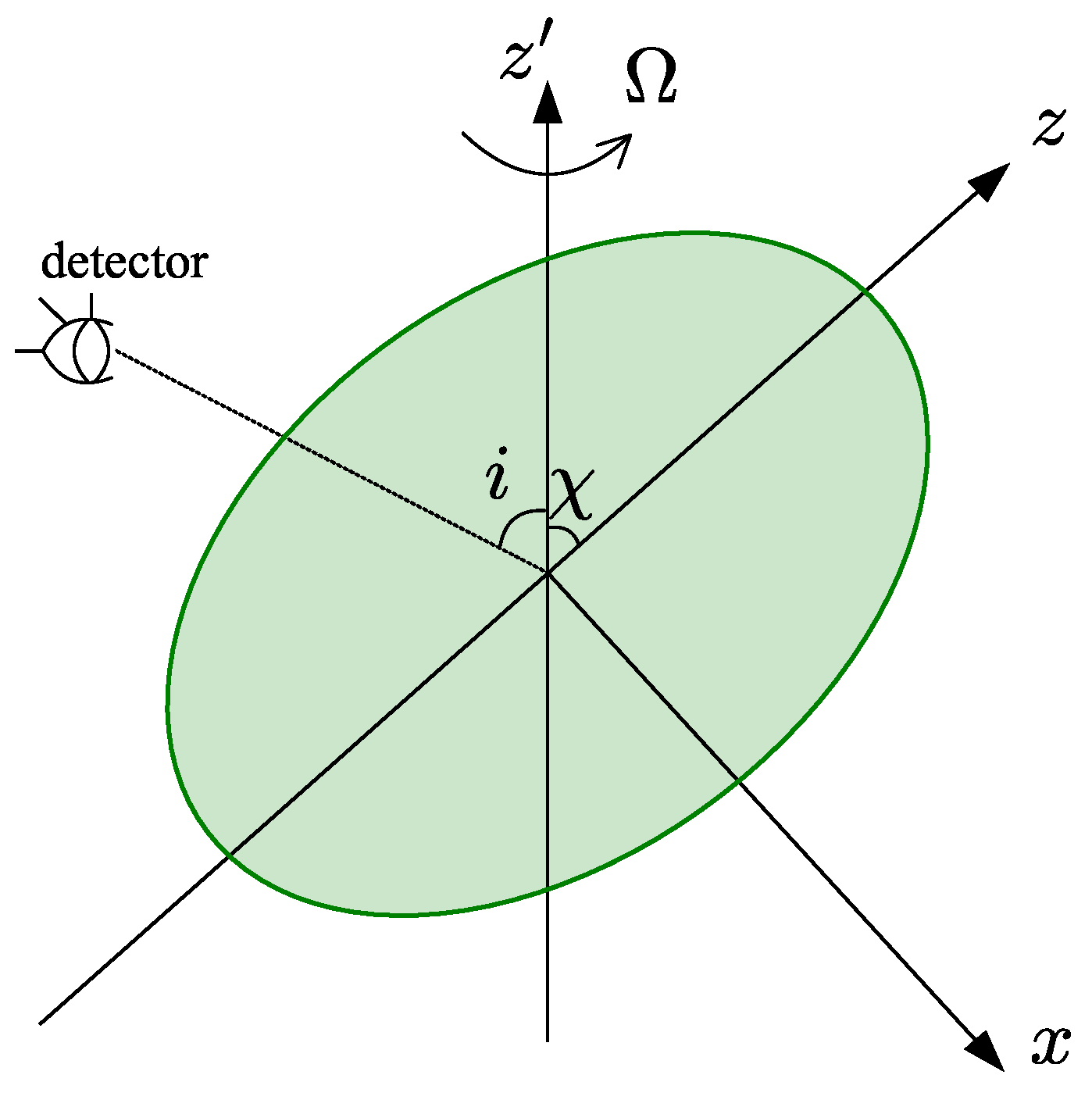
3. Gravitational Radiation Emitting from Rotating Magnetized White Dwarfs
4. Timescale for Emission of Gravitational Radiation
5. Conclusions
Data Availability Statement
References
- Chandrasekhar, S. The Maximum Mass of Ideal White Dwarfs. Astrophys. J. 1931, 74, 81. [Google Scholar] [CrossRef]
- Howell, D.A.; Sullivan, M.; Nugent, P.E.; Ellis, R.S.; Conley, A.J.; Le Borgne, D.; Carlberg, R.G.; Guy, J.; Balam, D.; Basa, S.; et al. The type Ia supernova SNLS-03D3bb from a super-Chandrasekhar-mass white dwarf star. Nature 2006, 443, 308–311. [Google Scholar] [CrossRef]
- Scalzo, R.A.; Aldering, G.; Antilogus, P.; Aragon, C.; Bailey, S.; Baltay, C.; Bongard, S.; Buton, C.; Childress, M.; Chotard, N.; et al. Nearby Supernova Factory Observations of SN 2007if: First Total Mass Measurement of a Super-Chandrasekhar-Mass Progenitor. Astrophys. J. 2010, 713, 1073–1094. [Google Scholar] [CrossRef]
- Ostriker, J.P.; Hartwick, F.D.A. Rapidly Rotating Stars.IV. Magnetic White Dwarfs. Astrophys. J. 1968, 153, 797. [Google Scholar] [CrossRef]
- Das, U.; Mukhopadhyay, B. Strongly magnetized cold degenerate electron gas: Mass-radius relation of the magnetized white dwarf. Phys. Rev. D 2012, 86, 042001. [Google Scholar] [CrossRef] [Green Version]
- Subramanian, S.; Mukhopadhyay, B. GRMHD formulation of highly super-Chandrasekhar rotating magnetized white dwarfs: Stable configurations of non-spherical white dwarfs. Mon. Not. RAS 2015, 454, 752–765. [Google Scholar] [CrossRef] [Green Version]
- Kalita, S.; Mukhopadhyay, B. Continuous gravitational wave from magnetized white dwarfs and neutron stars: Possible missions for LISA, DECIGO, BBO, ET detectors. Mon. Not. RAS 2019, 490, 2692–2705. [Google Scholar] [CrossRef] [Green Version]
- Kalita, S.; Mukhopadhyay, B. Continuous gravitational waves from magnetized white dwarfs. IAU Symp. 2020, 357, 79–83. [Google Scholar] [CrossRef]
- Kalita, S.; Mukhopadhyay, B. Modified Einstein’s gravity to probe the sub- and super-Chandrasekhar limiting mass white dwarfs: A new perspective to unify under- and over-luminous type Ia supernovae. J. Cosmol. Astropart. Phys. 2018, 9, 7. [Google Scholar] [CrossRef] [Green Version]
- Ong, Y.C. Generalized uncertainty principle, black holes, and white dwarfs: A tale of two infinities. J. Cosmol. Astropart. Phys. 2018, 9, 015. [Google Scholar] [CrossRef] [Green Version]
- Kalita, S.; Mukhopadhyay, B.; Govindarajan, T.R. Violation of Chandrasekhar mass-limit in noncommutative geometry: A strong possible explanation for the super-Chandrasekhar limiting mass white dwarfs. arXiv 2021, arXiv:1912.00900. [Google Scholar]
- Gupta, A.; Mukhopadhyay, B.; Tout, C.A. Suppression of luminosity and mass-radius relation of highly magnetized white dwarfs. Mon. Not. RAS 2020, 496, 894–902. [Google Scholar] [CrossRef]
- Zimmermann, M.; Szedenits, E., Jr. Gravitational waves from rotating and precessing rigid bodies—Simple models and applications to pulsars. Phys. Rev. D 1979, 20, 351–355. [Google Scholar] [CrossRef]
- Bonazzola, S.; Gourgoulhon, E. Gravitational waves from pulsars: Emission by the magnetic-field-induced distortion. Astron. Astrophys. 1996, 312, 675–690. [Google Scholar]
- Pili, A.G.; Bucciantini, N.; Del Zanna, L. Axisymmetric equilibrium models for magnetized neutron stars in General Relativity under the Conformally Flat Condition. Mon. Not. RAS 2014, 439, 3541–3563. [Google Scholar] [CrossRef] [Green Version]
- Komatsu, H.; Eriguchi, Y.; Hachisu, I. Rapidly rotating general relativistic stars. I—Numerical method and its application to uniformly rotating polytropes. Mon. Not. RAS 1989, 237, 355–379. [Google Scholar] [CrossRef]
- Braithwaite, J. Axisymmetric magnetic fields in stars: Relative strengths of poloidal and toroidal components. Mon. Not. RAS 2009, 397, 763–774. [Google Scholar] [CrossRef] [Green Version]
- Maggiore, M. Gravitational Waves: Volume 1: Theory and Experiments; Oxford University Press: Oxford, UK, 2008; Volume 1. [Google Scholar]
- Sathyaprakash, B.S.; Schutz, B.F. Physics, Astrophysics and Cosmology with Gravitational Waves. Living Rev. Relativ. 2009, 12, 2. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.J.; Hu, Y.M.; Korol, V.; Li, P.C.; Liang, Z.C.; Lu, Y.; Wang, H.T.; Yu, S.; Mei, J. Science with the TianQin Observatory: Preliminary results on Galactic double white dwarf binaries. Phys. Rev. D 2020, 102, 063021. [Google Scholar] [CrossRef]
- Ruiter, A.J.; Belczynski, K.; Benacquista, M.; Larson, S.L.; Williams, G. The LISA Gravitational Wave Foreground: A Study of Double White Dwarfs. Astrophys. J. 2010, 717, 1006–1021. [Google Scholar] [CrossRef] [Green Version]
- Melatos, A. Radiative precession of an isolated neutron star. Mon. Not. RAS 2000, 313, 217–228. [Google Scholar] [CrossRef] [Green Version]
- Kalita, S.; Mukhopadhyay, B.; Mondal, T.; Bulik, T. Timescales for Detection of Super-Chandrasekhar White Dwarfs by Gravitational-wave Astronomy. Astrophys. J. 2020, 896, 69. [Google Scholar] [CrossRef]
- Guseinov, O.K.; Novruzova, K.I.; Rustamov, I.S. He-rich white dwarfs: Birth-rate and kinematics of different groups of white dwarfs. Astrophys. Space Sci. 1983, 97, 305–322. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalita, S. Timescales for Detecting Magnetized White Dwarfs in Gravitational Wave Astronomy. Phys. Sci. Forum 2021, 2, 12. https://doi.org/10.3390/ECU2021-09310
Kalita S. Timescales for Detecting Magnetized White Dwarfs in Gravitational Wave Astronomy. Physical Sciences Forum. 2021; 2(1):12. https://doi.org/10.3390/ECU2021-09310
Chicago/Turabian StyleKalita, Surajit. 2021. "Timescales for Detecting Magnetized White Dwarfs in Gravitational Wave Astronomy" Physical Sciences Forum 2, no. 1: 12. https://doi.org/10.3390/ECU2021-09310
APA StyleKalita, S. (2021). Timescales for Detecting Magnetized White Dwarfs in Gravitational Wave Astronomy. Physical Sciences Forum, 2(1), 12. https://doi.org/10.3390/ECU2021-09310





