Position in Models of Quantum Mechanics with a Minimal Length ^†

Abstract

Candidate theories of quantum gravity predict the presence of a minimal measurable length at high energies. Such feature is in contrast with the Heisenberg Uncertainty Principle. Therefore, phenomenological approaches to quantum gravity introduced models spelled as modifications of quantum mechanics including a minimal length. The effects of such modification are expected to be relevant at large energies/small lengths. One first consequence is that position eigenstates are not included in such models due to the presence of a minimal uncertainty in position. Furthermore, depending on the particular modification of the position–momentum commutator, when such models are considered from momentum space, the position operator is changed, and a measure factor appears to let the position operator be self-adjoint. As a consequence, the (quasi-)position representation acquires numerous issues. For example, the position operator is no longer a multiplicative operator, and the momentum of a free particle does not correspond directly to its wave number. Here, we will review such issues, clarifying aspects of minimal length models, with particular reference to the representation of the position operator. Furthermore, we will show how such a (quasi-)position description of quantum mechanical models with a minimal length affects results concerning simple systems.

1. Introduction

Several approaches to quantum gravity, as well as gedanken experiments in black holes and high energy physics, suggest the presence of a minimal measurable length [1,2,3,4,5,6,7,8]. Such minimal length may be due to structural properties of space time (e.g., causal dynamical triangulation, loop quantum gravity, etc.) or to a fundamental minimal uncertainty in position (e.g., string theory, re-elaborations of the Heisenberg microscope including gravity, etc.). Regardless of its nature, such minimal length is in contrast with one of the cornerstones of quantum mechanics, viz. The Heisenberg uncertainty principle. Therefore, a modification of quantum mechanics accounting for such minimal measurable length is often considered in phenomenological approaches to quantum gravity. This modification is referred to as the generalized uncertainty principle (GUP). Several different approaches to GUP have been proposed in the past. In fact, GUP can be cast as a modification of the uncertainty relation between position and momentum, with no necessary modification of the representations of the corresponding operators [8,9,10]; alternatively, modifications of Poisson brackets have been considered in the classical sector, inducing modified classical dynamics [11,12,13,14]; finally, a modified commutation relation between position and momentum is studied, related with a modified uncertainty relation via the Schrödinger–Robertson relation [15,16,17,18]. In this work, we will consider this last approach. Specifically, we will consider a generic commutation relation of the form

$$\left[\widehat{q},\widehat{p}\right]=i\hslash f\left(\widehat{p}\right).$$

(1)

To study such relation and its implications, we will use [16] as a guideline. In particular, based on the work [19], we will study the action of the position operator in models with a minimal length described by Equation (1). It is worth pointing out at this stage that, as Equation (1) introduces a minimal uncertainty in position, position eigenstates are not included in such a model. We will thus see how a new representation is possible, following the ideas developed in [16] and the implications of such alternative perspective.

2. Quasi-Position Representation

Let us start from the momentum–space representation, in which the momentum operator acts on a wavefunction $\psi \left(p\right)$ by multiplying by the momentum variable $p$. In this space, a possible representation for the position operator is

$$\widehat{q}\psi \left(p\right)=i\hslash f\left(p\right)\frac{d}{dp}\psi \left(p\right).$$

(2)

As mentioned in the introduction, position eigenstates are not present in such model. Thus, we do not have a meaningful representation in which the operator $\widehat{q}$ acts multiplicatively. However, we can introduce maximally localized states as those states with the smallest position uncertainty possible, and write any state as a superposition of such maximally localized states. For practical reasons, we will specialize our analysis to the case in which the function $f\left(p\right)$ in Equation (1) is given as

$$f\left(p\right)=1-2\delta p+\left({\delta }^2+ϵ\right)p^2,$$

(3)

with

$$\delta =\frac{{\delta }_0}{M_{Pl}c},ϵ=\frac{{ϵ}_0}{M_{Pl}^2{c}^2}.$$

(4)

Here, $M_{Pl}$ is the Planck mass, $c$ is the speed of light in vacuum, and ${\delta }_0$ and ${ϵ}_0$ are dimensionless parameters. Similar results in a more general setting can be found in [19]. A function of minimal uncertainty in position can be found, as usually implemented in quantum mechanics, as the function ${\psi }_{⟨q⟩}\left(p\right)$ of position expectation value $⟨q⟩$ fulfilling the following equation

$$\left(\widehat{q}-⟨q⟩\right){\psi }_{⟨q⟩}=\frac{-i\hslash ⟨f\left(p\right)⟩}{{\left(\Delta p\right)}^2}\left(\widehat{p}-⟨p⟩\right){\psi }_{⟨q⟩}.$$

(5)

Using Equations (2) and (3), we find a differential equation of solution

$${\psi }_{⟨q⟩}\left(p\right)=\frac{1}{\sqrt{1-2\delta p+\left({\delta }^2+ϵ\right)p^2}}exp\left[-i\frac{⟨q⟩p_0\left(p\right)}{\hslash }\right],$$

(6)

where $p_0\left(p\right)$ is defined as

$$p_0\left(p\right)={\int }_0^p\frac{d{p}^{\prime }}{f\left(p^{\prime }\right)}=\frac{1}{\sqrt{ϵ}}arctan\left[\frac{-\delta +\left({\delta }^2+ϵ\right)p}{\sqrt{ϵ}}\right]+\frac{1}{\sqrt{ϵ}}arctan\left(\frac{\delta }{\sqrt{ϵ}}\right).$$

(7)

It is important to notice that, in general, the quantity $p_0$ is bounded on subset of $R$. In fact, in the particular case of Equation (3), we find

$$p_0\in \left(\frac{1}{\sqrt{ϵ}}arctan\left(\frac{\delta }{\sqrt{ϵ}}\right)-\frac{\pi }{2\sqrt{ϵ}},\frac{1}{\sqrt{ϵ}}arctan\left(\frac{\delta }{\sqrt{ϵ}}\right)+\frac{\pi }{2\sqrt{ϵ}}\right).$$

(8)

Such property is in agreement with the existence of a minimal length as, as we will see below, the two extremes correspond to the shorter wavelength allowed in the model. Furthermore, it is worth noticing that such an interval is not symmetric with respect to 0. This is a consequence of the linear term in $p$ in Equation (3), which introduces a difference between the left and right direction.

Considering the function in Equation (6) as a function of both $p$ and $\xi =⟨q⟩$ and using it as a kernel for an integral transform, we obtain the following two transforms, which generalize the Fourier transform in the case of GUP.

$$\begin{array}{c}{T}^{-1}\left[\varphi \right]\left(\xi \right)=\frac{1}{\sqrt{2\pi \hslash }}{\int }_{-\infty }^{\infty }\frac{dp}{f\left(p\right)}{\psi }^{}\left(p,\xi \right)\varphi \left(p\right),\\ T\left[\varphi \right]\left(p\right)=\frac{1}{\sqrt{2\pi \hslash }}{\int }_{-\infty }^{\infty }d\xi {\left[{\psi }^{}\left(p,\xi \right)\right]}^{-1}\varphi \left(\xi \right).\end{array}$$

(9)

Such transform allows for representing a state as a superposition of maximally localized states of different position expectation values $\xi$. We can then use them to find the momentum eigenstates in such new “quasi-position” representation

$${\varphi }_{\tilde{p}}\left(\xi \right)=T^{-1}\left[\delta \left(\tilde{p}-p\right)\right]\left(\xi \right)=\frac{1}{\sqrt{2\pi \hslash }}\frac{1}{{\left[1-2\delta \tilde{p}+\left({\delta }^2+ϵ\right){\tilde{p}}^2\right]}^{3/2}}exp\left[i\frac{\xi p_0\left(\tilde{p}\right)}{\hslash }\right].$$

(10)

We thus see that a momentum eigenstate, i.e., a free-particle state, in quasi-position space corresponds to a plane wave of wave number $k=p_0\left(\tilde{p}\right)/\hslash$. Therefore, GUP changes the de Broglie relation between wave number and momentum. Furthermore, in models in which $f\left(p\right)$ is not an even function, e.g., ${\delta }_0\ne 0$, we have two different wave numbers for left- and right-moving waves or, equivalently, a different dispersion relation for left- and right-moving particles.

Furthermore, the same transformations allow for writing the position and momentum operators in quasi-position space. In fact, we find

$$\begin{array}{c}\widehat{q}=\xi +i\hslash \left[\left({\delta }^2+ϵ\right)\widehat{p}-\delta \right],\\ \widehat{p}=\frac{\sqrt{ϵ}tan\left[\sqrt{ϵ}{\widehat{p}}_0-arctan\left(\frac{\delta }{\sqrt{ϵ}}\right)\right]+\delta }{{\delta }^2+ϵ},{\widehat{p}}_0=-i\hslash \frac{d}{d\xi }\end{array}$$

(11)

We then see that the position operator in such representation is not a multiplicative operator, as in standard quantum mechanics. This result is due to the rich structure of models with a minimal length.

3. Examples

We are now going to consider two special systems in which a minimal length, via the results found in the previous section, has interesting consequences.

3.1. Particle in a Box

Let us consider a one-dimensional box of side $L$. Such a system, similarly to what is implemented in ordinary quantum mechanics, can be described in terms of a discontinuous potential, which is 0 between $\xi =0$ and $\xi =L$, and infinite anywhere else. Proceeding as usual, one considers a superposition of left- and right- moving waves with same momentum eigenvalue $p$ up to a sign, and imposes the relevant boundary conditions. However, as in GUP models the wavelengths of left- and right- moving waves are, in general, different, we cannot directly conclude that a solution of the Schrödinger equation is a standing wave with $L$ a semi-integer multiple of the wavelength. In fact, after the necessary calculation, one may find that, in this case, the condition is that the sum of wavelengths of the left- and right-moving waves be a divider of the box width or, in terms of the quantity $p_0$,

$$\left[p_0\left(p_n\right)-p_0\left(-p_n\right)\right]=\frac{2n\pi \hslash }{L},$$

(12)

where $p_n$ is the momentum eigenvalue associated with the $n$’s energy state. The relation above can then be inverted to find the possible values of the momentum eigenvalue. However, as $p_0$ is bounded, as shown in the previous section, Equation (12) admits only a finite number of integers $n$. The maximum number of possible energy eigenstates is in fact related with the ratio $L/l_{Pl}$, with $l_{Pl}$ the Planck length. Specifically, one finds for the maximum number

$$n_{max}=⎣\frac{L}{2l_{Pl}\sqrt{{ϵ}_0}}⎦.$$

(13)

In Figure 1, two different choices for the parameters ${\delta }_0$ and ${ϵ}_0$ are compared to the standard case. The vertical dashed lines correspond to the higher energy state allowed in each model. Such effect becomes more relevant the narrower the box is, for example, when $L=20l_{Pl}$ and ${ϵ}_0=1$, one find that only 10 energy states are allowed. Conversely, one can find that boxes narrower than a particular width do not allow any state, that is, when

$$L<2l_{Pl}\sqrt{{ϵ}_0}.$$

(14)

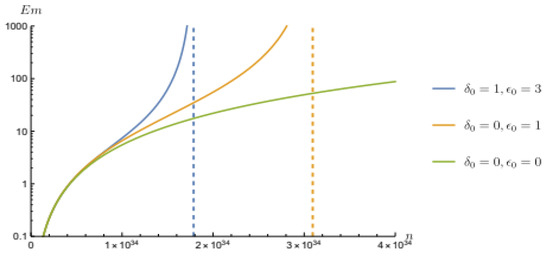
Figure 1. Energy times mass of a particle in a box of width 1 m. The green line represents the ordinary case, and the blue and orange lines represent two different GUP parametrizations. The dashed vertical lines represent the maximum integer n allowed for that particular model.

3.2. Potential Barrier

As a second example, let us consider a potential barrier of width $L$ and height $U_0$ between $\xi =0$ and $\xi =L$. As in ordinary quantum mechanics, considering a particle approaching the barrier from the left, a generic energy eigenstate is given by a superposition of a left- and a right-moving wave on the left of the barrier, corresponding to a reflected and an incoming wave, respectively; a left- and a right-moving wave in the region of the barrier; and a right-moving wave on the right of the barrier, corresponding to a transmitted wave. Imposing the corresponding boundary conditions, one can then find a relation for the transmission and reflection coefficients. Carrying out the calculations, one can find that resonances in the transmission amplitudes appear at different energies than in the standard case. Furthermore, contrary to ordinary quantum mechanics, only a finite number of resonances are allowed. As in the case of a particle in a box, resonances are related with the sum of the wavelengths of left- and right-moving waves in the region of the barrier. Specifically, a resonance is obtained when the width of the barrier is a half-integer multiple of such a sum. In terms of the quantity $p_0$, we have

$$p_0\left({p^{\prime }}_n\right)-p_0\left(-{p^{\prime }}_n\right)=\frac{2n\pi }{L},$$

(15)

with ${p^{\prime }}_n$ the momentum eigenvalue of the stationary states corresponding to a resonance, i.e.,

$$p_n=\sqrt{2m\left(E_n-U_0\right)}.$$

(16)

In this case as well, as $p_0$ acquires values on a limited interval, we can conclude that only finitely many resonances are allowed, as shown in Figure 2. The maximum number of resonances depend on the ratio $L/l_{Pl}$ and is given by

$$n_{max}=⎣\frac{L}{2l_{Pl}\sqrt{{ϵ}_0}}⎦.$$

(17)

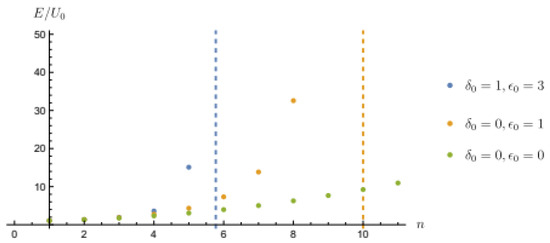
Figure 2. Resonance energies with a minimal length (blue and orange dots) and in the standard case (green dots). The vertical lines represent the maximum number of resonances allowed in the models. Here, a barrier of width $L=20l_{Pl}$ and height $U_0=120{\hslash }^2/{\mathrm{mL}}^2$ has been used.

4. Conclusions

The generalized uncertainty principle is a quantum model describing the existence of a minimal uncertainty in position. In this paper, we considered such a model modifying the commutation relation between position and momentum. Due to the presence of a minimal uncertainty in position, it is not possible to define a position representation, and we had to resort to an alternative description, often referred to as “quasi-position”. However, such methodology introduces various issues that we have tried to clarify here. In particular, the position operator does not act multiplicatively in such new representation. Rather, it contains a term proportional to the momentum operator and another which is an imaginary constant. Such an imaginary constant is related to the position expectation value on states of minimal uncertainty in position. Furthermore, by studying momentum eigenstates in the quasi-position representation, we saw that they can be described as plane waves with a wave number which is not proportional to the momentum eigenvalue, suggesting a modification of de Broglie relations. In fact, left- and right-moving waves, characterized by the same momentum eigenvalue, are described by different wavelengths. Furthermore, in general, the wave number of a free wave acquires its value on a limited interval, thus introducing a maximum wave number or a minimal wavelength, compatible with the introduction of a minimal length. All this has interesting implications when quantum systems are analyzed, as in the two examples presented here. In fact, we have seen that, in contrast to ordinary quantum mechanics, only a finite number of stationary states are allowed in a box. Furthermore, depending on the width of the box and on the parameters of the adopted model, a box may even present no state at all. As a second example, we considered the case of a potential barrier. Here, a minimal length also has relevant implications. In fact, we found a finite number of resonance energies for a wave crossing the barrier. Such number depends on the width of the barrier and on the parameters of the model. Furthermore, when no resonance is present, the reflection coefficient is strongly suppressed, even for energies below the potential energy of the barrier, as seen in Figure 3. Again, these last features are compatible with the presence of a minimal length.

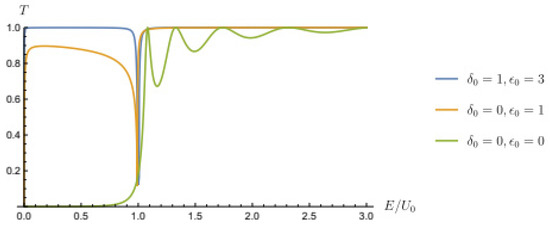
Figure 3. Transmission coefficient as a function of the ratio between the energy of the incoming wave and the barrier height. Here, a barrier of width $L=1l_{Pl}$ and height $U_0=120{\hslash }^2/{\mathrm{mL}}^2$ has been used. It is worth noticing that the transmission coefficient is equal to 1, or close to 1, even when $E<U_0$.

The present analysis, although limited to a one-dimensional case and to a specific model, serves to shed some light on the issues concerning a description of quantum mechanics with a minimal length. In fact, this is often the playground of phenomenological studies in quantum gravity [20,21,22]. A detailed and careful analysis is therefore necessary in order to potentially compare such features with experimental observations.