Curvature Change in Laser-Assisted Bending of Inconel 718 ^†

Abstract

Laser heating is industrially applied to facilitate plastic shaping, especially for materials difficult to form due to their high hardness or brittleness. The effects of thermal softening and thermal forming in the total plastic deformation of pre-stressed beams are investigated in the study. Laser-assisted bending experiments were performed using the moving CO₂ laser beam and cantilever thin beams made of the factory-annealed Inconel 718 nickel-based superalloy. The deformation process is simulated numerically using the Finite Element Method and the Johnson–Cook constitutive material model. Curvature changes in thermo-mechanical bending are calculated numerically. Phenomenological moment–curvature relations for the laser-assisted bending process are formulated. The curvature in hybrid bending can be estimated as a sum of components resulting from the elastic deformation and inelastic deformations due to the pure thermal bending and thermally enhanced mechanical bending. For the effective hybrid bending, the external mechanical load should be applied consistently with the deformation effect of the heat source alone.

1. Introduction

With a growing interest in the application of high-strength and difficult-to-form materials, the processes of forming aided by local heating have been under development in recent years. Laser assistance has been successfully introduced into many forming technologies, such as stamping, bending, single-point incremental forming (SPIF), spinning, stretch forming, roll profiling, deep drawing, wire drawing or hydroforming [1,2,3]. In particular, it proved to be useful for brittle or high-hardness materials, such as ceramics, cast iron, and nickel alloys.

Plastic deformation of many metallic and non-metallic materials can be produced solely due to laser heating, without any application of external forces. Investigations on laser thermal forming were initiated in the 1970s and originated from the research on the line heating method [4,5]. Laser forming techniques turned out to be very efficient in mass production of the electronic industry because of its ability to achieve high accuracy in touchless positioning and alignment of components during assembly [6,7]. Unfortunately, considerable time-consumption is related to the application of laser forming when larger deformations are needed [8]. Hence, the combined use of laser heating and external forces is studied in recent years [9,10,11,12,13,14,15].

The contribution of laser thermal forming mechanisms in thermo-mechanical bending has neither been separated nor estimated so far. The curvature is a quantity of fundamental importance in describing the mechanical bending process. To the best knowledge of the authors, the effect of thermal loading (due to the heating with a moving laser beam) combined with the initial mechanical loading (pre-stress condition) on the workpiece curvature has not been quantitatively described for the process of thermo-mechanical bending up to now. Therefore, the aim of this study is an attempt to quantify the contribution of laser heating in the laser-assisted bending process. It is a continuation of investigations on the application of hybrid laser-mechanical forming in manufacturing of components for the aerospace industry [16,17,18].

At first, thermo-mechanical bending experiments were performed using thin-walled beams loaded with an external mechanical loading in the elastic stress range and then heated with a moving laser beam. The experimental measurements results were subsequently used in calibration of a numerical model of the hybrid bending process. This model allowed then an analysis of thermo-elastic-plastic deformations of a thin-walled beam. Based on numerically calculated moment–curvature relations, a phenomenological model was formulated for the thermo-mechanical bending process.

2. Materials and Methods

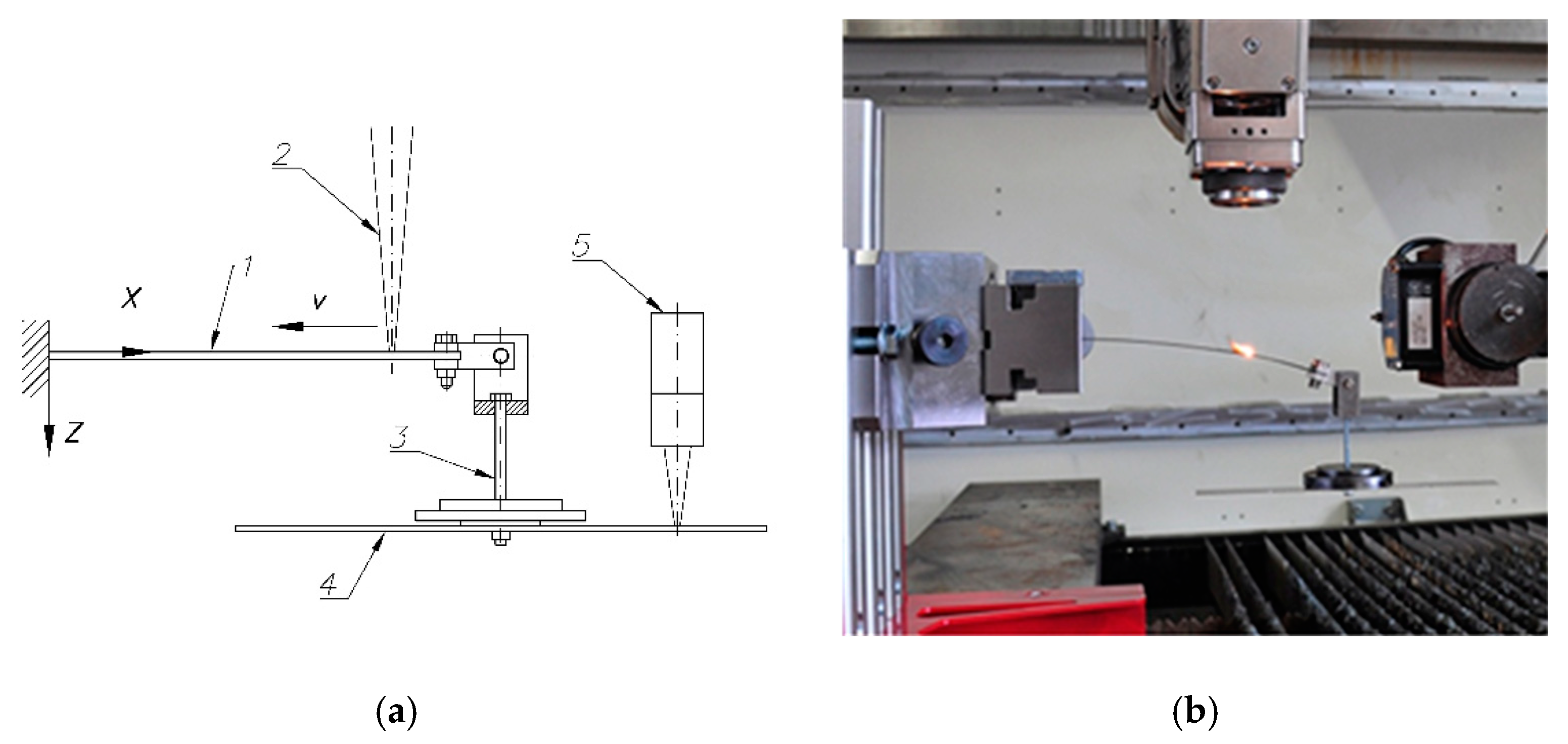
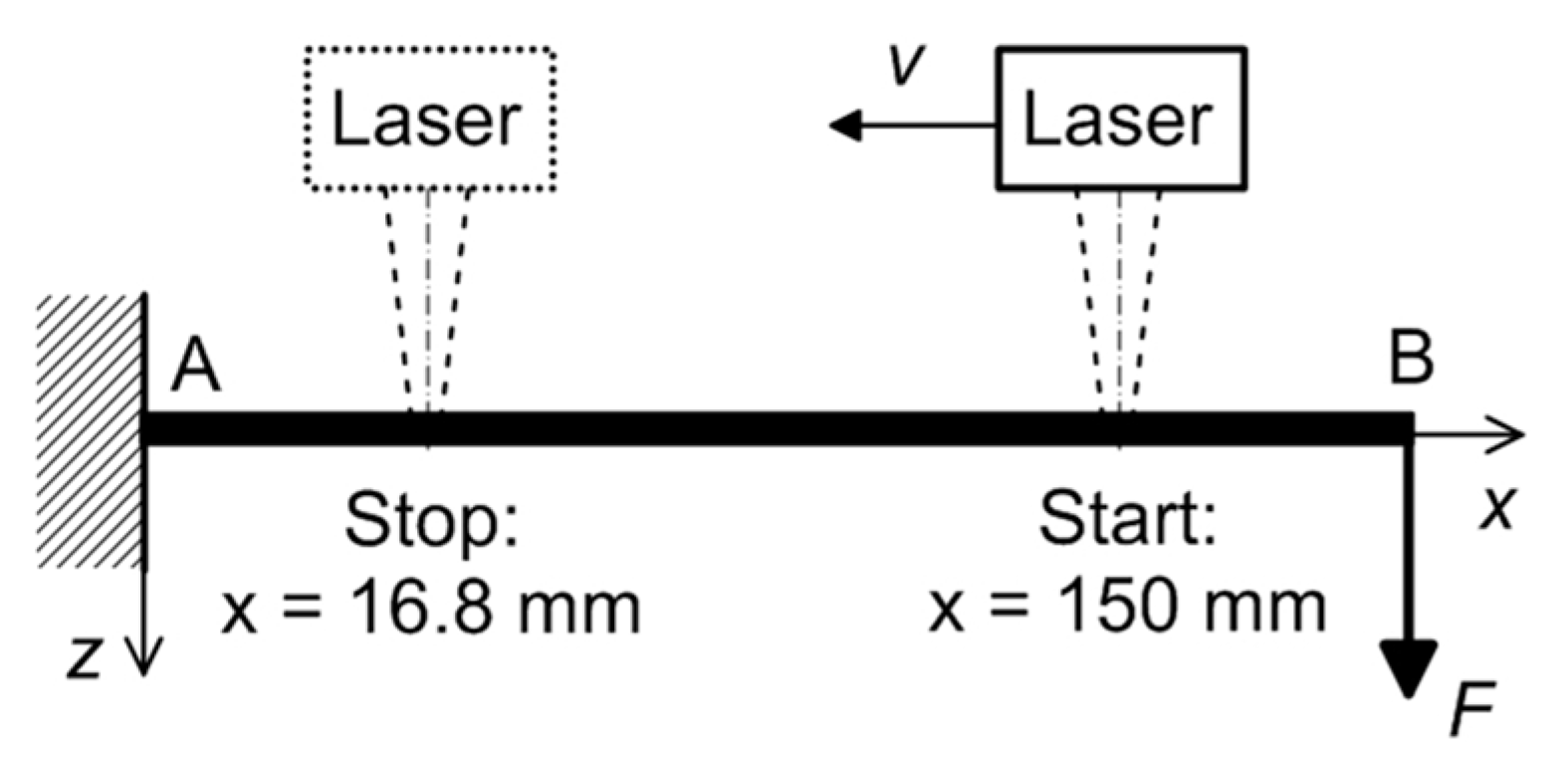
2.1. Experimental Investigation

Experiments were conducted on beams, 1 mm thick, made of commercial solution annealed Inconel 718. The samples were cut from a rolled sheet using a laser to minimize any residual stresses. Rectangular specimens, 20 mm wide, were clamped in a cantilever arrangement (Figure 1).

Table 1. Chemical composition (wt%) of Inconel 718.

Ni	Nb	Cr	Mo	Mn	Si	Ti	Al	Co	Fe
52.9	4.83	19.83	3.12	0.29	0.14	1.04	0.60	0.05	Balance

presents the chemical composition of the material.

Mechanical pre-stress was introduced by the gravity acting on weights mounted at the free end (at x = 175 mm, Figure 1a) and on the own mass of the sample. In a series of experiments, the mechanical loading system provided vertical dead load, denoted as F, of the following values: 1.08 N, 1.57 N, 2.55 N, 3.04 N and 4.51 N. Samples were pre-loaded within the elastic stress state.

Pre-stressed beams were subsequently subject to heating with a laser beam of power 500 W moving from position x = 150 mm in the direction of the specimen fixture (x = 0). The TruFlow6000 CO₂ laser (TRUMPF GmbH + Co. KG, Ditzingen, Germany) operating in the continuous-wave (CW) mode was used. A rectangular 20 mm × 2 mm laser spot had velocity v = 3.33 mm/s. Samples were covered with an absorptive layer (a black paint) in order to increase the transfer of the laser beam energy into the material.

Non-contact temperature measurements were performed to provide data needed for determination of the laser radiation absorption coefficient. OPTRIS CTL G5H CF2 pyrometer (Optris GmbH, Berlin, Germany) was used. It operates at a 5.2 µm radiation wavelength; therefore, the reflected CO₂ laser radiation (10.6 µm radiation wavelength) had no influence on temperature measurements. The thermo-mechanically induced deformation was measured with a non-contact optical displacement sensor MicroEpsilon LLT1700 (MICRO-EPSILON MESSTECHNIK GmbH & Co. KG, Ortenburg, Germany) and a flat metal plate attached to the holder of weights.

2.2. Numerical Simulations

Thermo-mechanical bending experiments were modelled numerically using the ABAQUS finite element (FE) program [19]. Numerical simulations were aimed first at calibrating parameters of the material constitutive model. Afterwards, computer calculations were used to analyse how the curvature produced under hybrid loading depends on the bending moment of the pre-stress state.

A dedicated DFLUX user subroutine was used in modelling of laser heating. As the laser radiation penetration depth is very small for metallic materials, the laser beam was treated as a surface heat source. The top-hat model was assumed for the radiation intensity distribution over the laser spot.

Sequentially coupled thermo-mechanical analysis was performed taking into account that heat generated due to material deformation is negligible as compared to the heat delivered by the laser beam. As the considered deformation process is relatively slow, any dynamic effects were also neglected. However, heat dissipation due to convection and radiation was accounted for.

A regular mesh of finite elements consisted of hexahedral DC3D8 elements for the heat transfer analysis in the initial configuration, and compatible C3D8 elements for the quasi-static mechanical analysis with 3D time-dependent temperature field and the external mechanical load. One half of the specimen was descretized by the mesh, as the beam, the loads and boundary conditions were symmetric with respect to the xz plane (Figure 1a). In order to achieve a high accuracy of temperature gradient and bending effects in numerical modelling, the mesh was built of 141,600 elements having dimensions 0.2 mm × 0.5 mm × 0.1 mm.

Using numerical simulations and surface temperature measurements taken with the pyrometer, the laser radiation absorption coefficient value 0.37 was determined.

2.3. Material Constitutive Model

The Johnson–Cook material model [20] was used to account for strain hardening, strain rate hardening or softening, and thermal softening effects in elastic-plastic incremental analysis:

$${\sigma }_Y^T=\left[A+B\cdot {\left({\epsilon }^{pl}\right)}^n\right]\left[1+C_{JC}\cdot \ln \left(\frac{\stackrel{•}{{\epsilon }^{pl}}}{\stackrel{•}{{\epsilon }_0}}\right)\right]\left[1-{\left(T^{\ast }\right)}^m\right]$$

(1)

where: ${\sigma }_Y^T$ is the strain-, strain rate- and temperature-dependent yield stress, ${\epsilon }^{pl}$ is plastic strain, $\stackrel{•}{{\epsilon }^{pl}}$ is plastic strain rate, $\stackrel{•}{{\epsilon }_0}$ is the reference strain rate (0.001 s⁻¹), $T^{\ast }=\left(T-T_r\right)/\left(T_m-T_r\right)$, T is temperature, $T_m$ is the melting temperature (1250 °C), $T_r$ is the transition temperature (20 °C), $A$, $B$, $C_{JC}$, $m$ and $n$ are material parameters.

Parameters of the Johnson–Cook material model (

Table 2. The Johnson–Cook material model parameters.

A (MPa)	B (MPa)	CJC	m	n
450	2100.95	0.02	1.5	0.76

) were identified using the data from hybrid bending experiments. Thermophysical material data used in numerical simulations are described in [21].

The numerical predictions of the free-end deflection (Figure 2) are in fairly close agreement with the experimental data for a wide range of the pre-load value. Visible discrepancies between the obtained results most probably result from the deviations in properties of the absorptive layer for individual specimens.

2.4. Beam Curvature

The curvature is a convenient and commonly applied quantity in analyses of the bending behaviour of beams. The parametric description of the beam axis makes it possible to account for arbitrary large curvatures. Treating the longitudinal beam axis as a curve $\overrightarrow{r}=x(s)\overrightarrow{i}+z(s)\overrightarrow{k}$, with $\overrightarrow{i},\overrightarrow{k}$—unit vectors of the axes $x$ and $z$, respectively (Figure 1a), the values of parameter $s$ referred to the x-coordinates of nodes that in the unloaded (initial) configuration were located on the beam axis.

The curvature $C$ of a plane curve in the parametric description can be calculated as [22].

$$C=\frac{\left|\frac{d^{2}z}{d{s}^2}\frac{dx}{ds}-\frac{d^{2}x}{d{s}^2}\frac{dz}{ds}\right|}{{\left({\left(\frac{dx}{ds}\right)}^2+{\left(\frac{dz}{ds}\right)}^2\right)}^{3/2}}$$

(2)

The bending moment and curvature values are presented here with the positive sign, without adherence to the commonly used sign conventions. With the assumed coordinate system, all these values otherwise should have the negative sign [23].

To calculate the derivatives $\frac{dx}{ds}$ and $\frac{dz}{ds}$ the finite difference method was used. For the first derivative the symmetric difference quotient formula was applied

$$\frac{df}{ds}\approx \frac{f(s+h)-f(s-h)}{2h},$$

(3)

The central difference approximation was used in calculating of the second derivatives $\frac{d^{2}x}{d{s}^2}$ and $\frac{d^{2}z}{d{s}^2}$

$$\frac{d^{2}f}{d{s}^2}\approx \frac{f(s+h)-2f(s)+f(s-h)}{h^2},$$

(4)

Numerical differentiation is often sensitive to errors resulting from the limited representation precision of numerical data (round-off errors). In this work, low round-off and truncation errors were achieved assuming the value of parameter $h$ equal 3 mm, with $x(s)$, $z(s)$ and $s$ expressed in millimeters.

3. Results and Discussion

The developed numerical model, validated with the experimental data, was used to simulate the behavior of a cantilever beam AB heated with a moving laser beam between the start position x = 150 mm and the stop position x = 16.8 mm (Figure 3), without and with the external mechanical loading. Three levels of the applied laser beam power were considered (450, 500 and 550 W). Other processing conditions were the same as for experimental validation of the numerical model.

Even without applying any mechanical load (no gravity, F = 0), the laser-heated beam underwent a considerable plastic deformation, solely due to the laser heating. Such a case will be called “the pure laser bending”. The so-called “convex bending” occurred, i.e., when the laser-heated surface of the workpiece becomes convex after processing [24].

Figure 4 presents a diagram of the beam curvature as a function of parameter s, calculated for the following loading conditions:

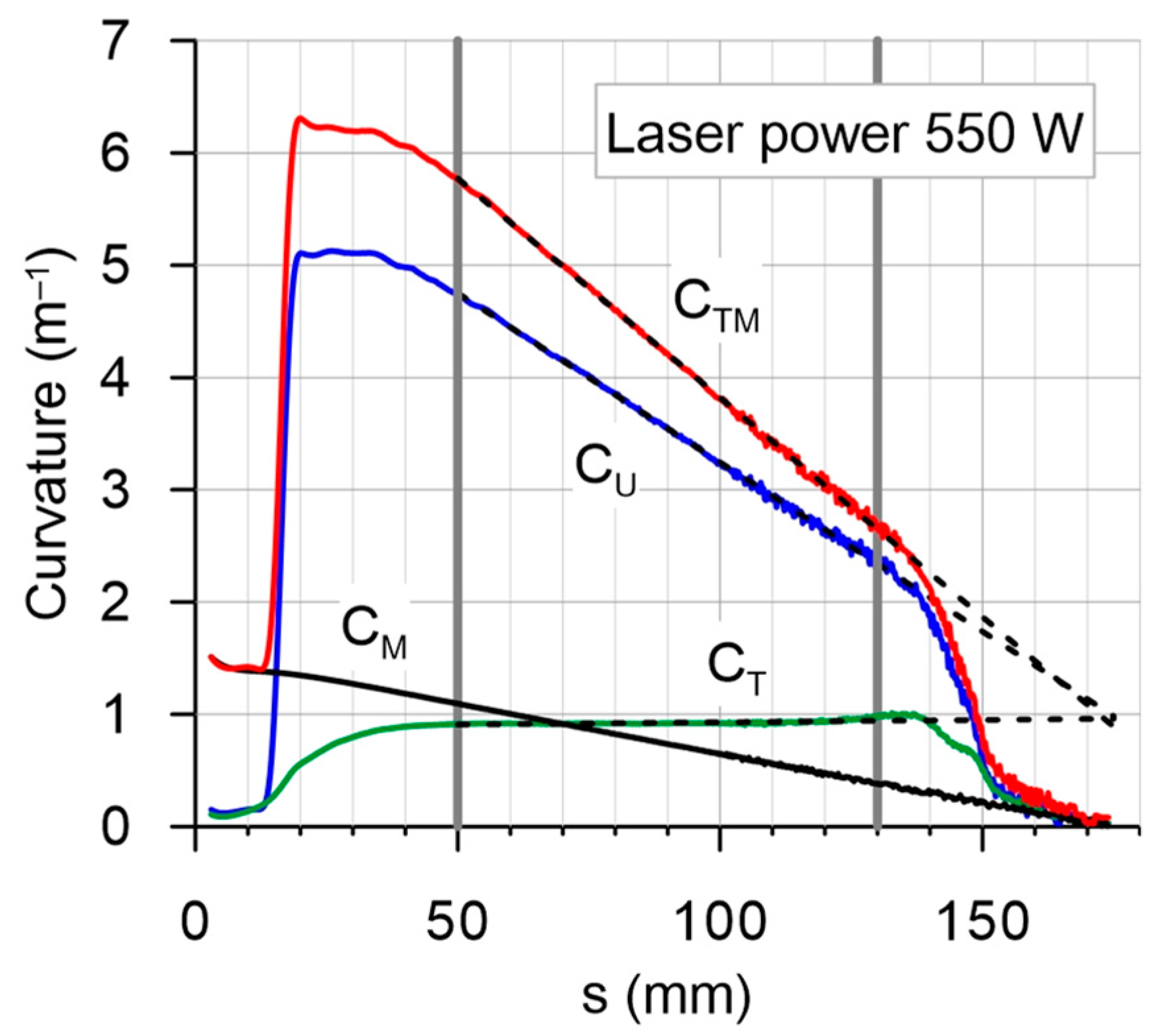
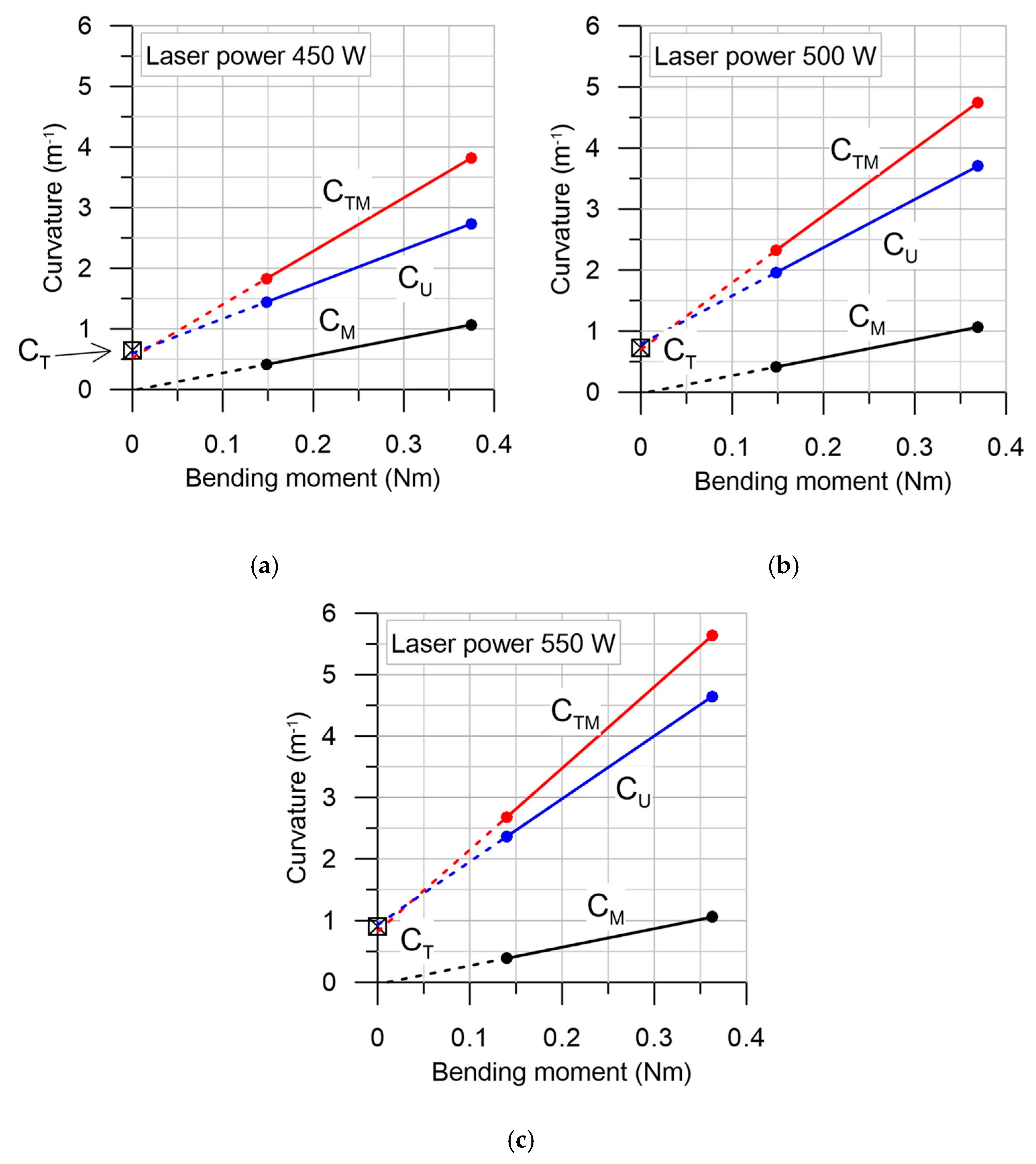
• Pure thermal loading (laser bending with laser power 550 W; curvature $C_T$).
• Pure mechanical loading (F= 3.04 N; curvature $C_M$).
• Thermo-mechanical bending, i.e., mechanical loading (F = 3.04 N) followed by laser heating (laser power 550 W; curvature $C_{TM}$).
• Complete unloading after thermo-mechanical bending (cooling, removal of mechanical loads; final curvature $C_U$).

Curvatures $C_T$, $C_{TM}$ and $C_U$, which were obtained for cases with the laser heating involved, exhibit strong instability related to the temperature field instability in the vicinity of the heating start and stop positions. The lines representing calculated curvature also show an effect of the applied numerical derivation procedure, visible as some dense oscillations (‘noise’).

The moment–curvature dependences (Figure 5a–c) were calculated using linear approximations of the curvature diagrams (Figure 4) in the middle range $50\le s\le 130$. The effect of large deformations was taken into account. Dashed lines in Figure 5a–c represent linear extrapolations of the curvature results.

Based on the obtained moment–curvature diagrams (Figure 5a–c), the following observations and conclusions can be formulated:

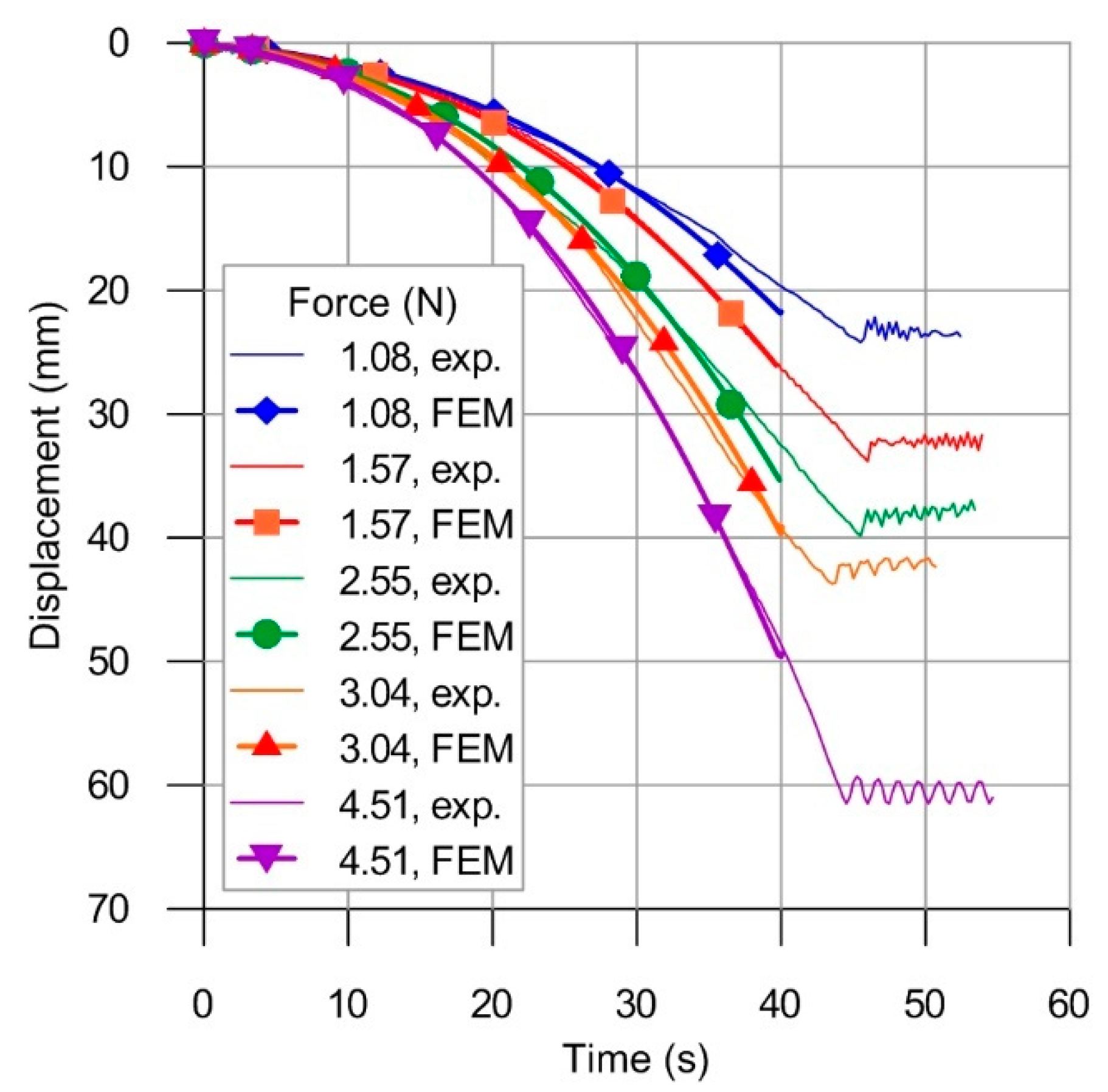
• Calculated curvature $C_M$ of the beam loaded only mechanically differs by no more than 0.5% from the well-known solution of the classical Bernoulli–Euler beam theory $C_{B-E}=M/\left(EI\right)$, where $M$ is the bending moment, $E$ is the Young’s modulus, $I$ is the moment of inertia of the beam cross-section. The difference may be attributed mainly due to: (1) the effect of shear stresses, which is not considered in the Bernoulli–Euler theory, and (2) the limited accuracy of numerical simulation and numerical derivation calculations.
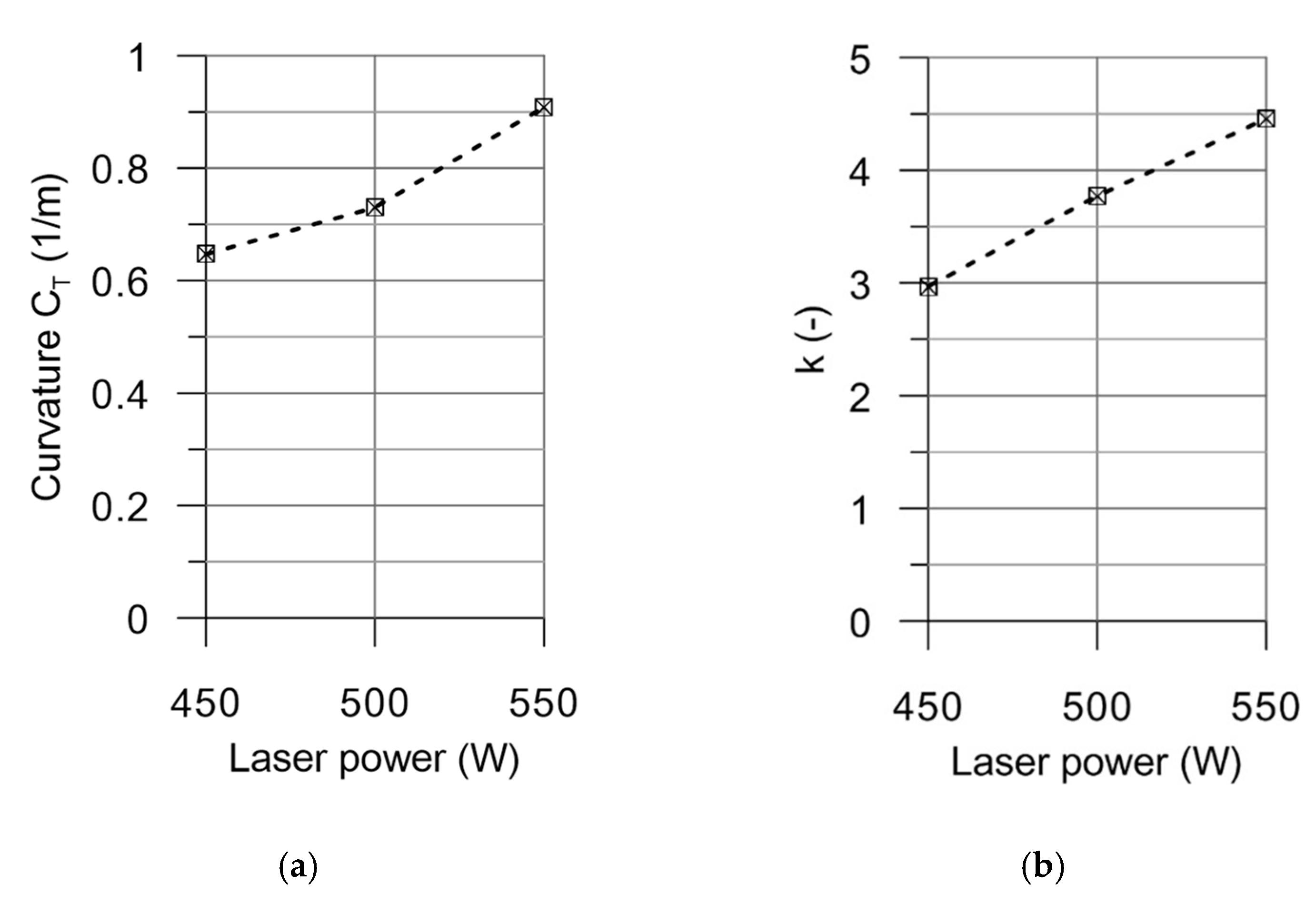
• For all considered heat load cases (laser power 450, 500 and 550 W), the curvature $C_{TM}$, calculated after thermo-mechanical processing, but still under mechanical loading, for the zero value of the bending moment has a value close to the pure thermal bending curvature value $C_T$. The dependence of curvature $C_T$ on the applied laser power, for the considered processing conditions, is presented in Figure 6a.
• Similarly, for all considered heat load cases, the final curvature $C_U$, calculated after thermo-mechanical processing and complete unloading, for the zero value of the bending moment has a value close to the pure thermal bending curvature value $C_T$.
• The dependence of curvature $C_{TM}$ on the bending moment $M$ may be described by the following phenomenological relation:

  $$C_{TM}(M)=C_T+k{C}_M(M)$$

  (5)

  where $k$ is the multiplication (scaling) factor, a constant dependent on processing conditions. The curvature after the laser heating step can be estimated by scaling the elastic solution for the mechanically induced curvature and adding the curvature produced by the pure laser bending. The dependence of the scaling factor $k$ on the applied laser power, for the considered processing conditions, is presented in Figure 6b.
• The effect of unloading may be estimated as the opposite to the effect of elastic loading:

  $$C_U(M)=C_{TM}(M)-C_M(M)$$

  (6)

  Equation (5) describes the effect of combined thermal and mechanical loading on curvature in the considered thermo-mechanical bending process. For the effective hybrid bending, the external mechanical load should be applied consistently with the deformation effect of the heat source alone.