The Geometry of Quivers †
Abstract
1. A First Look at Quivers
1.1. Quiver Representations
1.2. Examples and Basic Notions
1.3. Double Quivers
1.4. Quiver Varieties
2. The Electric Side
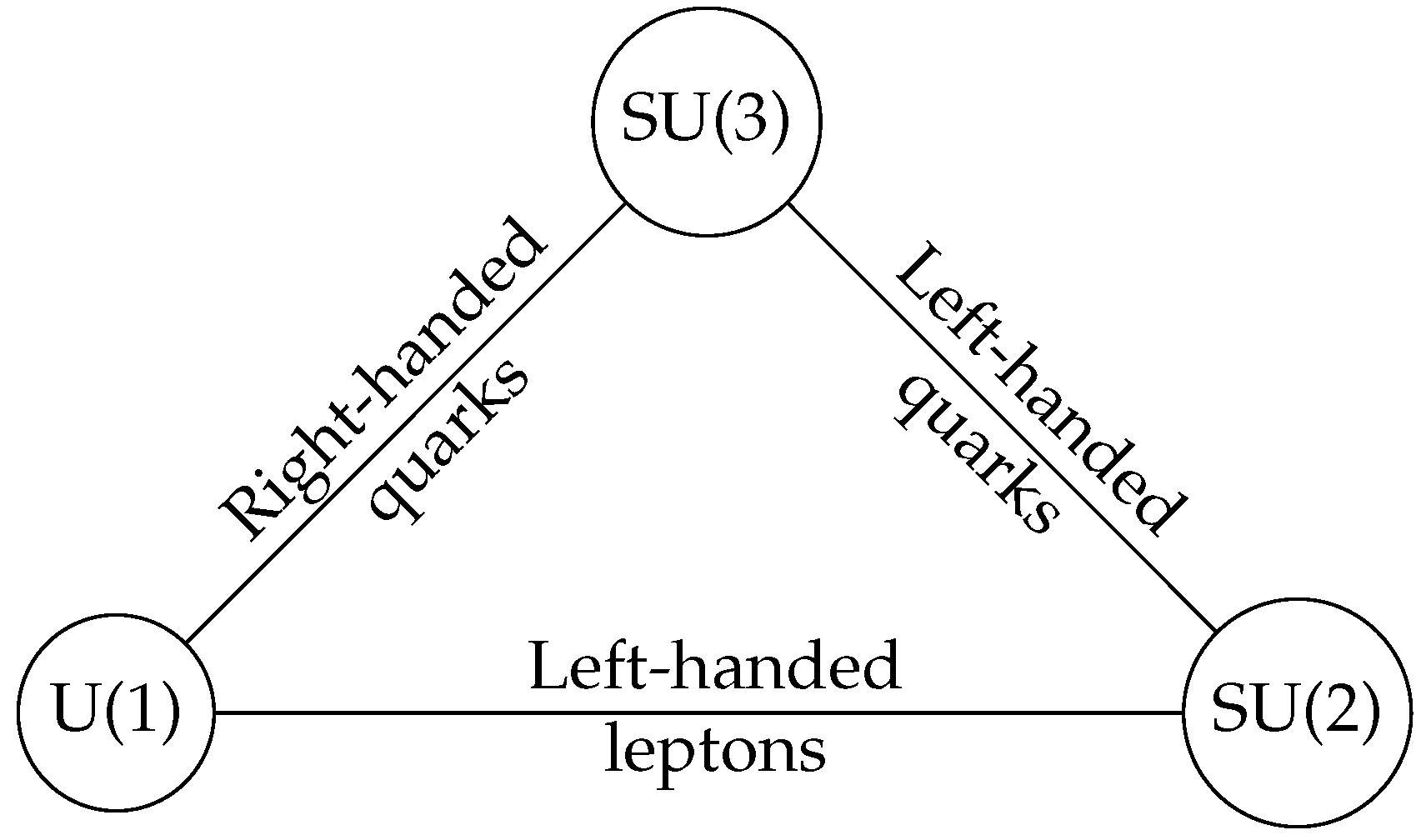
2.1. Physical Theories and Quivers
- A gauge group, which encodes the fundamental forces (electromagnetism, weak and strong forces). This is a Lie group whose complexified Lie algebra is . The forces are mediated by massless gauge bosons, which are vector fields valued in the adjoint representation of that algebra.
- Matter constituents, which are fermion fields valued in bifundamental (a bifundamental representation of a semisimple Lie algebra is the product of a fundamental representation of a simple summand of with the antifundamental representation of a summand of .) representations of . This matter content can be encoded in a quiver where the vertices are the simple summands of and the arrows are the matter fields.
2.2. Supersymmetric Quiver Gauge Theories
- The gauge bosons are part of vector multiplets, which contain spin gauginos and one complex scalar field in the adjoint representation of the gauge algebra.
- The matter fermions are part of hypermultiplets, which contain a pair of complex scalar fields that transforms in a representation of the form of the gauge algebra.
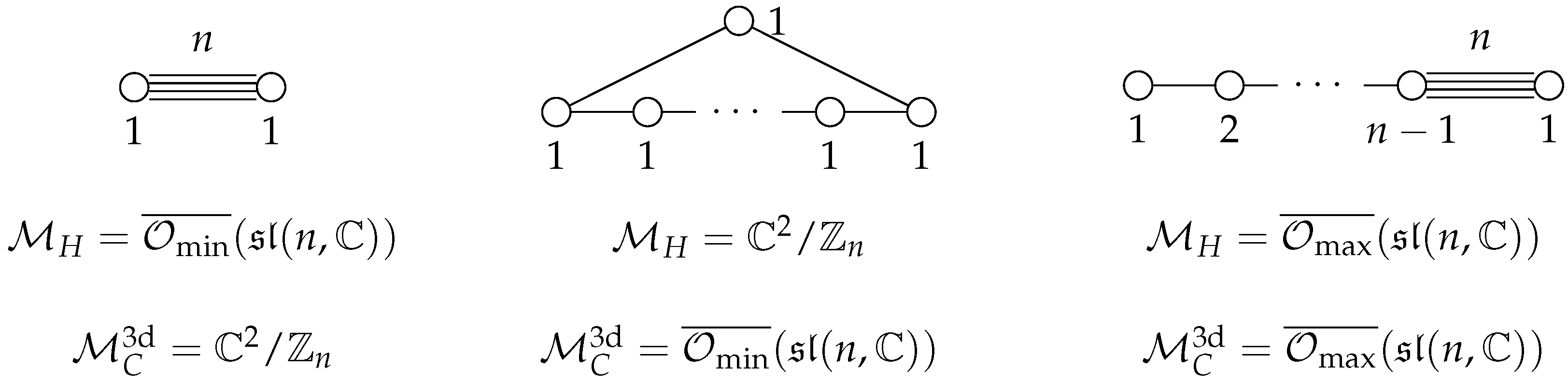
2.3. Higgs Branches, Quiver Varieties, and Beyond
3. The Magnetic Side
3.1. Three-Dimensional Coulomb Branches and Magnetic Quivers
3.2. The Scope of Magnetic Quivers
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ginzburg, V. Lectures on Nakajima’s quiver varieties. arXiv 2009, arXiv:0905.0686. [Google Scholar]
- Kirillov, A., Jr. Quiver Representations and Quiver Varieties; American Mathematical Soc.: Providence, RI, USA, 2016; Volume 174. [Google Scholar]
- Mumford, D.; Fogarty, J.; Kirwan, F. Geometric Invariant Theory; Springer Science & Business Media: Berlin, Germany, 1994; Volume 34. [Google Scholar]
- Crawley-Boevey, W. Geometry of the moment map for representations of quivers. Compos. Math. 2001, 126, 257–293. [Google Scholar] [CrossRef]
- Nakajima, H. Instantons on ALE spaces, quiver varieties, and Kac-Moody algebras. Duke Math. J. 1994, 76, 365–416. [Google Scholar] [CrossRef]
- Nakajima, H. Quiver varieties and Kac-Moody algebras. Duke Math. J. 1998, 91, 515–560. [Google Scholar] [CrossRef]
- Gaiotto, D. N = 2 dualities. JHEP 2012, 8, 034. [Google Scholar] [CrossRef]
- Argyres, P.C.; Douglas, M.R. New phenomena in SU(3) supersymmetric gauge theory. Nucl. Phys. B 1995, 448, 93–126. [Google Scholar] [CrossRef]
- Beauville, A. Symplectic singularities. arXiv 1999, arXiv:math/9903070. [Google Scholar] [CrossRef]
- Freed, D.S. Special Kahler manifolds. Commun. Math. Phys. 1999, 203, 31–52. [Google Scholar] [CrossRef]
- Cecotti, S.; Ferrara, S.; Girardello, L. Geometry of Type II Superstrings and the Moduli of Superconformal Field Theories. Int. J. Mod. Phys. A 1989, 4, 2475. [Google Scholar] [CrossRef]
- Nakajima, H. Towards a mathematical definition of Coulomb branches of 3-dimensional N=4 gauge theories, I. Adv. Theor. Math. Phys. 2016, 20, 595–669. [Google Scholar] [CrossRef]
- Braverman, A.; Finkelberg, M.; Nakajima, H. Towards a mathematical definition of Coulomb branches of 3-dimensional N=4 gauge theories, II. Adv. Theor. Math. Phys. 2018, 22, 1071–1147. [Google Scholar] [CrossRef]
- Seiberg, N.; Witten, E. Gauge dynamics and compactification to three-dimensions. arXiv 1996, arXiv:hep-th/9607163. [Google Scholar]
- Cremonesi, S.; Hanany, A.; Zaffaroni, A. Monopole operators and Hilbert series of Coulomb branches of 3d N = 4 gauge theories. JHEP 2014, 1, 005. [Google Scholar] [CrossRef]
- Bullimore, M.; Dimofte, T.; Gaiotto, D. The Coulomb Branch of 3d N=4 Theories. Commun. Math. Phys. 2017, 354, 671–751. [Google Scholar] [CrossRef]
- Hooft, G. On the Phase Transition Towards Permanent Quark Confinement. Nucl. Phys. B 1978, 138, 1–25. [Google Scholar] [CrossRef]
- Borokhov, V.; Kapustin, A.; Wu, X.K. Topological disorder operators in three-dimensional conformal field theory. J. High Energy Phys. 2003, 2002, 049. [Google Scholar] [CrossRef]
- Cabrera, S.; Hanany, A. Quiver Subtractions. JHEP 2018, 9, 008. [Google Scholar] [CrossRef]
- Bourget, A.; Cabrera, S.; Grimminger, J.F.; Hanany, A.; Sperling, M.; Zajac, A.; Zhong, Z. The Higgs mechanism—Hasse diagrams for symplectic singularities. JHEP 2020, 1, 157. [Google Scholar] [CrossRef]
- Bourget, A.; Grimminger, J.F.; Hanany, A.; Sperling, M.; Zhong, Z. Branes, Quivers, and the Affine Grassmannian. arXiv 2021, arXiv:2102.06190. [Google Scholar]
- Bourget, A.; Grimminger, J.F.; Hanany, A.; Zhong, Z. The Hasse Diagram of the Moduli Space of Instantons. arXiv 2022, arXiv:2202.01218. [Google Scholar] [CrossRef]
- Intriligator, K.A.; Seiberg, N. Mirror symmetry in three-dimensional gauge theories. Phys. Lett. B 1996, 387, 513–519. [Google Scholar] [CrossRef]
- Braden, T.; Licata, A.; Proudfoot, N.; Webster, B. Quantizations of conical symplectic resolutions II: Category O and symplectic duality. Asterisque 2016, 384, 75–179. [Google Scholar]
- Dancer, A.; Hanany, A.; Kirwan, F. Symplectic duality and implosions. arXiv 2020, arXiv:2004.09620. [Google Scholar] [CrossRef]
- Bourget, A.; Dancer, A.; Grimminger, J.F.; Hanany, A.; Kirwan, F.; Zhong, Z. Orthosymplectic implosions. JHEP 2021, 8, 012. [Google Scholar] [CrossRef]
- Bourget, A.; Dancer, A.; Grimminger, J.F.; Hanany, A.; Zhong, Z. Partial Implosions and Quivers. J. High Energ. Phys. 2022. [Google Scholar] [CrossRef]
- Bourget, A.; Grimminger, J.F.; Hanany, A.; Sperling, M.; Zafrir, G.; Zhong, Z. Magnetic quivers for rank 1 theories. JHEP 2020, 9, 189. [Google Scholar] [CrossRef]
- Bourget, A.; Grimminger, J.F.; Martone, M.; Zafrir, G. Magnetic quivers for rank 2 theories. JHEP 2022, 3, 208. [Google Scholar] [CrossRef]
- Carta, F.; Giacomelli, S.; Mekareeya, N.; Mininno, A. Conformal manifolds and 3d mirrors of Argyres–Douglas theories. JHEP 2021, 8, 015. [Google Scholar] [CrossRef]
- Xie, D. 3D mirror for Argyres–Douglas theories. arXiv 2021, arXiv:2107.05258. [Google Scholar]
- Dey, A. Higgs Branches of Argyres–Douglas theories as Quiver Varieties. arXiv 2021, arXiv:2109.07493. [Google Scholar]
- Bourget, A.; Grimminger, J.F.; Hanany, A.; Kalveks, R.; Zhong, Z. Higgs branches of U/SU quivers via brane locking. JHEP 2022, 8, 061. [Google Scholar] [CrossRef]
- Bourget, A.; Grimminger, J.F. Fibrations and Hasse diagrams for 6d SCFTs. JHEP 2022, 12, 159. [Google Scholar] [CrossRef]
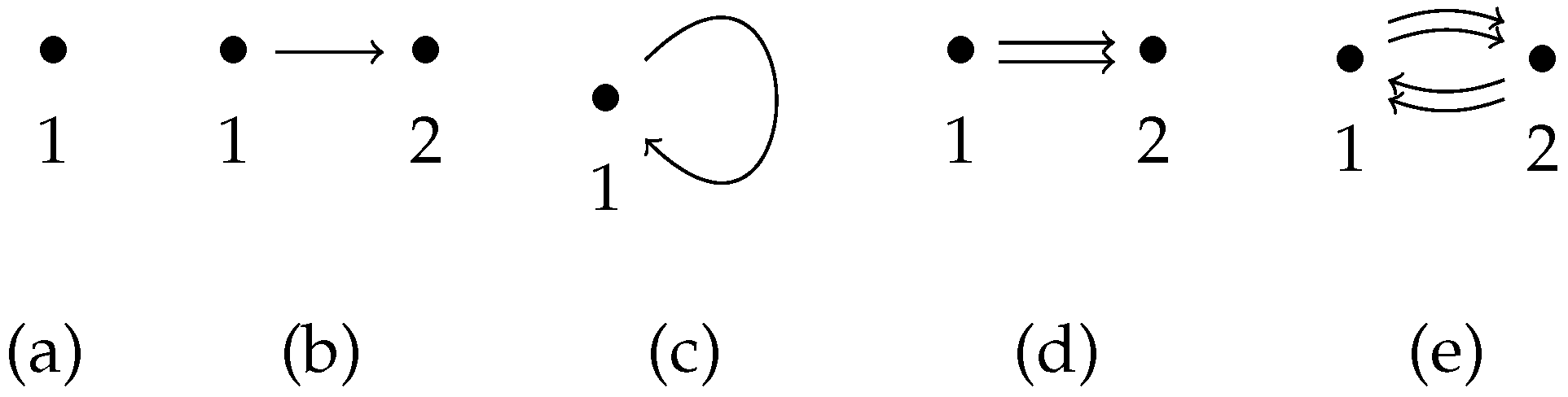

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bourget, A. The Geometry of Quivers. Phys. Sci. Forum 2022, 5, 42. https://doi.org/10.3390/psf2022005042
Bourget A. The Geometry of Quivers. Physical Sciences Forum. 2022; 5(1):42. https://doi.org/10.3390/psf2022005042
Chicago/Turabian StyleBourget, Antoine. 2022. "The Geometry of Quivers" Physical Sciences Forum 5, no. 1: 42. https://doi.org/10.3390/psf2022005042
APA StyleBourget, A. (2022). The Geometry of Quivers. Physical Sciences Forum, 5(1), 42. https://doi.org/10.3390/psf2022005042





