Gapless Superfluidity and Neutron Star Cooling †
Abstract
1. Introduction
2. Gapless Superfluidity
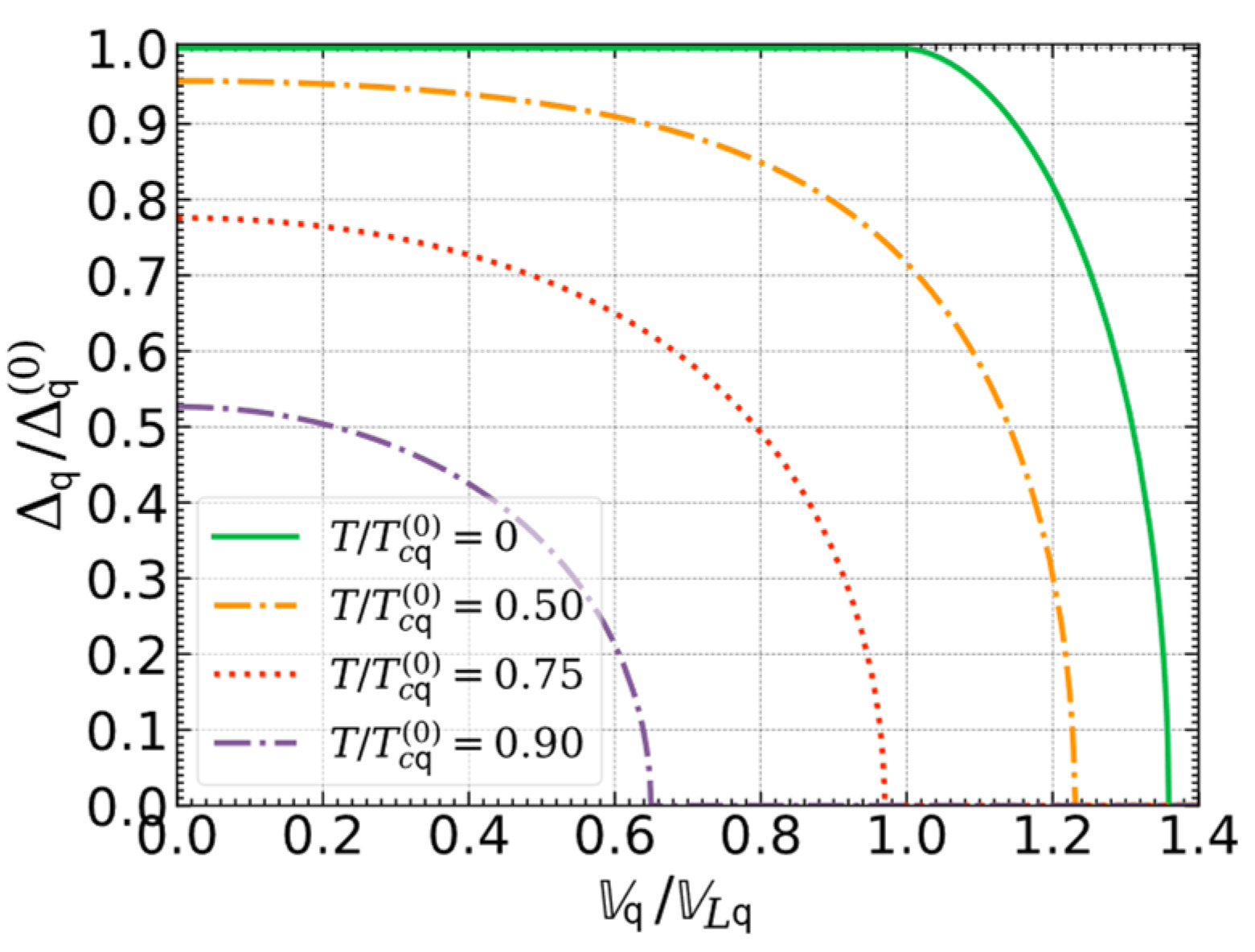
2.1. Order Parameter
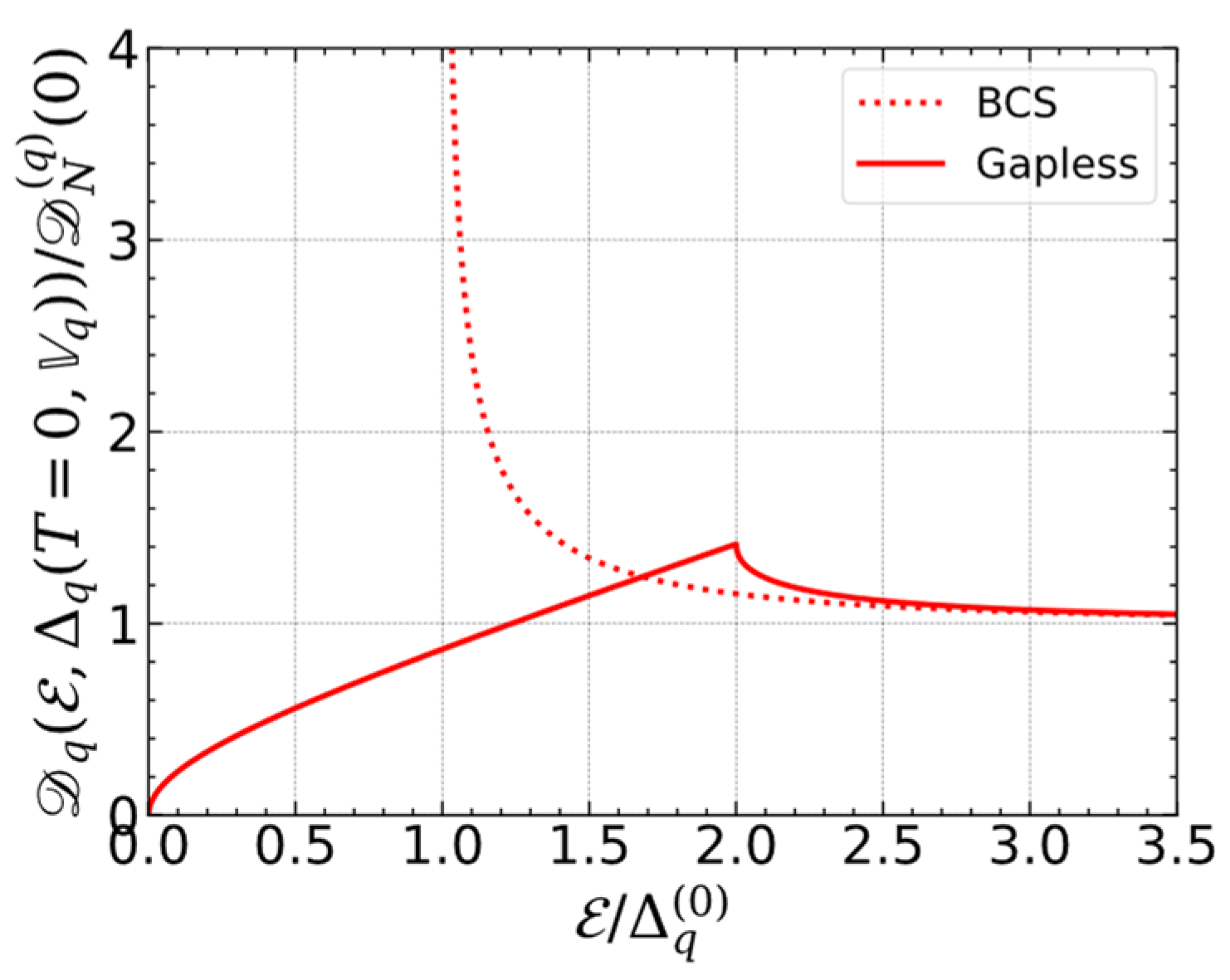
2.2. Gapless State and Specific Heat
3. Astrophysical Consequences
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Potekhin, A.Y.; Pons, J.A.; Page, D. Neutron Stars—Cooling and Transport. Space Sci. Rev. 2015, 191, 239–291. [Google Scholar] [CrossRef]
- Chamel, N. Superfluidity and Superconductivity in Neutron Stars. J. Astrophys. Astron. 2017, 38, 43. [Google Scholar] [CrossRef]
- Page, D.; Prakash, M.; Lattimer, J.M.; Steiner, A.W. Rapid Cooling of the Neutron Star in Cassiopeia A Triggered by Neutron Superfluidity in Dense Matter. Phys. Rev. Lett. 2011, 106, 081101. [Google Scholar] [CrossRef] [PubMed]
- Shternin, P.S.; Yakovlev, D.G.; Heinke, C.O.; Ho, W.C.G.; Patnaude, D.J. Cooling Neutron Star in the Cassiopeia A Supernova Remnant: Evidence for Superfluidity in the Core: Cooling Cas A Neutron Star. Mon. Not. R. Astron. Soc. Lett. 2011, 412, L108–L112. [Google Scholar] [CrossRef]
- Elshamouty, K.G.; Heinke, C.O.; Sivakoff, G.R.; Ho, W.C.G.; Shternin, P.S.; Yakovlev, D.G.; Patnaude, D.J.; David, L. Measuring the Cooling of the Neutron Star in Cassiopeia A with all Chandra X-ray Observatory Detectors. Astrophys. J. 2013, 777, 22. [Google Scholar] [CrossRef]
- Posselt, B.; Pavlov, G.G. Upper Limits on the Rapid Cooling of the Central Compact Object in Cas A. Astrophys. J. 2018, 864, 135. [Google Scholar] [CrossRef]
- Wijngaarden, M.J.P.; Ho, W.C.G.; Chang, P.; Heinke, C.O.; Page, D.; Beznogov, M.; Patnaude, D.J. Diffusive Nuclear Burning in Cooling Simulations and Application to New Temperature Data of the Cassiopeia A Neutron Star. Mon. Not. R. Astron. Soc. 2019, 484, 974–988. [Google Scholar] [CrossRef]
- Ho, W.C.G.; Zhao, Y.; Heinke, C.O.; Kaplan, D.L.; Shternin, P.S.; Wijngaarden, M.J.P. X-Ray Bounds on Cooling, Composition, and Magnetic Field of the Cassiopeia A Neutron Star and Young Central Compact Objects. Mon. Not. R. Astron. Soc. 2021, 506, 5015–5029. [Google Scholar] [CrossRef]
- Posselt, B.; Pavlov, G.G. The Cooling of the Central Compact Object in Cas A from 2006 to 2020. Astrophys. J. 2022, 932, 83. [Google Scholar] [CrossRef]
- Manchester, R.N. Pulsar Glitches. Proc. IAU 2017, 13, 197–202. [Google Scholar] [CrossRef]
- Anderson, P.W.; Itoh, N. Pulsar Glitches and Restlessness as a Hard Superfluidity Phenomenon. Nature 1975, 256, 25–27. [Google Scholar] [CrossRef]
- Pines, D.; Alpar, M.A. Superfluidity in Neutron Stars. Nature 1985, 316, 27–32. [Google Scholar] [CrossRef]
- Haskell, B.; Melatos, A. Models of Pulsar Glitches. Int. J. Mod. Phys. D 2015, 24, 1530008. [Google Scholar] [CrossRef]
- Sedrakian, A.; Clark, J.W. Superfluidity in Nuclear Systems and Neutron Stars. Eur. Phys. J. A 2019, 55, 167. [Google Scholar] [CrossRef]
- Allard, V.; Chamel, N. Entrainment Effects in Neutron-Proton Mixtures within the Nuclear Energy-Density Functional Theory. II. Finite Temperatures and Arbitrary Currents. Phys. Rev. C 2021, 103, 025804. [Google Scholar] [CrossRef]
- Allard, V.; Chamel, N. 1S0 Pairing Gaps, Chemical Potentials and Entrainment Matrix in Superfluid Neutron-Star Cores for the Brussels–Montreal Functionals. Universe 2021, 7, 470. [Google Scholar] [CrossRef]
- Allard, V.; Chamel, N. Gapless superfluidity in neutron stars—I. thermal properties. Phys. Rev. C 2022, Submitted. [Google Scholar]
- Allard, V.; Chamel, N. Evidence of gapless neutron superfluidity from the late time cooling of transiently accreting neutron stars. Phys. Rev. Lett. 2022, Submitted. [Google Scholar]
- Landau, L. Theory of the Superfluidity of Helium II. Phys. Rev. 1941, 60, 356–358. [Google Scholar] [CrossRef]
- Lifshitz, E.M.; Pitaevskii, L. Course of Theoretical Physics, v.9: Statistical Physics, Pt.2; Pergamon: Oxford, UK, 1980; pp. 88–94. [Google Scholar]
- Abrikosov, A.A. Fundamentals of the Theory of Metals; North Holland Publishing Company: Amsterdam, The Netherlands, 1988; p. 350. [Google Scholar]
- Wijnands, R.; Degenaar, N.; Page, D. Cooling of Accretion-Heated Neutron Stars. J. Astrophys. Astron. 2017, 38, 49. [Google Scholar] [CrossRef]
- Chamel, N.; Haensel, P. Physics of Neutron Star Crusts. Living Rev. Relativ. 2008, 11, 10. [Google Scholar] [CrossRef] [PubMed]
- Henyey, L.; L’Ecuyer, J. Studies in Stellar Evolution. VIII. The Time Scale for the Diffusion of Energy in the Stellar Interior. Astrophys. J. 1969, 156, 549. [Google Scholar] [CrossRef]
- Turlione, A.; Aguilera, D.N.; Pons, J.A. Quiescent Thermal Emission from Neutron Stars in Low-Mass X-Ray Binaries. Astron. Astrophys. 2015, 577, A5. [Google Scholar] [CrossRef]
- Deibel, A.; Cumming, A.; Brown, E.F.; Reddy, S. Late-Time Cooling of Neutron Star Transients and the Physics of the Inner Crust. Astrophys. J. 2017, 839, 95. [Google Scholar] [CrossRef]
- Gandolfi, S.; Palkanoglou, G.; Carlson, J.; Gezerlis, A.; Schmidt, K.E. The 1S0 Pairing Gap in Neutron Matter. Condens. Matter 2022, 7, 19. [Google Scholar] [CrossRef]
- Drissi, M.; Rios, A. Many-Body Approximations to the Superfluid Gap and Critical Temperature in Pure Neutron Matter. Eur. Phys. J. A 2022, 58, 90. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Allard, V.; Chamel, N. Gapless Superfluidity and Neutron Star Cooling. Phys. Sci. Forum 2023, 7, 9. https://doi.org/10.3390/ECU2023-14022
Allard V, Chamel N. Gapless Superfluidity and Neutron Star Cooling. Physical Sciences Forum. 2023; 7(1):9. https://doi.org/10.3390/ECU2023-14022
Chicago/Turabian StyleAllard, Valentin, and Nicolas Chamel. 2023. "Gapless Superfluidity and Neutron Star Cooling" Physical Sciences Forum 7, no. 1: 9. https://doi.org/10.3390/ECU2023-14022
APA StyleAllard, V., & Chamel, N. (2023). Gapless Superfluidity and Neutron Star Cooling. Physical Sciences Forum, 7(1), 9. https://doi.org/10.3390/ECU2023-14022






