Abstract
In this work, a machine learning methodology is used to predict the progress of the glycemic values of six patients with diabetes. Eight different algorithms are compared i.e., ANN, PNN, Polynomial Regression, Gradient Boosted Trees Regression, Random Forest Regression, Simple Regression Tree, Tree Ensemble Regression, Linear Regression. The algorithms are classified based on the ability to minimize four statistical errors, namely: Mean Absolute Error, Mean Squared Error, Root Mean Squared Error, Mean Signed Difference. Following the analysis, an ordering of the algorithms by predictive efficiency is proposed. Data are collected within the “Smart District 4.0 Project” with the contribution of the Italian Ministry of Economic Development.
1. Introduction
In the following analysis, the use of machine learning algorithms for the prediction of the glycemic state of two patients is proposed. Through the analysis of a historical series detected with a frequency of 3 min, it was possible to predict the future trend of the patients’ glycemic status. However, to better choose the algorithms to be used for the prediction, a comparative analysis of eight different algorithms was carried out, i.e., ANN-Artificial Neural Network with Perceptron Multilayer, PNN-Probabilistic Neural Network, Polynomial Regression, Gradient Boosted Trees Regression, Random Forest Regression, Simple Regression Tree, Tree Ensemble Regression, and Linear Regression. The choice of the best performing algorithm was made considering both the value of the R-square and also the ability to minimize various statistical errors detected.
The data that were processed were produced within a research project carried out by LUM Enterprise S.r.l. in collaboration with the company Noovle S.r.l. and financed by the Ministry of Economic Development of the Government of the Italian Republic. Specifically, the objective of the research project was to monitor the health status of some bus drivers from a glycemic point of view to verify whether they had any problems that could cause danger to passengers during travel. The monitoring of the glycemic health status of the drivers was carried out using special detection devices capable of detecting the condition of the individuals every 3 min. Specifically, the analysis was conducted for two different patients, indicated as Patient A and Patient B. The historical series of the data collected differs significantly for Patient A and for Patient B. For Patient A there are 243 observations while in the case of Patient B, there are about 13,204 observations.
Thanks to the use of telemedicine systems, it is possible to assist the patient population by means of a set of remotely-operating medical tools. The detected data can be analyzed using DSS systems integrated with models of artificial neural networks applied to the prediction of the values detected from patients [1] This prediction is useful for identifying critical elements and to foresee interventions. In particular, the use of the Artificial Neural Network-ANN with Multilayer Perceptron aids the de-hospitalization process thanks to the use of intelligent sensors oriented to the measurement of patient data [2]. The relevant data using telemedicine tools can also be integrated in the analysis of big data for the analysis of the state of health of the patient population [3]. The solution is therefore efficient both for the individual analysis of the patient’s health condition and for the implementation of real health policies.
Telemedicine platforms can be used both to monitor the physical condition of individual patients and to carry out overall analyses of the reference population. Telemedicine platforms can therefore be used both for the specific objectives of medicine aimed at individual patients and for more general purposes aimed at solving public health issues [4].
The article continues as follows: the second paragraph contains “Machine Learning and Predictions” while the third paragraph concludes the article.
2. Machine Learning and Predictions
Eight different machine learning algorithms for predicting the glycemic status of six different diabetes patients are analyzed below. Predictions are made for each patient by identifying the most efficient algorithm based on the historical series of surveys. Specifically, 70% of the dataset has been used as learning rate while the remaining 30% has been used for prediction. The choice of the algorithm in terms of predictive efficiency is made based on the analysis of four different statistical errors. The four statistical errors analyzed were: “Mean Absolute Error”, “Mean Squared Error”, “Root Mean Squared Error”, “Mean Signed Difference”.
Patient A. In the case of Patient A, the best predictor of the glycemic state is the Artificial Neural Network-ANN algorithm with Perceptron Multilayer. Specifically, in the case of Patient A, the following order of algorithms in terms of prediction is proposed:
- Artificial Neural Network-ANN with a payoff equal to 7;
- Polynomial Regression with a payoff equal to 7;
- Gradient Boosted Trees Regression with a payoff equal to 14;
- Random Forest Regression with a payoff equal to 16;
- Simple Regression Tree with a payoff equal to 18;
- Tree Ensemble Regression with a payoff equal to 23;
- Linear Regression with a payoff equal to 27;
- Probabilistic Neural Network-PNN with a payoff equal to 32.
In Table 1 are listed the performances of adopted algorithms.

Table 1.
Machine learning algorithms to predict the glycemic status of Patient A.
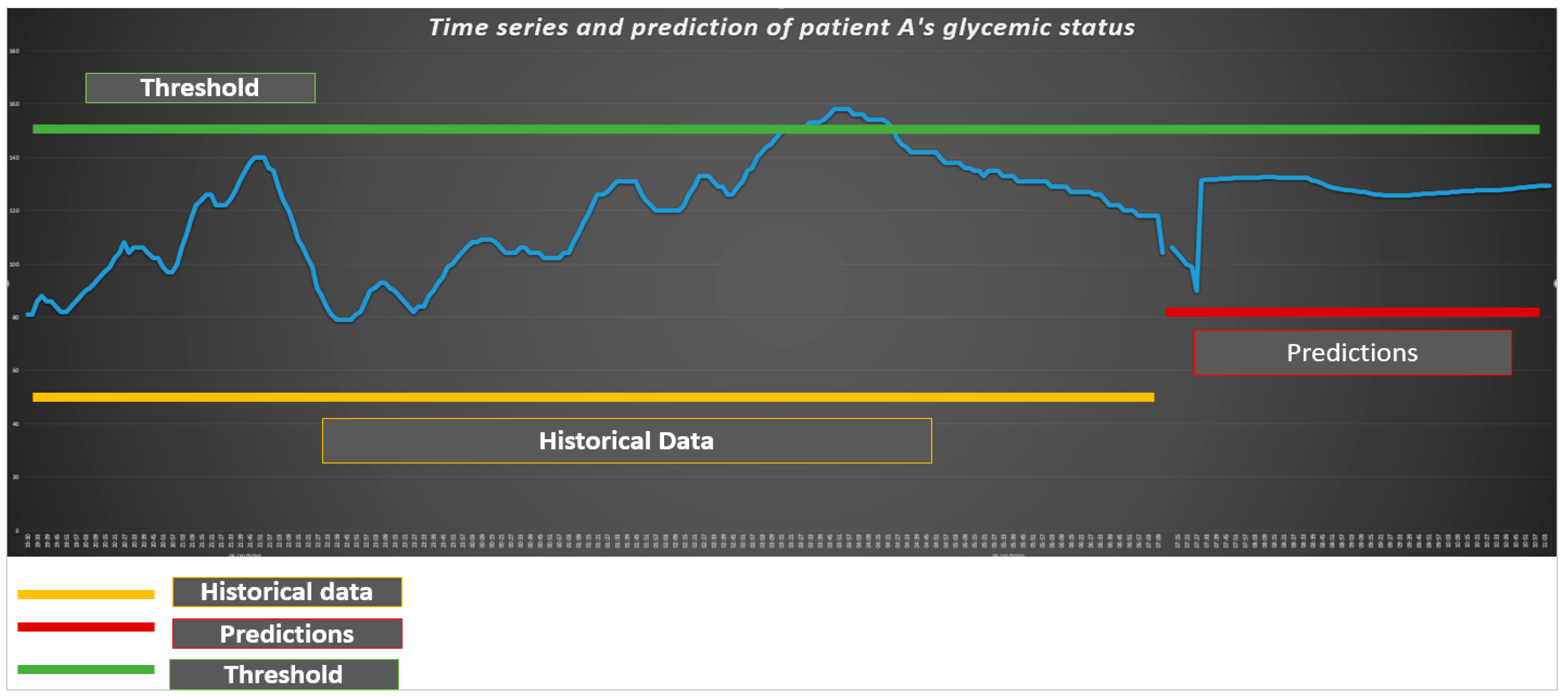
In this case, the Artificial Neural Network-ANN with Multilayer Perceptron has the following parameters: the maximum number of iterations is equal to 100, the number of hidden layers is equal to 1, the number of hidden neurons per layer is equal to 10. Since the value of threshold is equal to 150, as can be viewed in Figure 1, the glycemic status of Patient A is essentially under the critical level of 150. The algorithm predicts a level of glycemic status for Patient A lower than the threshold of 150.
Figure 1.
Machine learning algorithms to predict the glycemic status of Patient A.
Patient B. In the case of Patient B, the best predictor of the glycemic state is the Probabilistic Neural Network-PNN. In the case of Patient B, the choice of the best predictor is realized through either the maximization of the R-Squared or the minimization of the four statistical errors indicated. Specifically, in the case of Patient B, the following order of algorithms in terms of prediction is proposed:
- Probabilistic Neural Networks-PNN with a payoff equal to 6;
- Simple Regression Tree with a payoff equal to 13;
- Gradient Boosted Trees Regression and Random Forest Regression with a payoff equal to 19;
- Linear Regression with a payoff equal to 27;
- Tree Ensemble Regression and Artificial Neural Network-ANN with a payoff equal to 28;
- Polynomial Regression with a payoff equal to 40.
In Table 2 are listed the performances of adopted algorithms.

Table 2.
Synthesis of the main results of machine learning algorithms for the prediction of the glycemic status of Patient B.
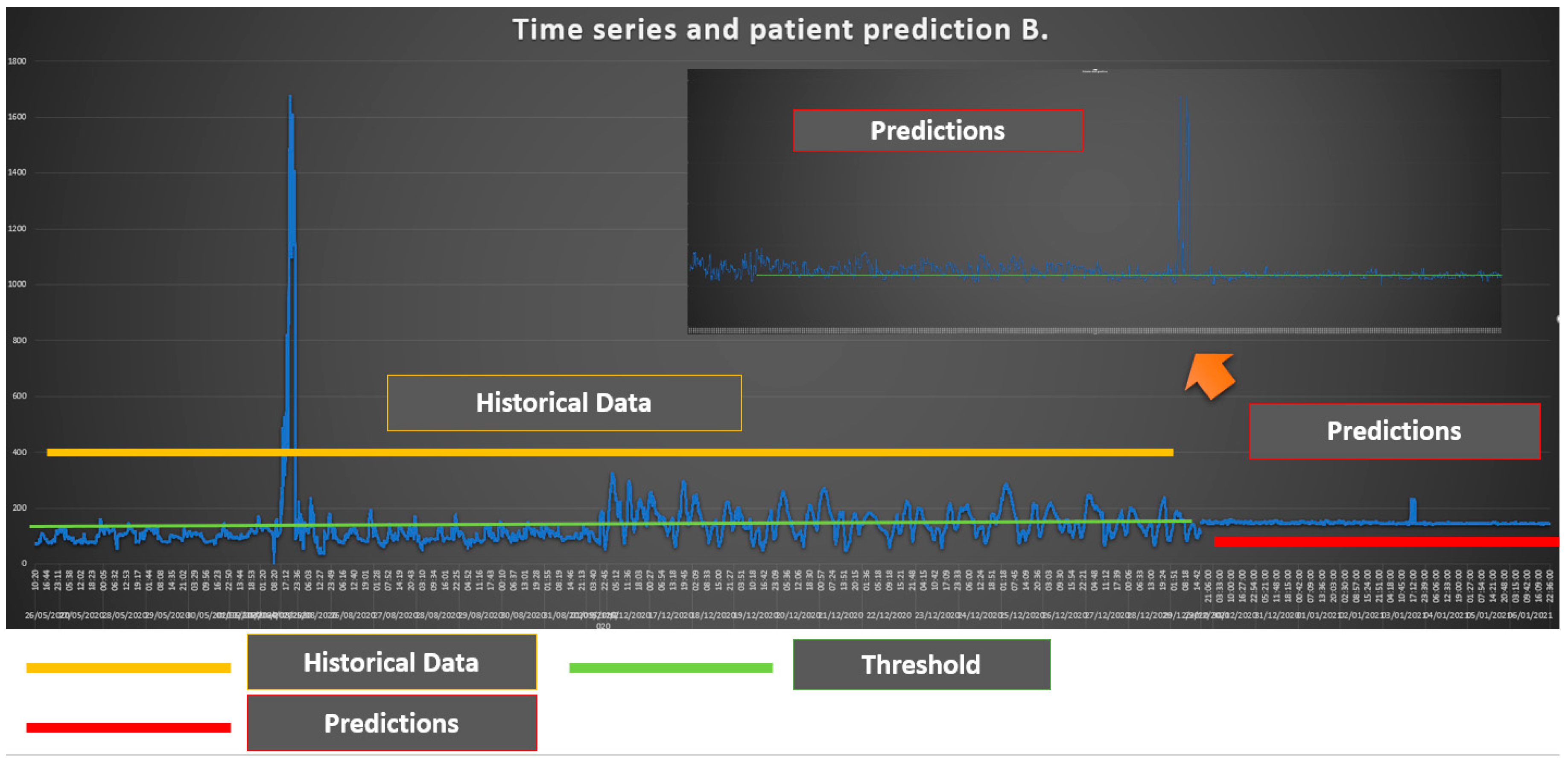
As we can see from Figure 2 the glycemic status of Patient B is generally over the level of 150 which is considered the threshold. In particular, in the second part of the historical data, the glycemic status of the Patient B is over the threshold level. The prediction shows the presence of values that are very close to the threshold level with some maximums in which Patient B exceeds the threshold values.
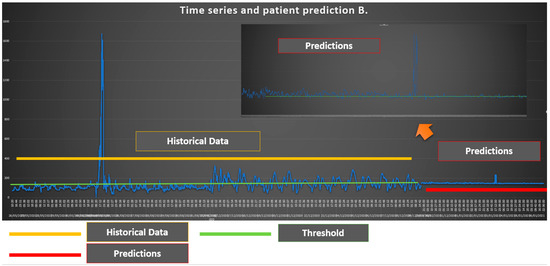
Figure 2.
Time Series and Patient B prediction.
There are many differences between the dataset of Patient A and the dataset of Patient B. Specifically, the dataset of Patient A is composed of 243 observations that are time-consecutive while the dataset of the Patient B is composed of 13,204 discontinuous observations. The analysis shows that the Artificial Neural Network-ANN with Multilayer Perceptron is more efficient than the PNN-Probabilistic Neural Network in the prediction applied to smaller and more timely coherent datasets. On the other hand, the PNN-Probabilistic Neural Network has a better performance in prediction in the case of larger and time- discontinuous datasets.
The confrontation between the value of the prediction of Patient A and the value of the prediction of Patient B is presented in Table 3 and shows that for both the patients, the glycemic status is under the threshold level. The following equation has been used to de-normalize data [5] where y’ is the predicted value and y is the value in the input dataset.

Table 3.
Metrics characteristics of the predicted values for Patient A and Patient B.
However, in the case of Patient B, there is a risk greater than that of Patient A as shown in the mean, median and maximum levels. In Table 3 are listed the parameters about basic statistics.
As we can see from data in Table 3, Patient B has a worse glycemic status than Patient B. In addition, in the prediction of the glycemic state of health of Patient B there are data which are very close, and in some cases higher than the threshold values.
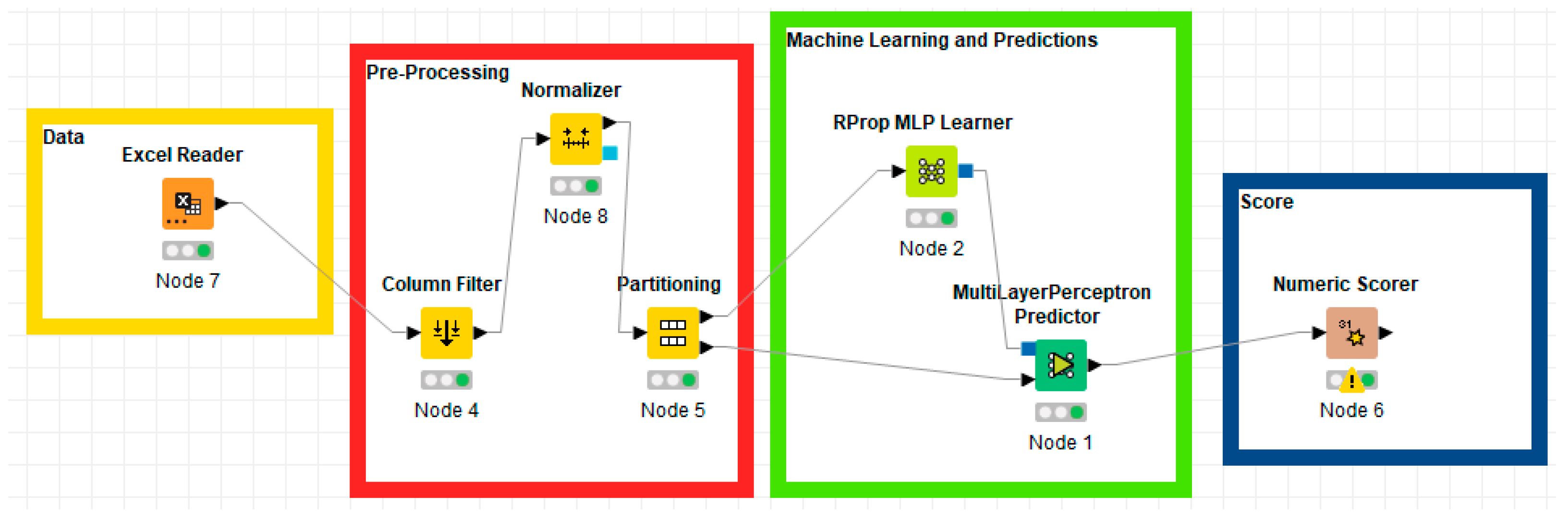
Figure 3 shows the four phases of the creation of a machine learning algorithm with predictive capability based on the Artificial Neural Network-ANN with Multilayer Perceptron. As can be seen from Figure 3, there are four phases:
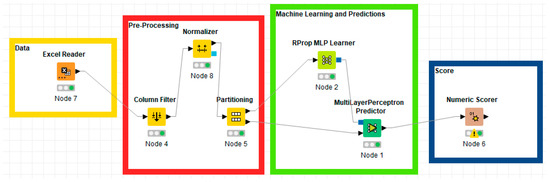
Figure 3.
KNIME workflows of the Artificial Neural Network-ANN with Multilayer Perceptron.
- Data: consists of a single KNIME node which has the function of reading the data entered in the Excel format;
- Preprocessing: consists of a group of three different KNIME nodes. The first node consists of “Column Filter” and is a node in which it is possible to select the columns of interest through which to carry out the prediction activity. The second node consists of “Normalizer” and it is a node that compresses data in the range from 0 to 1. The third node consists of “Partitioning” and is a node in which the data is divided into two different groups: 70% is used for the training of the neural network while the remaining 30% is used for the actual prediction;
- Machine Learning and predictions: is the central part of the data analysis process aimed at predictions and consists of two nodes. The first, known as “RProp MLP Learner” is used for neural network training. It has hyperparameters that can be modified according to the analytical needs and which, in the analyzed case, were used in the basic version. The second node of KNIME is “Multilayer Perceptron Predictor” and is the node containing the real data prediction.
- Score: the last phase consists of the “Numeric Scorer” node which allows the evaluation of the predictive efficiency of the neural network through the analysis of both the R-square and the statistical errors.
3. Conclusions
In this article, eight different machine learning algorithms were used to predict the health status of two patients with blood glucose. The choice of the best predictor among the eight algorithms was made considering the performance of the algorithms in terms of maximization of the R-square and minimization of statistical errors. Subsequently, the metric characteristics of the series were analyzed to verify the trend of the performance status of both Patient A and Patient B. Finally, the structure of the artificial neural network used was analyzed in detail with an indication of the various KNIME nodes used for prediction.
The use of machine learning algorithms for prediction makes it possible to identify the critical elements in the health management of patients with diabetes and can also have a life-saving impact on the monitored patients.
Author Contributions
Conceptualization, A.M.; methodology, A.M.; software, A.M., G.C. and A.L; validation, A.M.; formal analysis, G.C., A.L., N.M., F.C. and A.M.; investigation, G.C., A.L., N.M., F.C. and A.M.; resources, G.C., A.L., N.M. and A.M.; data curation, G.C., A.L., N.M. and A.M.; writing—original draft preparation, A.L. and A.M.; writing—review and editing, G.C., A.L., N.M. and A.M.; visualization, G.C., A.L., N.M. and A.M.; supervision, G.C., A.L., N.M. and A.M.; project administration, G.C., A.L., N.M. and A.M.; funding acquisition, G.C., A.L., N.M. and A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable (data anonymous for model testing).
Data Availability Statement
Not applicable.
Acknowledgments
All the applications have been deployed by a unique IT collaborative framework developed within the Smart District 4.0 Project: the Italian Fondo per la Crescita Sostenibile, Bando “Agenda Digitale”, D.M. 15 October 2014, funded by ”Ministero dello Sviluppo Economico”. This is an initiative funded with the contribution of the Italian Ministry of Economic Development aiming to sustain the digitization process of the Italian SMEs. The authors thank their partner Emtesys S.r.l. for the collaboration provided during the work development.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Massaro, A.; Maritati, V.; Savino, N.; Galiano, A.; Convertini, D.; De Fonte, E.; Di Muro, M. A Study of a health resources management platform integrating neural networks and DSS telemedicine for homecare assistance. Information 2018, 7, 176. [Google Scholar] [CrossRef]
- Massaro, A.; Maritati, V.; Savino, N.; Galiano, A. Neural networks for automated smart health platforms oriented on heart predictive diagnostic big data systems. In Proceedings of the 2018 AEIT International Annual Conference, Bari, Italy, 3–5 October 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Massaro, A.; Maritati, V.; Giannone, D.; Convertini, D.; Galiano, A. LSTM DSS automatism and dataset optimization for diabetes prediction. Appl. Sci. 2019, 9, 3532. [Google Scholar] [CrossRef]
- Massaro, A. Electronics in Advanced Research Industries: Industry 4.0 to Industry 5.0 Advances; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Denormalization of Predicted Data in Neural Networks. Available online: https://stackoverflow.com/questions/32888108/denormalization-of-predicted-data-in-neural-networks (accessed on 7 January 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).