Discussion of Design Wind Loads on a Vaulted Free Roof
Abstract
:1. Introduction
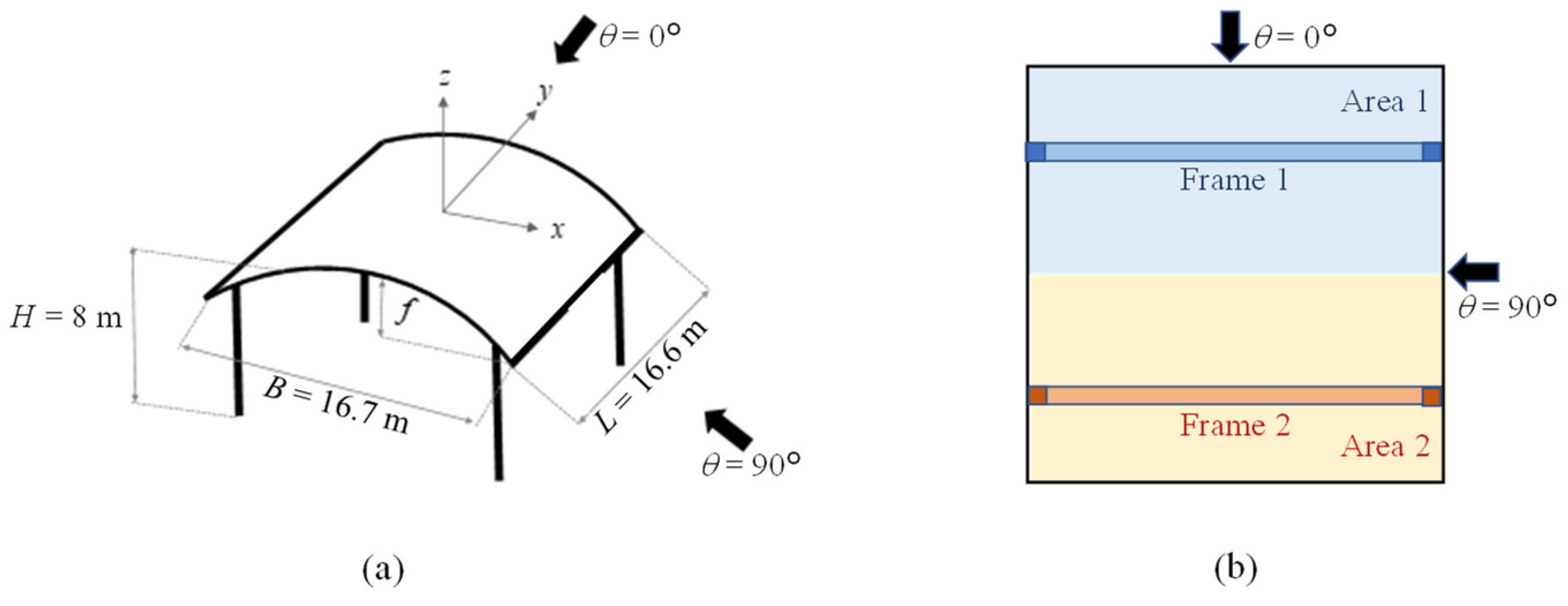
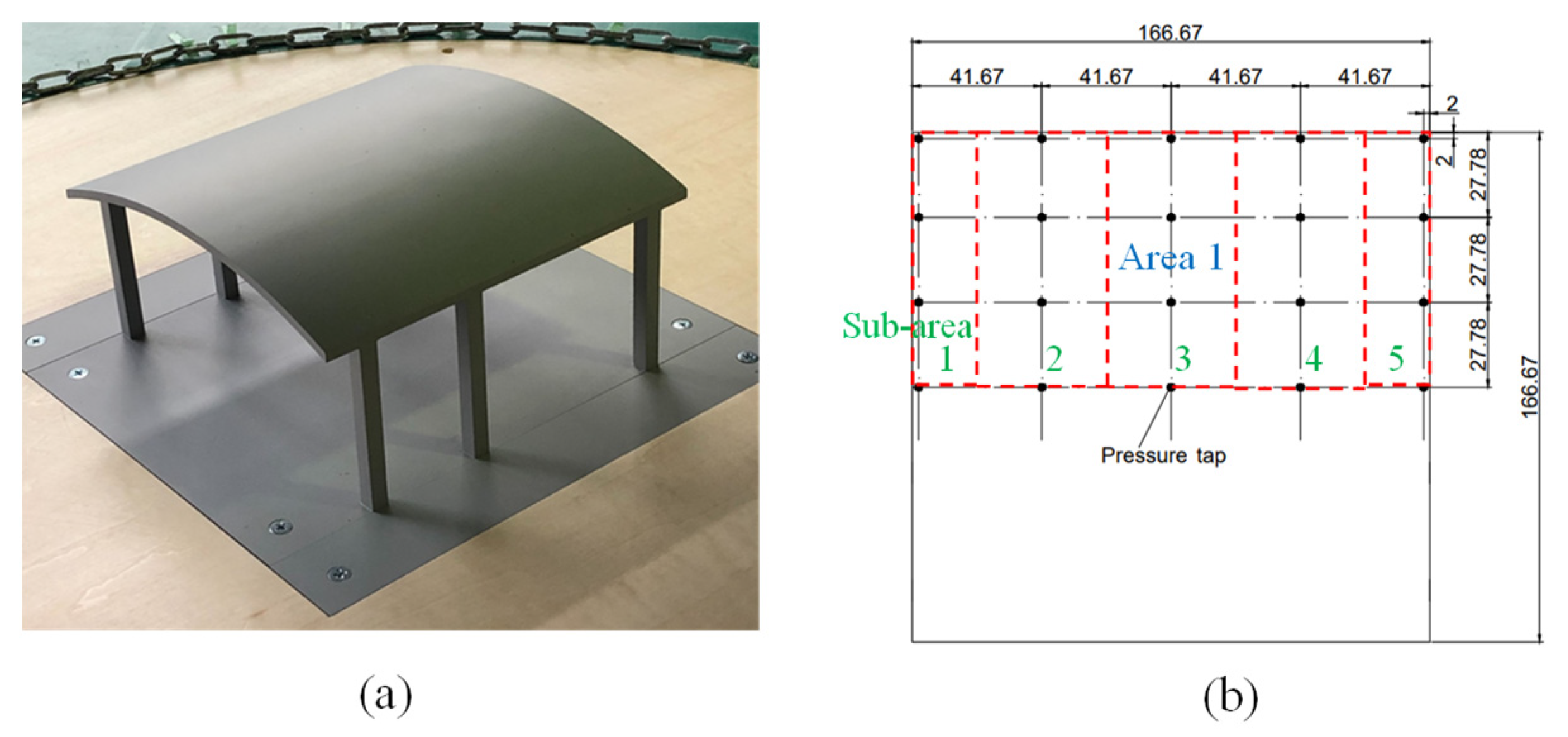
2. Wind Tunnel Model
3. Experimental Procedure
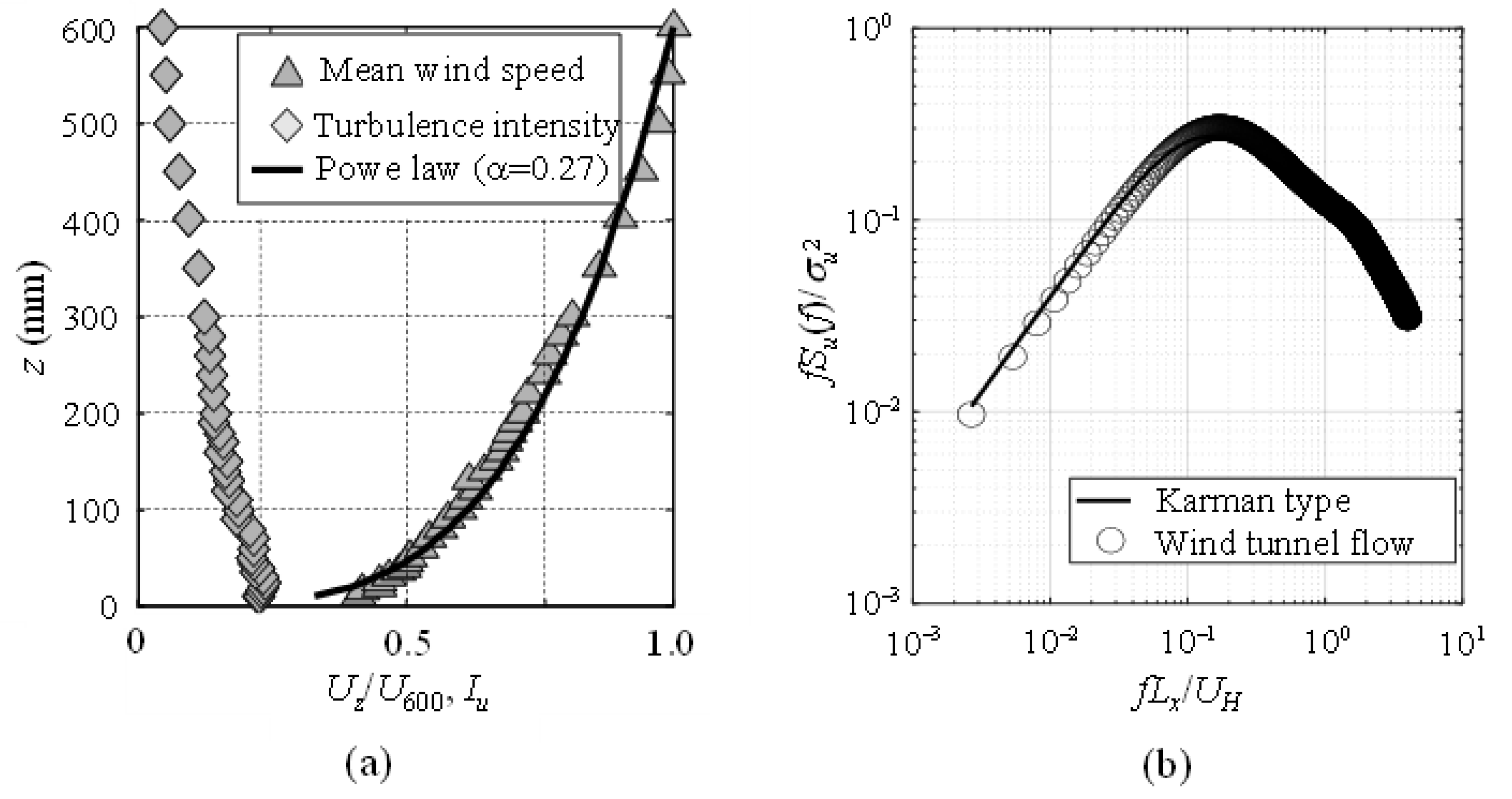
3.1. Wind Tunnel Flow
3.2. Pressure Measurement
4. Wind Force Coefficients for the Main Wind Force Resisting System
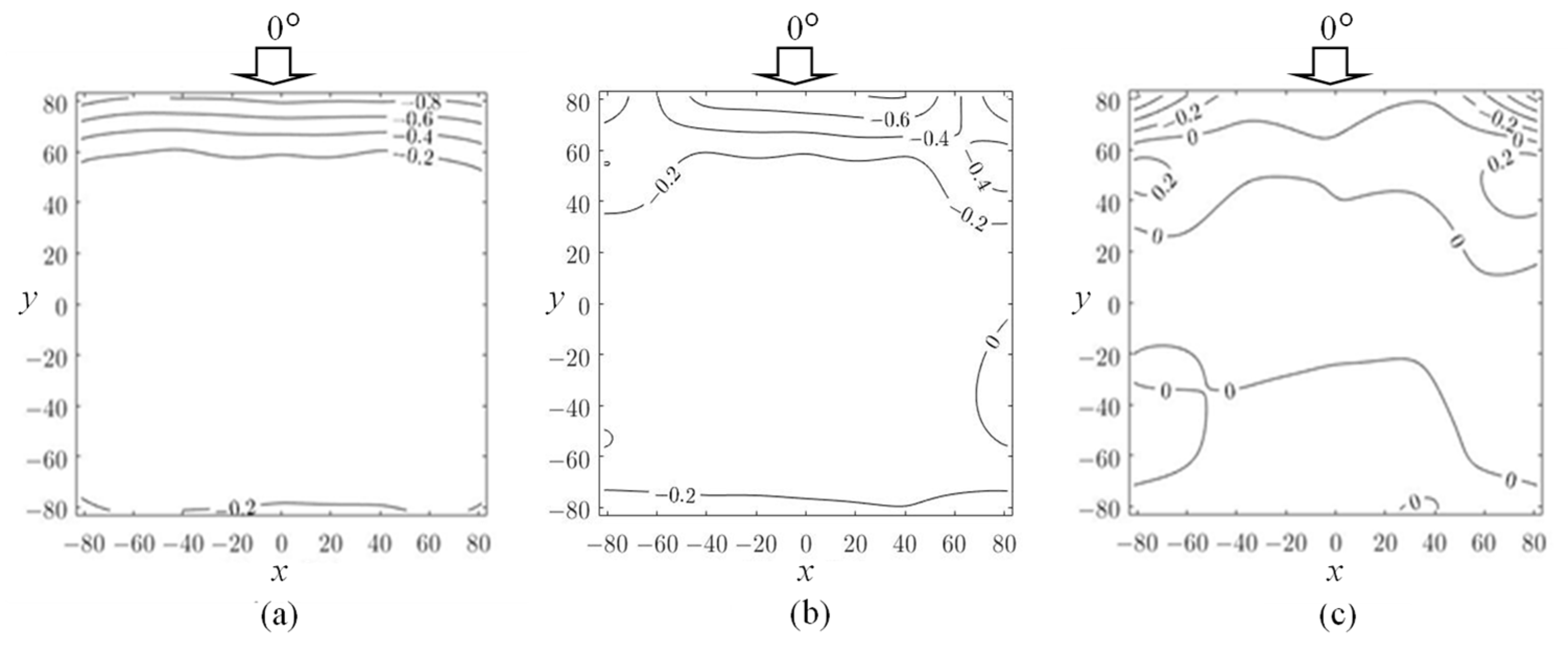
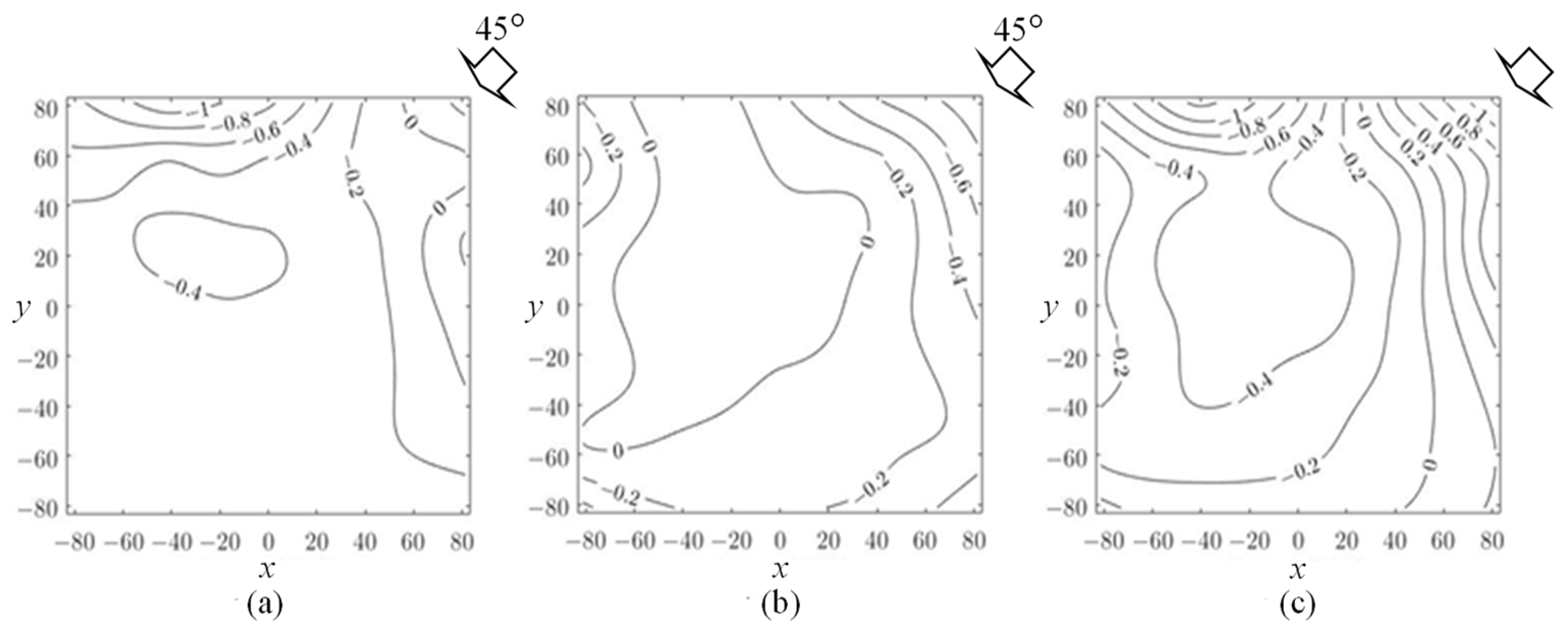
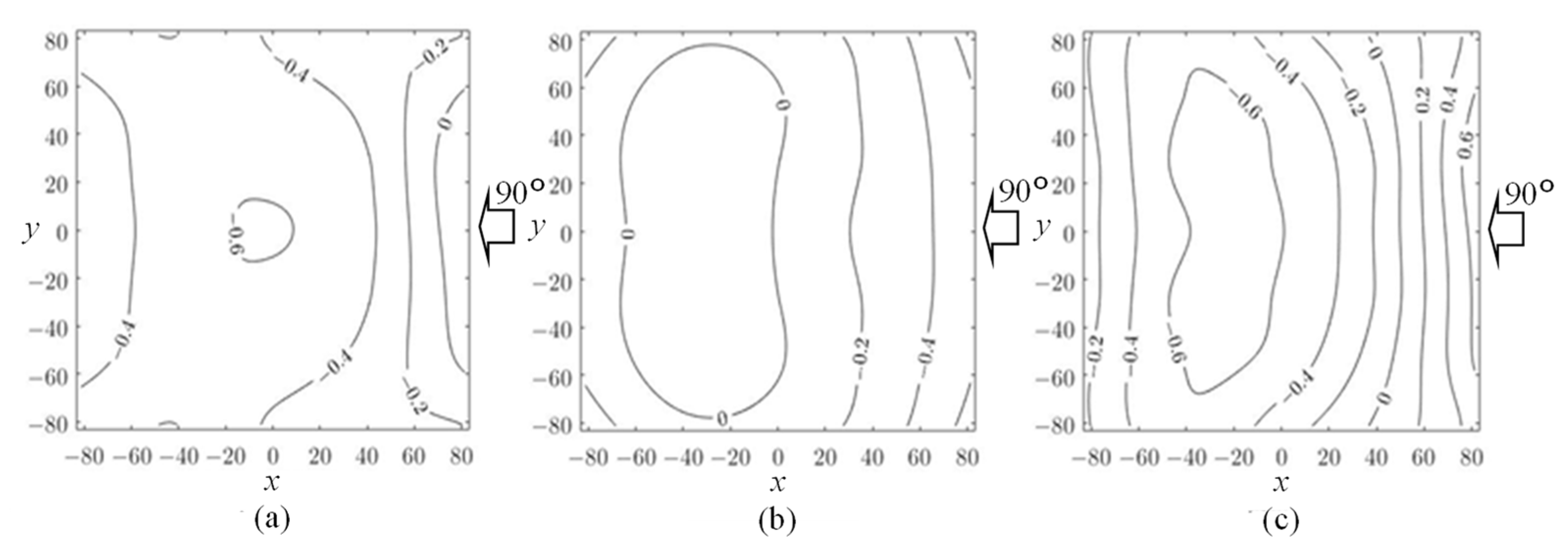
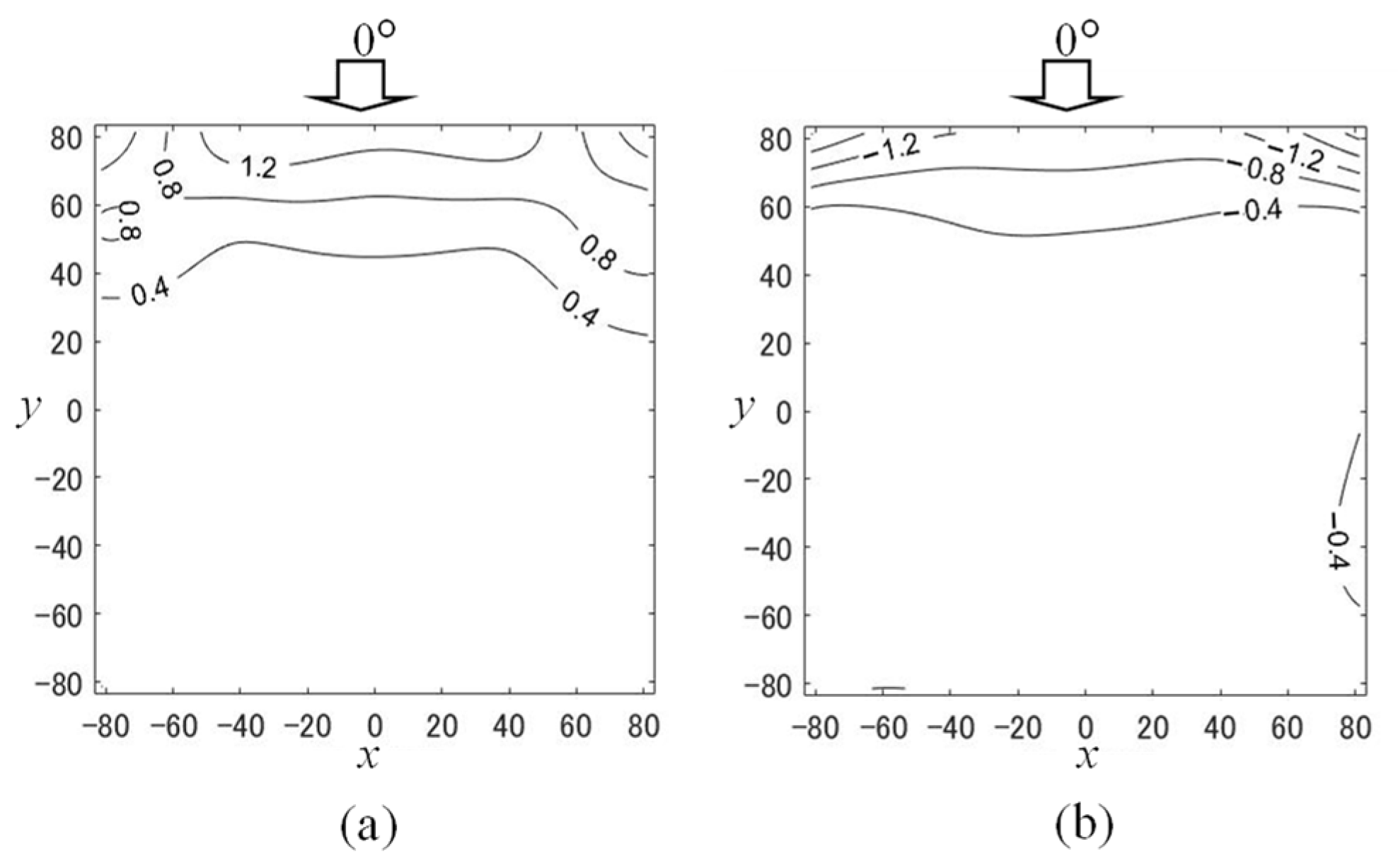
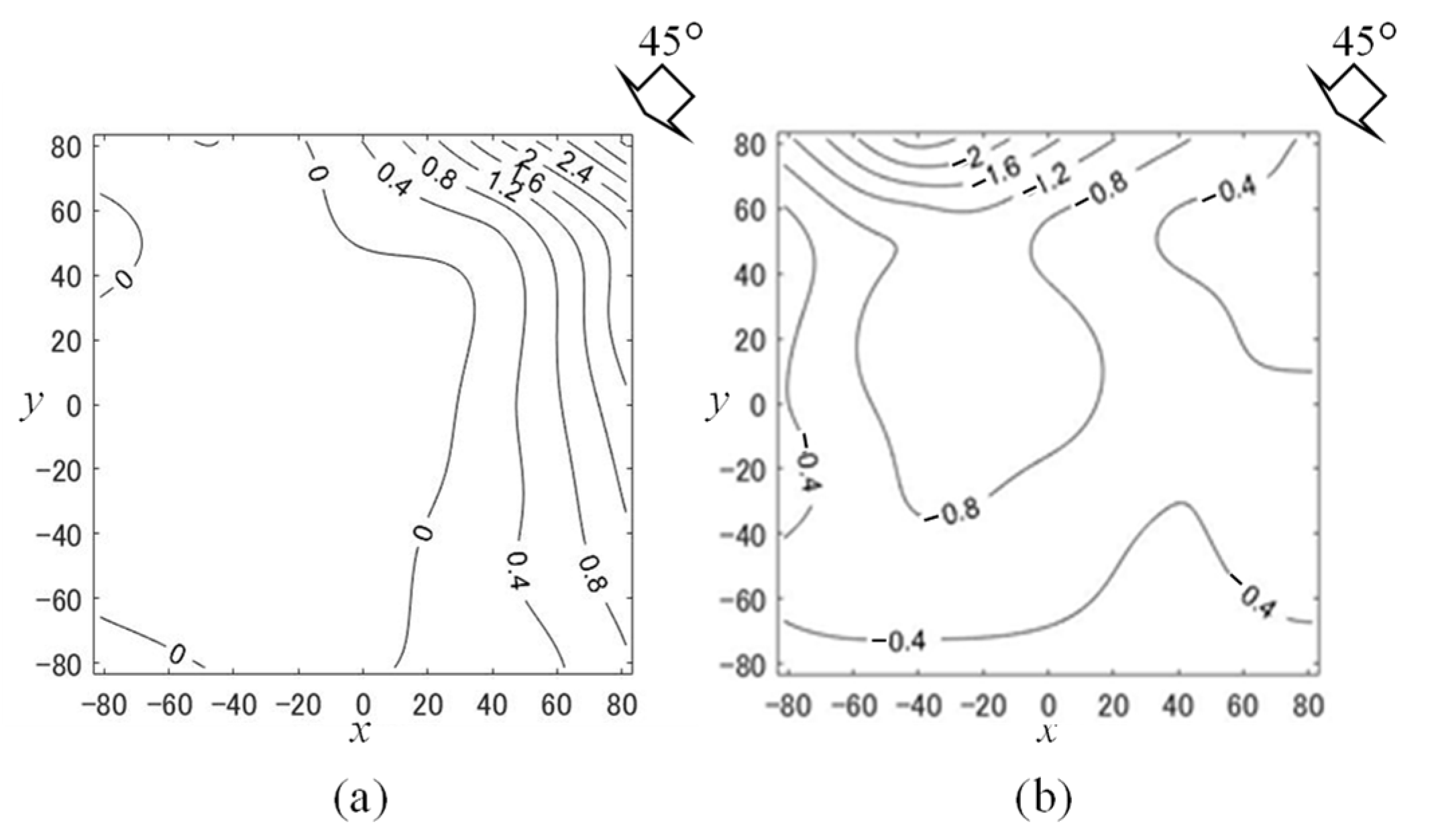
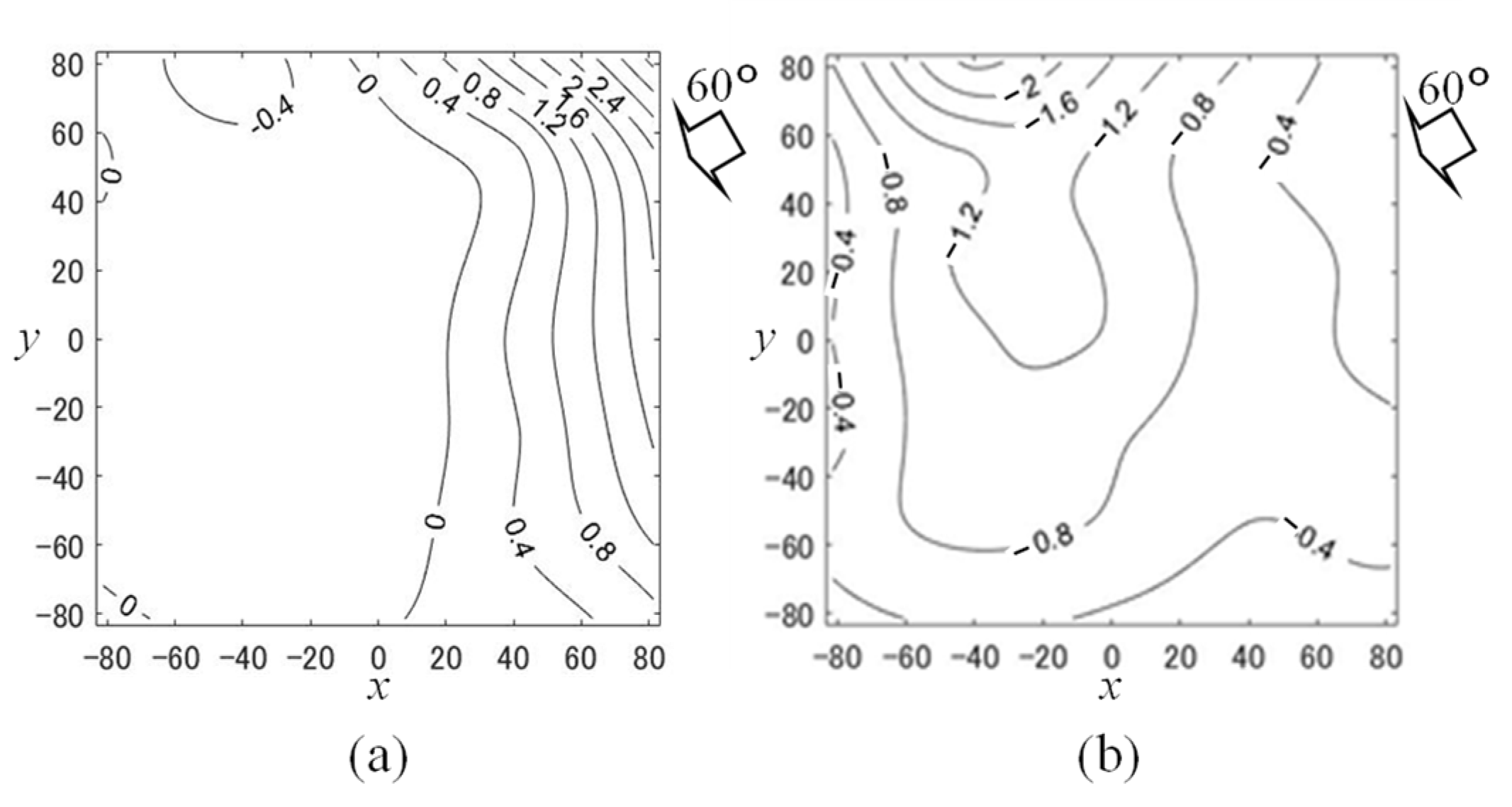
4.1. Mean Wind Pressure and Force Coefficients
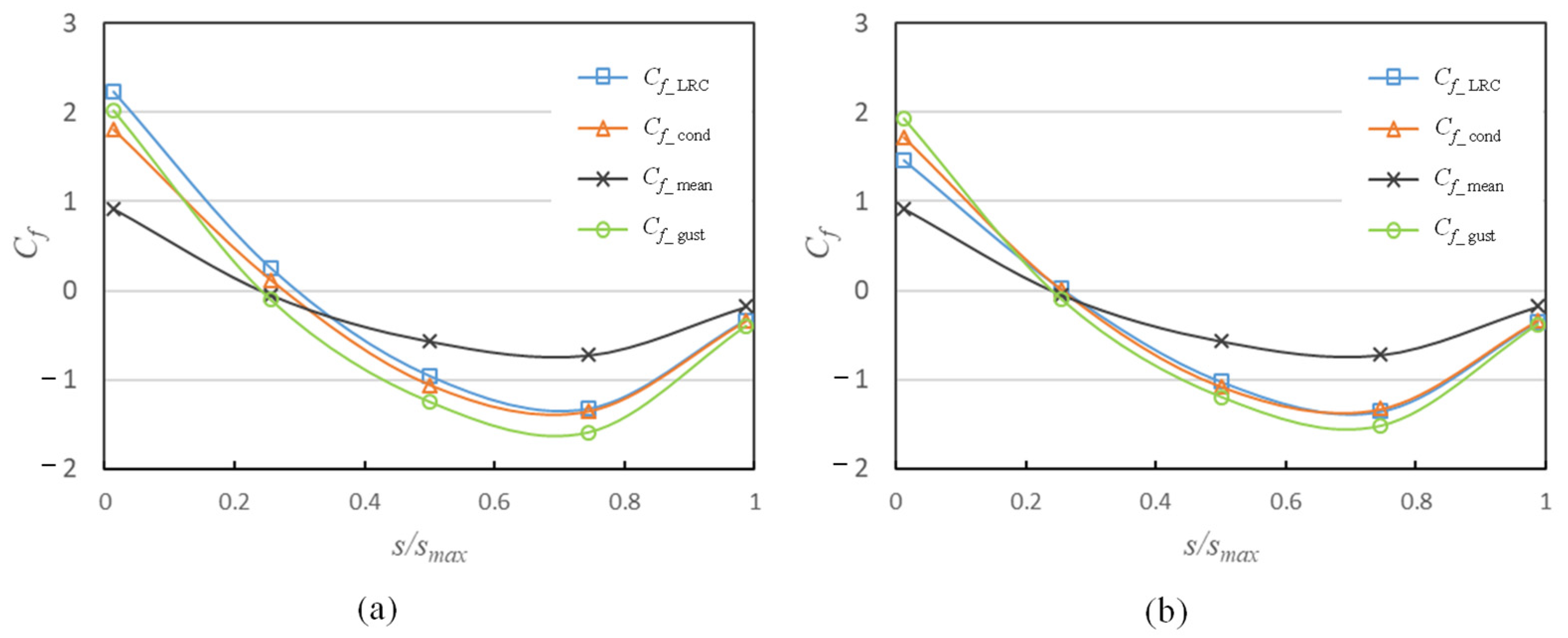
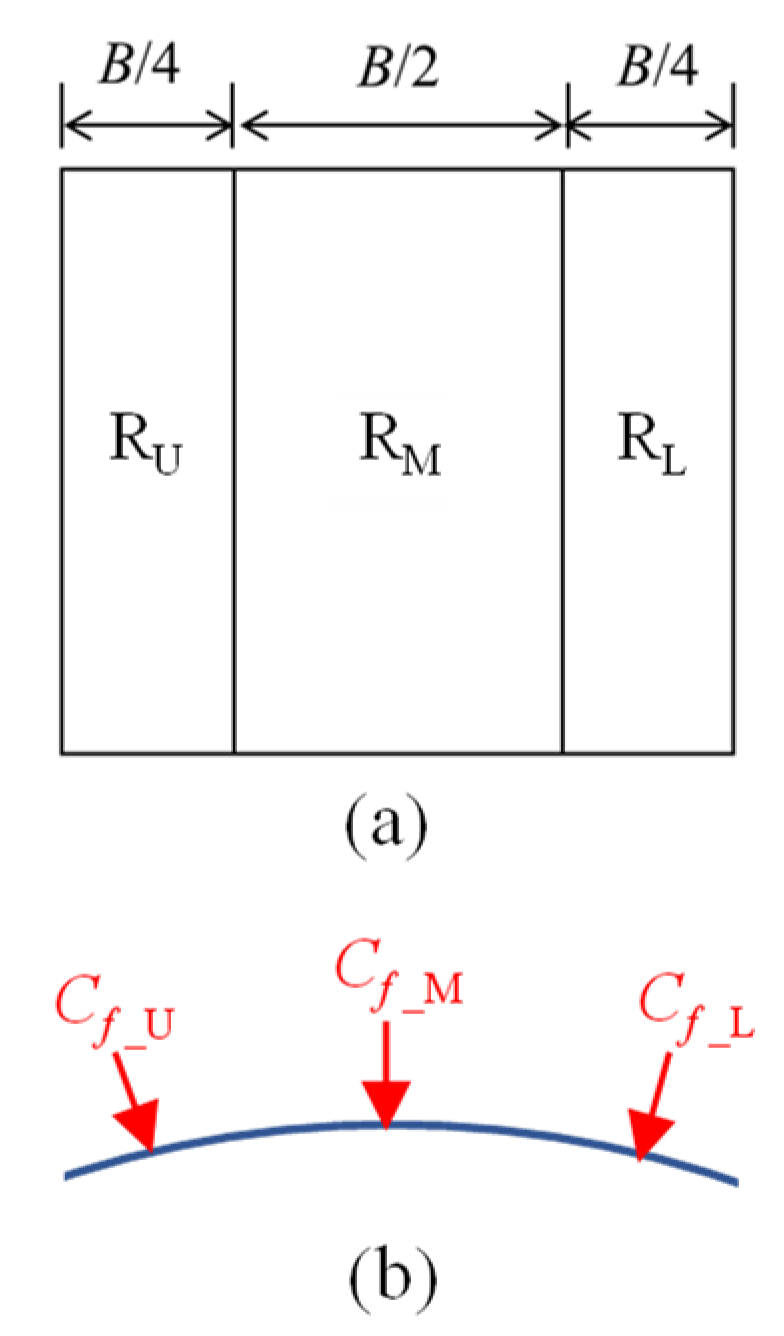
4.2. Estimation of the Equivalent Static Wind Force Coefficients
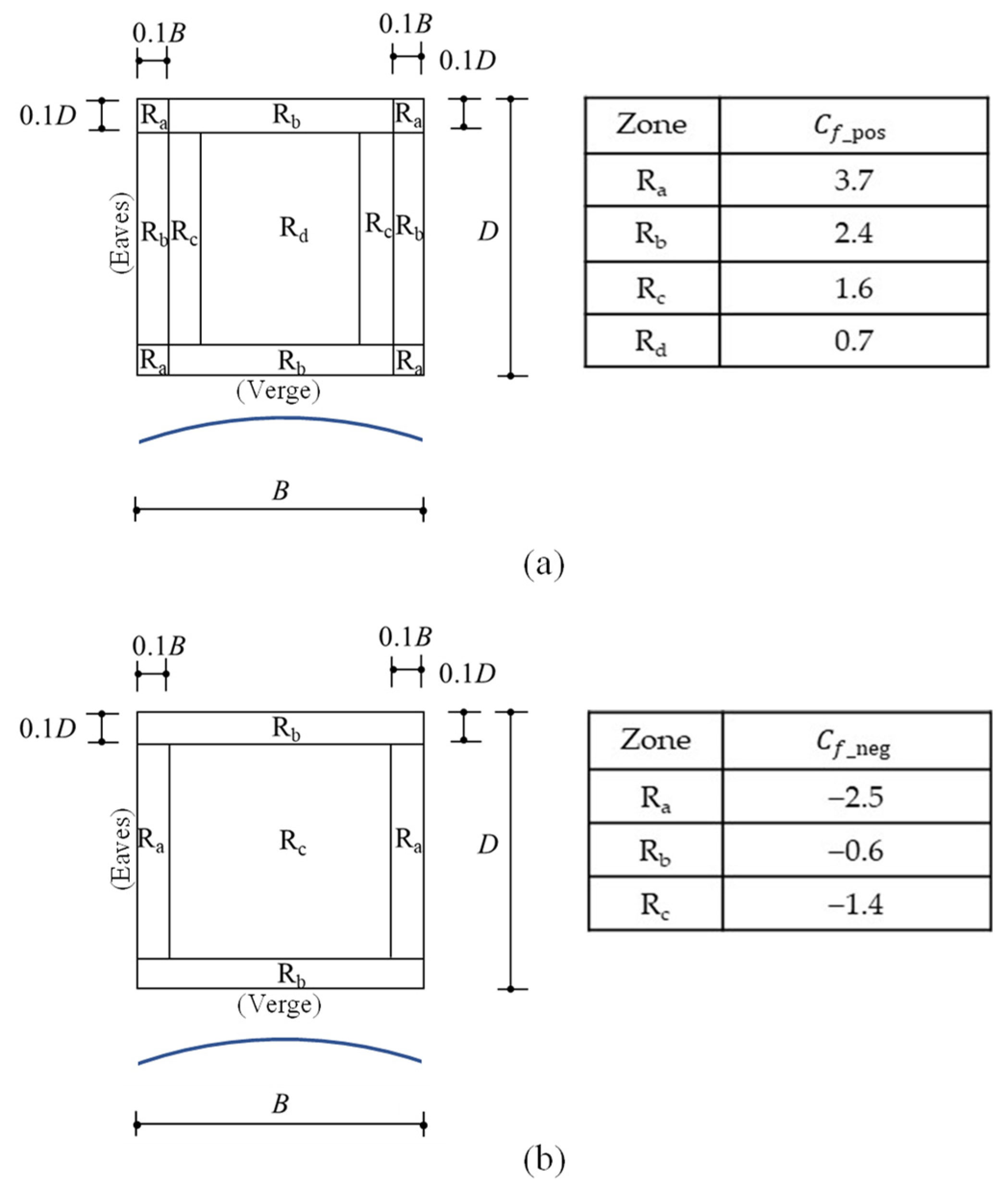
5. Peak Wind Force Coefficients for Designing Cladding
6. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gumley, S.J. A parametric study of extreme pressures for the static design of canopy structures. J. Wind. Eng. Ind. Aerodyn. 1984, 16, 43–56. [Google Scholar] [CrossRef]
- Letchford, C.W.; Ginger, J.D. Wind loads on planar canopy roofs, Part 1 Mean pressure distributions. J. Wind. Eng. Ind. Aerodyn. 1992, 45, 25–45. [Google Scholar] [CrossRef]
- Ginger, J.D.; Letchford, C.W. Wind loads on planar canopy roofs, Part 2 Fluctuating pressure, distributions and correlations. J. Wind. Eng. Ind. Aerodyn. 1994, 51, 353–370. [Google Scholar] [CrossRef]
- Natalini, B.; Marighetti, J.O.; Natalini, M.B. Wind tunnel modeling of mean pressures on planar canopy roof. J. Wind. Eng. Ind. Aerodyn. 2002, 90, 427–439. [Google Scholar] [CrossRef]
- Uematsu, Y.; Iizumi, E.; Stathopoulos, T. Wind loads on free-standing canopy roofs: Part 1 local wind pressures. J. Wind. Eng. Ind. Aerodyn. 2008, 96, 1015–1028. [Google Scholar] [CrossRef]
- Uematsu, Y.; Iizumi, E.; Stathopoulos, T. Wind loads on free-standing canopy roofs: Part 2 overall wind forces. J. Wind. Eng. Ind. Aerodyn. 2008, 96, 1029–1042. [Google Scholar] [CrossRef]
- ASCE/SEI 7-16; Minimum Design Loads and Associated Criteria for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2017.
- Architectural Institute of Japan. Recommendations of Loads on Buildings; Architectural Institute of Japan: Tokyo, Japan, 2015. [Google Scholar]
- AS/NZ 1170.2; Structural Design Actions, Part 2: Wind Actions. Standards New Zealand: Wellington, New Zealand; Standards Australia: Sydney, Australia, 2021. Available online: https://www.standards.govt.nz/shop/asnzs-1170-22021/ (accessed on 15 May 2022).
- Kaseya, T.; Okada, A.; Miyasato, N.; Hiroishi, S.; Nagai, Y.; Yoshino, S.; Matsumoto, R.; Kanda, M. Study on wind response on H.P.-shaped membrane roof, Part 1: Effect of Reynolds number on wind pressure distribution. Summ. Tech. Pap. Annu. Meet. Archit. Inst. Jpn. 2013, Structure I, 181–182. (In Japanese) [Google Scholar]
- Nakagawa, R.; Okada, A.; Miyasato, N.; Hiroishi, S.; Nagai, Y.; Yoshino, S.; Matsumoto, R.; Kanda, M. Study on wind response on H.P.-shaped membrane roof, Part 2: Effect of Reynolds number on static and dynamic response. Summ. Tech. Pap. Annu. Meet. Archit. Inst. Jpn. 2013, Structure I, 183–184. (In Japanese) [Google Scholar]
- Colliers, J.; Mollaert, M.; Degroote, J.; Laet, L.D. Prototyping of thin shell wind tunnel models to facilitate experimental wind load analysis on curved canopy structures. J. Wind. Eng. Ind. Aerodyn. 2019, 188, 308–322. [Google Scholar] [CrossRef]
- Uematsu, Y.; Miyamoto, Y.; Gavanski, E. Wind loading on a hyperbolic paraboloid free roof. J. Civ. Eng. Archit. 2014, 8, 1233–1242. [Google Scholar]
- Uematsu, Y.; Yamamura, R. Experimental Study of Wind Loads on Domed Free Roofs. In XV Conference of the Italian Association for Wind Engineering; IN-NENO; Ricciardelli, F., Avossa, A.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; Volume 27, pp. 716–729. [Google Scholar]
- Natalini, M.B.; Morel, C.; Natalini, B. Mean loads on vaulted canopy roofs. J. Wind. Eng. Ind. Aerodyn. 2013, 119, 102–113. [Google Scholar] [CrossRef]
- Uematsu, Y.; Yamamura, R. Wind loads for designing the main wind force resisting systems of cylindrical free-standing canopy roofs. Tech. Trans. Civ. Eng. 2019, 116, 125–143. [Google Scholar] [CrossRef] [Green Version]
- Wen, L.; Uematsu, Y. Characteristics of wind pressures and forces on a cylindrical free roof focusing on the special and temporal variations. Res. Pap. Membr. Struct. 2019, 33, 39–52. (In Japanese) [Google Scholar]
- Kasperski, M. Extreme wind load distributions for linear and non-linear design. Eng. Struct. 1992, 14, 27–34. [Google Scholar] [CrossRef]
- Tieleman, H.W.; Reinhold, T.A.; Marshall, R.D. On the wind-tunnel simulation of the atmospheric surface layer for the study of wind loads on low-rise buildings. J. Wind. Eng. Ind. Aerodyn. 1978, 3, 21–38. [Google Scholar] [CrossRef]
- Tieleman, H.W. Pressures on surface-mounted prisms: The effects of incident turbulence. J. Wind. Eng. Ind. Aerodyn. 1993, 49, 289–299. [Google Scholar] [CrossRef]
- Tieleman, H.W.; Hajj, M.R.; Reinhold, T.A. Wind tunnel simulation requirements to assess wind loads on low-rise buildings. J. Wind. Eng. Ind. Aerodyn. 1998, 74–76, 675–686. [Google Scholar] [CrossRef]
- ASCE/SEI 49-12; Wind Tunnel Testing for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2012.
- Uematsu, Y.; Orimo, T.; Watanabe, S.; Kitamura, S.; Iwaya, M. Wind loads on a steel greenhouse with a wing-like cross section. In Proceedings of the Fourth European & African Conference on Wind Engineering, Prague, Czech Republic, 11–15 July 2005. [Google Scholar]
- Cook, N.J.; Mayne, J.R. A novel working approach to the assessment of wind loads for equivalent static design. J. Wind. Eng. Ind. Aerodyn. 1979, 4, 149–164. [Google Scholar] [CrossRef]
- Cook, N.J.; Mayne, J.R. A refined working approach to the assessment of wind loads for equivalent static design. J. Wind. Eng. Ind. Aerodyn. 1980, 6, 125–137. [Google Scholar] [CrossRef]
- Hariris, R.I. An improved method for the prediction of extreme values of wind effects on simple buildings and structures. J. Wind. Eng. Ind. Aerodyn. 1982, 9, 343–379. [Google Scholar] [CrossRef]
- Harris, R.I. A new direct version of the Cook-Mayne method for wind pressure probabilities in temperate storms. J. Wind. Eng. Ind. Aerodyn. 2005, 93, 581–600. [Google Scholar] [CrossRef]
- Kasperski, M. Specification of design wind loads based on wind tunnel experiments. J. Wind. Eng. Ind. Aerodyn. 2003, 91, 527–541. [Google Scholar] [CrossRef]
- Kasperski, M. Specification of the design wind loads—A critical review of code concepts. J. Wind. Eng. Ind. Aerodyn. 2009, 97, 335–357. [Google Scholar] [CrossRef]
- Hui, Y.; Tamura, Y.; Yang, Q.S.; Li, Z.N. Estimation of extreme wind load on structures and claddings. J. Eng. Mech. 2015, 143, 04017081. [Google Scholar] [CrossRef]
- Uematsu, Y.; Isyumov, N. Peak gust pressures acting on the roof and wall edges of a low-rise building. J. Wind. Eng. Ind. Aerodyn. 1998, 77–78, 217–231. [Google Scholar] [CrossRef]
- Lawson, T.V. Wind Effects on Buildings Vol. 1 Design Applications; Applied Science Publishers Ltd.: London, UK, 1980. [Google Scholar]
- Aihara, T.; Asami, Y.; Nishimura, H.; Takamori, K.; Asami, R.; Somekawa, D. An area correct factor for the wind pressure coefficient for cladding of hip roof—The case of square plan hip roof with roof pitch of 20 degrees. In Proceedings of the National Symposium on Wind Engineering, Tokyo, Japan, 3–5 December 2008; pp. 463–466. (In Japanese). [Google Scholar]





| Load Effect Considered | |||
|---|---|---|---|
| Axial force N | 0.74 | −1.11 | −0.85 |
| Bending moment M | 1.23 | −1.05 | −0.83 |
| Load Effect Considered | |||
|---|---|---|---|
| Axial force N | 0.35 | −0.53 | −0.41 |
| Bending moment M | 0.56 | −0.48 | −0.38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, W.; Uematsu, Y. Discussion of Design Wind Loads on a Vaulted Free Roof. Wind 2022, 2, 479-494. https://doi.org/10.3390/wind2030026
Ding W, Uematsu Y. Discussion of Design Wind Loads on a Vaulted Free Roof. Wind. 2022; 2(3):479-494. https://doi.org/10.3390/wind2030026
Chicago/Turabian StyleDing, Wei, and Yasushi Uematsu. 2022. "Discussion of Design Wind Loads on a Vaulted Free Roof" Wind 2, no. 3: 479-494. https://doi.org/10.3390/wind2030026
APA StyleDing, W., & Uematsu, Y. (2022). Discussion of Design Wind Loads on a Vaulted Free Roof. Wind, 2(3), 479-494. https://doi.org/10.3390/wind2030026






