A Statistical–Dynamical Downscaling Technique for Wind Resource Mapping: A Regional Atmospheric-Circulation-Type Approach with Numerical Weather Prediction Modeling
Abstract
1. Introduction
2. Materials and Methods
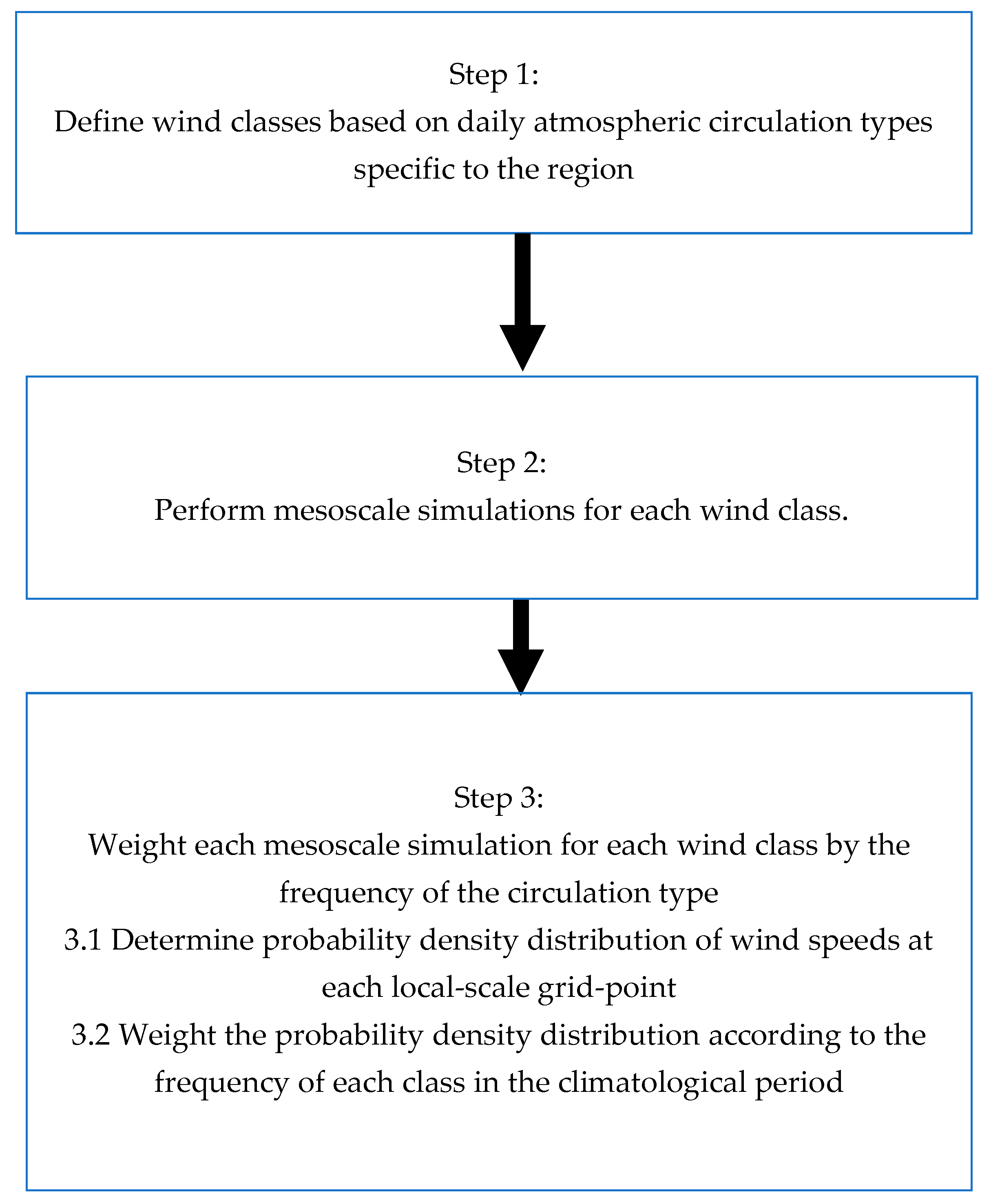
2.1. Statistical–Dynamical Downscaling Methodology to Develop High-Resolution Wind Maps
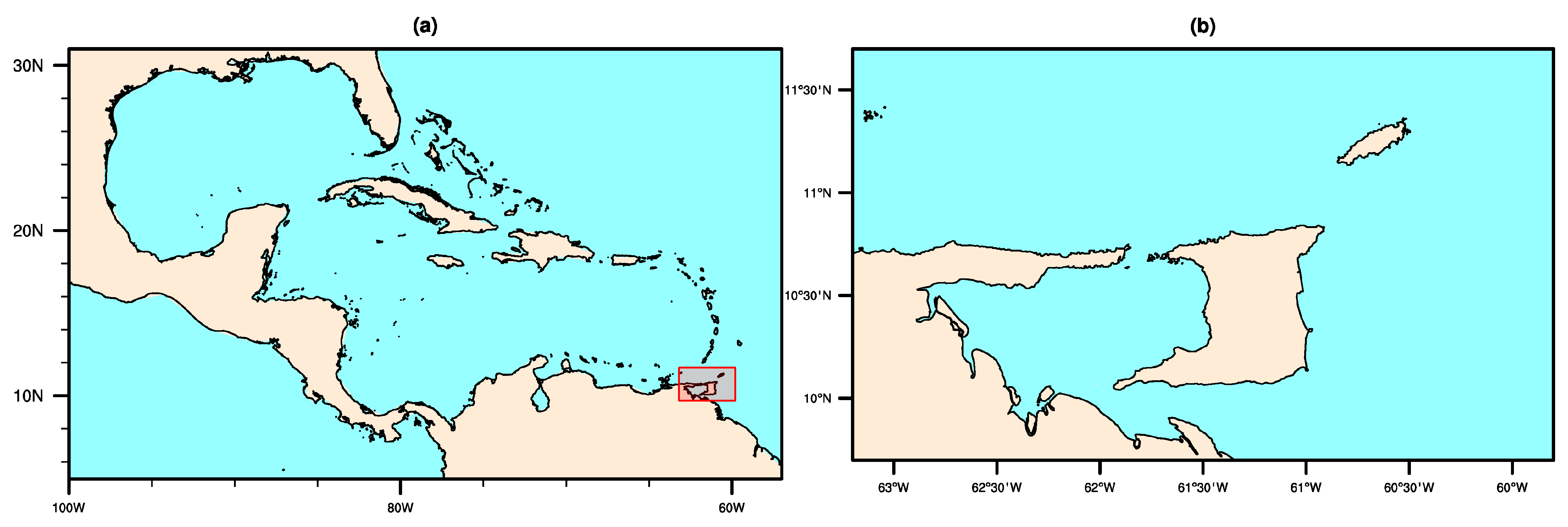
2.2. Study Region of the Case Study—Location, Climate, and Energy Situation
2.3. Wind Class Definition from an Atmospheric-Circulation-Type Catalog
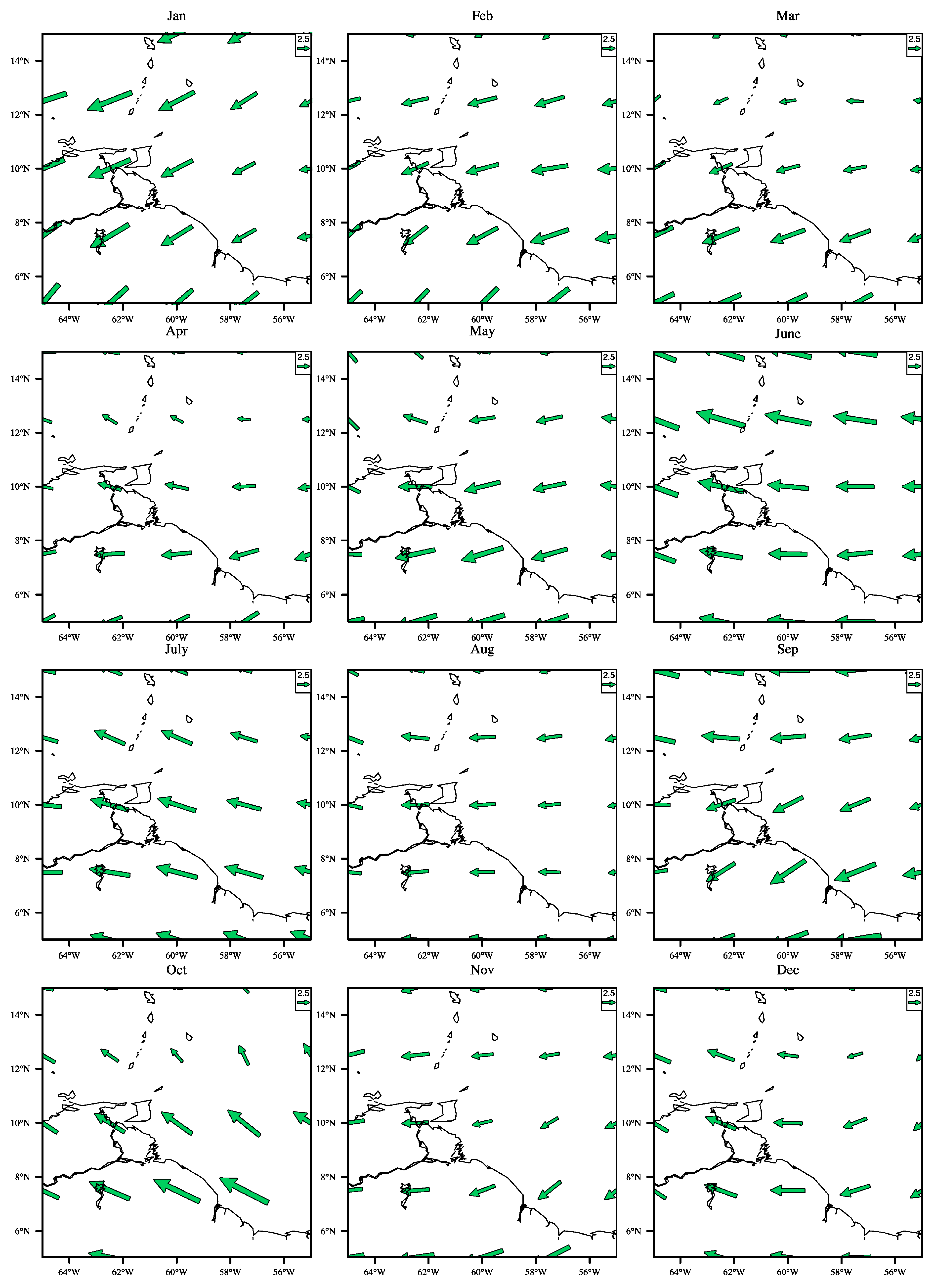
2.3.1. An Atmospheric Circulation Catalog for the Caribbean
2.3.2. Defining the Wind Classes from the Atmospheric Circulation Types
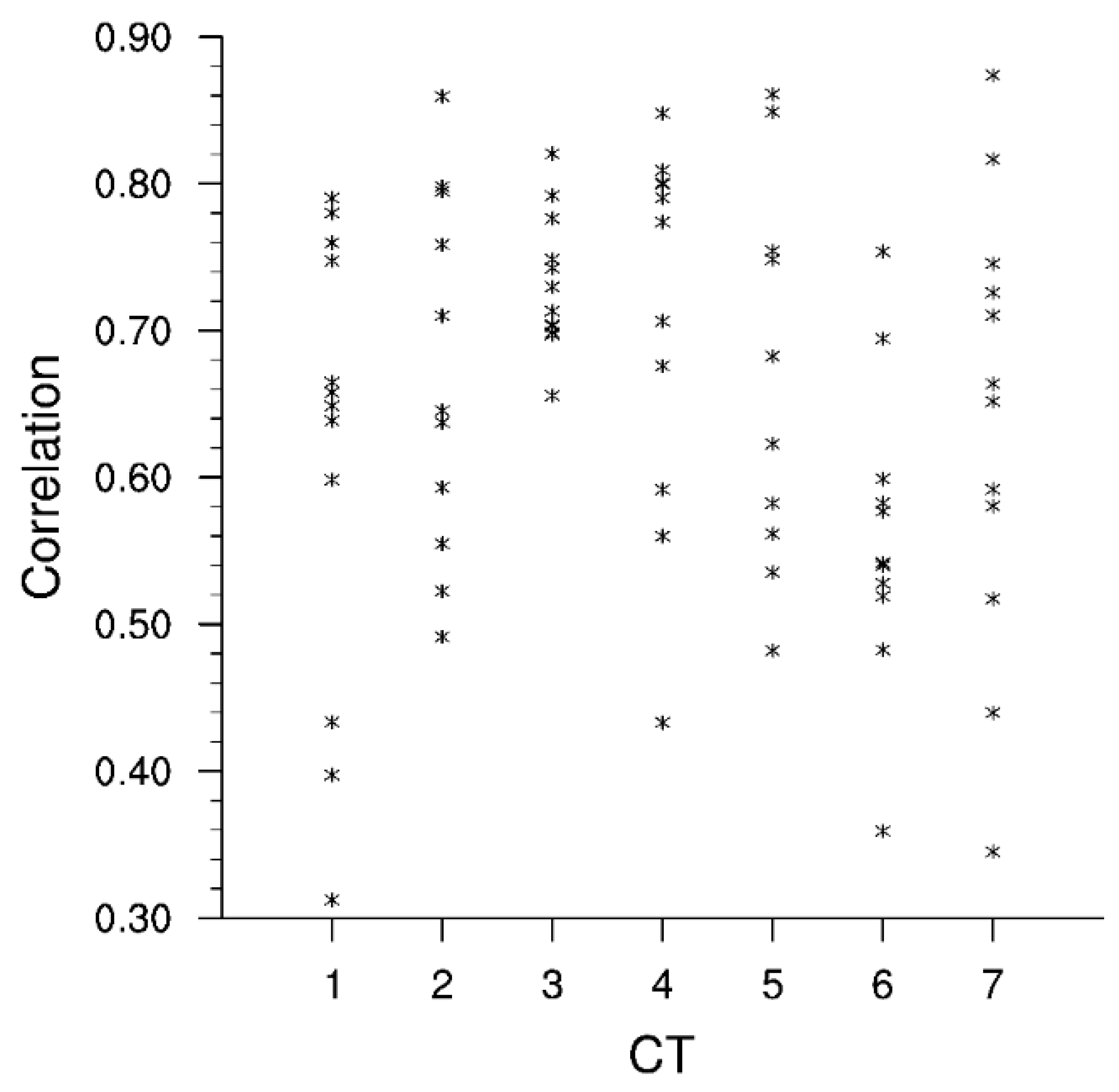
2.3.3. Accuracy of Eighty-Two Wind Classes Versus Seven Wind Classes in Reproducing the Long-Term Mean Wind-Field Pattern at the 10 m Level
2.4. Downscaling the Large-Scale Wind Fields Using a Numerical Weather Prediction Model
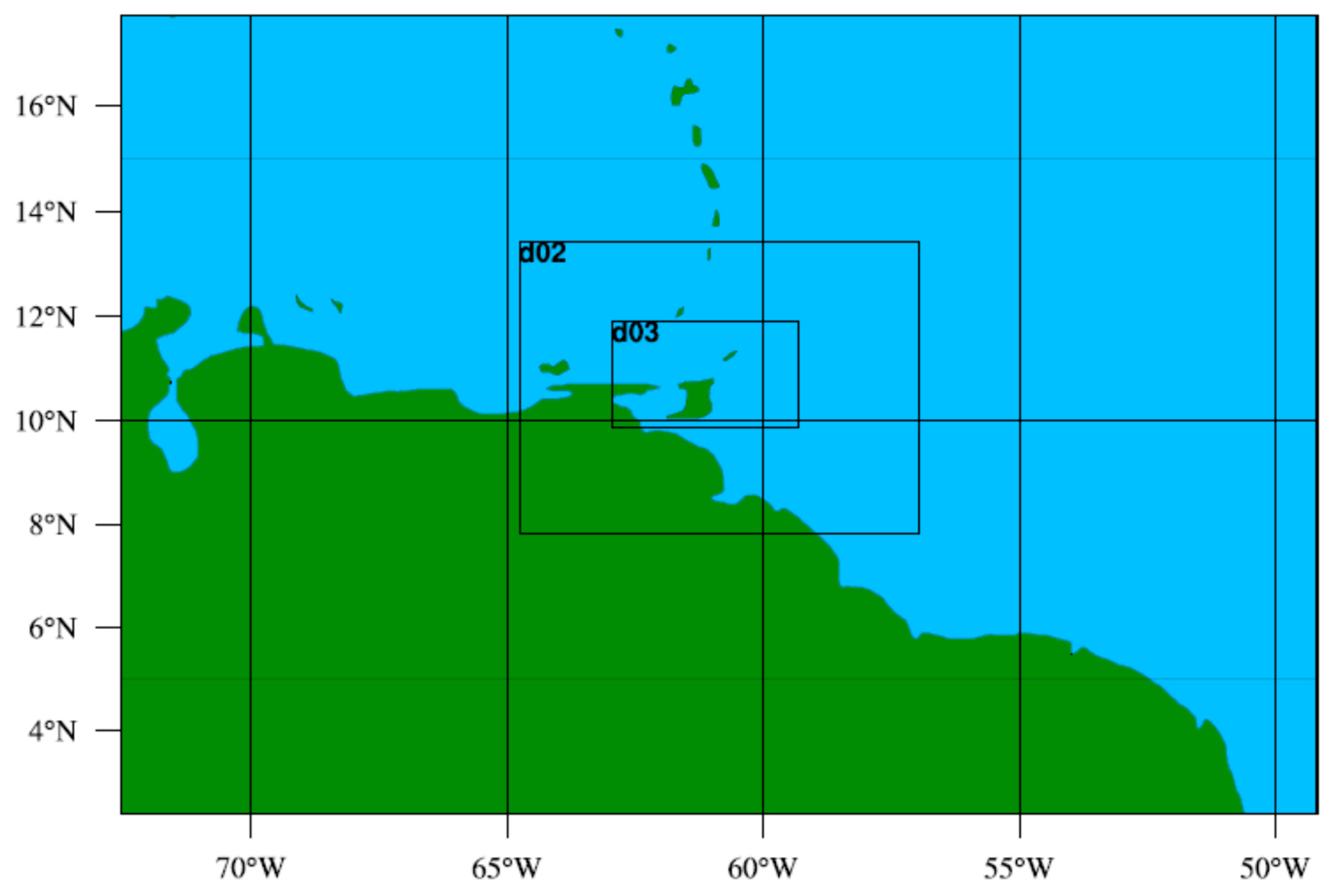
2.4.1. Modeling Domain
2.4.2. WRF’s Parameterization Schemes
2.4.3. Input Surface and Terrain Datasets
2.4.4. Initial and Boundary Input Conditions for Each Wind Class
2.4.5. Processing of the WRF’s Wind Speed Output
2.4.6. Summary of Step 2 of the SDD Method
2.5. Climatological Wind Map Creation
2.5.1. Wind Speed and Wind Power Densities
2.5.2. Processing High-Resolution Simulations to Create Wind Maps
2.5.3. Validation of the Wind Maps at the 10 m Height
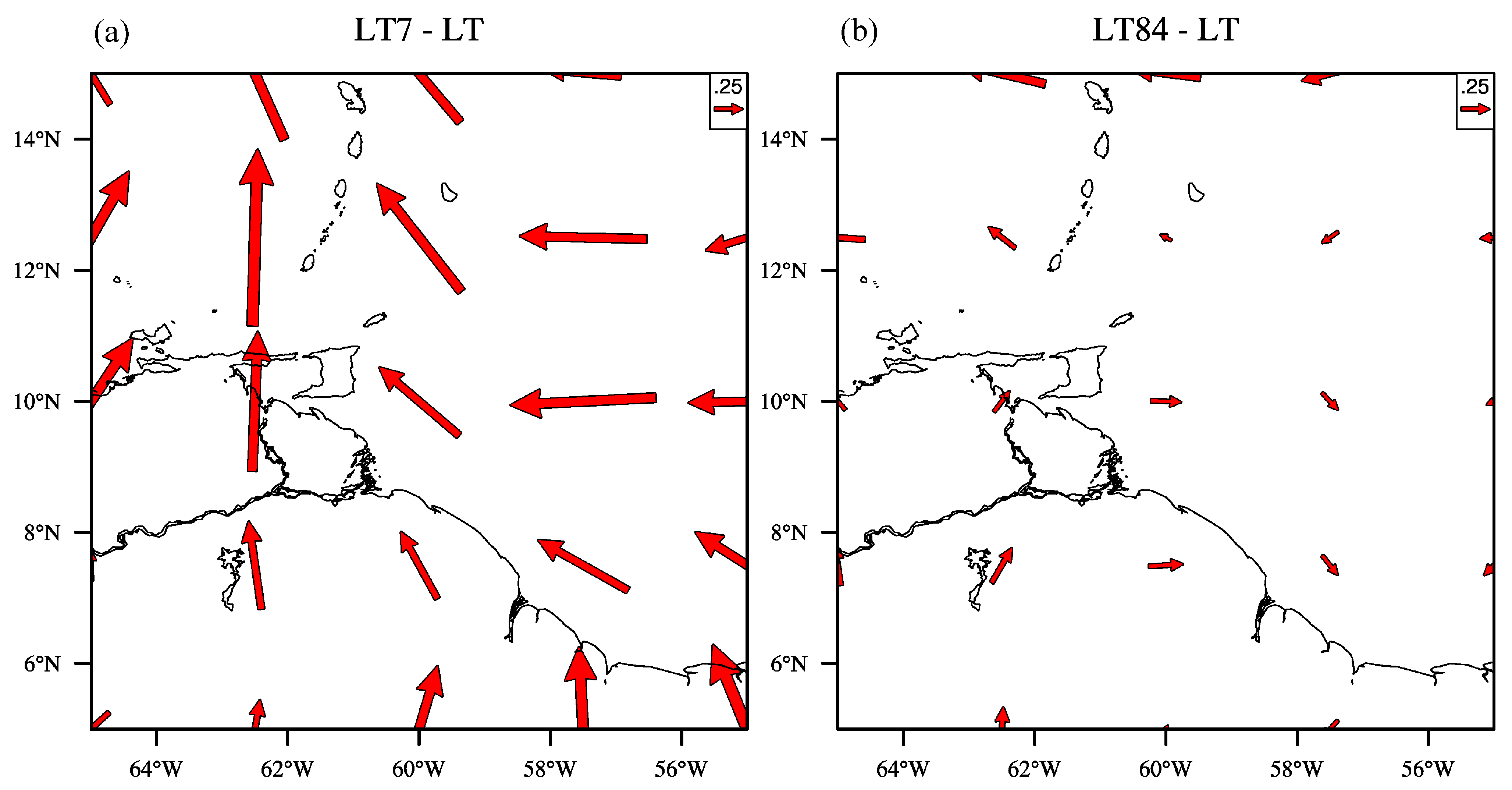
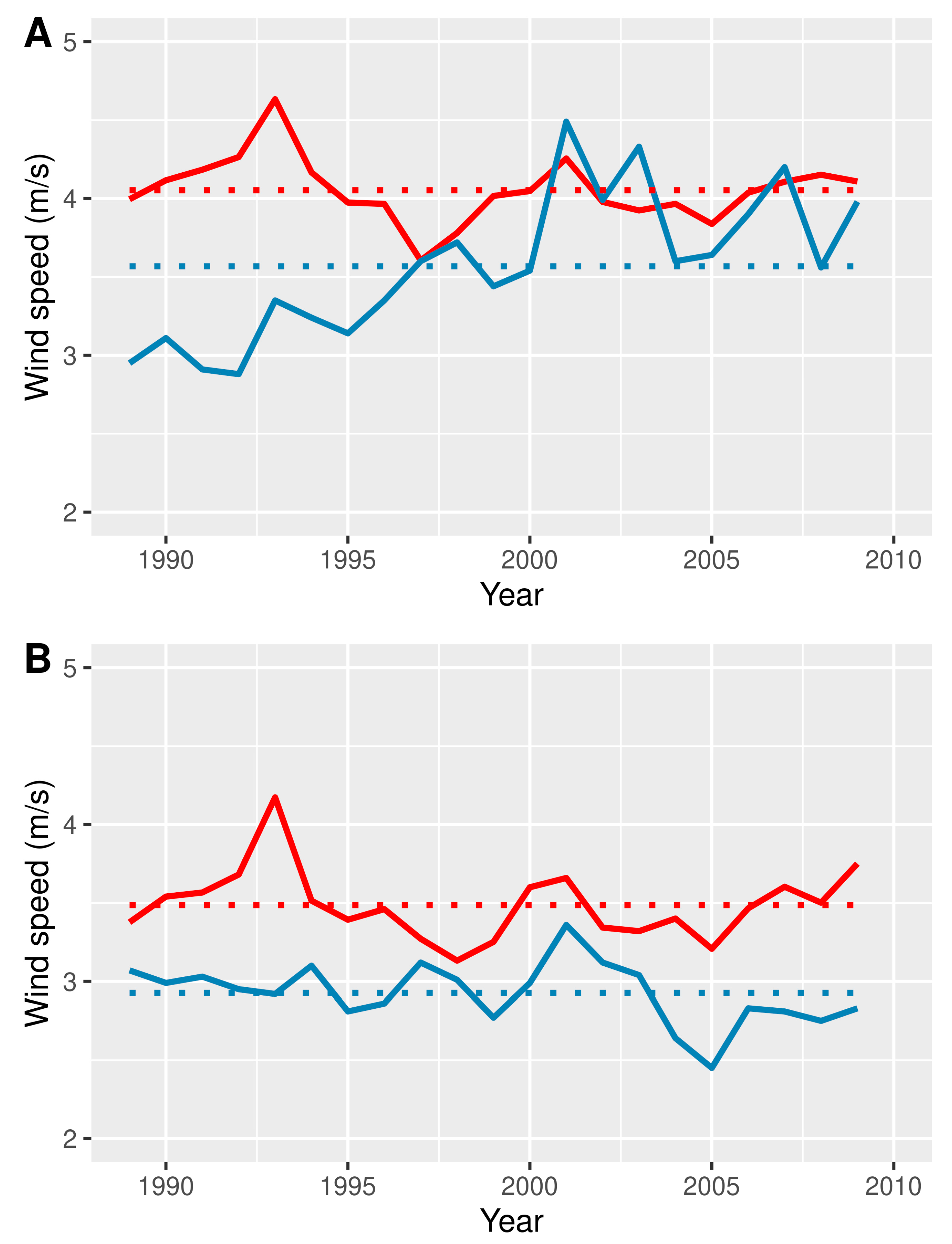
2.5.4. Interannual Variability
3. Results and Discussion
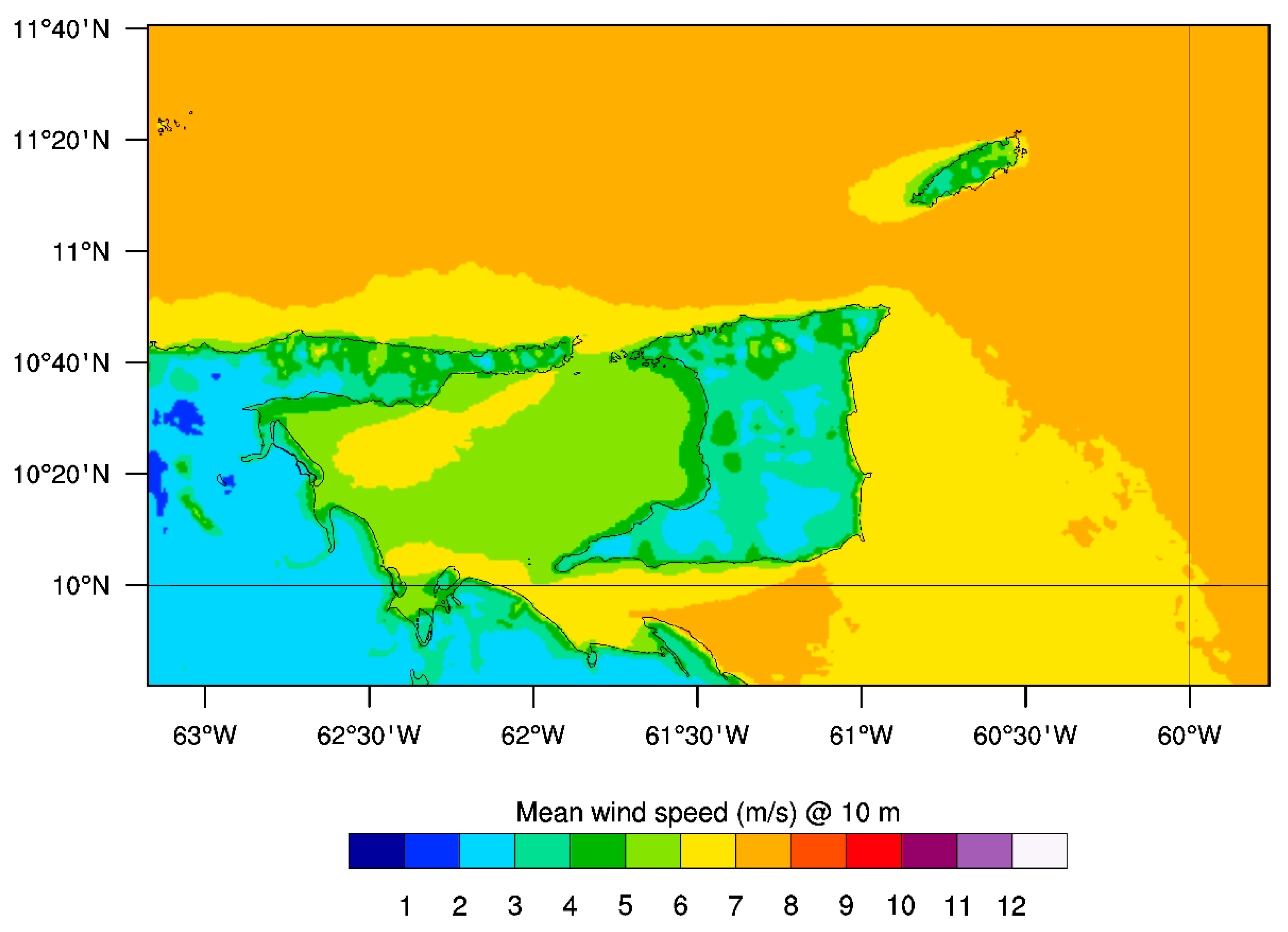
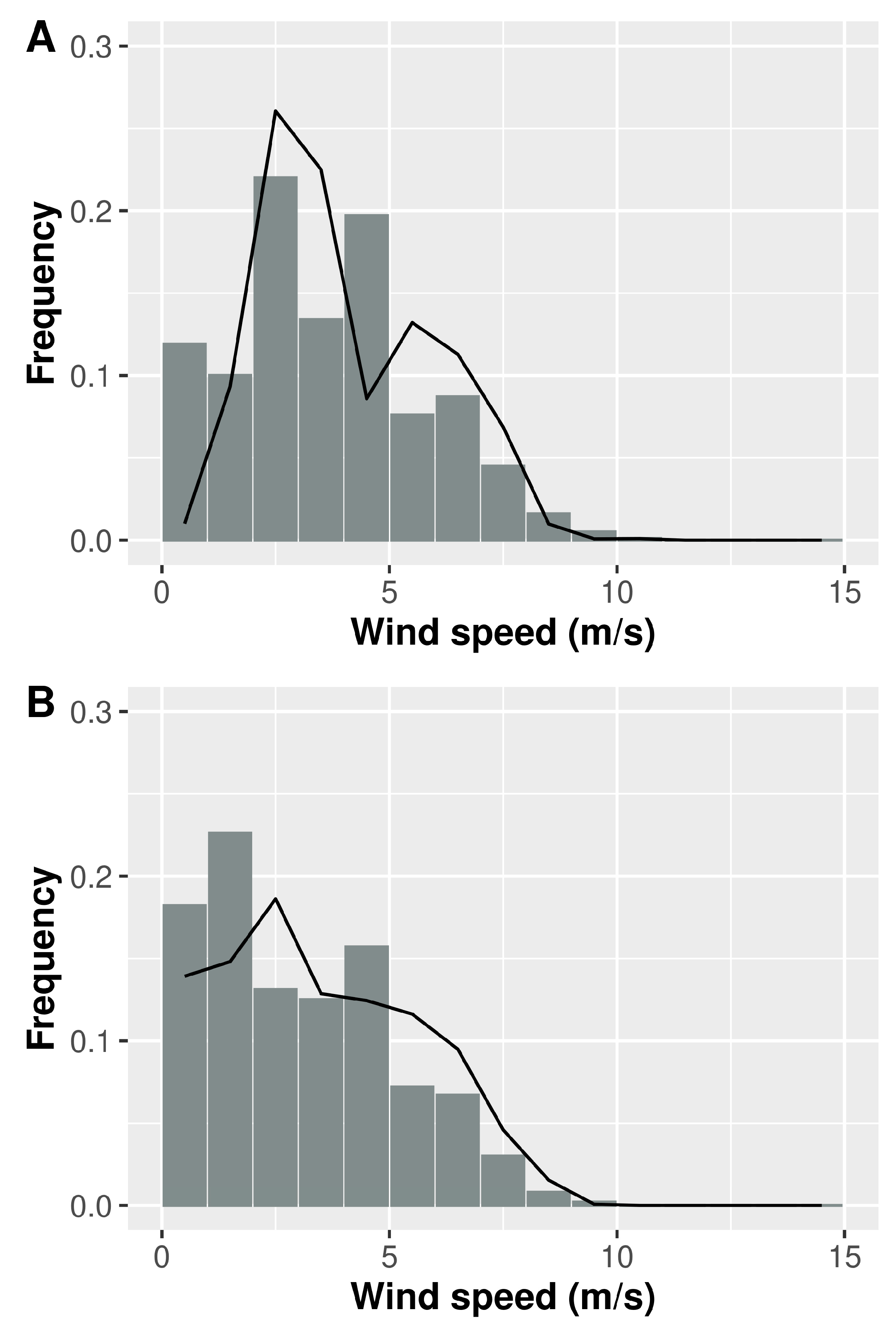
3.1. The Validation of the 10 m Wind Maps
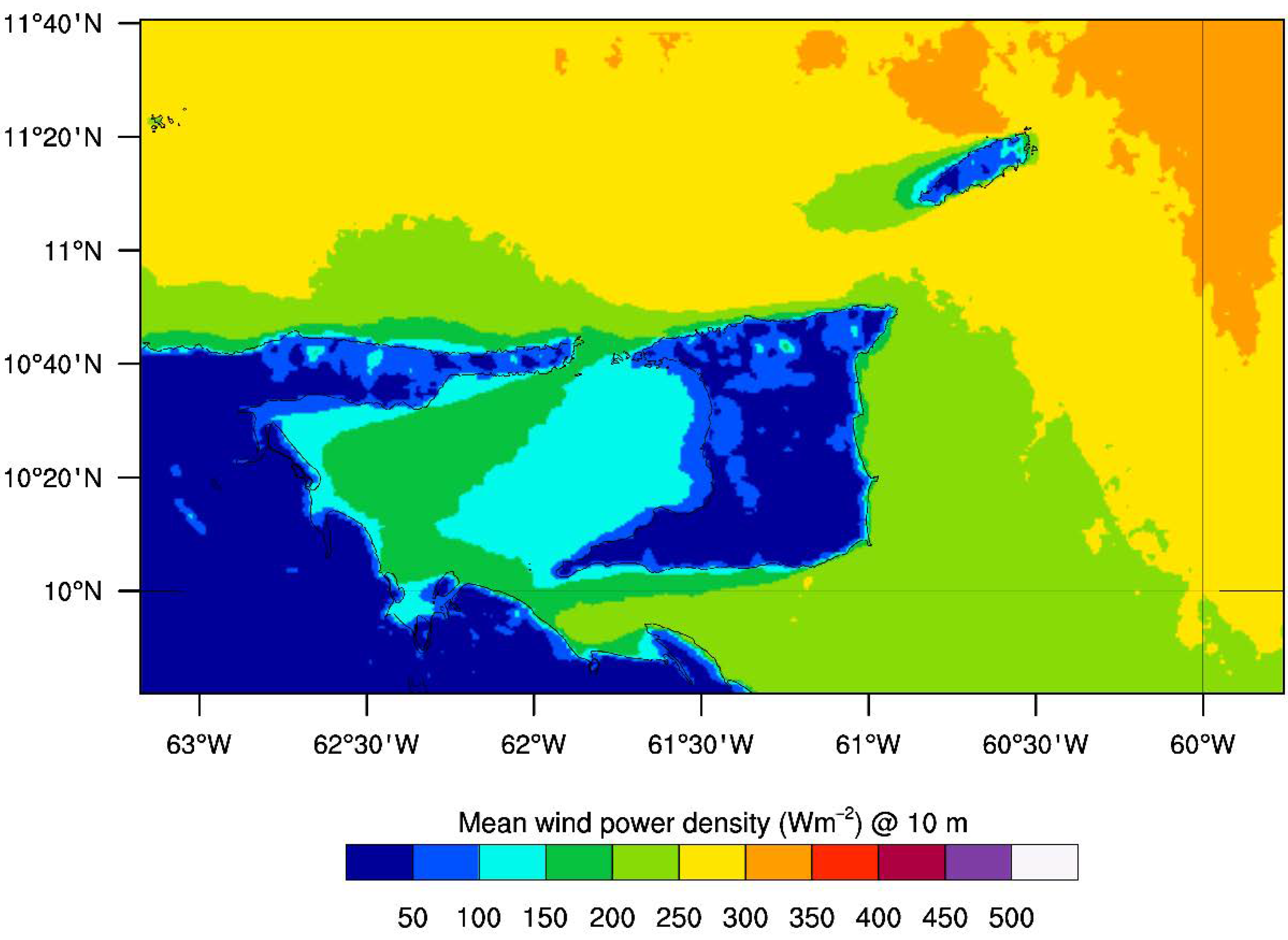
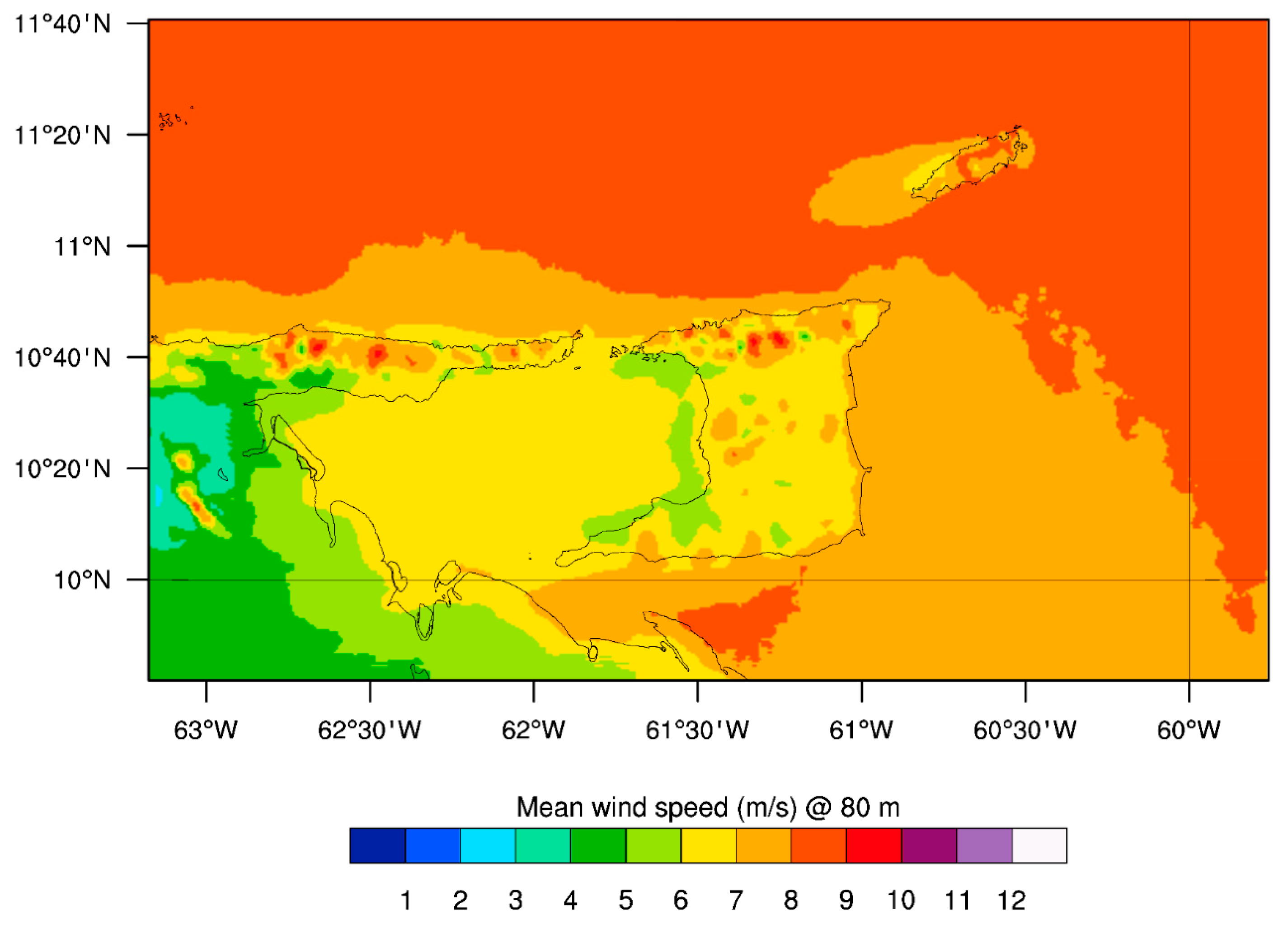
3.2. The 50 m and 80 m Wind Maps for Trinidad and Tobago
3.3. Implications
3.3.1. Small-Scale Wind Power
3.3.2. Utility-Scale Wind Power
3.3.3. Backup Energy Storage
3.3.4. Higher-Resolution Modeling and Climate Impact Studies
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BESS | battery energy storage system |
| CT | circulation type |
| EOF | empirical orthogonal function |
| GWA | Global Wind Atlas |
| ICBCs | initial and boundary conditions |
| IEA | International Energy Agency |
| IRENA | International Renewable Energy Agency |
| LCC | land cover characterization |
| LIDAR | Light detection and ranging |
| NCEP-DOE | National Center for Environmental Prediction/Department of Energy |
| NWP | numerical weather prediction |
| PBL | planetary boundary layer |
| SDD | statistical–dynamical downscaling |
| SDG | sustainable development goal |
| SIDS | small island developing states |
| SODAR | sound detection and ranging |
| SST | sea surface temperature |
| UN | United Nations |
| WMO | World Meteorological Organization |
| WPD | wind power density |
| WPS | WRF’s preprocessor |
| WRF | Weather Research and Forecasting |
References
- Global Wind Energy Council (GWEC). Global Wind Report 2024. 2024. Available online: https://www.gwec.net/reports (accessed on 19 February 2025).
- IRENA. World Energy Transitions Outlook: 1.5 °C Pathway; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2021; Available online: https://www.irena.org/Publications/2021/Jun/World-Energy-Transitions-Outlook (accessed on 20 November 2022).
- IEA. Net Zero by 2050: A Roadmap for the Global Energy Sector; IEA: Paris, France, 2021; Available online: https://www.iea.org/reports/net-zero-by-2050 (accessed on 22 November 2021).
- United Nations. The 17 Goals. Available online: https://sdgs.un.org/goals (accessed on 3 April 2024).
- Nor, K.M.; Shaaban, M.; Rahman, H.A. Feasibility assessment of wind energy resources in Malaysia based on NWP models. Renew. Energy 2014, 62, 147–154. [Google Scholar] [CrossRef]
- Carvalho, D.; Rocha, A.; Gómez-Gesteira, M.; Silva Santos, C. WRF wind simulation and wind energy production estimates forces by different reanalyses: Comparison with observed data for Portugal. Appl. Energy 2014, 117, 116–126. [Google Scholar] [CrossRef]
- Potter, C.W.; Lew, D.; McCaa, J.; Cheng, S.; Eichelberger, S.; Grimit, E. Creating the dataset for the Western Wind and Solar Integration Study (U.S.A.). Wind Eng. 2008, 32, 325–338. [Google Scholar] [CrossRef]
- Yim, S.H.L.; Fung, J.C.H.; Lau, A.K.H.; Kot, S.C. Developing a high resolution wind map for a complex terrain with a coupled MM5/CALMET system. J. Geophys. Res. 2007, 112, D05106. [Google Scholar] [CrossRef]
- Dvorak, M.J.; Archer, C.L.; Jacobson, M.Z. California offshore wind energy potential. Renew. Energy 2010, 35, 1244–1255. [Google Scholar] [CrossRef]
- Larsén, X.G.; Mann, J.; Berg, J.; Göttel, H.; Jacob, D. Wind climate from the regional climate model REMO. Wind Energy 2010, 13, 279–296. [Google Scholar] [CrossRef]
- Frank, H.P.; Rathmann, O.; Mortensen, N.G.; Landberg, L. The Numerical Wind Atlas—The KAMM/WasP Method; Report Risø-R-1252(EN); Risø National Laboratory: Roskilde, Denmark, 2001; Available online: https://orbit.dtu.dk/en/publications/the-numerical-wind-atlas-the-kammwasp-method-2 (accessed on 27 November 2022).
- Nygaard, I.; Rasmussen, K.; Badger, J.; Nielsen, T.T.; Hansen, L.B.; Stisen, S.; Larsen, S.; Mariko, A.; Togola, I. Using modelling, satellite images and existing global datasets for rapid preliminary assessments of renewable energy resources: The Case of Mali. Renew. Sustain. Energy Rev. 2010, 14, 2359–2371. [Google Scholar] [CrossRef]
- Mortensen, N.G.; Hansen, J.C.; Badger, J.; Jørgensen, B.H.; Hasager, C.B.; Paulsen, U.S.; Hansen, O.F.; Enevoldsen, K.; Youssef, L.G.; Said, U.S.; et al. Wind Atlas for Egypt: Measurements, micro- and mesoscale modelling. In Proceedings of the 2006 European Wind Energy Conference and Exhibition, Athens, Greece, 27 February–2 March 2006; EWEA: Brussels, Belgium, 2006. [Google Scholar]
- Charabi, Y.; Al-Yahyai, S.; Gastli, A. Evaluation of NWP performance for wind energy resource assessment in Oman. Renew. Sustain. Energy Rev. 2011, 15, 1545–1555. [Google Scholar] [CrossRef]
- Kotroni, V.; Lagouvardos, K.; Lykoudis, S. High-resolution model-based wind atlas for Greece. Renew. Sustain. Energy Rev. 2014, 30, 479–489. [Google Scholar] [CrossRef]
- Yu, W.; Benoit, R.; Girard, C.; Glazer, A.; Lemarquis, D.; Salmon, J.R.; Pinard, J.-P. Wind Energy Simulation Toolkit (WEST): A wind mapping system for use by the wind-energy industry. Wind Eng. 2006, 30, 15–33. [Google Scholar] [CrossRef]
- Schwartz, M.; Elliott, D. Validation of Updated State Wind Resource Maps for the United States; NREL/CP-500-36200; National Renewable Energy Lab: Golden, CO, USA, 2004. Available online: http://www.nrel.gov/docs/fy04osti/36200.pdf (accessed on 20 November 2022).
- Alonso, Y.; Martinez, Y.; Roque, A.; Yu, W.; Borrajero, I. A post-processing module based on Cressman’s analysis to improve the Wind Energy Simulation Toolkit mapping system. Wind Eng. 2019, 43, 277–298. [Google Scholar] [CrossRef]
- Badger, J.; Frank, H.; Hahmann, A.N.; Giebel, G. Wind-climate estimation based on mesocale and microscale modeling: Statistical-dynamical downscaling for wind energy applications. J. Appl. Meteorol. Climatol. 2014, 53, 1901–1919. [Google Scholar] [CrossRef]
- Prieto-Herráez, D.; Frías-Paredes, L.; Cascón, J.M.; Lagüela-López, S.; Gastón-Romeo, M.; Asensio-Sevilla, M.I.; Martín-Nieto, I.; Fernandes-Correia, P.M.; Laiz-Alonso, P.; Carrasco-Díaz, O.F.; et al. Local wind speed forecasting based on WRF-HDWind coupling. Atmos. Res. 2021, 248, 105219. [Google Scholar] [CrossRef]
- Badger, J.; Bauwens, I.; Casso, P.; Davis, N.; Hahmann, A.; Hansen, S.B.K.; Hansen, B.O.; Heathfield, D.; Knight, O.J.; Lacave, O.; et al. The Global Wind Atlas: Introduction (Version 3.0). Available online: https://globalwindatlas.info/en/about/introduction (accessed on 5 May 2024).
- Le Roy, B.; Lemonsu, A.; Schoetter, R. A statistical-dynamical downscaling methodology for the urban heat island applied to the EURO-CORDEX ensemble. Clim. Dyn. 2021, 56, 2487–2508. [Google Scholar] [CrossRef]
- Schoetter, R.; Hidalgo, J.; Jougla, R.; Masson, V.; Rega, M.; Pergaud, J. A statistical-dynamical downscaling for the urban heat island and building energy consumption—Analysis of its uncertainties. J. Appl. Meteorol. Climatol. 2020, 59, 859–993. [Google Scholar] [CrossRef]
- Schubert, D.; van der Linden, R.; Reyers, M.; Fink, A.H.; Massmeyer, K.; Pinto, J.G. Statistical-dynamical downscaling of precipitation for Vietnam: Methodology and evaluation for the recent climate. Int. J. Climatol. 2017, 37, 4211–4228. [Google Scholar] [CrossRef]
- Chávez-Arroyo, R.; Lozano-Galiana, S.; Sanz-Rodrigo, J.; Probst, O. On the application of principal component analysis for accurate statistical-dynamical downscaling of wind fields. Energy Procedia 2013, 40, 67–76. [Google Scholar] [CrossRef][Green Version]
- Martinez, Y.; Yu, W.; Lin, H. A new statistical-dynamical downscaling procedure based on EOF analysis for regional time series generation. J. Appl. Meteorol. Climatol. 2013, 52, 935–952. [Google Scholar] [CrossRef]
- Barry, R.G.; Chorley, R.J. Atmosphere, Weather and Climate, 9th ed.; Routledge: London, UK, 2010. [Google Scholar]
- Danzer, J.; Pieler, M.; Kirchengast, G. Closing the gap in the tropics: The added value of radio-occultation data for wind field monitoring across the Equator. Atmos. Meas. Tech. 2024, 17, 4979–4995. [Google Scholar] [CrossRef]
- Chadee, X.T.; Clarke, R.M. Daily near-surface large-scale atmospheric circulation patterns over the wider Caribbean. Clim. Dyn. 2015, 44, 2927–2946. [Google Scholar] [CrossRef]
- Hadjipetrou, S.; Kyriakidis, P. High-resolution wind speed estimates for the Eastern Mediterranean Basin: A statistical comparison against coastal meteorological observations. Wind 2024, 4, 311–341. [Google Scholar] [CrossRef]
- Kozyrakis, G.V.; Condaxakis, C.; Parasyris, A.; Kampanis, N.A. Wind resource assessment over the Hellenic Seas using dynamical downscaling techniques and meteorological station observations. Energies 2023, 16, 5965. [Google Scholar] [CrossRef]
- Xu, D.; Xue, F.; Wu, Y.; Li, Y.; Liu, W.; Xu, C.; Sun, J. Analysis of wind resource characteristics in the Ulanqab wind power base (wind farm): Mesoscale modeling approach. Energies 2024, 17, 3540. [Google Scholar] [CrossRef]
- Placide, G.; Lollchund, M.R. An evaluation of the reliability of the Weather Research Forecasting (WRF) model in predicting wind data: A case study of Burundi. BMC Environ. Sci. 2024, 1, 2. [Google Scholar] [CrossRef]
- Sperati, S.; Alessandrini, S.; D’Amico, F.; Cheng, W.; Rozoff, C.M.; Bonanno, R.; Lacavalla, M.; Aiello, M.; Airoldi, D.; Amaranto, A.; et al. A new wind atlas to support the expansion of the Italian wind power fleet. Wind Energy 2024, 27, 298–316. [Google Scholar] [CrossRef]
- Chadee, X.T.; Seegobin, N.R.; Clarke, R.M. Optimizing the Weather Research and Forecasting (WRF) model for mapping the near-surface wind resources over the southernmost Caribbean islands of Trinidad and Tobago. Energies 2017, 7, 931. [Google Scholar] [CrossRef]
- Frey-Buness, F.; Heimann, D.; Sausen, R. A statistical-dynamical downscaling procedure for global climate simulations. Theor. Appl. Climatol. 1995, 50, 117–131. [Google Scholar] [CrossRef]
- Commonwealth Chamber of Commerce. Trinidad and Tobago. Available online: https://commonwealthchamber.com/member-countries/trinidad-and-tobago/ (accessed on 31 January 2025).
- UNESCO. Tobago Main Ridge Forest Reserve. Available online: https://whc.unesco.org/en/tentativelists/5646/ (accessed on 31 January 2025).
- Trinidad and Tobago Meteorological Service. Climate. Available online: https://www.metoffice.gov.tt/Climate (accessed on 31 January 2025).
- Doodnath, A. 10 of the Deadliest Storms and Hurricanes to Hit Trinidad and Tobago. Loop T&T News, 24 July 2020. Available online: https://tt.loopnews.com/content/10-deadliest-storms-and-hurricanes-hit-trinidad-and-tobago (accessed on 31 January 2025).
- Extractive Industries Transparency Initiative & PKF Limited. Trinidad and Tobago EITI Report FY 2022. 2024. Available online: https://eiti.org/sites/default/files/2024-10/TTEITI%20Report%202022.pdf (accessed on 31 January 2025).
- Ministry of Energy and Energy Industries. Oil and Gas Industry Overview. Available online: https://www.energy.gov.tt/our-business/oil-and-gas-industry/ (accessed on 31 January 2025).
- World Integrated Trade Solutions. Anhydrous Ammonia Exports by Country in 2021. Available online: https://wits.worldbank.org/trade/comtrade/en/country/ALL/year/2021/tradeflow/Exports/partner/WLD/product/281410 (accessed on 31 January 2025).
- World Integrated Trade Solutions. Methanol (Methyl Alcohol) Exports by Country in 2022. Available online: https://wits.worldbank.org/trade/comtrade/en/country/ALL/year/2022/tradeflow/Exports/partner/WLD/product/290511 (accessed on 31 January 2025).
- The Energy Chamber of Trinidad and Tobago. Can Trinidad & Tobago and Venezuela Help Fill Europe’s Gas shortfall? 2022. Available online: https://energynow.tt/blog/can-trinidad-amp-tobago-and-venezuela-help-fill-europes-gas-shortfall (accessed on 31 January 2025).
- Shaw, T.A.; Arblaster, J.M.; Birner, T.; Butler, A.H.; Domeisen, D.I.V.; Garfinkel, C.I.; Garny, H.; Grise, K.M.; Karpechko, A.Y. Emerging climate change signals in atmospheric circulation. AGU Adv. 2024, 5, e2024AV001297. [Google Scholar] [CrossRef]
- Tveito, O.E. An assessment of circulation type classifications for precipitation distribution in Norway. Phys. Chem. Earth 2010, 35, 395–402. [Google Scholar] [CrossRef]
- Dijkstra, I.; Bloomfield, H.C.; Hunt, K.M.R. Identifying weather patterns responsible for renewable energy droughts over India. Adv. Geosci. 2025, 65, 127–140. [Google Scholar] [CrossRef]
- Couto, A.; Costa, P.; Simões, T. Identification of extreme wind events using a weather type classification. Energies 2021, 14, 3944. [Google Scholar] [CrossRef]
- Vozila, A.B.; Prtenjak, M.T.; Güttler, I. A weather-type classification and its application to near-surface wind climate change projections over the Adriatic Region. Atmosphere 2021, 12, 948. [Google Scholar] [CrossRef]
- Cortesi, N.; Torralba, V.; González-Reviriego, N.; Soret, A.; Dobals-Reyes, F.J. Characterization of European wind speed variability using weather regimes. Clim. Dyn. 2019, 53, 4961–4976. [Google Scholar] [CrossRef]
- Philip, A.; Bartholy, J.; Beck, C.; Erpicum, M.; Esteban, P.; Fettweis, X.; Huth, R.; James, P.; Jourdain, S.; Kreienkamp, F.; et al. Cost733cat—A database of weather and circulation type classifications. Phys. Chem. Earth Parts A/B/C 2010, 35, 360–373. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.-Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; NCAR Technical Note NCAR/TN-475+STR; National Center for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar]
- Chadee, X.T.; Clarke, R.M. Air density climate of two Caribbean tropical islands and relevance to wind power. ISRN Renew. Energy 2013. [Google Scholar] [CrossRef]
- World Meteorological Organization. Guide to Meteorological Instruments and Methods of Observation, 7th ed.; World Meteorological Organization: Geneva, Switzerland, 2008. [Google Scholar]
- Chadee, X.T.; Clarke, R.M. Wind resources and the levelized cost of wind generated electricity in the Caribbean islands of Trinidad and Tobago. Renew. Sustain. Energy Rev. 2018, 81, 2526–2540. [Google Scholar] [CrossRef]
- Jain, P. Wind Energy Engineering. The McGraw-Hill Companies, Inc.: New York, NY, USA, 2011. [Google Scholar]

| Physical Parameterization | Name of the Parameterization Scheme |
|---|---|
| Planetary boundary layer | Yonsei University PBL scheme with topographic drag enabled |
| Surface layer | Monin–Obukhov |
| Longwave radiation | RRTM |
| Shortwave radiation | Dudhia |
| Land surface model | Thermal diffusion |
| Microphysics | WSM 3 |
| Cumulus | Betts–Miller–Janjic (on d01 only; cloud formation is explicitly resolved on nests d02 and d03 (5 km and 1 km resolutions, respectively.) |
| Station Name | Location | Elevation | Closest Grid Point |
|---|---|---|---|
| Piarco, Trinidad | 15 m | ||
| Crown Point, Tobago | 12 m |
| Location | Interannual Variability In | |||
|---|---|---|---|---|
| Wind Speed | Wind Power Density (WPD) | |||
| Simulated (%) | Measured (%) | Simulated (%) | Measured (%) | |
| Crown Point | (−11.6,13.6) | (−19.3, 25.9) | (−23.9, 40.3) | (−47.7, 63.5) |
| Piarco | (−10.7,18.9) | (−16.3, 14.8) | (−18.8, 44.3) | (−27.4, 22.3) |
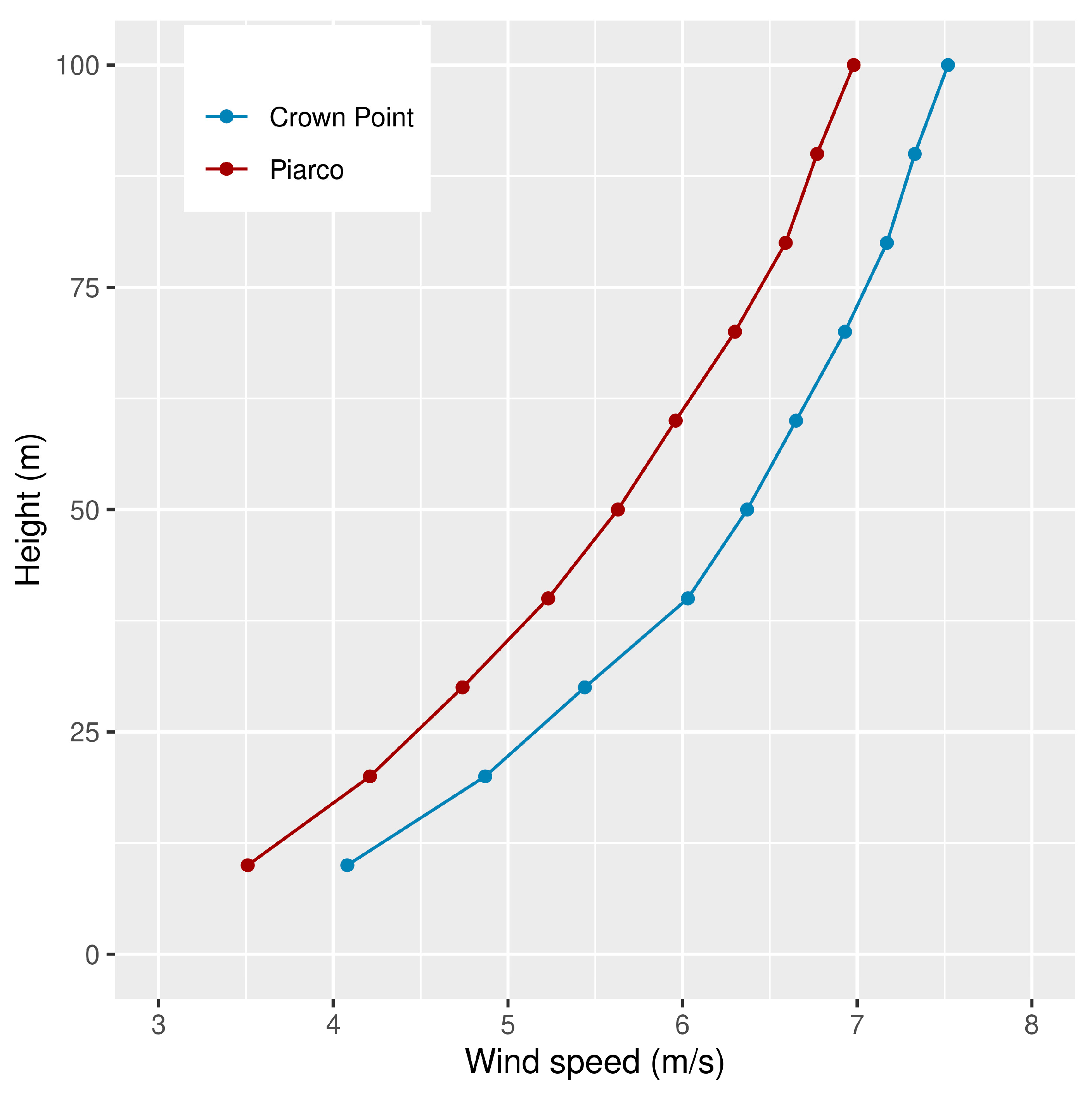
| Wind Speed Shear Exponents | ||
|---|---|---|
| Crown Point | Piarco | |
| 50 m vs. 10 m | 0.277 | 0.293 |
| 100 m vs. 10 m | 0.266 | 0.299 |
| 100 m vs. 50 m | 0.239 | 0.310 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chadee, X.T.; Seegobin, N.R.; Clarke, R.M. A Statistical–Dynamical Downscaling Technique for Wind Resource Mapping: A Regional Atmospheric-Circulation-Type Approach with Numerical Weather Prediction Modeling. Wind 2025, 5, 7. https://doi.org/10.3390/wind5010007
Chadee XT, Seegobin NR, Clarke RM. A Statistical–Dynamical Downscaling Technique for Wind Resource Mapping: A Regional Atmospheric-Circulation-Type Approach with Numerical Weather Prediction Modeling. Wind. 2025; 5(1):7. https://doi.org/10.3390/wind5010007
Chicago/Turabian StyleChadee, Xsitaaz T., Naresh R. Seegobin, and Ricardo M. Clarke. 2025. "A Statistical–Dynamical Downscaling Technique for Wind Resource Mapping: A Regional Atmospheric-Circulation-Type Approach with Numerical Weather Prediction Modeling" Wind 5, no. 1: 7. https://doi.org/10.3390/wind5010007
APA StyleChadee, X. T., Seegobin, N. R., & Clarke, R. M. (2025). A Statistical–Dynamical Downscaling Technique for Wind Resource Mapping: A Regional Atmospheric-Circulation-Type Approach with Numerical Weather Prediction Modeling. Wind, 5(1), 7. https://doi.org/10.3390/wind5010007






