Trends in the Frequency of Water and Heat Stress in Mid-Latitude North America since 1980
Abstract
:1. Background
2. Introduction
- Are episodes of acute HS becoming more or less frequent?
- Are different regions experiencing similar or divergent trends in HS?
- What are the proximate drivers of these trends in HS?
3. Methods
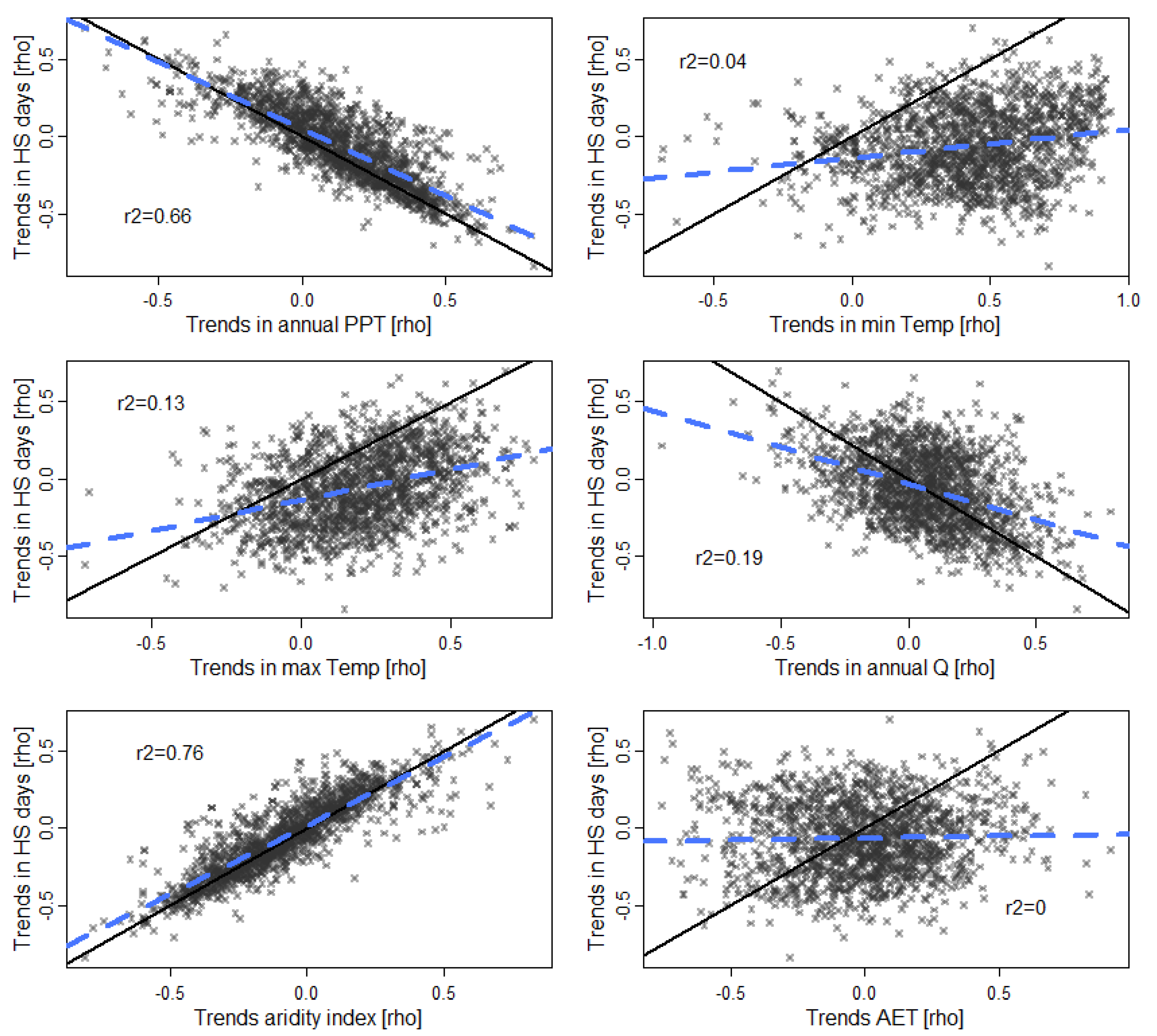
4. Results
5. Discussion
6. Contextualization
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barnabás, B.; Jäger, K.; Fehér, A. The effect of drought and heat stress on reproductive processes in cereals. Plant Cell Environ. 2008, 31, 11–38. [Google Scholar] [CrossRef]
- Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; McDowell, N.; Vennetier, M.; Cobb, N. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 2010, 259, 660–684. [Google Scholar] [CrossRef] [Green Version]
- Craufurd, P.Q.; Peacock, J.M. Effect of heat and drought stress on sorghum (Sorghum bicolor). II. Grain yield. Exp. Agric. 1993, 29, 77–86. [Google Scholar] [CrossRef] [Green Version]
- Ullah, I.; Ma, X.; Yin, J.; Asfaw, T.G.; Azam, K.; Syed, S.; Shahzaman, M. Evaluating the meteorological drought characteristics over Pakistan using in situ observations and reanalysis products. Int. J. Climatol. 2021, 41, 4437–4459. [Google Scholar] [CrossRef]
- Ullah, I.; Saleem, F.; Iyakaremye, V.; Yin, J.; Ma, X.; Syed, S.; Omer, A. Projected changes in socioeconomic exposure to heatwaves in South Asia under changing climate. Earths Future 2022, 10, e2021EF002240. [Google Scholar] [CrossRef]
- Dracup, J.A.; Lee, K.S.; Paulson, E.G., Jr. On the definition of droughts. Water Resour. Res. 1980, 16, 297–302. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Glantz, M.H. Understanding the drought phenomenon: The role of definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef] [Green Version]
- Keyantash, J.; Dracup, J.A. The quantification of drought: An evaluation of drought indices. Bull. Am. Meteorol. Soc. 2002, 83, 1167–1180. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration and moisture stress across the continental United States based on thermal remote sensing: 2. Surface moisture climatology. J. Geophys. Res. Atmos. 2007, 112, D11112. [Google Scholar] [CrossRef]
- Tashie, A.; Scaife, C.I.; Band, L.E. Transpiration and subsurface controls of streamflow recession characteristics. Hydrol. Processes 2019, 33, 2561–2575. [Google Scholar] [CrossRef]
- Tashie, A.M.; Mirus, B.B.; Pavelsky, T.M. Identifying long-term empirical relationships between storm characteristics and episodic groundwater recharge. Water Resour. Res. 2016, 52, 21–35. [Google Scholar] [CrossRef] [Green Version]
- Tashie, A.; Pavelsky, T.; Band, L.; Topp, S. Watershed-Scale Effective Hydraulic Properties of the Continental United States. J. Adv. Model. Earth Syst. 2021, 13, e2020MS002440. [Google Scholar] [CrossRef]
- Tashie, A.; Pavelsky, T.; Emanuel, R.E. Spatial and temporal patterns in baseflow recession in the continental United States. Water Resour. Res. 2020, 56, e2019WR026425. [Google Scholar] [CrossRef]
- Budyko, M.I. Climate and Life; Academic Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Choudhury, B.J. Synergism of multispectral satellite observations for estimating regional land surface evaporation. Remote Sens. Environ. 1994, 49, 264–274. [Google Scholar] [CrossRef]
- Mianabadi, A.; Coenders-Gerrits, M.; Shirazi, P.; Ghahraman, B.; Alizadeh, A. A global Budyko model to partition evaporation into interception and transpiration. Hydrol. Earth Syst. Sci. 2019, 23, 4983–5000. [Google Scholar] [CrossRef] [Green Version]
- Christensen, L.; Adams, H.R.; Tai, X.; Barnard, H.R.; Brooks, P.D. Increasing plant water stress and decreasing summer streamflow in response to a warmer and wetter climate in seasonally snow-covered forests. Ecohydrology 2021, 14, e2256. [Google Scholar] [CrossRef]
- Lhomme, J.P.; Moussa, R. Matching the Budyko functions with the complementary evaporation relationship: Consequences for the drying power of the air and the Priestley–Taylor coefficient. Hydrol. Earth Syst. Sci. 2016, 20, 4857–4865. [Google Scholar] [CrossRef]
- De Cicco, L.A.; Hirsch, R.M.; Lorenz, D.; Watkins, W.D. dataRetrieval: R Packages for Discovering and Retrieving Water Data Available from Federal Hydrologic Web Services; US Geological Survey: Reston, VA, USA, 2021. [Google Scholar] [CrossRef]
- Albers, S.J. tidyhydat: Extract and tidy Canadian hydrometric data. J. Open Source Softw. 2017, 2, 511. [Google Scholar] [CrossRef] [Green Version]
- Falcone, J.A. GAGES-II: Geospatial Attributes of Gages for Evaluating Streamflow; US Geological Survey: Reston, VA, USA, 2011. [Google Scholar]
- Brimley, B.; Cantin, J.F.; Harvey, D.; Kowalchuk, M.; Marsh, P.; Ouarda, T.B.M.J.; Phinney, B.; Pilon, P.; Renouf, M.; Tassone, B.; et al. Establishment of the Reference Hydrometric Basin Network (RHBN); Environment Canada Research Report: Kelowna, ON, Canada, 1999; 41p. [Google Scholar]
- Lehner, B.; Verdin, K.; Jarvis, A. New global hydrography derived from spaceborne elevation data. Eos Trans. AGU 2008, 89, 93–94. [Google Scholar] [CrossRef]
- Thornton, M.M.; Shrestha, R.; Wei, Y.; Thornton, P.E.; Kao, S.; Wilson, B.E. Daymet: Daily Surface Weather Data on a 1-km Grid for North America, Version 3; ORNL DAAC: Oak Ridge, TN, USA, 2020. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weath. Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Fuka, D.R.; Walter, M.T.; Archibald, J.A.; Steenhuis, T.S.; Easton, Z.M.; Fuka, M.D.; KeepSource, T.R.U.E. Package ‘EcoHydRology’. 2014. Available online: https://cran.r-project.org/web/packages/EcoHydRology/index.html (accessed on 24 February 2022).
- Arora, V.K. The use of the aridity indices to acces climate change effect on annual runoff. J. Hydrol. 2002, 265, 164–177. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis. Prat I–III. Nederl. Akad. Wetensch. Proc. 1950, 53, 386–392. [Google Scholar]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1948. [Google Scholar]
- Clow, D.W. Changes in the timing of snowmelt and streamflow in Colorado: A response to recent warming. J. Clim. 2010, 23, 2293–2306. [Google Scholar] [CrossRef]
- Nitze, I.; Grosse, G.; Jones, B.M.; Romanovsky, V.E.; Boike, J. Remote sensing quantifies widespread abundance of permafrost region disturbances across the Arctic and Subarctic. Nat. Commun. 2018, 9, 5423. [Google Scholar] [CrossRef]
- Powell, J.W. The irrigable lands of the arid region. Cent. Mag. 1890, 39, 766–776. [Google Scholar]
- Seager, R.; Lis, N.; Feldman, J.; Ting, M.; Williams, A.P.; Nakamura, J.; Henderson, N. Whither the 100th meridian? The once and future physical and human geography of America’s arid–humid divide. Part I: The story so far. Earth Interact. 2018, 22, 1–22. [Google Scholar] [CrossRef] [Green Version]
- McVicar, T.R.; Roderick, M.L.; Donohue, R.J.; Li, L.T.; Van Niel, T.G.; Thomas, A.; Dinpashoh, Y. Global review and synthesis of trends in observed terrestrial near-surface wind speeds: Implications for evaporation. J. Hydrol. 2012, 416, 182–205. [Google Scholar] [CrossRef]
- Tian, L.; Jin, J.; Wu, P.; Niu, G.Y. Quantifying the impact of climate change and human activities on streamflow in a semi-arid watershed with the budyko equation incorporating dynamic vegetation information. Water 2018, 10, 1781. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Pan, M.; Cong, Z.; Zhang, L.; Wood, E. Vegetation control on water and energy balance within the Budyko framework. Water Resour. Res. 2013, 49, 969–976. [Google Scholar] [CrossRef]
- Wang, W.; Ertsen, M.W.; Svoboda, M.D.; Hafeez, M. Propagation of drought: From meteorological drought to agricultural and hydrological drought. Adv. Meteorol. 2016, 2016, 6547209. [Google Scholar] [CrossRef]
- Pandžić, K.; Likso, T. Homogeneity of average annual air temperature time series for Croatia. Int. J. Climatol. 2010, 30, 1215–1225. [Google Scholar] [CrossRef]
- Pandžić, K.; Kobold, M.; Oskoruš, D.; Biondić, B.; Biondić, R.; Bonacci, O.; Curić, O. Standard normal homogeneity test as a tool to detect change points in climate-related river discharge variation: Case study of the Kupa River Basin. Hydrol. Sci. J. 2020, 65, 227–241. [Google Scholar] [CrossRef]
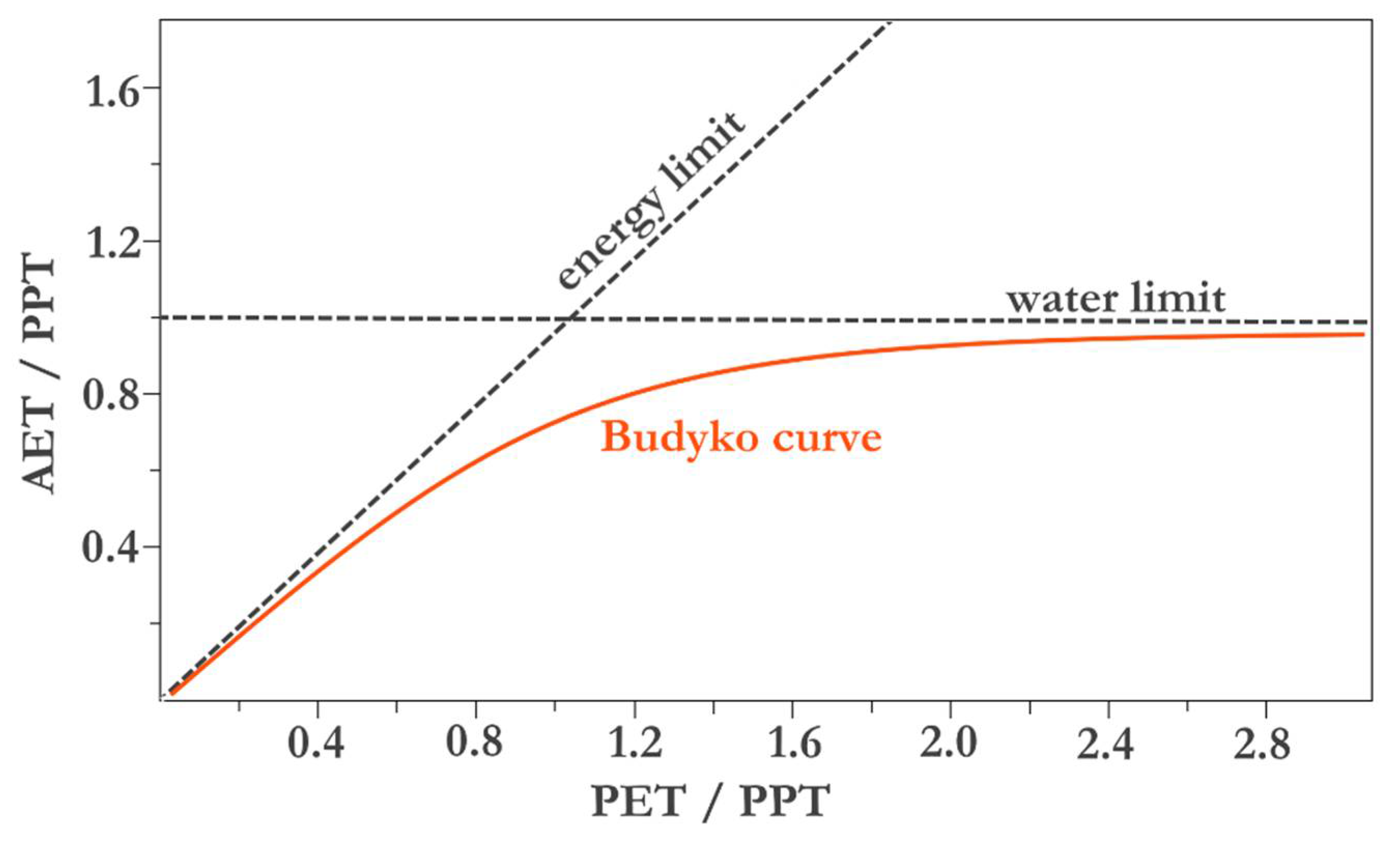
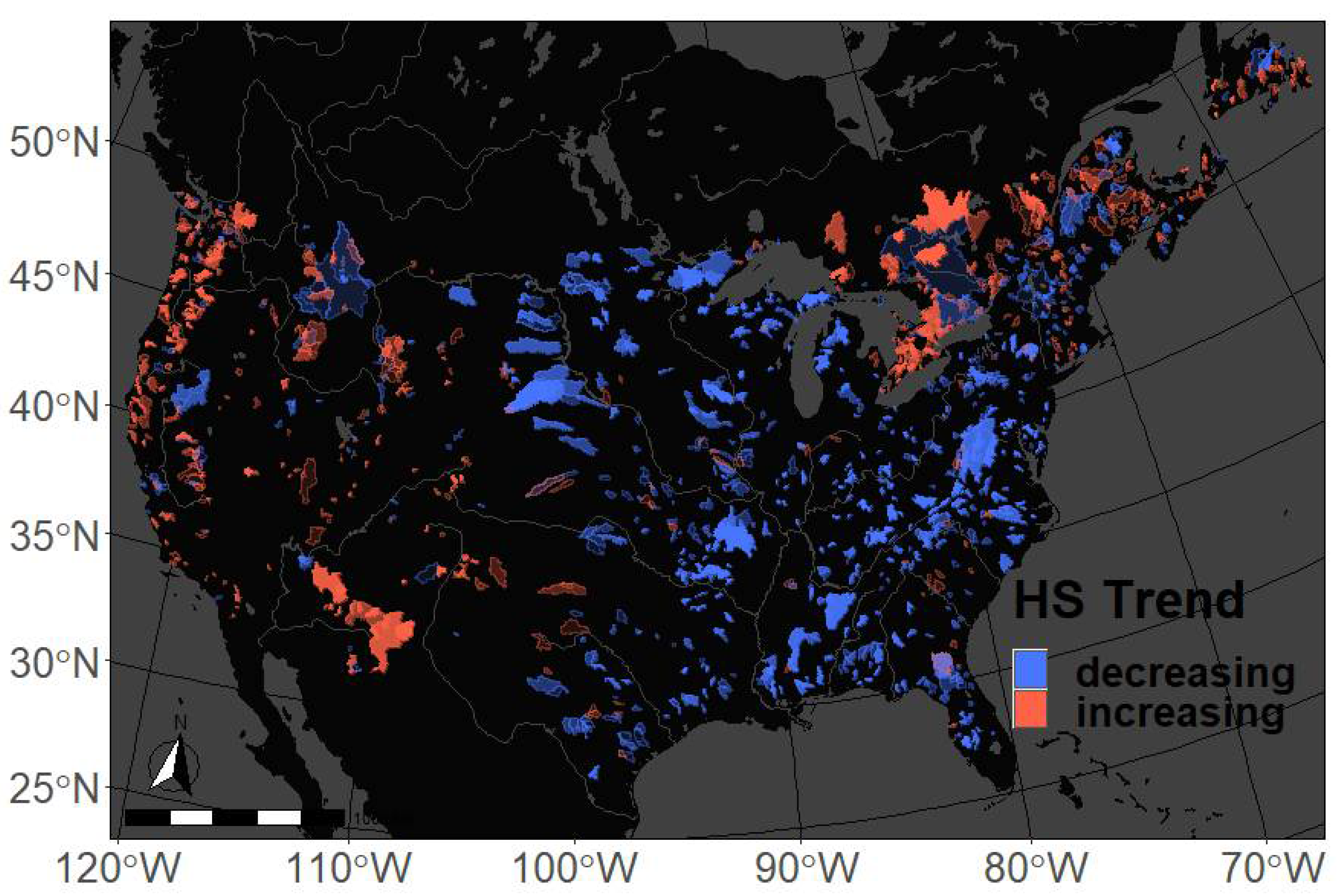
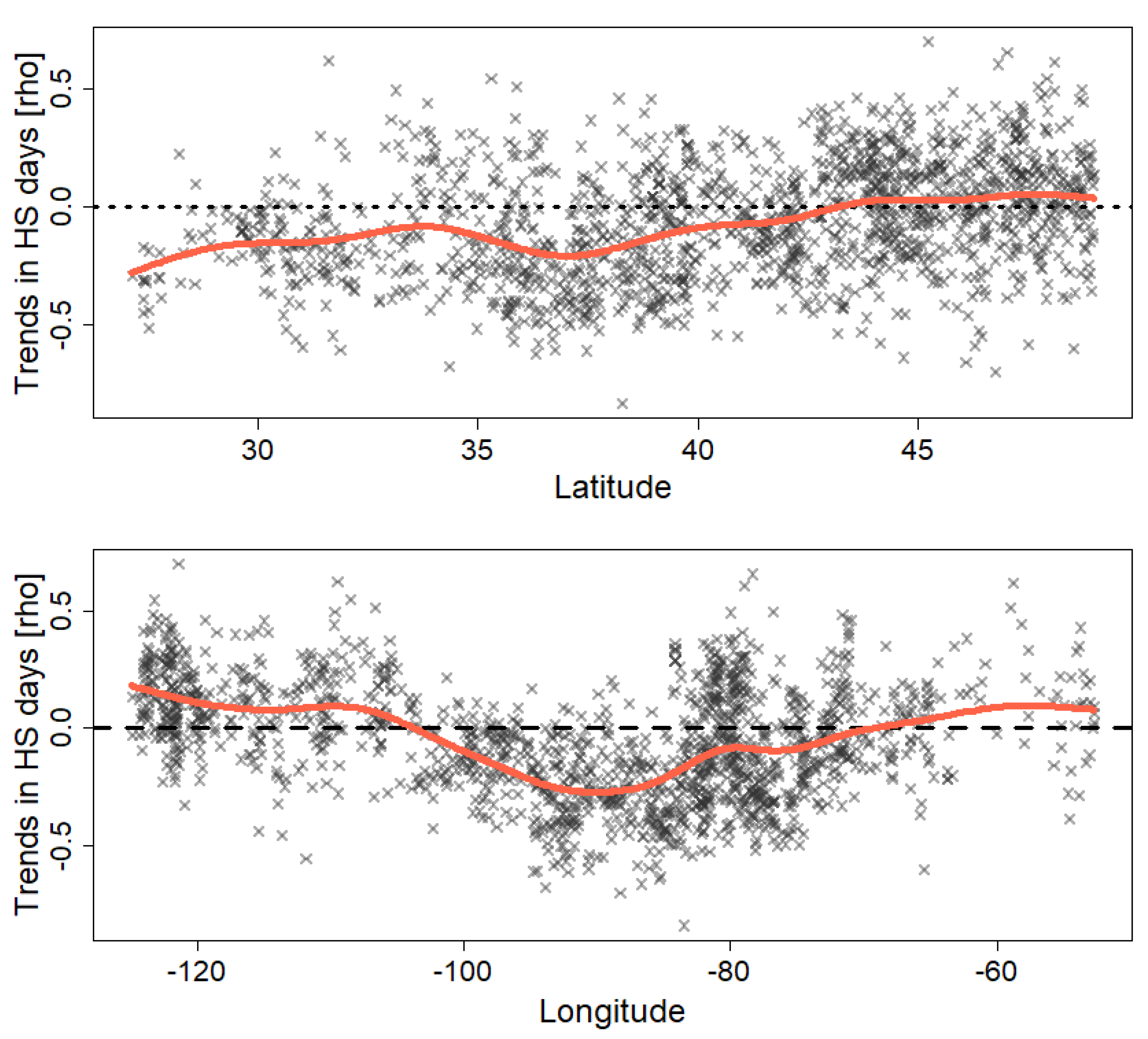
| 1st Quartile | Median | Mean | 3rd Quartile | |
|---|---|---|---|---|
| Decreasing HS | −1.1 | −2.9 | −3.6 | −5.0 |
| Significantly Decreasing HS | −3.8 | −5.0 | −6.2 | −6.7 |
| Increasing HS | 0.7 | 1.6 | 2.6 | 3.1 |
| Significantly Increasing HS | 2.1 | 2.9 | 4.2 | 4.6 |
| Min | 1st Quartile | Median | Mean | 3rd Quartile | Max | |
|---|---|---|---|---|---|---|
| Heat Stress (HS) slope | −3.63 | −0.34 | −0.07 | −0.11 | 0.11 | 12.00 |
| Heat Stress (HS) rho | −0.84 | −0.24 | −0.06 | −0.06 | 0.12 | 0.70 |
| Heat Stress (HS) pval | 0.00 | 0.10 | 0.32 | 0.38 | 0.63 | 1.00 |
| PPT slope | −44.26 | −0.25 | 2.37 | 2.82 | 5.66 | 54.80 |
| PPT rho | −0.75 | −0.01 | 0.13 | 0.13 | 0.29 | 0.81 |
| PPT pval | 0.00 | 0.08 | 0.33 | 0.39 | 0.66 | 1.00 |
| Min Temp slope | −0.12 | 0.02 | 0.04 | 0.04 | 0.05 | 0.26 |
| Min Temp rho | −0.69 | 0.27 | 0.45 | 0.43 | 0.62 | 0.94 |
| Min Temp pval | 0.00 | 0.00 | 0.01 | 0.14 | 0.14 | 1.00 |
| Max Temp slope | −0.18 | 0.00 | 0.02 | 0.02 | 0.03 | 0.33 |
| Max Temp rho | −0.72 | 0.04 | 0.19 | 0.19 | 0.34 | 0.78 |
| Max Temp pval | 0.00 | 0.05 | 0.25 | 0.33 | 0.58 | 1.00 |
| Streamflow (Q) slope | −11.37 | −0.69 | 0.72 | 2.42 | 3.02 | 48.17 |
| Streamflow (Q) rho | −0.96 | −0.07 | 0.07 | 0.07 | 0.21 | 0.79 |
| Streamflow (Q) pval | 0.00 | 0.16 | 0.42 | 0.44 | 0.70 | 1.00 |
| Aridity Index slope | −0.20 | 0.00 | 0.00 | 0.00 | 0.00 | 0.30 |
| Aridity Index rho | −0.81 | −0.25 | −0.09 | −0.09 | 0.07 | 0.83 |
| Aridity Index pval | 0.00 | 0.10 | 0.35 | 0.40 | 0.66 | 1.00 |
| AET slope | −13.17 | −0.89 | −0.13 | 0.11 | 1.12 | 27.11 |
| AET rho | −0.75 | −0.18 | 0.00 | −0.01 | 0.16 | 0.91 |
| AET pval | 0.00 | 0.10 | 0.34 | 0.40 | 0.68 | 1.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tashie, A. Trends in the Frequency of Water and Heat Stress in Mid-Latitude North America since 1980. Meteorology 2022, 1, 142-153. https://doi.org/10.3390/meteorology1020009
Tashie A. Trends in the Frequency of Water and Heat Stress in Mid-Latitude North America since 1980. Meteorology. 2022; 1(2):142-153. https://doi.org/10.3390/meteorology1020009
Chicago/Turabian StyleTashie, Arik. 2022. "Trends in the Frequency of Water and Heat Stress in Mid-Latitude North America since 1980" Meteorology 1, no. 2: 142-153. https://doi.org/10.3390/meteorology1020009
APA StyleTashie, A. (2022). Trends in the Frequency of Water and Heat Stress in Mid-Latitude North America since 1980. Meteorology, 1(2), 142-153. https://doi.org/10.3390/meteorology1020009






