Multiple-Instance Regression for Metal Powder Hall Flow Rate Prediction Using Augmented Particle Size and Shape Data
Abstract
:1. Introduction
1.1. Data-Driven Insights
1.2. Influence of Powder Flowability in CSAM
1.3. Present Contributions
- Developed the first (to our knowledge) known data augmentation technique that derives multiple-instance data utilizing an aggregated label for instances in mixed samples for powder-based metal AM applications;
- Introduced the first usage (to our knowledge) of MIR for processing powder-based data in metal AM; and
- Developed a comparative study of various MIR frameworks to determine the most promising framework for addressing said problem.
2. Problem Setting
2.1. Powder Flowability through the Lens of HFRs
2.2. Data Analysis for Predicting HFRs
3. Proposed Frameworks and Approaches
3.1. Processing Using Multiple-Instance Learning
3.1.1. Aggregated MIR
3.1.2. Instance MIR
3.1.3. Pruning MIR
3.2. Target Variable Engineering
3.3. Class Balancing
3.4. Proposed Strategy for Powder and Particle Data Augmentation
3.5. Hall Flow Prediction Using Classification
4. Results and Evaluation
4.1. Dataset
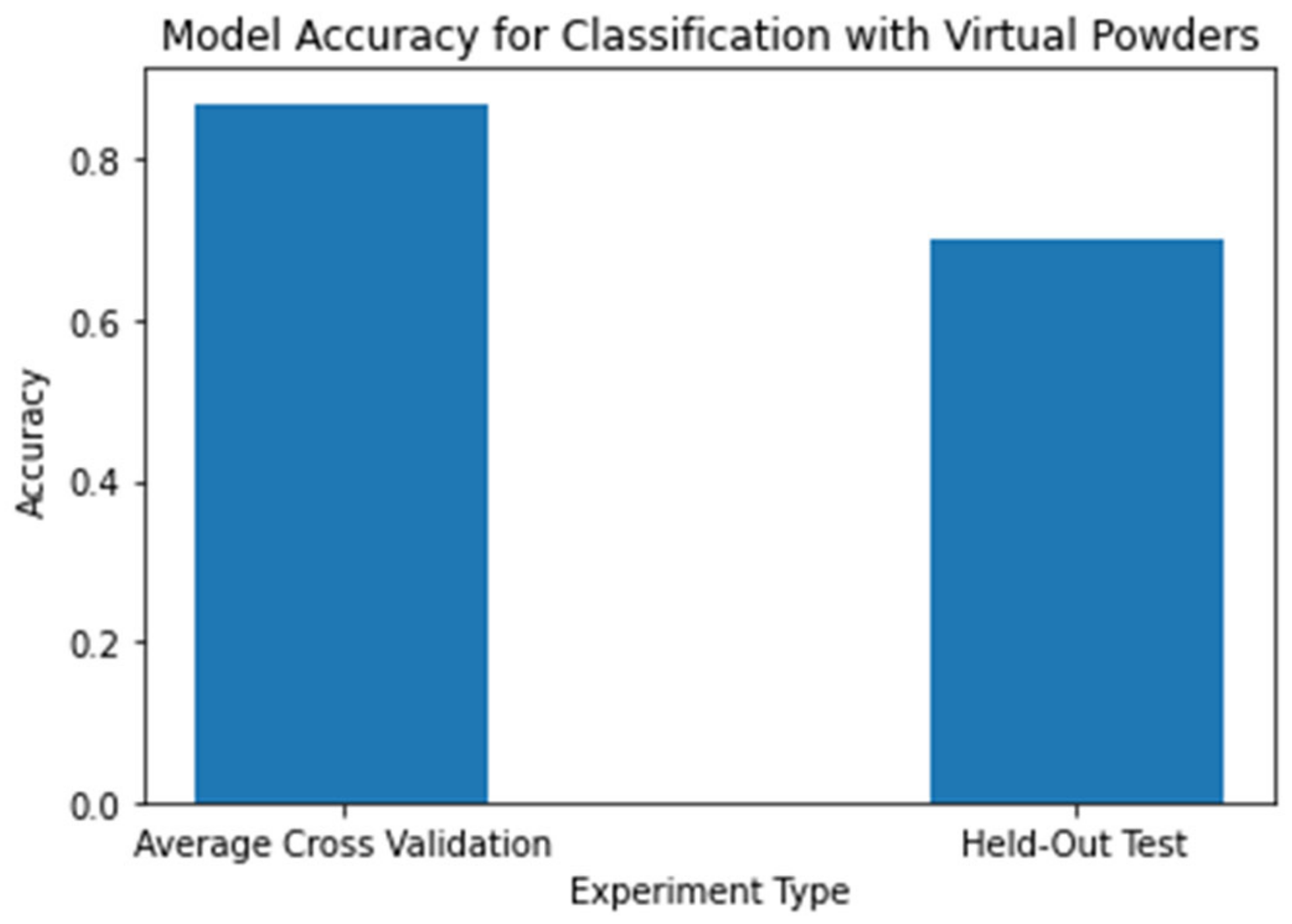
4.2. MIR Classification Results
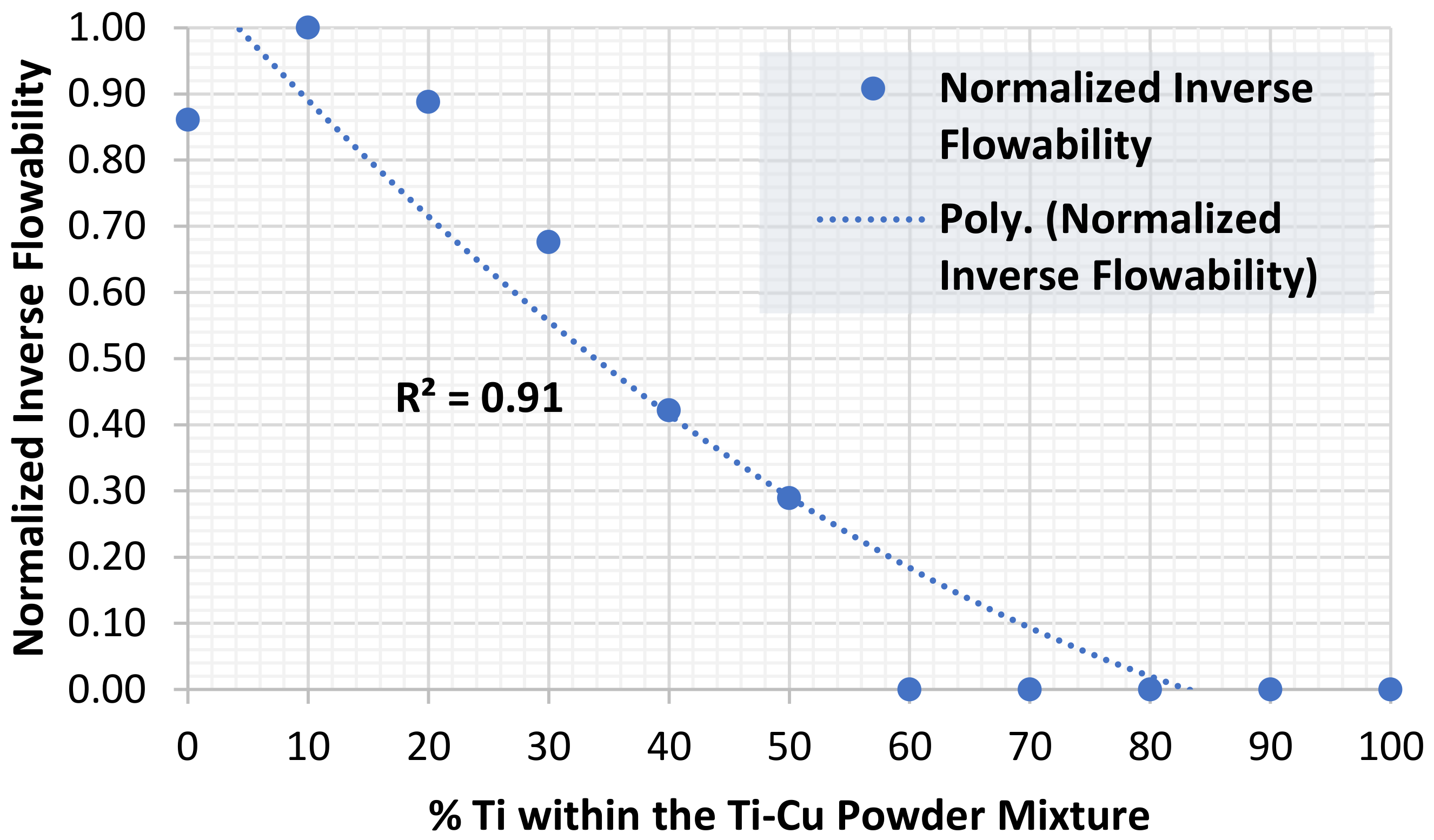
4.3. Data Augmentation Evaluation
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zheng, Z.; Xu, T.; Legut, D.; Zhang, R. High-throughput informed machine learning models for ultrastrong B-N solids. Comput. Mater. Sci. 2022, 215, 111789. [Google Scholar] [CrossRef]
- Kouraytem, N.; Li, X.; Tan, W.; Kappes, B.; Spear, A.D. Modeling process–structure–property relationships in metal additive manufacturing: A review on physics-driven versus data-driven approaches. J. Physics Mater. 2021, 4, 032002. [Google Scholar] [CrossRef]
- Ma, B.; Wei, X.; Liu, C.; Ban, X.; Huang, H.; Wang, H.; Xue, W.; Wu, S.; Gao, M.; Shen, Q.; et al. Data augmentation in microscopic images for material data mining. NPJ Comput. Mater. 2020, 6, 125. [Google Scholar] [CrossRef]
- Zhang, Y.; Ling, C. A strategy to apply machine learning to small datasets in materials science. NPJ Comput. Mater. 2018, 4, 25. [Google Scholar] [CrossRef] [Green Version]
- Valent, R.C.; Ostapenko, A.; Sousa, B.C.; Grubbs, J.; Massar, C.J.; Cote, D.B.; Neamtu, R. Classifying Powder Flowability for Cold Spray Additive Manufacturing Using Machine Learning. In Proceedings of the 2nd International Workshop on Big Data Tools, Methods, and Use Cases for Innovative Scientific Discvery, IEEE BigData Conference, Atlanta, GA, USA, 10–13 December 2020; pp. 2919–2928. [Google Scholar]
- Kroeger, J.; Poirié, T.; Moghimian, P.; Marion, F.; Larouche, F. Flow rate ranges for spherical metallic powders for additive manufacturing. Prog. Addit. Manuf. 2021, 7, 411–418. [Google Scholar] [CrossRef]
- Standard Test Methods for Flow Rate of Metal Powders Using the Hall Flowmeter Funnel. Available online: https://www.astm.org/b0213-20.html (accessed on 21 February 2023).
- Kudo, Y.; Yasuda, M.; Matsusaka, S. Effect of particle size distribution on flowability of granulated lactose. Adv. Powder Technol. 2019, 31, 121–127. [Google Scholar] [CrossRef]
- Kiani, P.; Bertoli, U.S.; Dupuy, A.D.; Ma, K.; Schoenung, J.M. A Statistical Analysis of Powder Flowability in Metal Additive Manufacturing. Adv. Eng. Mater. 2020, 22, 2000022. [Google Scholar] [CrossRef]
- Zhang, J.; Habibnejad-Korayem, M.; Liu, Z.; Lyu, T.; Sun, Q.; Zou, Y. A Computer Vision Approach to Evaluate Powder Flowability for Metal Additive Manufacturing. Integr. Mater. Manuf. Innov. 2021, 10, 429–443. [Google Scholar] [CrossRef]
- Vieira, C.; Schuliger, A. Cleaning on Demand with a Recommender System (CODeRS); Worcester Poly-Technic Institute: Worcester, MA, USA, 2022; Available online: https://digital.wpi.edu/concern/student_works/9306t271v?locale=en (accessed on 21 February 2023).
- Dietterich, T.G.; Lathrop, R.H.; Lozano-Pérez, T. Solving the multiple instance problem with axis-parallel rectangles. Artif. Intell. 1997, 89, 31–71. [Google Scholar] [CrossRef] [Green Version]
- Maron, O.; Lozano-Pérez, T. A Framework for Multiple-Instance Learning. Adv. Neural Inf. Process Syst. 1997, 10, 570–576. [Google Scholar]
- Chen, Y.; Bi, J.; Wang, J. MILES: Multiple-Instance Learning via Embedded Instance Selection. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1931–1947. [Google Scholar] [CrossRef]
- Yang, C.; Dong, M.; Fotouhi, F. Region based image annotation through multiple-instance learning. In Proceedings of the 13th ACM International Conference on Multimedia, Hilton, Singapore, 6–11 November 2005; pp. 435–438. [Google Scholar] [CrossRef]
- Ray, S.; Page, D. Multiple Instance Regression. In Proceedings of the 18th International Conference on Machine Learning, Williamstown, MA, USA, 28 June–1 July 2001. [Google Scholar]
- Zhang, Y.; Charoenphakdee, N.; Wu, Z.; Sugiyama, M. Learning from aggregate observations. Adv. Neural Inf. Process. Syst. 2020, 33, 7993–8005. [Google Scholar]
- Trabelsi, M.; Frigui, H. Robust fuzzy clustering for multiple instance regression. Pattern Recognit. 2019, 90, 424–435. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Lan, L.; Vucetic, S. Mixture Model for Multiple Instance Regression and Applications in Remote Sensing. IEEE Trans. Geosci. Remote. Sens. 2011, 50, 2226–2237. [Google Scholar] [CrossRef]
- Wagstaff, K.L.; Lane, T.; Roper, A. Multiple-Instance Regression with Structured Data. In Proceedings of the IEEE International Conference on Data Mining Workshops, ICDM Workshops 2008, Pisa, Italy, 15–19 December 2008; pp. 291–300. [Google Scholar] [CrossRef]
- Wang, Z.; Radosavljevic, V.; Han, B.; Obradovic, Z.; Vucetic, S. Aerosol Optical Depth Prediction from Satellite Observations by Multiple Instance Regression. In Proceedings of the Society for Industrial and Applied Mathematics–8th SIAM International Conference on Data Mining 2008, Proceedings in Applied Mathematics, Atlanta, GA, USA, 24–26 April 2008; Volume 1, pp. 165–176. [Google Scholar] [CrossRef] [Green Version]
- Lin, W.-C.; Tsai, C.-F.; Hu, Y.-H.; Jhang, J.-S. Clustering-based undersampling in class-imbalanced data. Inf. Sci. 2017, 409–410, 17–26. [Google Scholar] [CrossRef]
- Fernández, A.; García, S.; Galar, M.; Prati, R.C.; Krawczyk, B.; Herrera, F. Learning from Imbalanced Data Sets. IEEE Trans. Knowl. Data Eng. 2018, 21, 1263–1284. [Google Scholar] [CrossRef]
- Horton, M.K.; Woods-Robinson, R. Addressing the critical need for open experimental databases in materials science. Patterns 2021, 2, 100411. [Google Scholar] [CrossRef]
- Ohno, H. Auto-encoder-based generative models for data augmentation on regression problems. Soft Comput. 2019, 24, 7999–8009. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, W.; Shi, F.; Qi, L.; Xie, X.; Wei, Y.; Ding, Z.; Gao, Y.; Wu, S.; Liu, J.; et al. A novel multiple instance learning framework for COVID-19 severity assessment via data augmentation and self-supervised learning. Med. Image Anal. 2021, 69, 101978. [Google Scholar] [CrossRef]
- Shen, L.; Qian, Q. A virtual sample generation algorithm supporting machine learning with a small-sample dataset: A case study for rubber materials. Comput. Mater. Sci. 2022, 211, 111475. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. Available online: http://jmlr.org/papers/v12/pedregosa11a.html (accessed on 20 February 2023).
- Anguita, D.; Ghelardoni, L.; Ghio, A.; Oneto, L.; Ridella, S. The ‘K’ in K-fold Cross Validation. Available online: http://www.i6doc.com/en/livre/?GCOI=28001100967420 (accessed on 20 February 2023).
- Price, S.E.; Gleason, M.A.; Sousa, B.C.; Cote, D.L.; Neamtu, R. Automated and Refined Application of Convolutional Neural Network Modeling to Metallic Powder Particle Satellite Detection. Integr. Mater. Manuf. Innov. 2021, 10, 661–676. [Google Scholar] [CrossRef]
- Price, S.; Neamtu, R. Identifying, Evaluating, and Addressing Nondeterminism in Mask R-CNNs. In Lecture Notes in Computer Science, Proceedings of the Pattern Recognition and Artificial Intelligence: Third International Conference, ICPRAI 2022, Paris, France, 1–3 June 2022; Springer: Berlin/Heidelberg, Germany, 2022; Volume 13363 LNCS, pp. 3–14. [Google Scholar] [CrossRef]
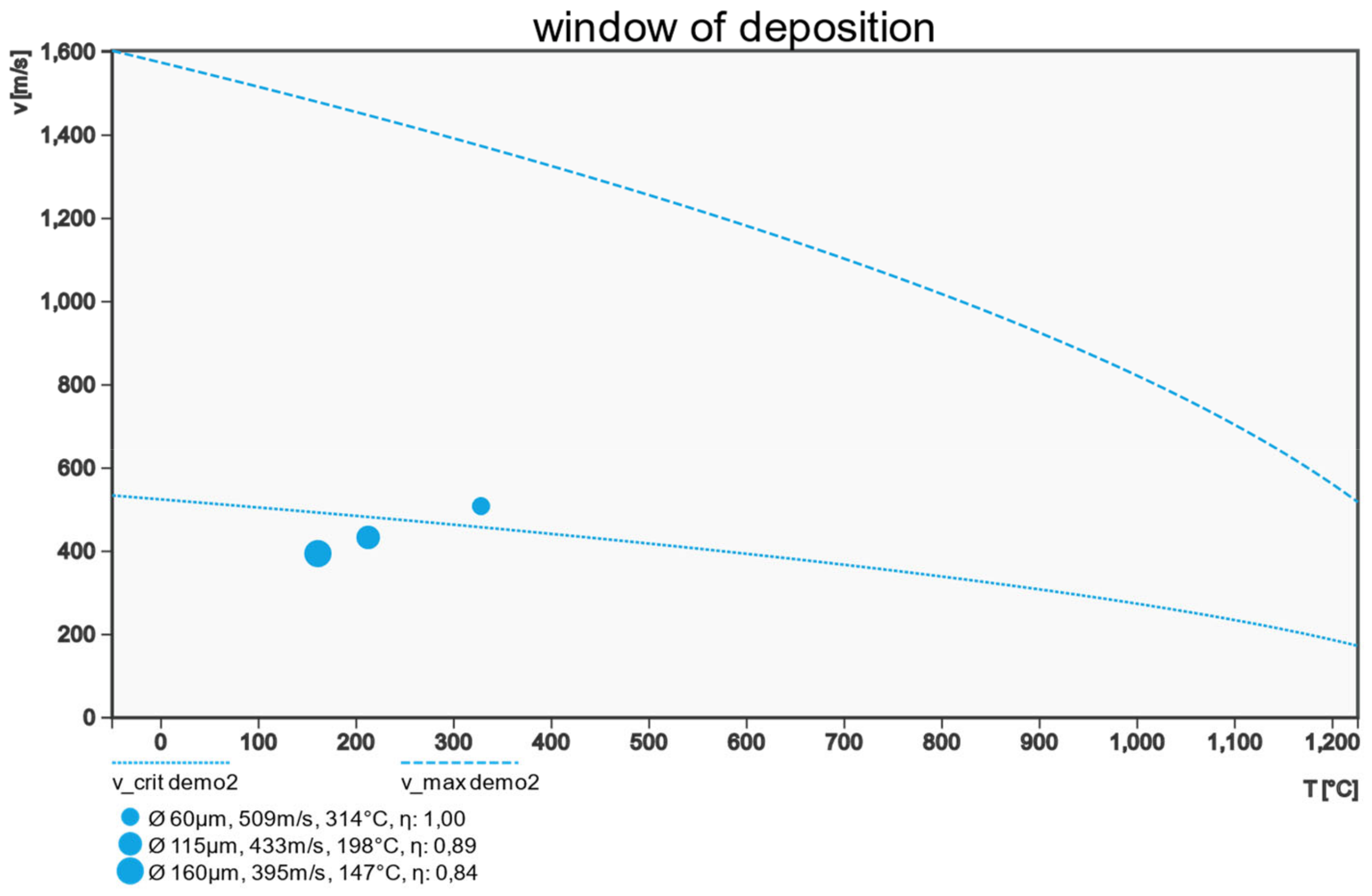
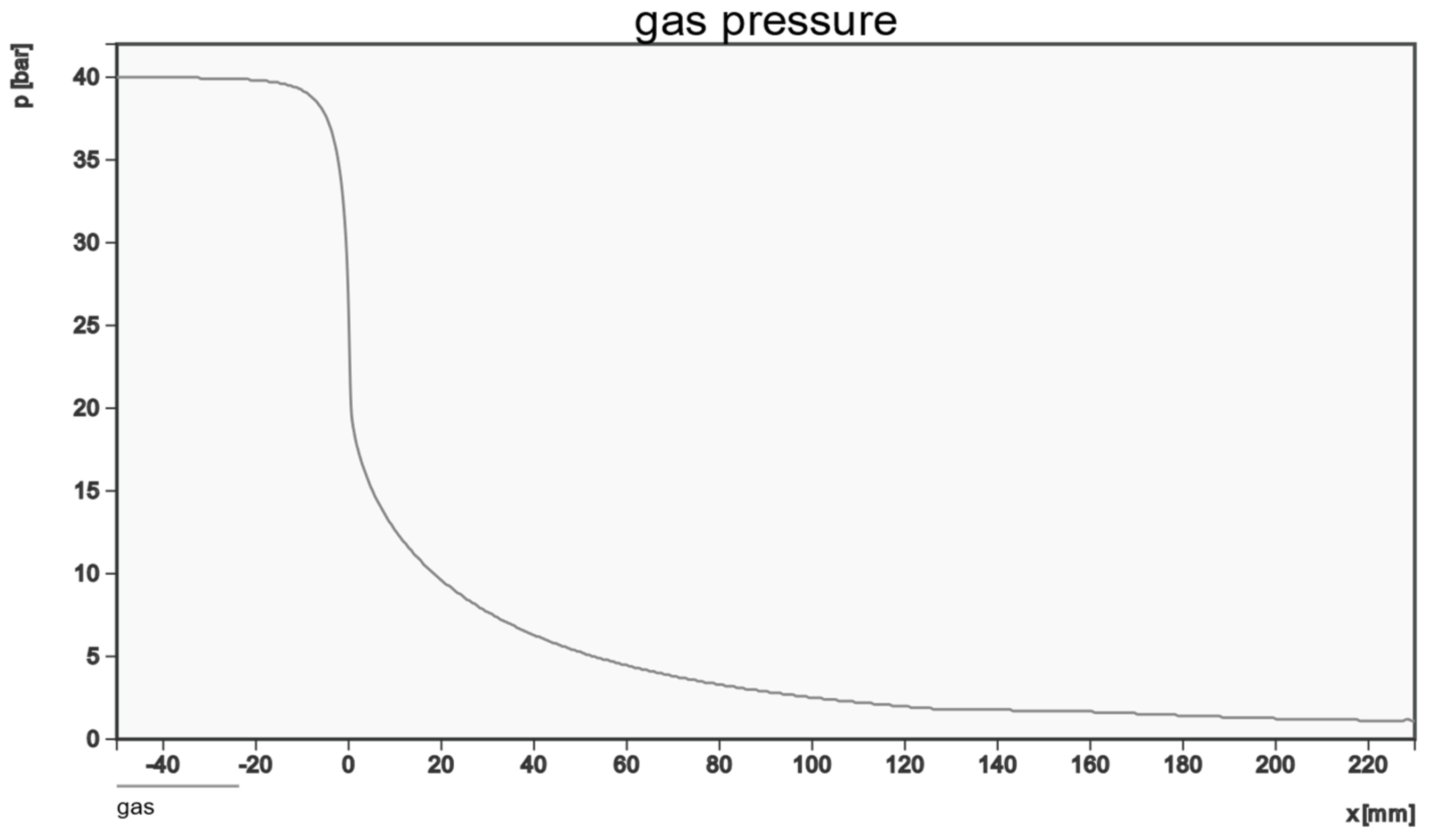

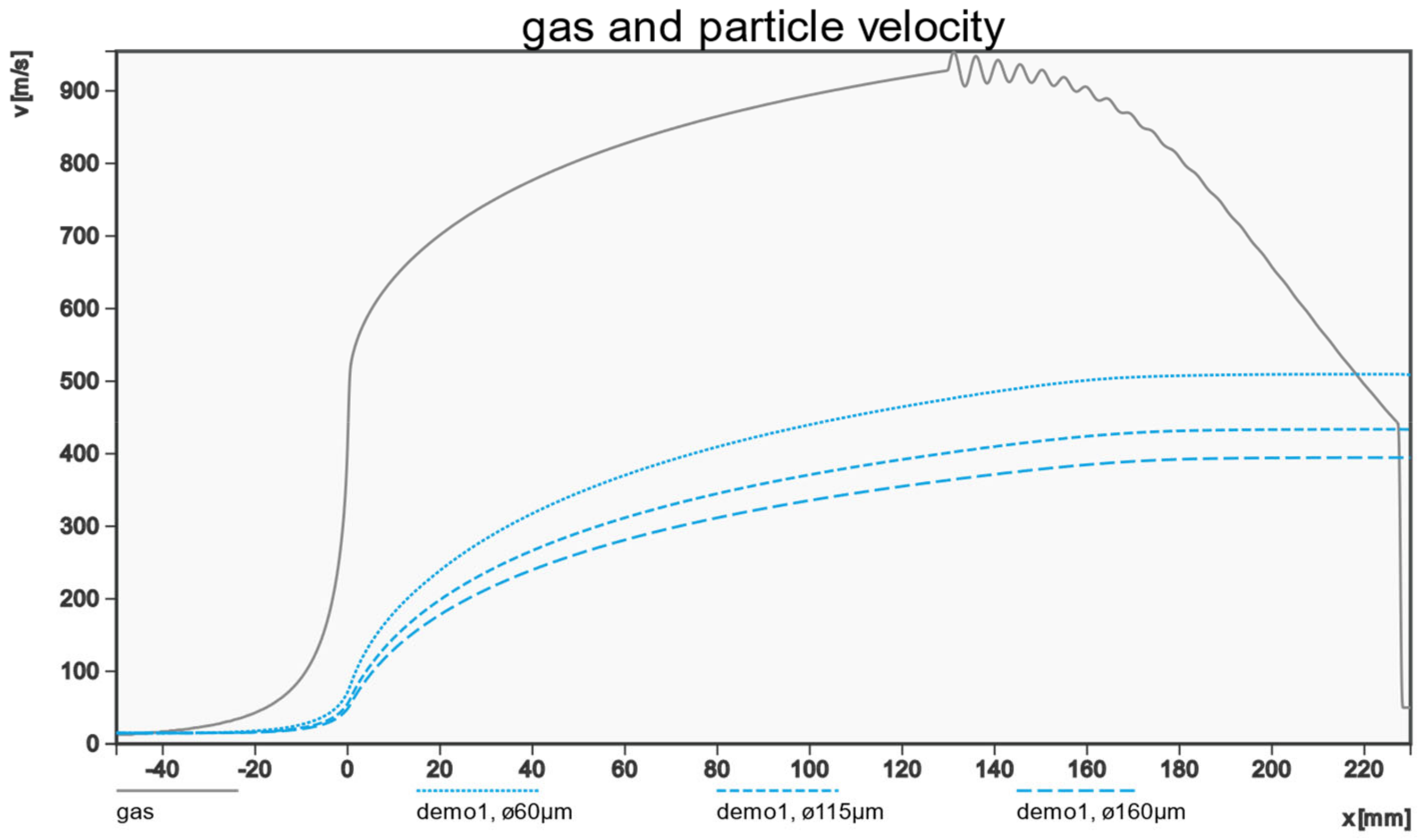
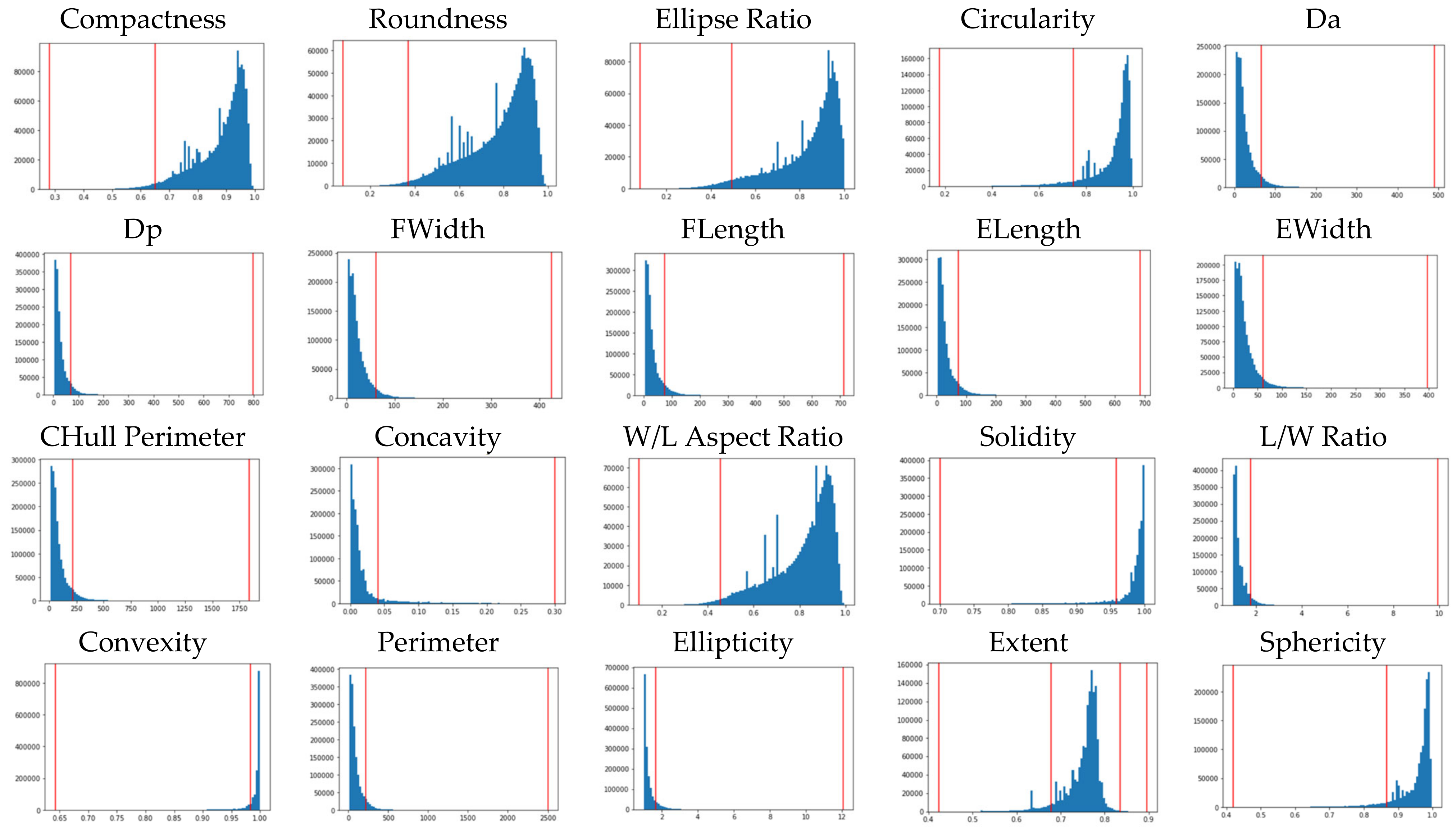




| Feature | Unit | Description | Group |
|---|---|---|---|
| Da | μm | Area equivalent diameter | Size |
| Dp | μm | Perimeter equivalent diameter | Size |
| FLength | μm | Feret length | Size |
| FWidth | μm | Feret width | Size |
| ELength | μm | Legendre ellipse length | Size |
| EWidth | μm | Legendre ellipse width | Size |
| Area | μm2 | Projected 2D area | Size |
| Volume | μm3 | Calculated from Da | Size |
| Perimeter | μm | Projected 2D perimeter | Size |
| Surface Area | μm2 | Spherical surface area from Da | Size |
| CHull Area | μm2 | Area of the convex Hull in 2D | Size |
| CHull Surface Area | μm2 | Spherical area parameter | Size |
| Fiber Length | μm | Function of area and perimeter | Size |
| Fiber Width | μm | Function of area and fiber width | Size |
| Sphericity | n/a | Measure of the proximity to a circle | Shape/form |
| Circularity | n/a | Sensitive measure of the proximity to a circle | Shape/form |
| Roundness | n/a | Shape indicator in relation to proximal circle | Shape/form |
| Extent | n/a | Function of area, FLength and FWidth | Shape/form |
| Ellipse Ratio | n/a | Measure of overall form | Shape/form |
| W/L Aspect Ratio | n/a | Ratio of FWidth to FLength | Shape/form |
| L/W Ratio | n/a | Ratio of FLength to FWidth | Shape/form |
| Ellipticity | n/a | Degree of deviation from a circularity | Shape/form |
| Angularity | n/a | Morphological characteristic | Shape/form |
| Compactness | n/a | Function of area and FLength | Shape/form |
| Convexity | n/a | Measure of surface roughness | Surface roughness |
| Solidity | n/a | Measure of surface roughness | Surface roughness |
| Concavity | n/a | Measure of surface roughness | Surface roughness |
| Transparency | n/a | Light intensity via longest vertical line | Intensity |
| Curvature | n/a | Middle 50% of the line from transparency | Intensity |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schuliger, A.; Price, S.; Sousa, B.C.; Cote, D.L.; Neamtu, R. Multiple-Instance Regression for Metal Powder Hall Flow Rate Prediction Using Augmented Particle Size and Shape Data. Powders 2023, 2, 189-204. https://doi.org/10.3390/powders2010013
Schuliger A, Price S, Sousa BC, Cote DL, Neamtu R. Multiple-Instance Regression for Metal Powder Hall Flow Rate Prediction Using Augmented Particle Size and Shape Data. Powders. 2023; 2(1):189-204. https://doi.org/10.3390/powders2010013
Chicago/Turabian StyleSchuliger, Ashley, Stephen Price, Bryer C. Sousa, Danielle L. Cote, and Rodica Neamtu. 2023. "Multiple-Instance Regression for Metal Powder Hall Flow Rate Prediction Using Augmented Particle Size and Shape Data" Powders 2, no. 1: 189-204. https://doi.org/10.3390/powders2010013
APA StyleSchuliger, A., Price, S., Sousa, B. C., Cote, D. L., & Neamtu, R. (2023). Multiple-Instance Regression for Metal Powder Hall Flow Rate Prediction Using Augmented Particle Size and Shape Data. Powders, 2(1), 189-204. https://doi.org/10.3390/powders2010013








