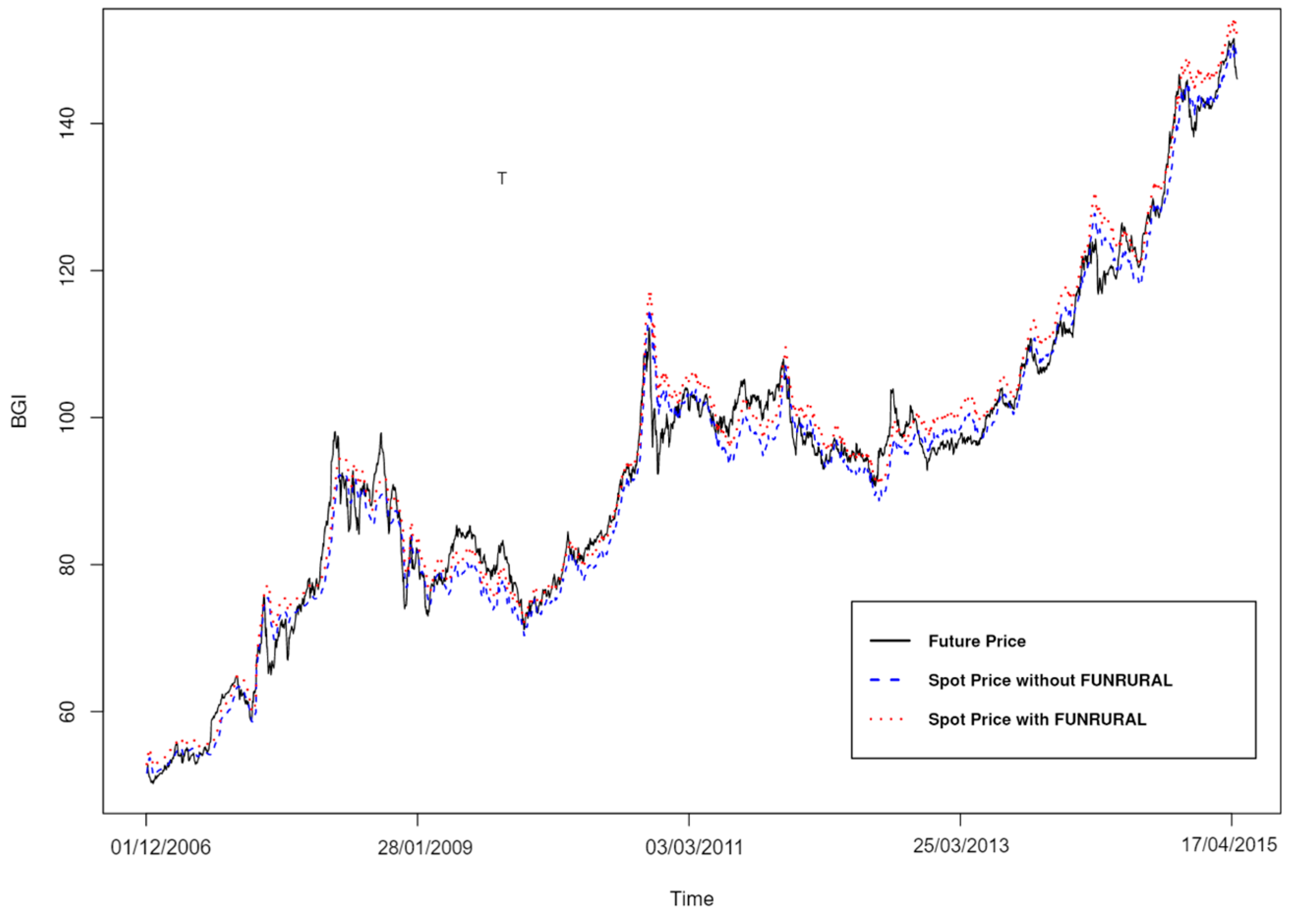
The data consisted of BGI futures prices acquired with GrapherOC software and BGI spot prices taken from the CEPEA-USP website. The futures price data referred to the period from 11 February 2005 to 30 December 2014, whereas the spot prices came from trades between 23 July 1997 and 30 April 2015.
When a future contract is due in March and another in April, for instance, both contracts will be available to buy and will have a price months before March. In other words, futures contracts’ terms overlap, and a common market strategy is also to operate using futures with short maturities. If a contract’s last month is chosen, the value in the last days will converge on the spot value, and, after launching the series, the next contract will diverge again, because it will be due in 30 days at the end of the futures contract’s term. Thus, the data included the next-to-last month of each futures contract along with the spot prices for the same dates. The resulting period used in the data modelling was from 1 December 2006 to 30 April 2015.
Complementing this visual portrayal,
Table 1 provides a statistical overview, displaying the minimum, first quartile, median, mean, third quartile, maximum and standard deviation. As anticipated, the spot price inclusive of the
Funrural tax consistently registers higher values than its counterpart without the tax. This difference aligns with the inherent nature of the
Funrural as an added tax. Meanwhile, the futures price demonstrates its own unique distribution and fluctuations, reflective of market dynamics and anticipations.
For the futures price, the mean stands at 94.02, with a standard deviation of 21.7942, ranging from a minimum of 50.20 to a maximum of 151.55. This indicates that there has been an overall upward trend in the ’Future Price’ from its start to its end, though the actual movement has intermediate ’ups’ and ’downs’. The seasonal components are approximately −0.04887 and 0.05295, respectively. This shows that the seasonal fluctuations (or oscillations) around the trend have a fairly small magnitude. The seasonal patterns go both above and below the trend. Finally, the random component range goes from about −3.279720 to 3.254873. This shows that the fluctuations or irregularities are relatively larger than the seasonal component. The spot price without Funrural exhibits a mean value of 93.09 and a standard deviation of 21.99908 and spans from 51.31 to 150.65. When considering the Funrural contribution, the mean spot price slightly rises to 95.28, with a standard deviation of 22.51686 and a range between 52.52 and 154.20.
3.1. Exponential Smoothing Algorithms
This research relied on simple, Holt and Holt–Winters exponential smoothing models. At first glance, the simple exponential smoothing method resembles the moving-average technique in that both approaches extract random behaviour from time series observations by smoothing historical data (see [
27], chapter 10). The innovation introduced by the simple exponential smoothing model is that this method assigns different weights to each observation in the series. In the moving-average technique, the observations used to formulate future value forecasts contribute equally to calculating the predicted values. Simple exponential smoothing, in contrast, uses the latest information by applying a factor that determines its importance (see [
28], chapter 4). According to [
29], the argument in favour of the latter treatment of time series observations is that the latest observations are assumed to contain more information about futures and thus are more relevant to the forecast process.
The simple exponential smoothing model is represented as follows. If
then Equations (1) and (2) can be written:
in which
is the forecast at time
and
is the weight assigned to observation
. In the present model’s fit,
and the forecast coefficient is
.
Figure 4 presents the fitted values of the simple exponential smoothing algorithm applied.
Figure 5 shows a ‘zoom in’ image of the data, with only the last 31 daily entries. This facilitated a comparison of the real dataset not used in the data modelling with the model’s predictions in blue. The dashed blue line is the confidence interval. The mean squared error is
. This figure highlights the model’s forecasting inadequacies.
When the simple exponential smoothing method is applied to predicting time series that involve trends in past observations, the predicted values overestimate or underestimate the actual values [
27]. Thus, the forecast’s accuracy is impaired. The linear exponential smoothing method was developed to avoid this systematic error, in an effort to reflect the trends present in data series [
29].
The latter method obtains forecast values by applying Equation (3):
in which
corresponds to the forecast at time
.
represents the trend component obtained with Equation (4), and
is the forecast horizon:
in which
is the weight attributed to the observation
, and
is the smoothing coefficient. The present study’s Holt exponential smoothing model has the values
and
. The coefficients for the forecast are 150.6 and 0.1450552.
Figure 6 shows, in red, the fitted values for the Holt exponential smoothing model. This graph looked similar to
Figure 4 above, so the next step was to zoom in on the data’s last part.
Figure 7 shows the results with the simple exponential smoothing model’s values in blue and the Holt exponential smoothing model’s values in red. This graph highlights the differences between the latter two models.
Figure 8 presents the daily entries from 1980 to 2015 and, in red, the fitted values with the posterior predictions. The dashed lines are the confidence interval, and the mean squared error for the predictions is
. This figure again shows the Holt model’s forecasting inadequacy, as the values are clearly overestimated.
The third exponential smoothing algorithm considered was the Holt–Winters approach. In addition to the unobservable components present in the previous model, this algorithm also incorporates a third—seasonality [
30]. Since the analysed data did not present seasonality, the current study only used the simple and Holt exponential smoothing models. Of these two models, the best fit was the simple exponential smoothing option. Despite only giving fixed-value predictions, this model presented a lower mean squared error in the forecasts.
3.2. ARIMA
This section discusses the fit obtained for the futures prices using an ARIMA approach. The ARIMA model was proposed by [
31]. The present research’s first model was the traditional ARIMA(1,1,0) and ARIMA(2,1,1), after which a regression variable was used, namely, an ARIMAX model. A seasonal ARIMA model was not included because, as mentioned previously, the data did not have a seasonal component.
The futures price series were differentiated once, and the autocorrelation function (ACF) was obtained as shown in
Figure 9. This graph confirmed that one differentiation was enough, so
.
The first line in
Figure 9 above represents the ARIMA(1,1,0) results, with an autoregressive coefficient equal to
and an Akaike information criterion (AIC)
. Regarding the diagnostic analysis of this model, the standardised residuals behaved as a white noise sequence, and they did not present either an autoregressive or moving-average component.
The second model shown in
Figure 9 above is ARIMA(2,1,1), with autoregressive coefficients of
and a moving-average coefficient of
. This model has an AIC
, which is smaller than the previous model’s criterion. Regarding the diagnostic analysis of the ARIMA(2,1,1) model, the standardised residuals again behaved as a white noise sequence, and they did not present either an autoregressive or moving-average component.
In both models, the
p-values for Ljung–Box Q-statistics are higher than 0.05. The futures prices were predicted for 16 days.
Figure 10 shows in blue and red the ARIMA(1,1,0) and ARIMA(2,1,1) models’ results, respectively.
Figure 11 zooms in on only these two models’ predictions and presents the futures prices’ real value. Neither prediction clearly captured the fall in values happening in the real data. The sum of the predictions’ squared errors is
and
for the ARIMA(1,1,0) and ARIMA(2,1,1) models, respectively.
The results support the conclusion that neither prediction and, consequently, neither model was a good fit for this time series. However, more information was available to use in the modelling process, that is, the spot prices. Thus, the next step was to estimate the ARIMAX model with the spot prices as a regression variable. Orders c(1,1,0) and c(2,1,1) were used, as previously, for the purposes of comparison, but this time—after using the auto.arima function in R—order c(0,0,5) was also included.
The ARIMAX(1,1,0) model has an autoregressive coefficient of and a regression coefficient of . The ARIMAX(2,1,1) model produced autoregressive coefficients of 0.0681 and 0.0116, a moving-average coefficient of and a regression coefficient of 0.4388. The ARIMAX(0,0,5) model’s coefficients are for the moving-average component, and was obtained for the intercept and for the regression.
The models’ AICs are 4711.76, 4715.48 and 5606.42, respectively.
Figure 12 presents the predictions generated by the ARIMAX models, with a sum of squared errors of
,
and 18.64785, respectively. Although the predictions looked somewhat better, the ARIMAX models presented a higher sum of squared errors compared to the ARIMA approach.
Overall, the ARIMA(1,1,0) model presented the lowest sum of squared errors for its predictions, that is, . This figure is not only the lowest as opposed to the ARIMA or ARIMAX models’ results but also compared with the exponential smoothing algorithms and ARIMAX(0,0,5). The results obtained by using the auto.arima function in R include the highest sum of squared errors for the predictions: . Another class of models was estimated to facilitate a retrospective comparison.
3.3. GARCH
The GARCH approach was originally proposed by [
32]. In the present study, this model was developed using the ‘rugarch package’ written in R. As described in the previous section, the futures prices series were differentiated for modelling purposes, and, after the predictions were generated, the data were transformed back into their original form to compare the forecasts with the real data. Given the dynamic conditional variance, the GARCH model estimated was configured as GARCH(1,1), the mean model was ARFIMA(1,0,1), and the conditional distribution was normal. All model parameters and distributions were statistically significant with a
p-value of 0.05.
The optimal parameters are
0.0538910,
,
,
,
and
, in which
and
represent the autoregressive and moving-average coefficients. The AIC is 2.2184.
Figure 13 shows that the lines are close to each other, and the sum of squared errors is
—the lowest value up to this point.
After comparing the GARCH, ARIMA or ARIMAX and exponential smoothing models, the GARCH(1,1) version was found to be the best fit for the data. To finalise the modelling process, one more type of model, GARMA, was estimated for comparison purposes.
3.4. GARMA
To apply the GARMA method, the most appropriate family of distributions needed to be determined, as mentioned above in
Section 3. The
t-Student distribution was selected because the weight of the tails matches the financial data analysed. Formal tests were conducted to confirm the suitability of this distribution choice, using a significance threshold of 0.05. The orders that best fitted the real figures were
and
. The models with and without intercept were considered to ascertain the best fit.
In this study, the VaR at 5% was always used, as it corresponds to the lower limit of a 90% confidence interval in terms of the predictions, that is, a
t-Student distribution quantile. A confidence interval of 90% means 5% in each tail of the distributions, and only the 5% lower weight was of interest in this research. Regarding the distribution, the
t-Student family was used. Ref. [
33] report that the data binding function for
should be identity and, for
and
logarithmic.
The GARMA model was developed with order
, that is, a GAR(1) model with intercept. Every estimation has a
p-value lower than 1%. The resulting model is represented by Equations (5) and (6):
with
in which
is the function that represents the autoregressive term, with an associated parameter
.
The GARMA model with order
and without intercept was also a generalised autoregressive GAR(1), except that it had no intercept. All estimates have a
-value less than 1%. The model developed is shown in Equations (7) and (8):
with
in which
A is the function that represents the autoregressive term, with an associated parameter
.
This model was not just autoregressive, because it also included a moving-average component. The GARMA model used order
, namely, the autoregressive part had order 2, and the moving average component had order 1. As mentioned previously, all this model’s estimations have a
-value below 1%. This model is expressed in Equations (9) and (10):
with
in which
is the function that represents the autoregressive term, with the associated parameter
.
represents the moving-average component that has as an associated parameter
.
These three models’ results are presented in
Figure 14;
Figure 15. All three are similar, so they are not shown separately. These graphs focus only on the data’s last part to be able to show the models by zooming in closely enough. The straight blue line separates the data used for modelling from the part utilised to compare the real data with the models’ prediction.
Figure 15 above presents the models’ forecasts. Of the four options analysed, the ones with order
with and without intercept and the one with order
with intercept also provided similar results in terms of forecasts. The predictions overlap regarding both goodness of fit (see
Figure 14 above) and forecasts (see
Figure 15 above). In this graph, the three models’ futures price values cross the estimated VaR line.
The last model estimated also had an order of
, without intercept. As in the previous cases, all this model’s estimations present a
-value lower than 1%. The model is shown in Equations (11) and (12):
with
in which
A is the function that represents the autoregressive term, with an associated parameter
. In addition,
M represents the moving-average component, with an associated parameter
.
Figure 16 presents the real data in black, and the blue line marks the separation between data used in the final model and data separated for comparison with the forecasts. The fitted values are in orange. This graph zooms in to show only the last 60 days in order to display the overlapping lines correctly.
Figure 17 displays the futures price forecasts. This model with order
and without intercept stands out as having a better fit. Notably, the graph reveals that the model’s forecast curve closely follows the real figures. In addition, the lower confidence interval, that is, the estimated VaR using 95% confidence, is always below the actual future prices at all points, which supports the conclusion that the estimated VaR is reliable. The analyses also included finding the mean square deviation of the four GARMA models estimated. The results are presented in
Table 2.
Table 2 highlights in bold that the forecast generated by the GARMA model with order
is considerably more adequate, and this model’s mean square deviation is the smallest. Thus, this model was chosen among the GARMA options as the best way to obtain the VaR of futures prices, as shown in bold in
Table 2.
The conclusions drawn from the models’ fits and
Table 2 are that the two exponential smoothing models did not have as good a fit as the GARMA models, and that these two models presented a higher mean square deviation in the forecasts. Therefore, the best model to estimate futures prices’ VaR is the GARMA with order
and without intercept.
The body of work in the domain of forecasting using GARMA models, especially with commodity prices, has recently been enriched with studies exploring novel hybrid techniques. A pivotal study by [
12] brought forward the GARMAWLLWNN process, a hybrid model that synthesises the k-factor GARMA process, empirical wavelet transform and the local linear wavelet neural network (LLWNN) methods. When evaluated using data from the Polish electricity markets, their hybrid model showed enhanced predicting performance, outdoing both the dual generalised long-memory k-factor GARMA-G-GARCH model and the individual WLLWNN.
On the other hand, [
13] proposed the k-factor GARMA-EWLLWNN model, an inventive hybrid approach linking the dual long-memory process (GARMA and G-GARCH), the empirical wavelet transform (EWT) and the local linear wavelet neural network (LLWNN). Their model, tested using data from the same Polish electricity markets, demonstrated superior forecasting capabilities in comparison to the GARMA-G-GARCH process and the hybrid EWLLWNN.
In our research, though we leveraged the GARMA model to forecast commodity prices, we found results that parallel the performance of the models proposed in both studies. Our forecasts, derived using the GARMA model, align with the strong predictive capacities observed in both these studies. It is imperative to note, however, that though these studies combine several techniques to enhance the prediction accuracy, our research provides a testament to the robustness and efficacy of the GARMA model in its capacity.
Moreover, though both aforementioned studies focus on the Polish electricity markets, our analysis extends to a broader range of data spanning from 1997 to 2015. This provides a comprehensive insight into the model’s utility across varying datasets and time frames.
Our results contribute to the growing literature that attests to the utility of the GARMA model and its hybrids in forecasting, further cementing its position as an invaluable tool for time series forecasting, particularly in the context of commodity prices.