Time Domain Vibration Analysis of Cracked Ice Shelf
Abstract
:1. Introduction
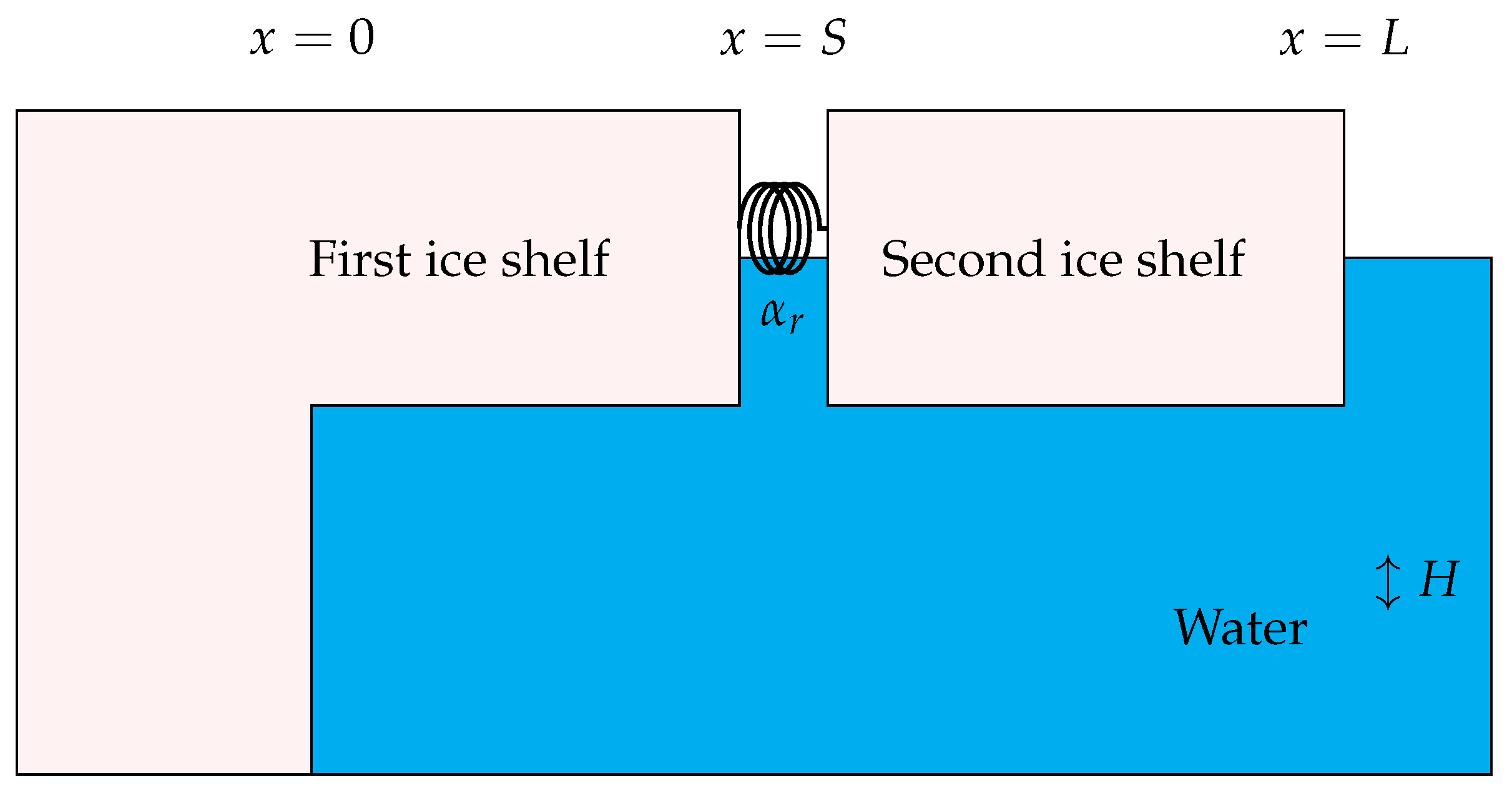
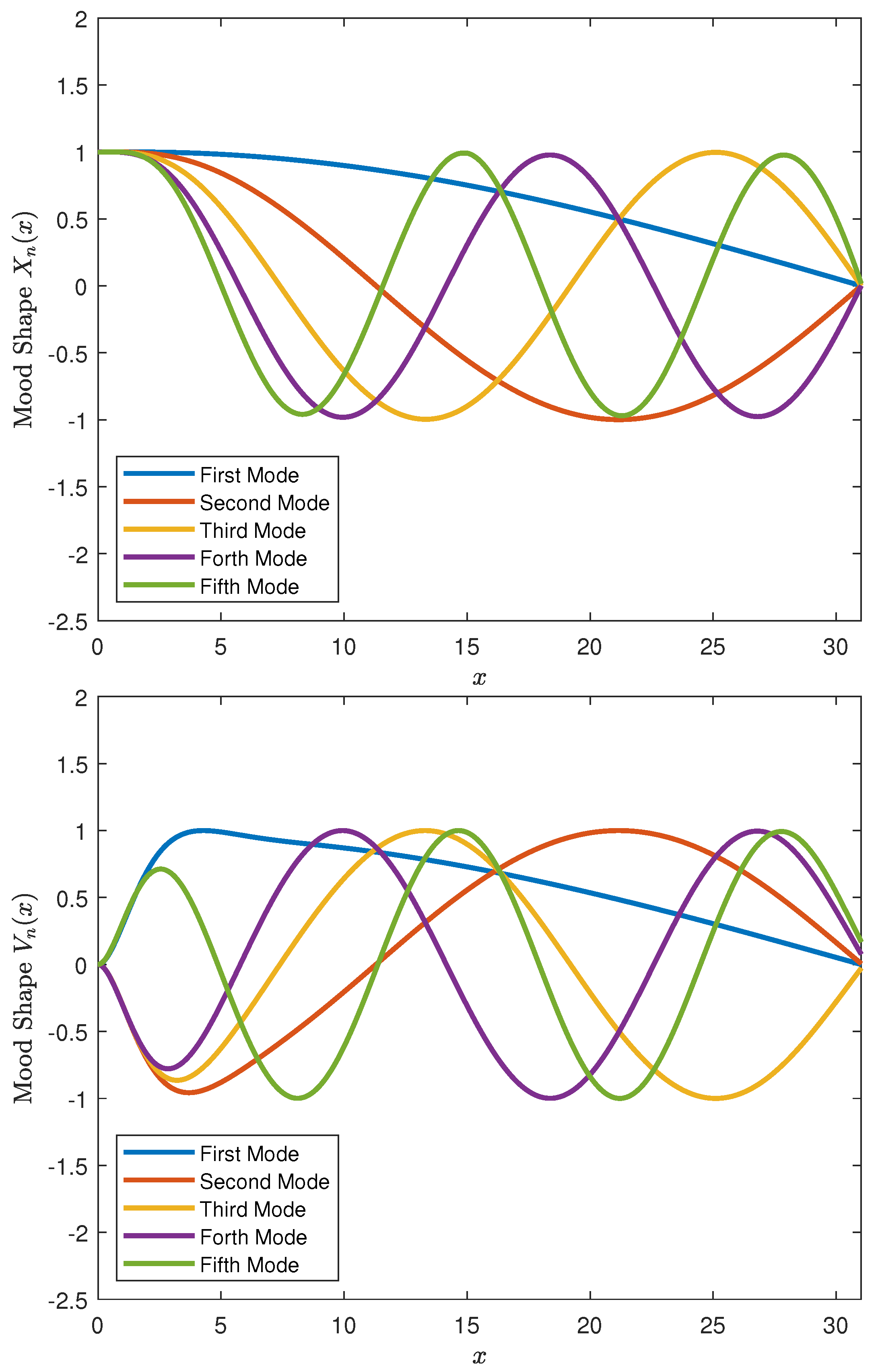
2. Mathematical Model
- are the roots of k of the characteristic polynomial:
3. Simulating Cracked Ice Shelf Vibrations
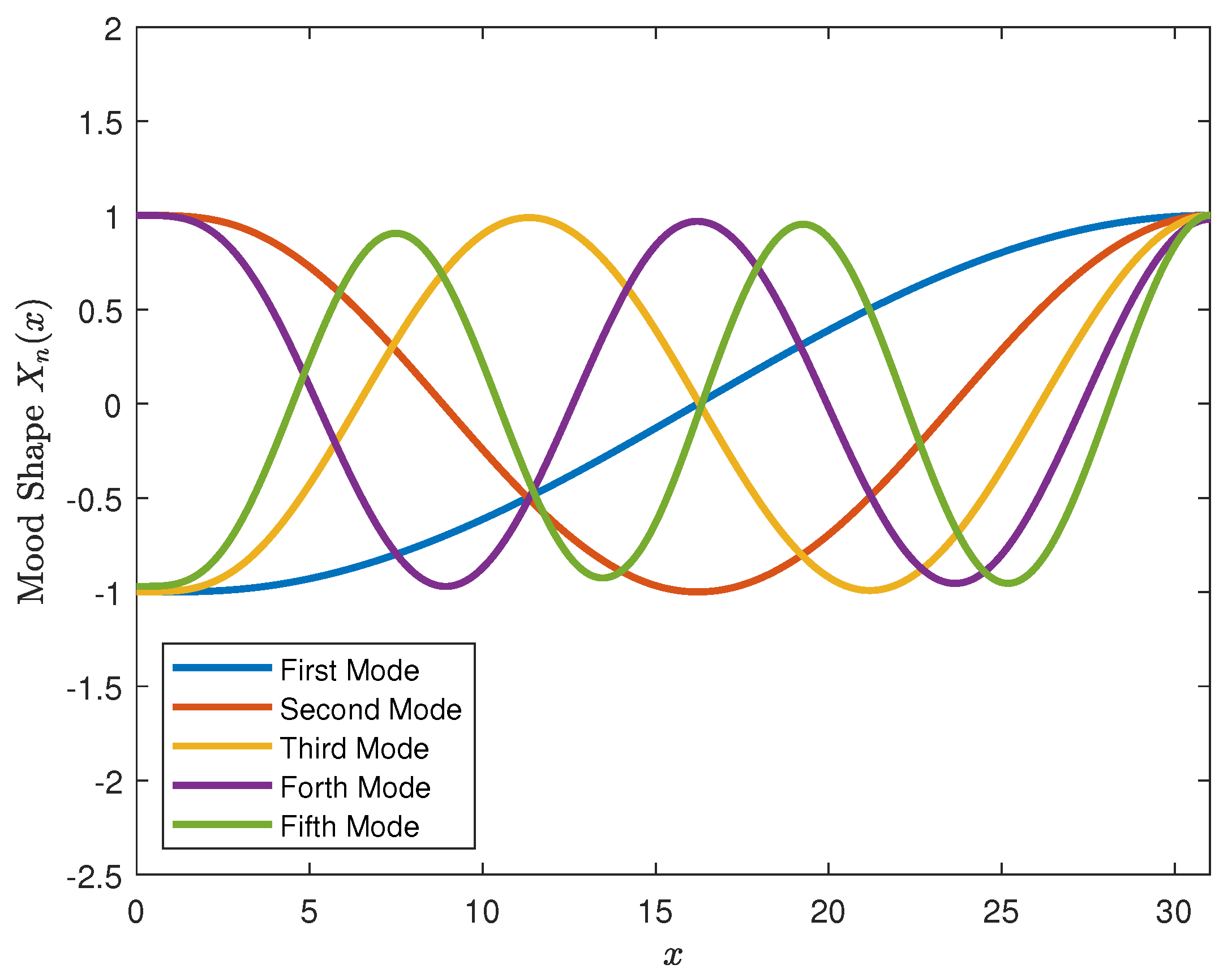
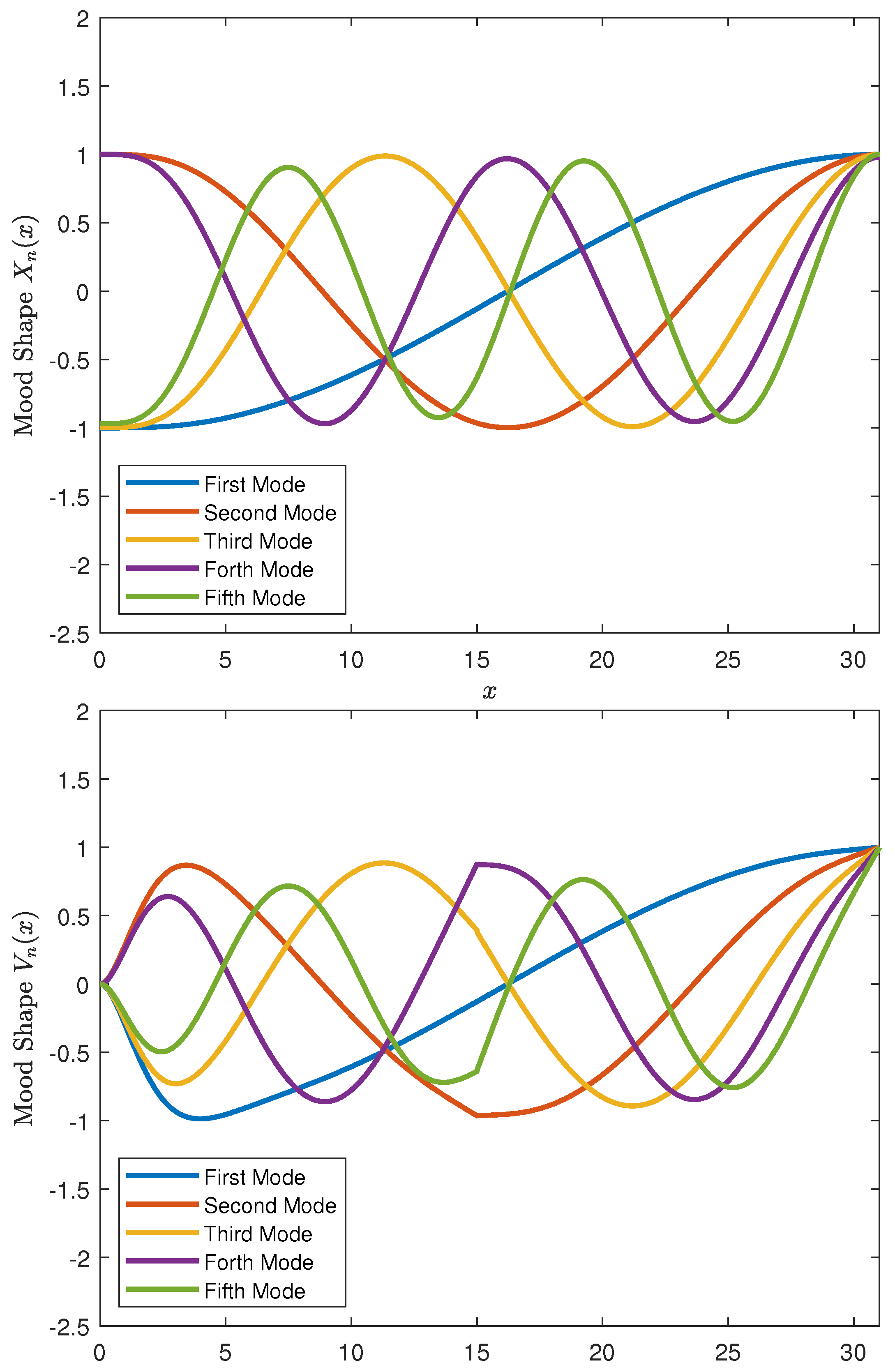
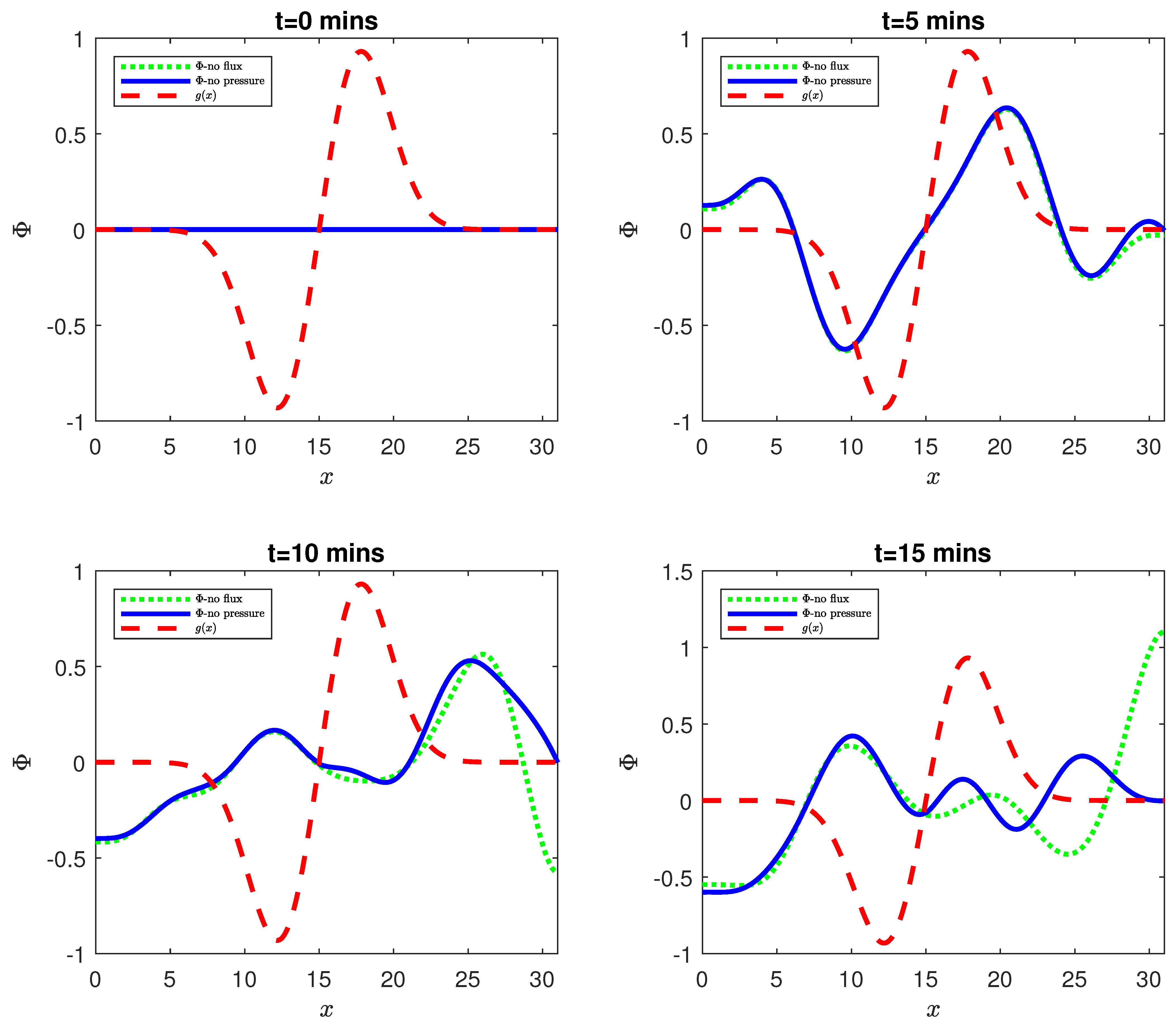
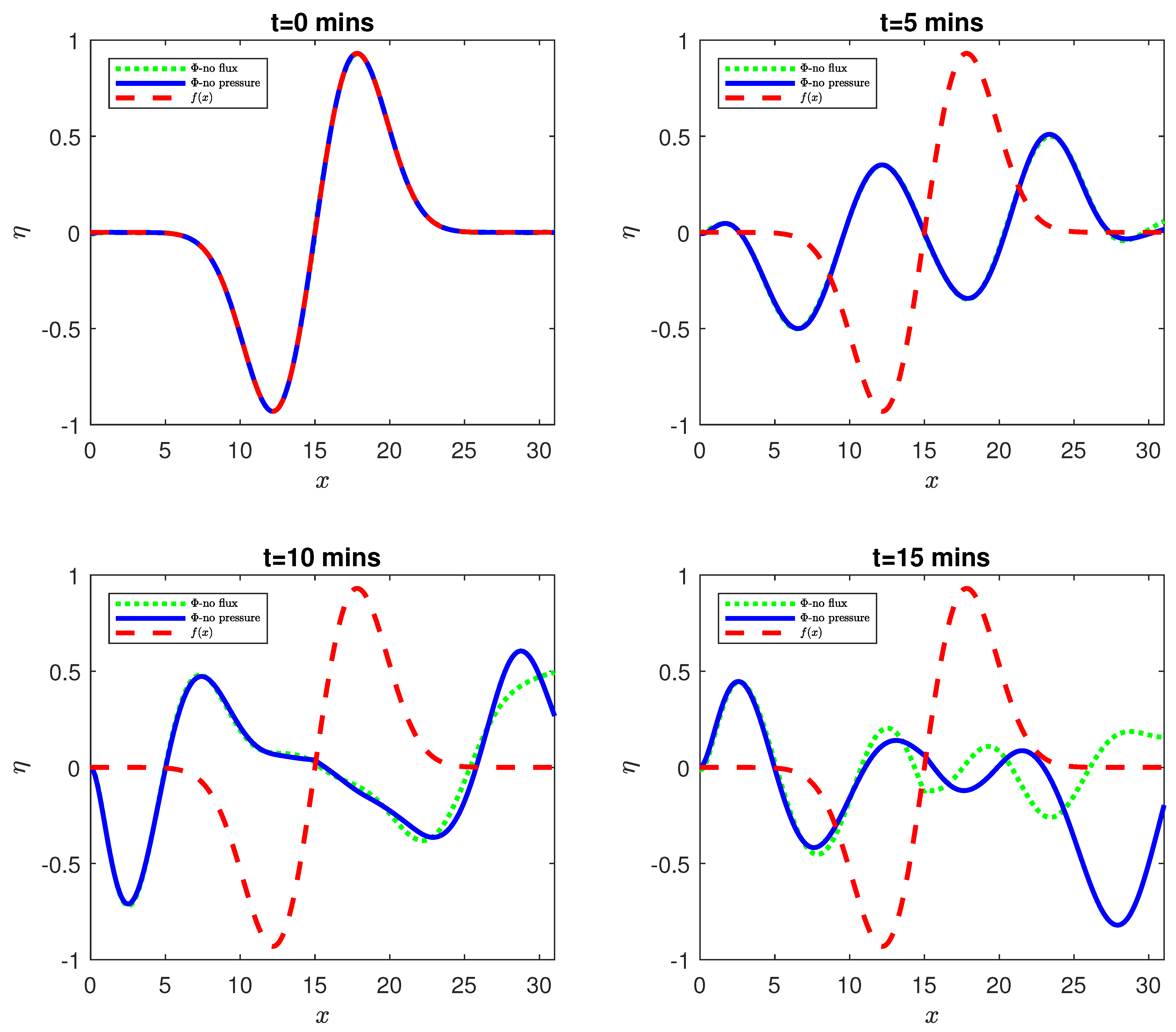
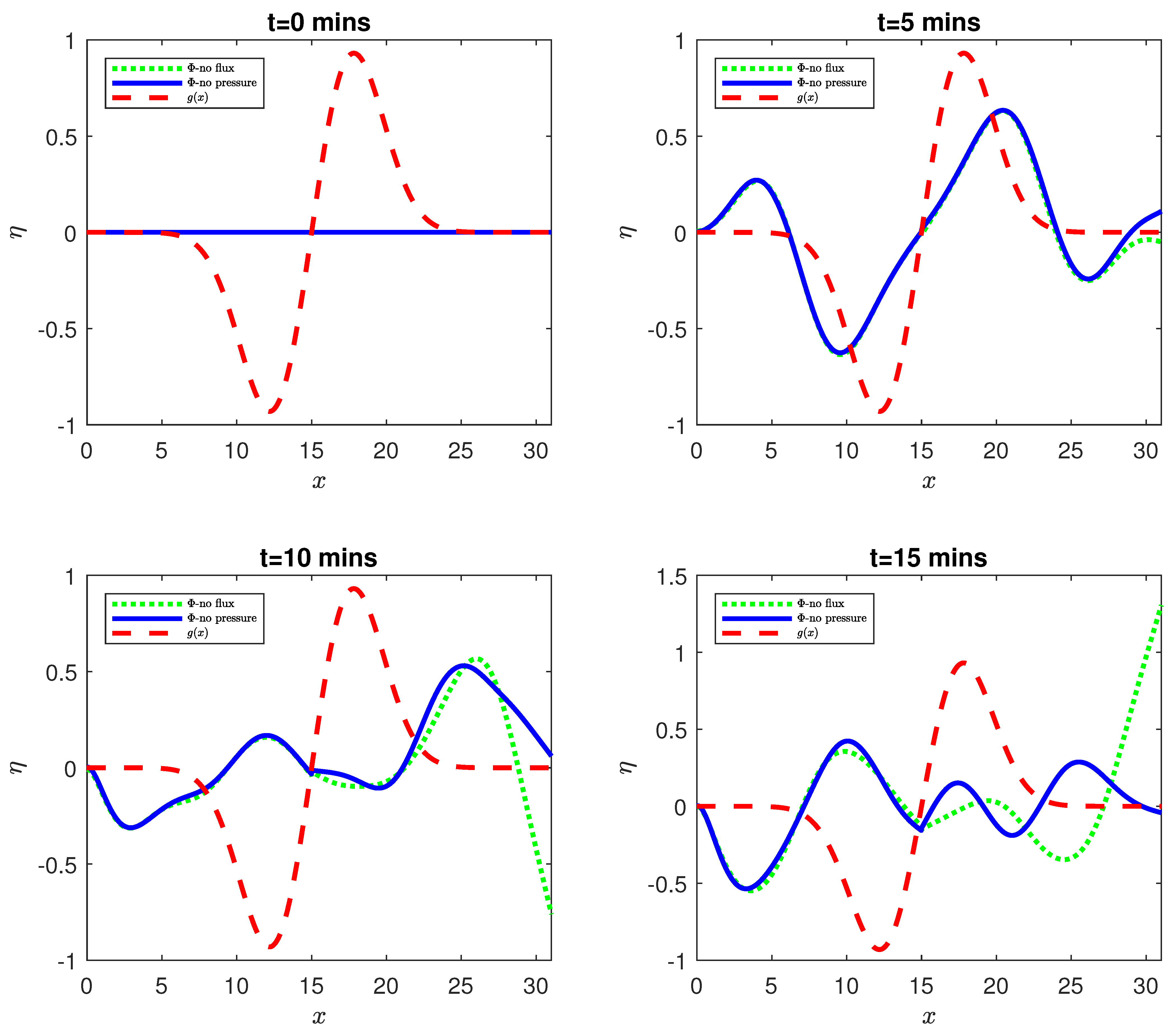
4. Results
5. Discussion: Application to Ice Shelf Breakup
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- DeConto, R.M.; Pollard, D. Contribution of Antarctica to past and future sea-level rise. Nature 2016, 531, 591–597. [Google Scholar] [CrossRef]
- Rignot, E.; Jacobs, S.; Mouginot, J.; Scheuchl, B. Ice-shelf melting around Antarctica. Science 2013, 341, 266–270. [Google Scholar] [CrossRef]
- Snow, N.; Center, I.D. Why Ice Shelves Matter. National Snow and Ice Data Center a Part of CIRES at the University of Colorado Boulder. Available online: https://nsidc.org/learn/parts-cryosphere/ice-shelves/why-ice-shelves-matter#:~:text=on%20ice%20shelves-,Why%20they%20matter,are%20already%20floating%20on%20water (accessed on 24 January 2023).
- NASA Earth Observatory. Breakup at Brunt. NASA Earth Observatory. 2021. Available online: https://earthobservatory.nasa.gov/images/150880/antarcticas-brunt-ice-shelf-finally-breaks (accessed on 24 January 2023).
- British Antarctic Survey. Brunt Ice Shelf in Antarctica Calves Giant Iceberg; British Antarctic Survey: Cambridge, UK, 2023. [Google Scholar]
- U.S. National Ice Center Latest News. Brunt Ice Shelf; U.S. National Ice Center Latest News: Suitland, MD, USA, 2023.
- Sun, S.; Cornford, S.L.; Liu, Y.; Moore, J.C. Dynamic response of Antarctic ice shelves to bedrock uncertainty. Cryosphere 2014, 8, 1561–1576. [Google Scholar] [CrossRef]
- Brunt, K.M.; Okal, E.A.; MacAyeal, D.R. Antarctic ice-shelf calving triggered by the Honshu (Japan) earthquake and tsunami, March 2011. J. Glaciol. 2011, 57, 785–788. [Google Scholar] [CrossRef]
- Massom, R.A.; Scambos, T.A.; Bennetts, L.G.; Reid, P.; Squire, V.A.; Stammerjohn, S.E. Antarctic ice shelf disintegration triggered by sea ice loss and ocean swell. Nature 2018, 558, 383–389. [Google Scholar] [CrossRef] [PubMed]
- Bromirski, P.D.; Chen, Z.; Stephen, R.A.; Gerstoft, P.; Arcas, D.; Diez, A.; Aster, R.C.; Wiens, D.A.; Nyblade, A. Tsunami and infragravity waves impacting A ntarctic ice shelves. J. Geophys. Res. Ocean. 2017, 122, 5786–5801. [Google Scholar]
- Liang, J.; Pitt, J.P.; Bennetts, L.G. Pan-Antarctic assessment of ice shelf flexural responses to ocean waves. J. Geophys. Res. Ocean. 2024, 129, e2023JC020824. [Google Scholar]
- Holdsworth, G.; Glynn, J. Iceberg calving from floating glaciers by a vibrating mechanism. Nature 1978, 274, 464–466. [Google Scholar] [CrossRef]
- Reeh, N. On the calving of ice from floating glaciers and ice shelves. J. Glaciol. 1968, 7, 215–232. [Google Scholar] [CrossRef]
- Meylan, M.H.; Bennetts, L.G.; Hosking, R.J.; Catt, E. On the calculation of normal modes of a coupled ice-shelf/sub-ice-shelf cavity system. J. Glaciol. 2017, 63, 751–754. [Google Scholar] [CrossRef]
- Sergienko, O.V. Normal modes of a coupled ice-shelf/sub-ice-shelf cavity system. J. Glaciol. 2013, 59, 76–80. [Google Scholar] [CrossRef]
- Kalyanaraman, B.; Meylan, M.H.; Bennetts, L.G.; Lamichhane, B.P. A coupled fluid-elasticity model for the wave forcing of an ice-shelf. J. Fluids Struct. 2020, 97, 103074. [Google Scholar] [CrossRef]
- Papathanasiou, T.; Karperaki, A.; Theotokoglou, E.; Belibassakis, K. A higher order FEM for time-domain hydroelastic analysis of large floating bodies in an inhomogeneous shallow water environment. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20140643. [Google Scholar] [CrossRef]
- Bennetts, L.G.; Meylan, M.H. Complex resonant ice shelf vibrations. SIAM J. Appl. Math. 2021, 81, 1483–1502. [Google Scholar] [CrossRef]
- Aljabri, R.; Meylan, M.H. Time Domain Vibration Analysis of an Ice Shelf. J. Mar. Sci. Eng. 2024, 12, 468. [Google Scholar] [CrossRef]
- Alshahrani, F.; Meylan, M.H.; Wilks, B. Transient Shallow Water Wave Interactions with a Partially Fragmented Ice Shelf. Fluids 2024, 9, 192. [Google Scholar] [CrossRef]
- Bennetts, L.G.; Williams, T.D.; Porter, R. A thin-plate approximation for ocean wave interactions with an ice shelf. J. Fluid Mech. 2024, 984, A48. [Google Scholar]
- Chondros, T.; Dimarogonas, A.; Yao, J. A continuous cracked beam vibration theory. J. Sound Vib. 1998, 215, 17–34. [Google Scholar] [CrossRef]
- Mungla, M.J.; Sharma, D.; Makwana, H.; Bhavsar, R. Inverse dynamics of cracked cantilever beam. In Proceedings of the International Conference in Advanced Design and Manufacturing, Montreal, QC, Canada, 13–15 August 2014; pp. 331–336. [Google Scholar]
- Mungla, M.J.; Sharma, D.S.; Trivedi, R.R. Identification of a crack in clamped-clamped beam using frequency-based method and genetic algorithm. Procedia Eng. 2016, 144, 1426–1434. [Google Scholar] [CrossRef]
- Chati, M.; Rand, R.; Mukherjee, S. Modal analysis of a cracked beam. J. Sound Vib. 1997, 207, 249–270. [Google Scholar] [CrossRef]
- Saavedra, P.; Cuitino, L. Crack detection and vibration behavior of cracked beams. Comput. Struct. 2001, 79, 1451–1459. [Google Scholar] [CrossRef]
- Nguyen, K.V. Mode shapes analysis of a cracked beam and its application for crack detection. J. Sound Vib. 2014, 333, 848–872. [Google Scholar] [CrossRef]
- Chang, C.C.; Chen, L.W. Detection of the location and size of cracks in the multiple cracked beam by spatial wavelet based approach. Mech. Syst. Signal Process. 2005, 19, 139–155. [Google Scholar] [CrossRef]
- Dimarogonas, A.D.; Paipetis, S.A.; Chondros, T.G. Analytical Methods in Rotor Dynamics; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Papathanasiou, T.K.; Karperaki, A.E.; Belibassakis, K.A. On the resonant hydroelastic behaviour of ice shelves. Ocean Model. 2019, 133, 11–26. [Google Scholar] [CrossRef]
- Stoker, J.J. Water Waves: The Mathematical Theory with Applications; John Wiley & Sons: Hoboken, NJ, USA, 1992; Volume 36. [Google Scholar]
- Fox, C. A scaling law for the flexural motion of floating ice. In Proceedings of the IUTAM Symposium on Scaling Laws in Ice Mechanics and Ice Dynamics: Proceedings of the IUTAM Symposium, Fairbanks, AK, USA, 13–16 June 2000; Springer: Berlin/Heidelberg, Germany, 2001; pp. 135–148. [Google Scholar] [CrossRef]
- Humbert, A.; Gross, D.; Müller, R.; Braun, M.; Van De Wal, R.; Van Den Broeke, M.; Vaughan, D.; Van De Berg, W. Deformation and failure of the ice bridge on the Wilkins Ice Shelf, Antarctica. Ann. Glaciol. 2010, 51, 49–55. [Google Scholar] [CrossRef]
- Borstad, C.; McGrath, D.; Pope, A. Fracture propagation and stability of ice shelves governed by ice shelf heterogeneity. Geophys. Res. Lett. 2017, 44, 4186–4194. [Google Scholar] [CrossRef]
- De Rydt, J.; Gudmundsson, G.H.; Nagler, T.; Wuite, J.; King, E.C. Recent rift formation and impact on the structural integrity of the Brunt Ice Shelf, East Antarctica. Cryosphere 2018, 12, 505–520. [Google Scholar] [CrossRef]
- Larour, E.; Rignot, E.; Poinelli, M.; Scheuchl, B. Physical processes controlling the rifting of Larsen C Ice Shelf, Antarctica, prior to the calving of iceberg A68. Proc. Natl. Acad. Sci. USA 2021, 118, e2105080118. [Google Scholar] [CrossRef]
- McNeil, S.; Meylan, M.H. Time-Dependent Modelling of the Wave-Induced Vibration of Ice Shelves. J. Mar. Sci. Eng. 2023, 11, 1191. [Google Scholar] [CrossRef]



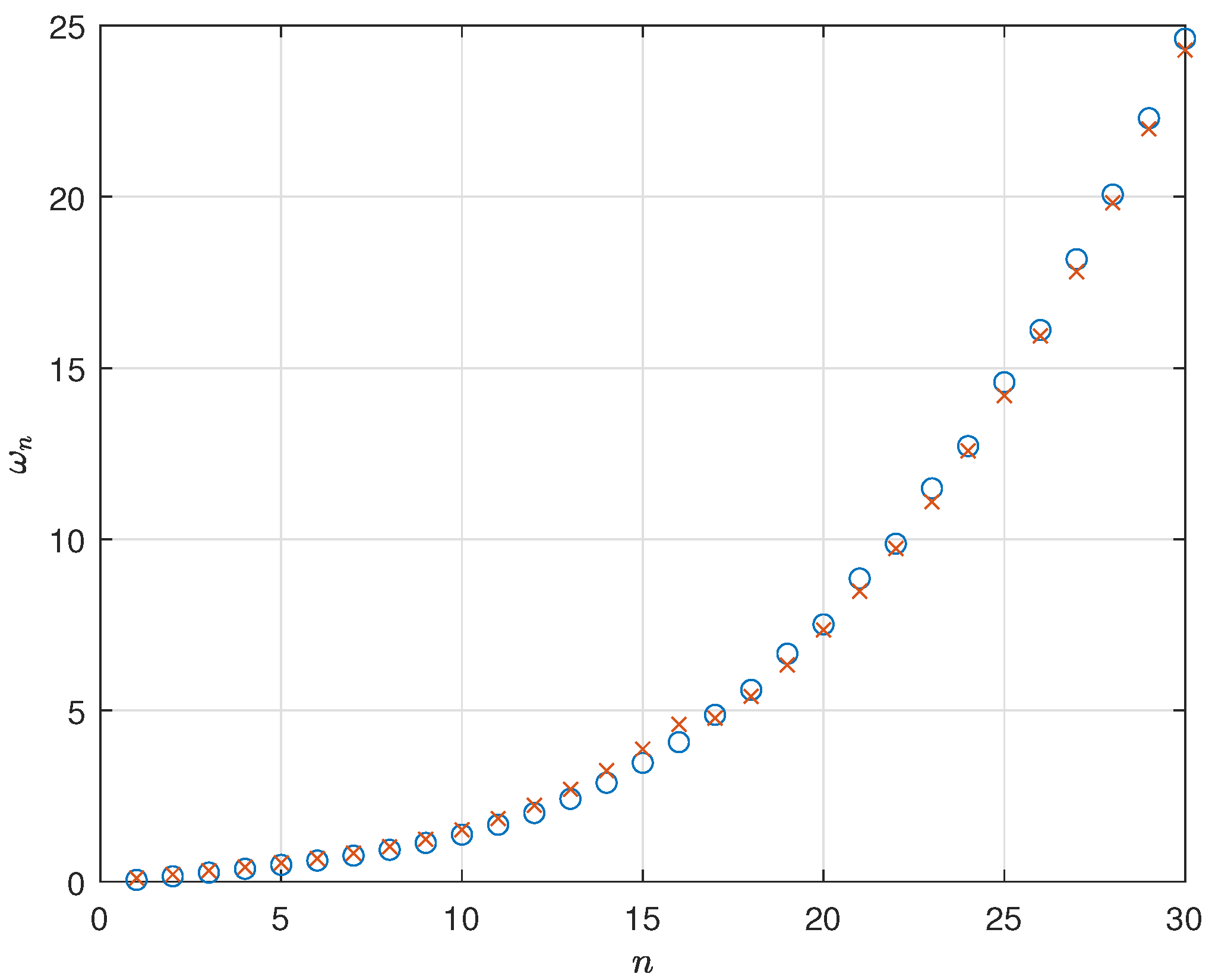


| n | ||||
| 1 | 0.10613 | 0.67701 h | 0.10614 | 0.67695 h |
| 2 | 0.21253 | 0.33808 h | 0.21261 | 0.33796 h |
| 3 | 0.32014 | 0.22445 h | 0.32039 | 0.22427 h |
| 4 | 0.43116 | 0.16665 h | 0.43178 | 0.16641 h |
| 5 | 0.54961 | 0.13073 h | 0.55082 | 0.13045 h |
| 10 | 1.51175 | 171.113 s | 1.52461 | 169.669 s |
| 15 | 3.87393 | 66.7747 s | 3.94702 | 65.5383 s |
| 20 | 7.35072 | 35.1913 s | 8.76451 | 29.5146 s |
| 25 | 14.1932 | 18.2256 s | 16.7541 | 15.4398 s |
| 30 | 24.2845 | 10.6521 s | 28.6811 | 9.01921 s |
| n | ||||
| 1 | 0.05306 | 1.35422 h | 0.05306 | 1.35419 h |
| 2 | 0.15930 | 0.45107 h | 0.15933 | 0.45098 h |
| 3 | 0.26626 | 0.26986 h | 0.26641 | 0.26971 h |
| 4 | 0.37566 | 0.19127 h | 0.37607 | 0.19106 h |
| 5 | 0.49087 | 0.14638 h | 0.49176 | 0.14611 h |
| 10 | 1.37497 | 188.139 s | 1.38673 | 186.539 s |
| 15 | 3.47097 | 74.5270 s | 3.54124 | 73.0482 s |
| 20 | 7.51409 | 34.4261 s | 6.86932 | 37.6574 s |
| 25 | 14.5845 | 17.7366 s | 13.3130 | 19.4306 s |
| 30 | 24.6155 | 10.5088 s | 23.9252 | 10.8120 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshammari, A.; Meylan, M.H. Time Domain Vibration Analysis of Cracked Ice Shelf. Glacies 2025, 2, 5. https://doi.org/10.3390/glacies2020005
Alshammari A, Meylan MH. Time Domain Vibration Analysis of Cracked Ice Shelf. Glacies. 2025; 2(2):5. https://doi.org/10.3390/glacies2020005
Chicago/Turabian StyleAlshammari, Alyah, and Michael H. Meylan. 2025. "Time Domain Vibration Analysis of Cracked Ice Shelf" Glacies 2, no. 2: 5. https://doi.org/10.3390/glacies2020005
APA StyleAlshammari, A., & Meylan, M. H. (2025). Time Domain Vibration Analysis of Cracked Ice Shelf. Glacies, 2(2), 5. https://doi.org/10.3390/glacies2020005







