Impact of Nanoparticles on Heat Transfer Enhancement and Thermal Performance Improvement in HTS Power Transformers
Abstract
:1. Introduction
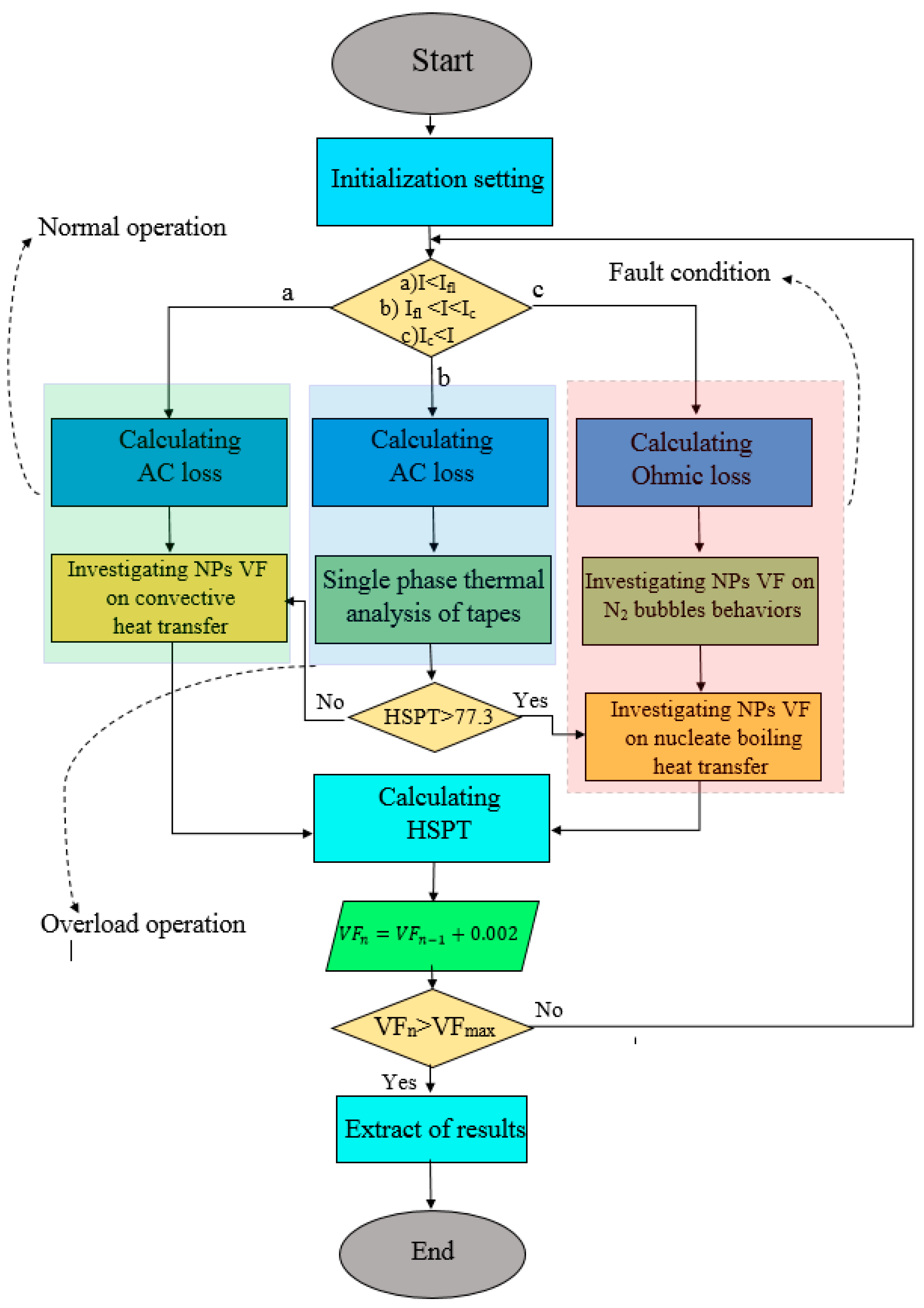
2. Governing Equations
2.1. AC Loss Calculation
2.2. Overload Losses
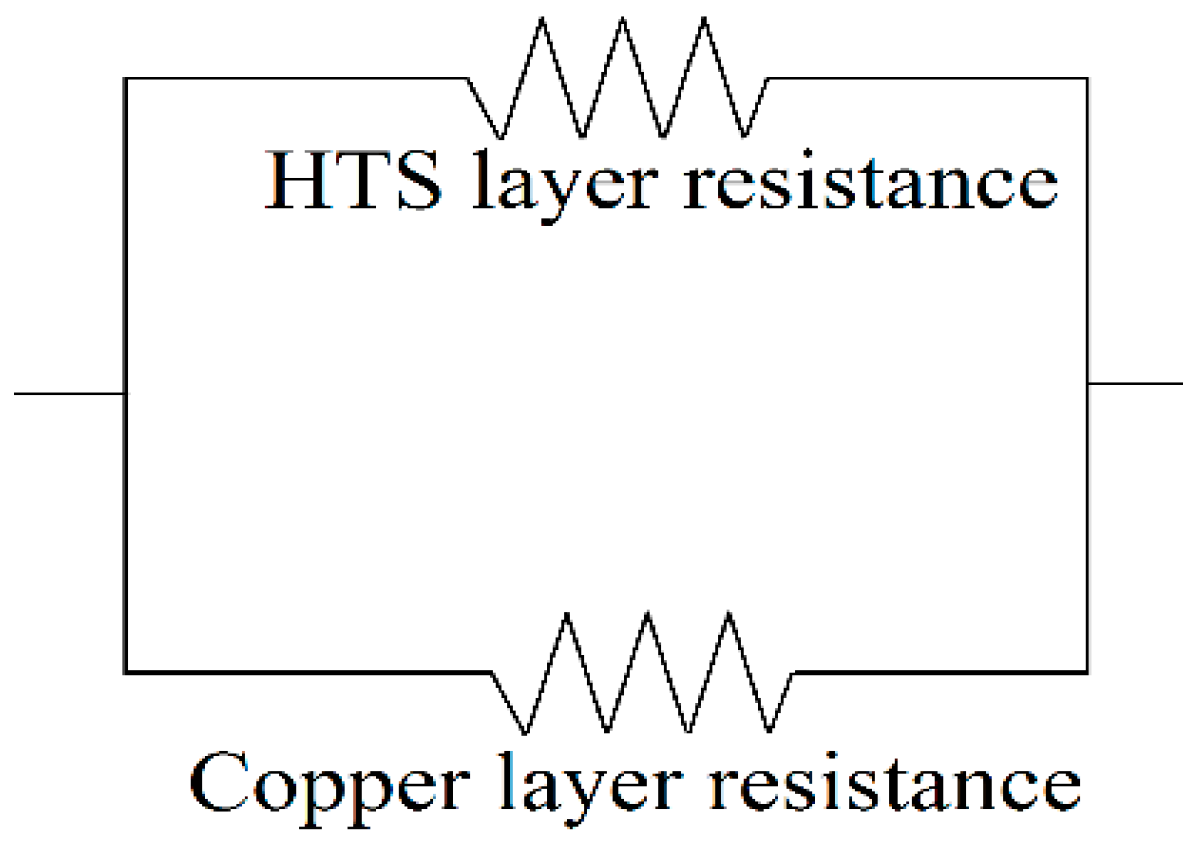
2.3. Fault Current Loss
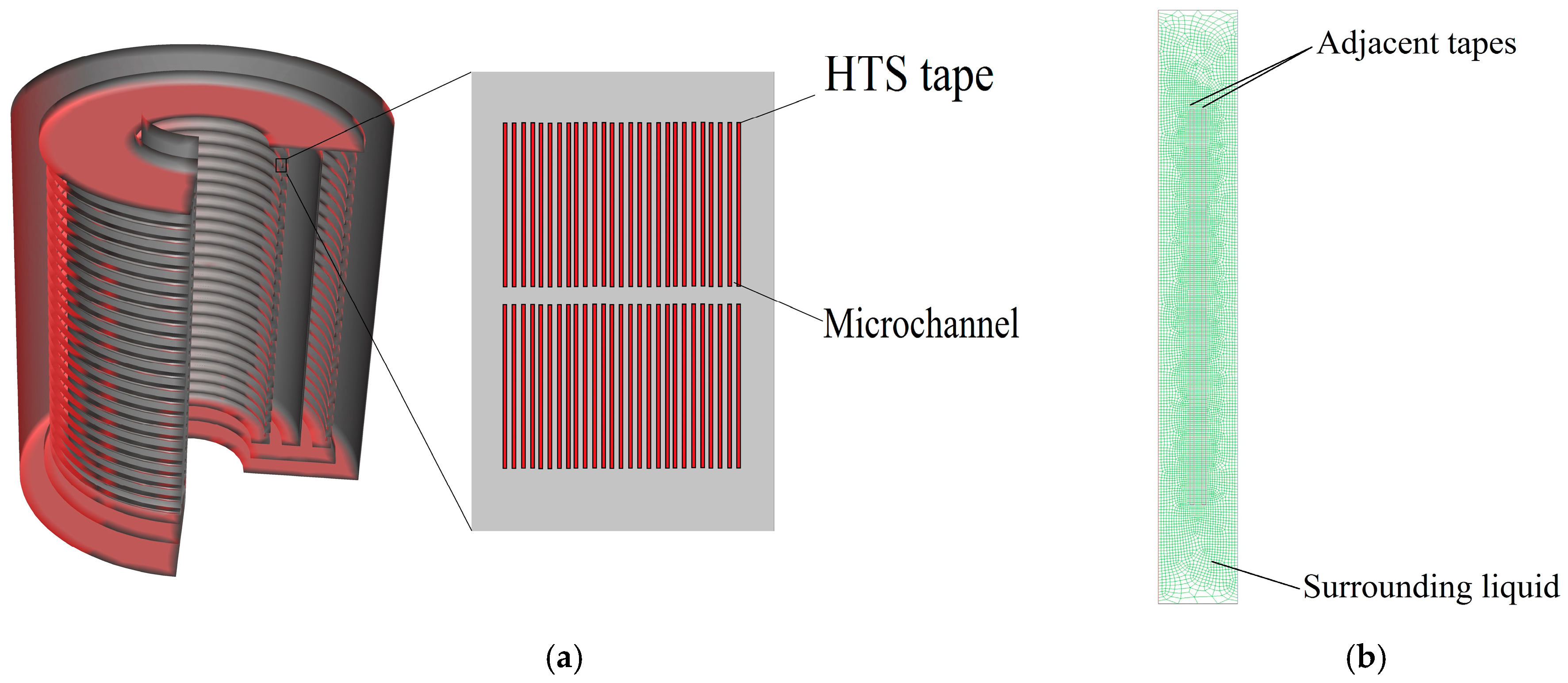
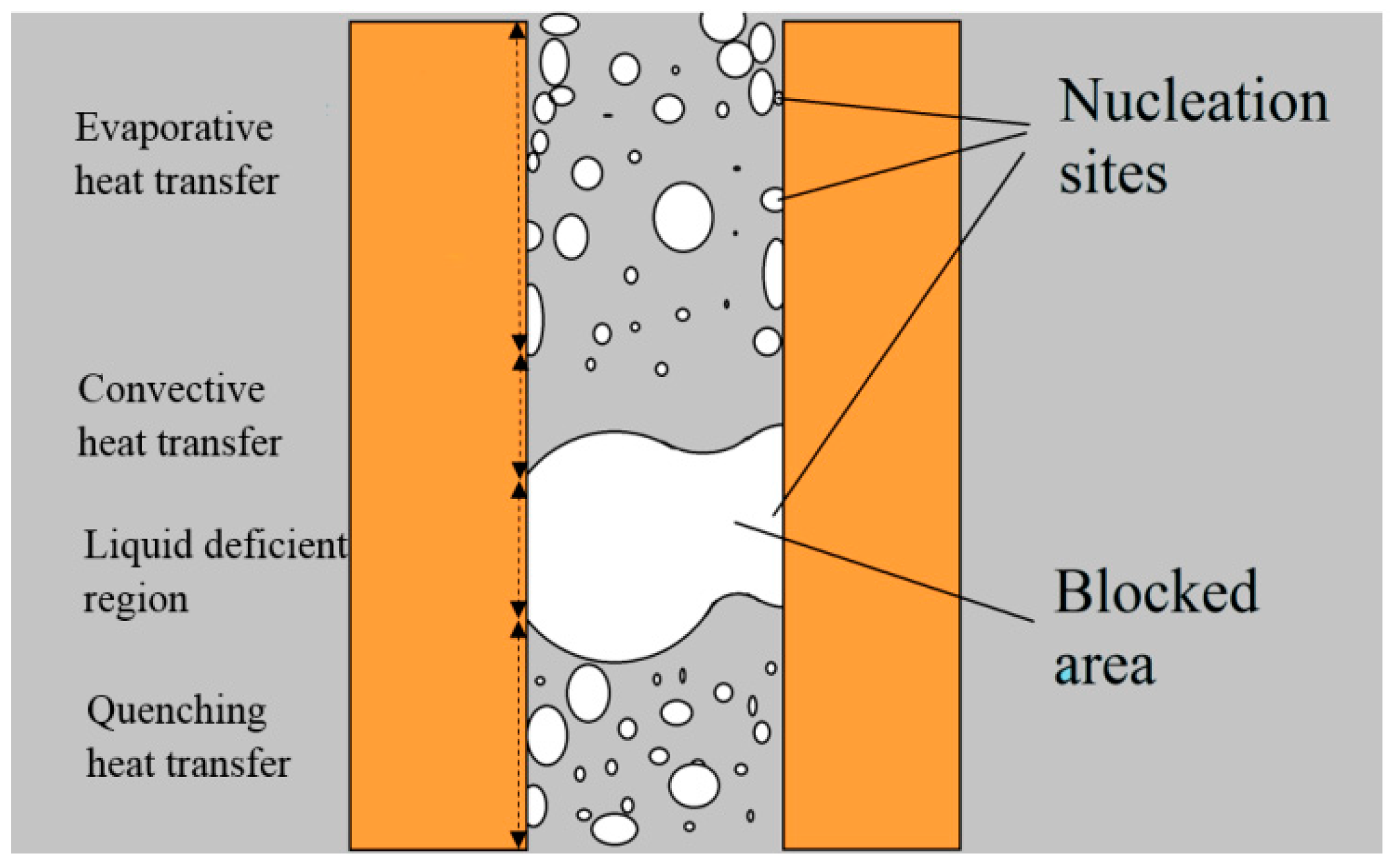
2.4. Heat Transfer
2.4.1. Convection Heat Transfer
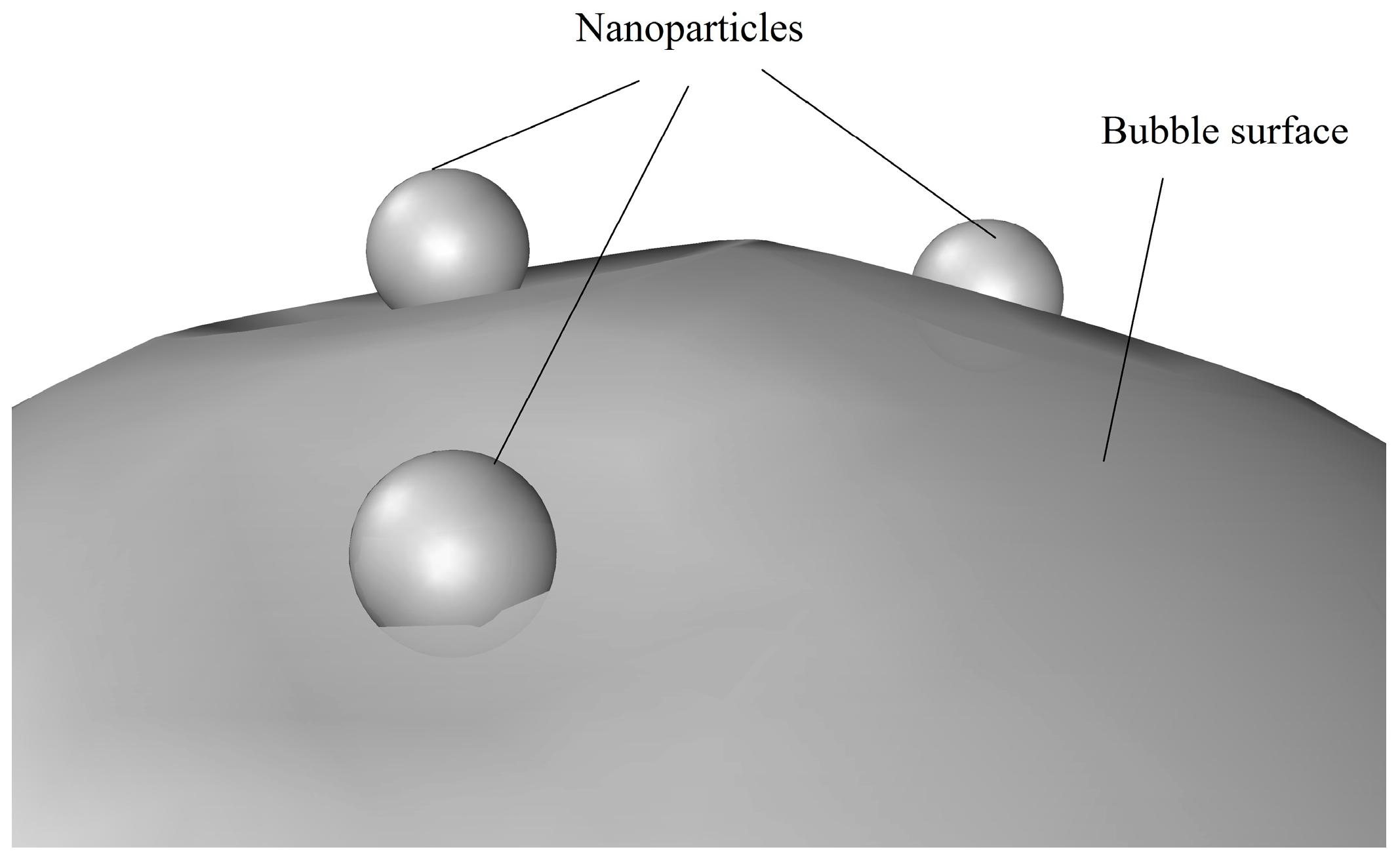
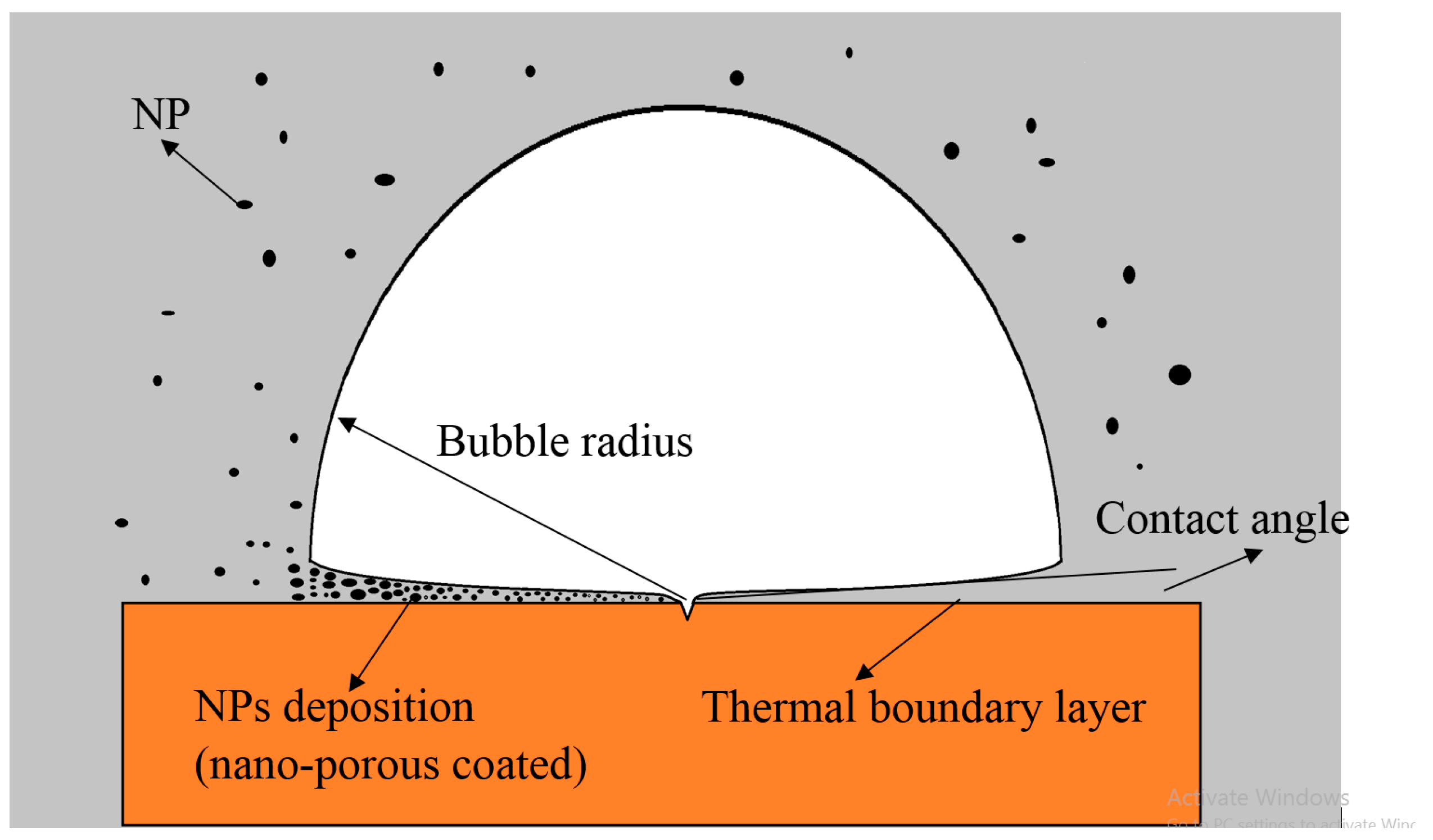
2.4.2. Nucleated Boiling Heat Transfer
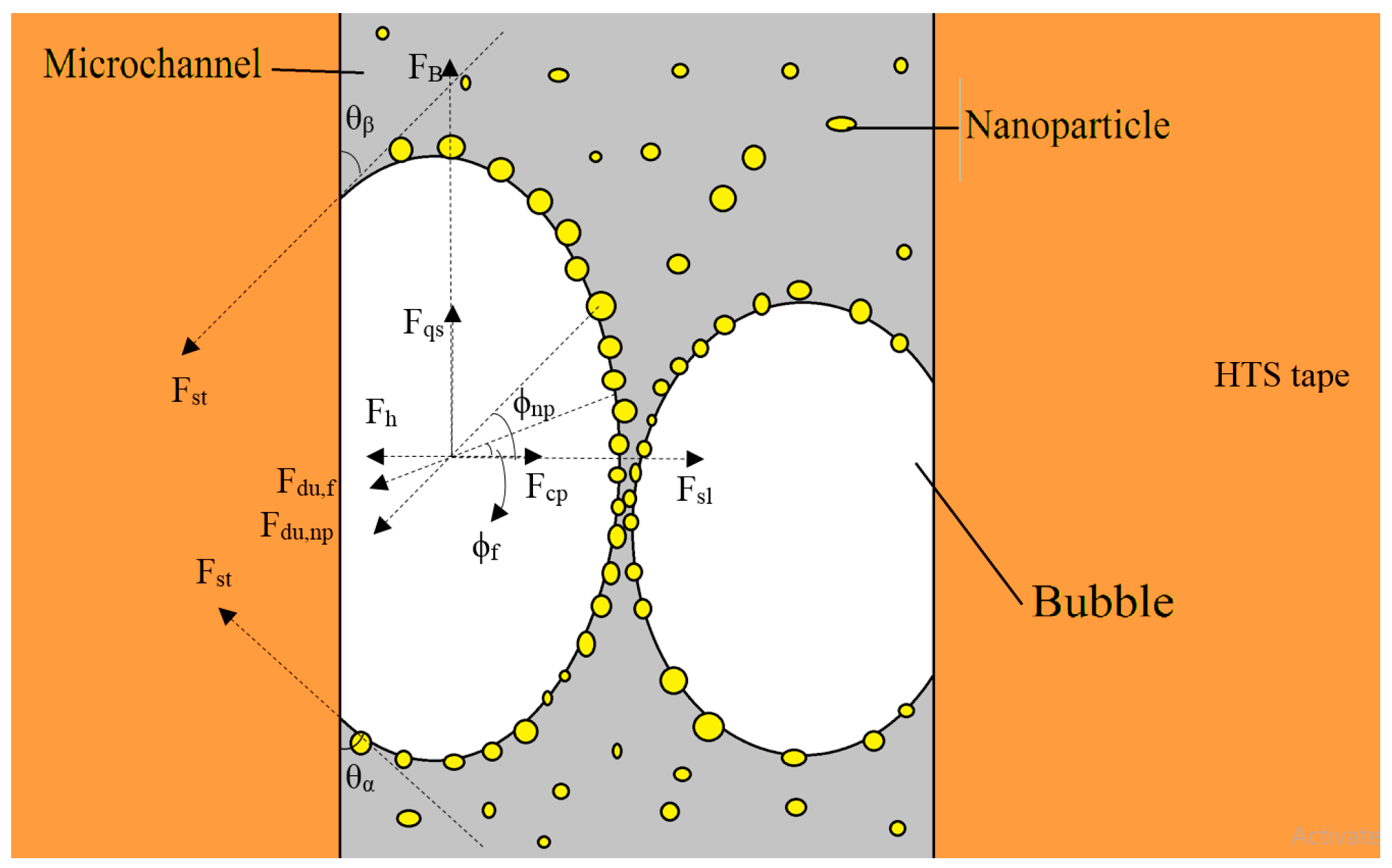
2.5. Bubbles Behaviors
2.5.1. Void Fraction
2.5.2. Governer Equations
3. Results
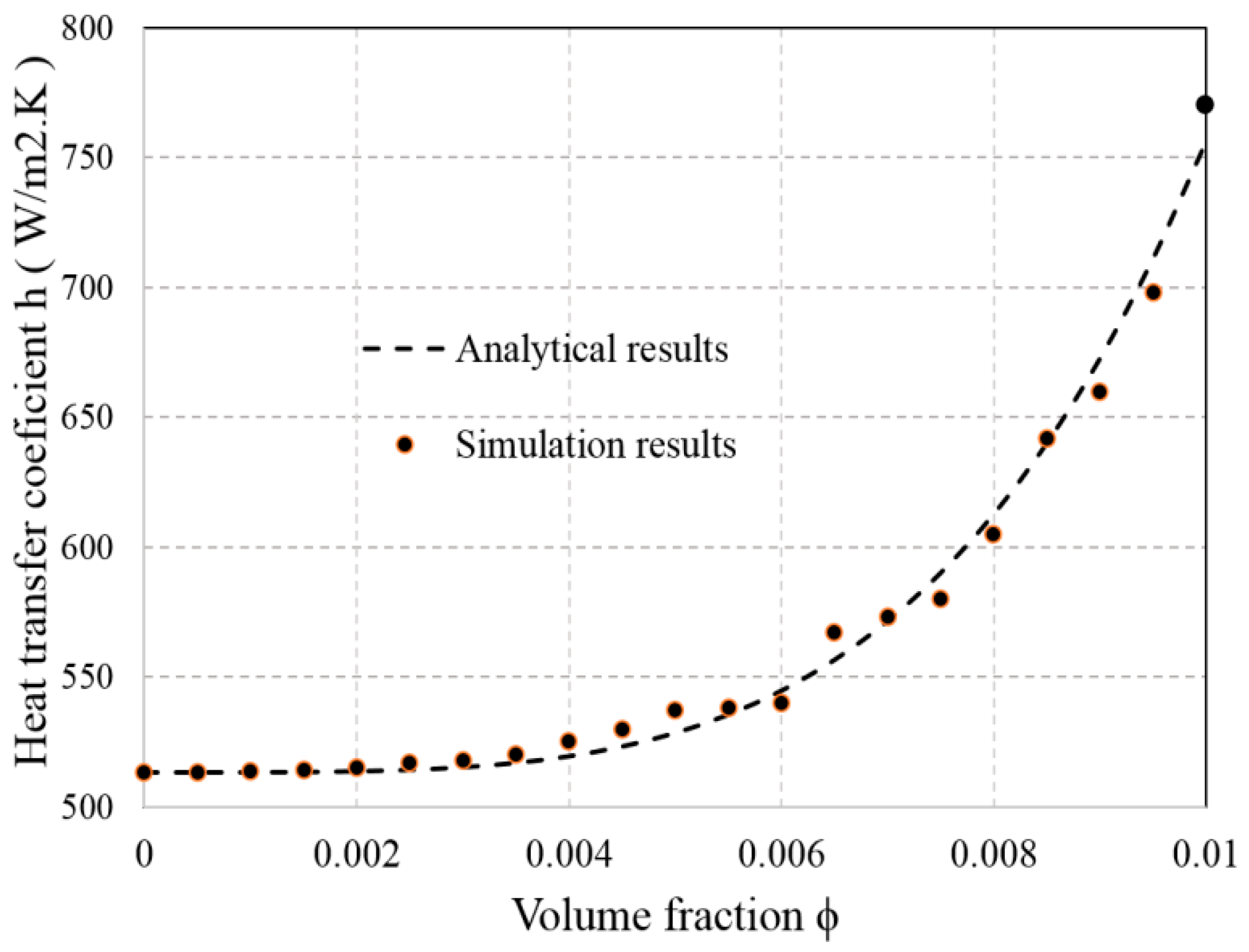
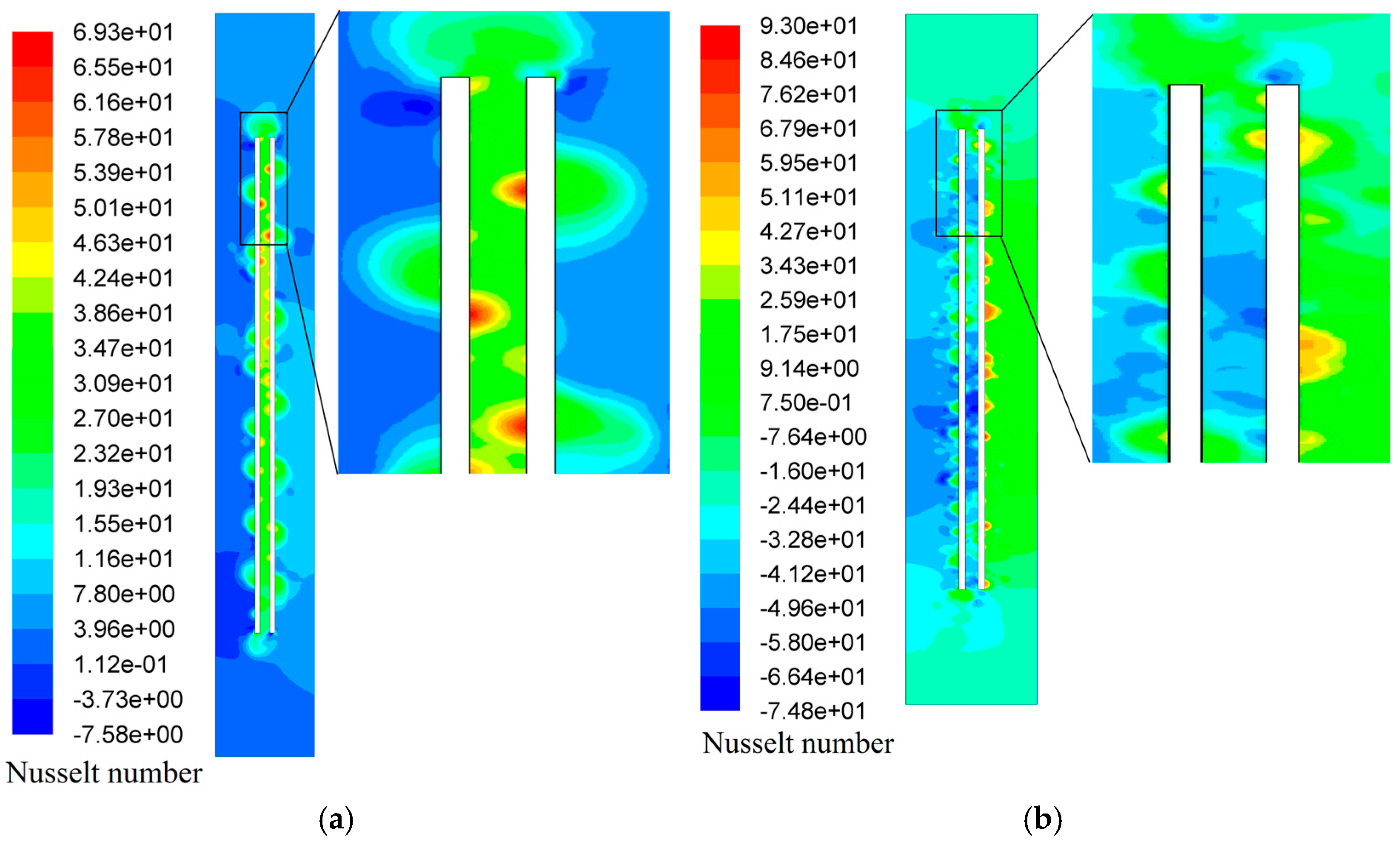
3.1. Steady-State Heat Transfer
3.2. Overload Thermal Analysis
3.3. Fault Current Condition
3.3.1. Bubble Behavior Analysis
3.3.2. Fault Condition Heat Transfer
Comparison
4. Conclusions
- Adding nanoparticles to fluids increases the heat transfer coefficient both in convection and nucleated boiling mode.
- Nanoparticles can decrease the coalescence rate between the bubbles and reduce the bubbles’ size. These results improve the cooling performance of the cooling system described in this paper.
- The results have shown that nanoparticles with a VF of 1% had the greatest effect on heat transfer and temperature distribution in microchannels.
- By adding nanoparticles, the blocked area inside the microchannels disappears. This result prevents the tapes from burning during the intense fault currents.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclatures
| Symbol | Description (unit) |
| AC loss (W) | |
| Current density (A) | |
| Electrical field (V/m) | |
| Electrical specific resistance (Ω) | |
| Critical criterion of superconductor (V/m) | |
| Critical current density (A) | |
| Self-field critical current (A) | |
| Parallel components of magnetic field (T) | |
| Perpendicular components of magnetic field (T) | |
| Fault current loss (W) | |
| l | Tape length (m) |
| S | Tape cross-section (m2) |
| Volume (m3) | |
| Density (g/m3) | |
| Specific heat capacity (J/kg.K) | |
| Thermal conductivity (W/m.K) | |
| Pressure (P) | |
| h | Heat transfer coefficient (W/m2.K) |
| Tape surface temperature (K) | |
| Fluid temperature (K) | |
| Tb | Boiling point temperature (K) |
| VF (%) | |
| Thermal expansion coefficient (1/K) | |
| Dynamic viscosity (Ns/m2) | |
| Latent heat (J/kg) | |
| Rayleigh number | |
| Nu | Nusselt number |
| Re | Reynolds number |
| Pr | Prandtl number |
| Thermal diffusivity (m2/s) | |
| Bubble contact area (m2) | |
| Tape surface are (m2) | |
| Nucleation sites density (sites/m2) | |
| Shear lift force (N) | |
| Hydrodynamic force (N) | |
| Bubble growth’s unsteady drag force from base fluid (N) | |
| Bubble growth’s unsteady drag force from nanoparticles (N) | |
| Surface tension force (N) | |
| Contact force (N) | |
| Quasi-steady drag in the flow direction (N) | |
| Gravity force (N) | |
| Buoyancy force (N) | |
| Bubble departure diameter (m) | |
| Energy dissipation rate per mass (m2/s2) | |
| R | Bubble radius (m) |
| ф | Inclined angle (rad) |
| Advancing contact angle (rad) | |
| Receding contact angle (rad) | |
| σ | Surface tension (N/m) |
| Nanoparticles porosity factor (%) | |
| Characteristic length of nanoparticle (m) | |
| Characteristic length of fluid (m) | |
| First minimum of potential well (m) | |
| Total potential energy at first minimum (van der Waals potential energy)(J) | |
| kB | Boltzmann constant (J/K) |
| Maximum surface concentration (mol/m2) | |
| M | Molar mass fluid molecule |
| Ifl | Full load current amplitude |
| Ic | Critical current |
| VFn VFmax | Volume fraction in step n Maximum volume fraction considered |
| Subscript | |
| cd | conductor |
| nf | nanofluid |
| np | nanoparticle |
| nb | nucleated boiling |
| b | bubble |
| s | solid |
| f | fluid |
| g | gas |
| l | liquid |
| v | vapor |
| bf | base fluid |
References
- Yazdani-Asrami, M.; Mirzaie, M.; Akmal, A.A.S. No-Load Loss Calculation of Distribution Transformers Supplied by Nonsinusoidal Voltage Using Three-Dimensional Finite Element Analysis. Energy 2013, 50, 205–219. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Mirzaie, M.; Akmal, A.S.; Gholamian, S.A. Life Estimation of Distribution Transformers Under Non-Linear Loads Using Calculated Loss by 2D-FEM. J. Elect. Syst. 2011, 7, 12–24. [Google Scholar]
- Yazdani-Asrami, M.; Mirzaie, M.; Akmal, A.A.S. Investigation on Impact of Current Harmonic Contents on the Distribution Transformer Losses and Remaining Life. In Proceedings of the 2010 IEEE International Conference on Power and Energy, Kuala Lumpur, Malaysia, 29 November–1 December 2010; pp. 689–694. [Google Scholar] [CrossRef]
- Sadeghi, A.; Barzegar, S.Μ.S.; Yazdani-Asrami, M. A Simple and Fast Computation Equivalent Circuit Model to Investigate the Effect of Tape Twisting on the AC Loss of HTS Cables. Eng. Technol. Appl. Sci. Res. 2022, 12, 8168–8174. [Google Scholar] [CrossRef]
- Song, W.; Pei, X.; Zeng, X.; Yazdani-Asrami, M.; Fang, X.; Fang, J.; Jiang, Z. AC Losses in Noninductive SFCL Solenoidal Coils Wound by Parallel Conductors. IEEE Trans. Appl. Supercond. 2020, 30, 5602509. [Google Scholar] [CrossRef]
- Sadeghi, A.; Seyyedbarzegar, S.; Yazdani-Asrami, M. Investigation on the Electrothermal Performance of a High-Temperature Superconducting Cable in an Offshore Wind Farm Integrated Power System: Fault and Islanding Conditions. IEEE Trans. Appl. Supercond. 2022, 32, 5401011. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Seyyedbarzegar, S.; Sadeghi, A.; de Sousa, W.T.; Kottonau, D. High Temperature Superconducting Cables and Their Performance Against Short Circuit Faults: Current Development, Challenges, Solutions, and Future Trends. Supercond. Sci. Technol. 2022, 35, 083002. [Google Scholar] [CrossRef]
- Sadeghi, A.; Bonab, S.A.; Song, W.; Yazdani-Asrami, M. Intelligent Estimation of Critical Current Degradation in HTS Tapes Under Repetitive Overcurrent Cycling for Cryo-Electric Transportation Applications. Mater. Today Phys. 2024, 42, 101365. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Song, W.; Morandi, A.; De Carne, G.; Murta-Pina, J.; Pronto, A.; Oliveira, R.; Grilli, F.; Pardo, E.; Parizh, M.; et al. Roadmap on Artificial Intelligence and Big Data Techniques for Superconductivity. Supercond. Sci. Technol. 2023, 36, 043501. [Google Scholar] [CrossRef]
- Sadeghi, A.; Song, W.; Yazdani-Asrami, M. Superconducting Transformers for Power, Energy, and Transportation Applications: An Introduction to Superconducting Technology for Transformer Engineers. Transform. Mag. 2024, 11, 98–110. [Google Scholar]
- Yazdani-Asrami, M.; Taghipour-Gorjikolaie, M.; Song, W.; Zhang, M.; Chakraborty, S.; Yuan, W. Artificial Intelligence for Superconducting Transformers. Transform. Mag. 2021, 8, 22–30. [Google Scholar]
- Yazdani-Asrami, M.; Sadeghi, A.; Song, W.; Madureira, A.; Murta-Pina, J.; Morandi, A.; Parizh, M. Artificial Intelligence Methods for Applied Superconductivity: Material, Design, Manufacturing, Testing, Operation, and Condition Monitoring. Supercond. Sci. Technol. 2022, 35, 123001. [Google Scholar] [CrossRef]
- Ghabeli, A.; Yazdani-Asrami, M.; Gholamian, S.A. A Novel Unsymmetrical Multi-Segment Concentric Winding Scheme for Electromagnetic Force and Leakage Flux Mitigation in HTS Power Transformers. IEEE Trans. Appl. Supercond. 2015, 25, 5500410. [Google Scholar] [CrossRef]
- Glasson, N.; Staines, M.; Buckley, R.; Pannu, M.; Kalsi, S. Development of a 1 MVA 3-Phase Superconducting Transformer Using YBCO Roebel Cable. IEEE Trans. Appl. Supercond. 2010, 21, 1393–1396. [Google Scholar] [CrossRef]
- Glasson, N.D.; Staines, M.P.; Jiang, Z.; Allpress, N.S. Verification Testing for a 1 MVA 3-Phase Demonstration Transformer Using 2G-HTS Roebel Cable. IEEE Trans. Appl. Supercond. 2012, 23, 5500206. [Google Scholar] [CrossRef]
- Glasson, N.; Staines, M.; Allpress, N.; Pannu, M.; Tanchon, J.; Pardo, E.; Badcock, R.; Buckley, R. Test Results and Conclusions From a 1 MVA Superconducting Transformer Featuring 2G HTS Roebel Cable. IEEE Trans. Appl. Supercond. 2016, 27, 5500205. [Google Scholar] [CrossRef]
- Staines, M.; Glasson, N.; Pannu, M.; Thakur, K.P.; Badcock, R.; Allpress, N.; D’souza, P.; Talantsev, E. The Development of a Roebel Cable Based 1 MVA HTS Transformer. Supercond. Sci. Technol. 2011, 25, 014002. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Gholamian, S.A.; Mirimani, S.M.; Adabi, J. Influence of Field-Dependent Critical Current on Harmonic AC Loss Analysis in HTS Coils for Superconducting Transformers Supplying Non-Linear Loads. Cryogenics 2021, 113, 103234. [Google Scholar] [CrossRef]
- Mahamed, M.; Seyyedbarzegar, S. Design and Thermal Analysis of a 250 MVA HTS Transformer for Substation of Offshore Wind Farms. Phys. C Supercond. Appl. 2024, 620, 1354503. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Staines, M.; Sidorov, G. Heat Transfer in HTS Transformer and Current Limiter Windings. In Proceedings of the 2nd International Workshop on Cooling Systems for HTS Applications (IWC-HTS), Karlsruhe, Germany, 13–15 September 2017. [Google Scholar]
- Staines, M.; Yazdani-Asrami, M.; Glasson, N.; Allpress, N.; Jolliffe, L.; Pardo, E. Cooling Systems for HTS Transformers: Impact of Cost, Overload, and Fault Current Performance Expectations. In Proceedings of the 2nd International Workshop on Cooling Systems for HTS Applications (IWC-HTS), Karlsruhe, Germany, 13–15 September 2017. [Google Scholar]
- Mahamed, M.; Seyyedbarzegar, S. Temperature Reduction of an HTS Transformer Under Short Circuit Fault by Modifying the Cryostat Structure: Impact of Perlator and Valve Location. Phys. C Supercond. Appl. 2024, 618, 1354429. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Staines, M.; Sidorov, G.; Eicher, A. Heat Transfer and Recovery Performance Enhancement of Metal and Superconducting Tapes Under High Current Pulses for Improving Fault Current-Limiting Behavior of HTS Transformers. Supercond. Sci. Technol. 2020, 33, 095014. [Google Scholar] [CrossRef]
- Mahamed, M.; Yazdani-Asrami, M.; Behjat, V.; Yazdani, A.; Sharifzadeh, M. Impact of Perlator on the Cooling Liquid Flow and Hottest Point Temperature of Superconducting Windings in HTS Transformer. Superconductivity 2022, 3, 100021. [Google Scholar] [CrossRef]
- Sadeghi, A.; Bonab, S.A.; Song, W.; Yazdani-Asrami, M. Short Circuit Analysis of a Fault-Tolerant Current-Limiting High Temperature Superconducting Transformer in a Power System in Presence of Distributed Generations. Superconductivity 2024, 9, 100085. [Google Scholar] [CrossRef]
- Song, W.; Jiang, Z.; Zhang, X.; Staines, M.; Badcock, R.A.; Fang, J.; Sogabe, Y.; Amemiya, N. AC Loss Simulation in a HTS 3-Phase 1 MVA Transformer Using H Formulation. Cryogenics 2018, 94, 14–21. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Staines, M.; Sidorov, G.; Davies, M.; Bailey, J.; Allpress, N.; Glasson, N.; Gholamian, S.A. Fault Current Limiting HTS Transformer with Extended Fault Withstand Time. Supercond. Sci. Technol. 2019, 32, 035006. [Google Scholar] [CrossRef]
- Jiang, Z.; Endo, N.; Wimbush, S.C.; Brooks, J.M.; Song, W.; Badcock, R.; Miyagi, D.; Tsuda, M. Exploiting Asymmetric Wire Critical Current for the Reduction of AC Loss in HTS Coil Windings. J. Phys. Commun. 2019, 3, 095017. [Google Scholar] [CrossRef]
- Pi, W.; Tian, B.; Wang, T.; Ma, Y.; Meng, Y.; Wang, Y.; Shi, Q.; Dong, J. Fault Current Characteristics of Parallel Stainless Steel & REBCO Tapes and a 6 kV/400 V HTS Transformer. IEEE Trans. Appl. Supercond. 2021, 31, 5500206. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Sadeghi, A.; Seyyedbarzegar, S.; Song, W. Role of Insulation Materials and Cryogenic Coolants on Fault Performance of MW-Scale Fault-Tolerant Current-Limiting Superconducting Transformers. IEEE Trans. Appl. Supercond. 2022, 33, 5500215. [Google Scholar] [CrossRef]
- Song, W.; Jiang, Z.; Yazdani-Asrami, M.; Staines, M.; Badcock, R.A.; Fang, J. Role of Flux Diverters in Reducing AC Loss in a Single-Phase 6.5 MVA HTS Traction Transformer for Chinese High-Speed Train Carrying High-Order Harmonic Currents. IEEE Access 2022, 10, 69650–69658. [Google Scholar] [CrossRef]
- Fang, X.; Wang, X.; Sun, Y.; Song, W.; Pei, X.; Jiang, Z.; Badcock, R.; Long, N.; Fang, J. Application of Flux Diverters in High Temperature Superconducting Transformer Windings for AC Loss Reduction. IEEE Trans. Appl. Supercond. 2021, 31, 5501005. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Song, W.; Zhang, M.; Yuan, W.; Pei, X. AC Transport Loss in Superconductors Carrying Harmonic Current With Different Phase Angles for Large-Scale Power Components. IEEE Trans. Appl. Supercond. 2020, 31, 5900205. [Google Scholar] [CrossRef]
- Ghabeli, A.; Yazdani-Asrami, M.; Besmi, M.; Gholamian, S.A. Optimization of Distributive Ratios of Apportioned Winding Configuration in HTS Power Transformers for Hysteresis Loss and Leakage Flux Reduction. J. Supercond. Nov. Magn. 2015, 28, 3463–3479. [Google Scholar] [CrossRef]
- Song, W.; Jiang, Z.; Staines, M.; Wimbush, S.C.; Badcock, R.; Fang, J. AC Loss Calculation on a 6.5 MVA/25 kV HTS Traction Transformer with Hybrid Winding Structure. IEEE Trans. Appl. Supercond. 2020, 30, 5500405. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Song, W.; Pei, X.; Zhang, M.; Yuan, W. AC Loss Characterization of HTS Pancake and Solenoid Coils Carrying Nonsinusoidal Currents. IEEE Trans. Appl. Supercond. 2020, 30, 5900709. [Google Scholar] [CrossRef]
- Jiang, Z.; Song, W.; Pei, X.; Fang, J.; Badcock, R.; Wimbush, S.C. 15% reduction in AC loss of a 3-phase 1 MVA HTS Transformer by Exploiting Asymmetric Conductor Critical Current. J. Phys. Commun. 2021, 5, 025003. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Taghipour-Gorjikolaie, M.; Song, W.; Zhang, M.; Yuan, W. Prediction of Nonsinusoidal AC Loss of Superconducting Tapes Using Artificial Intelligence-Based Models. IEEE Access 2020, 8, 207287–207297. [Google Scholar] [CrossRef]
- Bonab, S.A.; Yazdani-Asrami, M. Machine Learning-Based Model for the Intelligent Estimation of Critical Heat Flux in Nanofluids. Nano Express 2024, 5, 025012. [Google Scholar] [CrossRef]
- Uppada, V.R.; Dondapati, R.S. Role of Nanocryogenic Fluids in Optimizing the Thermohydraulic Characteristics of High Temperature Superconducting (HTS) Cables with Entropy Generation Minimization Strategy. Phys. C Supercond. Appl. 2020, 571, 1353620. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Sadeghi, A.; Atrey, M.D. Selecting a Cryogenic Cooling System for Superconducting Machines: General Considerations for Electric Machine Designers and Engineers. Int. J. Refrig. 2022, 140, 70–81. [Google Scholar] [CrossRef]
- Adnan Ashraf, W.; Khan, U.; Al-Johani, A.S.; Ahmed, N.; Mohyud-Din, S.T.; Khan, I.; Andualem, M. Impact of Freezing Temperature (Tfr) of Al2O3 and Molecular Diameter (H2O) d on Thermal Enhancement in Magnetized and Radiative Nanofluid with Mixed Convection. Sci. Rep. 2022, 12, 703. [Google Scholar]
- Lone, S.A.; Raizah, Z.; Saeed, A.; Bognár, G. Statistical Computation for Heat and Mass Transfers of Water-Based Nanofluids Containing Cu, Al2O3, and TiO2 Nanoparticles Over a Curved Surface. Sci. Rep. 2024, 14, 6908. [Google Scholar] [CrossRef]
- Noman, M.T.; Petru, M.; Amor, N.; Louda, P. Thermophysiological Comfort of Zinc Oxide Nanoparticles Coated Woven Fabrics. Sci. Rep. 2020, 10, 21080. [Google Scholar] [CrossRef]
- Ekiciler, R.; Çetinkaya, M.S.A.; Arslan, K. Heat Transfer Enhancement in An Equilateral Triangular Duct by Using an Al2o3/Water Nanofluid: Effect of Nanoparticle Shape and Volume Fraction. Heat Transf. Res. 2020, 51, 741–757. [Google Scholar] [CrossRef]
- Mahamed, M.; Seyyedbarzegar, S. Thermal Analysis of the HTS Transformer in the Fault Current Condition Considering the Tape Roughness Effect. Phys. C Supercond. Appl. 2024, 623, 1354548. [Google Scholar] [CrossRef]
- Qi, C.; Wan, Y.; Liang, L.; Rao, Z.; Li, Y. Numerical and Experimental Investigation Into the Effects of Nanoparticle Mass Fraction and Bubble Size on Boiling Heat Transfer of TiO2–Water Nanofluid. J. Heat Transf. 2016, 138, 081503. [Google Scholar] [CrossRef]
- Yahyaee, A. Influence of nanoparticle shapes in nanofluid film boiling on vertical cylinders: A numerical study. Int. J. Thermofluids 2024, 22, 100631. [Google Scholar] [CrossRef]
- You, S.M.; Kim, J.H.; Kim, K.H. Effect of Nanoparticles on Critical Heat Flux of Water in Pool Boiling Heat Transfer. Appl. Phys. Lett. 2003, 83, 3374–3376. [Google Scholar] [CrossRef]
- Mohebali, M.M.; Baniamerian, Z. Effect of Nanofluid Sedimentation on Heat Transfer and Critical Heat Flux in Boiling Flows. J. Therm. Anal. Calorim. 2024, 149, 8225–8244. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhou, X.; Wang, Y. Effects of Nanoparticle Shapes on Heat and Mass Transfer of Nanofluid Thermocapillary Convection Around a Gas Bubble. Microgravity Sci. Technol. 2020, 32, 167–177. [Google Scholar] [CrossRef]
- Puli, U. Effect of AL2O3-Water Nano Fluid on Bubble Spacing in Subcooled Flow Boiling in a Horizontal Annulus. In Proceedings of the 10th International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics, Orlando, FL, USA, 14–16 July 2014. [Google Scholar]
- Zhang, P.; Zhou, L.; Jin, L.; Zhao, H.; Du, X. Effect of Nanostructures on Rapid Boiling of Water Films: A Comparative Study by Molecular Dynamics Simulation. Appl. Phys. A 2019, 125, 142. [Google Scholar] [CrossRef]
- Li, S.; Yang, Q.; Ye, L.; Du, H.; Zhang, Z.; Huang, X.; Xu, J. Effect of Nano-Particle Concentration on Physical and Heat-Transfer Properties and Evaporation Characteristics of Graphite/N-Decane Nanofluid Fuels. ACS Omega 2022, 7, 3284–3292. [Google Scholar] [CrossRef]
- Mehrvarz, B.; Bahadori, F.; Moghaddam, S.Z. Heat Transfer Enhancement in Distribution Transformers Using TiO2 Nanoparticles. Adv. Powder Technol. 2018, 30, 221–226. [Google Scholar] [CrossRef]
- Moraveji, M.K.; Haddad, S.M.H.; Darabi, M. Modeling of Forced Convective Heat Transfer of a Non-Newtonian Nanofluid in the Horizontal Tube Under Constant Heat Flux with Computational Fluid Dynamics. Int. Commun. Heat Mass Transf. 2012, 39, 995–999. [Google Scholar] [CrossRef]
- Vontas, K.; Pavarani, M.; Miché, N.; Marengo, M.; Georgoulas, A. Validation of the Eulerian–Eulerian Two-Fluid Method and the RPI Wall Partitioning Model Predictions in OpenFOAM with Respect to the Flow Boiling Characteristics within Conventional Tubes and Micro-Channels. Energies 2023, 16, 4996. [Google Scholar] [CrossRef]
- Enjadat, S.M. CFD Comparison of Multiphase Models in the Pool Boiling State. Curved Layer. Struct. 2022, 9, 382–389. [Google Scholar] [CrossRef]
- Lee, C.Y.; Zhang, B.J.; Kim, K.J. Morphological Change of Plain and Nano-Porous Surfaces During Boiling and Its Effect on Nucleate Pool Boiling Heat Transfer. Exp. Therm. Fluid Sci. 2012, 40, 150–158. [Google Scholar] [CrossRef]
- Wu, W.; Chen, P.; Jones, B.G.; Newell, T. A Study on Bubble Detachment and the Impact of Heated Surface Structure in Subcooled Nucleate Boiling Flows. Nucl. Eng. Des. 2008, 238, 2693–2698. [Google Scholar] [CrossRef]
- Pistorius, P.C. Bubbles in Process Metallurgy. In Treatise on Process Metallurgy; Elsevier: Amsterdam, The Netherlands, 2014; pp. 179–196. [Google Scholar]
- Wenzel, R.N. Surface Roughness and Contact Angle. J. Phys. Chem. 1949, 53, 1466–1467. [Google Scholar] [CrossRef]
- Traciak, J.; Żyła, G. Effect of Nanoparticles Saturation on the Surface Tension of Nanofluids. J. Mol. Liq. 2022, 363, 119937. [Google Scholar] [CrossRef]
- Machrafi, H. Surface Tension of Nanoparticle Dispersions Unravelled by Size-Dependent Non-Occupied Sites Free Energy Versus Adsorption Kinetics. NPJ Microgravity 2022, 8, 47. [Google Scholar] [CrossRef]
- Mathure, N. Study of Flow Patterns and Void Fraction in Horizontal Two-Phase Flow; Oklahoma State University: Stillwater, OK, USA, 2010. [Google Scholar]
- Jabbarzadeh, A.; Halfina, B. Unravelling the Effects of Size, VF, and Shape of Nanoparticle Additives on Crystallization of Nanocomposite Polymers. Nanoscale Adv. 2019, 1, 4704–4721. [Google Scholar] [CrossRef]
- Elreafay, A.M.; Salem, K.M.; Abumandour, R.M.; Dawood, A.S.; Al Nuaimi, S. Effect of Particle Diameter and Void Fraction on Gas–Solid Two-Phase Flow: A Numerical Investigation Using the Eulerian–Eulerian Approach. Comput. Part. Mech. 2024, 1–23. [Google Scholar] [CrossRef]
- Zuber, N.; Findlay, J.A. Average Volumetric Concentration in Two-Phase Flow Systems. J. Heat Transf. 1965, 87, 453–468. [Google Scholar] [CrossRef]
- Wang, Y.; Deng, K.H.; Liu, B.; Wu, J.M.; Su, G.H. Experimental Study on ALN/H2O and Al2O3/H2O Nanofluid Flow Boiling Heat Transfer and Its Influence Factors in a Vertical Tube. In International Conference on Nuclear Engineering; American Society of Mechanical Engineers: New York, NY, USA, 2016; Volume 50039, p. V003T09A031. [Google Scholar]
- Wang, Y.; Deng, K.H.; Liu, B.; Wu, J.M.; Su, G.H. Experimental Study on Al2O3/H2O Nanofluid Flow Boiling Heat Transfer Under Different Pressures. In International Conference on Micro/Nanoscale Heat Transfer; American Society of Mechanical Engineers: New York, NY, USA, 2016; Volume 49651, p. V001T02A002. [Google Scholar]
- Wang, Y.; Deng, K.; Liu, B.; Wu, J.; Su, G. A Correlation of Nanofluid Flow Boiling Heat Transfer Based on the Experimental Results of ALN/H2O and Al2O3/H2O Nanofluid. Exp. Therm. Fluid Sci. 2017, 80, 376–383. [Google Scholar] [CrossRef]
- Choi, Y.J.; Kam, D.H.; Jeong, Y.H. Analysis of CHF Enhancement by Magnetite Nanoparticle Deposition in the Subcooled Flow Boiling Region. Int. J. Heat Mass Transf. 2017, 109, 1191–1199. [Google Scholar] [CrossRef]
- Sarafraz, M.M.; Arya, H.; Saeedi, M.; Ahmadi, D. Flow Boiling Heat Transfer to MgO-Therminol 66 Heat Transfer Fluid: Experimental Assessment and Correlation Development. Appl. Therm. Eng. 2018, 138, 552–562. [Google Scholar] [CrossRef]
- Balasubramanian, K.R.; Krishnan, R.A.; Suresh, S. Transient Flow Boiling Performance and Critical Heat Flux Evaluation of Al2O3-Water Nanofluid in Parallel Microchannels. J. Nanofluids 2018, 7, 1035–1044. [Google Scholar] [CrossRef]
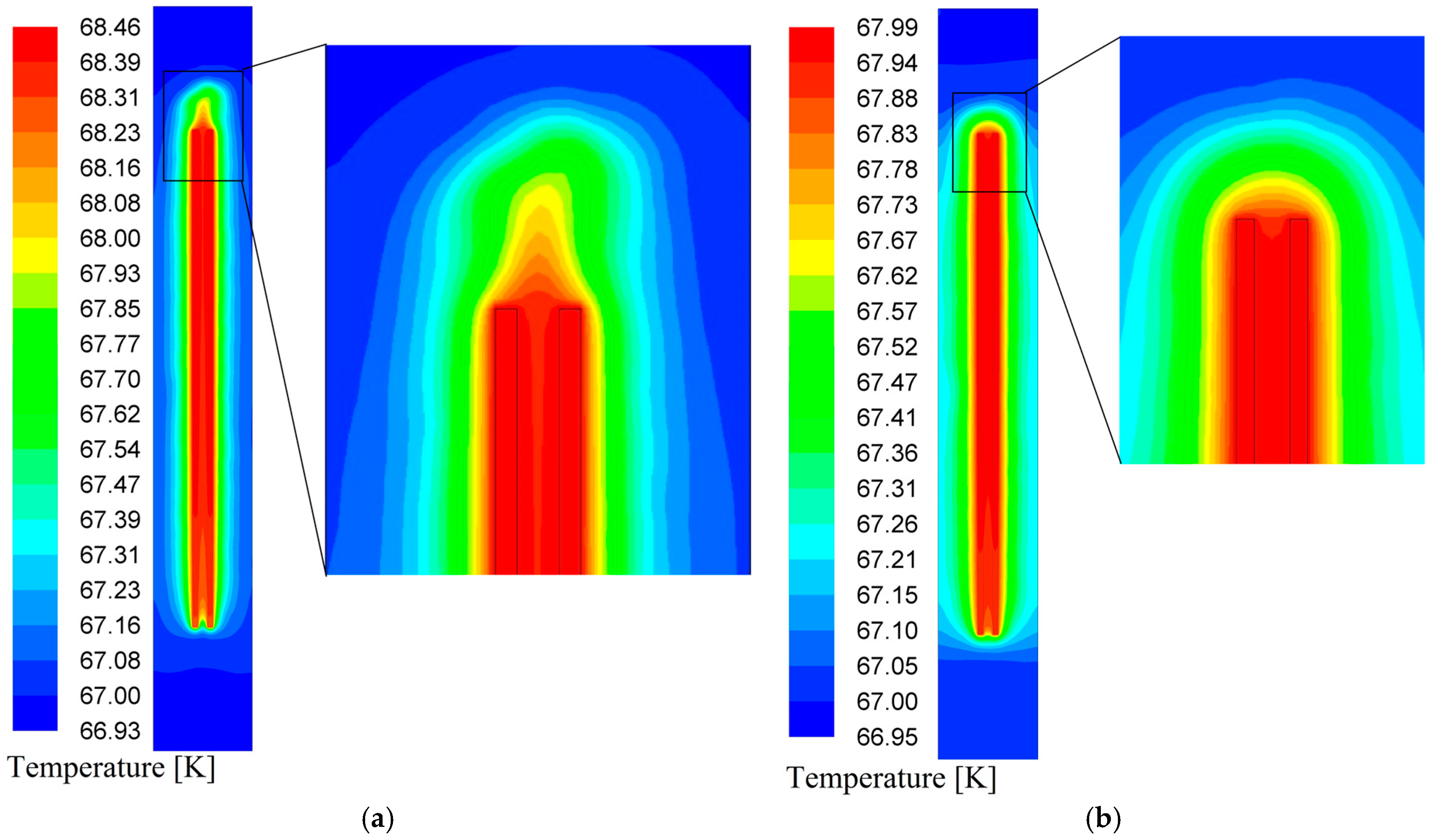
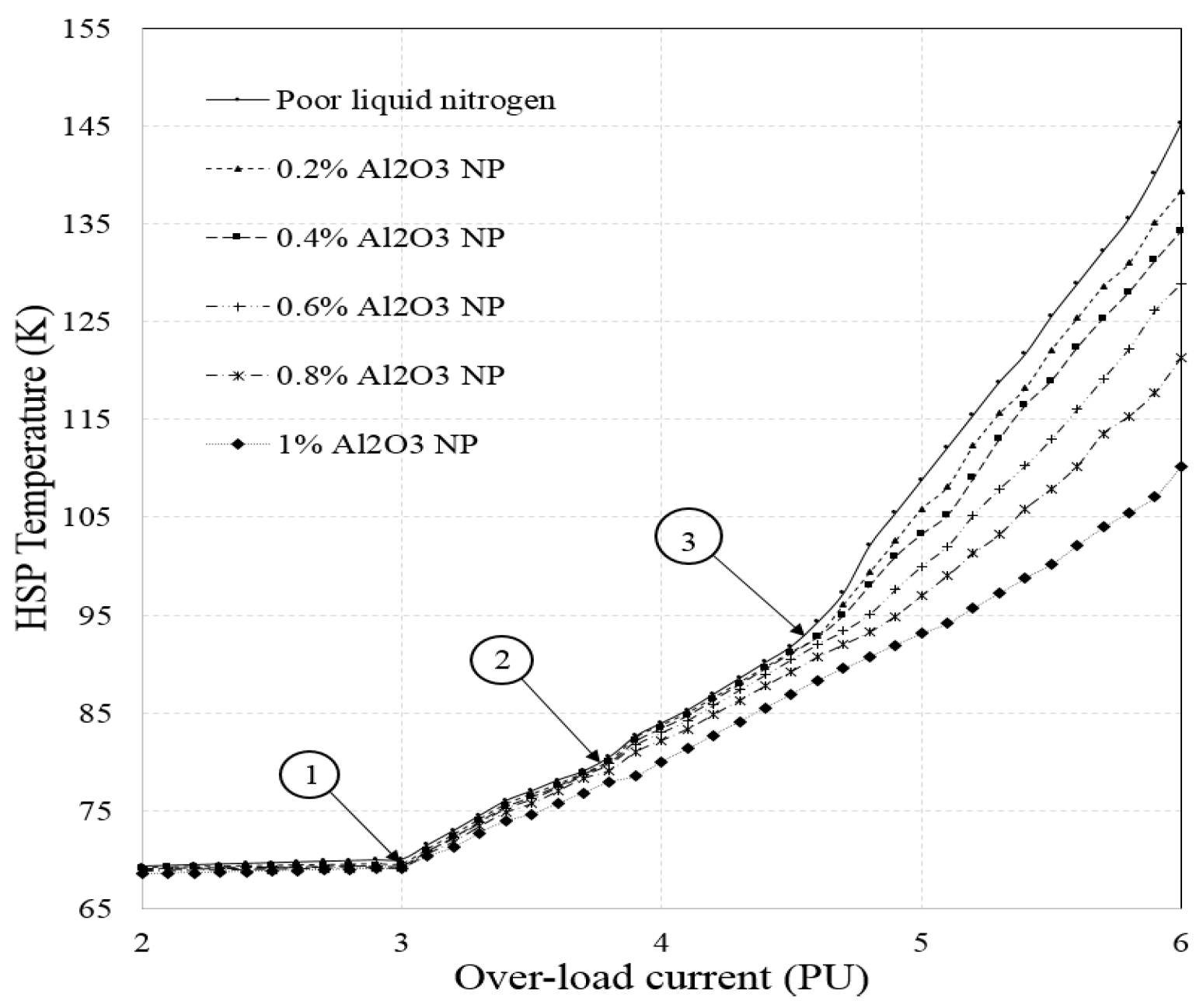
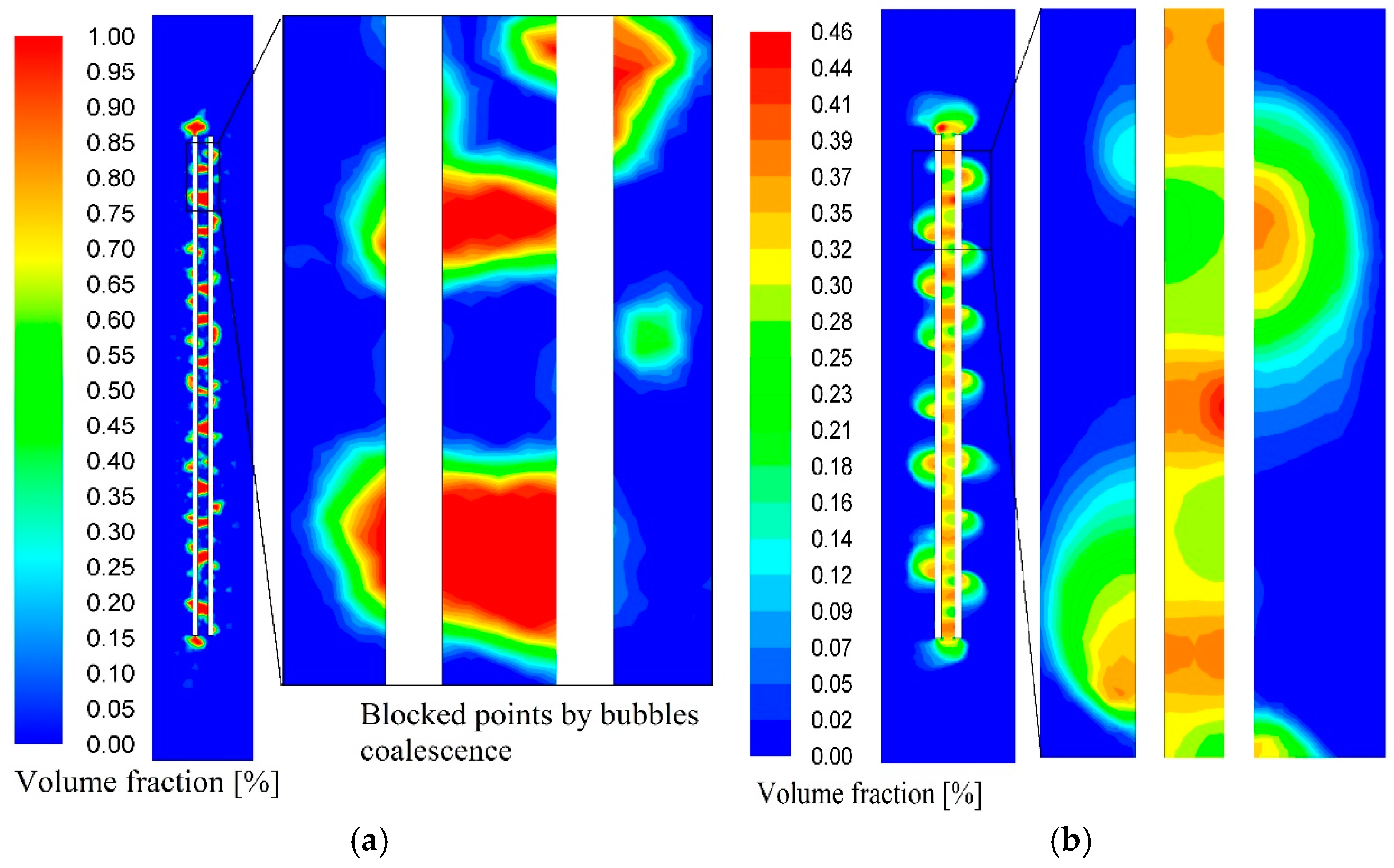
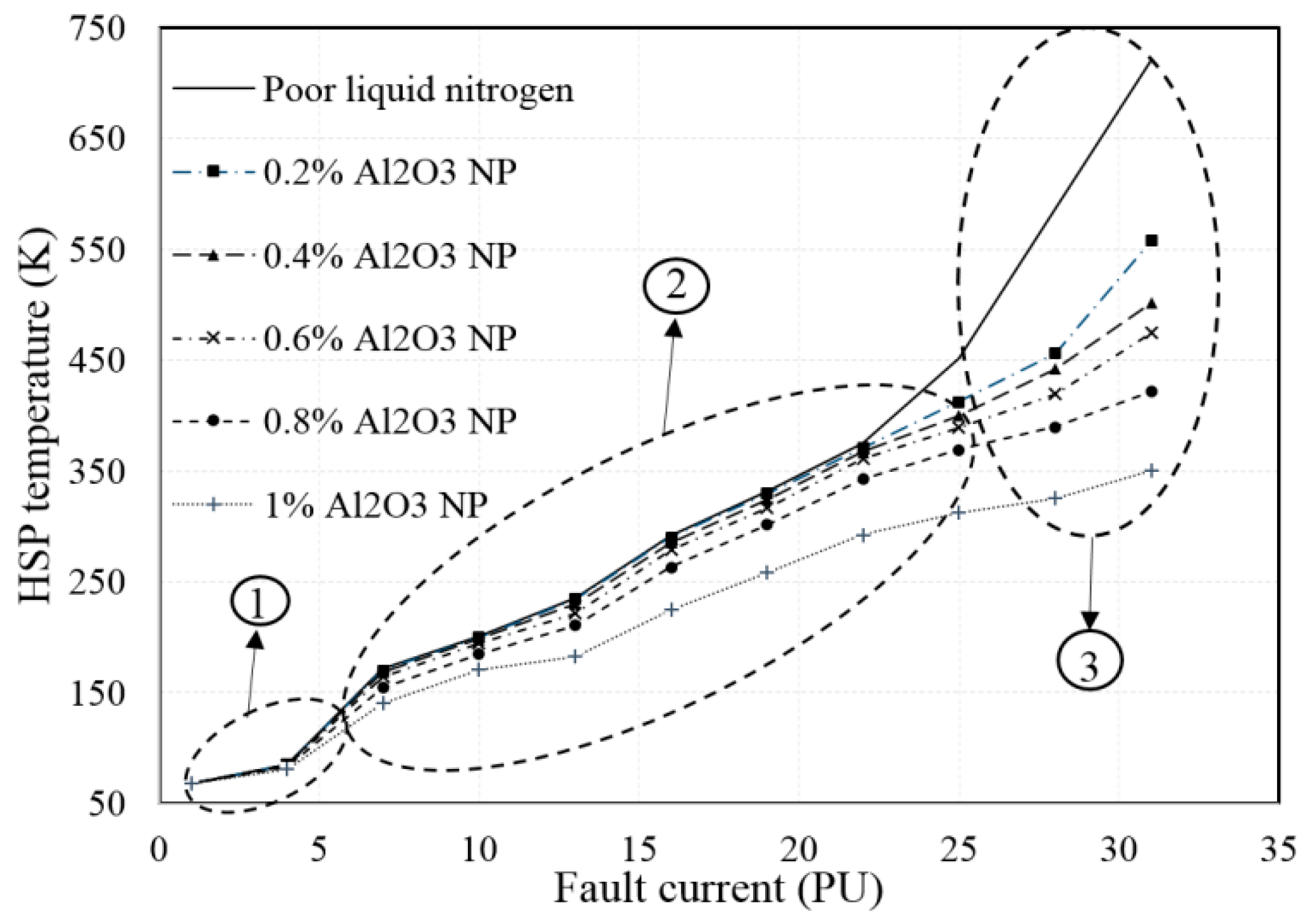

| Parameter | Value |
|---|---|
| Capacity | 250 MVA |
| HV/LV voltage | 220/33 kV |
| HV/LV current | 655/4182.5 A |
| Tape material | YBCO |
| Tape dimension | 0.12 × 10 mm2 |
| Critical current | 300 A (65 K) 200 A (77 K) |
| Microchannel width | 0.1 mm |
| Element | Dimension | Material |
|---|---|---|
| HV winding | 10 × 2500 mm | 40% Cupper, 50% Hastelloy, 4% silver, 1% YBCO, 5% other materials |
| LV winding | 2 × 5 × 2600 mm | 40% Cupper, 50% Hastelloy, 4% silver, 1% YBCO, 5% other materials |
| Cryostat | 1100 × 3000 mm | GFRP with vacuum layer |
| Windings holders | 150 × 2600 mm | GFRP |
| Core | 7500 × 4000 mm | laminated silicon steel |
| Parameter | Value |
|---|---|
| Density | 2719 kg/m3 |
| Specific heat | 843 (in 300 k) |
| Thermal conductivity | 0.045 W/m−k |
| Viscosity | 1.72 × 10−5 kg/m−s |
| Molecular weight | 26.98 kg/kmol |
| Particle size | <100 nm |
| Paper | Impact of Nanoparticle Conditions on Heat Transfer Coefficient Change (%) |
|---|---|
| Qi et al. [58] | Improved up to 77.7% in low concentrations and decreased 30.3% in high concentrations |
| You et al. [60] | Increased up to 200% |
| Mohebali et al. [61] | Reduced to 31% due to the sedimentation |
| Wang et al. [69] | Improved about 64%, 61% compared to water for AlN and c-Al2O3, respectively |
| Wang et al. [70] | Enhanced about 86% using nanofluid compared to water |
| Wang et al. [71] | Improved about 64%, 61% compared to water for AlN and c-Al2O3, respectively |
| Choi et al. [72] | Enhanced up to 40% for nanofluid compared to water |
| Sarafraz et al. [73] | Increased about 23.7% for 0.1 mass% |
| Balasubramanian et al. [74] | Enhanced during the transient state/improved up to 15% for moderate volume concentration |
| Our study | Improved up to 52% for various NP concentrations |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahamed, M.; Seyyedbarzegar, S. Impact of Nanoparticles on Heat Transfer Enhancement and Thermal Performance Improvement in HTS Power Transformers. Cryo 2025, 1, 2. https://doi.org/10.3390/cryo1010002
Mahamed M, Seyyedbarzegar S. Impact of Nanoparticles on Heat Transfer Enhancement and Thermal Performance Improvement in HTS Power Transformers. Cryo. 2025; 1(1):2. https://doi.org/10.3390/cryo1010002
Chicago/Turabian StyleMahamed, Mahdi, and Seyyedmeysam Seyyedbarzegar. 2025. "Impact of Nanoparticles on Heat Transfer Enhancement and Thermal Performance Improvement in HTS Power Transformers" Cryo 1, no. 1: 2. https://doi.org/10.3390/cryo1010002
APA StyleMahamed, M., & Seyyedbarzegar, S. (2025). Impact of Nanoparticles on Heat Transfer Enhancement and Thermal Performance Improvement in HTS Power Transformers. Cryo, 1(1), 2. https://doi.org/10.3390/cryo1010002






