Capacitive Phase Shift Detection for Measuring Water Holdup in Horizontal Oil–Water Two-Phase Flow
Abstract
:1. Introduction
2. Model of Concave Capacitance Sensor
2.1. Structure of Concave Capacitance Sensor
2.2. Equivalent Circuit Model of CCS for ST Flow
2.3. Finite Element Model of CCS for ST Flow
3. Design of the Phase Shift Detection System
3.1. Phase Shift Detection System
3.2. Basic Phase Shift Circuit
4. Parameter Optimization of the Sensor
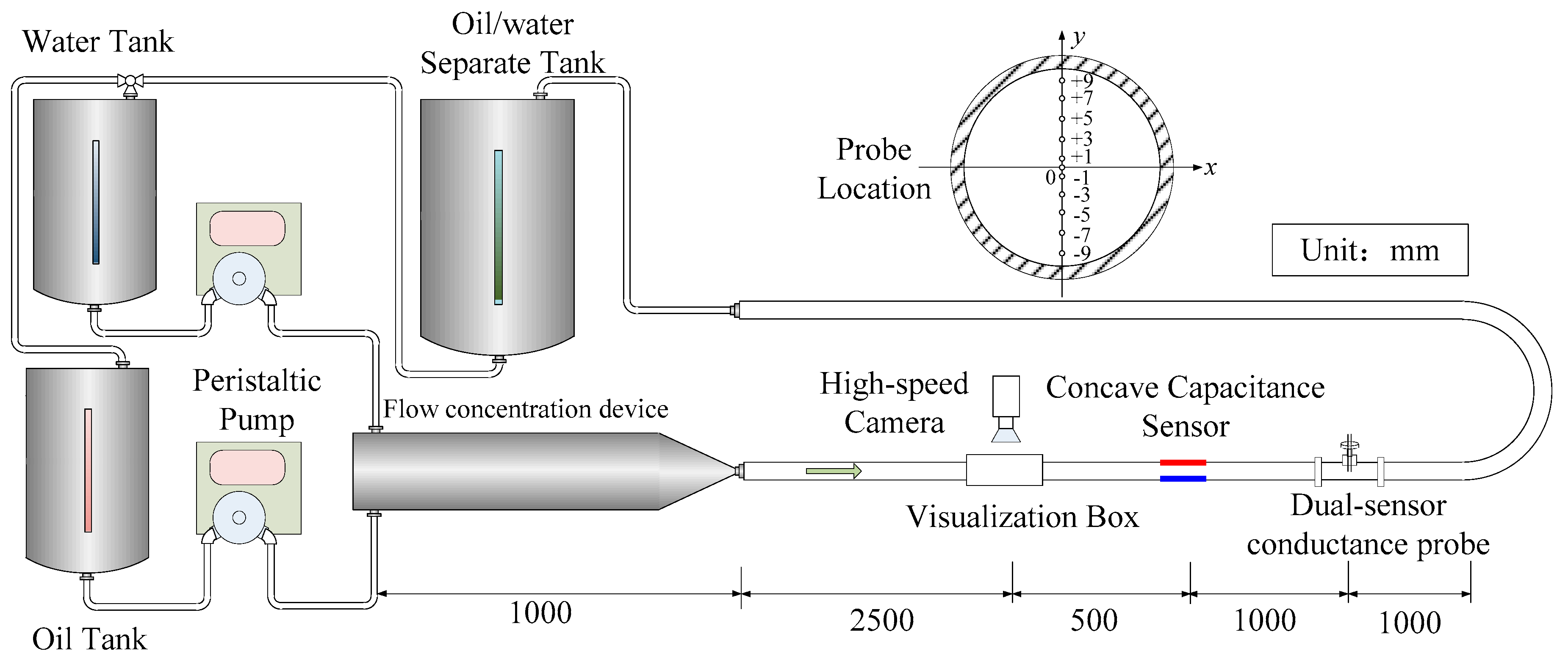
5. Experiment with Oil–Water Two-Phase Flow
5.1. Experimental Setup
5.2. Experimental Results and Discussions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Abouelwafa, M.S.A.; Kendall, E.J.M. The use of capacitance sensors for phase percentage determination in multiphase pipelines. IEEE Trans. Instrum. Meas. 1993, 29, 24–27. [Google Scholar] [CrossRef]
- Strizzolo, C.N.; Concerti, J. Capacitance sensors for measurement of phase volume fraction in two-phase pipelines. IEEE Trans. Instrum. Meas. 1993, 42, 726–729. [Google Scholar] [CrossRef]
- Ahmed, H. Capacitance sensors for void-fraction measurements and flow-pattern identification in air–oil two-phase Flow. IEEE Sens. J. 2006, 6, 1153–1163. [Google Scholar] [CrossRef]
- Salehi, S.M.; Karimi, H.; Dastranj, A.A. A capacitance sensor for gas/oil two phase flow measurement: Exciting frequency analysis and static experiment. IEEE Sens. J. 2017, 17, 679–686. [Google Scholar] [CrossRef]
- Ghai, L.L.; Pao, W.K.; Hisham, H.N.; Tang, T.B. Design of helical capacitance sensor for holdup measurement in two-phase stratified flow: A sinusoidal function approach. Sensors 2016, 16, 1032. [Google Scholar]
- Salehi, S.M.; Karimi, H.; Moosavi, R.; Dastranj, A.A. Different configurations of capacitance sensor for Gas/oil two phase flow measurement: An experimental and numerical study. Exp. Therm. Fluid Sci. 2017, 82, 349–358. [Google Scholar] [CrossRef]
- Liu, X.B.; Qiang, X.F.; Qiao, H.T.; Ma, G.; Xiong, J.; Qiao, Z. A theoretical model for a capacitance tool and its application to production logging. Flow. Meas. Instrum. 1998, 9, 249–257. [Google Scholar] [CrossRef]
- Zhang, H.X.; Zhai, L.S.; Han, Y.F.; Chen, X.; Gao, Z.K.; Jin, N. The response characteristics of coaxial capacitance sensor for horizontal segregated and non-uniform oil–water two-phase flows. IEEE Sens. J. 2017, 17, 359–368. [Google Scholar] [CrossRef]
- Zhao, A.; Jin, N.D.; Zhai, L.S.; Gao, Z.K. Liquid holdup measurement in horizontal oil–water two-phase flow by using concave capacitance sensor. Measurement 2014, 49, 153–163. [Google Scholar]
- Zhai, L.S.; Jin, N.D.; Gao, Z.K.; Wang, Z. Liquid holdup measurement with double helix capacitance sensor in horizontal oil–water two-phase flow pipes. Chin. J. Chem. Eng. 2015, 23, 268–275. [Google Scholar] [CrossRef]
- Wu, H.; Tan, C.; Dong, X.X.; Dong, F. Design of a conductance and capacitance combination sensor for water holdup measurement in oil–water two-phase flow. Flow. Meas. Instrum. 2015, 46, 218–225. [Google Scholar] [CrossRef]
- Demori, M.; Ferrari, V.; Strazza, D.; Poesio, P. A capacitive sensor system for the analysis of two-phase flows of oil and conductive water. Sens. Actuators A Phys. 2010, 163, 172–179. [Google Scholar] [CrossRef]
- Strazza, D.; Demori, M.; Ferrari, V.; Poesio, P. Capacitance sensor for hold-up measurement in high-viscous-oil/conductive-water core-annular flows. Flow Meas. Instrum. 2011, 22, 360–369. [Google Scholar] [CrossRef]
- Huang, Z.Y.; Long, J.; Xu, W.B.; Ji, H.; Wang, B.; Li, H. Design of capacitively coupled contactless conductivity detection sensor. Flow Meas. Instrum. 2012, 27, 67–70. [Google Scholar] [CrossRef]
- Ji, H.F.; Lyu, Y.C.; Wang, B.L.; Huang, Z.; Li, H.; Yan, Y. An improved capacitively coupled contactless conductivity detection sensor for industrial applications. Sens. Actuators A Phys. 2015, 235, 273–280. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, Z.Y.; Wang, B.L.; Ji, H.; Li, H. A new method for void fraction measurement of gas–liquid two-phase flow in millimeter-scale pipe. Int. J. Multiph. Flow 2015, 72, 298–305. [Google Scholar] [CrossRef]
- Wolffenbuttel, R.F.; Regtien, P.P.L. Capacitance-to-phase angle conversion for the detection of extremely small capacities. IEEE Trans. Instrum. Meas. 1987, 1001, 868–872. [Google Scholar] [CrossRef]
- Jaworek, A.; Krupa, A. Phase-shift detection for capacitance sensor measuring void fraction in two-phase flow. Sens. Actuators A Phys. 2010, 160, 78–86. [Google Scholar] [CrossRef]
- Zhai, L.S.; Jin, N.D.; Zong, Y.B.; Hao, Q.Y.; Gao, Z.K. Experimental flow pattern map, slippage and time-frequency representation of oil–water two-phase flow in horizontal small diameter pipes. Int. J. Multiph. Flow 2015, 76, 168–186. [Google Scholar] [CrossRef]
- Salvi, D.; Boldor, D.; Aita, G.M.; Sabliov, C.M. COMSOL Multiphusics model for continuous flow microwave heating of liquids. J. Food Eng. 2011, 104, 422–429. [Google Scholar] [CrossRef]
- Zhai, L.S.; Jin, N.D.; Zong, Y.B.; Wang, Z.; Gu, M. The development of a conductance method for measuring liquid holdup in horizontal oil–water two-phase flows. Meas. Sci. Technol. 2012, 23, 025304. [Google Scholar] [CrossRef]
- Zhai, L.S.; Bian, P.; Gao, Z.K.; Jin, N.D. The measurement of local flow parameters for gas–liquid two-phase bubbly flows using a dual-sensor probe array. Chem. Eng. Sci. 2016, 144, 346–363. [Google Scholar] [CrossRef]
- Edomwonyi-Otu, L.C.; Angeli, P. Pressure drop and holdup predictions in horizontal oil–water flows for curved and wavy interfaces. Chem. Eng. Res. Des. 2015, 93, 55–65. [Google Scholar] [CrossRef]















| Hw | No Error | 3° Assembly Angle Error | 5° Assembly Angle Error | 10° Assembly Angle Error | |||
|---|---|---|---|---|---|---|---|
| ϕ (°) | ϕ (°) | Relative Error | ϕ (°) | Relative Error | ϕ (°) | Relative Error | |
| 10% | −17.96 | −17.97 | 0.05% | −17.98 | 0.13% | −18.05 | 0.52% |
| 20% | −18.98 | −19.00 | 0.10% | −19.03 | 0.27% | −19.19 | 1.08% |
| 30% | −20.39 | −20.41 | 0.12% | −20.46 | 0.32% | −20.65 | 1.27% |
| 40% | −22.15 | −22.17 | 0.13% | −22.22 | 0.34% | −22.44 | 1.33% |
| 50% | −24.26 | −24.29 | 0.13% | −24.35 | 0.36% | −24.35 | 0.36% |
| 60% | −26.84 | −26.88 | 0.14% | −26.94 | 0.39% | −27.25 | 1.55% |
| 70% | −30.03 | −30.07 | 0.13% | −30.14 | 0.38% | −30.47 | 1.45% |
| 80% | −34.01 | −34.04 | 0.08% | −34.12 | 0.32% | −34.37 | 1.05% |
| 90% | −38.72 | −38.73 | 0.02% | −38.74 | 0.04% | −38.79 | 0.18% |
| Flow Pattern | Prediction Model |
|---|---|
| ST | |
| SW | |
| DC and DO/W&W |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Zhai, L.; Yan, C.; Wang, H.; Jin, N. Capacitive Phase Shift Detection for Measuring Water Holdup in Horizontal Oil–Water Two-Phase Flow. Sensors 2018, 18, 2234. https://doi.org/10.3390/s18072234
Zhang H, Zhai L, Yan C, Wang H, Jin N. Capacitive Phase Shift Detection for Measuring Water Holdup in Horizontal Oil–Water Two-Phase Flow. Sensors. 2018; 18(7):2234. https://doi.org/10.3390/s18072234
Chicago/Turabian StyleZhang, Hongxin, Lusheng Zhai, Cong Yan, Hongmei Wang, and Ningde Jin. 2018. "Capacitive Phase Shift Detection for Measuring Water Holdup in Horizontal Oil–Water Two-Phase Flow" Sensors 18, no. 7: 2234. https://doi.org/10.3390/s18072234
APA StyleZhang, H., Zhai, L., Yan, C., Wang, H., & Jin, N. (2018). Capacitive Phase Shift Detection for Measuring Water Holdup in Horizontal Oil–Water Two-Phase Flow. Sensors, 18(7), 2234. https://doi.org/10.3390/s18072234






