Development of Low-Cost Air Quality Stations for Next Generation Monitoring Networks: Calibration and Validation of PM2.5 and PM10 Sensors
Abstract
:1. Introduction
2. System Development
2.1. System Hardware
2.2. Sensors’ Specifications
- air temperature and relative humidity: AM2315 (Adafruit, New York City, NY, USA);
- CO: TGS-2600 (Figaro Inc., Arlington Heights, IL, USA);
- CO2: S8 (SenseAir, Delsbo, Sweden);
- NO2: MiCS-2714 (SGX-Sensortech, Neuchatel, Switzerland);
- O3: MiCS-2614 (SGX-Sensortech);
- VOC: MiCS-5524 (SGX-Sensortech).
3. Laboratory Calibration
3.1. Laboratory Calibration Setup
3.2. Reference Instrumentation for PM2.5 and PM10 Calibration
3.3. Calibration Procedure
- timescale alignment of both data series along the common interval;
- optimized time interpolation and resampling every 1 min;
- preliminary scatter-plot of sensor signal vs. reference signal as compared to the least squares line to detect a possible linear relationship;
- “simple” linear regression, i.e., without outliers removal, based on least squares minimization;
- robust linear regression, aimed at reducing the influence of outliers on least square fitting [38] using the M-estimation method [39], which performs an iterative weighted least squares estimation ultimately achieving a weight matrix [40]; the M-estimation function is given in the form of a weight function w(e) of residuals e, with the default tuning constant k giving coefficient estimates that are approximately 95% as statistically efficient as the ordinary least squares estimates, provided that the response has a normal distribution with no outliers [41]; in applying the M-estimation, the following weight functions have been used [42]: (i) Andrews; (ii) Bisquare; (iii) Cauchy; (iv) Fair; (v) Huber; (vi) Logistic; (vii) Talwar; (viii) Welsch;
- non-linear regressions: polynomial, i.e., (i) quadratic and (ii) cubic; (iii) exponential; (iv) power; for exponential and power regressions, a MATLAB implementation of Levenberg-Marquardt non-linear least squares algorithm has been employed which requires initial estimates of the parameters as input to successfully converge [43].
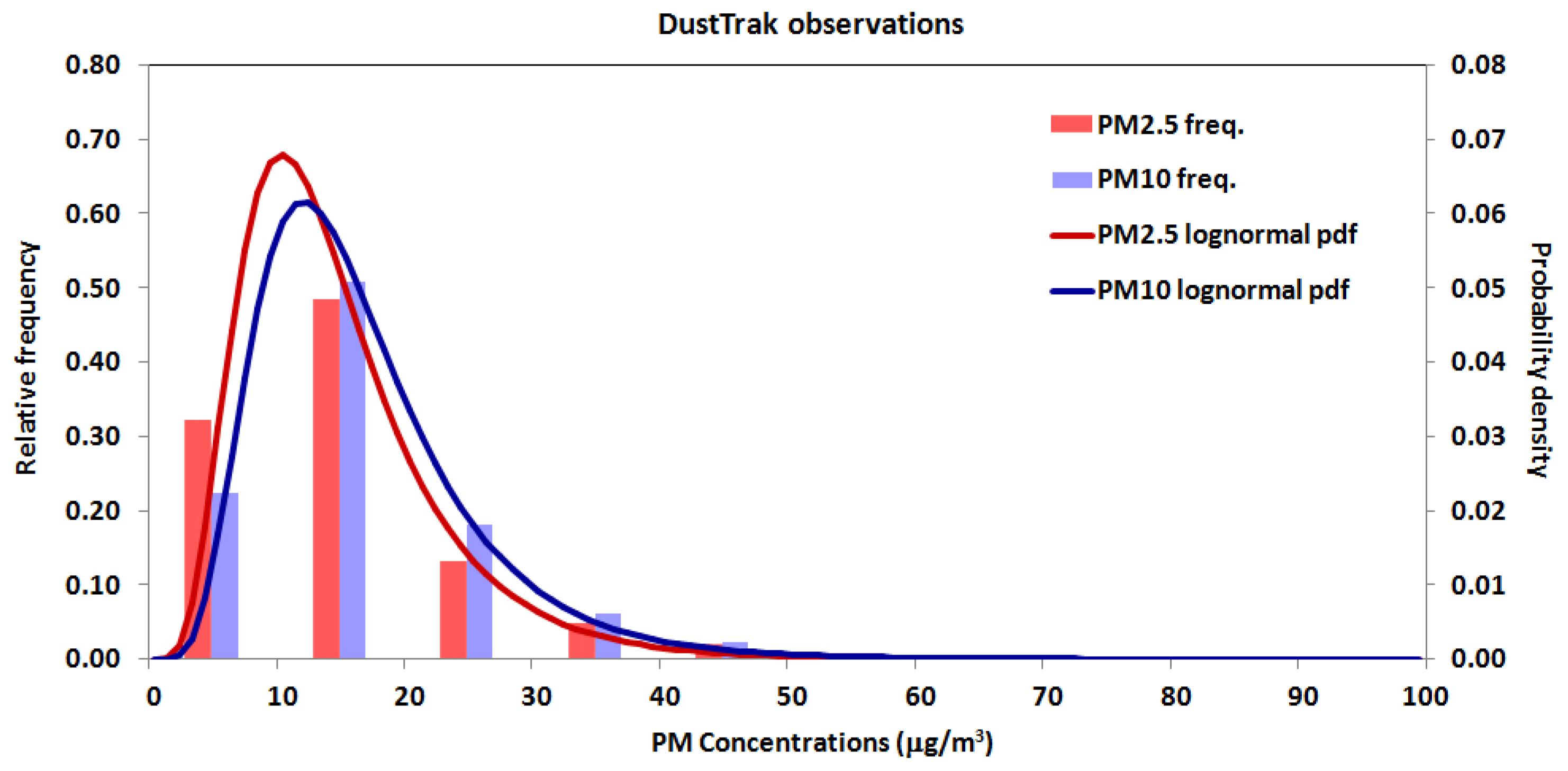
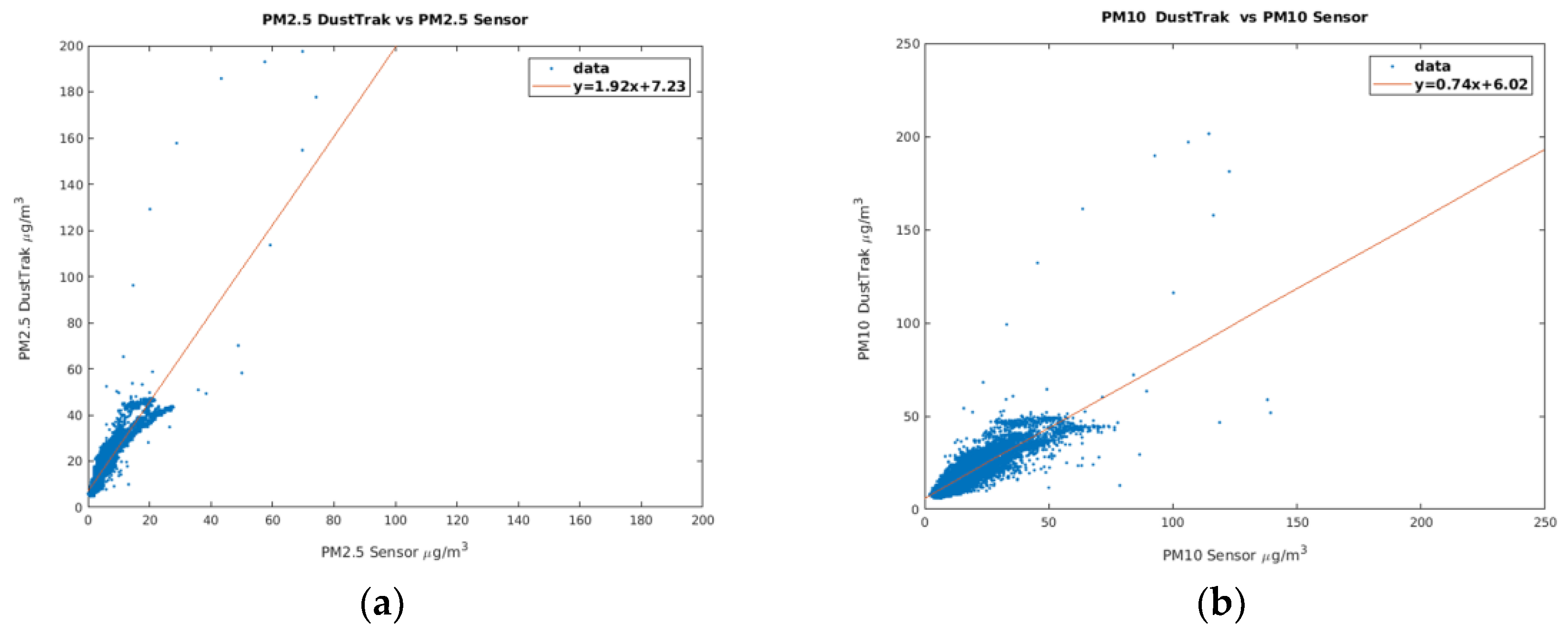
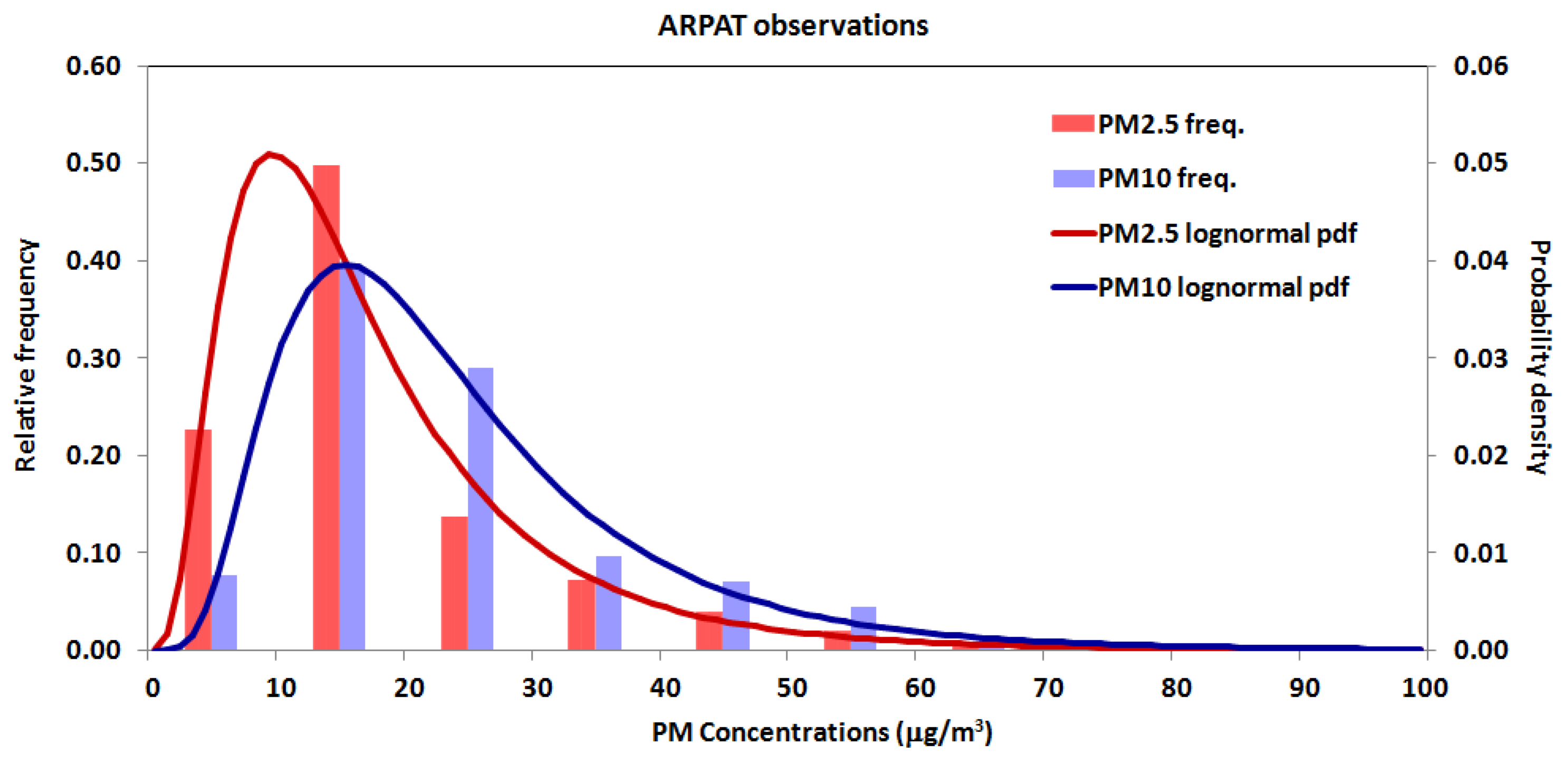
3.4. PM2.5 and PM10 Calibration Results
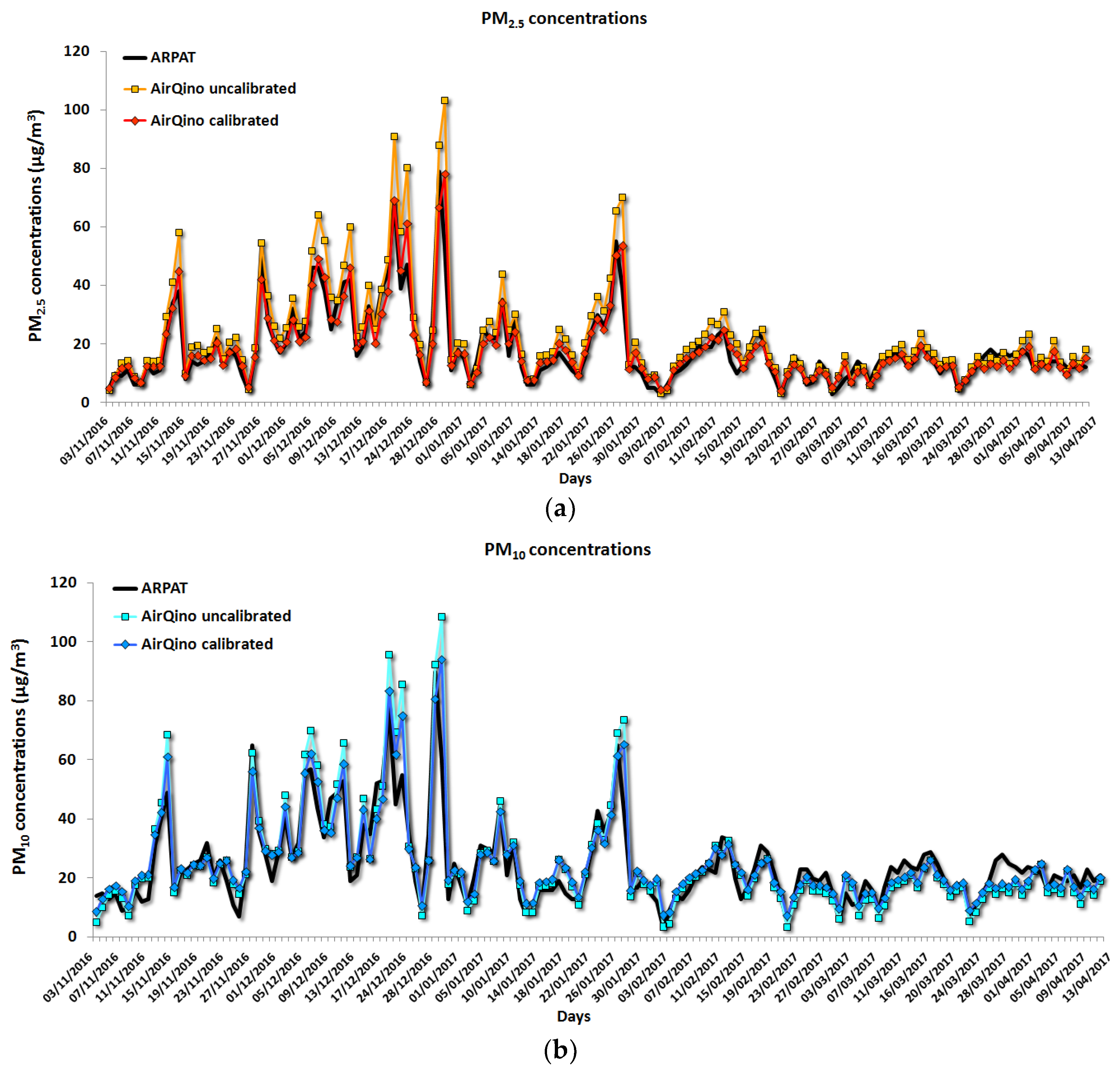
4. Field Validation
5. Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Velasco, A.; Ferrero, R.; Gandino, F.; Montrucchio, B.; Rebaudengo, M. A mobile and low-cost system for environmental monitoring: A case study. Sensors 2016, 16, 710. [Google Scholar] [CrossRef] [PubMed]
- Pope, C.A., III; Ezzati, M.; Dockery, D.W. Fine particulate air pollution and life expectancy in the United States. N. Engl. J. Med. 2009, 360, 376–386. [Google Scholar] [CrossRef] [PubMed]
- Kheirbek, I.; Wheeler, K.; Walters, S.; Kass, D.; Matte, T. PM2.5 and ozone health impacts and disparities in New York City: Sensitivity to spatial and temporal resolution. Air Qual. Atmos. Health 2013, 6, 473–486. [Google Scholar] [CrossRef] [PubMed]
- Ambient (Outdoor) Air Quality and Health. Available online: http://www.who.int/news-room/fact-sheets/detail/ambient-(outdoor)-air-quality-and-health (accessed on 10 July 2018).
- Directive 2008/50/EC of the European Parliament and of the Council of 21 May 2008 on Ambient Air Quality and Cleaner Air for Europe. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:32008L0050 (accessed on 10 July 2018).
- Kumar, P.; Morawska, L.; Martani, C.; Biskos, G.; Neophytou, M.; Di Sabatino, S.; Bell, M.; Norford, L.; Britter, R. The rise of low-cost sensing for managing air pollution in cities. Environ. Int. 2015, 75, 199–205. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chong, C.-Y.; Kumar, S.P. Sensor networks: Evolution, opportunities, and challenges. Proc. IEEE 2003, 91, 1247–1256. [Google Scholar] [CrossRef] [Green Version]
- Mead, M.I.; Popoola, O.A.M.; Stewart, G.B.; Landshoff, P.; Calleja, M.; Hayes, M.; Baldovi, J.J.; McLeod, M.W.; Hodgson, T.F.; Dicks, J.; et al. The use of electrochemical sensors for monitoring urban air quality in low-cost, high-density networks. Atmos. Environ. 2013, 70, 186–203. [Google Scholar] [CrossRef]
- Tsujita, W.; Yoshino, A.; Ishida, H.; Moriizumi, T. Gas sensor network for air-pollution monitoring. Sens. Actuators B Chem. 2005, 110, 304–311. [Google Scholar] [CrossRef]
- Kamionka, M.; Breuil, P.; Pijolat, C. Calibration of a multivariate gas sensing device for atmospheric pollution measurement. Sens. Actuators B Chem. 2006, 118, 323–327. [Google Scholar] [CrossRef]
- Clements, A.L.; Griswold, W.G.; Johnston, J.E.; Herting, M.M.; Thorson, J.; Collier-Oxandale, A.; Hannigan, M. Low-cost air quality monitoring tools: From research to practice (A Workshop Summary). Sensors 2017, 17, 2478. [Google Scholar] [CrossRef] [PubMed]
- Measuring Air Pollution with Low-Cost Sensors. EU, 2017. Available online: https://ec.europa.eu/jrc/en/publication/brochures-leaflets/measuring-air-pollution-low-cost-sensors (accessed on 7 August 2018).
- Evaluation of Low-Cost Sensors for Air Pollution Monitoring: Effect of Gaseous Interfering Compounds and Meteorological Conditions. EU, 2017. Available online: https://ec.europa.eu/jrc/en/publication/evaluation-low-cost-sensors-air-pollution-monitoring-effect-gaseous-interfering-compounds-and (accessed on 7 August 2018).
- Spinelle, L.; Gerboles, M.; Villani, M.G.; Aleixandre, M.; Bonavitacola, F. Field calibration of a cluster of low-cost commercially available sensors for air quality monitoring. Part B: NO, CO and CO2. Sens. Actuators B Chem. 2017, 238, 706–715. [Google Scholar] [CrossRef]
- Piedrahita, R.; Xiang, Y.; Masson, N.; Ortega, J.; Collier, A.; Jiang, Y.; Li, K.; Dick, R.P.; Lv, Q.; Hannigan, M.; et al. The next generation of low-cost personal air quality sensors for quantitative exposure monitoring. Atmos. Meas. Tech. 2014, 7, 3325–3336. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.; Wong, K.C.; Wei, P.; Ye, S.; Huang, H.; Yang, F.; Westerdahl, D.; Louie, P.K.K.; Luk, C.W.Y.; Ning, Z. Development and application of a next generation air sensor network for the Hong Kong marathon 2015 air quality monitoring. Sensors 2016, 16, 211. [Google Scholar] [CrossRef] [PubMed]
- Spinelle, L.; Gerboles, M.; Villani, M.G.; Aleixandre, M.; Bonavitacola, F. Field calibration of a cluster of low-cost available sensors for air quality monitoring. Part A: Ozone and nitrogen dioxide. Sens. Actuators B Chem. 2015, 215, 249–257. [Google Scholar] [CrossRef]
- Gualtieri, G.; Camilli, F.; Cavaliere, A.; De Filippis, T.; Di Gennaro, F.; Di Lonardo, S.; Dini, F.; Gioli, B.; Matese, A.; Nunziati, W.; et al. An integrated low-cost road traffic and air pollution monitoring platform to assess vehicles’ air quality impact in urban areas. In Proceedings of the 20th EURO Working Group on Transportation Meeting, Budapest, Hungary, 4–6 September 2017. [Google Scholar]
- Cheadle, L.; Deanes, L.; Sadighi, K.; Gordon Casey, J.; Collier-Oxandale, A.; Hannigan, M. Quantifying neighborhood-scale spatial variations of ozone at open space and urban sites in Boulder, Colorado using low-cost sensor technology. Sensors 2017, 17, 2072. [Google Scholar] [CrossRef] [PubMed]
- Williams, R.; Kilaru, V.J.; Snyder, E.G.; Kaufman, A.; Dye, T.; Rutter, A.; Russell, A.; Hafner, H. Air Sensor Guidebook; EPA/600/R-14/159; U.S. EPA: Washington, DC, USA, 2014.
- Spinelle, L.; Gerboles, M.; Kok, G.; Persijn, S.; Sauerwald, T. Review of portable and low-cost sensors for the ambient air monitoring of benzene and other volatile organic compounds. Sensors 2017, 17, 1520. [Google Scholar] [CrossRef] [PubMed]
- Ng, C.L.; Kai, F.M.; Tee, M.H.; Tan, N.; Hemond, H.F. A prototype sensor for in situ sensing of fine particulate matter and volatile organic compounds. Sensors 2018, 18, 265. [Google Scholar] [CrossRef] [PubMed]
- Holstius, D.M.; Pillarisetti, A.; Smith, K.R.; Seto, E. Field calibrations of a low-cost aerosol sensor at a regulatory monitoring site in California. Atmos. Meas. Tech. 2014, 7, 1121–1131. [Google Scholar] [CrossRef]
- Shao, W.; Zhang, H.; Zhou, H. Fine particle sensor based on multi-angle light scattering and data fusion. Sensors 2017, 17, 1033. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, A.; Stanton, L.G.; Graham, A.R.; Roberts, P.T. Assessing the utility of low-cost particulate matter sensors over a 12-week period in the Cuyama Valley of California. Sensors 2017, 17, 1805. [Google Scholar] [CrossRef] [PubMed]
- Zikova, N.; Hopke, P.K.; Ferro, A.R. Evaluation of new low-cost particle monitors for PM2.5 concentrations measurements. J. Aerosol Sci. 2017, 105, 24–34. [Google Scholar] [CrossRef]
- Zikova, N.; Masiol, M.; Chalupa, D.C.; Rich, D.Q.; Ferro, A.R.; Hopke, P.K. Estimating hourly concentrations of PM2.5 across a metropolitan area using low-cost particle monitors. Sensors 2017, 17, 1922. [Google Scholar] [CrossRef] [PubMed]
- Caubel, J.J.; Cados, T.E.; Kirchstetter, T.W. A new black carbon sensor for dense air quality monitoring networks. Sensors 2018, 18, 738. [Google Scholar] [CrossRef] [PubMed]
- Snyder, E.G.; Watkins, T.H.; Solomon, P.A.; Thoma, E.D.; Williams, R.W.; Hagler, G.S.; Shelow, D.; Hindin, D.A.; Kilaru, V.J.; Preuss, P.W. The changing paradigm of air pollution monitoring. Environ. Sci. Technol. 2013, 47, 11369–11377. [Google Scholar] [CrossRef] [PubMed]
- Khedo, K.K.; Perseedoss, R.; Mungur, A. A wireless sensor network air pollution monitoring system. Int. J. Wirel. Mob. Netw. 2010, 2. [Google Scholar] [CrossRef]
- Zaldei, A.; Camilli, F.; De Filippis, T.; Di Gennaro, F.; Di Lonardo, S.; Dini, F.; Gioli, B.; Gualtieri, G.; Matese, A.; Nunziati, W.; et al. An integrated low-cost road traffic and air pollution monitoring platform for next citizen observatories. Transp. Res. Procedia 2017, 24, 531–538. [Google Scholar] [CrossRef]
- Rossi, M.; Tosato, P. Energy Neutral Design of an IoT System for Pollution Monitoring. In Proceedings of the 2017 IEEE Workshop on Environmental, Energy, and Structural Monitoring Systems (EESMS), Milan, Italy, 24–25 July 2017. [Google Scholar]
- Brunelli, D.; Rossi, M. Enhancing lifetime of WSN for natural gas leakages detection. Microelectron. J. 2014, 45, 1665–1670. [Google Scholar] [CrossRef]
- Rossi, M.; Brunelli, D. Ultra low power wireless gas sensor network for environmental monitoring applications. In Proceedings of the 2012 IEEE Workshop on Environmental Energy and Structural Monitoring Systems (EESMS), Perugia, Italy, 28 September 2012. [Google Scholar]
- Rossi, M.; Brunelli, D.; Adami, A.; Lorenzelli, L.; Menna, F.; Remondino, F. Gas-drone: Portable gas sensing system on UAVs for gas leakage localization. In Proceedings of the 2014 IEEE SENSORS, Valencia, Spain, 2–5 November 2014. [Google Scholar]
- Chambers, J.M. Graphical Methods for Data Analysis; Wadsworth International Group: Belmont, CA, USA; Duxbury Press: Boston, MA, USA, 1983. [Google Scholar]
- Cook, R.D. Detection of influential observation in linear regression. Technometrics 1977, 19, 15–18. [Google Scholar]
- Fox, J.; Weisberg, S. Robust Regression. October 2013. Available online: http://users.stat.umn.edu/~sandy/courses/8053/handouts/robust.pdf (accessed on 10 July 2018).
- Stefanski, L.A.; Boos, D.D. The calculus of M-estimation. Am. Statist. 2002, 56, 29–38. [Google Scholar] [CrossRef]
- Kutner, M.H.; Nachtsheim, C.; Neter, J. Applied Linear Regression Models; McGraw-Hill/Irwin: New York, NY, USA, 2004. [Google Scholar]
- Chatterjee, S.; Mächler, M. Robust regression: A weighted least squares approach. Commun. Stat. Theory Methods 1997, 26, 1381–1394. [Google Scholar] [CrossRef]
- Holland, P.W.; Welsch, R.E. Robust regression using iteratively reweighted least-squares. Commun. Stat. Theory Methods 1977, 6, 813–827. [Google Scholar] [CrossRef]
- Lourakis, M.I.A. A brief description of the Levenberg-Marquardt algorithm implemented by levmar. Found. Res. Technol. 2005, 4, 1–6. [Google Scholar]
- Draper, N.R.; Smith, H. Applied Regression Analysis, 3rd ed.; John Wiley: Hoboken, NJ, USA, 1998; ISBN 0-471-17082-8. [Google Scholar]
- Spiess, A.N.; Neumeyer, N. An evaluation of R 2 as an inadequate measure for nonlinear models in pharmacological and biochemical research: A Monte Carlo approach. BMC Pharmacol. 2010, 10, 6. [Google Scholar] [CrossRef] [PubMed]
- Fox, J. Applied Regression Analysis and Generalized Linear Models; Sage Publications, Inc.: Thousand Oaks, CA, USA, 2008. [Google Scholar]
- Annual Report on Air Quality in the Tuscany Region—Year 2016. Technical Report; Tuscany Region Environmental Protection Agency (ARPAT). March 2017. Available online: http://www.arpat.toscana.it/documentazione/catalogo-pubblicazioni-arpat/relazione-annuale-sullo-stato-della-qualita-dellaria-nella-regione-toscana-anno-2016 (accessed on 10 July 2018). (In Italian).
- Jiao, W.; Hagler, G.; Williams, R.; Sharpe, R.; Brown, R.; Garver, D.; Judge, R.; Caudill, M.; Rickard, J.; Davis, M.; et al. Community Air Sensor Network (CAIRSENSE) project: Evaluation of low-cost sensor performance in a suburban environment in the southeastern United States. Atmos. Meas. Tech. 2016, 9, 5281–5292. [Google Scholar] [CrossRef]
- Cross, E.S.; Williams, L.R.; Lewis, D.K.; Magoon, G.R.; Onasch, T.B.; Kaminsky, M.L.; Worsnop, D.R.; Jayne, J.T. Use of electrochemical sensors for measurement of air pollution: Correcting interference response and validating measurements. Atmos. Meas. Tech. 2017, 10, 3575–3588. [Google Scholar] [CrossRef]
- Esposito, E.; De Vito, S.; Salvato, M.; Bright, V.; Jones, R.L.; Popoola, O. Dynamic neural network architectures for on field stochastic calibration of indicative low cost air quality sensing systems. Sens. Actuators B Chem. 2016, 231, 701–713. [Google Scholar] [CrossRef]
- Borrego, C.; Costa, A.M.; Ginja, J.; Amorim, M.; Coutinho, M.; Karatzas, K.; Sioumis, T.; Katsifarakis, N.; Konstantinidis, K.; De Vito, S.; et al. Assessment of air quality microsensors versus reference methods: The EuNetAir joint exercise. Atmos. Environ. 2016, 147, 246–263. [Google Scholar] [CrossRef]
- Riani, M.; Cerioli, A.; Atkinson, A.C.; Perrotta, D. Monitoring robust regression. Electron. J. Stat. 2014, 8, 646–677. [Google Scholar] [CrossRef]
- Rousseeuw, P.J.; Perrotta, D.; Riani, M.; Hubert, M. Robust monitoring of many time series with application to fraud detection. arXiv, 2017; arXiv:1708.08268. [Google Scholar]







| Regression Laws | Equation |
|---|---|
| Linear | F(x) = β0 + β1 x |
| Quadratic | F(x) = β0 + β1 x + β2 x2 |
| Cubic | F(x) = β0 + β1 x + β2 x2 + β3 x3 |
| Exponential | F(x) = β0 exp(β1 x) |
| Power | F(x) = β0 xβ1 |
| Regression Model | R2 | MB (µg/m3) | RMSE (µg/m3) | SSR (mg/m3)2 | SSE (mg/m3)2 | SST (mg/m3)2 |
|---|---|---|---|---|---|---|
| Linear | ||||||
| Without outlier removal | 0.8095 | −0.0342 | 3.3 | 0.6228 | 0.1475 | 0.7743 |
| With outlier removal (3.36%) | 0.7655 | 0.0388 | 2.6 | 0.2793 | 0.0852 | 0.3645 |
| Robust linear | ||||||
| Andrew | 0.8499 | −0.2461 | 2.7 | 0.5855 | 0.1033 | 0.6888 |
| Bisquare | 0.8501 | −0.2456 | 2.7 | 0.5856 | 0.1032 | 0.6888 |
| Cauchy | 0.8484 | −0.2453 | 2.8 | 0.5841 | 0.1043 | 0.6885 |
| Fair | 0.8447 | −0.2209 | 2.8 | 0.5897 | 0.1084 | 0.6981 |
| Huber | 0.8532 | −0.2446 | 2.7 | 0.5857 | 0.1007 | 0.6864 |
| Logistic | 0.8478 | −0.2344 | 2.8 | 0.5876 | 0.1054 | 0.6931 |
| Talwar | 0.8634 | −0.1993 | 2.6 | 0.5785 | 0.0915 | 0.6701 |
| Welsh | 0.8499 | −0.2453 | 2.7 | 0.5853 | 0.1033 | 0.6887 |
| Non-linear | ||||||
| Quadratic | 0.8098 | −0.0462 | 3.3 | 0.6270 | 0.1473 | 0.7743 |
| Cubic | 0.8197 | −0.1001 | 3.2 | 0.6347 | 0.1396 | 0.7743 |
| Exponential | - | −0.7755 | 5.4 | 0.3729 | 0.2629 | 0.7683 |
| Power | - | −0.0643 | 3.4 | 0.1531 | 0.6513 | 0.7683 |
| Regression Model | R2 | MB (µg/m3) | RMSE (µg/m3) | SSR (mg/m3)2 | SSE (mg/m3)2 | SST (mg/m3)2 |
|---|---|---|---|---|---|---|
| Linear | ||||||
| Without outlier removal | 0.6747 | 0.0836 | 4.5 | 0.5532 | 0.2667 | 0.8199 |
| With outlier removal (3.72%) | 0.7221 | 0.0312 | 3.2 | 0.3448 | 0.1342 | 0.4830 |
| Robust linear | ||||||
| Andrew | 0.7499 | −0.1249 | 3.5 | 0.4998 | 0.1666 | 0.6665 |
| Bisquare | 0.7500 | −0.1240 | 3.5 | 0.4999 | 0.1665 | 0.6665 |
| Cauchy | 0.7485 | −0.1184 | 3.5 | 0.5000 | 0.1679 | 0.6680 |
| Fair | 0.7459 | −0.0977 | 3.6 | 0.5056 | 0.1721 | 0.6778 |
| Huber | 0.7480 | −0.1043 | 3.5 | 0.5023 | 0.1692 | 0.6715 |
| Logistic | 0.7481 | −0.1047 | 3.5 | 0.5039 | 0.1696 | 0.6735 |
| Talwar | 0.7679 | −0.1109 | 3.3 | 0.4921 | 0.1486 | 0.6408 |
| Welsh | 0.7500 | −0.1204 | 3.5 | 0.5005 | 0.1667 | 0.6673 |
| Non-linear | ||||||
| Quadratic | 0.6981 | 0.1574 | 4.3 | 0.5806 | 0.2475 | 0.8199 |
| Cubic | 0.7081 | 0.0115 | 4.3 | 0.5724 | 0.2393 | 0.8199 |
| Exponential | - | −0.1506 | 4.9 | 0.3098 | 0.3892 | 0.8145 |
| Power | - | −0.0556 | 4.6 | 0.2721 | 0.6122 | 0.8145 |
| Pollutant | Regression Model | β0 | β1 | R2 | MB (µg/m3) | RMSE (µg/m3) | SSR (mg/m3)2 | SSE (mg/m3)2 | SST (mg/m3)2 |
|---|---|---|---|---|---|---|---|---|---|
| PM2.5 | Robust linear: Talwar | 6.3 | 2.0 | 0.8634 | −0.8634 | 2.6 | 0.5785 | 0.0915 | 0.6701 |
| PM10 | Robust linear: Talwar | 5.0 | 0.7 | 0.7679 | −0.7679 | 3.3 | 0.4921 | 0.1486 | 0.6408 |
| Pollutant | Station | Mean | Standard Deviation | Range |
|---|---|---|---|---|
| PM2.5 | ARPAT | 18.45 | 12.64 | 3.00–79.00 |
| AIRQino uncalibrated | 22.85 | 17.32 | 3.11–103.53 | |
| AIRQino calibrated | 18.49 | 12.79 | 3.92–78.06 | |
| PM10 | ARPAT | 24.80 | 14.31 | 3.00–90.00 |
| AIRQino uncalibrated | 25.52 | 18.41 | 3.49–108.79 | |
| AIRQino calibrated | 25.40 | 15.17 | 7.25–94.00 |
| Pollutant | Score | AIRQino Station | |
|---|---|---|---|
| Uncalibrated | Calibrated | ||
| PM2.5 | MB (µg/m3) | 4.394 | 0.036 |
| NMB (%) | 21.401 | 0.196 | |
| MAE (µg/m3) | 4.827 | 2.683 | |
| RMSE (µg/m3) | 7.955 | 4.056 | |
| NRMSE (%) | 38.746 | 21.959 | |
| R2 | 0.900 | 0.957 | |
| FAC2 | 0.987 | 1.000 | |
| PM10 | MB (µg/m3) | 0.720 | 0.598 |
| NMB (%) | 2.863 | 2.384 | |
| MAE (µg/m3) | 5.103 | 4.309 | |
| RMSE (µg/m3) | 7.802 | 6.084 | |
| NRMSE (%) | 31.011 | 24.240 | |
| R2 | 0.840 | 0.909 | |
| FAC2 | 0.987 | 0.987 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cavaliere, A.; Carotenuto, F.; Di Gennaro, F.; Gioli, B.; Gualtieri, G.; Martelli, F.; Matese, A.; Toscano, P.; Vagnoli, C.; Zaldei, A. Development of Low-Cost Air Quality Stations for Next Generation Monitoring Networks: Calibration and Validation of PM2.5 and PM10 Sensors. Sensors 2018, 18, 2843. https://doi.org/10.3390/s18092843
Cavaliere A, Carotenuto F, Di Gennaro F, Gioli B, Gualtieri G, Martelli F, Matese A, Toscano P, Vagnoli C, Zaldei A. Development of Low-Cost Air Quality Stations for Next Generation Monitoring Networks: Calibration and Validation of PM2.5 and PM10 Sensors. Sensors. 2018; 18(9):2843. https://doi.org/10.3390/s18092843
Chicago/Turabian StyleCavaliere, Alice, Federico Carotenuto, Filippo Di Gennaro, Beniamino Gioli, Giovanni Gualtieri, Francesca Martelli, Alessandro Matese, Piero Toscano, Carolina Vagnoli, and Alessandro Zaldei. 2018. "Development of Low-Cost Air Quality Stations for Next Generation Monitoring Networks: Calibration and Validation of PM2.5 and PM10 Sensors" Sensors 18, no. 9: 2843. https://doi.org/10.3390/s18092843
APA StyleCavaliere, A., Carotenuto, F., Di Gennaro, F., Gioli, B., Gualtieri, G., Martelli, F., Matese, A., Toscano, P., Vagnoli, C., & Zaldei, A. (2018). Development of Low-Cost Air Quality Stations for Next Generation Monitoring Networks: Calibration and Validation of PM2.5 and PM10 Sensors. Sensors, 18(9), 2843. https://doi.org/10.3390/s18092843












