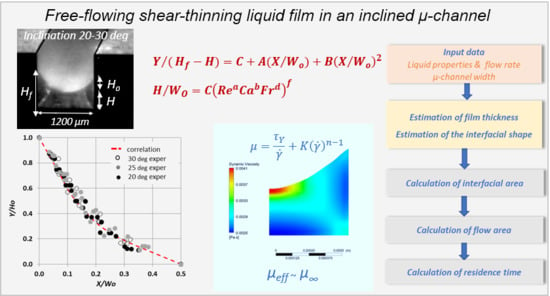
Free-Flowing Shear-Thinning Liquid Film in Inclined μ-Channels

Abstract

Among the most important variables in the design of falling film microreactors (FFMRs) is the liquid film thickness as well as the gas/liquid interfacial area, which dictate the mass and heat transfer rates. In a previous work conducted in our lab the characteristics of a free-falling Newtonian liquid film have been studied and appropriate correlations have been proposed. In this work the geometrical characteristics of a non-Newtonian shear thinning liquid, flowing in an inclined open microchannel, have been experimentally investigated and design correlations that can predict with reasonable accuracy the features of a FFMR have been proposed. The test section used was an open μ-channel with square cross section (W_O = 1200 μm) made of brass which can be set to various inclination angles. The liquid film characteristics were measured by a non-intrusive technique that is based on the features of a micro Particle Image Velocimetry (μ-PIV) system. Relevant computational fluid dynamics (CFD) simulations revealed that the volume average dynamic viscosity over the flow domain is practically the same as the corresponding asymptotic viscosity value, which can thus be used in the proposed design equations. Finally, a generalized algorithm for the design of FFMRs, containing non-Newtonian shear thinning liquids, is suggested.

1. Introduction

The term process intensification describes the methodology which aims to build smaller, more compact and cheaper systems. Microfluidics, i.e., the technology that concerns the manipulation of fluids at the submillimeter scale, has shown considerable promise for improving diagnostics and biology research [1]. Among other potential applications, microfluidics includes fluid handling and quantitative analysis in healthcare and veterinary medicine [2]. During the last decades, engineers have developed various micro-devices which have at least one characteristic dimension less than 1 mm and can be potentially used in biological and medical applications. These microdevices are also characterized by low consumption of reagents and multifunctionality, as various unit operations can be combined in a single piece of equipment.

Microreactors are among the widely studied microdevices, since they have significant advantages over conventional ones [3]. Falling film microreactors (FFMRs) are liquid–gas phase contact devices in which the aim is to generate thin liquid films and to achieve large contact areas between the two phases. The large gas/liquid interface which provides enhanced mass transfer rates between the phases is included between the main advantages of micro-reactors [4]. Biomedical applications involve body fluids, such as blood, saliva, semen, mucus, that are fluids which exhibit non-Newtonian shear thinning behavior.

Most of the published work concerning FFMR deals with the conversion rate of specific reactions (e.g., [4,5]), while limited work [6,7] has been published on the characteristics of the interface in such devices. For example, Ishikawa et al. [8], have studied the CO₂ absorption into a wavy falling film of NaOH aqueous solution on a micro-baffled plate using two methods for visualizing the liquid film thickness. The first method uses the light reflection from a small angle (5°), that illuminates the liquid surface of a liquid film at another angle (45°). The second one is a particle injection method. More specifically the particles are PMMA slurry that can be detected and form the liquid film layer. Lokhat et al. [9], also studied, via CO₂ absorption experiments, the influence of a reaction plate orientation and gas flow rate on liquid phase mass transfer coefficient. They proposed correlations that are based on Nusselt’s condensation theory. Tourvieille et al. [6], have visualized the liquid film thickness using fluorescence confocal microscopy, and they proposed correlations for determining the mass transfer coefficient, using Nusselt and Kapitza numbers. Yang et al. [10], who have investigated the liquid film thickness and the shape of the interface on an open channel FFMR using stereo digital microscopy, also proposed an empirical correlation, that predicts their experimentally measured liquid film thickness with 7% deviation. Patel et al. [11], have proposed another technique for the characterization of the interface between the liquid and the gas phase in a microchannel, using tracing particles and a microscope, and proved that this technique can reach the accuracy of 1.06 μm, without proposing any correlations for this specific method. Yu et al. [7], have experimentally measured the meniscus shape and the characteristics of the flow in inclined open rectangular microgrooves heat sinks using micro Particle Image Velocimetry (μ-PIV), and found that the meniscus shape is a parabolic arc.

In a previous work conducted in our lab the characteristics of a free falling Newtonian liquid film have been studied [12] and correlations have been proposed [13]. The aim of the present study is to extend our previous work [12,13] by performing experiments with non-Newtonian shear-thinning liquids and to check whether these correlations are valid for this type of fluids. Our ultimate goal is to propose an algorithm for the design of FFMRs.

2. Experimental Procedure

In a previous work of our group [12], a μ-PIV system, i.e., a non-intrusive method intended for measuring 2D velocity fields in microfluidics, was suitably adapted to measure the liquid film thickness and to reconstruct the shape of the interface of a free-flowing Newtonian liquid layer in an open μ-channel. In the proposed technique the area covered by the liquid phase is identified by recording the fluorescent particles used in μ-PIV for measuring the velocity field.

2.1. Experimental Setup

The experimental setup (Figure 1) comprises the test section, i.e., the open microchannel, which is connected to a syringe pump (AL-2000, World Precision Instruments^®, Sarasota, FL, USA) to feed the liquid and the μ-PIV system. The μ-PIV system used consists of a high sensitivity charge-coupled device (CCD) camera (Hisense MkII, Dantec Dynamics^®, Skovlunde, Denmark), which is connected to a microscope (Nikon Eclipse LV150, Nikon Corporation^®, Tokyo, Japan), while the acquired images were processed by the Flow Manager Software (Dantec Dynamics, v4.00). Prior to measurements the fluids were traced by adding Nile red fluorescent carboxylate microspheres (Invitrogen, Carlsbad, MA, USA) with mean diameter of 1 μm. The measurements were conducted 30 diameters downstream from the inlet of the microchannel, where fully developed flow is established. The test section was placed on the microscope stage, which can be moved along its vertical axis with ten-micron accuracy. To obtain sufficiently magnified images a 20× air immersion objective with numerical aperture (NA) equal to 0.45 was used, which results in 3 μm depth of field. The maximum recording frame rate of the camera is 12.2 fps and that restricts the maximum frequency of the measurements to 12 Hz. The field of view was covering the whole channel width.

The test section used (Figure 2) was an open μ-channel, with square cross section (W_O = 1200 μm), made of brass. The test section was constructed by employing ultrahigh precision micromachining techniques, which have the unique advantage of being able to manufacture geometrically complex miniature components to high accuracy, with fine surface finish, in a wide range of engineering materials. The test-section used in the present was constructed using a five-axis ultra-precision micro milling machine that ensures both minimal surface roughness and straightness of the channels. Typical overall values of repeatability, surface finish and straightness achievable by this procedure are in the range of 1.0 μm, 0.040 μm Ra, and 0.2 μm over 100 mm of travel respectively. The channel was milled using a 500 μm cutter at 200 μm steps, while to ensure minimal surface roughness, a final 20 μm cut was performed.

To assure continuous free flow, the liquid phase enters by overflowing a circular region preceding the inlet of the microchannel. To conduct the measurements, the lens axis must be perpendicular to the test section and so the microscope was placed on platform that can be tilted up to 45° from the horizontal position (Figure 1). The measurements were conducted at three inclination angles, namely 20°, 25°, and 30°.

Two non-Newtonian shear thinning fluids were used. Presented in

Table 1. Physical properties of liquids used.

Index	Liquid	Refractive Index	Contact Angle	Density	Surface Tension	Viscosity
		-	(°)	(kg/m3)	(mN/m)	(Pa·s)
nW	100% water + 0.03% xanthan gum	1.340	74	998	72.1	μ = 0.003698γ−1 + 0.004339γ−0.1819
nG20	75% water + 25% glycerol w/w + 0.03% xanthan gum	1.360	74	1059	66.7	μ = 0.002952γ−1 + 0.006295γ−0.1535

are their physical properties, i.e., density, ρ, surface tension, σ, and the contact angle (for brass) measured by a tensiometer (KSV Cam200, KSV Instruments^®, Helsinki, Finland), and dynamic viscosity, μ, measured by a magnetic rheometer (AR-G2, TA Instruments, Sussex, UK). All properties were evaluated at room temperature (20–22 °C), and the experiments were conducted under the same conditions. The viscosity of the shear-thinning non-Newtonian fluids used can be accurately described by the Herschel–Bulkley model [14]:

$$\begin{array}{c}\mu =\frac{{\tau }_Y}{\dot{\gamma }}+{\rm K}{\left(\dot{\gamma }\right)}^{n-1}\end{array}$$

(1)

where, ${\tau }_Y$, is the yield stress, K, the viscosity consistency and n, the power law index. The physical properties of the fluids are shown in Table 1, while, for the liquids employed, Figure 3 presents the dependence of viscosity on shear rate.

2.2. Measuring Procedure

As already mentioned at the experimental set-up section, μ-PIV measurements require the injection of fluorescent tracing particles into the fluid. Consequently, in each focusing plane, the liquid phase corresponds to areas where light spots are visible, the external dark areas are identified as the walls of the microchannel, whereas the inner dark area corresponds to the gas phase (Figure 4). The use of proper microscope objectives ensures a narrow depth of field, which in turn increases the measuring accuracy, since the focus plane can be moved with a steady step of 10–20 μm resulting in to the recording of 20–25 planes per measurement.

The measuring system was calibrated by measuring a known liquid film thickness, i.e., by measuring the thickness of the liquid layer obtained when a known liquid volume is placed in a vessel with known cross-section. It must be noted that during the measurements the displacement of the focusing plane due to refraction was also considered.

During each measurement, the plane, where the tracing particles are initially visible, is recognized as the first plane of the measurements. When the bottom of the meniscus, i.e., the plane where the liquid covers the entire area, is reached, no dark regions are observed. By further moving the focusing plane, an area where no particles are visible in reached, which is identified as the bottom of the microchannel. The liquid film thickness is the distance between the bottom of the meniscus and the bottom of the microchannel. The shape of the meniscus can be reconstructed by combining the results corresponding to the various focusing planes. A typical reconstruction of the film is presented in Figure 5. As expected, the film is symmetrical with respect to the center plane of the channel and thus, to minimize effort, the measurements were taken only at one half of the channel. Figure 6 shows the main geometrical characteristics of the liquid film and a typical photo of it.

3. Results and Discussion

3.1. Liquid Film Thickness Calculation

In our previous work [13], according to the Rayleigh method of dimensional analysis, it was found that the film thickness H can be calculated as a function of modified dimensionless numbers, i.e., Reynolds (Re), Froude (Fr) and Capillary (Ca) number.

$$H/W_O=C{\left(R{e}^{a}C{a}^{b}F{r}^d\right)}^f$$

(2)

The dimensionless numbers use the channel width (W_O) as the characteristic length and the superficial velocity (U_S) defined as the volumetric flow rate divided by cross section of the meniscus. By inserting the aforementioned quantities, the dimensionless numbers are defined as follows:

$$Re=U_s{W}_O\rho /\mu =Q\rho /\left(\mu h\right)$$

(3)

$$Fr=U_s{}^2/g_{\phi }{W}_O=Q^2/(g_{\phi }{W}_O{}^3{h}^2)$$

(4)

with g_φ being the component of the acceleration of gravity that acts in the direction of flow, i.e., g_φ = g sin(φ) and φ is the inclination angle from the horizontal.

$$Ca=\mu U_s/\sigma =\mu Q/W_{o}h\sigma$$

(5)

where ρ, μ and σ are the density, the viscosity and the surface tension of the fluid. In our case, where non-Newtonian liquids are used, an effective viscosity, i.e., a representative viscosity value along the whole domain, must be specified. To evaluate this viscosity, we have performed relevant CFD simulations.

3.2. Effective Viscosity Prediction

For the sake of computational simplicity, simulations were performed by forcibly imposing on the computational model the geometrical features of the liquid falling film, which are experimentally obtained. Namely, the experimentally measured parabolic surface profile was manually modeled and set as a free-slip wall boundary condition. At the bottom and at the two side walls of the domain the no-slip wall boundary condition was applied (Figure 7). Two liquid flow rate values were tested, i.e., 40 mL/h and 80 mL/h.

The governing equations for the fluid flow are the Navier–Stokes equations and the continuity equation for incompressible and non-Newtonian flow. The fluid domain was discretized using tetrahedral elements and a symmetry plane was used to halve the problem for lowering computational costs. Total cell number varied for every case tested; from about 180,000 to about 240,000 cells. All simulations were performed using a commercial CFD code, the ANSYS CFX^® (v. 19, ANSYS Inc., Canonsburg, PA, USA). ANSYS CFX^® provides a finite volume method, a fully coupled solver for pressure and velocity coupling. The Direct Numerical Simulation (DNS) method for laminar flow was employed for the solution, as the flow in the μ-channel does not present any turbulent phenomena. Figure 8, shows the dynamic viscosity distribution at cross section, which was placed 100 widths downstream from the inlet to minimize inlet disturbances.

Figure 8 presents typical dynamic viscosity distributions, calculated by CFD simulation, at a plane perpendicular to the flow direction and located 30 hydraulic diameters downstream from the liquid entrance. It worth mentioning that there are areas near the interface where the viscosity attains its higher value.

The volume averaged viscosity values predicted by the CFD simulation were compared with the asymptotic viscosity of the liquid, proving that the maximum difference is less than 8% (

Table 2. Average and asymptotic viscosity for the liquids tested.

Fluid	μ∞ (Pa·s)	μave (Pa·s)	% Difference
nG20_80	0.0025	0.00260	4.0
nG20_40	0.0025	0.00270	8.0
nW_80	0.0014	0.00145	4.0
nW_40	0.0014	0.00150	7.1

). We must also consider that the viscosity measurement has an inherent uncertainty of 8%. Consequently, the asymptotic viscosity, which is known a priori, can be used in Equations (3)–(5).

The acquired data were appropriately fitted and the constants of Equation (2) were estimated (

Table 3. Constants of Equation (2) for film thickness correlation.

Constants for Equation (1)	Present Work	Previous Work [13]
a	0.50	0.50
b	0.01	0.01
c	3.90	2.04
d	−0.56	−0.56
f	−0.86	−0.86

) and compared with the ones found for the same substrate type (i.e., brass) but for Newtonian fluids. It has been reported that for Newtonian fluids the constant C of Equation (2) depends on the type of the substrate material [15]. The present work proves that it also depends of the nature of the fluid, i.e., Newtonian or non-Newtonian, because for the same substrate type the non-Newtonian fluids result in thicker films. Although the volume averaged viscosity over the domain is almost the same as the corresponding asymptotic viscosity (Table 2), there are areas near the interface, where the viscosity values are much higher (Figure 8). Consequently, the liquid flow is expected to decelerate resulting in thicker films. As it can be seen in Figure 9, Equation (2) can predict with reasonable accuracy (less than ±15%) the liquid film thickness for the fluids, flow rates and inclination angles tested.

3.3. Meniscus Shape

It is obvious that in FFMRs the concave shape of the interface augments the interfacial area. Thus, a characteristic that we must be able to determine during the design of an FFMRs is the shape and length of the gas–liquid interface (Figure 6a). In our previous work [13] it was shown that the shape of the meniscus can be accurately represented by a second order polynomial:

$$Y/\left(H_f-H\right)=C+A\left(X/W_o\right)+B{\left(X/W_o\right)}^2$$

(6)

where X is the distance from the side wall, while the constants of the equation are defined as:

C = H_f − H

(7)

$$B=4\left(H_f-H\right)/W_o{}^2$$

(8)

A = −BW_O

(9)

where, H_f is the height where the three-phase contact is pinned, which for shallow μ-channels equals the channel’s depth and H is the height of the meniscus (Figure 6a) that can be calculated by Equation (2).

Figure 10 presents the variation the meniscus height over the substrate divided by its maximum height along the channel width for the liquids, flow rates, and inclination angles studied. Figure 11 presents a comparison between the experimentally obtained meniscus profile and the one calculated by Equation (6). It is proved that Equation (6) can estimate the meniscus shape with reasonable accuracy (less than ±10%), for all the cases studied.

Figure 12 verifies the assumption that the asymptotic viscosity (μ_∞) can be used for calculating the liquid layer characteristics in place of volume averaged viscosity (μ_ave), estimated by CFD. More precisely, the shape of the meniscus calculated by Equations (2)–(7) using either μ_∞ or μ_ave, is compared with the one defined experimentally. Although the curve corresponding to μ_ave fits the experimental data better, the curve calculated using μ_∞, which is a priori known, can also predict the meniscus shape with reasonable accuracy, i.e., ±8%, compared with the one based on the experimental data.

The length of the parabolic arc (L), i.e., the length of the meniscus (Figure 6a), can be calculated with the following formula [16]:

$$L=\frac{1}{2}\sqrt{W_O{}^2+16H_O{}^2}+\frac{W_O{}^2}{8H_O}ln\left(\frac{4H_O+\sqrt{W_O{}^2+16H_O}}{Wo}\right)$$

(10)

where H_O and W_O are parameters defined in Figure 6a. The liquid phase cross section (A) was calculated by:

$$A=H_f{W}_O-\frac{2}{3}{H}_O{W}_O$$

(11)

Consequently, the specific surface (a) is the gas–liquid interfacial area (S) divided by the total fluid volume (V) in the reactor, that is:

$$a=\frac{S}{V}=\frac{L·\left(reactorlength\right)}{A·\left(reactorlength\right)}=\frac{L}{A}$$

(12)

whereas the fluid residence time per unit length of the reactor (τ) can be calculated by:

τ = A/Q

(13)

Figure 13 and Figure 14 present the effect of flow rate and inclination angle on the specific area and the residence time respectively. It is obvious that for a given flow rate both the specific area and the corresponding residence time can be controlled by altering the inclination angle.

Figure 15 presents a typical meniscus shape that corresponds to a flow rate of 40 mL/h and 25° inclination angle. The interfacial area calculated by the suggested procedure, i.e., Equations (6)–(11), is 15% lower than the one estimated using the experimental data. However, the deviation is considerably higher (i.e., around 30%), if a flat interface is assumed.

As a capstone of this study, a generalized algorithm for the design of FFMRs, is proposed (Figure 16). The input parameters of the algorithm are the physical properties and the flow rate of the liquid phase as well as the geometrical characteristics and the inclination angle of the μ-channel. Initially, the film thickness (H) is calculated by Equation (2). Subsequently, the shape of the interface can be determined by Equation (6) using the calculated film thickness (H) and the characteristics of the μ-channel. Finally, based on the calculated shape of the meniscus, the liquid phase cross section (A) can be calculated. Derived from this, important reactor design parameters, i.e., the specific surface (α) and the residence time (τ), can be specified.

4. Conclusions

The most important features that must be considered during the design of FFMRs are the residence time of the liquid phase as well as the interfacial area per volume of fluid. Consequently, the thickness of the liquid film and the shape of the interface are key parameters for the design of such devices. In this work the geometrical characteristics of the liquid film, created when a non-Newtonian shear-thinning liquid flows in an inclined open microchannel made of brass, have been experimentally investigated.

Based on the experimental data, design correlations that can predict with reasonable accuracy the features of an FFMR design for biomedical applications have been proposed. The mean viscosity of the non-Newtonian fluid is calculated using relevant CFD simulations. It is also proved that the characteristics of the liquid film can be predicted with reasonable accuracy if the asymptotic viscosity (a priori known) is used in place of the calculated average one.

As a matter of fact, the design engineer could apply the proposed methodology to construct or rate an FFMR. Various input parameters, e.g., the inclination angle, can be changed and operating parameters (film thickness, interfacial area, residence time) can be recalculated by the same procedure. More work is certainly needed to investigate the dependence of the constant C (Equation (2)) on the channel material.