Time Stable Reduced Order Modeling by an Enhanced Reduced Order Basis of the Turbulent and Incompressible 3D Navier–Stokes Equations

Abstract

In the following paper, we consider the problem of constructing a time stable reduced order model of the 3D turbulent and incompressible Navier–Stokes equations. The lack of stability associated with the order reduction methods of the Navier–Stokes equations is a well-known problem and, in general, it is very difficult to account for different scales of a turbulent flow in the same reduced space. To remedy this problem, we propose a new stabilization technique based on an a priori enrichment of the classical proper orthogonal decomposition (POD) modes with dissipative modes associated with the gradient of the velocity fields. The main idea is to be able to do an a priori analysis of different modes in order to arrange a POD basis in a different way, which is defined by the enforcement of the energetic dissipative modes within the first orders of the reduced order basis. This enables us to model the production and the dissipation of the turbulent kinetic energy (TKE) in a separate fashion within the high ranked new velocity modes, hence to ensure good stability of the reduced order model. We show the importance of this a priori enrichment of the reduced basis, on a typical aeronautical injector with Reynolds number of 45,000. We demonstrate the capacity of this order reduction technique to recover large scale features for very long integration times (25 ms in our case). Moreover, the reduced order modeling (ROM) exhibits periodic fluctuations with a period of $2.2$ ms corresponding to the time scale of the precessing vortex core (PVC) associated with this test case. We will end this paper by giving some prospects on the use of this stable reduced model in order to perform time extrapolation, that could be a strategy to study the limit cycle of the PVC.

1. Introduction

Reduced order modeling (ROM) of the complete Navier–Stokes equations by the projection of these equations upon a reduced order space, that is generated by a minimal number of spatial modes, is still an attractive research area especially when we consider turbulent flows such as the ones encountered in aeronautical engines and that feature a large range of scales. The most important issue to be addressed when performing an order reduction of the turbulent and unsteady Navier–Stokes equations is the construction of a minimal reduced order space that could cover properly the large range of scales of a turbulent fluid flow. If we find a minimal subspace that could verify these properties, then we can do further studies concerning the efficient adaptivity of the associated reduced order equations in terms of design and optimization of the components of an aeronautical engine, such as the combustion chamber and the fuel injection system.

The large vortices carry the major amount of the turbulent kinetic energy (TKE), while small scales are responsible for the dissipation of TKE. The real time prediction of this physics, under strong unsteadiness and variable constraints, is a big challenge for the industrial design in aeronautical engineering. Reduced order modeling by proper orthogonal decomposition (POD) is a very good candidate for solving such problems. It enables approximation of the high-fidelity (HF) partial differential equations (PDE)s in a subspace of small dimension, which reproduces accurately the energy of the coherent structures of a fluid flow. Nevertheless, the ROMs by POD for the turbulent and incompressible Navier–Stokes equations suffer a time instability due to the misrepresentation of the energy of the small vortices of these convection dominated equations, by the coherent energetic POD modes. Many authors propose techniques to remedy time instability within ROMs by POD of the Navier–Stokes equations. By time stable reduced order model, we mean the capacity of the reduced equations to verify the energy balance and the mass conservation properties of the complete Navier–Stokes equations.

Improvement of the Galerkin reduced order modeling using mathematical approaches such as the stabilization based on the role of the neglected POD modes to enhance the dissipation of the TKE [1], or reduced order models based on deconvolution methods for large-eddy simulation (LES) have been proposed in the literature: Rowley et al. [2] proposed a Galerkin ROM-POD for the compressible Navier–Stokes equations, constructed by projection via an energy-based inner product. Codina et al. [3] proposed the enrichment of the ROM by increasing the dimension of the projection POD subspace, and computing the new temporal weights amplitudes by a least square minimization with respect to the initial temporal snapshots. The later sub-scale approach was applied for an incompressible and turbulent flow around a cylinder of which the Reynolds number varies from 32,000 to 74,000. Balajewicz et al. [4] proposed an enhanced Galerkin approximation by POD of the compressible Navier–Stokes equations based on an a priori implementation of a traditional eddy-viscosity based closure model in order to modify the overall eigenvalue distribution of the dissipative linear operator within the Galerkin reduced order modeling. This technique was applied for a 2D laminar airfoil at Reynolds 500. Xie et al. [5] proposed a deconvolution method for LES-based reduced order models in order to model the subfilter stress-scale tensor within the reduced order modeling. This approach was performed for the 1D Burgers equation and a 3D flow past a cylinder at Reynolds 1000. In [6], the authors propose to study theoretically and numerically the influence of different types of finite element on the ROM mass conservation. They tested the Taylor–Hood (TH) element and the Scott–Vogelius (SV) element. They showed that the SV-ROM yields to more accurate results when applied to a 2D flow past a circular cylinder at a Reynolds number $Re=100$, especially for coarser meshes and longer time intervals. We can find in literature also stabilization of reduced order models based on operator splitting, specifically the streamline-upwind Petrov–Galerkin (SUPG) stabilization method [7].

In the domain of model order reduction for finite volume numerics for computational fluid dynamics, we cite the work of Carlberg et al. [8], where it has been proposed a method for model reduction of finite-volume models that guarantees the resulting reduced-order model to be conservative. The proposed reduced order model is associated with optimization problems that explicitly enforce conservation over subdomains. In [9], the authors proposed a POD-Galerkin reduced order methods for CFD using finite volume discretization. This was performed as a consequence of the projection of the Navier–Stokes equations onto different reduced basis space for velocity and pressure, respectively. Stabile et al. [10], developed finite volume POD-Galerkin stabilized reduced order methods for the incompressible Navier–Stokes equations. These methods are based on the pressure Poisson equation and supremizer enrichment which ensures that a reduced version of the inf-sup condition is satisfied.

Among the work concerning the stabilisation of the POD-based ROM for turbulent fluids dynamics, Amsallem et al. [11] have proposed to perform the POD-based model reduction using the descriptor form of the discretized Euler or Navier–Stokes equations, i.e., the natural variables of these equations, whereas many computations are performed in CFD codes using the non-descriptor form of these equations. In [12], the authors proposed to use the stability of the reduced-order Galerkin models in incompressible flows in order to study the limit cycle of the hydrodynamic vortex acting on a circular cylinder. Amsallem et al. [13] have proposed a stabilization of the projection-based linear reduced order models because of a convex optimization problem that operates directly on available reduced order operators. This method was tested for computational fluid dynamics-based model of a linearized unsteady supersonic flow, the reduction of a computational structural dynamic system, and the stabilization of the reduction of a coupled computational fluid dynamics–computational structural dynamics model of a linearized aeroelastic system in the transonic flow regime.

Besides these reduced order techniques which are intrusive for the computational fluid dynamics physics, there are some new non-intrusive reduced order ones, as they rely only on the available snapshots data, without taking into account all the equations of physics as constraints, but rather some physical properties as the turbulent kinetic energy conservation by learning the orthogonal projection coefficients of the solutions over a POD basis using a metamodel or a neural network, see the work of Wang et al. [14]. These non-intrusive techniques would take into account also the parameters calibration of the closure terms and the turbulent sub-grid scale modeling in the large eddy simulation models or the reynolds average Navier–Stokes equations ones, see the work of Lapeyre et al. [15]. There are also some research directions towards combining the machine learning non-intrusive reduced order techniques with the physics based reduced order ones in order to improve the quality of these latters, see the work of Xie et al. [16].

In this paper, we are interested in the stabilization of POD-Galerkin reduced order modeling for the turbulent and incompressible Navier–Stokes equations and we propose a new stabilization and purely physical approach for the POD-Galerkin approximation of the turbulent and incompressible Navier–Stokes equations. More precisely, a simplified POD-Galerkin projection of the complete Navier–Stokes equations is performed within an extended and minimal reduced order subspace, which reproduces accurately all the scales contained in the different terms of the Navier–Stokes equations, in order to recover a proper evolution of the fluctuating TKE. The proposed approach is based on the POD representation of the velocity gradient. A solution for the issue due to the combination of POD velocity and POD gradient modes is proposed. Moreover, we point out that the proposed stabilization is based on the a priori analysis of the different velocity modes and gradient velocity modes, in order to enforce the energetic dissipative modes within the first vectors of the new reduced order basis. This a priori enrichment by scale seperation is a key point to our proposed approach, and this will lead to the desired time stability of the reduced order model. We also point out that our proposed strategy is different from the ones that propose a scalar product change while defining the correlations matrix of the singular value decomposition (SVD) step of the POD method, in order to take into account the gradient scales within the scalar product computations, typically as in [17].

The manuscript is organized as follows: the proposed theoretical framework for the construction of the enhanced reduced order basis is detailed in Section 2. In this section, we motivate the use of an a priori enhancement of the classical POD basis by POD modes associated with the gradient velocity. All the numerical results are detailed in Section 3 for a benchmark problem of a typical aeronautical injection system at $Re$ = 45,000 and 14 millions mesh elements. The flow solver of the High Fidelity Navier–Stokes equations is first exposed. Reduced order modeling via the enriched POD is presented and analyzed. In Section 4, we show the dynamic temporal coefficients obtained by running the enhanced fluid dynamics reduced order model for very long time integrations, even longer than the one of the high-fidelity solutions that generated the enhanced reduced order basis. In Section 5, we give some conclusions and prospects to this work. More precisely, we introduce our future work concerning the use of this stabilization technique for the extrapolation of the reduced order model in time so that, we can study efficiently the limit cycle of the PVC in an aeronautical injector [18]. It is well known that the Q-criterion of the smallest vortices is larger than the one of the large coherent structures, then the PVC is masked by small scales surrounding turbulence in the LES simulation. The enhanced ROM enables us to filter the PVC throughout the reduced order simulation even for large values of Q-criterion and for very long integration times.

2. Theoretical Framework

2.1. POD-Galerkin Reduced Order Modeling Applied to the Unsteady and Incompressible Navier–Stokes Equations

We denote by $X={\left[L^2\left(\mathsf{\Omega }\right)\right]}^3$ the functional Hilbert space of the squared integrable functions over a bounded $3D$—open set $\mathsf{\Omega }$. The corresponding inner product is the kinetic energy-based one associated with the X-functional norm. They will be denoted respectively by $(.,.)$ and $∥.∥$. Consider $v\left(t\right)\in X$ the velocity field of an unsteady incompressible flow. Denote $\overline{v}\left(t\right)$ the filtered field obtained by a given LES model. A reduced order POD subspace is obtained by the snapshots method [19]. More precisely, if we discretize the time interval to M points, then the snapshots set is given as follows: $\mathcal{S}=\{\overline{v}\left(t_i\right)i=1,\dots ,M\}$. The associated POD eigenmodes ${\mathsf{\Phi }}_n,$ $n=1,\dots ,M$ are solutions of the following eigenvalues problems given the temporal correlations matrix:

$$C_{ij}=(\overline{v}\left(t_i\right),\overline{v}\left(t_j\right)),$$

(1)

of size $M\times M$. We denote by $A_n={\left(A_{i,n}\right)}_{1\le i\le M}$ for $n=1,\dots ,M$, a set of orthonormal eigenvectors of the matrix C. Then, the POD-eigenmodes associated with $\overline{v}$, are given by:

$${\mathsf{\Phi }}_n\left(x\right)=\frac{1}{\sqrt{{\lambda }_{n}M}}\sum _{i=1}^M{A}_{i,n}\overline{v}(t_i,x),\forall x\in \mathsf{\Omega }\forall n=1,\dots ,M,$$

(2)

where ${\left({\lambda }_n\right)}_{n=1,\dots ,M}$ is the decreasing sequence of the positive eigenvalues of the correlations matrix C.

To achieve the POD reduced order modeling of the filtered incompressible Navier–Stokes equations, the approximated velocity field is expressed in the reduced order POD subspace:

$${\displaystyle \tilde{v}(t,x)=\sum _{n=1}^N{a}_n\left(t\right){\mathsf{\Phi }}_n\left(x\right),\forall x\in \mathsf{\Omega },}$$

(3)

where $N<<M$ denotes the number of retained high energetic POD modes, and $a_1\left(t\right)$, $a_2\left(t\right)$,..., $a_N\left(t\right)$ are the temporal weights which are solutions of the following coupled dynamical system:

$$\left\{\begin{array}{c}\frac{d{a}_n}{dt}+\left(div(\tilde{v}\left(t\right)\otimes \tilde{v}\left(t\right)),{\mathsf{\Phi }}_n\right)=\nu \left(\Delta \tilde{v}\left(t\right),{\mathsf{\Phi }}_n\right)-\frac{1}{\rho }\left(\nabla p\left(t\right),{\mathsf{\Phi }}_n\right)\hfill \\ {\left(q,div\left(\tilde{v}\left(t\right)\right)\right)}_{H^0}=0\forall q\in H^0\hfill \\ a_n\left(0\right)=\left(v_0,{\mathsf{\Phi }}_n\right)\hfill \end{array},\right.$$

(4)

where $div$ denotes the divergence operator, $p\left(t\right)$ is the pressure field, $\rho$ the density, $\nu$ denotes the kinematic viscosity, $v_0$ is the initial condition of the velocity field and $H^0$ is the subspace of the divergence free X-functions.

We point out the fact that the equations upon which we perform the POD-Galerkin projection are the continuous high-fidelity incompressible Navier–Stokes equations without any turbulence model taken into account. So, our reduced order modeling formulation is the one associated with the continuous Navier–Stokes equations. However, it is clear that the POD computation is associated with High-Fidelity snapshots $\overline{v}\left(t\right)$ which are usually obtained from LES of the Navier–Stokes equations.

In general, the first POD mode ${\mathsf{\Phi }}_1\left(x\right)$ which describes the mean topology of the fluid flow is not kept and a ROM of the fluid dynamics equations represents only the fluctuating part. However in our case the first POD mode ${\mathsf{\Phi }}_1\left(x\right)$ is kept within the ROM. This could be very valuable when we are interested in using the reduced order modeling in order to predict the flow with respect to parametric variations, or even for new geometries [20]. This enables the ROM to consider naturally the influence of the velocity fluctuations on the velocity mean.

We point out the following two remarks concerning our formulation of the reduced order modeling:

Remark 1.

The POD modes contain only the energetic scales of the flow. The dissipative scales at the Taylor macro-scale are not present in the basis.

Remark 2.

The flow rate in the flow domain is not guaranteed except if penalization is added in the pressure term to take into account the pressure difference between inlet and outlet.

We propose to tackle these remarks on account of a physical stabilization by satisfying the kinetic energy budget.

2.2. Physical Stabilization by Satisfying the Kinetic Energy Budget

2.2.1. Enrichment of the POD-Galerkin ROM with the Flow Rate Driving Forces

If we integrate by part the pressure term in the reduced order model (4), then we get the following equality:

$$\left(\nabla p\left(t\right),{\mathsf{\Phi }}_n\right)=-\left(p\left(t\right),div\left({\mathsf{\Phi }}_n\right)\right)+{\int }_{\delta \mathsf{\Omega }}p\left(t\right){({\mathsf{\Phi }}_n\left(x\right),\overrightarrow{n}\left(x\right))}_{{\mathbb{R}}^3}d\delta \mathsf{\Omega },$$

(5)

where $\overrightarrow{n}$ is the normal vector to the domain boundaries $\delta \mathsf{\Omega }$.

Using the fact that the incompressibility constraint is also verified by the velocity POD modes, the pressure term could be written:

$${\displaystyle \left(\nabla p\left(t\right),{\mathsf{\Phi }}_n\right)={\int }_{\delta \mathsf{\Omega }}p\left(t\right){({\mathsf{\Phi }}_n\left(x\right),\overrightarrow{n}\left(x\right))}_{{\mathbb{R}}^3}d\delta \mathsf{\Omega }.}$$

(6)

We propose to model the pressure difference between the inlet ${\mathsf{\Gamma }}_{in}$ and the outlet, because of a penalization for the flow rate. This could be written mathematically as follows:

$${\displaystyle \sum _{m=1}^N{a}_m\left(t\right){\int }_{{\mathsf{\Gamma }}_{in}}{\left({\mathsf{\Phi }}_n\left(x\right),{\mathsf{\Phi }}_m\left(x\right)\right)}_{{\mathbb{R}}^3}d{\mathsf{\Gamma }}_{in}={\int }_{{\mathsf{\Gamma }}_{in}}{\left({\mathsf{\Phi }}_n\left(x\right),v_{{\mathsf{\Gamma }}_{in}}\left(x\right)\right)}_{{\mathbb{R}}^3}d{\mathsf{\Gamma }}_{in},\forall n=1,\dots ,N,}$$

(7)

where $v_{{\mathsf{\Gamma }}_{in}}$ is the inlet boundary condition of the corresponding High-Fidelity Navier–Stokes equations.

The reduced order model satisfying the flow rate production forces is now written as follows: ∀ $n=1,\dots ,N$,

$$\left\{\begin{array}{c}\frac{d{a}_n}{dt}+\left(div(\tilde{v}\left(t\right)\otimes \tilde{v}\left(t\right)),{\mathsf{\Phi }}_n\right)=\nu \left(\Delta \tilde{v}\left(t\right),{\mathsf{\Phi }}_n\right)\hfill \\ +\tau \left[{\displaystyle \sum _{m=1}^N}{a}_m\left(t\right){\int }_{{\mathsf{\Gamma }}_{in}}{\left({\mathsf{\Phi }}_n\left(x\right),{\mathsf{\Phi }}_m\left(x\right)\right)}_{{\mathbb{R}}^3}d{\mathsf{\Gamma }}_{in}-{\int }_{{\mathsf{\Gamma }}_{in}}{\left({\mathsf{\Phi }}_n\left(x\right),v_{{\mathsf{\Gamma }}_{in}}\left(x\right)\right)}_{{\mathbb{R}}^3}d{\mathsf{\Gamma }}_{in}\right],\hfill \\ a_n\left(0\right)=\left(\overline{v}\left(0\right),{\mathsf{\Phi }}_n\right)\hfill \end{array}\right.$$

(8)

where $\tau$ is the penalization coefficient and which has been chosen equal to 10,000 in the online resolution of the reduced order modeling (8).

The flow rate penalization will enforce the following equality:

$$a_1\left(t\right){\mathsf{\Phi }}_1\left(x\right)=V\left(x\right),\forall x\in \mathsf{\Omega }\mathrm{and}\forall t,$$

where V is a steady velocity field, that should represents the mean motion. Denote by ${\displaystyle v^{reduced}\left(t\right)=\sum _{n=2}^N{a}_n\left(t\right){\mathsf{\Phi }}_n}$ the fluctuating reduced order velocity, then the evolution of the turbulent kinetic energy within the ROM (8) is given by:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{2}\frac{d}{dt}\sum _{n=2}^N{a}_n^2}& =& \nu \left(\Delta \tilde{v}\left(t\right)),\tilde{v}\left(t\right)\right)\hfill \end{array}$$

(9)

$$\begin{array}{c}-\left(div(v^{reduced}\left(t\right)\otimes V),v^{reduced}\left(t\right)\right)-\left(div(V\otimes V),v^{reduced}\left(t\right)\right)\hfill \end{array}$$

(10)

$$\begin{array}{c}-\left(div(V\otimes v^{reduced}\left(t\right)),V\right)-\left(div(v^{reduced}\left(t\right)\otimes v^{reduced}\left(t\right)),V\right)\hfill \end{array}$$

(11)

$$\begin{array}{cc}=& \nu \left(\Delta \tilde{v}\left(t\right)),\tilde{v}\left(t\right)\right)\hfill \end{array}$$

(12)

$$\begin{array}{c}-2\left(div(v^{reduced}\left(t\right)\otimes V),v^{reduced}\left(t\right)\right)-2\left(div(V\otimes V),v^{reduced}\left(t\right)\right)\hfill \end{array}$$

(13)

The terms (13) in the assessment of the kinetic energy represents the production rate of the kinetic energy.

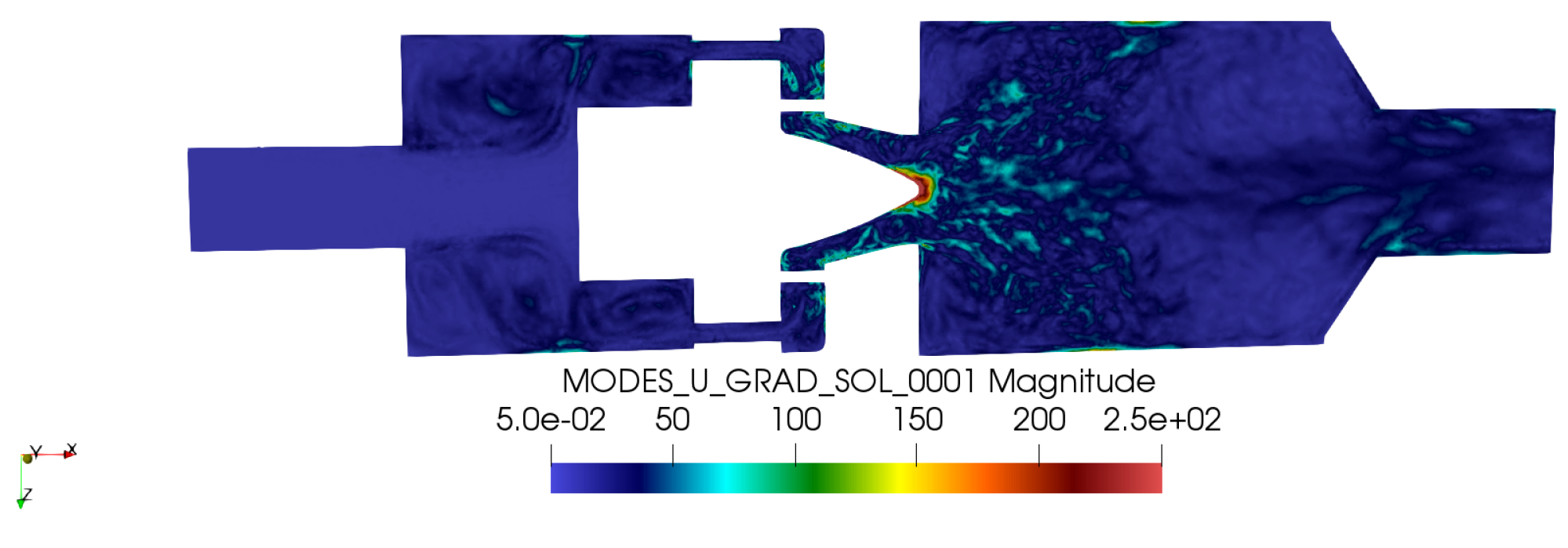
2.2.2. Enrichment of the POD-Galerkin ROM with the Most Dissipative Scales Based on the Velocity Gradient

To recover the dissipation rate of the fluctuating TKE in (8), we propose the following numerical algorithm, based on the enrichment of velocity-based POD modes by gradient velocity-based POD modes following a new a priori approach.

The proposed enrichment algorithm is the following:

• Compute the POD velocity modes ${\mathsf{\Phi }}_n=\frac{1}{\sqrt{{\lambda }_{n}M}}{\sum }_{i=1}^M{A}_{i,n}\overline{v}\left(t_i\right),$ $n=1,\dots ,M$ and truncate at $N<<M$ these POD modes. We note that N is intentionally chosen to be less than the needed number of the POD modes to represent all the features of the coherent energetic scales of the kinetic energy.
• Compute the fluctuating POD gradient modes ${\mathsf{\Psi }}_n=\frac{1}{\sqrt{{\beta }_{n}M}}{\sum }_{i=1}^M{B}_{i,n}\nabla \overline{v}\left(t_i\right),$ $n=1,\dots ,M$ and truncate at $N^{\prime }<<M$. Where $B_n={\left(B_{i,n}\right)}_{1\le i\le M}$ for $n=1,\dots ,M$, a set of orthonormal eigenvectors of the temporal correlations matrix on the fluctuating velocity gradient: ${\left(\nabla \overline{v}\left(t_i\right)-W,\nabla \overline{v}\left(t_j\right)-W\right)}_{{\left[L^2\left(\mathsf{\Omega }\right)\right]}^9},$ $i,j=1,\dots ,M$ (W the mean velocity gradient being removed from these correlations), and ${\left({\beta }_n\right)}_{n=1,\dots ,M}$ is the sequence of the eigenvalues of this latter matrix.
• Compute the following velocity basis functions: ${\mathsf{\Phi }}_n^E=\frac{1}{\sqrt{{\beta }_{n}M}}{\sum }_{i=1}^M{B}_{i,n}\overline{v}\left(t_i\right),$ $n=1,\dots ,N^{\prime }$.
• Perform the Gram–Schmidt orthonormalization process for the enriched set $\left\{{\mathsf{\Phi }}_1,\dots ,{\mathsf{\Phi }}_N,{\mathsf{\Phi }}_1^E,\dots ,{\mathsf{\Phi }}_{N^{\prime }}^E\right\}$ with respect to the energy-based inner product $(.,.)$. This step is the key of the enforcement of dissipative energy modes with high singular values ${\left({\beta }_n\right)}_{n=1,\dots ,N^{\prime }}$ in early ranks of the reduced order basis, which is the opposite case when considering only the classical velocity-based POD modes (dissipative energy modes are classified respectively with very small singular values).

We will show that the new reduced order basis features new modes that represent larger ranges of spatial scales than the ones encountered in the energetic classical velocity POD modes. We point out also that the intentional a priori enforcement of these new modes within the first ranks of the reduced order basis has a major role on the quality of the resulting reduced order model. We will show that it ensures the stability of the reduced order model in an efficient fashion as a result of the availability of the driving forces and the dissipative ones within a reduced number of velocity modes.

3. Application of the Stabilization Approach to a Typical Aeronautical Injector

3.1. Flow Solver

For the present simulations, the low-Mach number solver YALES2 [21] for unstructured grids is retained. This flow solver has been specifically tailored for the direct numerical simulation and large-eddy simulation of turbulent reacting flows on large meshes counting several billion cells using massively parallel super-computers [22,23]. It features a central fourth-order scheme for spatial discretization while time integration of convective terms is performed with an explicit fourth-order temporal scheme. The Poisson equation that arises from the low-Mach formulation of the Navier–Stokes equations is solved with a highly efficient Deflated Preconditioned conjugated gradient method [23].

3.2. Typical Aeronautical Injector of Re = 45,000 Lean Preccinsta Burner

3.2.1. Test Case Presentation

In what follows, we apply our new approach for a 3D unsteady, turbulent and incompressible fluid flow in a fuel injection system. The main objective is to be able to have an efficient strategy in order to compute precisely the aerodynamic field in the primary zone of the combustion chamber. The so-called PRECCINSTA test case [24,25] is presented in Figure 1. This lean-premixed burner has been widely studied in the combustion community to validate large-eddy simulation models [22,26,27,28,29,30,31].

The 3D turbulent flow in the complex configuration presented in Figure 1 is considered. The kinematic viscosity $\nu ={10}^{-5}{\mathrm{m}}^2/\mathrm{s}$ yields a Reynolds number 45,000 based on the inlet velocity and the length of the duct. The present High Fidelity simulation runs over 512 cores during 5 days in order to obtain a physical simulation time equal to 250 ms. A velocity-based POD-Galerkin reduced order modeling is performed, and an evaluation of its accuracy and efficiency is done before and after applying the a priori enrichment by the dissipative modes. By efficiency, we mean the online time needed to solve the mesh-independent ordinary differential Equation (8). In order to build the reduced basis, 2500 snapshots of the solution and its gradient are taken, extracted at each time step of the original HF simulation. We point out the fact that these 2500 snapshots are taken from 6644 time steps of the high fidelity simulation corresponding to the final 25 ms of its total physical time. We precise that these 25 ms represent two times the flow through time (FTT) of this test case.

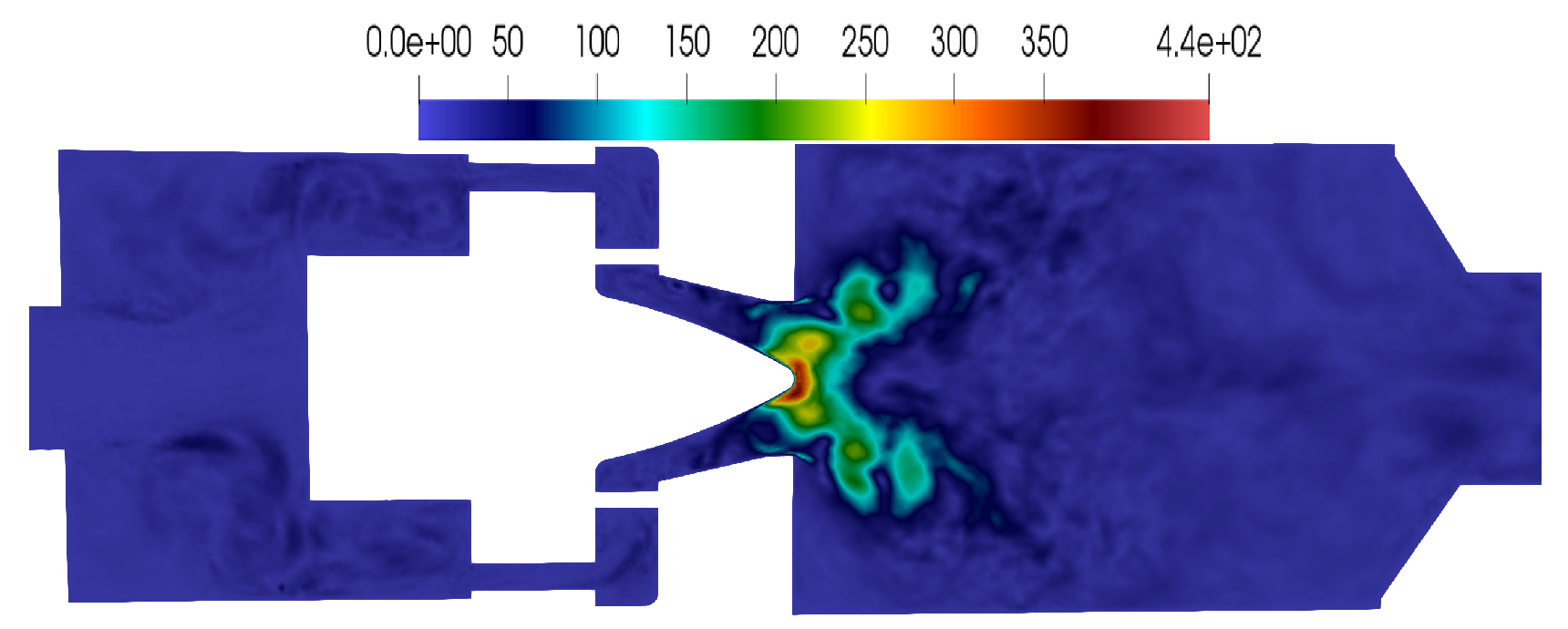
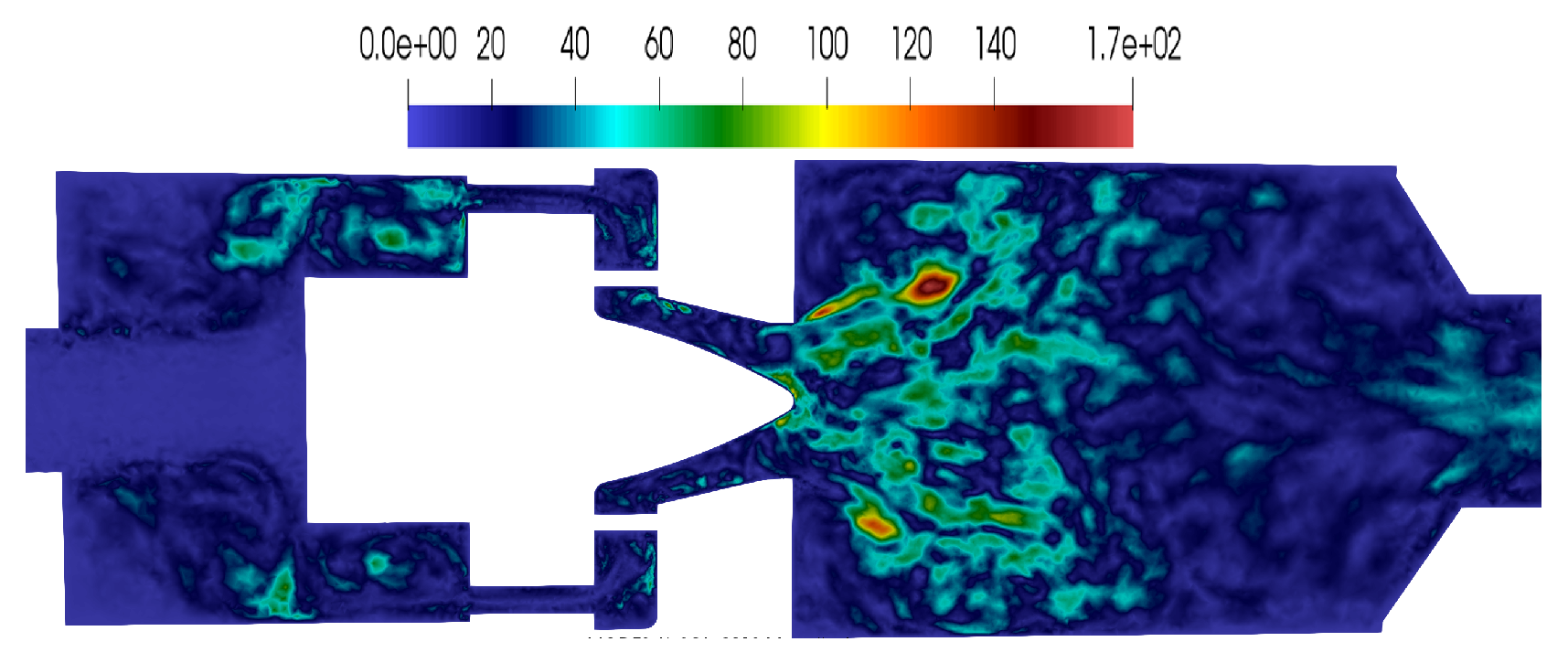
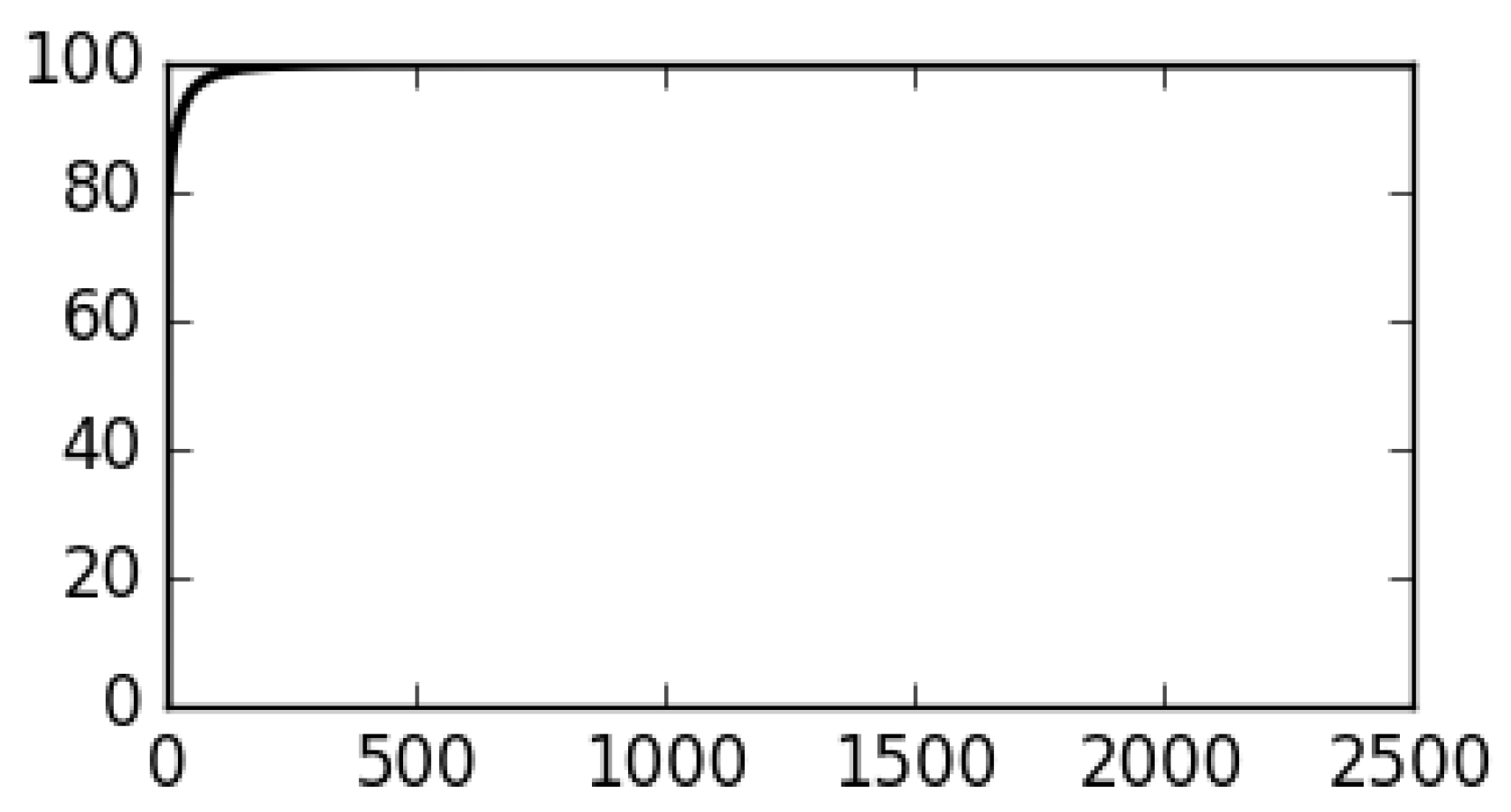
3.2.2. POD Modes Computation for the Preccinsta

The velocity-based and gradient velocity-based POD modes were computed through a distributed snapshots POD performed in the YALES2 code. The CPU ressources needed for this computation are 768 cores (24 nodes), to guarantee a memory availability to read the 2500 time snapshots. The computation runs during 6 hours for the velocity-based POD modes and 9 hours for the gradient velocity-based POD modes. These POD modes for the velocity and gradient velocity fields are shown respectively starting from Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17.

We can see that the velocity-based POD modes contain the high-scales of the principal coherent structures of the flow.

Interestingly, compared to the velocity-based POD modes, the velocity gradient-based POD ones feature high-scales in the dissipative regions such as in the wake of the two channels of the swirler and in the wake of the combustion chamber.

Moreover, if we compare the cumulative kinetic energies (Figure 18 and Figure 19) associated respectively with the velocity-based POD modes and the gradient velocity-based ones, we can see that fewer than 10 velocity-based POD modes are sufficient to reproduce $90\%$ of the high-scales TKE, however we need a larger number of velocity gradient-based POD modes in order to reproduce $90\%$ of the small and dissipatives scales of the TKE. Then, it is clear that the dissipative scales are not considered in the velocity-based POD modes and should be added in order to preserve the energy conservation within the ROM.

3.2.3. The Enhanced Reduced Order Basis

We apply our a priori enforcement of the dissipative velocity modes defined previously by our new approach in the following fashion:

• We choose $N=4$ and start the enforcement by the new velocity modes from the 5th rank. This choice is made because we want to limit the number of classical global POD modes which do not exhibit at the end very large features of spatial scales, as we can see on the modes ${\mathsf{\Phi }}_5,$ ${\mathsf{\Phi }}_6,$ ${\mathsf{\Phi }}_7$, ${\mathsf{\Phi }}_8$ and ${\mathsf{\Phi }}_9$.
• We choose $N^{\prime }=50$ because, as already discussed, we need a large number of velocity gradient-based POD modes in order to reproduce $90\%$ of the small and dissipatives scales of the TKE as shown on Figure 19.
• We perform the Gram–Schmidt orthonormalization process for the enriched set $\left\{{\mathsf{\Phi }}_1,\dots ,{\mathsf{\Phi }}_N,{\mathsf{\Phi }}_1^E,\dots ,{\mathsf{\Phi }}_{N^{\prime }}^E\right\}$ with respect to the energy-based inner product $(.,.)$.

By applying our proposed algorithm with the preceding choices, we get a new velocity-based reduced order basis as shown from Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27, Figure 28, Figure 29, Figure 30 and Figure 31.

We give some further remarks in what follows:

• We recall that the choice $N=4$ is done intentionally in order to retrieve some dissipative modes at earlier stages than in the classical POD technique where we can see that even after 12 modes we do not have any modes of large scale’s features.
• The fact that the dissipative energy modes appear at late stages in the classical POD technique with very small singular values is the reason why we are not able to exploit their physical significance even if we increase the dimension of the classical POD reduced order model.
• We add starting $n=5$ velocity-based modes of high singular values and large features of scales.
• This enrichment by small scale enforcement and separation is the key to multi-scale reproduction within the reduced order modeling. We precise once more that this approach is very different than the ones based on the change of the inner product that defines the matrix of the correlations between the instanteneous snapshots, typically the approach where the $H^1$ inner product is considered instead of the $L^2$ inner product. By our approach we enable scale separation, then small scale’s enforcement, which is very hard to distinguish when performing a $H^1$ correlations matrix and then retrieving a complete POD basis: the small scales will remain dominated by the $L^2$ correlated large scales even if we perform this inner product change. Some authors use mathematical calibration in order to retrieve the small scales [17].

The new velocity-based modes ${\mathsf{\Phi }}_5^E,$ ${\mathsf{\Phi }}_6^E,$ ${\mathsf{\Phi }}_7^E$, ${\mathsf{\Phi }}_8^E$ and ${\mathsf{\Phi }}_9^E$ show very large features of spatial scales which was not observed within the classical global POD modes ${\mathsf{\Phi }}_5,$ ${\mathsf{\Phi }}_6,$ ${\mathsf{\Phi }}_7$, ${\mathsf{\Phi }}_8$ and ${\mathsf{\Phi }}_9$. The margin of variation of these large features, as we can see on Figure 24, Figure 25, Figure 26, Figure 27 and Figure 28, ranges from 0 to 380 (see Figure 25, Figure 27 and Figure 28). Moreover, the largest scales exhibit local structures in the fluid domain which are the small vortices carrying out the dissipative energy by analogy with the gradient velocity-based POD modes (see Figure 14, Figure 15, Figure 16 and Figure 17).

In what follows, we call “dissipative ROM” the reduced order model computed using the proposed enriched basis ${\left({\mathsf{\Phi }}_n^E\right)}_n$, whereas “non-dissipative ROM” refers to the ROM using the classical POD basis ${\left({\mathsf{\Phi }}_n\right)}_n$.

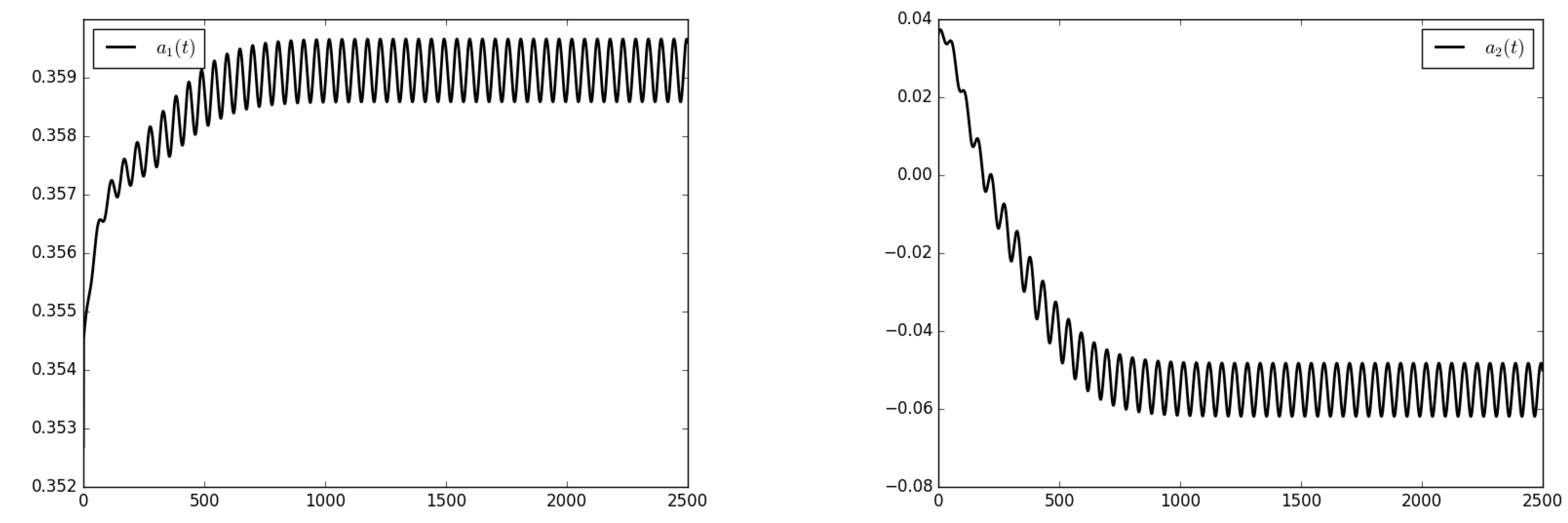
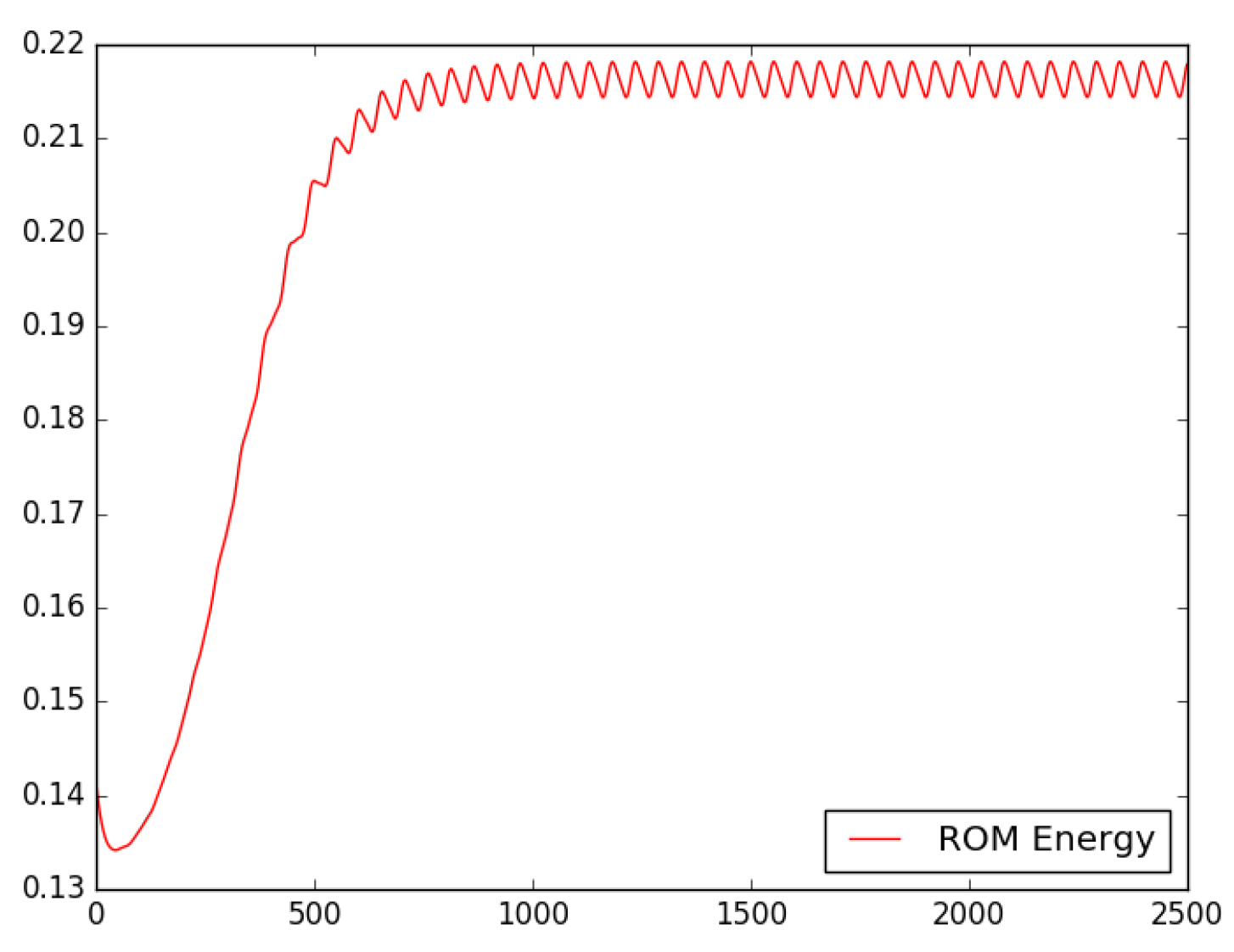
3.2.4. The Temporal Coefficients and Kinetic Energy of the Enriched Reduced Order Model and the Comparaison with the Classical POD-Galerkin Reduced Order Model

Figure 32, Figure 33, Figure 34, Figure 35 and Figure 36 show the time history of the stabilized ROM amplitudes, when the stabilization algorithm is performed by enrichment of $N=4$ POD velocity modes with $N^{\prime }=50$ dissipative modes. We can see that these temporal coefficients obtained from the resolution of the reduced order model for a time interval equal to 25 ms which corresponds to the total time from which our data set was extracted in order to compute the POD modes for the velocity and the gradient velocity fields, tend to stabilize at the end of this resolution (from time step 2000). This could be explained by the order reduction using a limited number of modes, which means that the ROM needs to retrieve its equilibrium before the conservation of the kinetic energy. The ROM exhibits periodic fluctuations with a period of $2.2$ ms which is the time scale of the precessing vortex core (PVC) associated with this test case.

This proves that the dissipative modes play a major role in the evolution of the Turbulent Kinetic Energy. Their introduction in the set of POD modes of the Galerkin ROM enables us to recover a better time evolution of the TKE in the system with fewer modes, see Figure 37. If we compare on this plot the kinetic energy evolutions respectively for the dissipative ROM and the non dissipative ROM, we can see that in the non dissipative case the plot of the kinetic energy is far from stabilization on the same time interval which is 25 ms.

These results are very encouraging to test the dynamic extrapolation of the stabilized reduced order model, so that we could access in real time (without any further offline operations) the evolution of the turbulent and incompressible flow outside the original snapshots data set. The first results of the dynamic extrapolation are shown in Section 4 in what follows.

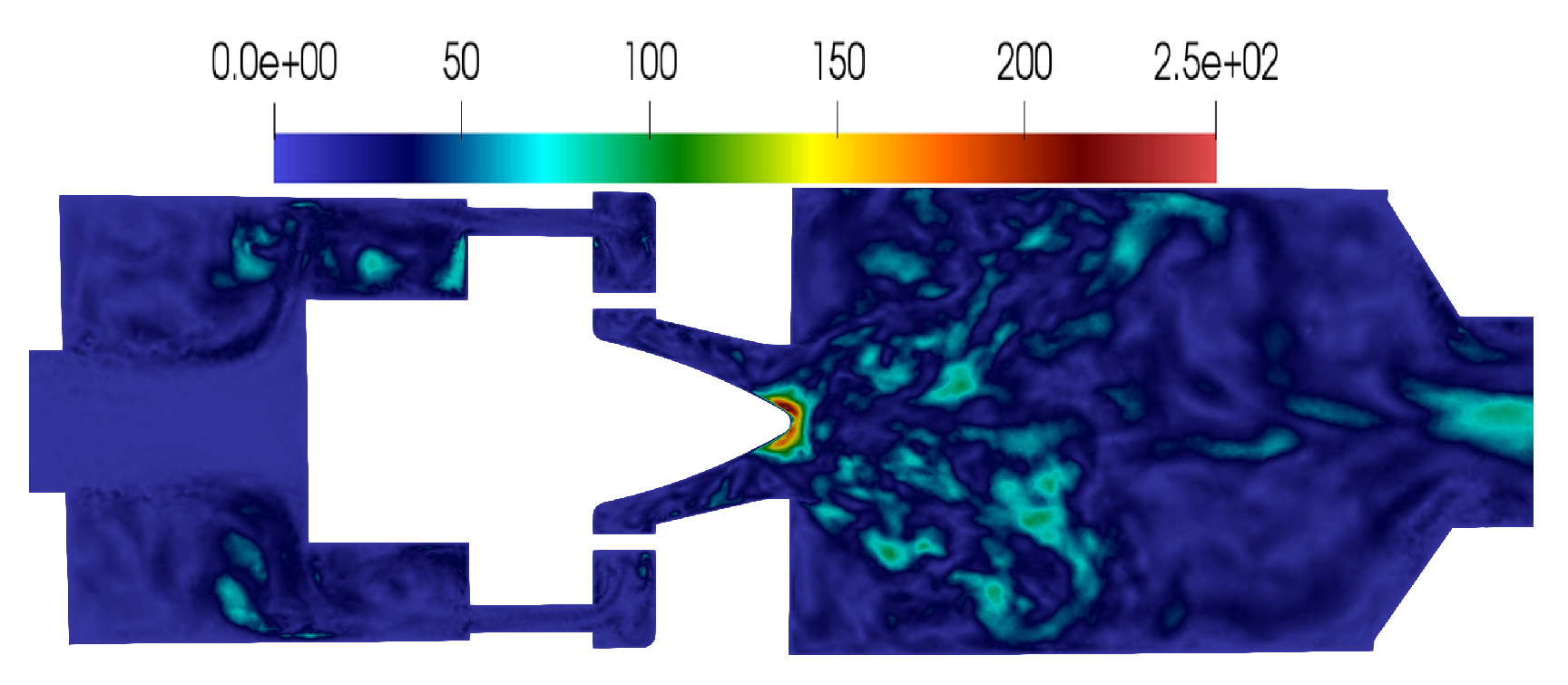
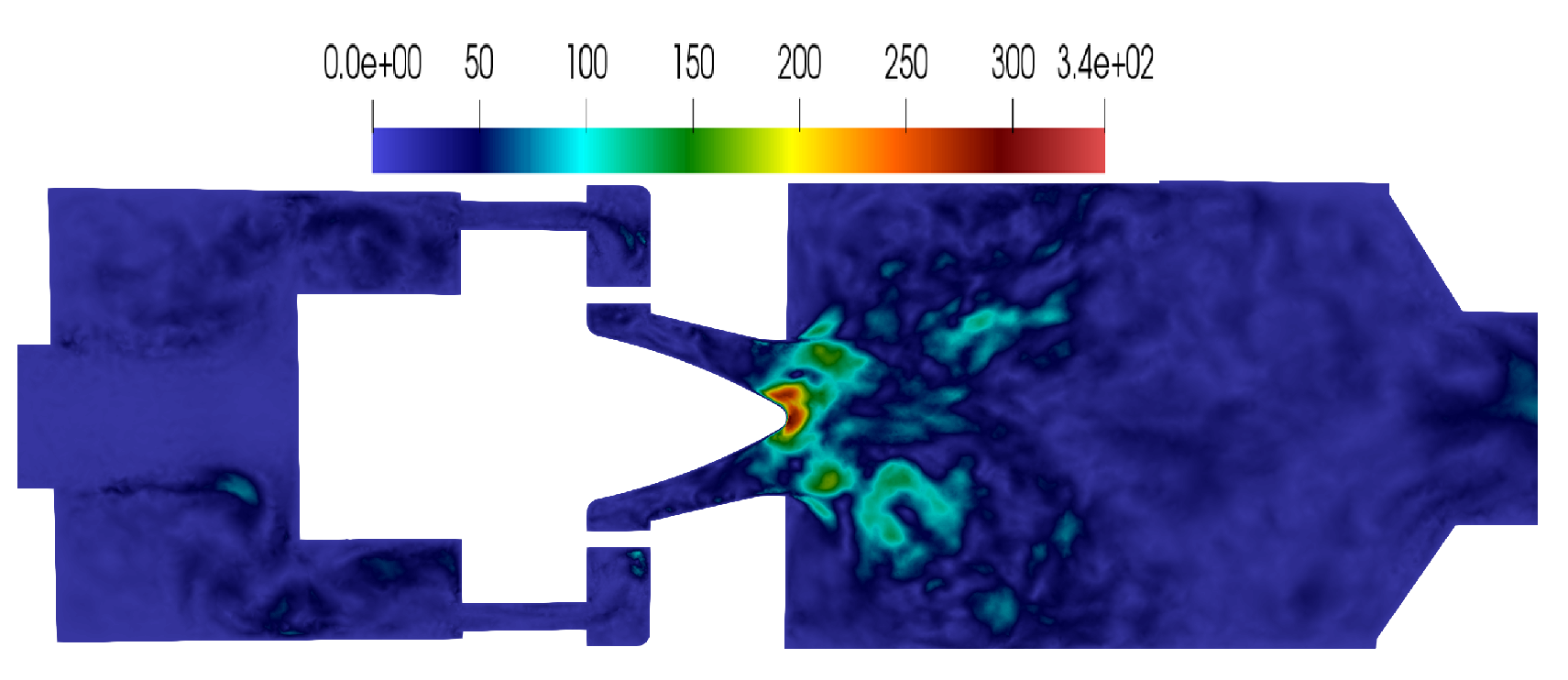
3.2.5. 3D Time Fields Obtained by the ROM and the High-Fidelity Model

In what follows we show in Figure 38 plots of the $3D$ reduced order velocity fields when the stabilized ROM is applied, compared to the $3D$ high fidelity velocity fields obtained by LES. Large scale features of the flow are clearly reproduced by the ROM even for very long time integrations.

3.2.6. CPU Time for Offline and Online Computation

In

Table 1. Offline and online computational cost.

Operation	Wall Clock Time
High-fidelity YALES2 solver (512 cores)	5 days
Velocity-based POD + Disipative modes computation (768 cores)	15 h
Stabilization by Gram–Schmidt (768 cores)	3 h
Galerkin projection (768 cores)	3 min
Time python ROM-POD solver (1 core)	$3.7$ s
Speed up factor	${10}^8$

, we evaluate the efficiency of the stabilized reduced order modeling with respect to the High Fidelity simulation. Furthermore, we evaluate approximately the cost of the offline phase (including the snapshots POD, the Galerkin projection and the stabilization when applied) and the online ROM phase.

We precise that the speed-up is defined by the ratio of the ROM return time and the YALES2 return time. As a consequence of the proposed strategy we are able to enhance the accuracy of the reduced order modeling with a very good efficiency, regarding the online resolution. Furthermore, the offline effort associated with the additional stabilization algorithm scales with the high fidelity YALES2 return time.

It is important to note that the steps which are the most CPU consuming in the offline stage are the velocity-based POD and the gradient velocity-based one computations, followed by the stabilization by Gram–Schmidt. This took 18 h over 768 cores (24 nodes are required), because of the memory cost needed to read all of the 2500 time snapshots. This operation was not well distributed over the 768 cores due to the following issue: a temporal snapshot was not post-processed as one file per subdomain, i.e. the number of solution files per time step was less than the number of mesh partitions. This means that the running cores are working the available memory on the saved nodes in order to read lots of data per process. However, the Galerkin projection of the Navier–Stokes equations’ operators took only three minutes over 768 cores. This is a consequence of the fact that we do not need to read any snapshots but, we read only the reduced number of the enhanced reduced order vectors and, we perform distributed scalar product and classical differentiation operations which scale with the mesh complexity but are very well parallelized due to distributed tasks on the mesh parts.

4. Temporal Extrapolation of the Dissipative ROM

Running the reduced order model for 250 ms (i.e., 10 times longer than 25 ms that is the time interval over which the POD basis has been performed), yields the dynamic weight coefficients (Figure 39, Figure 40, Figure 41, Figure 42 and Figure 43) and the evolution of the turbulent kinetic energy represented on Figure 44. These coefficients were obtained as a consequence of the run of the stable ROM over 1 core. In this case, we can legitimately state that the speed up of the reduced order modeling is ${10}^8$, due to the fact that we are accessing physical solutions that were not seen by the offline phase and the learning phase of the ROM.

5. Conclusions and Prospects

A new methodology is proposed for the stabilisation of Galerkin reduced order models by POD for the turbulent and incompressible 3D Navier–Stokes equations. The method is based on adding the necessary physics in the new reduced order space, so that all the scales modeled in the high-fidelity Navier–Stokes equations are taken into account by the reduced order model. The only ingredient which is not represented by the retained POD modes for the reduction process in the classical methodology, is the small rank scales which are responsible for the dissipation of the turbulent kinetic energy. This ingredient is added as a result of an a priori enrichment strategy and an enforcement to the velocity-based POD modes, by a minimal number of new velocity modes which contain the low dissipative energy in the new reduced order basis. This strategy shows a very good performance when applied to an unsteady turbulent flow of Reynolds 45,000 in a typical aeronautical injection system.

The prospects of this work are the use of the proposed stable reduced model in order to perform time extrapolation, that could be a way to study the limit cycle of the Precessing Vortex Core of an aeronautical injection system.