Microinjection Molding of Out-of-Plane Bistable Mechanisms
Abstract
:1. Introduction
2. Design of Double V-Beam Bistable Mechanism
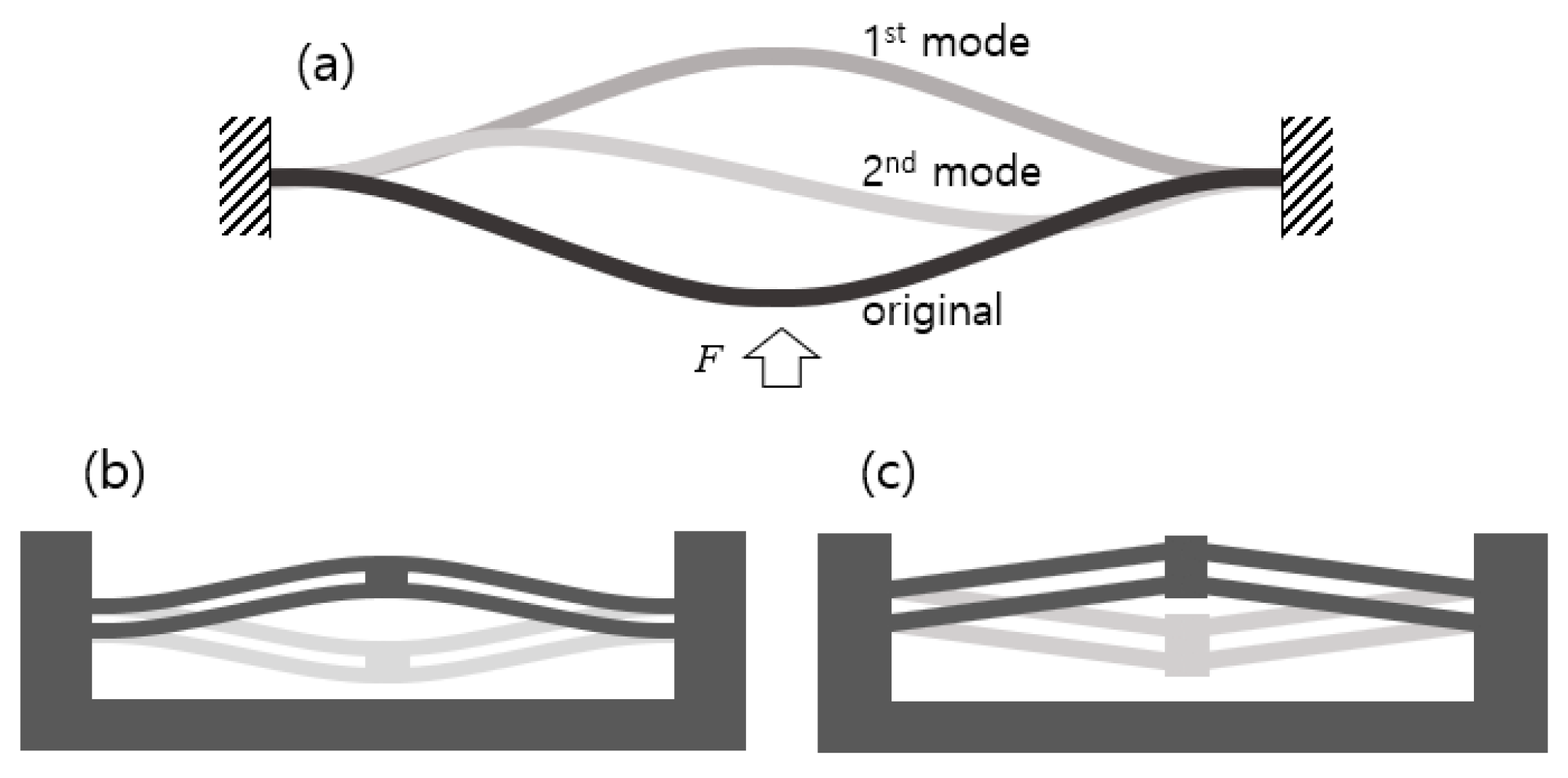
2.1. Beam-Based Bistable Mechanisms (BM)
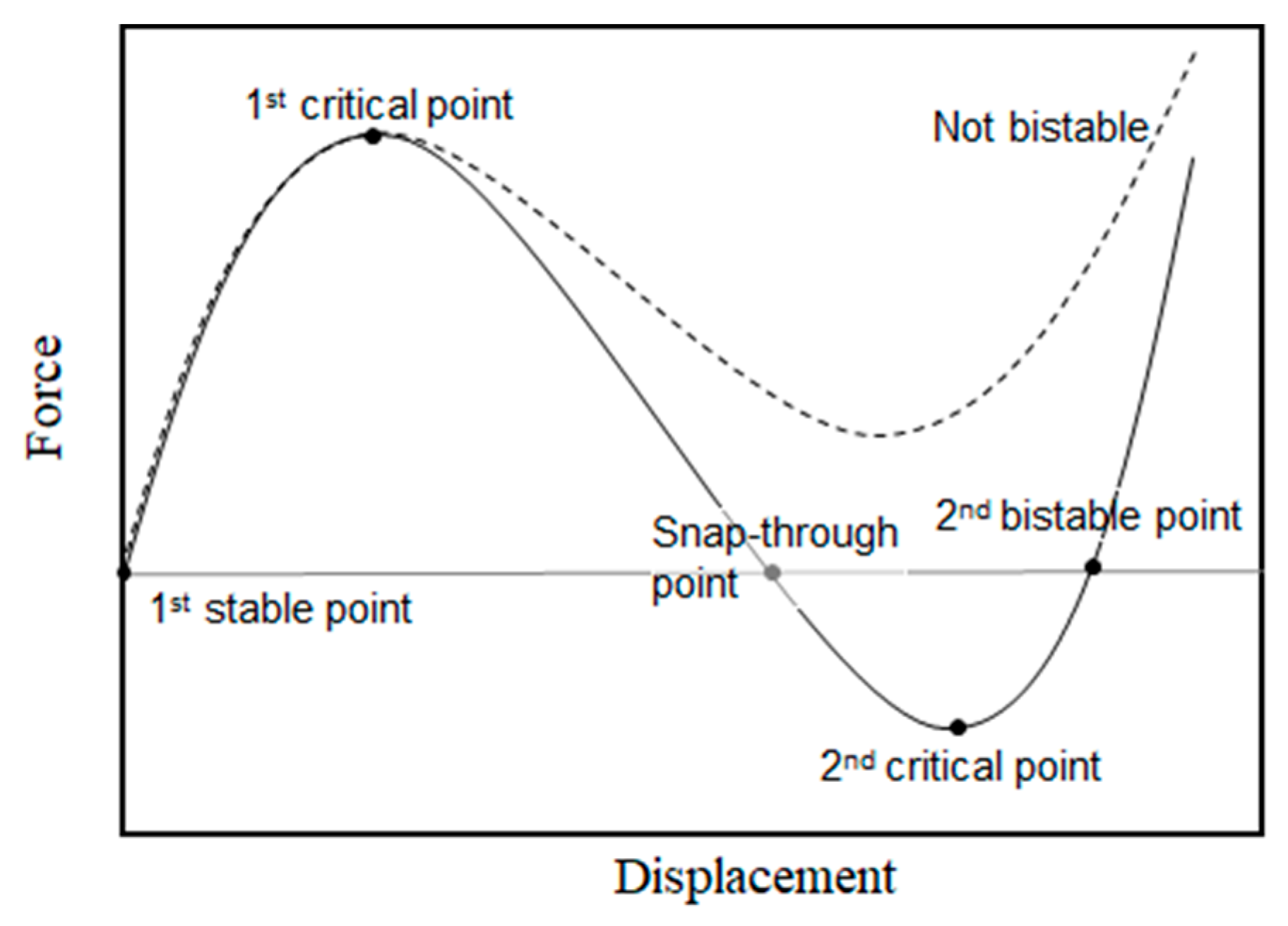
2.2. Design Consideration for Injection Molding (IM) of Single V-Beam and Bistability
3. Fabrication
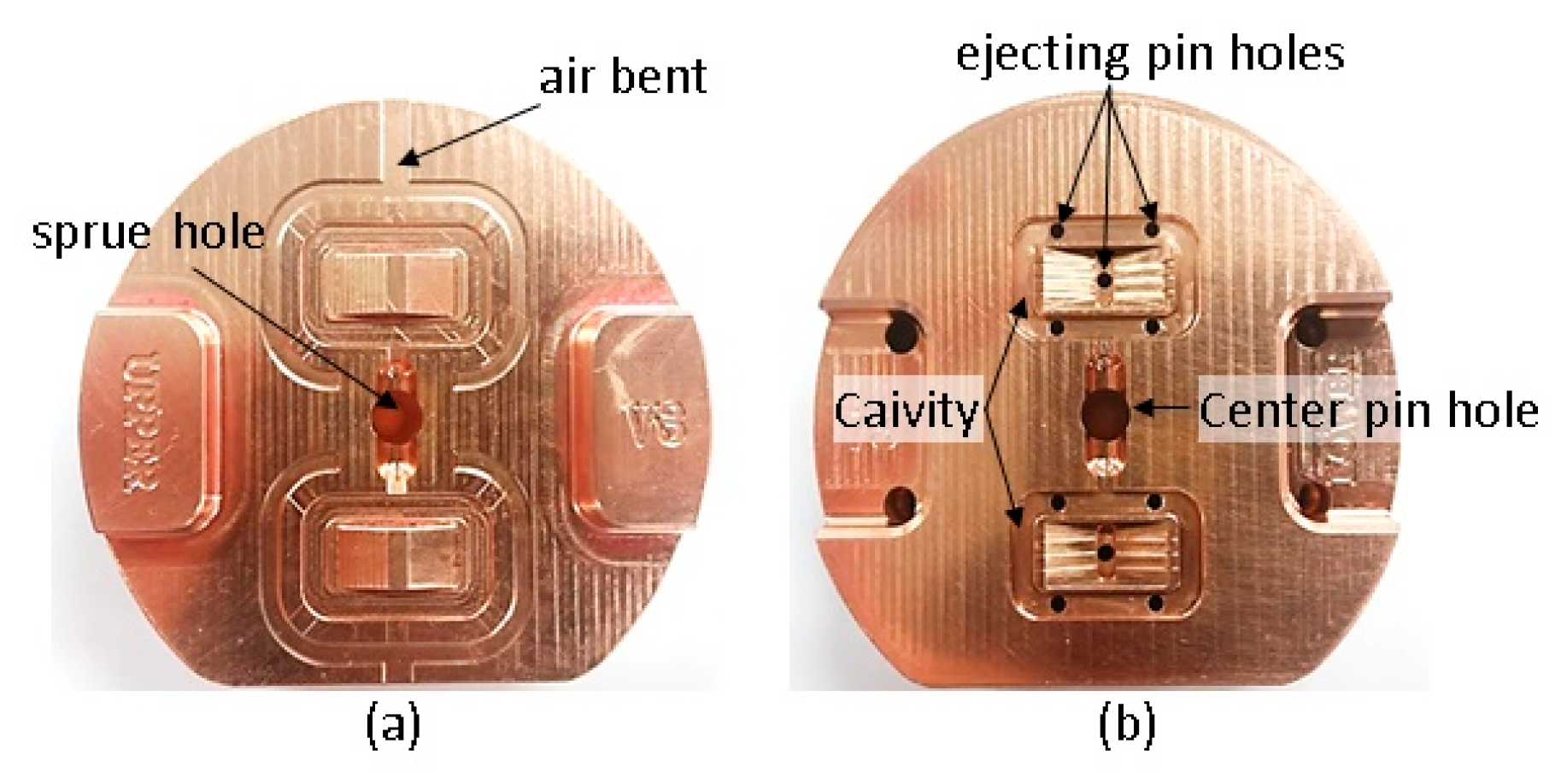
3.1. Layout and Tooling
3.2. Material and Injection Molding
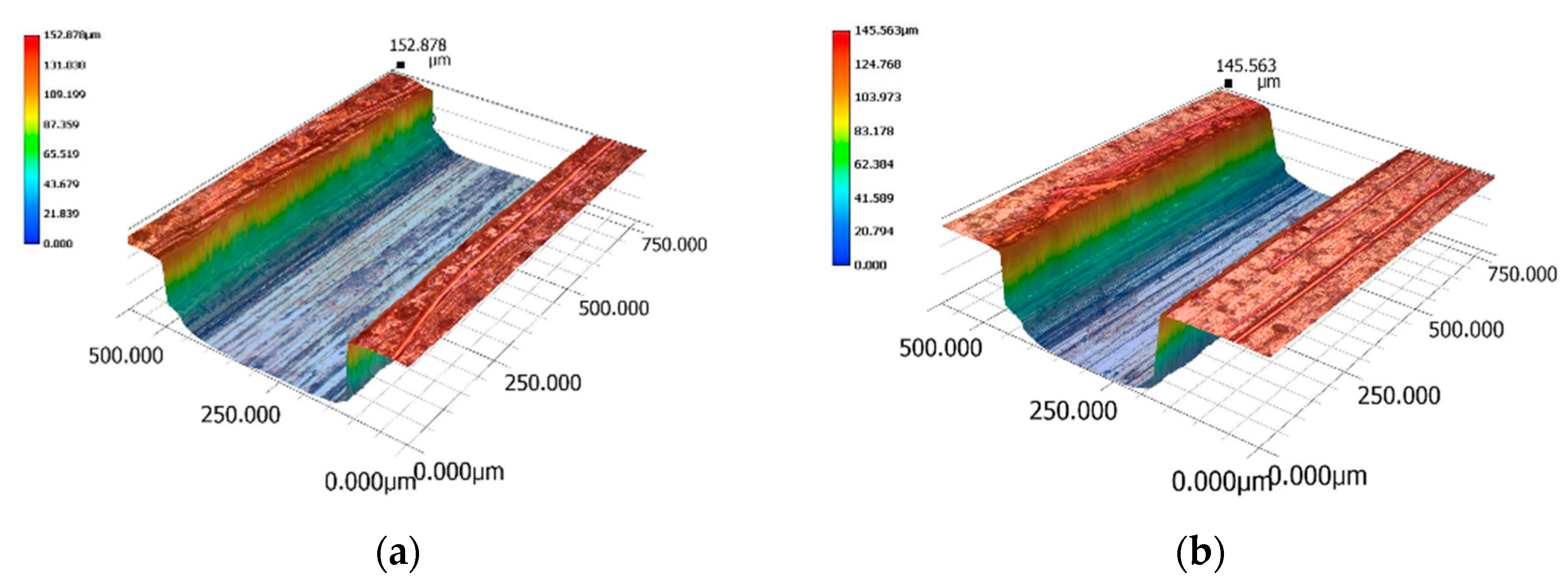
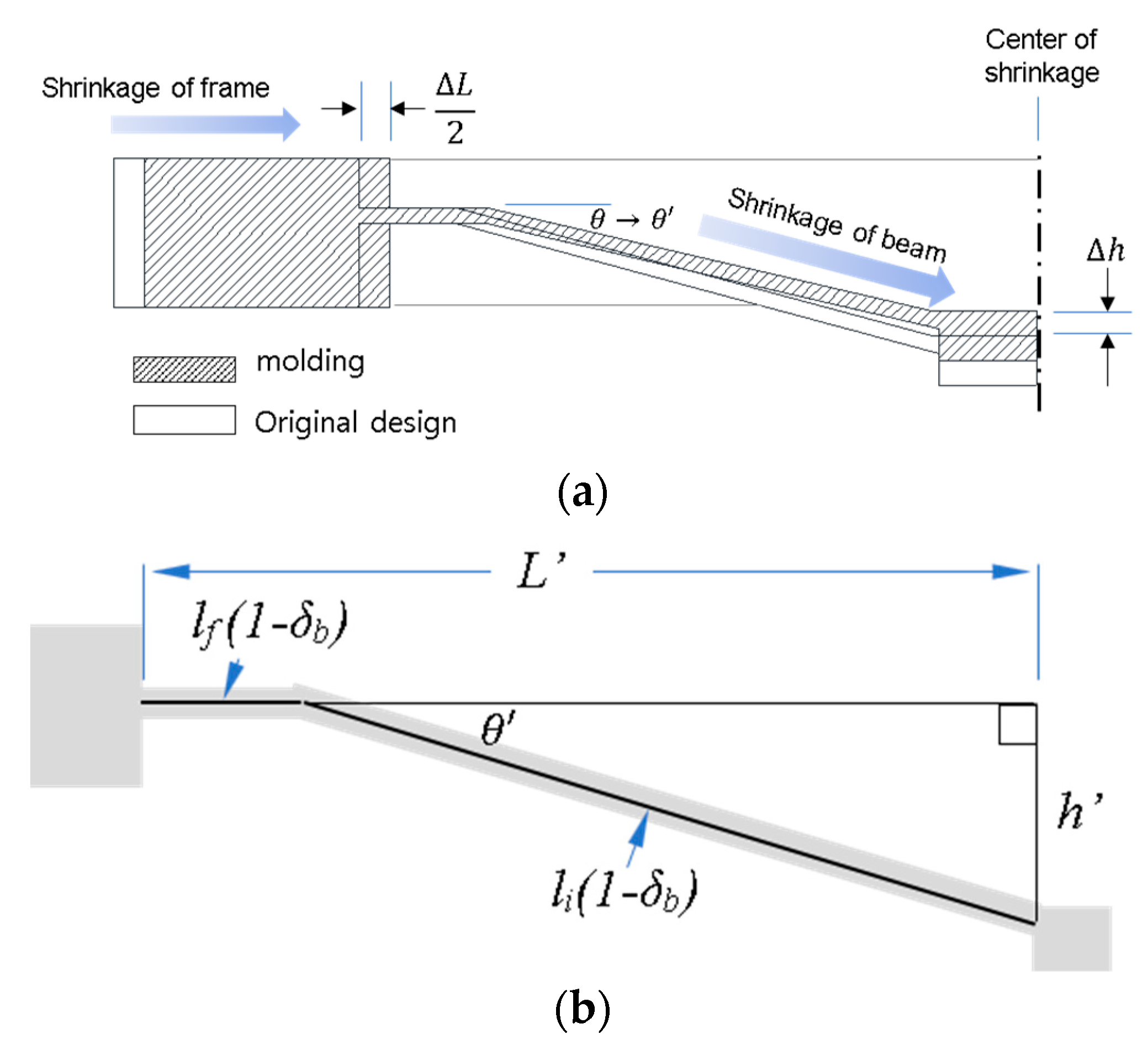
3.3. Shrinkage and Shape Error Compensation
4. Experiment
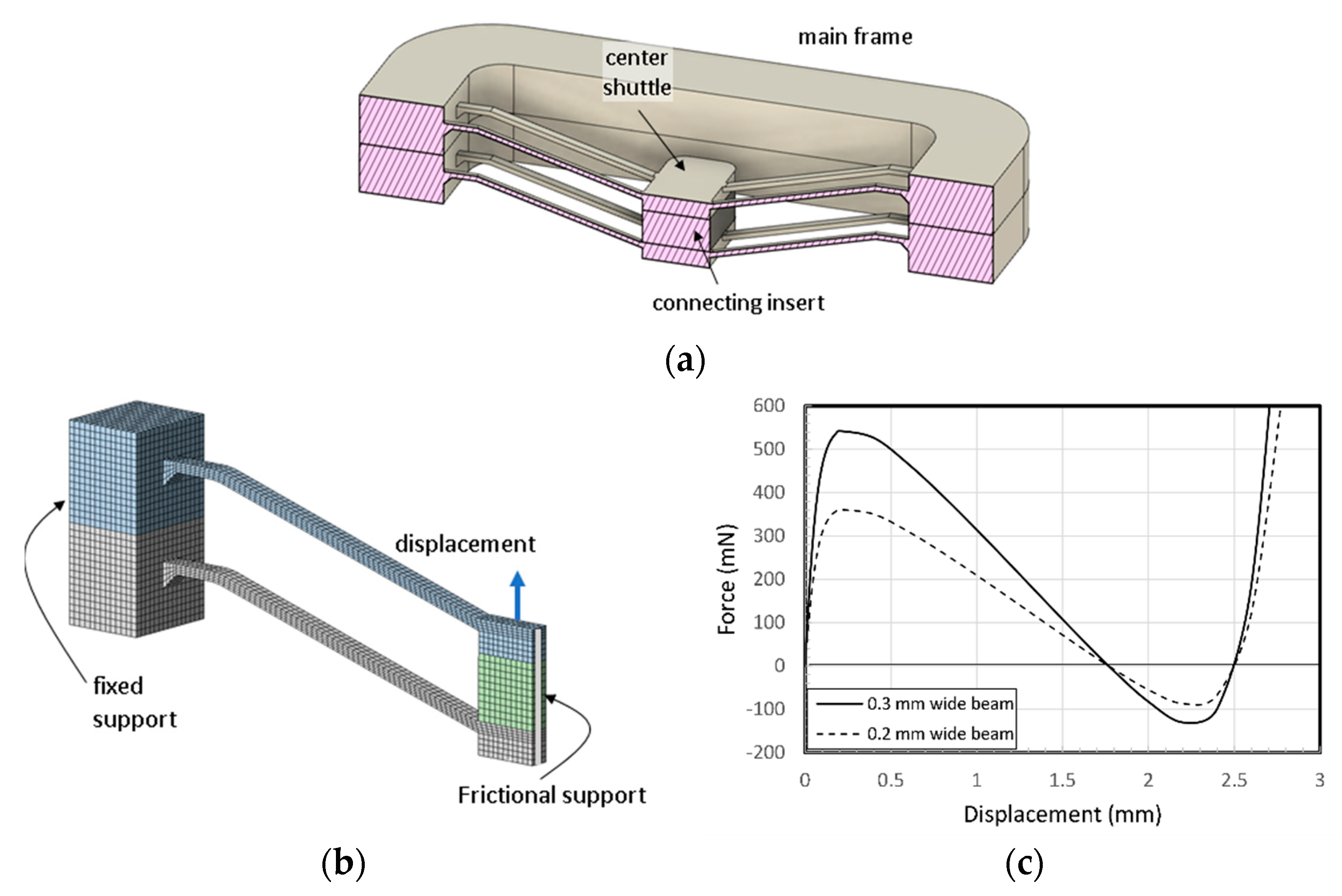
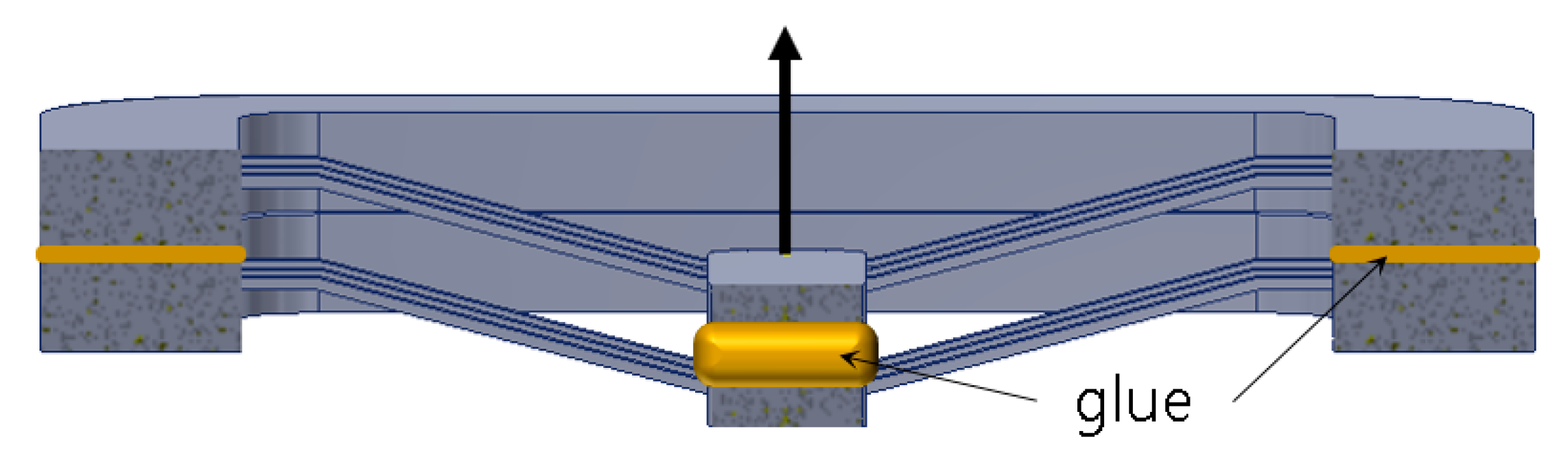
4.1. Setup for Measurement of Force-Displacement Behavior
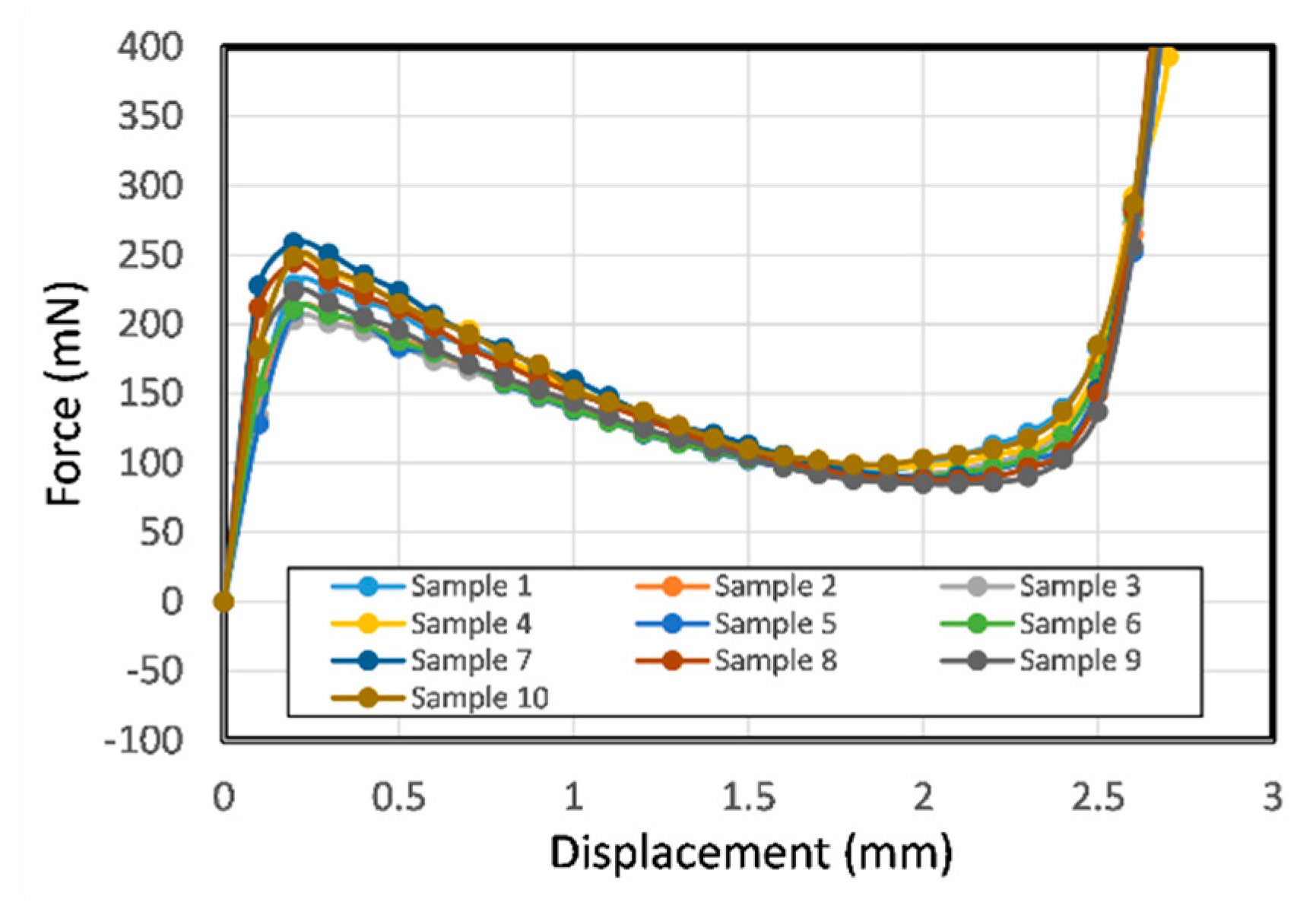
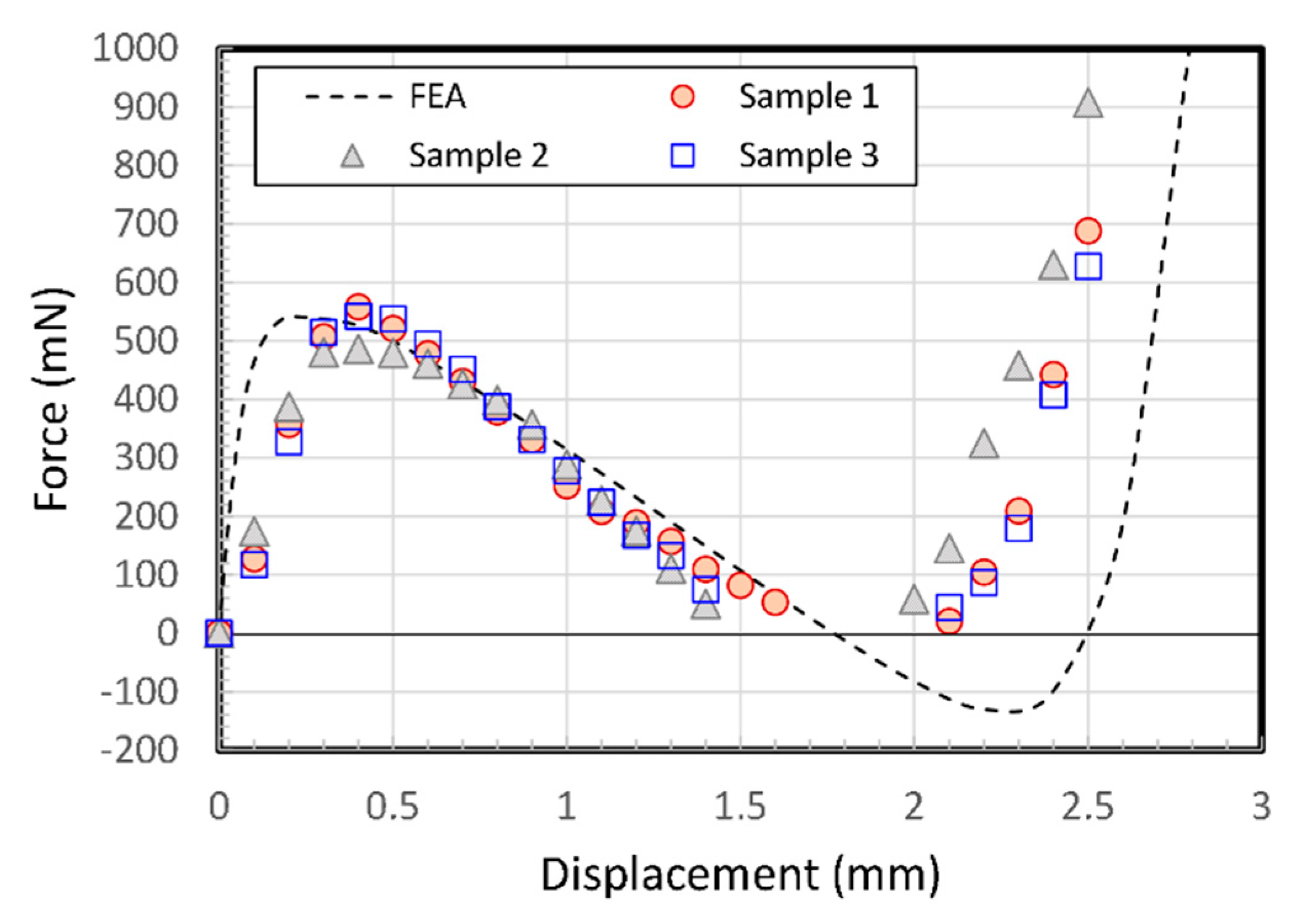
4.2. Force–Displacement Relationship of Molded V-beam Structures
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Baker, M.S.; Howell, L.L. On-chip actuation of an in-plane compliant bistable micromechanism. J. Microelectromech. Syst. 2002, 11, 566–573. [Google Scholar] [CrossRef]
- Qiu, J.; Lang, J.H.; Slocum, A.H. A curved-beam bistable mechanism. J. Microelectromech. Syst. 2004, 13, 137–146. [Google Scholar] [CrossRef]
- Casals-Terre, J.; Fargas-Marques, A.; Shkel, A.M. Snap-action bistable micromechanisms actuated by nonlinear resonance. J. Microelectromech. Syst. 2008, 17, 1082–1093. [Google Scholar] [CrossRef]
- Hansen, B.J.; Carron, C.J.; Jensen, B.D.; Hawkins, A.R.; Schultz, S.M. Plastic latching accelerometer based on bistable compliant mechanisms. Smart Mater. Struct. 2007, 16, 1967–1972. [Google Scholar] [CrossRef]
- Megnin, C.; Barth, J.; Kohl, M. A bistable SMA microvalve for 3/2-way control. Sens. Actuators Phys. 2012, 188, 285–291. [Google Scholar] [CrossRef]
- Hu, N.; Burgueño, R. Buckling-induced smart applications: Recent advances and trends. Smart Mater. Struct. 2015, 24, 063001. [Google Scholar] [CrossRef]
- Harne, R.L.; Wang, K.W. A review of the recent research on vibration energy harvesting via bistable systems. Smart Mater. Struct. 2013, 22, 023001. [Google Scholar] [CrossRef]
- Nguyen, S.D.; Halvorsen, E.; Paprotny, I. Bistable springs for wideband microelectromechanical energy harvesters. Appl. Phys. Lett. 2013, 102, 023904. [Google Scholar] [CrossRef] [Green Version]
- Saif, M.T.A. On a tunable bistable MEMS-theory and experiment. J. Microelectromech. Syst. 2000, 9, 157–170. [Google Scholar] [CrossRef]
- Ongaro, F.; Jin, Q.; Siciliani de Cumis, U.; Ghosh, A.; Denasi, A.; Gracias, D.H.; Misra, S. Force characterization and analysis of thin film actuators for untethered microdevices. AIP Adv. 2019, 9, 055011. [Google Scholar] [CrossRef] [Green Version]
- Zirbel, S.A.; Tolman, K.A.; Trease, B.P.; Howell, L.L. Bistable mechanisms for space applications. PLoS ONE 2016, 11, e0168218. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.-C.; Lin, M.-J.; Chen, R. The derivation of a bistable criterion for double V-beam mechanisms. J. Micromech. Microeng. 2013, 23, 115005. [Google Scholar] [CrossRef]
- Pustan, M.; Chiorean, R.; Birleanu, C.; Dudescu, C.; Muller, R.; Baracu, A.; Voicu, R. Reliability design of thermally actuated MEMS switches based on V-shape beams. Microsyst. Technol. 2017, 23, 3863–3871. [Google Scholar] [CrossRef]
- Hayes, G.R.; Frecker, M.I.; Adair, J.H. Fabrication of compliant mechanisms on the mesoscale. Mech. Sci. 2011, 2, 129–137. [Google Scholar] [CrossRef] [Green Version]
- Todd, B.; Jensen, B.D.; Schultz, S.M.; Hawkins, A.R. Design and testing of a thin-flexure bistable mechanism suitable for stamping from metal sheets. J. Mech. Des. 2010, 132, 071011. [Google Scholar] [CrossRef]
- Young, R.J.; Lovell, P.A. Introduction to Polymers; CRC Press: Boca Raton, FI, USA, 2011. [Google Scholar]
- Giboz, J.; Copponnex, T.; Mélé, P. Microinjection molding of thermoplastic polymers: Morphological comparison with conventional injection molding. J. Micromech. Microeng. 2009, 19, 025023. [Google Scholar] [CrossRef]
- Yang, C.; Yin, X.-H.; Cheng, G.-M. Microinjection molding of microsystem components: New aspects in improving performance. J. Micromech. Microeng. 2013, 23, 093001. [Google Scholar] [CrossRef]
- Lucchetta, G.; Masato, D.; Sorgato, M.; Crema, L.; Savio, E. Effects of different mould coatings on polymer filling flow in thin-wall injection moulding. CIRP Ann. 2016, 65, 537–540. [Google Scholar] [CrossRef]
- Griffiths, C.A.; Rees, A.; Kerton, R.M.; Fonseca, O.V. Temperature effects on DLC coated micro moulds. Surf. Coat. Technol. 2016, 307, 28–37. [Google Scholar] [CrossRef] [Green Version]
- Xu, G.; Yu, L.; Lee, L.J.; Koelling, K.W. Experimental and numerical studies of injection molding with microfeatures. Polym. Eng. Sci. 2005, 45, 866–875. [Google Scholar] [CrossRef]
- Sha, B.; Dimov, S.; Griffiths, C.; Packianather, M.S. Investigation of micro-injection moulding: Factors affecting the replication quality. J. Mater. Process. Technol. 2007, 183, 284–296. [Google Scholar] [CrossRef]
- Kim, W.-W.; Gang, M.G.; Min, B.-K.; Kim, W.-B. Experimental and numerical investigations of cavity filling process in injection moulding for microcantilever structures. Int. J. Adv. Manuf. Technol. 2014, 75, 293–304. [Google Scholar] [CrossRef]
- Eladl, A.; Mostafa, R.; Islam, A.; Loaldi, D.; Soltan, H.; Hansen, H.N.; Tosello, G. Effect of process parameters on flow length and flash formation in injection moulding of high aspect ratio polymeric micro features. Micromachines 2018, 9, 58. [Google Scholar] [CrossRef] [Green Version]
- Mélé, P.; Giboz, J. Micro-injection molding of thermoplastic polymers: Proposal of a constitutive law as function of the aspect ratios. J. Appl. Polym. Sci. 2018, 135, 45719. [Google Scholar] [CrossRef]
- Han, S.-Y.; Kim, W.-B. Microinjection moulding of miniaturised polymeric ortho-planar springs. Microsyst. Technol. 2016, 22, 1991–1999. [Google Scholar] [CrossRef]
- McFarland, A.W.; Poggi, M.A.; Bottomley, L.A.; Colton, J.S. Injection moulding of high aspect ratio micron-scale thickness polymeric microcantilevers. Nanotechnology 2004, 15, 1628–1632. [Google Scholar] [CrossRef]
- Urwyler, P.; Schift, H.; Gobrecht, J.; Häfeli, O.; Altana, M.; Battiston, F.; Müller, B. Surface patterned polymer micro-cantilever arrays for sensing. Sens. Actuators Phys. 2011, 172, 2–8. [Google Scholar] [CrossRef]
- Zhou, W.; Yu, H.; Chen, L.; Chen, Y.; Peng, B.; Peng, P. Stability analysis of two coupled pre-shaped beams in parallel. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 2482–2489. [Google Scholar] [CrossRef]
- Wilcox, D.L.; Howell, L.L. Fully compliant tensural bistable micromechanisms (FTBM). J. Microelectromech. Syst. 2005, 14, 1223–1235. [Google Scholar] [CrossRef]
- Xu, Q. Design of a large-stroke bistable mechanism for the application in constant-force micropositioning stage. J. Mech. Robot. 2017, 9, 011006. [Google Scholar] [CrossRef]
- Masters, N.D.; Howell, L.L. A self-retracting fully compliant bistable micromechanism. J. Microelectromech. Syst. 2003, 12, 273–280. [Google Scholar] [CrossRef]
- Yan, W.; Yu, Y.; Mehta, A. Analytical modeling for rapid design of bistable buckled beams. Theor. Appl. Mech. Lett. 2019, 9, 264–272. [Google Scholar] [CrossRef]
- Ghosh, A.; Yoon, C.; Ongaro, F.; Scheggi, S.; Selaru, F.M.; Misra, S.; Gracias, D.H. Stimuli-responsive soft untethered grippers for drug delivery and robotic Ssurgery. Front. Mech. Eng. 2017, 3, 7. [Google Scholar] [CrossRef] [PubMed]
- Tolou, N.; Henneken, V.A.; Herder, J.L. Statically balanced compliant micro mechanisms (SB-MEMS): Concepts and simulation. In Proceedings of the ASME 2010 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Montreal, QC, Canada, 15–18 August 2010; pp. 447–454. [Google Scholar]
- Synthesis of Mechanisms with Prescribed Elastic Load-Displacement Characteristics | TU Delft Repositories. Available online: https://repository.tudelft.nl/islandora/object/uuid:d518b379-462a-448f-83ef-5ba0e761c578 (accessed on 23 January 2020).
- Lamers, A.J.; Gallego Sánchez, J.A.; Herder, J.L. Design of a statically balanced fully compliant grasper. Mech. Mach. Theory 2015, 92, 230–239. [Google Scholar] [CrossRef]
- Shan, S.; Kang, S.H.; Raney, J.R.; Wang, P.; Fang, L.; Candido, F.; Lewis, J.A.; Bertoldi, K. Multistable architected materials for trapping elastic strain energy. Adv. Mater. 2015, 27, 4296–4301. [Google Scholar] [CrossRef]
- Che, K.; Yuan, C.; Qi, H.J.; Meaud, J. Viscoelastic multistable architected materials with temperature-dependent snapping sequence. Soft Matter 2018, 14, 2492–2499. [Google Scholar] [CrossRef]
- Yang, H.; Ma, L. Multi-stable mechanical metamaterials by elastic buckling instability. J. Mater. Sci. 2019, 54, 3509–3526. [Google Scholar] [CrossRef]
- Haghpanah, B.; Salari-Sharif, L.; Pourrajab, P.; Hopkins, J.; Valdevit, L. Multistable shape-reconfigurable architected materials. Adv. Mater. 2016, 28, 7915–7920. [Google Scholar] [CrossRef]
- Chen, T.; Mueller, J.; Shea, K. Integrated design and simulation of tunable, multi-state structures fabricated monolithically with multi-material 3D printing. Sci. Rep. 2017, 7, 1–8. [Google Scholar] [CrossRef]
- Wu, X.; Su, Y.; Shi, J. Perspective of additive manufacturing for metamaterials development. Smart Mater. Struct. 2019, 28, 093001. [Google Scholar] [CrossRef]
- Cao, L.; Dolovich, A.T.; Schwab, A.L.; Herder, J.L.; Zhang, W. (Chris). Toward a unified design approach for both compliant mechanisms and rigid-body mechanisms: Module optimization. J. Mech. Des. 2015, 137, 122301. [Google Scholar] [CrossRef] [Green Version]
- Cao, L.; Dolovich, A.T.; Chen, A.; Zhang, W. (Chris). Topology optimization of efficient and strong hybrid compliant mechanisms using a mixed mesh of beams and flexure hinges with strength control. Mech. Mach. Theory 2018, 121, 213–227. [Google Scholar] [CrossRef]






| Process Parameters | Value |
|---|---|
| Injection speed (mm/s) | 75 |
| Injection pressure (MPa) | 75 |
| Pressure holding time (s) | 4 |
| Melt temperature (°C) | 220 |
| Mold temperature (°C) | 130 (filling), 100 (ejecting) |
| Design | Geometric Variable | Mold | Part | Shrinkage (%) | Error (%) |
|---|---|---|---|---|---|
| Original | L (mm) | 5.83 | 5.726 | 1.78 | −1.78 |
| lf (mm) | 1.0 | 0.99 | 1.08 | −1 | |
| li (mm) | 5.0 | 4.95 | −1 | ||
| h (mm) | 1.294 | 1.175 | – | −9.1 | |
| θ (°) | 15.0 | 13.74 | – | −8.4 | |
| Compensation | L (mm) | 5.99 | 5.869 | 2.02 | 0.6 |
| lf (mm) | 1 | 0.99 | 1.01 | −1 | |
| li (mm) | 5.2 | 5.15 | 3 | ||
| h (mm) | 1.45 | 1.34 | – | 3.6 | |
| θ (°) | 16.4 | 15.08 | – | 0.6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, W.-B.; Han, S.-Y. Microinjection Molding of Out-of-Plane Bistable Mechanisms. Micromachines 2020, 11, 155. https://doi.org/10.3390/mi11020155
Kim W-B, Han S-Y. Microinjection Molding of Out-of-Plane Bistable Mechanisms. Micromachines. 2020; 11(2):155. https://doi.org/10.3390/mi11020155
Chicago/Turabian StyleKim, Wook-Bae, and Sol-Yi Han. 2020. "Microinjection Molding of Out-of-Plane Bistable Mechanisms" Micromachines 11, no. 2: 155. https://doi.org/10.3390/mi11020155
APA StyleKim, W.-B., & Han, S.-Y. (2020). Microinjection Molding of Out-of-Plane Bistable Mechanisms. Micromachines, 11(2), 155. https://doi.org/10.3390/mi11020155




