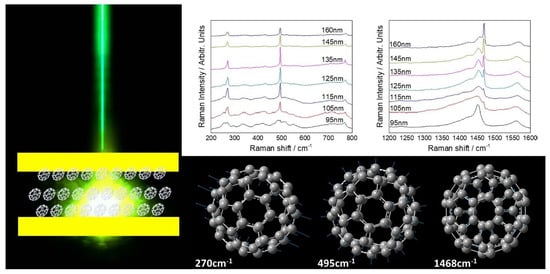
Microcavity Enhanced Raman Spectroscopy of Fullerene C60 Bucky Balls
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Cavity Preparation
2.2.2. Metrological Characterization
2.2.3. Photo-Luminescence and Raman Spectra
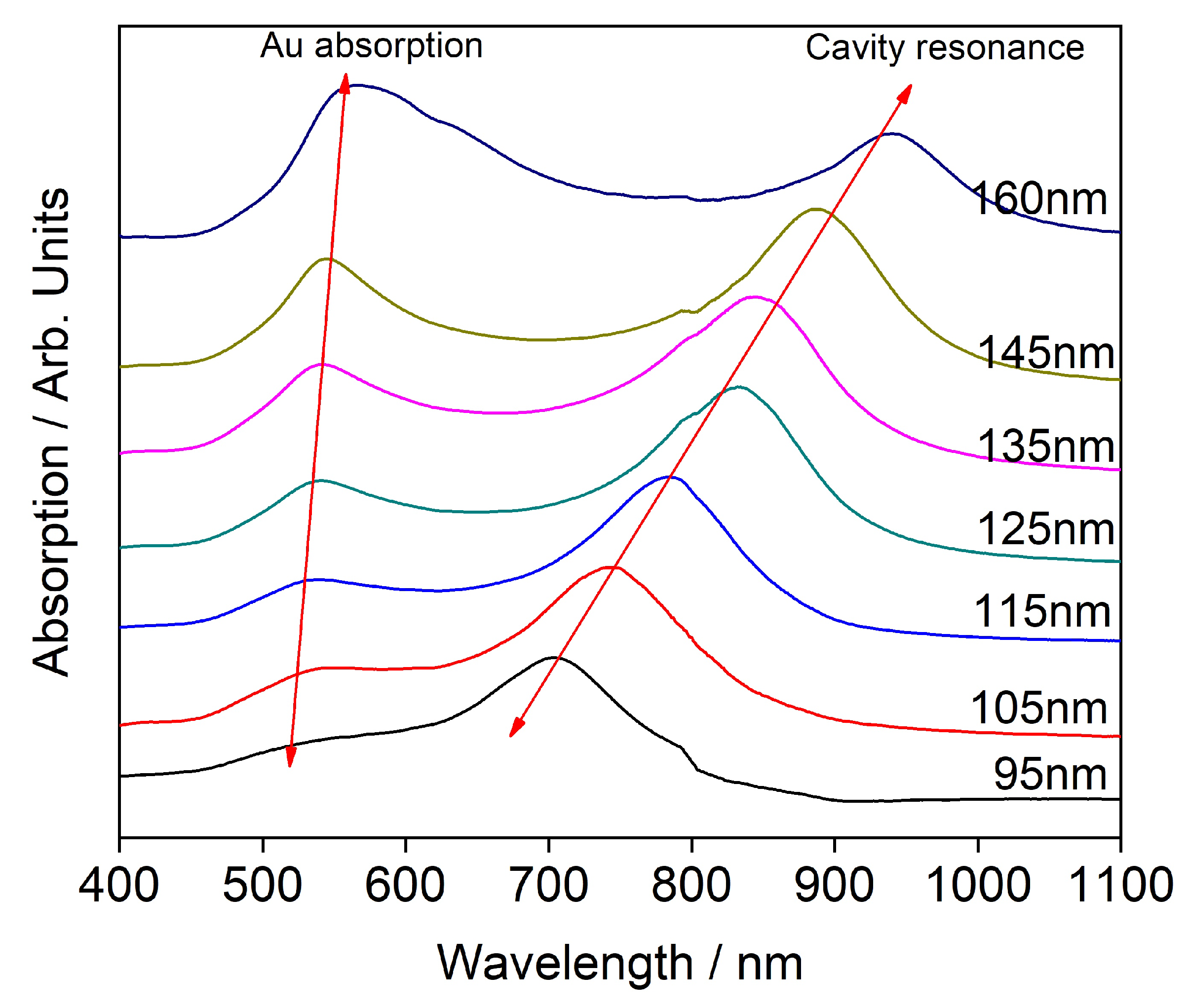
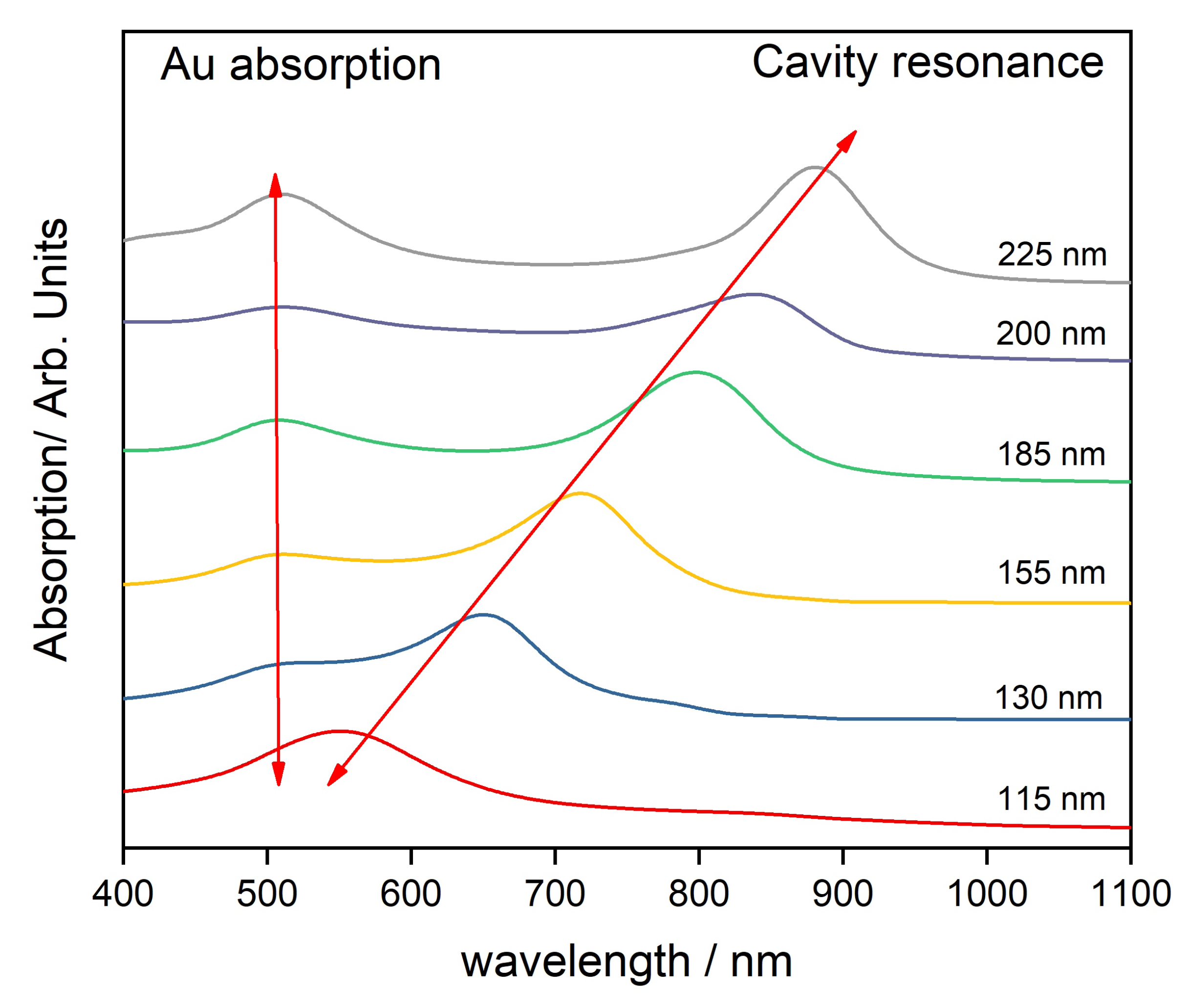
2.2.4. Transmission Spectroscopy
2.2.5. DFT Calculations
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PL | Photo-Luminescence |
| DFT | Density Functional Theory |
| SNR | Signal to Noise Ratio |
| SERS | Surfaced Enhanced Raman Spectroscopy |
| PERS | Plasmon Enhanced Raman Spectroscopy |
| TERS | Tip Enhanced Raman Spectroscopy |
| CERS | Cavity Enhanced Raman Spectroscopy |
| PS | Polystyrene |
| DI | Deionized |
| NA | Numerical Aperture |
References
- Dovesi, R.; Erba, A.; Orlando, R.; Zicovich-Wilson, C.M.; Civalleri, B.; Maschio, L.; Rérat, M.; Casassa, S.; Baima, J.; Salustro, S.; et al. Quantum-mechanical condensed matter simulations with CRYSTAL. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, 1360–1396. [Google Scholar] [CrossRef]
- Aprà, E.; Bhattarai, A.; Baxter, E.; Johnson, G.E.; Govind, N.; El-Khoury, P.Z. A Simplified Approach to Simulating Raman Spectra from Ab Initio Molecular Dynamics. arXiv 2019, arXiv:1909.03142. [Google Scholar]
- De Wolf, I. Micro-Raman spectroscopy to study local mechanical stress in silicon integrated circuits. Semicond. Sci. Tech. 1996, 11, 139–154. [Google Scholar] [CrossRef]
- Mohiuddin, T.; Lombardo, A.; Nair, R.; Bonetti, A.; Savini, G.; Jalil, R.; Bonini, N.; Basko, D.; Galiotis, C.; Marzari, N.; et al. Uniaxial strain in graphene by Raman spectroscopy: G peak splitting, Grüneisen parameters, and sample orientation. Phys. Rev. B 2009, 79, 1–8. [Google Scholar] [CrossRef]
- Hupp, J.T.; Williams, R.D. Using resonance Raman spectroscopy to examine vibrational barriers to electron transfer and electronic delocalization. Acc. Chem. Res. 2001, 34, 808–817. [Google Scholar] [CrossRef] [PubMed]
- Fleischmann, M.; Hendra, P.J.; McQuillan, A.J. Raman spectra of pyridine adsorbed at a silver electrode. Chem. Phys. Lett. 1974, 26, 163–166. [Google Scholar] [CrossRef]
- Shao, F.; Zenobi, R. Tip-enhanced Raman spectroscopy: Principles, practice, and applications to nanospectroscopic imaging of 2D materials. Anal. Bioanal. Chem. 2019, 411, 37–61. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Li, H.; Xu, S.; Zhao, B.; Xu, W. Integrated plasmon-enhanced Raman scattering (i PERS) spectroscopy. Sci. Rep. 2017, 7, 14630. [Google Scholar] [CrossRef] [Green Version]
- Ding, S.Y.; You, E.M.; Tian, Z.Q.; Moskovits, M. Electromagnetic theories of surface-enhanced Raman spectroscopy. Chem. Soc. Rev. 2017, 46, 4042–4076. [Google Scholar] [CrossRef]
- Wang, P.; Chen, W.; Wan, F.; Wang, J.; Hu, J. A review of cavity-enhanced Raman spectroscopy as a gas sensing method. App. Spect. Rev. 2019, 1–25. [Google Scholar] [CrossRef]
- Sandfort, V.; Goldschmidt, J.; Wöllenstein, J.; Palzer, S. Cavity-enhanced Raman spectroscopy for food chain management. Sensors 2018, 18, 709. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Uliel, T.B.; Gouda, L.; Aviv, H.; Itzhak, A.; Tischler, Y.R. Microcavity enhancement of low-frequency Raman scattering from a CsPbI3 thin film. J. Raman Spec. 2019, 50, 1672–1678. [Google Scholar] [CrossRef]
- Yakuphanoglu, F. Photovoltaic properties of the organic–inorganic photodiode based on polymer and fullerene blend for optical sensors. Sens. Actuators A Phys. 2008, 141, 383–389. [Google Scholar] [CrossRef]
- Bethune, D.S.; Meijer, G.; Tang, W.C.; Rosen, H.J.; Golden, W.G.; Seki, H.; Brown, C.A.; de Vries, M.S. Vibrational Raman and infrared spectra of chromatographically separated C60 and C70 fullerene clusters. Chem. Phys. Lett. 1991, 179, 181–186. [Google Scholar] [CrossRef] [Green Version]
- Wen, X.D.; Martin, R.L.; Henderson, T.M.; Scuseria, G.E. Density functional theory studies of the electronic structure of solid state actinide oxides. Chem. Rev. 2012, 113, 1063–1096. [Google Scholar] [CrossRef] [PubMed]
- Schettino, V.; Pagliai, M.; Ciabini, L.; Cardini, G. The vibrational spectrum of fullerene C60. J. Phys. Chem. A 2001, 105, 11192–11196. [Google Scholar] [CrossRef]
- Menéndez, J.; Page, J.B. Vibrational spectroscopy of C 60. In Light Scattering in Solids VIII; Springer: Berlin, Germany, 2000; pp. 27–95. [Google Scholar]
- Do, H.; Besley, N.A. Calculation of the vibrational frequencies of carbon clusters and fullerenes with empirical potentials. Phys. Chem. Chem. Phys. 2015, 17, 3898–3908. [Google Scholar] [CrossRef] [Green Version]
- Hashimoto, K.; Badarla, V.R.; Kawai, A.; Ideguchi, T. Complementary Vibrational Spectroscopy. arXiv 2019, arXiv:1904.02857. [Google Scholar] [CrossRef] [Green Version]
- Parker, S.F.; Williams, K.P.; Bortz, M.; Yvon, K. Inelastic neutron scattering, infrared, and Raman spectroscopic studies of Mg2FeH6 and Mg2FeD6. Inorg. Chem. 1997, 36, 5218–5221. [Google Scholar] [CrossRef]
- Altman, E.I.; Colton, R.J. The interaction of C60 with noble metal surfaces. Surf. Sci. 1993, 295, 13–33. [Google Scholar] [CrossRef]
- Sivadasan, A.; Parida, S.; Ghosh, S.; Pandian, R.; Dhara, S. Spectroscopically forbidden infra-red emission in Au-vertical graphene hybrid nanostructures. Nanotechnology 2017, 28, 465703. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sauvajol, J.; Graja, A.; Firlej, L.; Król, S. Raman study of the charge transfer C60 complexes with tetraphenylphosphonium halides. J. Mol. Sci. 1997, 436, 19–23. [Google Scholar] [CrossRef]
- Luo, Z.X.; Fang, Y. SERS of C60 coated with gold nanoparticles on filter paper and filter membrane. Sci. Access 2004, 2, 548–549. [Google Scholar]
- Luo, Z.; Loo, B.H.; Peng, A.; Ma, Y.; Fu, H.; Yao, J. Single-molecule surface-enhanced Raman scattering of fullerene C60. J. Raman Spec. 2011, 42, 319–323. [Google Scholar] [CrossRef]
- Yang, X.C.; Fang, Y. Surface-enhanced Raman scattering of C60 and C70 in gold hydrosols. J. Phys. Chem. B 2003, 107, 10100–10103. [Google Scholar] [CrossRef]
- Meletov, K. Photopolymerization in the Fullerene Layers of the Molecular Donor–Acceptor Complex {Pt (nPr 2 dtc) 2}·(C 60) 2. Phys. Sol. State 2018, 60, 2103–2108. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. IV. A new dynamical correlation functional and implications for exact-exchange mixing. J. Chem. Phys. 1996, 104, 1040–1046. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–790. [Google Scholar] [CrossRef] [Green Version]
- Stephens, P.J.; Devlin, F.; Chabalowski, C.; Frisch, M.J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Sinwani, M.; Muallem, M.; Tischler, Y.R. The effect of excitation wavelength and metallic nanostructure on SERS spectra of C60. J. Raman Spec. 2017, 48, 829–836. [Google Scholar] [CrossRef]
- Gupta, G.; Tanaka, D.; Ito, Y.; Shibata, D.; Shimojo, M.; Furuya, K.; Mitsui, K.; Kajikawa, K. Absorption spectroscopy of gold nanoisland films: Optical and structural characterization. Nanotechnology 2008, 20, 025703. [Google Scholar] [CrossRef] [PubMed]
- Liang, H.P.; Wan, L.J.; Bai, C.L.; Jiang, L. Gold hollow nanospheres: Tunable surface plasmon resonance controlled by interior-cavity sizes. J. Phys. Chem. B 2005, 109, 7795–7800. [Google Scholar] [CrossRef] [PubMed]
- Murphy, C.J.; Coffer, J.L. Quantum dots: A primer. Appl. Spec. 2002, 56, 16–27. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Ding, T. Optical tuning of plasmon-enhanced photoluminescence. Nanoscale 2019, 11, 10589–10594. [Google Scholar] [CrossRef]
- Jensen, L.; Van Duijnen, P.T. Refractive index and third-order nonlinear susceptibility of C60 in the condensed phase calculated with the discrete solvent reaction field model. Int. J. Quantum Chem. 2005, 102, 612–619. [Google Scholar] [CrossRef]
- Khinevich, N.; Girel, K.; Bandarenka, H.; Salo, V.; Mosunov, A. Surface enhanced Raman spectroscopy of fullerene C60 drop-deposited on the silvered porous silicon. J. Phys. Conf. Ser. 2017, 917, 062052. [Google Scholar] [CrossRef]






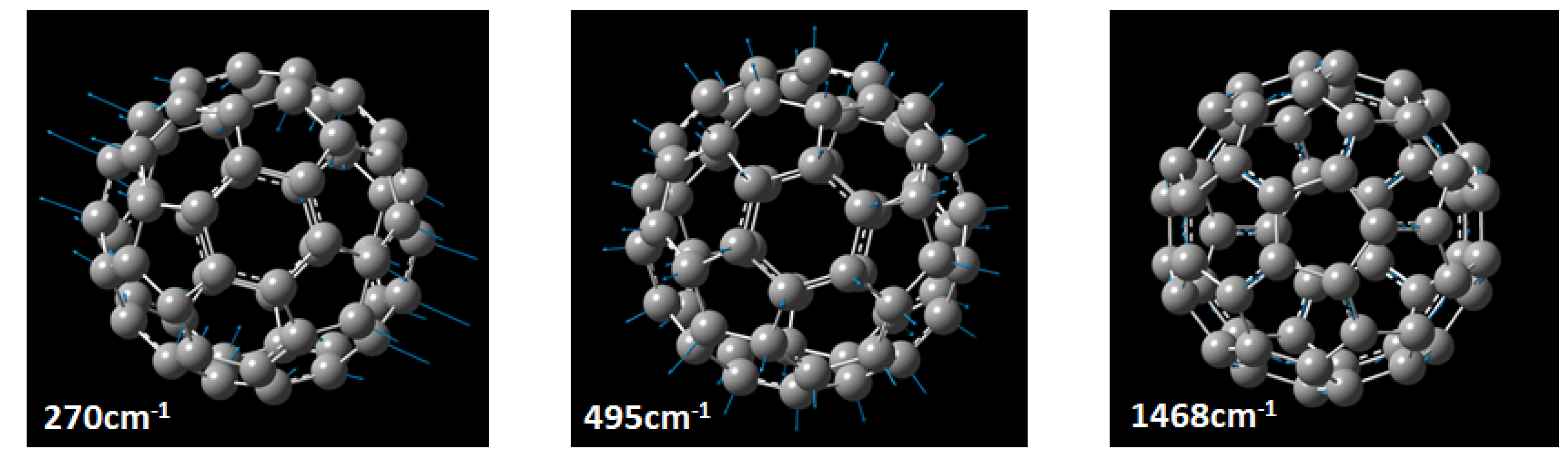
| Symmetry | Ag | Au | T1g | T1u | T3u | T3g | Gg | Gu | Hg | Hu |
|---|---|---|---|---|---|---|---|---|---|---|
| Number of Modes | 2 | 1 | 3 | 4 | 5 | 4 | 6 | 6 | 8 | 7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Damle, V.H.; Sinwani, M.; Aviv, H.; Tischler, Y.R. Microcavity Enhanced Raman Spectroscopy of Fullerene C60 Bucky Balls. Sensors 2020, 20, 1470. https://doi.org/10.3390/s20051470
Damle VH, Sinwani M, Aviv H, Tischler YR. Microcavity Enhanced Raman Spectroscopy of Fullerene C60 Bucky Balls. Sensors. 2020; 20(5):1470. https://doi.org/10.3390/s20051470
Chicago/Turabian StyleDamle, Vinayaka H., Miri Sinwani, Hagit Aviv, and Yaakov R. Tischler. 2020. "Microcavity Enhanced Raman Spectroscopy of Fullerene C60 Bucky Balls" Sensors 20, no. 5: 1470. https://doi.org/10.3390/s20051470
APA StyleDamle, V. H., Sinwani, M., Aviv, H., & Tischler, Y. R. (2020). Microcavity Enhanced Raman Spectroscopy of Fullerene C60 Bucky Balls. Sensors, 20(5), 1470. https://doi.org/10.3390/s20051470