Direct Use of the Savitzky–Golay Filter to Develop an Output-Only Trend Line-Based Damage Detection Method
Abstract
1. Introduction
2. Basic Theory of SGF
3. Proposed Method
4. The Numerical Model of Simply Supported Beam under Moving Sprung Mass
5. Trend Lines and Damage Localization
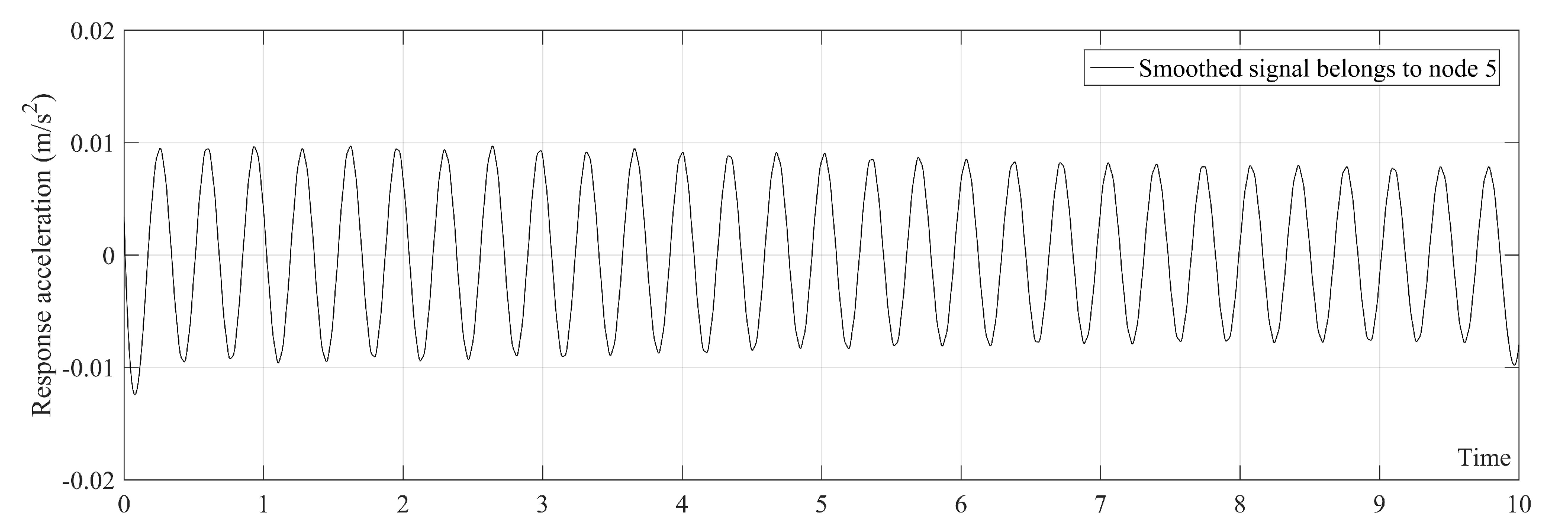
5.1. Applying SGF on Each Acceleration Data
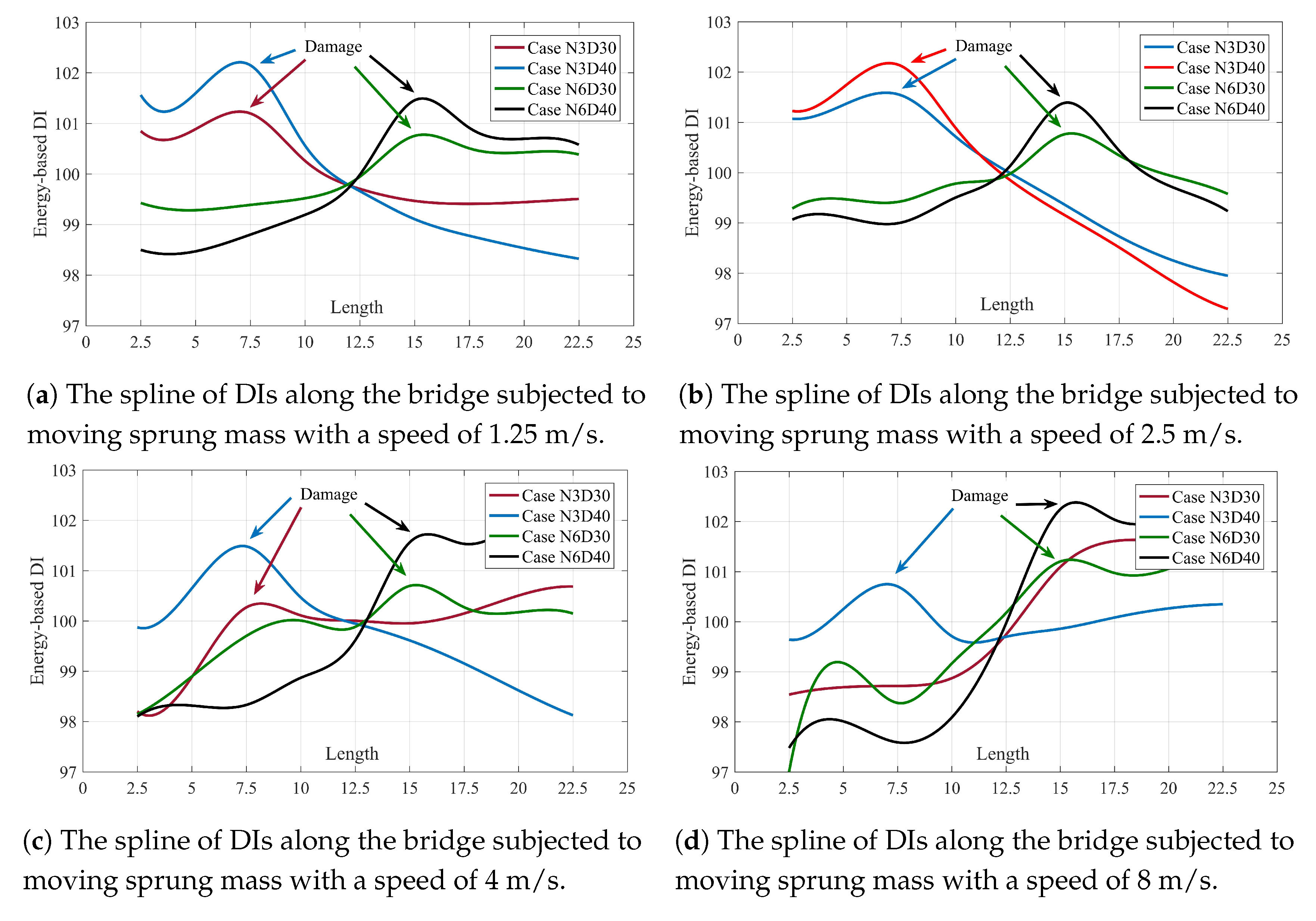
5.2. Damage Localization
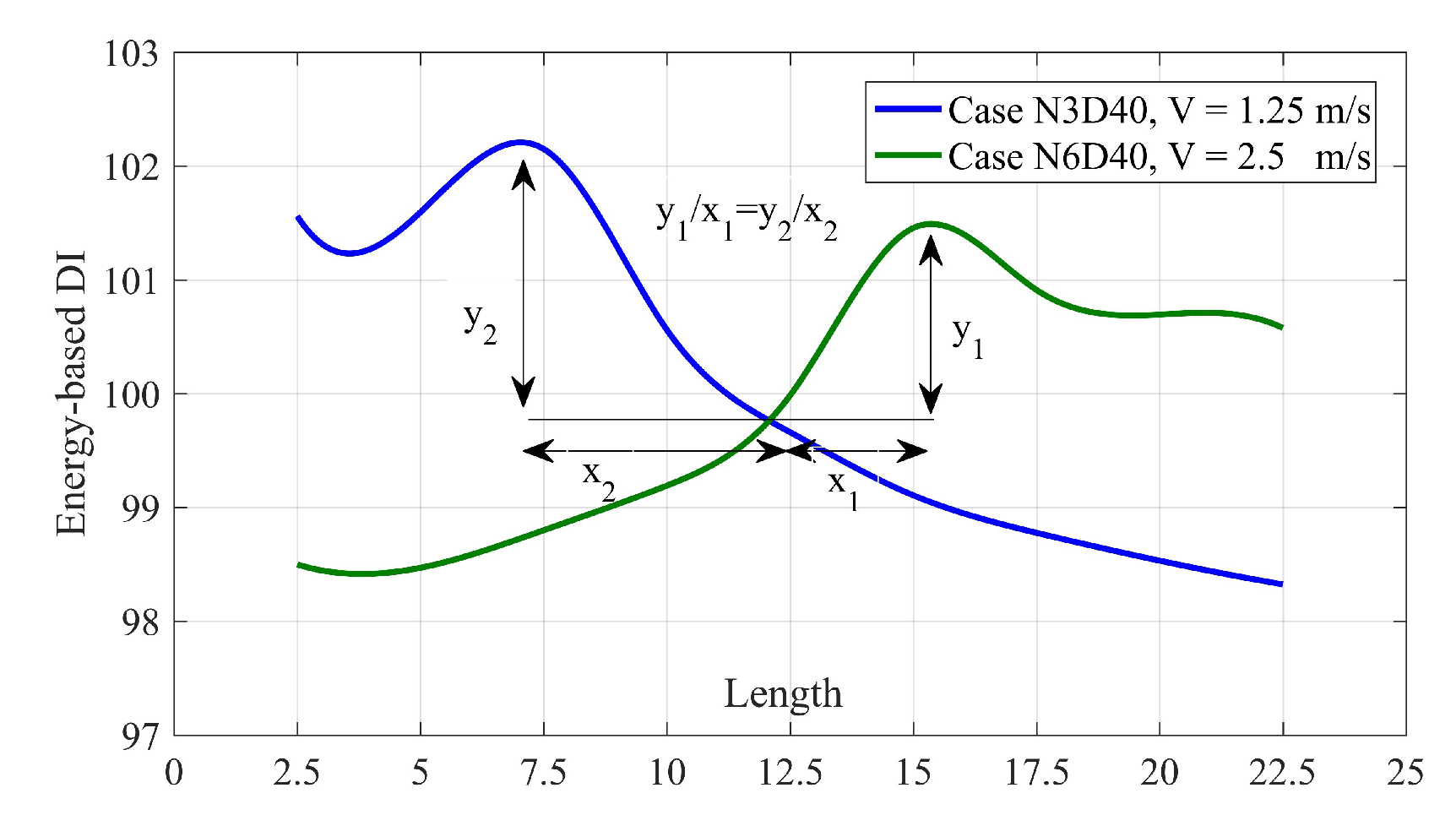
5.3. Damage Quantification for Single Damage Scenarios
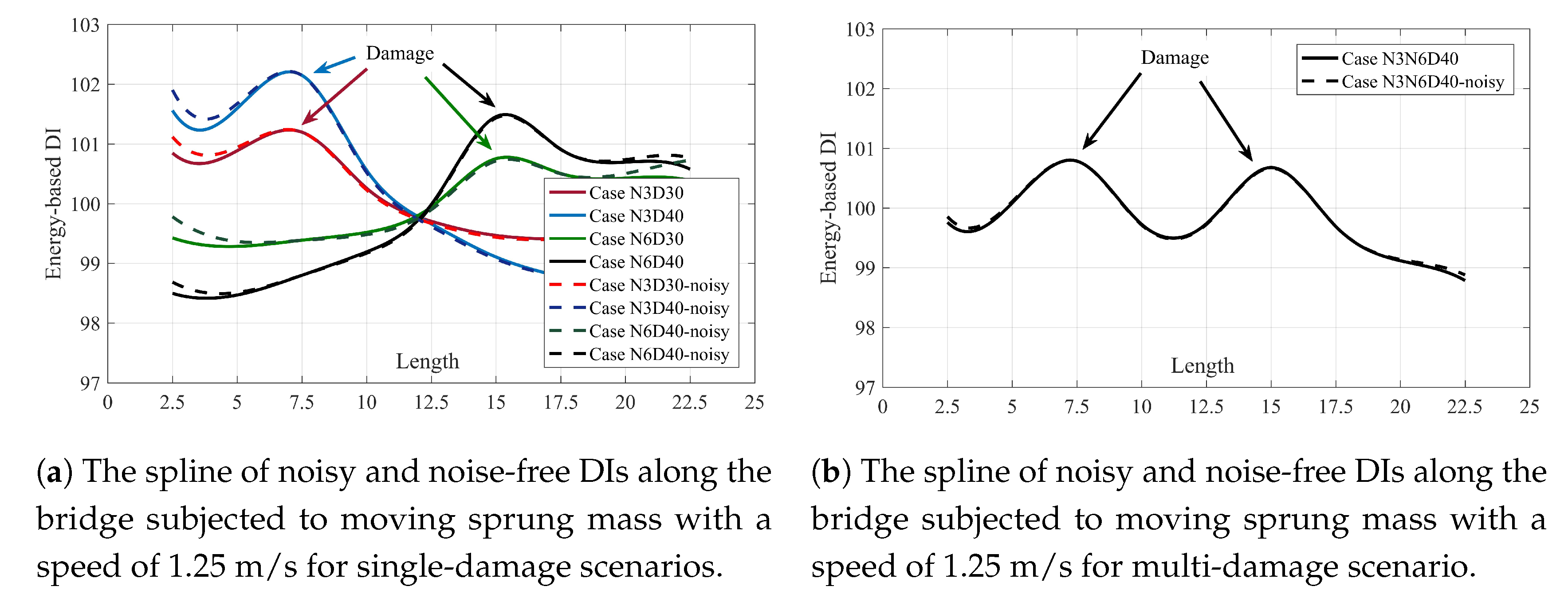
5.4. Considering the Noise
5.5. Baseline Estimation
6. Discussion
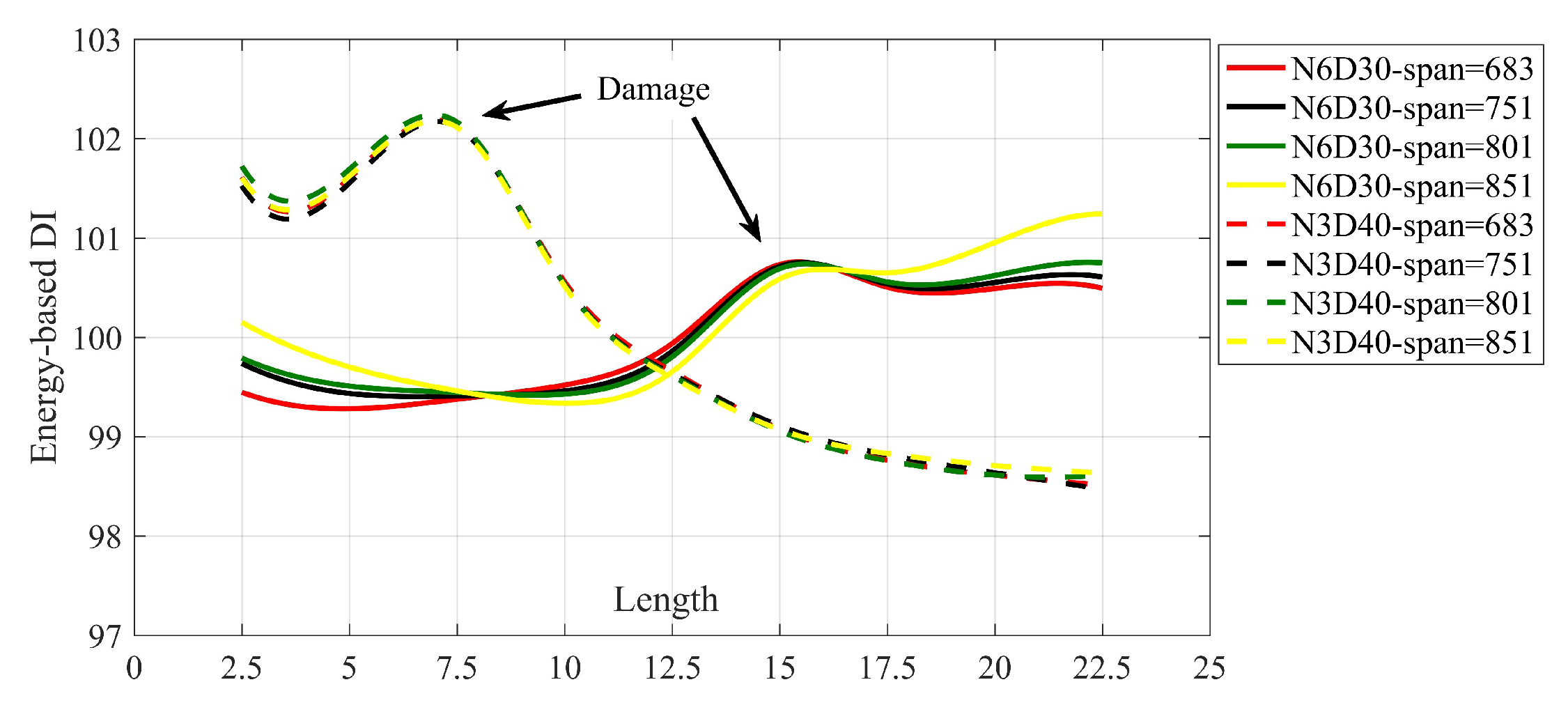
6.1. The Effect of Different Spans of SGF
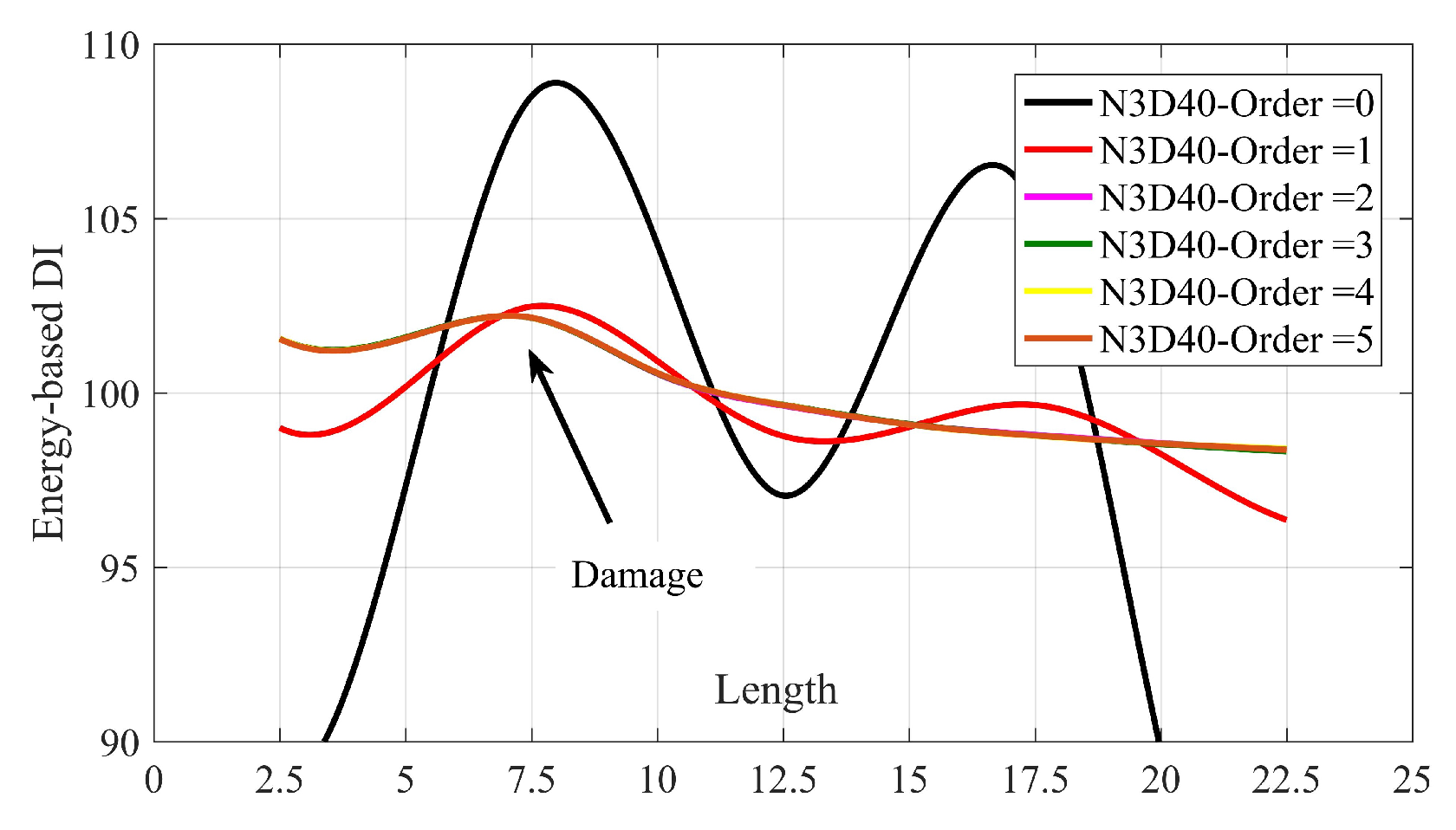
6.2. The Effect of Different Order of SGF
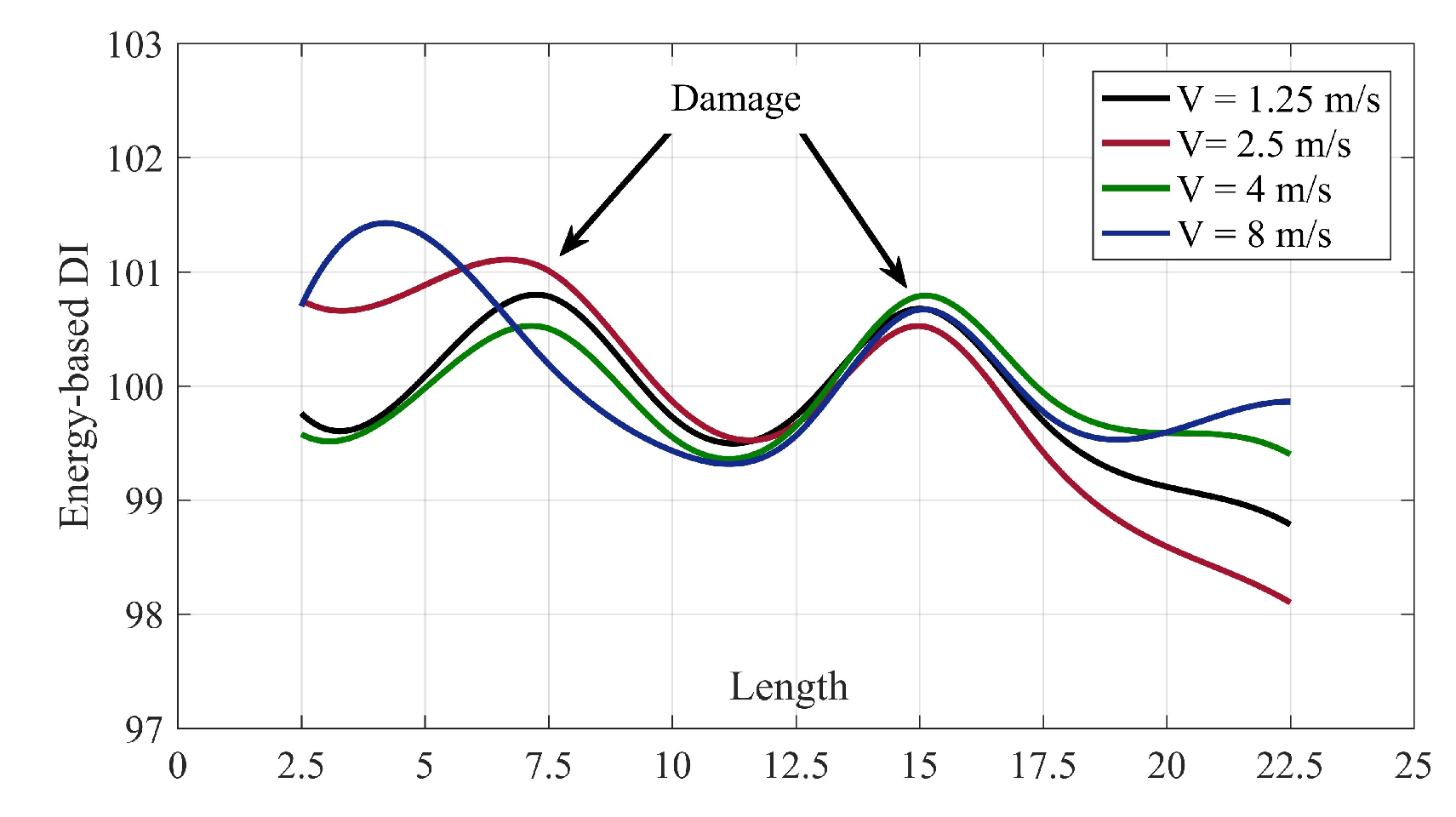
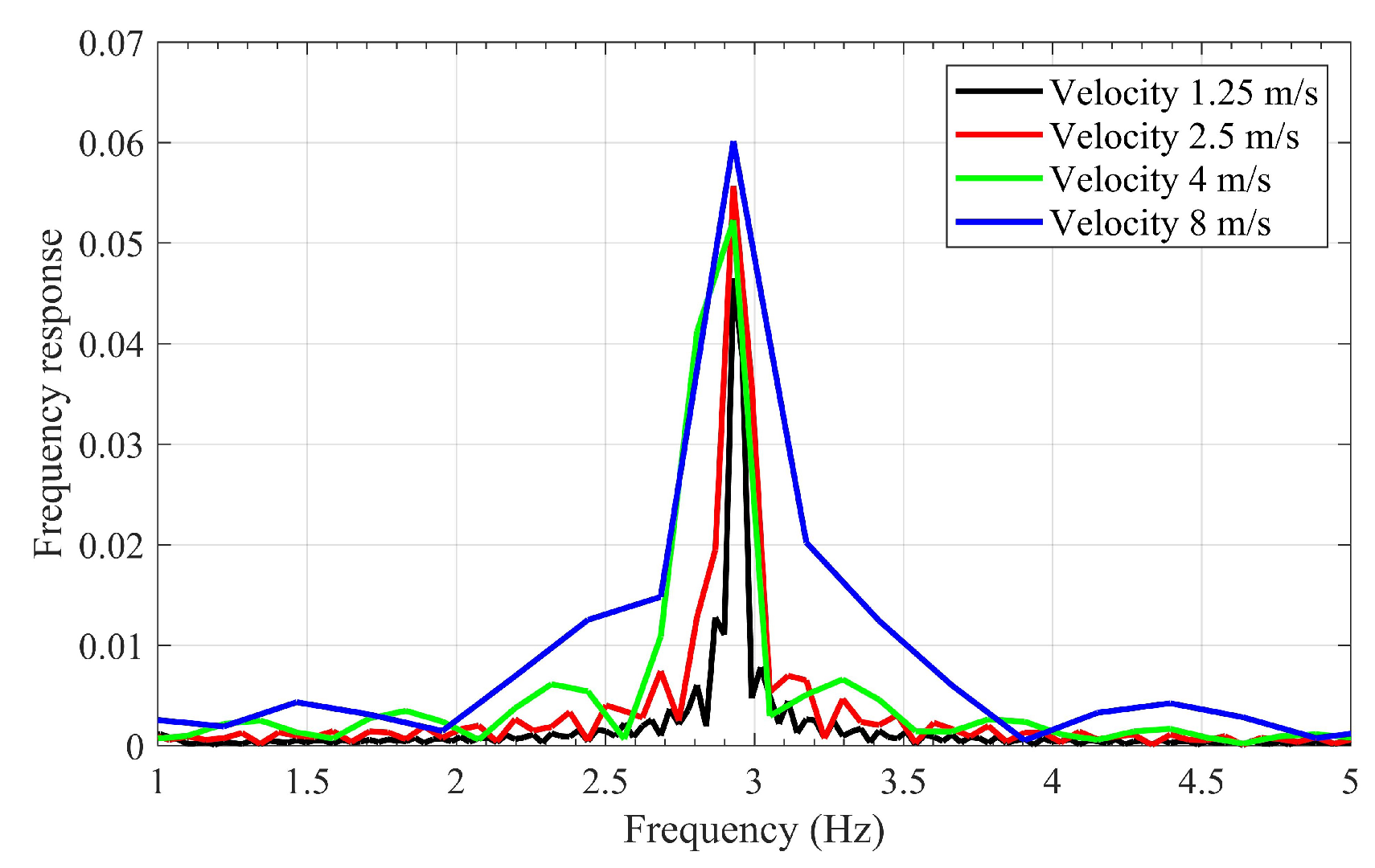
6.3. Vehicle-Bridge Interaction
6.4. The Effect of Damage on Natural Frequencies
7. Conclusions
- Since the SGF is a de-noising technique, the proposed method is essentially insensitive to the noise.
- The proposed method could locate/quantify the damage in noisy/noise-free environment.
- Fitting a Gaussian curve to the normalization factor makes the proposed method as a baseline-free method.
- The proposed method can locate the damage in a multi-damage scenario.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BHM | Bridge Health Monitoring |
| BSS | Blind Source Separation |
| DI | Damage Index |
| RDT | Random Decrement Technique |
| SGF | Savitzky–Golay filter |
| SHM | Structural Health Monitoring |
| SOBI | Second Order Blind Identification |
References
- Kordestani, H.; Xiang, Y.Q.; Ye, X.W. Output-only damage detection of steel beam using moving average filter. Shock Vib. 2018, 2018. [Google Scholar] [CrossRef]
- Kordestani, H.; Xiang, Y.Q.; Ye, X.W.; Jia, Y.K. Application of the random decrement technique in damage detection under moving load. Appl. Sci. 2018, 8, 753. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, C.; Zhu, X.; Kang, W.H.; Mao, X.; Uy, B. Design and experimental investigations of a vibration based wireless measurement system for bridge cable tension monitoring. Adv. Struct. Eng. 2014, 17, 1657–1668. [Google Scholar] [CrossRef]
- Sun, L.; Li, C.; Zhang, C.; Su, Z.; Chen, C. Early monitoring of rebar corrosion evolution based on FBG sensor. Int. J. Struct. Stab. Dyn. 2018, 18, 1840001. [Google Scholar] [CrossRef]
- OBrien, E.J.; Malekjafarian, A.; González, A. Application of empirical mode decomposition to drive-by bridge damage detection. Eur. J. Mech. 2017, 61, 151–163. [Google Scholar] [CrossRef]
- Pakrashi, V.; O’Connor, A.; Basu, B. A bridge-vehicle interaction based experimental investigation of damage evolution. Struct. Health Monit. 2010, 9, 285–296. [Google Scholar] [CrossRef]
- Hester, D.; Gonzalez, A. A wavelet-based damage detection algorithm based on bridge acceleration response to a vehicle. Mech. Syst. Signal. Process. 2012, 28, 145–166. [Google Scholar] [CrossRef]
- Balafas, K.; Kiremidjian, A.S. Development and validation of a novel earthquake damage estimation scheme based on the continuous wavelet transform of input and output acceleration measurements. Earthq. Eng. Struct. Dyn. 2015, 44, 501–522. [Google Scholar] [CrossRef]
- Cantero, D.; Basu, B. Railway infrastructure damage detection using wavelet transformed acceleration response of traversing vehicle. Struct. Control. Health Monit. 2015, 22, 62–70. [Google Scholar] [CrossRef]
- Hester, D.; González, A. Impact of road profile when detecting a localised damage from bridge acceleration response to a moving vehicle. Key Eng. Mater. 2013, 569, 199–206. [Google Scholar] [CrossRef]
- Zhu, X.; Law, S.S. Structural health monitoring based on vehicle-bridge interaction: Accomplishments and challenges. Adv. Struct. Eng. 2015, 18, 1999–2015. [Google Scholar] [CrossRef]
- Asayesh, M.; Khodabandeloo, B.; Siami, A. A random decrement technique for operational modal analysis in the presence of periodic excitations. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2009, 223, 1525–1534. [Google Scholar] [CrossRef]
- Rodrigues, J.; Brincker, R. Application of the random decrement technique in operational modal analysis. In Proceedings of the 1st International Operational Modal Analysis Conference (IOMAC), Copenhagen, Denmark, 26–27 April 2005; pp. 191–200. [Google Scholar]
- Lee, J.W.; Kim, J.D.; Yun, C.B.; Yi, J.H.; Shim, J.M. Health-monitoring method for bridges under ordinary traffic loadings. J. Sound Vib. 2002, 257, 247–264. [Google Scholar] [CrossRef][Green Version]
- He, X.H.; Hua, X.G.; Chen, Z.Q.; Huang, F.L. EMD-based random decrement technique for modal parameter identification of an existing railway bridge. Eng. Struct. 2011, 33, 1348–1356. [Google Scholar] [CrossRef]
- Wu, W.H.; Chen, C.C.; Liau, J.A. A multiple random decrement method for modal parameter identification of stay cables based on ambient vibration signals. Adv. Struct. Eng. 2012, 15, 969–982. [Google Scholar] [CrossRef]
- Buff, H.; Friedmann, A.; Koch, M.; Bartel, T.; Kauba, M. Design of a random decrement method based structural health monitoring system. Shock Vib. 2012, 19, 787–794. [Google Scholar] [CrossRef][Green Version]
- Poncelet, F.; Kerschen, G.; Golinval, J.C.; Verhelst, D. Output-only modal analysis using blind source separation techniques. Mech. Syst. Signal. Process. 2007, 21, 2335–2358. [Google Scholar] [CrossRef]
- Kerschen, G.; Poncelet, F.; Golinval, J.C. Physical interpretation of independent component analysis in structural dynamics. Mech. Syst. Signal. Process. 2007, 21, 1561–1575. [Google Scholar] [CrossRef]
- Zhou, W.; Chelidze, D. Blind source separation based vibration mode identification. Mech. Syst. Signal. Process. 2007, 21, 3072–3087. [Google Scholar] [CrossRef]
- Loh, C.H.; Hung, T.; Chen, S.; Hsu, W. Damage detection in bridge structure using vibration data under random travelling vehicle loads. J. Phys. Conf. Ser. 2015, 628, 012044. [Google Scholar] [CrossRef]
- Huang, C.; Nagarajaiah, S. Experimental study on bridge structural health monitoring using blind source separation method: arch bridge. Struct. Monit. Maint. 2014, 1, 69–87. [Google Scholar] [CrossRef]
- Nie, Z.; Ngo, T.; Ma, H. Reconstructed phase space-based damage detection using a single sensor for beam-Like structure subjected to a moving mass. Shock Vib. 2017. [Google Scholar] [CrossRef]
- Meredith, J.; González, A.; Hester, D. Empirical Mode Decomposition of the Acceleration Response of a Prismatic Beam Subject to a Moving Load to Identify Multiple Damage Locations. Shock. Vib. 2012, 19, 845–856. [Google Scholar] [CrossRef]
- Gonzalez, A.; Hester, D. An investigation into the acceleration response of a damaged beam-type structure to a moving force. J. Sound Vib. 2013, 332, 3201–3217. [Google Scholar] [CrossRef]
- Ostertagova, E.; Ostertag, O. Methodology and application of savitzky-golay moving average polynomial smoother. Global. J. Pure. Appl. Math. 2016, 12, 3201–3210. [Google Scholar]
- Guinon, J.; Ortega, E.; Garcia-Anton, J.; Perez-Herranz, V. Moving average and savitzki-golay smoothing filters using mathcad. In Proceedings of the International Conference on Engineering Education—ICEE 2007, Coimbra, Portugal, 3–7 September 2007. [Google Scholar]
- Quaranta, G.; Carboni, B.; Lacarbonara, W. Damage detection by modal curvatures: Numerical issues. J. Vib. Control 2016, 22, 1913–1927. [Google Scholar] [CrossRef]
- Mosti, F.; Quaranta, G.; Lacarbonara, W. Numerical and experimental assessment of the modal curvature method for damage detection in plate structures. In Structural Nonlinear Dynamics and Diagnosis; Springer: Cham, Switzerland, 2015; Volume 8, p. 02007. [Google Scholar] [CrossRef]
- Mario, D.O.; Nelcileno, A.; Rodolfo, D.S.; Tony, D.S.; Jayantha, E. Use of Savitzky–Golay Filter for Performances Improvement of SHM Systems Based on Neural Networks and Distributed PZT Sensors. Sensors 2018, 18, 152. [Google Scholar] [CrossRef]
- Kordestani, H.; Zhang, C.; Shadabfar, M. Beam Damage Detection Under a Moving Load Using Random Decrement Technique and Savitzky–Golay Filter. Sensors 2020, 20, 243. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Schafer, R. What Is a Savitzky-Golay Filter? (A lecture note). IEEE Signal Process. Mag. 2011, 28, 111–117. [Google Scholar] [CrossRef]
- Ouyang, H. Moving-load dynamic problems: A tutorial (with a brief overview). Mech. Syst. Signal Process. 2011, 25, 2039–2060. [Google Scholar] [CrossRef]
- Yang, Y.B.; Cheng, M.C.; Chang, K.C. Frequency variation in vehicle–bridge interaction systems. Int. J. Struct. Stab. Dyn. 2013, 13, 1350019. [Google Scholar] [CrossRef]
- Cantero, D.; OBrien, E.J. The non-stationarity of apparent bridge natural frequencies during vehicle crossing events. FME Trans. 2013, 41, 279–284. [Google Scholar]
- Cantero, D.; Rønnquist, A. Numerical Evaluation of Modal Properties Change of Railway Bridges during Train Passage. Procedia Eng. 2017, 199, 2931–2936. [Google Scholar] [CrossRef]
- Malekjafarian, A.; Brien, E.J. Identification of bridge mode shapes using short time frequency domain decomposition of the responses measured in a passing vehicle. Eng. Struct. 2014, 81, 386–397. [Google Scholar] [CrossRef]
- OBrien, E.J.; McGetrick, P.J.; Gonzalez, A. A drive-by inspection system via vehicle moving force identification. Smart. Struct. Syst. 2014, 13, 821–848. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, P. Vibration-based damage identification methods: a review and comparative study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Qiao, P.; Cao, M. Waveform fractal dimension for mode shape-based damage identification of beam-type structures. Int. J. Solids Struct. 2008, 45, 5946–5961. [Google Scholar] [CrossRef]
- Kordestani, H.; Xiang, Y.Q.; Ye, X.W.; Yun, C.B.; Shadabfar, M. Localization of damaged cable in a tied-arch bridge using Arias intensity of seismic acceleration response. Struct. Control Health Monit. 2019, e2491. [Google Scholar] [CrossRef]
- Farrar, C.R.; Doebling, S.W.; Cornwell, P.J.; Straser, E.G. Variability of Modal Parameters Measured on the Alamosa Canyon Bridge. Available online: https://www.osti.gov/biblio/432967 (accessed on 2 March 2020).
- Carboni, B.; Lacarbonara, W. A three-dimensional continuum approach to the thermoelastodynamics of large-scale structures. Eng. Struct. 2012, 40, 155–167. [Google Scholar] [CrossRef]
- Peeters, B.; De Roeck, G. One-year monitoring of the Z24-Bridge: Environmental effects versus damage events. Earthq. Eng. Struct. Dyn. 2001, 30, 149–171. [Google Scholar] [CrossRef]





| Properties | Unit | Symbol | Value |
|---|---|---|---|
| Length | m | L | 25 |
| Mass per unit | kg/m | μ | 18,360 |
| Stiffness | Nm2 | EI | 4.865 × 1010 |
| Properties | Unit | Symbol | Value |
|---|---|---|---|
| Body mass | kg | ||
| Axle mass | kg | 700 | |
| Suspension stiffness | Nm | 8 × 105 | |
| Suspension damping | Nm | 2 × 104 | |
| Tire stiffness | Nm | 3.5 × 106 | |
| Velocity | m/s | V |
| Scenario | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Crack depth to the beam height ratio | |||||
| Location | At node 3 | At node 3 | At node 6 | At node 6 | At node 3 and 6 |
| Name |
| Scenario | Velocity (m/s) | Slope | Scenario | Velocity (m/s) | Slope |
|---|---|---|---|---|---|
| 1.25 | 0.31 | N3D40 | 1.25 | 0.52 | |
| N3D30 | 2.5 | 0.34 | 2.5 | 0.47 | |
| 4 | 0.06 | 4 | 0.33 | ||
| 8 | −0.24 | 8 | 0.20 | ||
| 1.25 | 0.32 | N6D40 | 1.25 | 0.55 | |
| N6D30 | 2.5 | 0.25 | 2.5 | 0.46 | |
| 4 | 0.23 | 4 | 0.52 | ||
| 8 | 0.47 | 8 | 0.81 | ||
| Average | 0.27 | Average | 0.49 | ||
| Speed | Node 1 | Node 2 | Node 3 | Node 4 | Node 5 | Node 6 | Node 7 | Node 8 | Node 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1.25 | 0.1732 | 0.6233 | 1.1773 | 1.6273 | 1.8000 | 1.6286 | 1.1775 | 0.6212 | 0.1718 |
| 2.5 | 0.1732 | 0.6212 | 1.1759 | 1.6221 | 1.7980 | 1.6287 | 1.1815 | 0.6258 | 0.1736 |
| 4 | 0.1761 | 0.6283 | 1.1824 | 1.6270 | 1.7970 | 1.6254 | 1.1746 | 0.6184 | 0.1707 |
| 8 | 0.1753 | 0.6228 | 1.1813 | 1.6308 | 1.7997 | 1.6270 | 1.1758 | 0.6175 | 0.1697 |
| Velocity | 1.25 m/s | 2.5 m/s | 4 m/s | 8 m/s |
|---|---|---|---|---|
| Max acceleration | 0.0110 m/s | 0.0290 m/s | 0.0324 m/s | 0.0656 m/s |
| DAF | 1.55 | 1.76 | 1.96 | 2.01 |
| Scenarios | 1st Natural | Change | 2nd Natural | Change | 3rd Natural | Change |
|---|---|---|---|---|---|---|
| Frequency | % | Frequency | % | Frequency | % | |
| WD | 2.933 | — | 11.602 | — | 25.638 | — |
| N3D30 | 2.921 | 0.4 | 11.537 | 0.5 | 25.622 | 0.1 |
| N3D40 | 2.909 | 0.8 | 11.475 | 1.1 | 25.608 | 0.1 |
| N6D30 | 2.916 | 0.5 | 11.577 | 0.2 | 25.589 | 0.2 |
| N6D40 | 2.900 | 1.1 | 11.553 | 0.4 | 25.533 | 0.4 |
| N3N6D40 | 2.877 | 1.9 | 11.424 | 1.5 | 25.502 | 0.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kordestani, H.; Zhang, C. Direct Use of the Savitzky–Golay Filter to Develop an Output-Only Trend Line-Based Damage Detection Method. Sensors 2020, 20, 1983. https://doi.org/10.3390/s20071983
Kordestani H, Zhang C. Direct Use of the Savitzky–Golay Filter to Develop an Output-Only Trend Line-Based Damage Detection Method. Sensors. 2020; 20(7):1983. https://doi.org/10.3390/s20071983
Chicago/Turabian StyleKordestani, Hadi, and Chunwei Zhang. 2020. "Direct Use of the Savitzky–Golay Filter to Develop an Output-Only Trend Line-Based Damage Detection Method" Sensors 20, no. 7: 1983. https://doi.org/10.3390/s20071983
APA StyleKordestani, H., & Zhang, C. (2020). Direct Use of the Savitzky–Golay Filter to Develop an Output-Only Trend Line-Based Damage Detection Method. Sensors, 20(7), 1983. https://doi.org/10.3390/s20071983






