Interleaved Array Transducer with Polarization Inversion Technique to Implement Ultrasound Tissue Harmonic Imaging
Abstract
:1. Introduction
2. Materials and Methods
2.1. Polarization Inversion Technique
2.2. Design of Interleaved Array Transducer Based on FEA Simulation
2.3. FEA Simulation Results
3. Experimental Validation
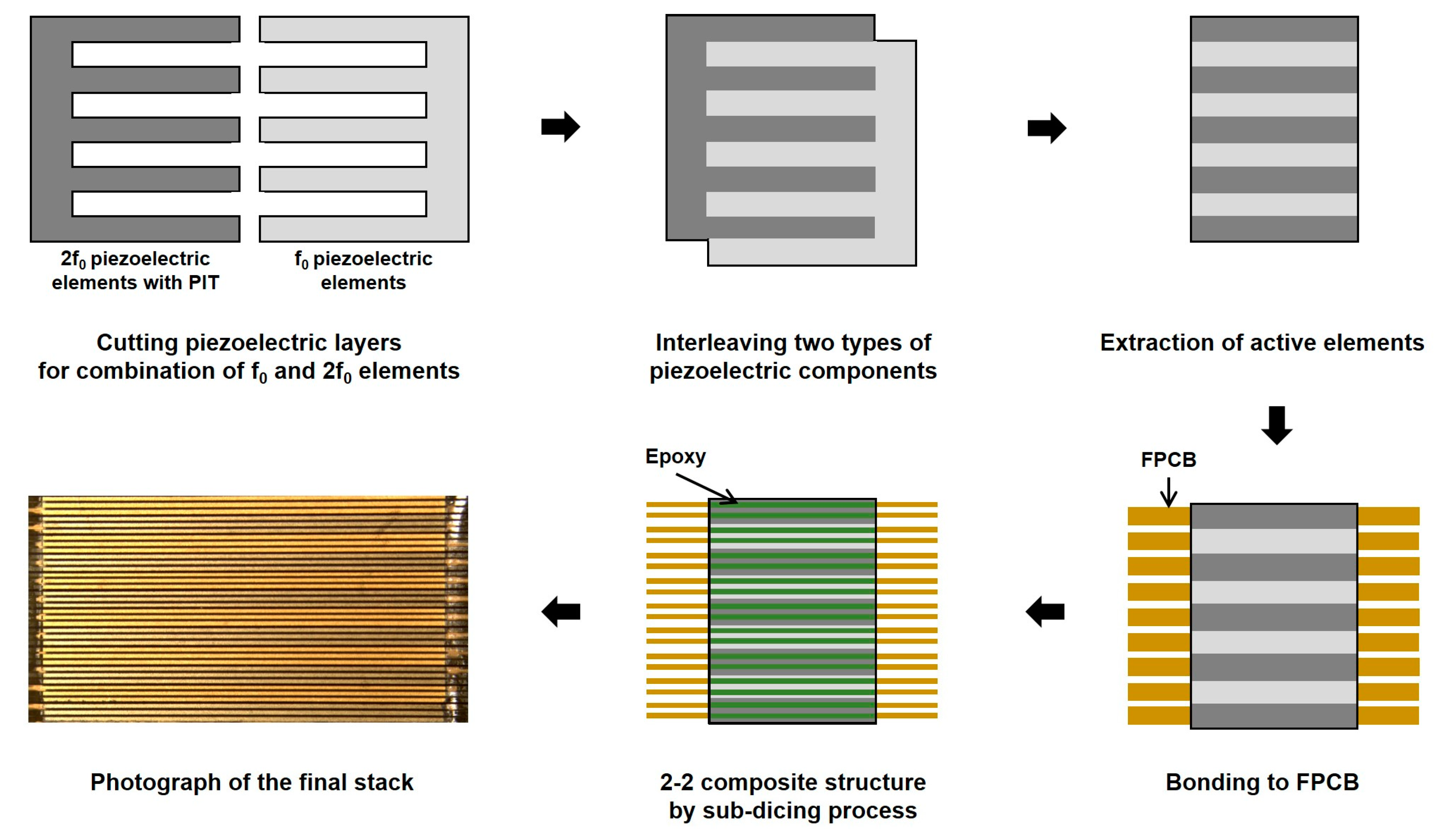
3.1. Fabrication of Prototype Array Transducer with PIT and Novel Interleaved Technique
3.2. Experimental Results
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hedrick, W.R.; Metzger, L. Tissue harmonic imaging: A review. J. Diagn. Med. Sonogr. 2005, 21, 183–189. [Google Scholar] [CrossRef] [Green Version]
- Averkiou, M.A.; Roundhill, D.N.; Powers, J.E. A new imaging technique based on the nonlinear properties of tissues. In Proceedings of the IEEE Ultrasonic Symposium, Toronto, ON, Canada, 5–8 October 1997; pp. 1561–1566. [Google Scholar]
- Song, J.H.; Kim, S.W.; Sohn, H.Y.; Yoo, Y.M. Coded excitation for ultrasound tissue harmonic imaging. Ultrasonics 2010, 50, 613–619. [Google Scholar] [CrossRef]
- Duck, F.A. Nonlinear acoustics in diagnostic ultrasound. Ultrasound Med. Biol. 2002, 28, 1–18. [Google Scholar] [CrossRef]
- Burns, P.N.; Simpson, D.H.; Averkiou, M.A. Nonlinear imaging. Ultrasound Med. Biol. 2000, 26, S19–S22. [Google Scholar] [CrossRef]
- Hirata, K.; Watanabe, H.; Beppu, S.; Muro, T.; Teragaki, M.; Yoshiyama, M.; Takeuchi, K.; Yoshikawa, J. Pitfalls of echocardiographic measurement in tissue harmonic imaging: In vitro and in vivo study. J. Am. Soc. Echocardiogr. 2002, 15, 1038–1044. [Google Scholar] [CrossRef] [PubMed]
- Lencioni, R.; Cioni, D.; Bartolozzi, C. Tissue harmonic and contrast-specific imaging: Back to gray scale in ultrasound. Eur. Radiol. 2002, 12, 151–165. [Google Scholar] [CrossRef] [PubMed]
- Uppal, T. Tissue harmonic imaging. AJUM 2010, 13, 29–31. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anvari, A.; Forsberg, F.; Samir, A.E. A primer on the physical principles of tissue harmonic imaging. Radiographics 2015, 35, 1955–1964. [Google Scholar] [CrossRef]
- Hossack, J.A.; Mauchamp, P.; Ratsimandresy, L. A high bandwidth transducer optimized for harmonic imaging. In Proceedings of the IEEE Ultrasonic Symposium, San Juan, PR, USA, 22–25 October 2000; pp. 1021–1024. [Google Scholar]
- Desser, T.S.; Jeffrey, R.B. Tissue harmonic imaging techniques: Physical principles and clinical applications. Semin. Ultrasound CT MRI 2001, 22, 1–10. [Google Scholar] [CrossRef]
- Chandrana, C.; Kharin, N.; Vince, G.D.; Roy, S.; Fleischman, A.J. Demonstration of second-harmonic IVUS feasibility with focused broadband miniature transducers. IEEE Trans. Ultrason. Ferroelctr. Freq. Control 2010, 57, 1077–1085. [Google Scholar] [CrossRef]
- Kim, M.J.; Kim, J.S.; Cao, W. Electromechanical coupling coefficient of an ultrasonic array element. J. Appl. Phys. 2006, 99, 074102/1–074102/6. [Google Scholar] [CrossRef]
- Yaralioglu, G.G.; Ergun, A.S.; Bayram, B.; Hæggström, E.; Khuri-Yakub, B.T. Calculation and measurement of electromechanical coupling coefficient of capacitive micromachined ultrasonic transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2003, 50, 449–456. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.M.; Proulx, T.L. Single Crystals vs. Single Crystals vs. PZT Ceramics for Medical Ultrasound Applications. In Proceedings of the IEEE Ultrasonic Symposium, Rotterdam, The Netherlands, 18–21 September 2005; pp. 227–230. [Google Scholar]
- Ritter, T.; Geng, X.; Shung, K.K.; Lopath, P.D.; Park, S.E.; Shrout, T.R. Single crystal PZN/PT-polymer composites for ultrasound transducer applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2000, 47, 792–800. [Google Scholar] [CrossRef]
- Nakamura, K.; Fukazawa, K.; Yamada, K.; Saitoh, S. Broadband ultrasonic transducers using a LiNbO3 plate with a ferroelectric inversion layer. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2003, 50, 1558–1562. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Cannata, J.M.; Guo, H.; Huang, C.; Marmarelis, V.Z.; Shung, K.K. Half-thickness inversion layer high-frequency ultrasonic transducers using LiNbO3 single crystal. IEEE Trans. Ultrason. Ferroelect. Freq. Control 2005, 52, 127–133. [Google Scholar] [CrossRef] [PubMed]
- Legros, M.; Novell, A.; Bouakaz, A.; Ferin, G.; Dufait, R.; Certon, D. Tissue Harmonic Imaging with CMUTs. In Proceedings of the 2011 IEEE International Ultrasonics Symposium, Orlando, FL, USA, 18–21 October 2011; pp. 2249–2252. [Google Scholar]
- Novell, A.; Escoffre, J.M.; Bouakaz, A. Second Harmonic and Subharmonic for Non-Linear Wideband Contrast Imaging Using a Capacitive Micromachined Ultrasonic Transducer Array. Ultrasound in Med. Biol. 2013, 39, 1500–1512. [Google Scholar] [CrossRef] [PubMed]
- Akasheh, F.; Myers, T.; Fraser, J.D.; Bose, S.; Bandyopadhyay, A. Development of piezoelectric micromachined ultrasonic transducers. Sens. Actuators A 2004, 111, 275–287. [Google Scholar] [CrossRef]
- Yongqiang, Q.; James, V.G.; Margeaux, W.; Flavio, G.; Christine, E.M.D.; Sandy, C.; Susan, T.M. Piezoelectric Micromachined Ultrasound Transducer (PMUT) Arrays for Integrated Sensing, Actuation and Imaging. Sensors 2015, 15, 8020–8041. [Google Scholar]
- Neer, P.L.M.J.V.; Matte, G.; Danilouchkine, M.G.; Prins, C.; Adel, F.V.D.; Jong, N.D. Super-Harmonic Imaging: Development of an Interleaved Phased-Array Transducer. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 455–468. [Google Scholar] [CrossRef]
- Bouakaz, A.; Frigstad, S.; Cate, F.J.T.; Jong, N.D. Super harmonic imaging: A new imaging technique for improved contrast detection. Ultrasound Med. Biol. 2002, 28, 59–68. [Google Scholar] [CrossRef]
- Bouakaz, A.; Cate, F.T.; Jong, N.D. A new ultrasonic transducer for improved contrast nonlinear imaging. Phys. Med. Biol. 2004, 49, 3515–3525. [Google Scholar] [CrossRef] [PubMed]
- Saitoh, S.; Izumi, M.; Mine, Y. A dual frequency ultrasonic probe for medical applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1995, 42, 294–300. [Google Scholar] [CrossRef]
- Zhou, Q.; Cannata, J.M.; Shung, K.K. Design and modeling of inversion layer ultrasonic transducers using LiNbO3 single crystal. Ultrasonics 2006, 44, e607–e611. [Google Scholar] [CrossRef]
- Sung, J.H.; Jeong, J.S. High-frequency ultrasound transducer by using inversion layer technique for intravascular ultrasound imaging. Electron. Lett. 2016, 52, 1003–1005. [Google Scholar] [CrossRef]
- Park, C.Y.; Sung, J.H.; Jeong, J.S. Design and fabrication of ultrasound linear array transducer based on polarization inversion technique. Sens. Actuators A Phys. 2018, 280, 484–494. [Google Scholar] [CrossRef]
- Sung, J.H.; Jeong, E.Y.; Jeong, J.S. Intravascular ultrasound transducer by using polarization inversion technique for tissue harmonic imaging: Modeling and experiments. IEEE Trans. Biomed. Eng. 2020. [Google Scholar] [CrossRef]
- Shui, Y.; Xue, Q. Dynamic characteristics of 2-2 piezoelectric composite transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1997, 44, 1110–1119. [Google Scholar] [CrossRef]
- Ritter, T.A.; Shrout, T.R.; Shung, K.K. A 30-MHz piezo-composite ultrasound array for medical imaging applications. IEEE Trans. Ultrason. Ferroelect. Freq. Control 2002, 49, 217–230. [Google Scholar] [CrossRef]
- Lukacs, M.; Yin, J.; Pang, G.; Garcia, R.C.; Cherin, E.; Williams, R.; Mehi, J.; Foster, F.S. Performance and characterization of new micromachined high-frequency linear arrays. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2006, 53, 1719–1729. [Google Scholar] [CrossRef]
- Yuan, J.R.; Jiang, X.; Cao, P.J.; Sadaka, A.; Bautista, R.; Snook, K.; Rehrig, P.W. High frequency piezo composites microfabricated ultrasound transducers for intravascular imaging. In Proceedings of the IEEE Ultrasonics Symposium, Vancouver, BC, Canada, 2–6 October 2006; pp. 264–268. [Google Scholar]
- Brown, J.A.; Foster, F.S.; Needles, A.; Cherin, E.; Lockwood, G.R. Fabrication and performance of a linear array based on a 1-3 composite with geometric elevation focusing. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2007, 54, 1888–1894. [Google Scholar] [CrossRef]
- Liu, R.; Harasiewicz, K.A.; Foster, F.S. Interdigital pair bonding for high frequency (20–50 MHz) ultrasonic composite transducers. IEEE Trans. Ultrason. Ferroelect. Freq. Control 2001, 48, 299–306. [Google Scholar]
- Yin, J.; Lukacs, M.; Harasiewicz, K.A.; Foster, F.S. Design and fabrication of ultrafine piezoelectric composites. Ultrason. Imaging 2005, 27, 54–64. [Google Scholar] [CrossRef] [PubMed]
- Cannata, J.M.; Williams, J.A.; Hu, C.-H.; Shung, K.K. Development of high frequency linear arrays using interdigital bonded composites. In Proceedings of the IEEE Ultrasonics Symposium, Beijing, China, 2–5 November 2008; pp. 686–689. [Google Scholar]
- Cannata, J.M.; Williams, J.A.; Zhang, L.; Hu, C.H.; Shung, K.K. High-Frequency Linear Ultrasonic Array Utilizing an Interdigitally Bonded 2-2 Piezo-Composite. IEEE Trans. Ultrason. Ferroelect. Freq. Control 2011, 58, 2202–2212. [Google Scholar] [CrossRef] [Green Version]
- Chabok, H.R.; Cannata, J.M.; Kim, H.H.; Williams, J.A.; Park, J.H.; Shung, K.K. A High-Frequency Annular-Array Transducer Using an Interdigital Bonded 1-3 Composite. IEEE Trans. Ultrason. Ferroelect. Freq. Control 2011, 58, 206–214. [Google Scholar] [CrossRef] [PubMed]









| Conventional f0 Element | PIT 2f0 Element | |
|---|---|---|
| Center frequency [MHz] | 5 | 10 |
| Element number | 4 | 4 |
| Element width [μm] | 301 | |
| Sub-element width [μm] | 75 | |
| Kerf size [μm] | 38 | |
| Total thickness of piezoelectric layer [μm] | 280 | |
| Thickness of 1st matching layer [μm] | 80 | |
| Thickness of 2nd matching layer [μm] | 100 | |
| Piezoelectric material | PZT-5H | |
| 1st Matching layer material | Aluminum powder filled epoxy | |
| 2nd Matching layer material | Unloaded epoxy | |
| Backing layer material | Tungsten powder filled epoxy | |
| PZT-5H (CTS3203HD) | ||
|---|---|---|
| Elastic stiffness | 13.7 | |
| 8.8 | ||
| 9.23 | ||
| 12.6 | ||
| 2.2 | ||
| 2.5 | ||
| Mechanical Q | 90 | |
| Dielectric permittivity | 1305.8 | |
| 1200.2 | ||
| Piezoelectric stress e | −9.4 | |
| 22.5 | ||
| 16.1 | ||
| Density | 7820 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, C.Y.; Sung, J.H.; Jeong, E.Y.; Lee, H.S.; Jeong, J.S. Interleaved Array Transducer with Polarization Inversion Technique to Implement Ultrasound Tissue Harmonic Imaging. Sensors 2020, 20, 3915. https://doi.org/10.3390/s20143915
Park CY, Sung JH, Jeong EY, Lee HS, Jeong JS. Interleaved Array Transducer with Polarization Inversion Technique to Implement Ultrasound Tissue Harmonic Imaging. Sensors. 2020; 20(14):3915. https://doi.org/10.3390/s20143915
Chicago/Turabian StylePark, Chan Yuk, Jin Ho Sung, Eun Young Jeong, Hee Su Lee, and Jong Seob Jeong. 2020. "Interleaved Array Transducer with Polarization Inversion Technique to Implement Ultrasound Tissue Harmonic Imaging" Sensors 20, no. 14: 3915. https://doi.org/10.3390/s20143915




