Interdigital Capacitor-Based Passive LC Resonant Sensor for Improved Moisture Sensing
Abstract
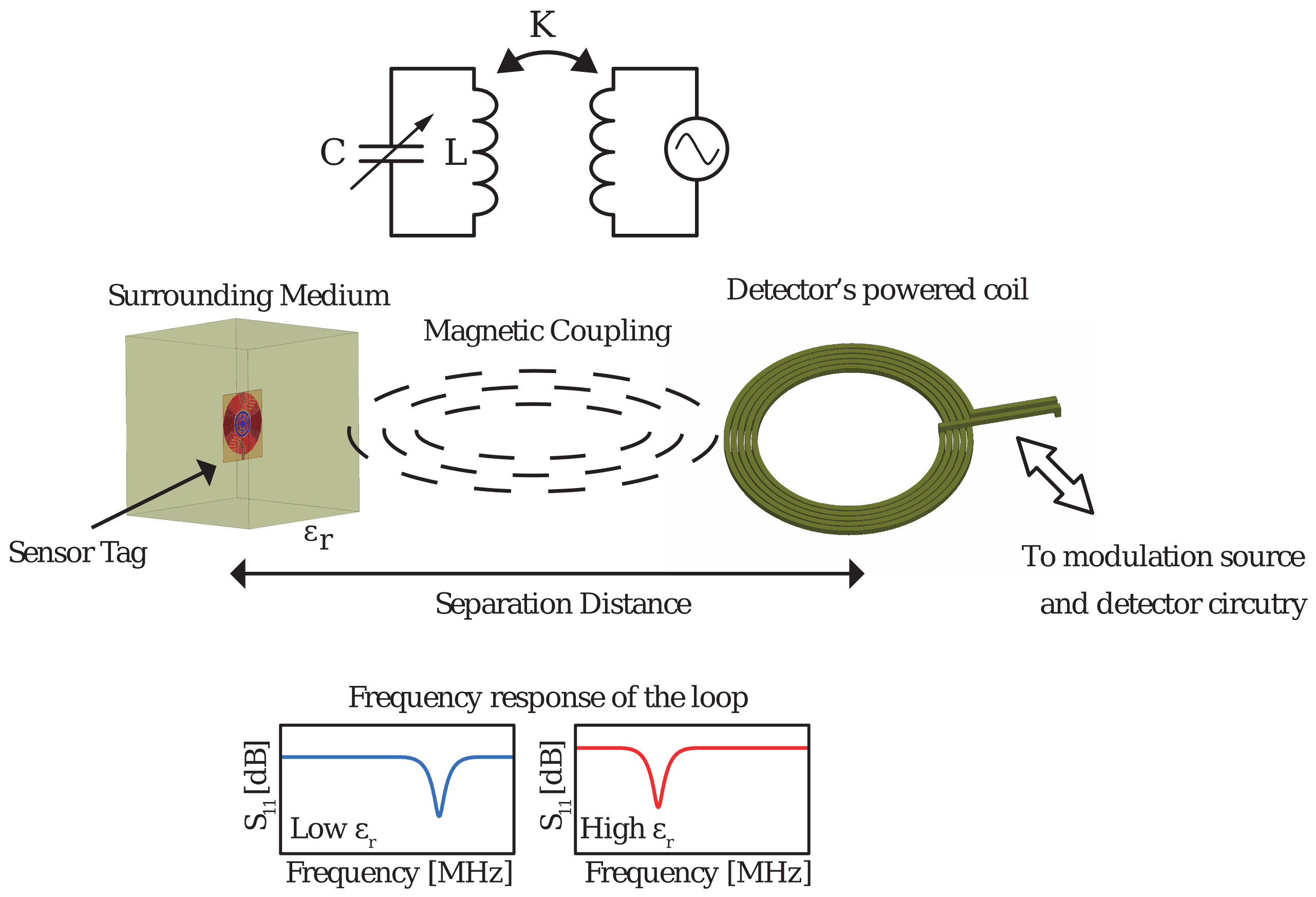
:1. Introduction
2. Materials and Methods
2.1. Fringing Capacitance
2.2. Calculation of Capacitor Loss and Q-Factor
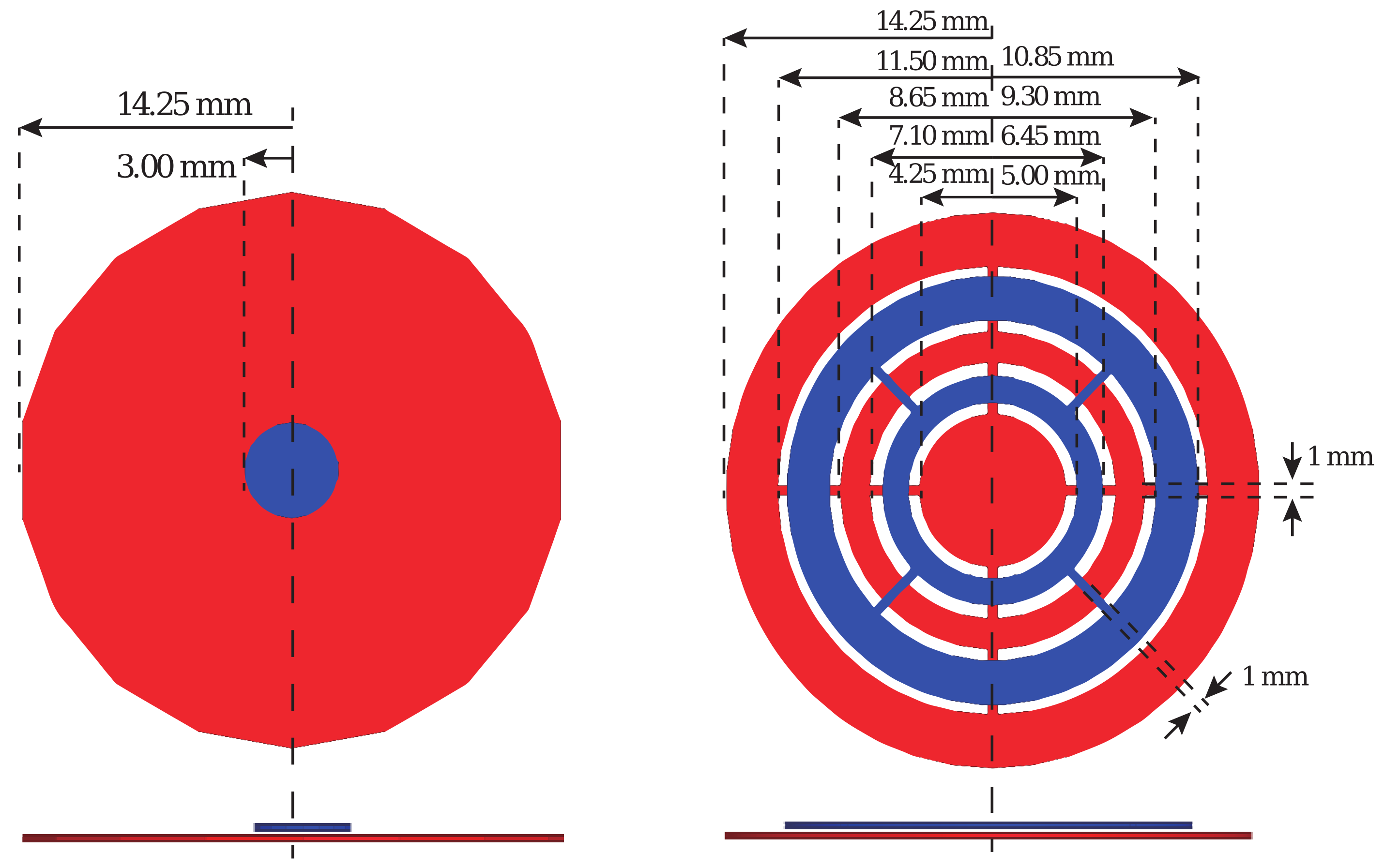
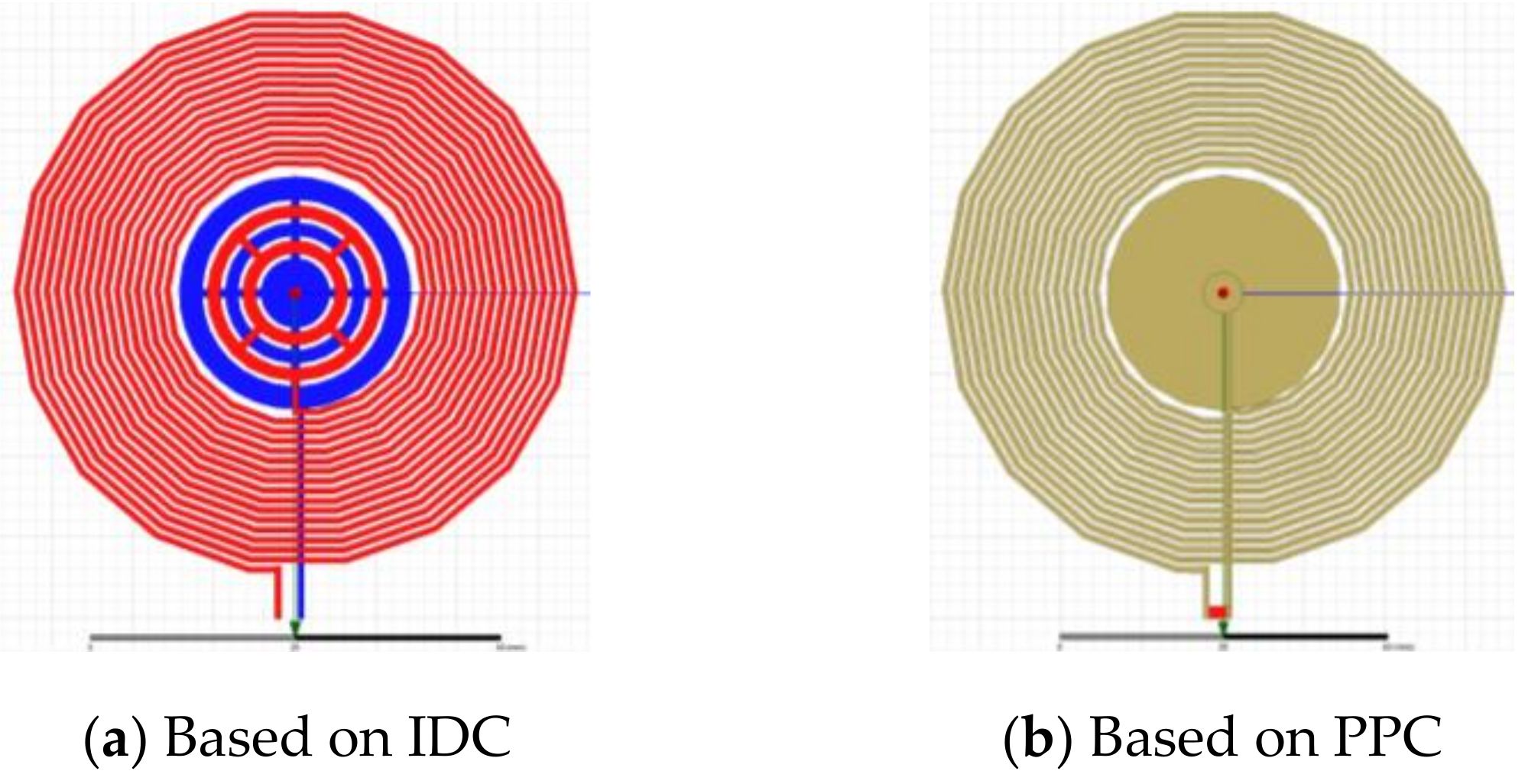
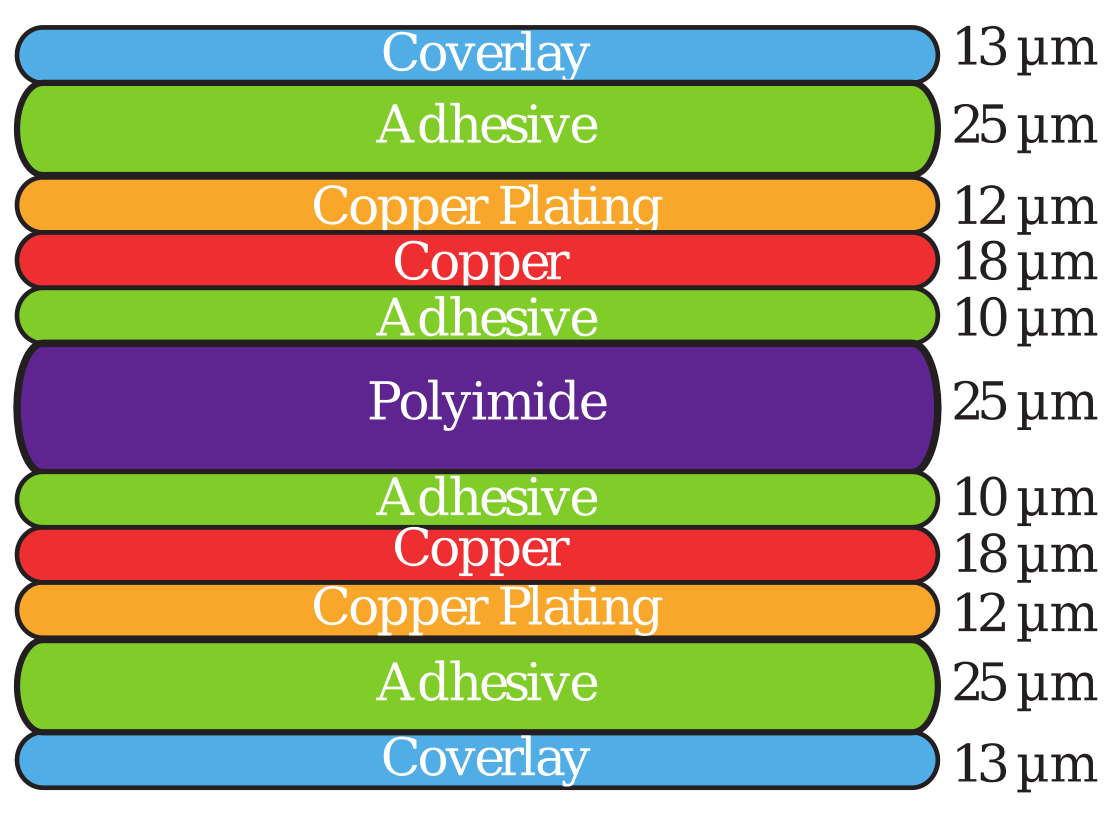
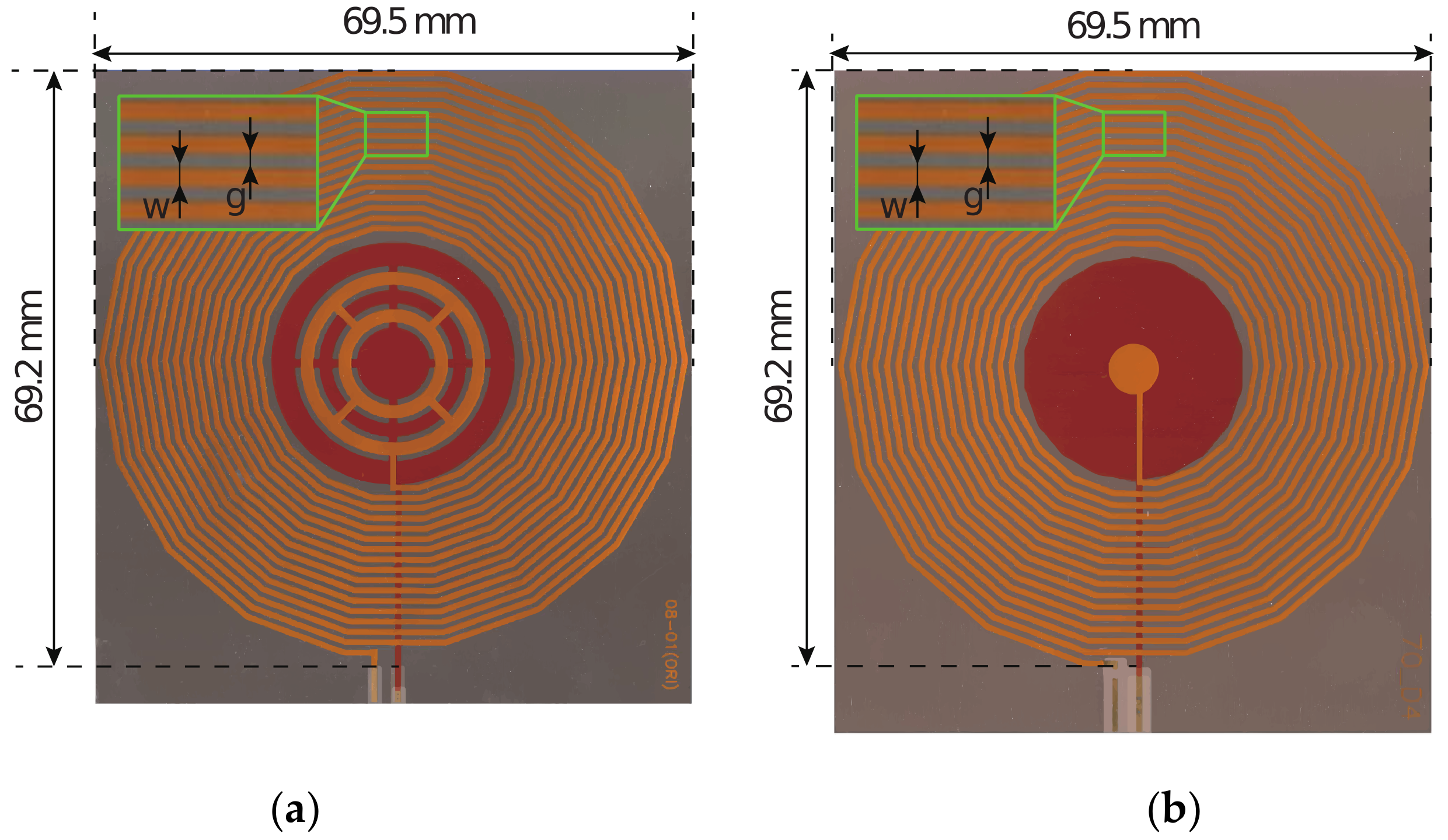
2.3. Sensor Design
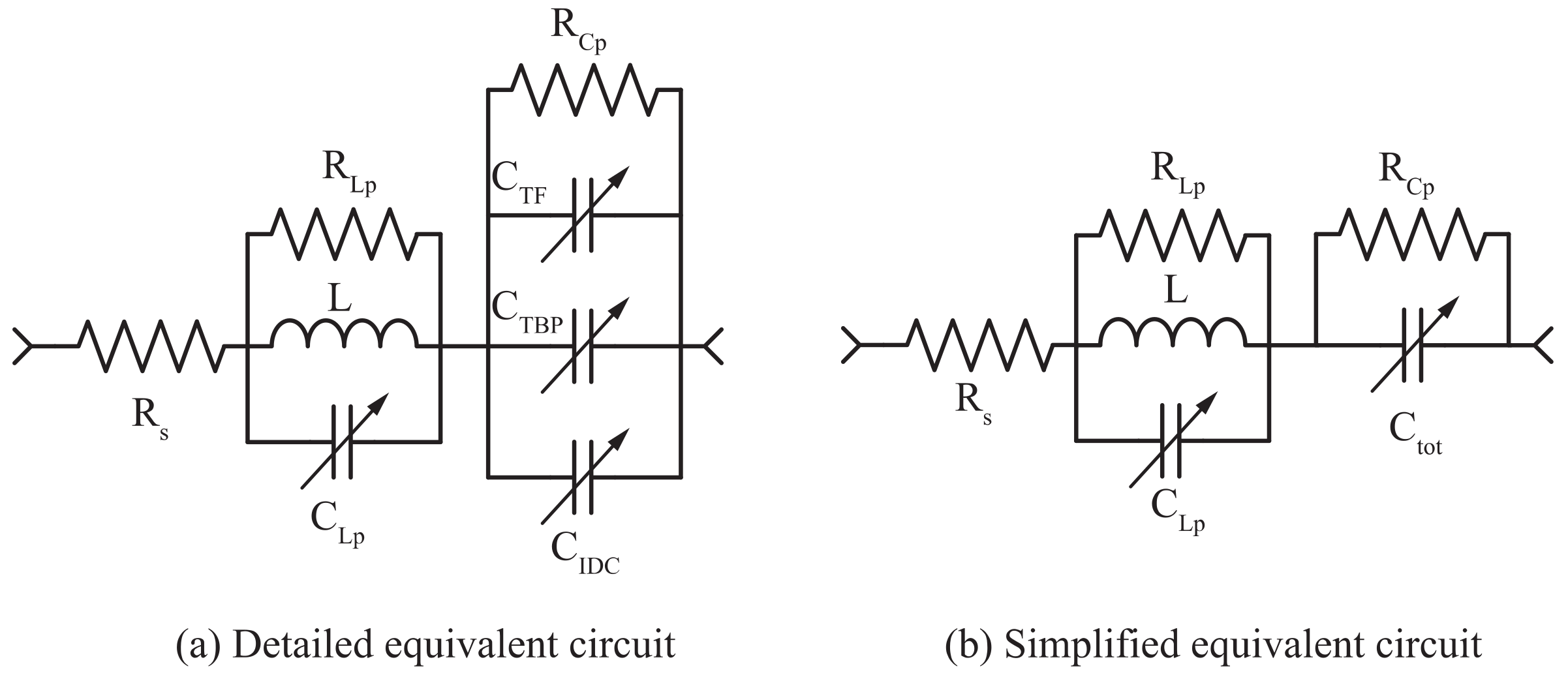
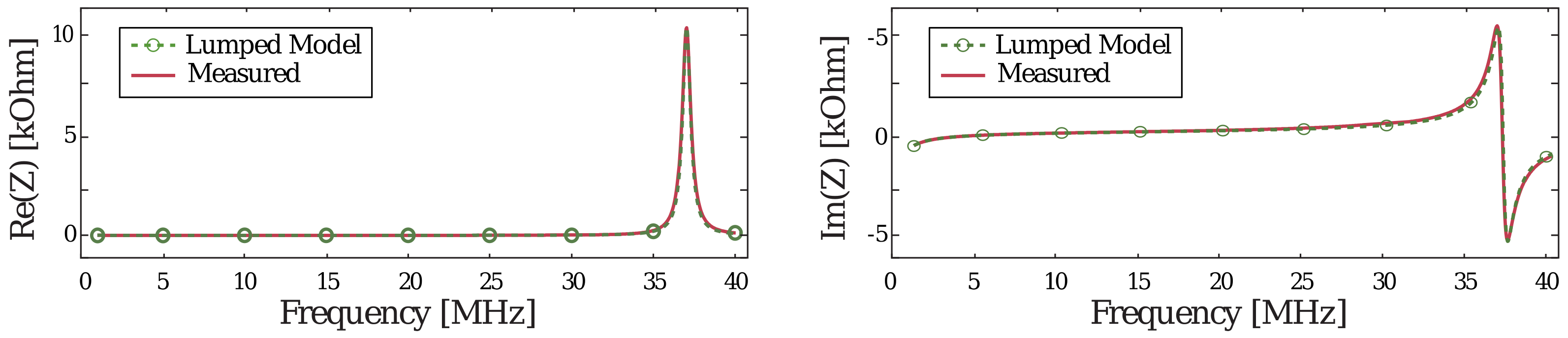
2.4. Equivalent Circuit
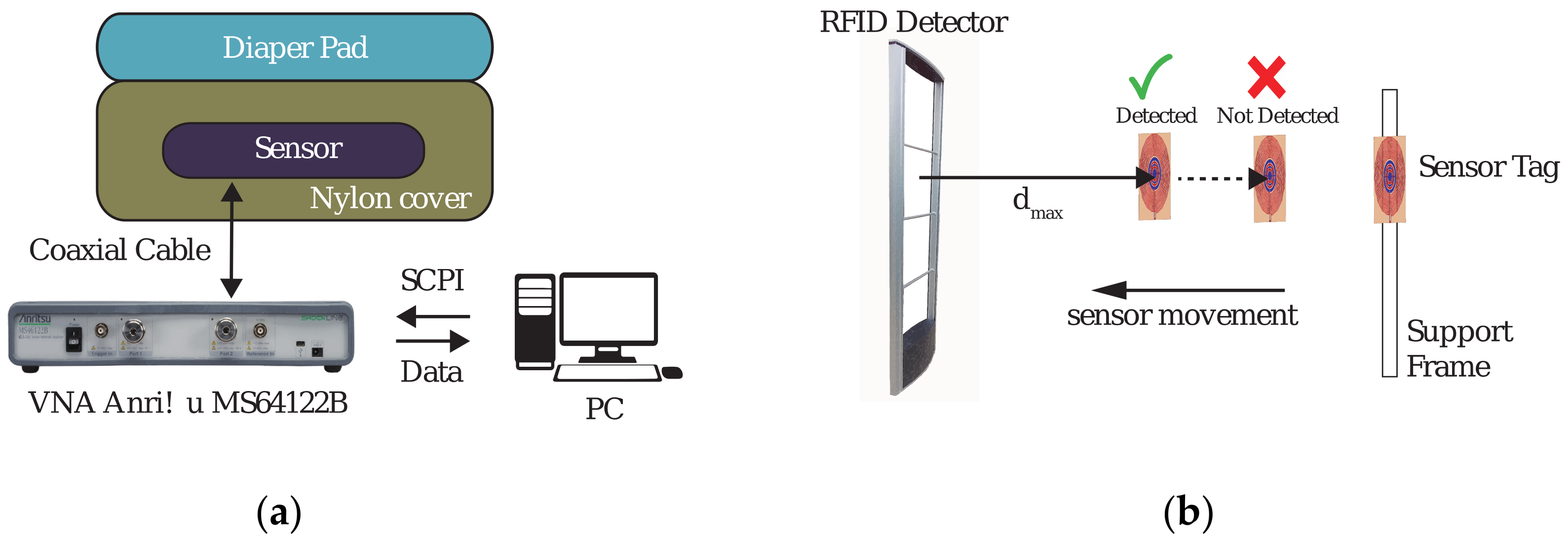
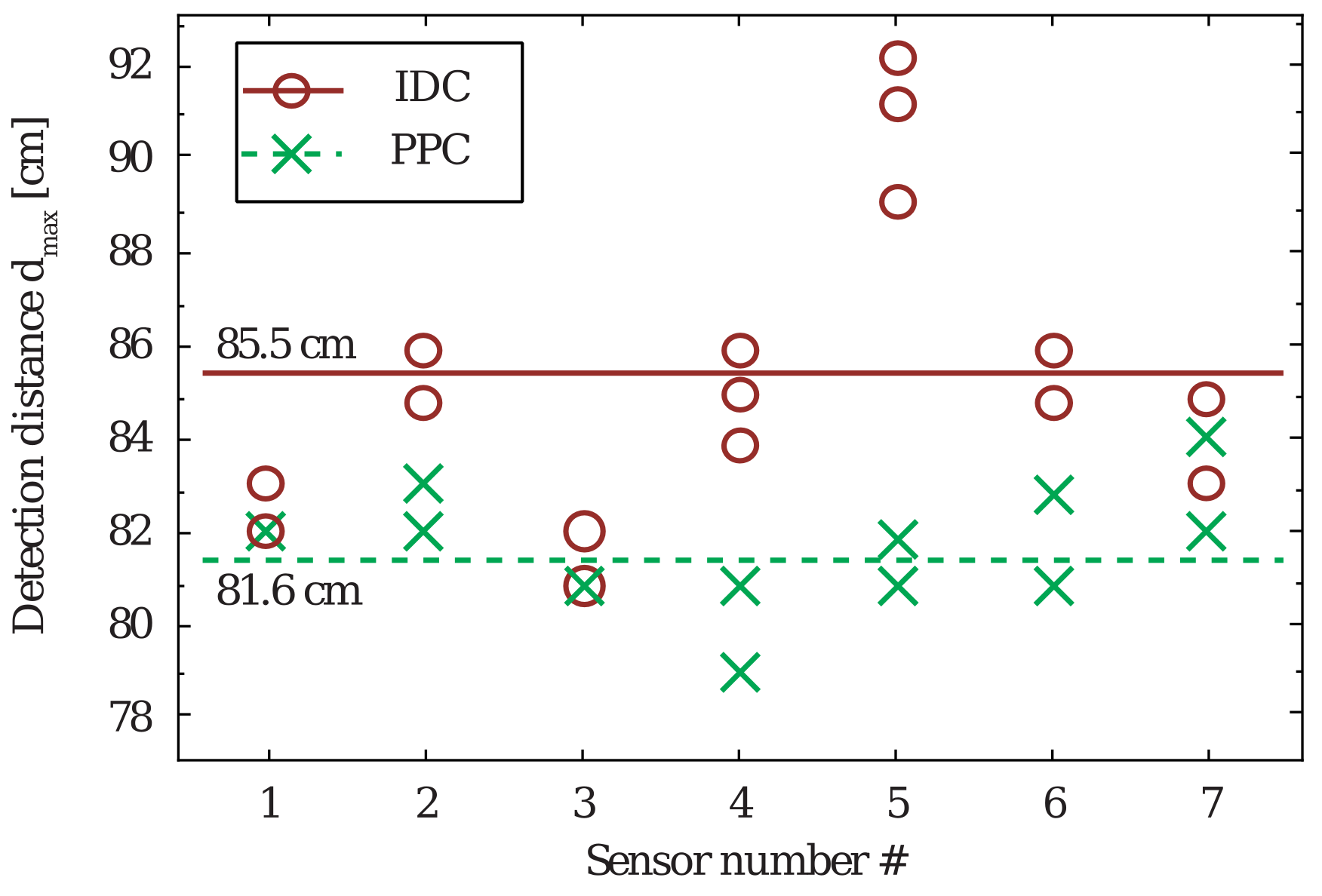
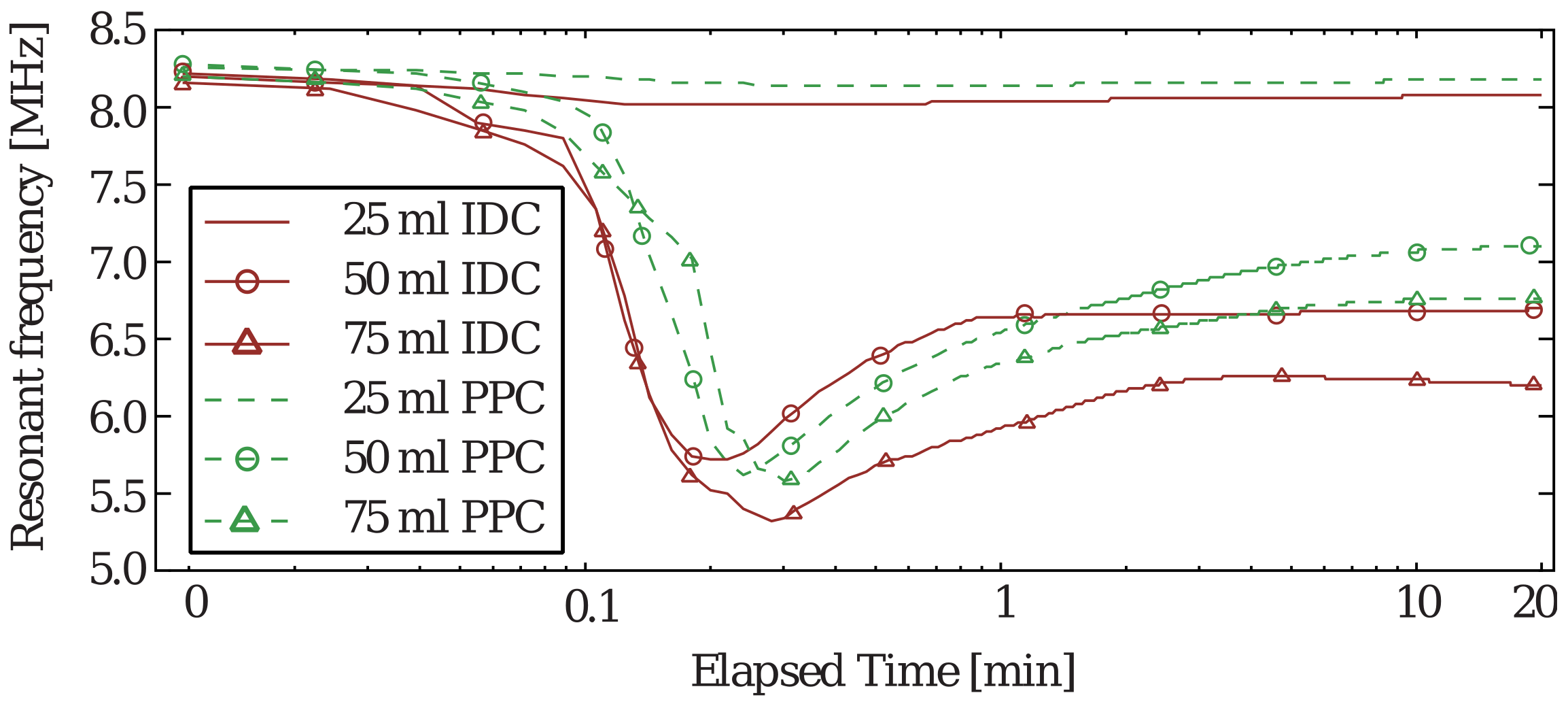
3. Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gaubert, V.; Gidik, H.; Koncar, V. Boxer Underwear Incorporating Textile Moisture Sensor to Prevent Nocturnal Enuresis. Sensors 2020, 20, 3546. [Google Scholar] [CrossRef] [PubMed]
- Ngo, H.-D.; Hoang, T.H.; Baeuscher, M.; Wang, B.; Mackowiak, P.; Grabbert, N.; Weiland, T.; Ehrmann, O.; Lang, K.-D.; Schneider-Ramelow, M.; et al. A Novel Low Cost Wireless Incontinence Sensor System (Screen-Printed Flexible Sensor System) for Wireless Urine Detection in Incontinence Materials. Proceedings 2018, 2, 716. [Google Scholar] [CrossRef] [Green Version]
- Ziai, M.A.; Batchelor, J.C. Smart radio-frequency identification tag for diaper moisture detection. Healthc. Technol. Lett. 2015, 2, 18–21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cabezas, J.; Sanchez-Rodriguez, T.; Gomez-Galan, J.; Cifuentes, H.; Carvajal, R. Compact Embedded Wireless Sensor-Based Monitoring of Concrete Curing. Sensors 2018, 18, 876. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Millán, S.; Campillo, C.; Casadesús, J.; Pérez-Rodríguez, J.M.; Prieto, M.H. Automatic Irrigation Scheduling on a Hedgerow Olive Orchard Using an Algorithm of Water Balance Readjusted with Soil Moisture Sensors. Sensors 2020, 20, 2526. [Google Scholar] [CrossRef] [PubMed]
- Saleh, M.; Elhajj, I.H.; Asmar, D.; Bashour, I.; Kidess, S. Experimental evaluation of low-cost resistive soil moisture sensors. In Proceedings of the IEEE International Multidisciplinary Conference on Engineering Technology (IMCET), Beirut, Lebanon, 2–4 November 2016; pp. 179–184. [Google Scholar] [CrossRef]
- Tadav, B.C.; Srivastava, R.; Dwivedi, C.D.; Pramanik, P. Syntesis of nano-sized ZnO using drop wise method and its performance as moisture sensor. Sens. Actuators A Phys. 2009, 153, 137–141. [Google Scholar]
- Huan, Z.; Wang, H.; Li, C.; Wan, C. The soil moisture sensor based on soil dielectric property. Pers. Ubiquit. Comput. 2017, 21, 67–74. [Google Scholar] [CrossRef]
- Bobrov, P.P.; Belyaeva, T.A.; Kroshka, E.S.; Radionova, O.V. Soil Moisture Measurement by the Dielectric Method. Eurasian Soil Sc. 2019, 52, 822–833. [Google Scholar] [CrossRef]
- Zhu, H.-T.; Chen, Y.; Xiong, Y.-F.; Xu, F.; Lu, Y.-Q. A Flexible Wireless Dielectric Sensor for Noninvasive Fluid Monitoring. Sensors 2020, 20, 174. [Google Scholar] [CrossRef] [Green Version]
- Archer, G.; Wang, P. The Dielectric Constant of Water and Debye-Hückel Limiting Law Slopes. J. Phys. Chem. Ref. Data 1990, 19, 371–411. [Google Scholar] [CrossRef] [Green Version]
- Hutson, V. The circular plate condenser at small separations. Math. Proc. Camb. Philos. Soc. 1963, 59, 211–224. [Google Scholar] [CrossRef]
- Yambem, L.; Yapici, M. A New Wireless Sensor System for Smart Diapers. IEEE Sens. J. 2008, 8, 238–239. [Google Scholar] [CrossRef]
- Tanaka, A. Wearable Self-Powered Diaper- Shaped Urinary-Incontinence Sensor Suppressing Response-Time Variation with 0.3V Star-Up Converter. IEEE Sens. J. 2015, 16, 3472–3479. [Google Scholar] [CrossRef]
- Chetpattananondh, K.; Tapoanoi, T.; Phukpattaranont, P.; Jindapetch, N. A self-calibration water level measurement using an interdigital capacitive sensor. Sens. Actuators A Phys. 2014, 209, 175–182. [Google Scholar] [CrossRef]
- Kumar, A.; Wang, C.; Meng, F.-Y.; Zhou, Z.-L.; Zhao, M.; Yan, G.-F.; Kim, E.-S.; Kim, N.-Y. High-Sensitivity, Quantified, Linear and Mediator-Free Resonator-Based Microwave Biosensor for Glucose Detection. Sensors 2020, 20, 4024. [Google Scholar] [CrossRef]
- Gong, C.A.; Chiu, H.K.; Huang, L.R.; Lin, C.H.; Hsu, Z.D.; Tu, P. Low-Cost Comb-Electrode Capacitive Sensing Device for Liquid-Level Measurement. IEEE Sens. J. 2016, 16, 2896–2897. [Google Scholar] [CrossRef]
- Karygiannis, T.; Eydt, B.; Barber, G. Guidelines for Securing Radio Frequency Identification (RFID) Systems. NIST Spec. Publ. 2007, 80, 800–898. [Google Scholar]
- Gevorgian, S.S.; Martinsson, T.; Linner, P.L.J.; Kollberg, E.L. CAD models for multilayered substrate interdigital capacitors. IEEE Trans. Microw. Theory Tech. 1996, 44, 896–904. [Google Scholar] [CrossRef]
- Chaniotakis, C. Frequency Response: Resonance, Bandwidth, Q Factor. Available online: https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-071j-introduction-to-electronics-signals-and-measurement-spring-2006/lecture-notes/resonance_qfactr.pdf (accessed on 29 September 2020).
- Dupont Kapton Summary of Properties. Available online: https://www.dupont.com/content/dam/dupont/amer/us/en/products/ei-transformation/documents/DEC-Kapton-summary-of-properties.pdf (accessed on 29 September 2020).
- Salmerón, J.F.; Albrecht, A.; Kaffah, S.; Becherer, M.; Lugli, P.; Rivadeneyra, A. Wireless Chipless System for Humidity Sensing. Sensors 2018, 18, 2275. [Google Scholar] [CrossRef] [Green Version]
- Stojanović, G.; Radovanović, M.; Malešev, M.; Radonjanin, V. Monitoring of Water Content in Building Materials Using a Wireless Passive Sensor. Sensors 2010, 10, 4270–4280. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Su, S.; Lv, W.; Zhang, T.; Tan, Q.; Zhang, W.; Xiong, J. A MoS2 Nanoflakes-Based LC Wireless Passive Humidity Sensor. Sensors 2018, 18, 4466. [Google Scholar] [CrossRef] [Green Version]


| Design | Center Capacitor | ||
|---|---|---|---|
| C [pF] (εr = 1/10) | ΔC | ||
| [pF] | [%] | ||
| PPC | 18.3/20.5 | 2.2 | 12 |
| IDC | 15.6/33.9 | 18.3 | 117 |
| Design | Total Capacitance | Frequency Shift | Q | |||||
|---|---|---|---|---|---|---|---|---|
| C [pF] (εr = 1/10) | ΔC | F [MHz] (εr = 1/10) | ΔF | εr = 1 | εr = 10 | |||
| [pF] | [%] | [MHz] | [%] | |||||
| PPC | 27.9/49.0 | 21.1 | 76 | 8.2/6.1 | 2.1 | 26 | 30.0 | 22.6 |
| IDC | 28.6/59.8 | 31.2 | 109 | 8.2/5.5 | 2.7 | 33 | 37.0 | 23.6 |
| Design | Q-Factor (In Free Space) | |
|---|---|---|
| Simulated | Measured | |
| PPC | 30 | 21 |
| IDC | 37 (+23%) | 27 (+29%) |
| Work | Sensor Type by | Base Material | Advantages | Disadvantages | ||
|---|---|---|---|---|---|---|
| Powered | Sense Location | Sense Mechanism | ||||
| [1] | Active | Local | Resistive | Fabric | Accuracy | Expensive Requires power |
| [2] | Active | Local | Capacitive/Resistive | Diaper Foil | ||
| [3] | Passive | Remote (RF 13.56 MHz) | LC Resonance | Paper/Polyacrylate | Binary detection | |
| [22] | Passive | Remote (RF 14.00 MHz) | LC Resonance | Polyamide | Low cost | Large size |
| [23] | Passive | Remote (RF 35.75 MHz) | LC Resonance | PCB | Low efficiency | |
| [24] | Passive | Remote (RF 177.00 MHz) | LC Resonance | LTCC | Sensitivity | Versatility |
| This work | Passive | Remote (RF 8.20 MHz) | LC Resonance | Polyamide | Low cost | Versatility |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dimitrov, K.C.; Song, S.; Chang, H.; Lim, T.; Lee, Y.; Kwak, B.-J. Interdigital Capacitor-Based Passive LC Resonant Sensor for Improved Moisture Sensing. Sensors 2020, 20, 6306. https://doi.org/10.3390/s20216306
Dimitrov KC, Song S, Chang H, Lim T, Lee Y, Kwak B-J. Interdigital Capacitor-Based Passive LC Resonant Sensor for Improved Moisture Sensing. Sensors. 2020; 20(21):6306. https://doi.org/10.3390/s20216306
Chicago/Turabian StyleDimitrov, Kristian Chavdarov, Sanghun Song, Hyungjun Chang, Taejun Lim, Yongshik Lee, and Byung-Jae Kwak. 2020. "Interdigital Capacitor-Based Passive LC Resonant Sensor for Improved Moisture Sensing" Sensors 20, no. 21: 6306. https://doi.org/10.3390/s20216306
APA StyleDimitrov, K. C., Song, S., Chang, H., Lim, T., Lee, Y., & Kwak, B.-J. (2020). Interdigital Capacitor-Based Passive LC Resonant Sensor for Improved Moisture Sensing. Sensors, 20(21), 6306. https://doi.org/10.3390/s20216306






