Constrained Image-Based Visual Servoing of Robot Manipulator with Third-Order Sliding-Mode Observer
Abstract
:1. Introduction
- A new MPC control strategy is proposed based on the TOSM observer. Considering the nonlinear dynamics of the robot, the MPC controller output the optimal sequence of joint torque with visibility constraints and actuator constraints, and the TOSM observer is employed to observe the system centralized uncertainties together with joint velocities.
- Compared with the classical traditional control method in [30,31], the proposed strategy in this paper can achieve better servo performance with model errors and system constraints in a 2-DOF robot manipulator. Compared with the recent visual servo control method proposed in [27], the proposed strategy in this paper provides faster convergence speed and more accurate control with time-varying disturbances in both 2-DOF and 6-DOF robot manipulators.
- The global stability of the system when combining MPC controller and TOSM observer is proved by the Lyapunov stability theory.
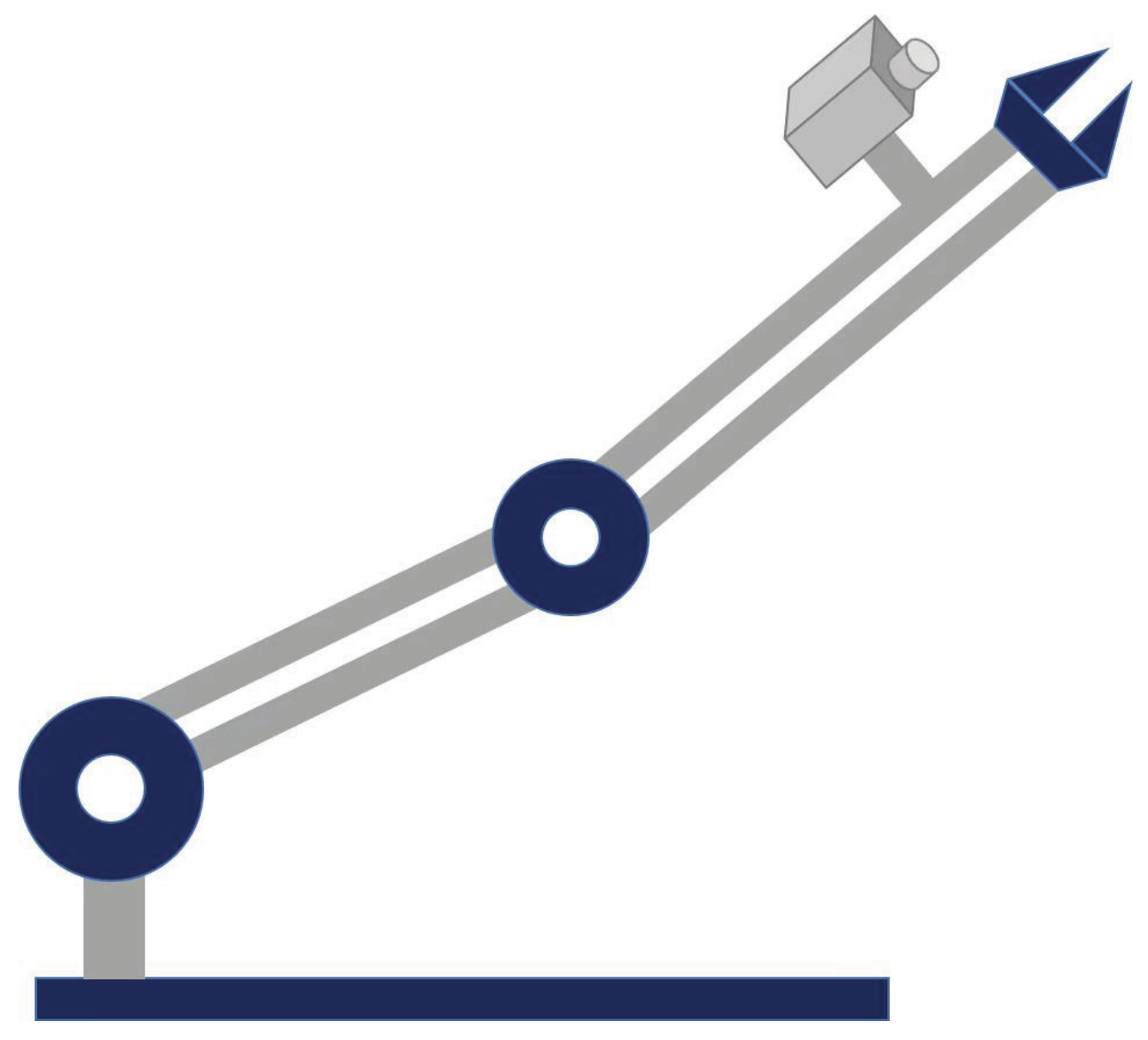
2. Visual Servoing System Modeling
2.1. Kinematics of Visual Servoing Systems
2.2. Robot Dynamics
3. Third-Order Sliding-Mode Observer
4. MPC Controller Design
5. Simulation Results
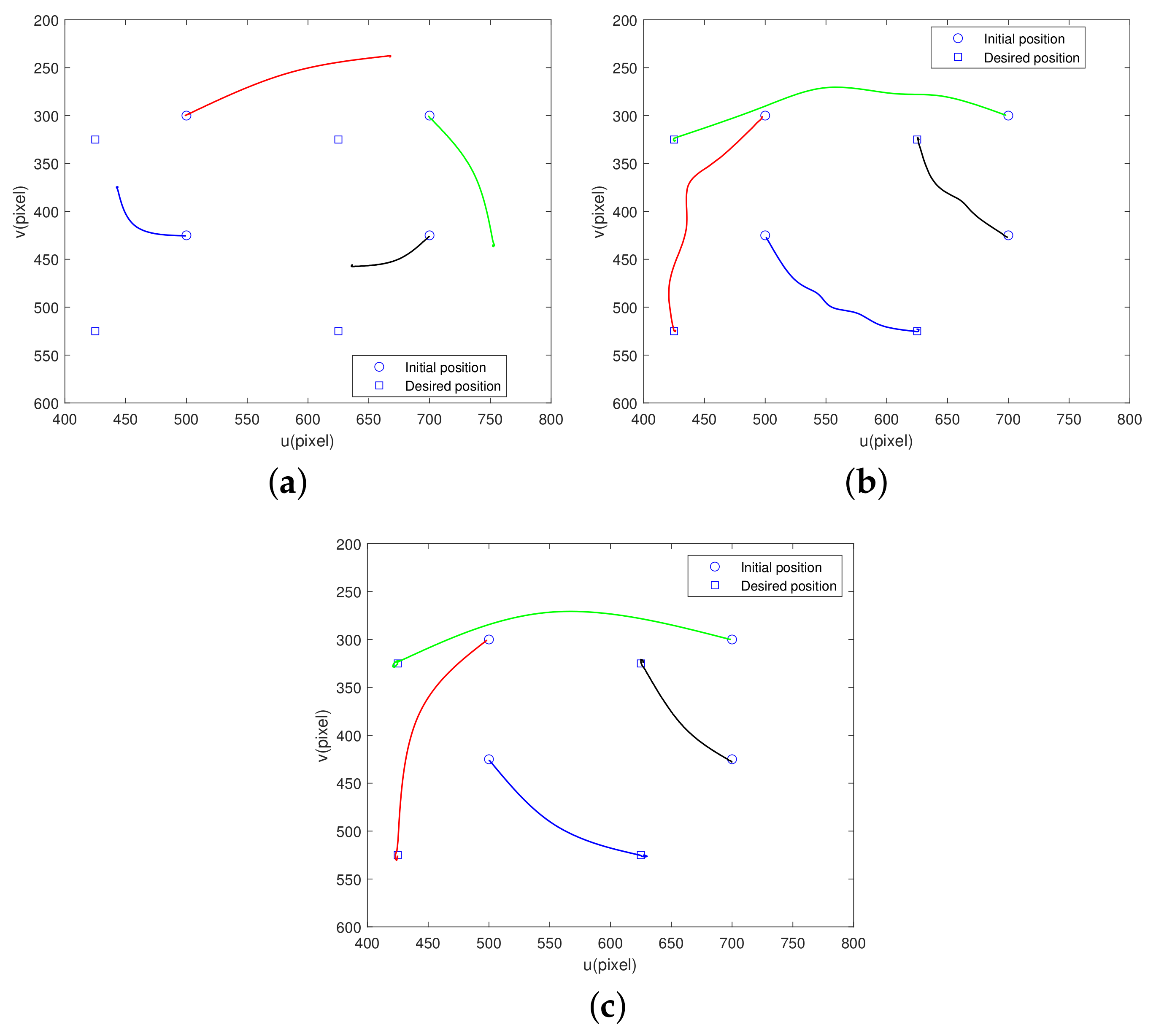
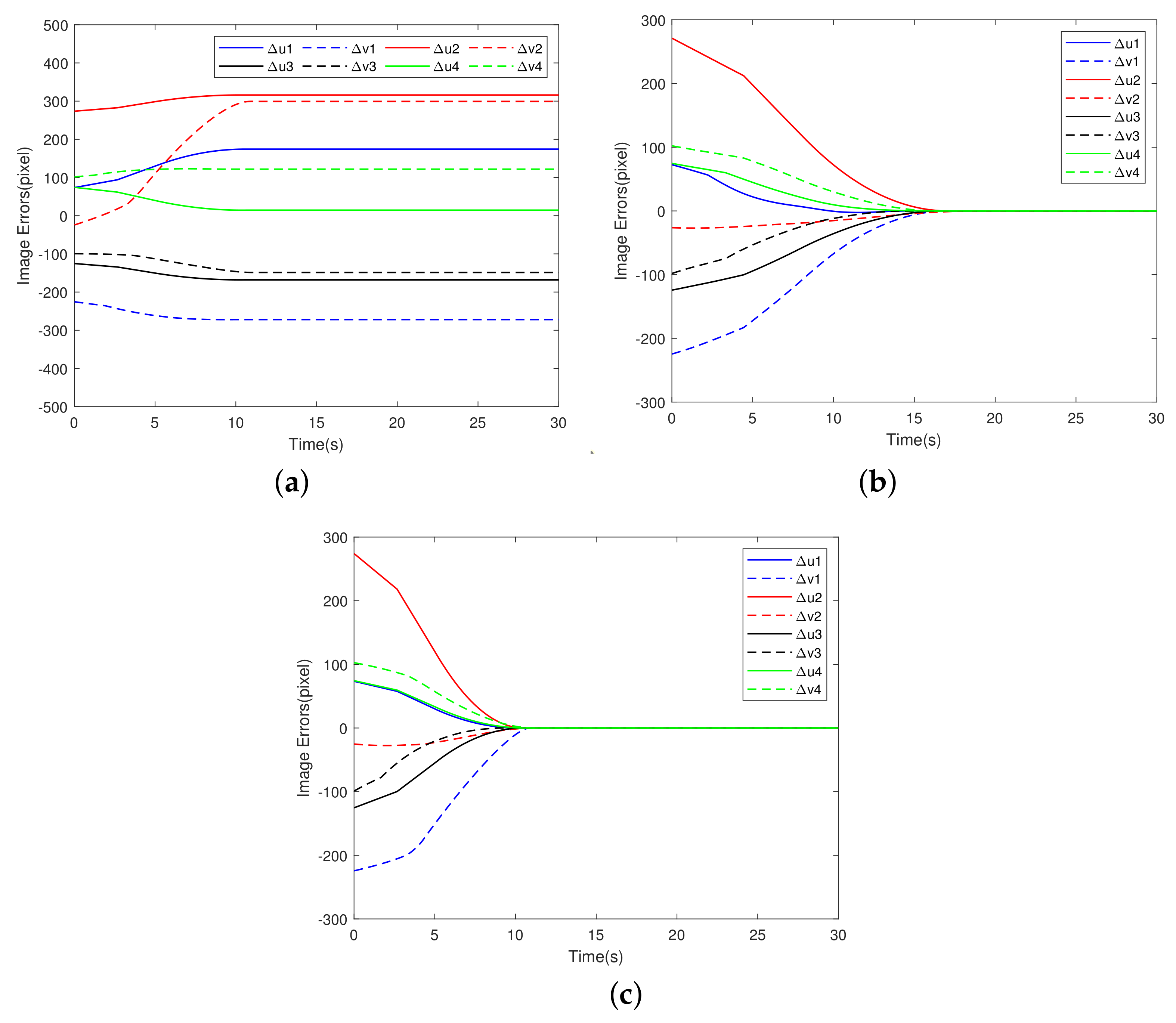
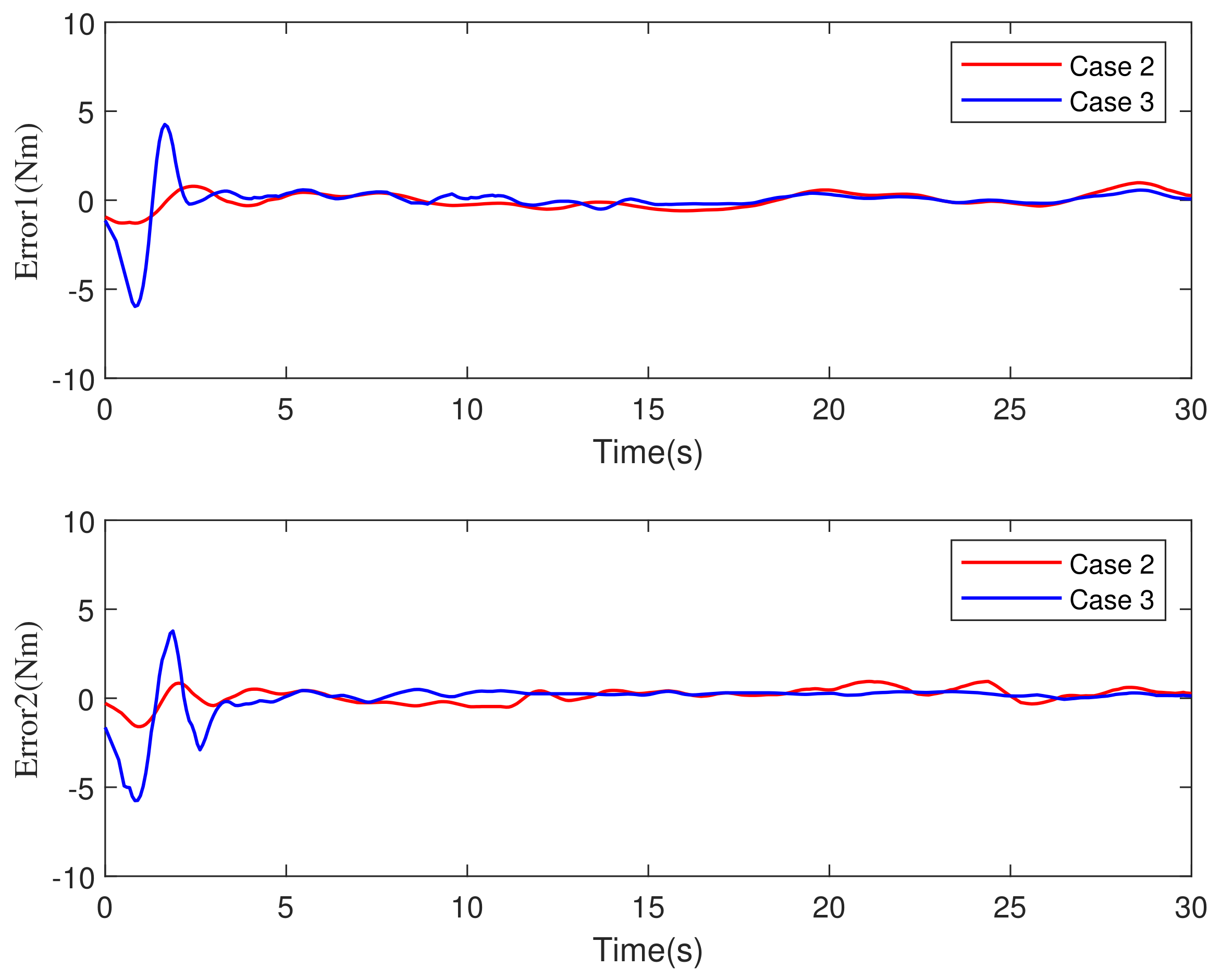
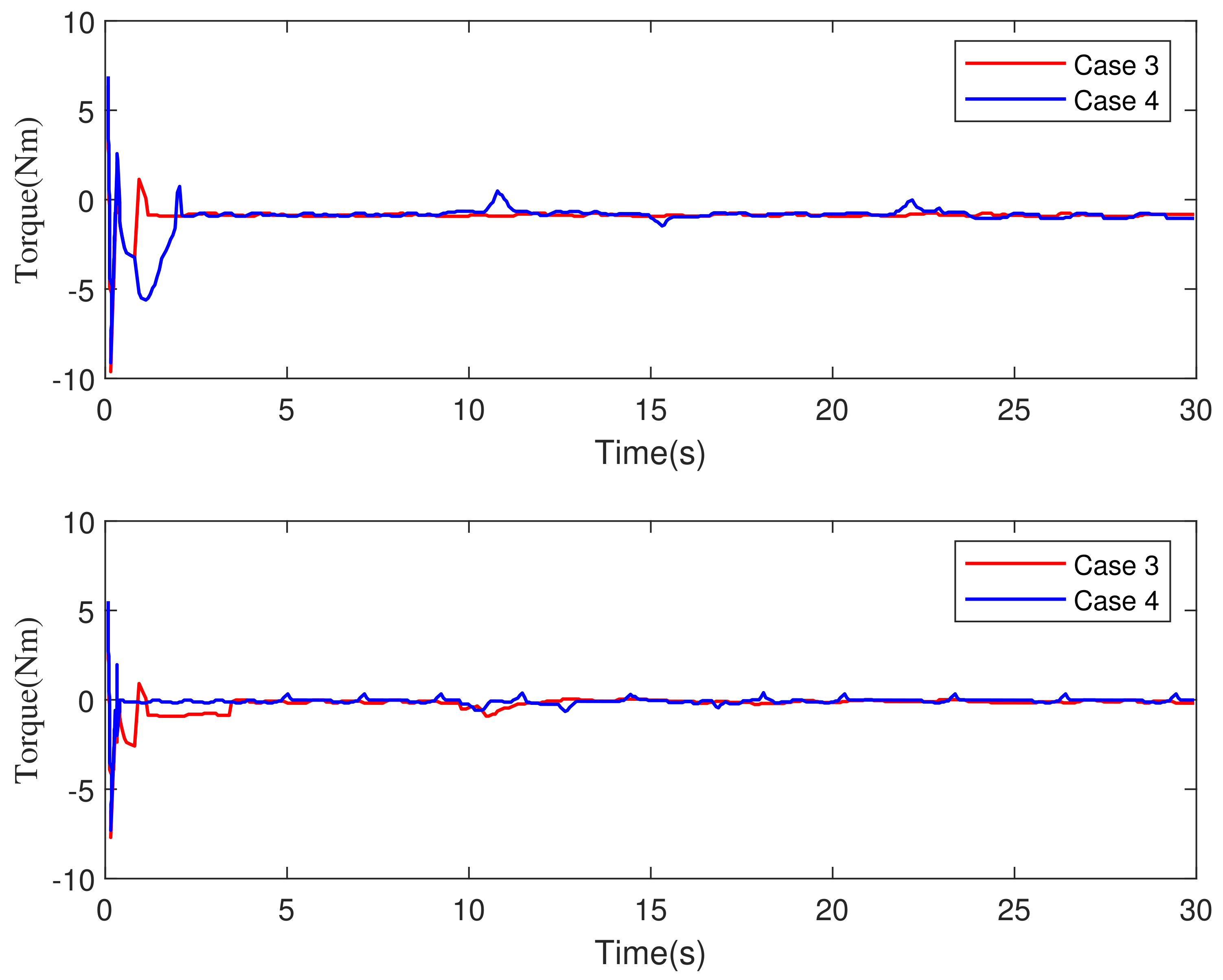
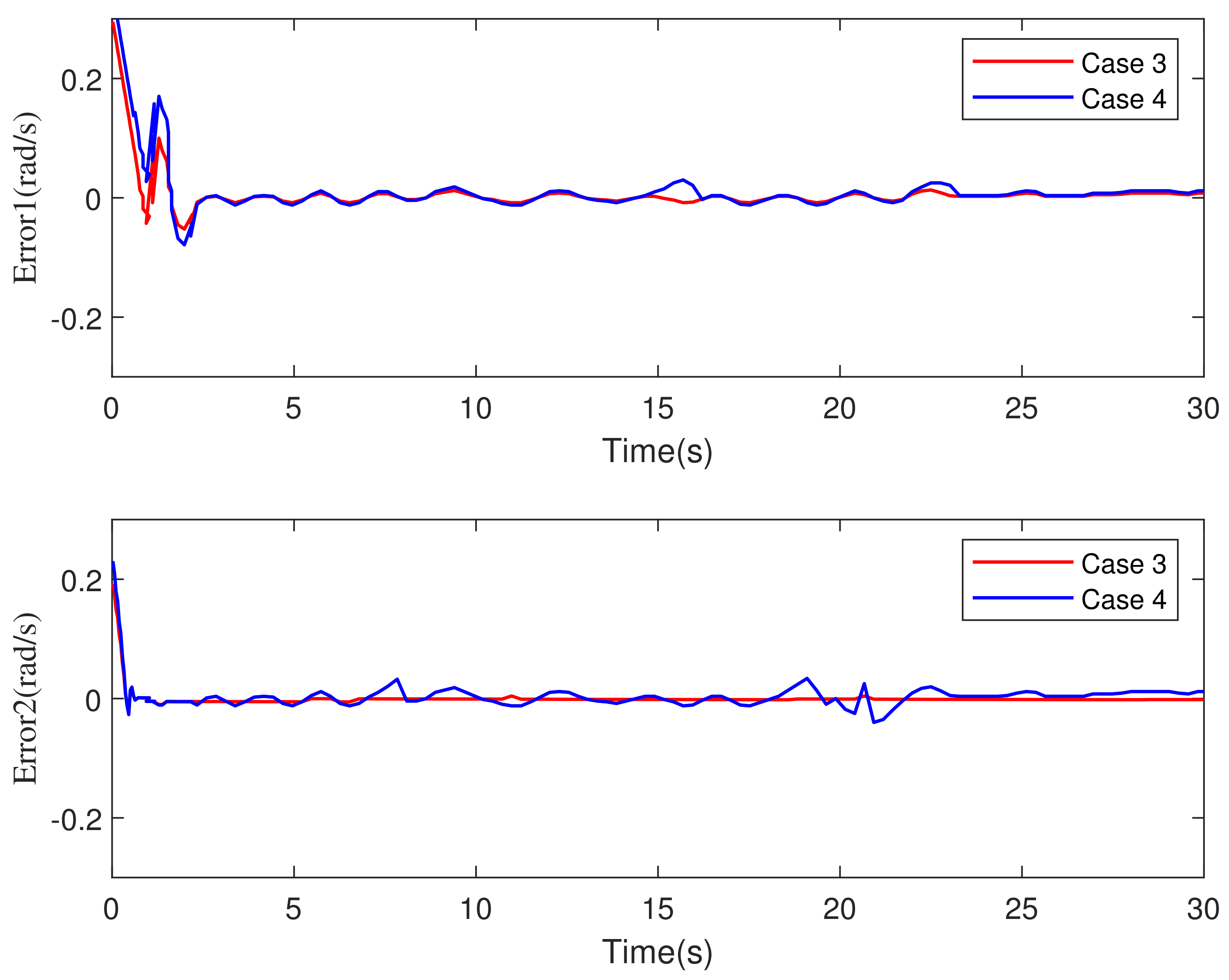
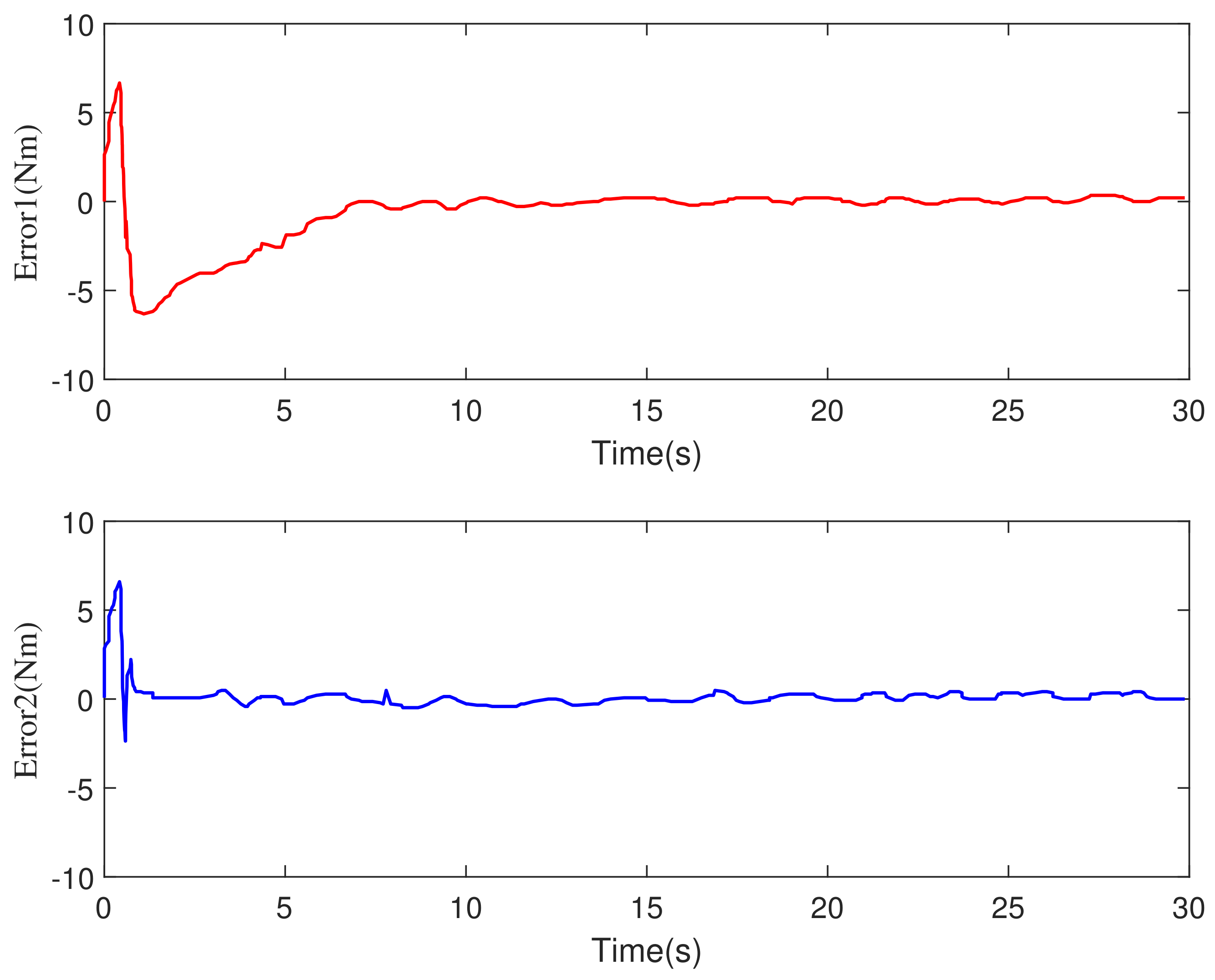
5.1. Comparative Simulations with Model Uncertainty
- Case 1: The control strategy is the traditional visual servo control method in [30].
- Case 2: The control method is MPC and the observer is a traditional SMO in [31].
- Case 3: The control strategy is the MPC-TOSM method proposed in this paper.
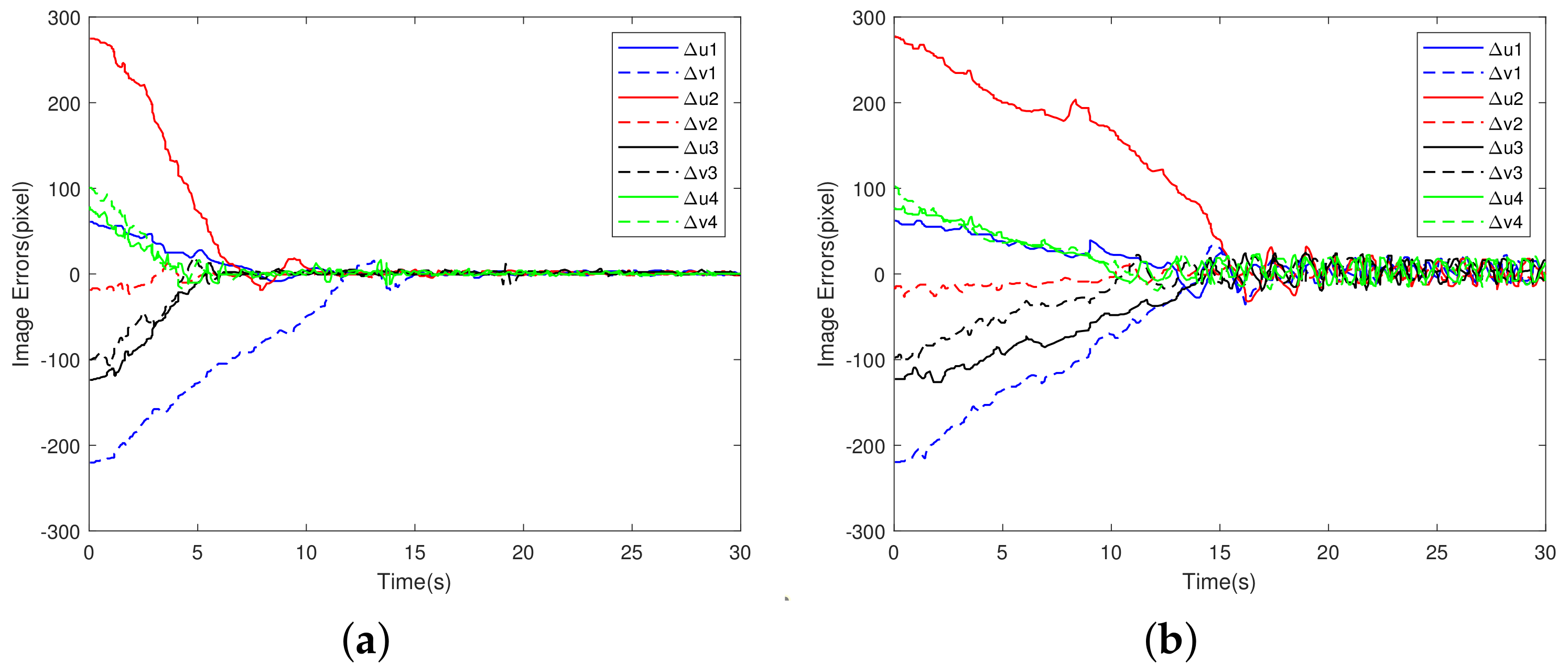
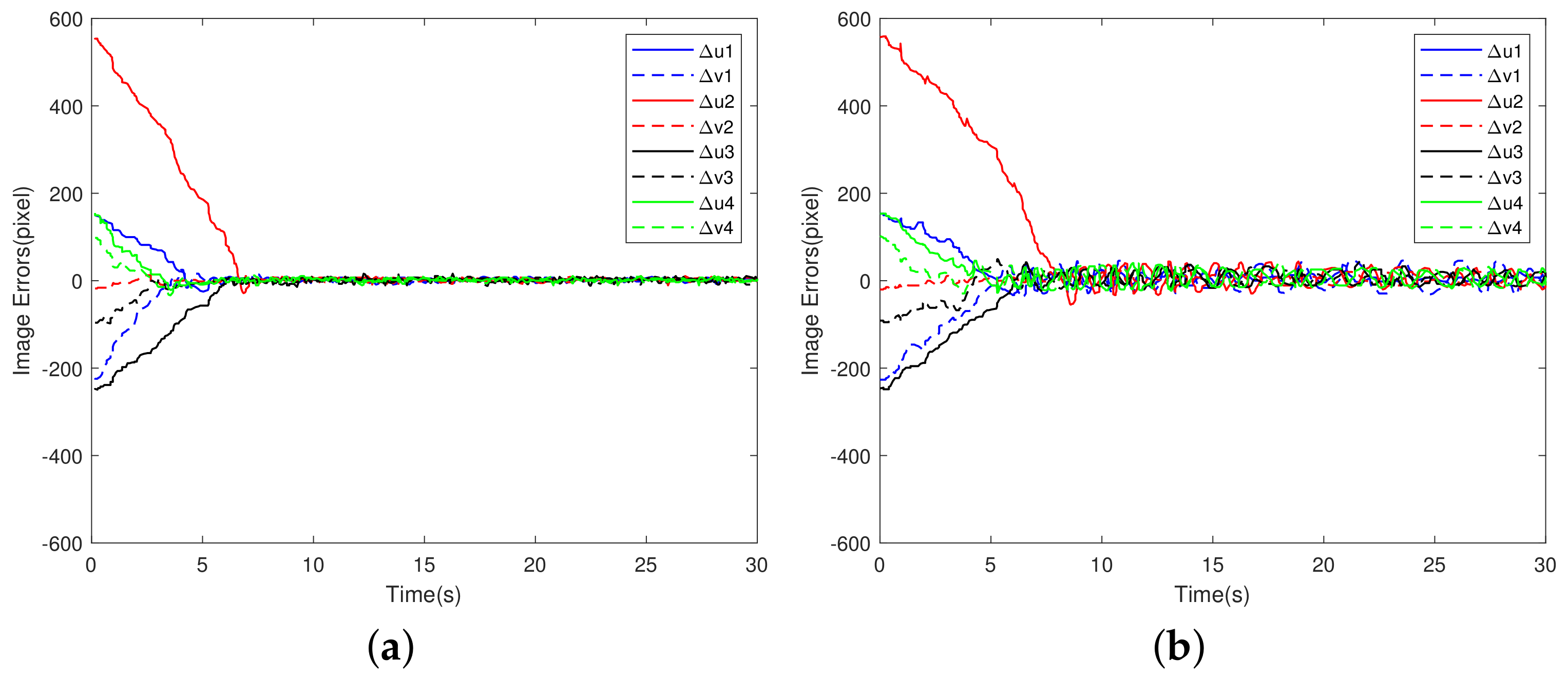
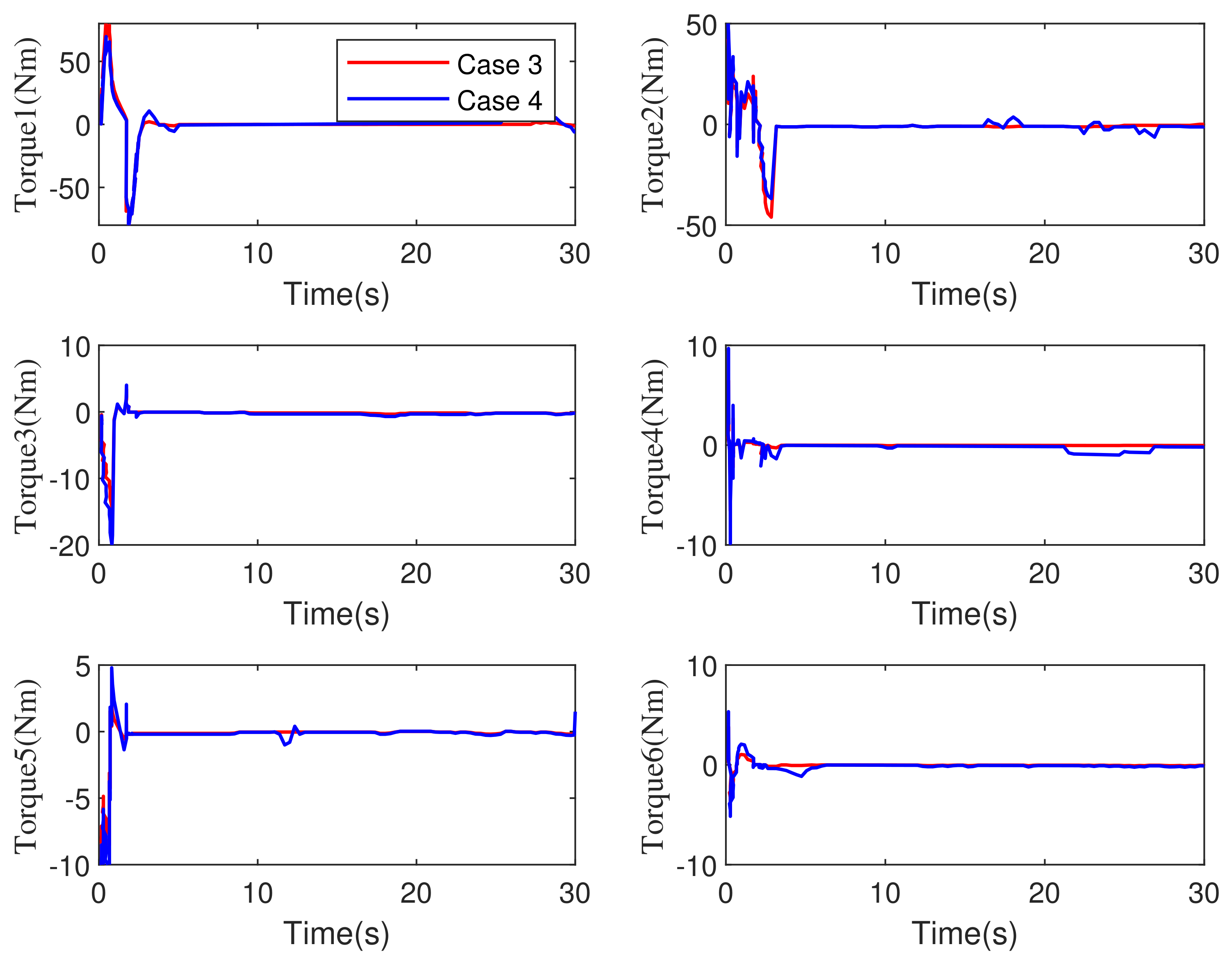
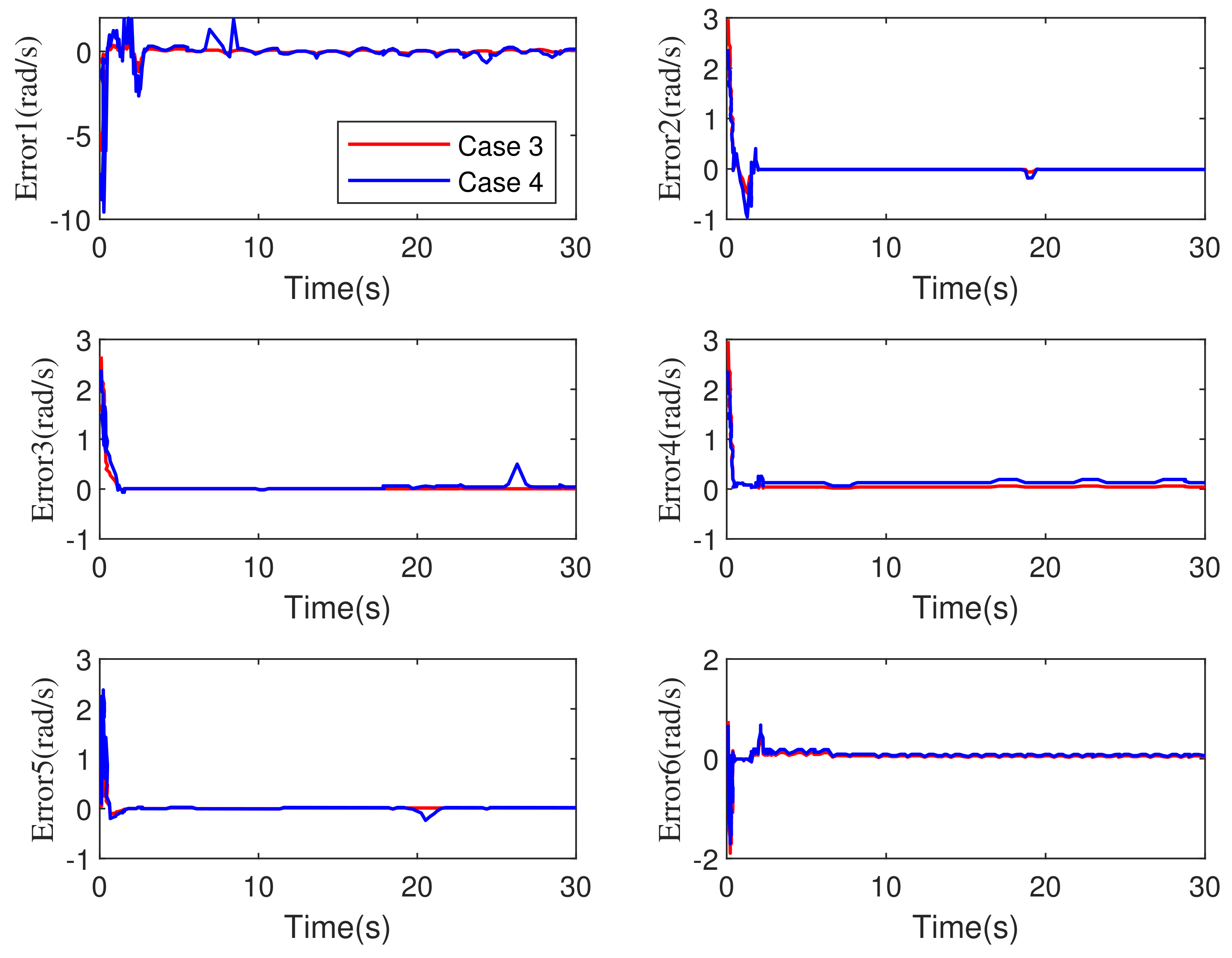
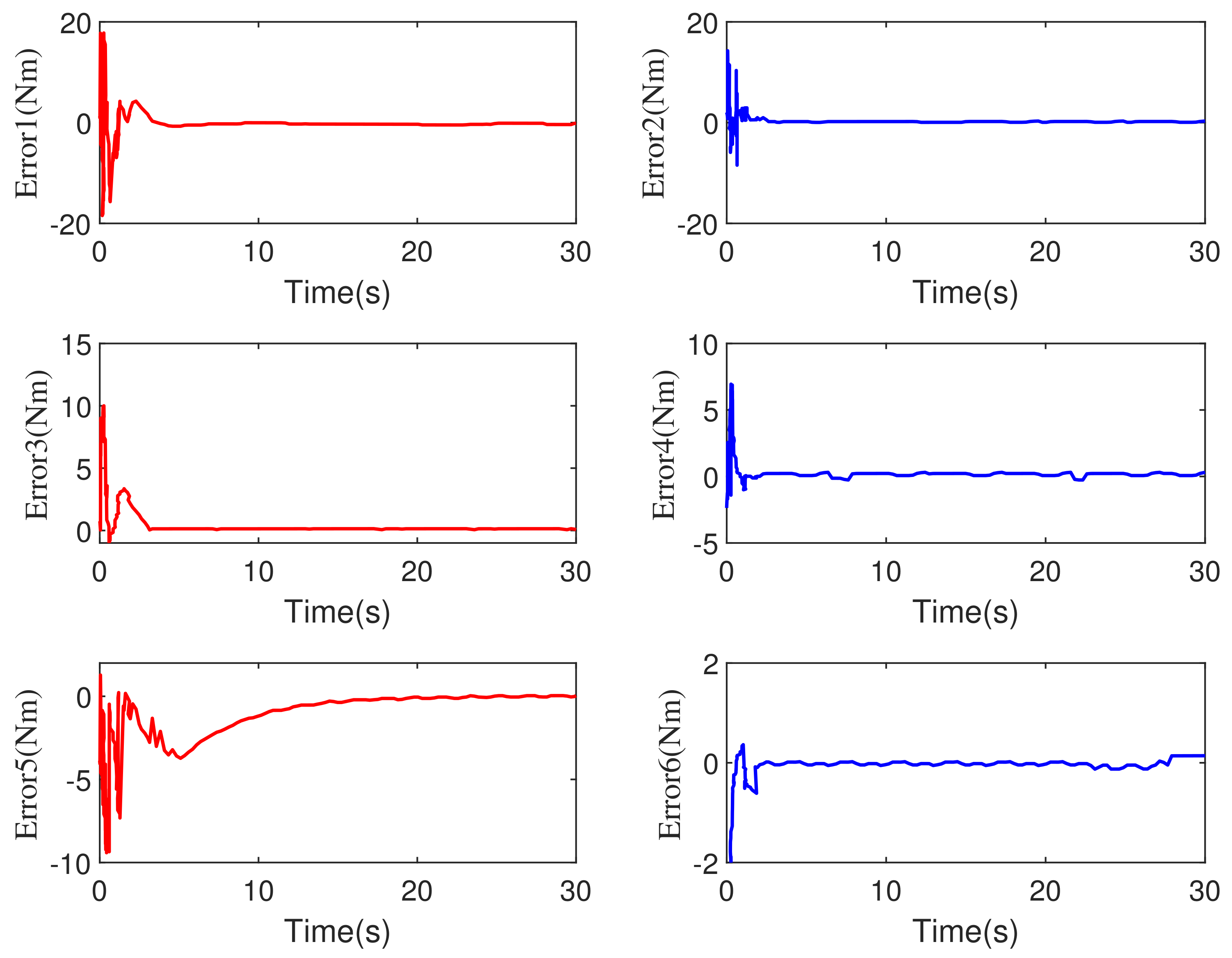
5.2. Comparative Simulations with Time-Varying External Disturbances
5.2.1. 2-DOF Robot Manipulator
5.2.2. 6-DOF Robot Manipulator
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wurll, C.; Fritz, T.; Hermann, Y.; Hollnaicher, D. Production logistics with mobile robots. In Proceedings of the ISR 2018; 50th International Symposium on Robotics, Munich, Germany, 20–21 June 2018; pp. 1–6. [Google Scholar]
- Madhusanka, B.G.D.A.; Jayasekara, A.G.B.P. Design and development of adaptive vision attentive robot eye for service robot in domestic environment. In Proceedings of the IEEE International Conference on Information and Automation for Sustainability, Galle, Sri Lanka, 16–19 December 2016; pp. 1–6. [Google Scholar]
- Cai, K.; Chi, W.; Meng, M.Q. A vision-based road surface slope estimation algorithm for mobile service robots in indoor environments. In Proceedings of the IEEE International Conference on Information and Automation (ICIA), Fujian, China, 11–13 August 2018; pp. 621–626. [Google Scholar]
- Gupta, S.; Mishra, S.R.R.S.; Singal, G.; Badal, T.; Garg, D. Corridor segmentation for automatic robot navigation in indoor environment using edge devices. Comput. Netw. 2020, 178, 107374. [Google Scholar] [CrossRef]
- Sim, R.; Little, J.J. Autonomous vision-based robotic exploration and mapping using hybrid maps and particle filters. Image Vis. Comput. 2009, 17, 167–177. [Google Scholar] [CrossRef]
- Lazar, C.; Burlacu, A. A Control Predictive Framework for Image-Based Visual Servoing Applications. In Proceedings of the The 24th International Conference on Robotics in Alpe-Adria-Danube Region (RAAD), Bucharest, Romania, 6–8 May 2016. [Google Scholar]
- Garcia-Aracil, N.; Perez-Vidal, C.; Sabater, J.M.; Morales, R.; Badesa, F.J. Robust and Cooperative Image-Based Visual Servoing System Using a Redundant Architecture. Sensors 2011, 11, 11885–11900. [Google Scholar] [CrossRef] [PubMed]
- Parsapour, M.; RayatDoost, S.; Taghirad, H.D. A 3D sliding mode control approach for position based visual servoing system. Sci. Iran. 2015, 22, 844–853. [Google Scholar]
- Park, D.-H.; Kwon, J.-H.; Ha, I.-J. Novel position-based visual servoing approach to robust global stability under field-of-view constraint. IEEE Trans. Ind. Electron. 2012, 59, 4735–4752. [Google Scholar] [CrossRef]
- Yan, F.; Li, B.; Shi, W.; Wang, D. Hybrid Visual Servo Trajectory Tracking of Wheeled Mobile Robots. IEEE Access 2018, 6, 24291–24298. [Google Scholar] [CrossRef]
- Luo, R.C.; Chou, S.C.; Yang, X.Y.; Peng, N. Hybrid Eye-to-hand and Eye-in-hand visual servo system for parallel robot conveyor object tracking and fetching. In Proceedings of the Iecon 2014—40th Annual Conference of the Ieee Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014. [Google Scholar]
- Yoshimi, B.H.; Allen, P.K. Alignment using an uncalibrated camera system. IEEE Trans. Robot. Autom. 1995, 11, 516–521. [Google Scholar] [CrossRef]
- Wang, H.; Liu, M. Design of robotic visual servo controlbased on neural network and genetic algorithm. Int. J. Autom. Comput. 2012, 9, 24–29. [Google Scholar] [CrossRef]
- Zhong, X.; Zhong, X.; Peng, X. Robust Kalman Filtering Cooperated Elman Neural Network Learning for Vision-Sensing-Based Robotic Manipulation with Global Stability. Sensors 2013, 13, 13464–13486. [Google Scholar] [CrossRef]
- Yuksel, T. Intelligent visual servoing with extreme learning machine and fuzzy logic. Expert Syst. Appl. 2017, 22, 344–356. [Google Scholar] [CrossRef]
- Kang, M.; Chen, H.; Dong, J. Adaptive Visual Servoing with an Uncalibrated Camera UsingExtreme Learning Machine and Q-leaning. Neurocomputing 2020, 22, 384–394. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, Y.X.; Gao, J.; An, X.M. Visual Servo Control of Underwater Vehicles Based on Image Moments. In Proceedings of the 6th IEEE International Conference on Advanced Robotics and Mechatronics (ICARM), Chongqing, China, 3–5 July 2021. [Google Scholar]
- Anwar, A.; Lin, W.; Deng, X.; Qiu, J.; Gao, H. Quality inspection of remote radio units using depth-free image based visual servo with acceleration command. IEEE Trans. 2019, 66, 8214–8223. [Google Scholar] [CrossRef]
- Keshmiri, M.; Xie, W.; Ghasemi, A. Visual Servoing Using an Optimized Trajectory Planning Technique for a 4 DOFs Robotic Manipulator. Int. J. Control. Autom. Syst. 2017, 15, 1362–1373. [Google Scholar] [CrossRef]
- Wang, J.P.; Liu, A.; Cho, H.S. Direct path planning in image plane and tracking for visual servoing. In Proceedings of the Optomechatronic Systems Control III, Lausanne, Switzerland, 8–10 October 2007. [Google Scholar]
- McFadyen, A.; Jabeur, M.; Corke, P. Image-Based Visual Servoing With Unknown Point Feature Correspondence. IEEE Robot. Autom. Lett. 2017, 2, 601–607. [Google Scholar] [CrossRef]
- Jin, Z.H.; Wu, J.H.; Liu, A.D.; Zhang, W.A.; Yu, L. Policy-Based Deep Reinforcement Learning for Visual Servoing Control of Mobile Robots With Visibility Constraints. IEEE Trans. Ind. Electron. 2022, 69, 1898–1908. [Google Scholar] [CrossRef]
- Wang, Z.; Kim, D.J.; Behal, A. Design of Stable Visual Servoing Under Sensor and Actuator Constraints via a Lyapunov-Based Approach. IEEE Trans. Control. Syst. Technol. 2012, 20, 1575–1582. [Google Scholar] [CrossRef]
- Munoz-Benavent, P.; Gracia, L.; Solanes, J.E.; Esparza, A.; Tornero, J. Robust fulfillment of constraints in robot visual servoing. Control. Eng. Pract. 2018, 71, 79–95. [Google Scholar] [CrossRef]
- Li, Z.J.; Yang, C.G.; Su, C.Y.; Deng, J.; Zhang, W.D. Vision-Based Model Predictive Control for Steering of a Nonholonomic Mobile Robot. IEEE Trans. Control. Syst. Technol. 2016, 24, 553–564. [Google Scholar] [CrossRef]
- Lazar, C.; Burlacu, A. Predictive control strategy for image based visual servoing of robot manipulators. In Proceedings of the 9th WSEAS International Conference on Automation and Information, Bucharest, Romania, 24–26 June 2008. [Google Scholar]
- Qiu, Z.J.Z.; Hu, S.Q.; Liang, X.W. Model Predictive Control for Constrained Image-Based Visual Servoing in Uncalibrated Environments. Asian J. Control. 2019, 21, 783–799. [Google Scholar] [CrossRef]
- Wang, T.T.; Xie, W.F.; Liu, G.D.; Zhao, Y.M. Quasi-min-max Model Predictive Control for Image-Based Visual Servoing with Tensor Product Model transformation. Asian J. Control. 2015, 17, 402–416. [Google Scholar] [CrossRef]
- Gao, J.; Zhang, G.J.; Wu, P.G.; Zhao, X.Y.; Wang, T.H.; Yan, W.S. Model Predictive Visual Servoing of Fully-Actuated Underwater Vehicles with a Sliding Mode Disturbance Observer. IEEE Access 2019, 3, 25516–25526. [Google Scholar] [CrossRef]
- Chaumette, F.; Hutchinson, S. Visual servo control. I. Basic approaches. IEEE Robot. Autom. Mag. 2006, 13, 82–90. [Google Scholar] [CrossRef]
- Davila, J.; Fridman, L.; Levant, A. Second-order sliding-mode observer for mechanical systems. IEEE Trans. Automat. Contr. 2005, 50, 1785–1789. [Google Scholar] [CrossRef]
- Levant, A. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Control. 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Universal Robots A/S. Universal Robots Support-Faq. Available online: www.universal-robots.com/how-tos-and-faqs/faq/ur-faq/ (accessed on 20 April 2022).






| ith Joint | (m) | (kg) | (m) | (kgm) |
|---|---|---|---|---|
| 1 | 0.18 | 23.9 | 0.091 | 1.27 |
| 2 | 0.15 | 4.44 | 0.105 | 0.24 |
| ith Joint | (m) | (kg) | (m) | (kgm) |
|---|---|---|---|---|
| 1 | 0.05 | 20 | 0.05 | 1.0 |
| 2 | 0.05 | 4 | 0.05 | 0.2 |
| Focal Length (m) | Coordinates of the Camera Stagnation Point in the Image Frame (pixels) | Scaling Factors along u Axis and v Axis (pixels/m) | |
|---|---|---|---|
| Real camera parameters | 0.0005 | (646, 482) | (269,167, 267,778) |
| Initial rough camera parameters | 0.0005 | (500, 500) | (250,000, 250,000) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, X.; Li, J.; Li, B.; Wu, J. Constrained Image-Based Visual Servoing of Robot Manipulator with Third-Order Sliding-Mode Observer. Machines 2022, 10, 465. https://doi.org/10.3390/machines10060465
Peng X, Li J, Li B, Wu J. Constrained Image-Based Visual Servoing of Robot Manipulator with Third-Order Sliding-Mode Observer. Machines. 2022; 10(6):465. https://doi.org/10.3390/machines10060465
Chicago/Turabian StylePeng, Xiuyan, Jiashuai Li, Bing Li, and Jiawei Wu. 2022. "Constrained Image-Based Visual Servoing of Robot Manipulator with Third-Order Sliding-Mode Observer" Machines 10, no. 6: 465. https://doi.org/10.3390/machines10060465
APA StylePeng, X., Li, J., Li, B., & Wu, J. (2022). Constrained Image-Based Visual Servoing of Robot Manipulator with Third-Order Sliding-Mode Observer. Machines, 10(6), 465. https://doi.org/10.3390/machines10060465







