Stress Triaxial Constraint and Fracture Toughness Properties of X90 Pipeline Steel
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experiment Model
2.2. Numerical Simulation Model
3. Results and Discussion
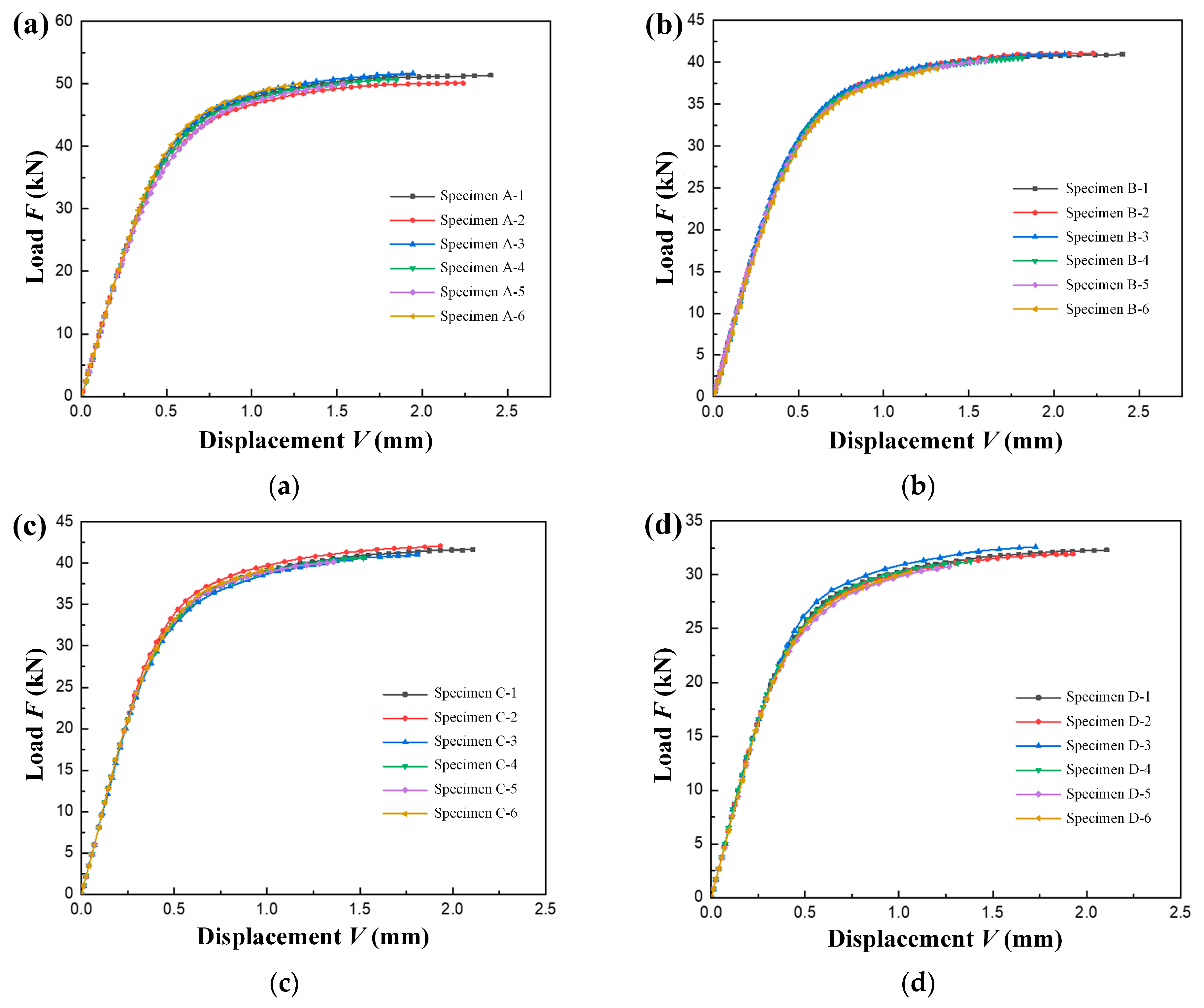
3.1. Comparison between Experimental and Simulation Results
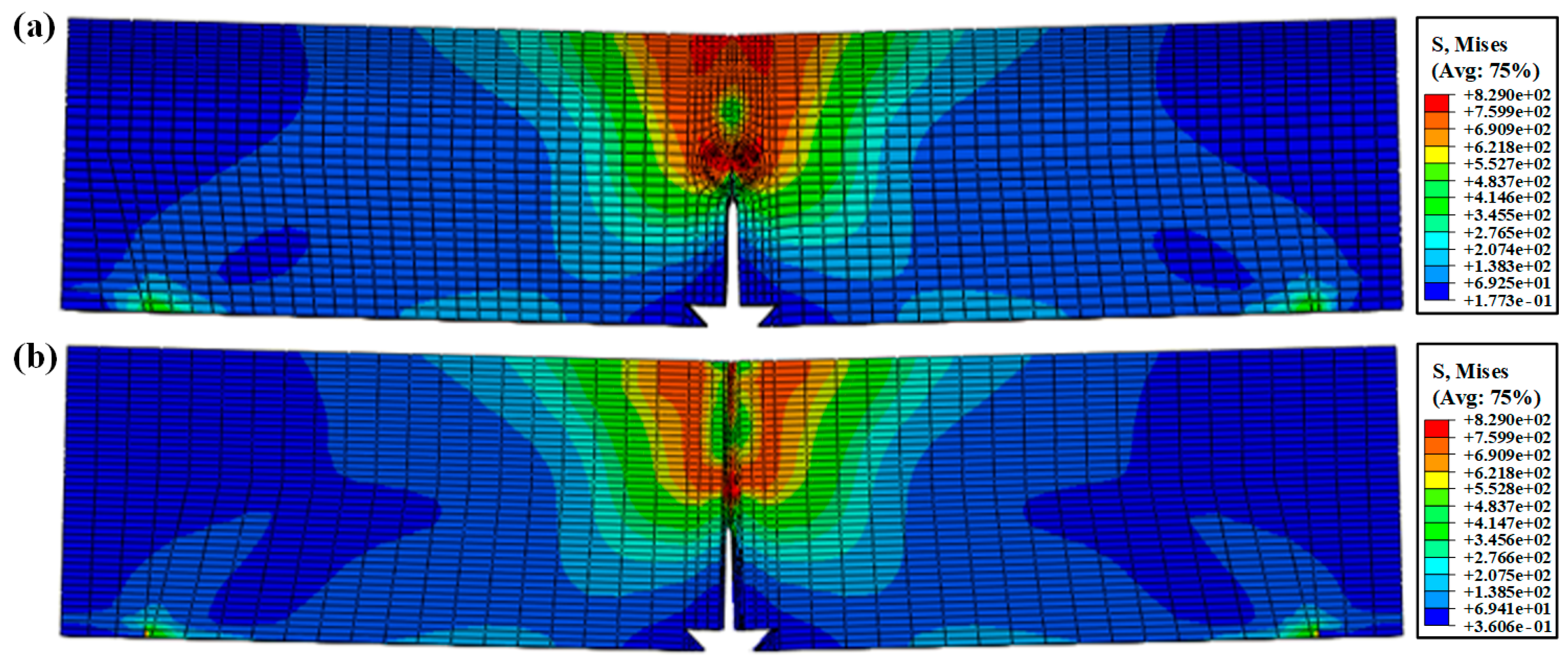
3.2. Overall Stress Distribution of Specimens
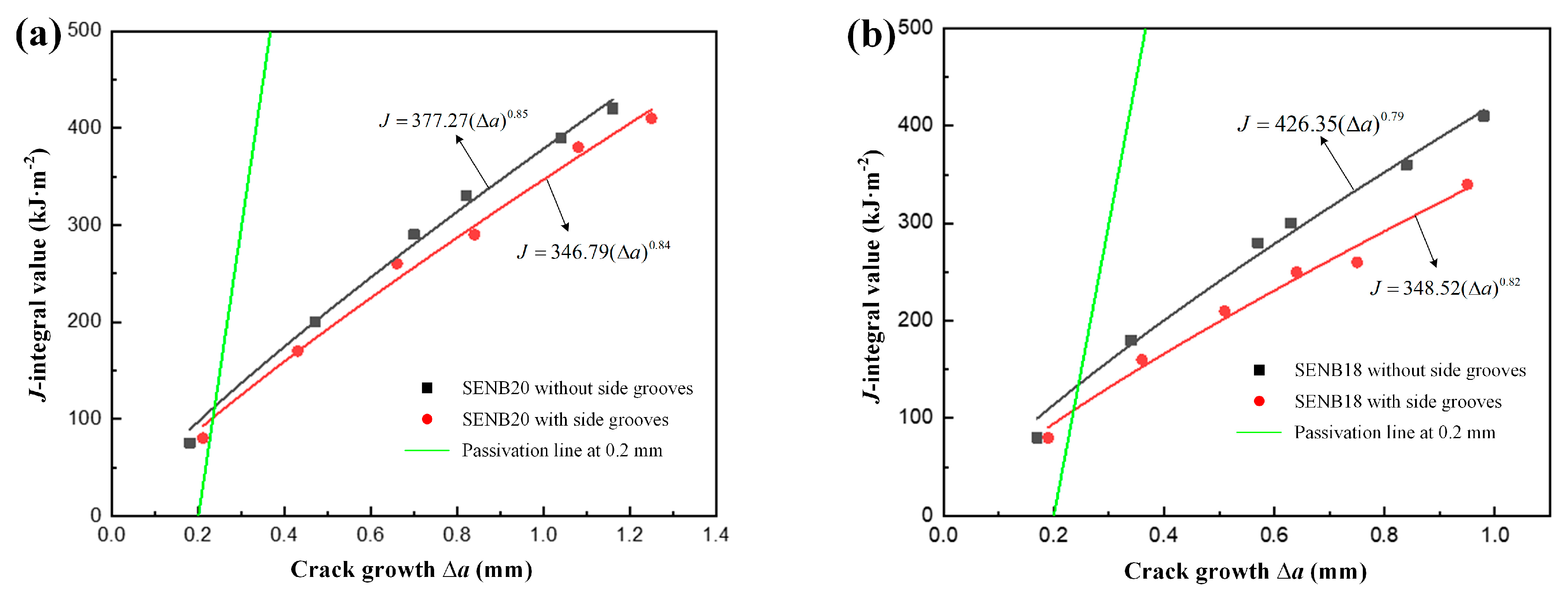
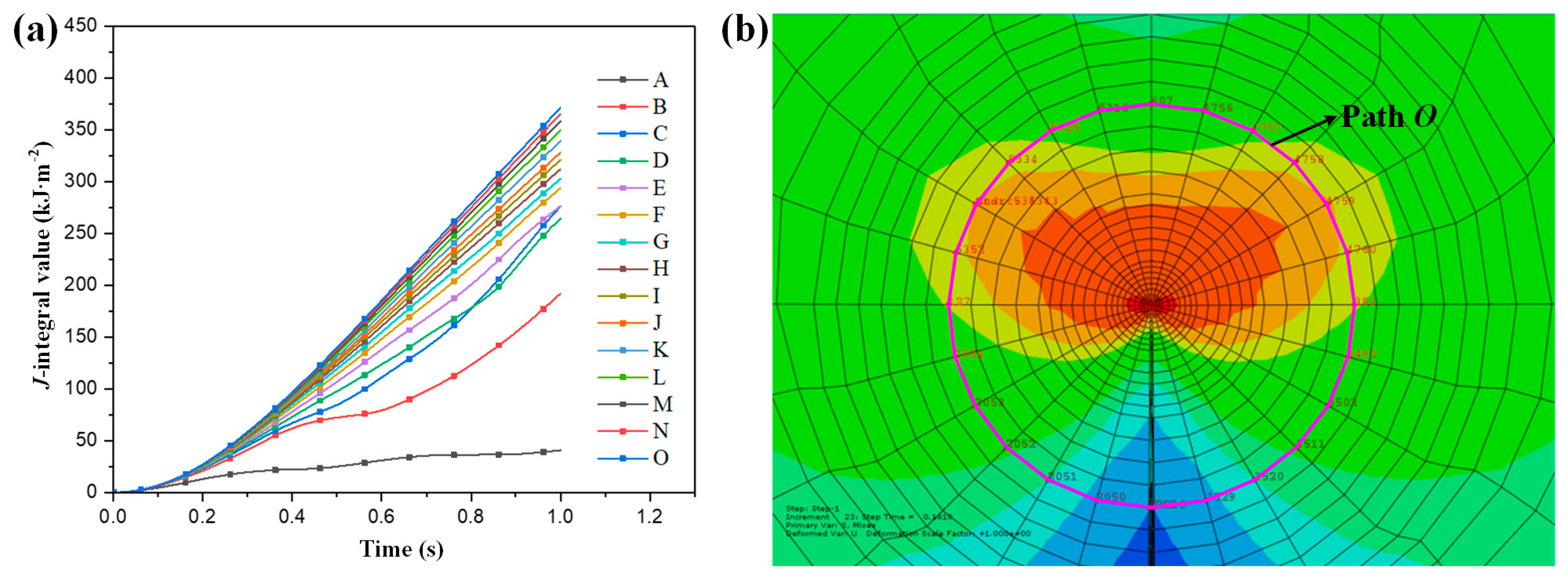
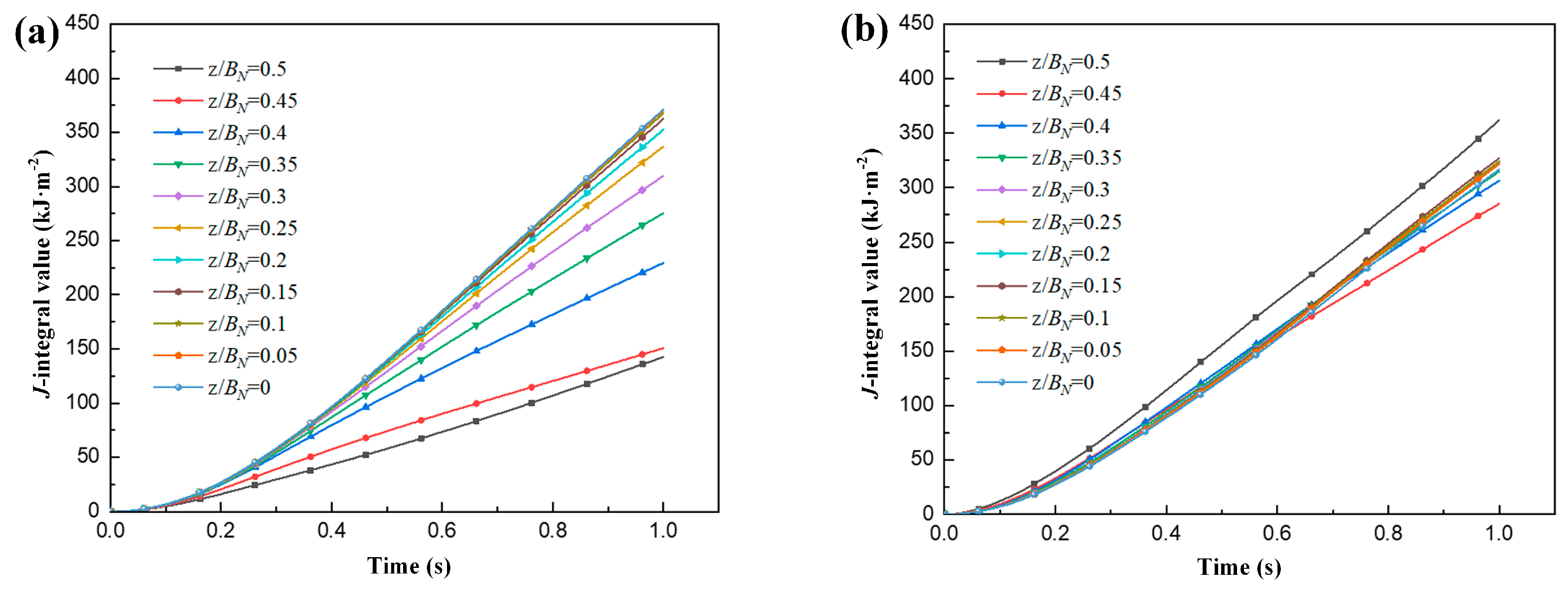
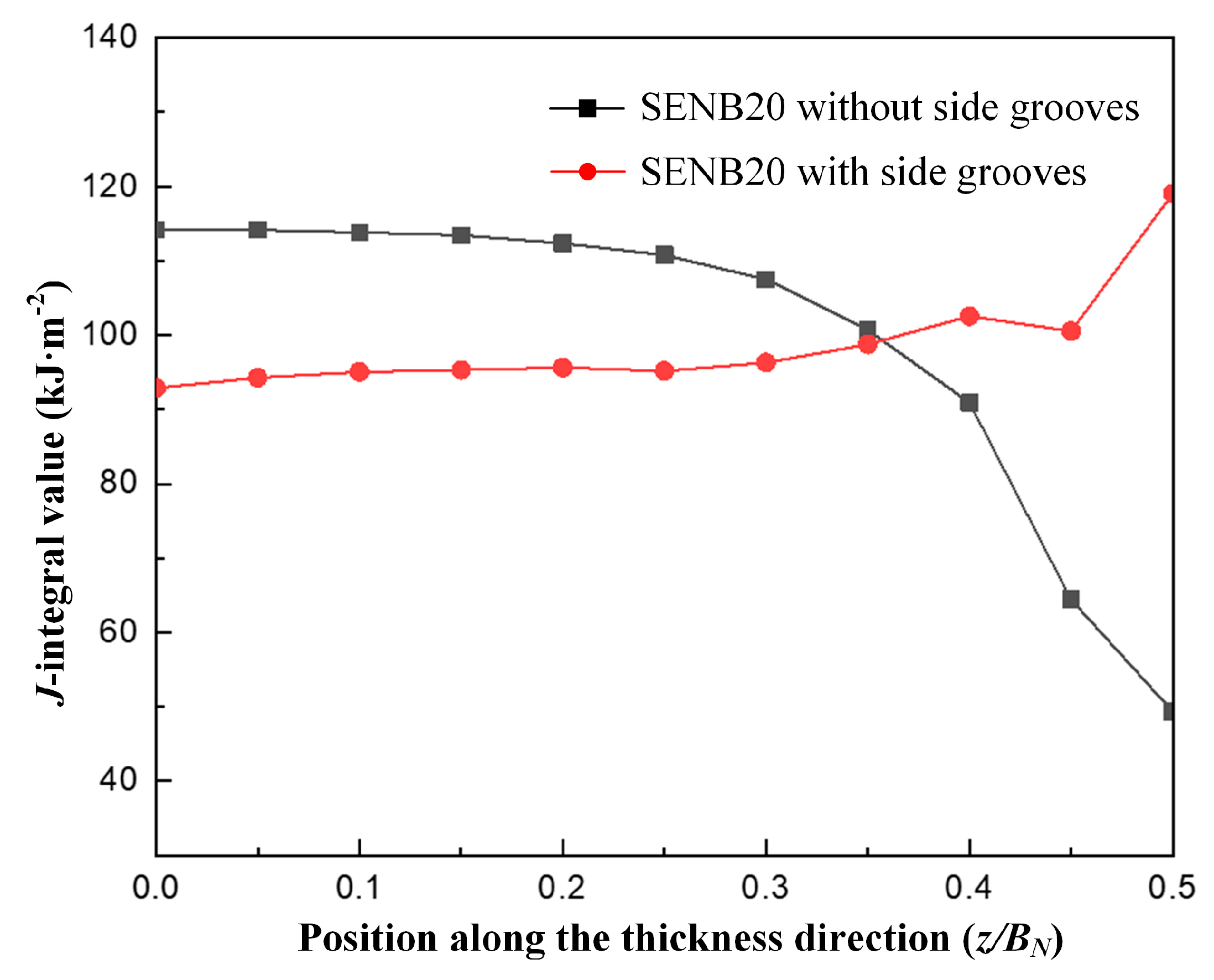
3.3. J-Integral Distribution of Specimens
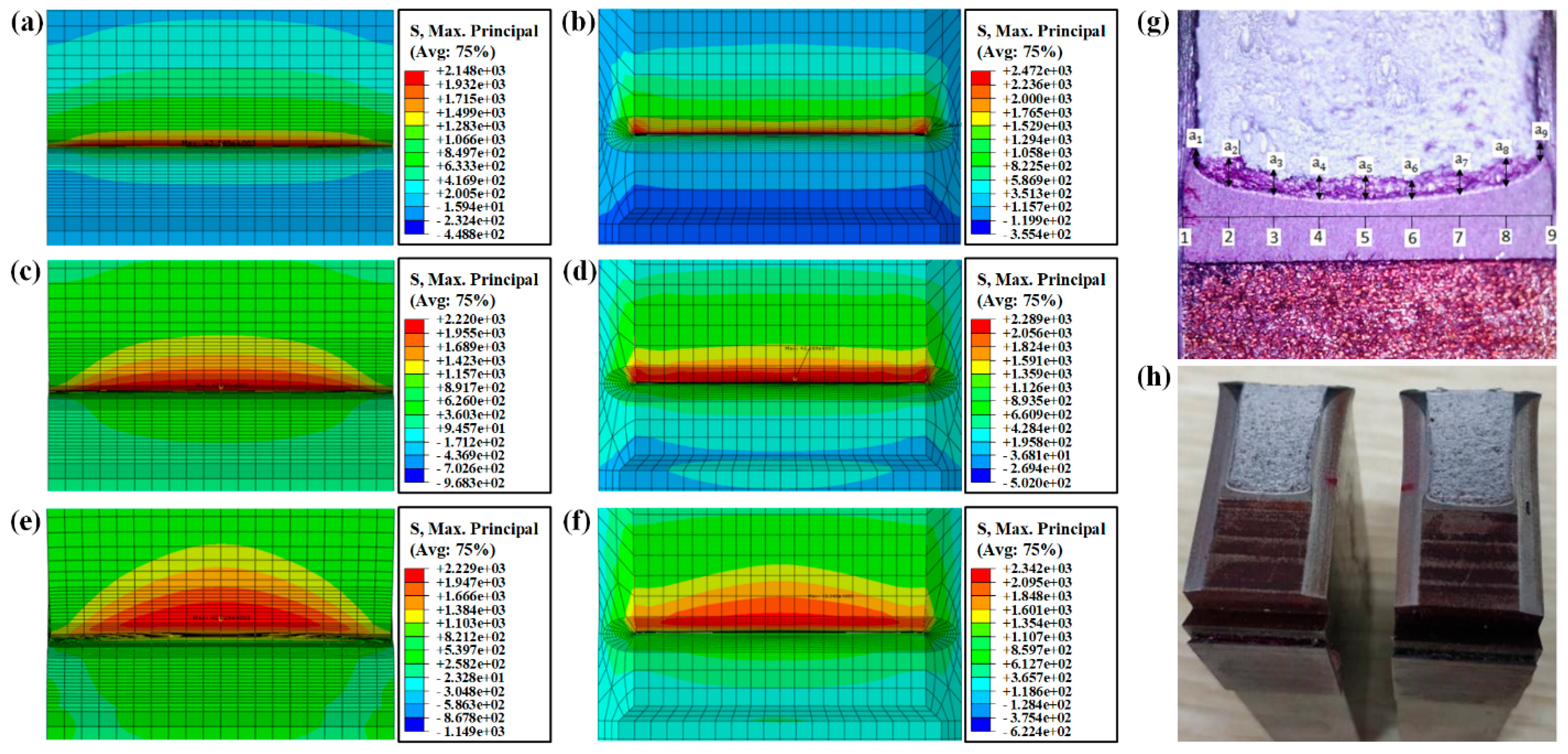
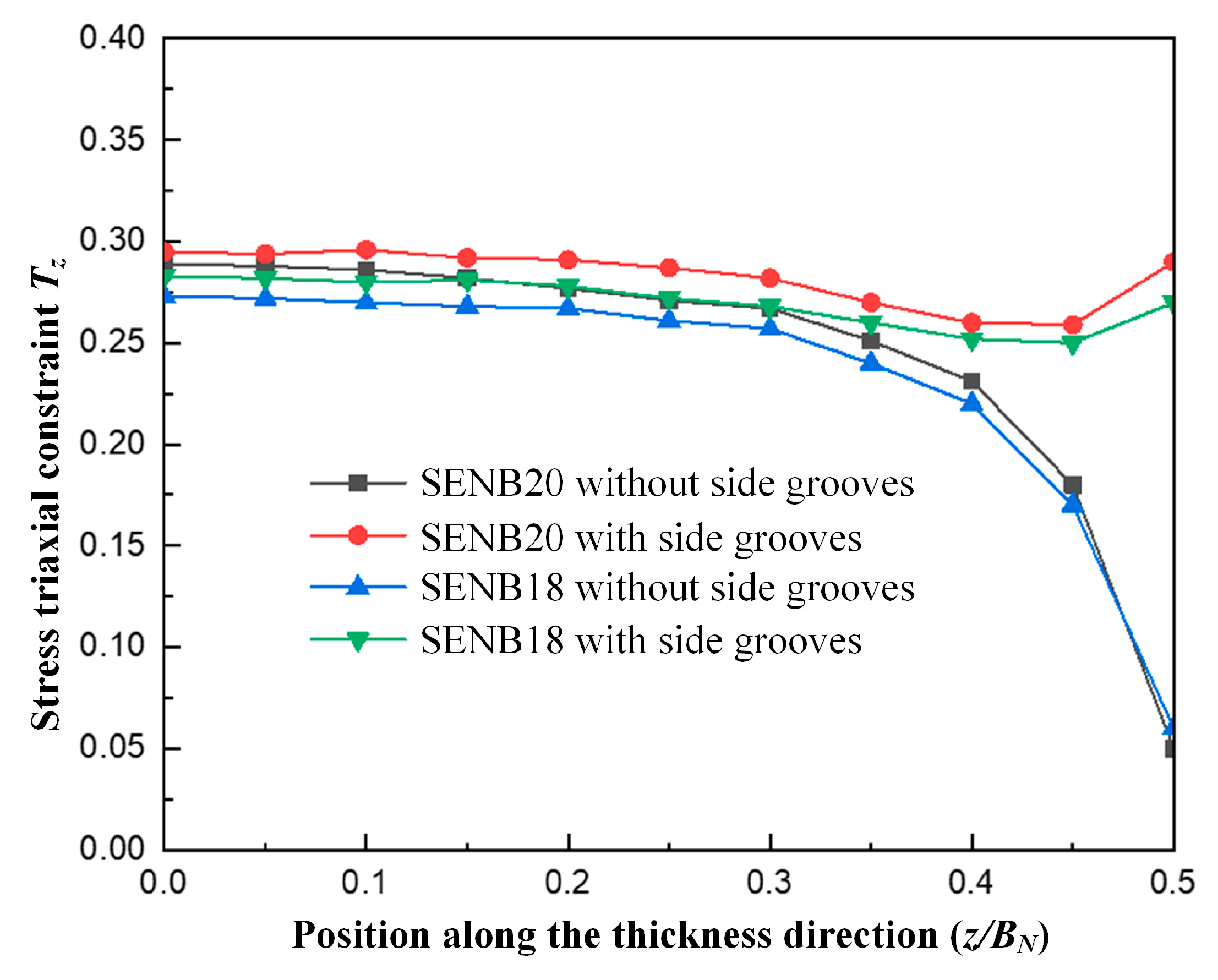
3.4. Stress Triaxial Constraint Distribution of Specimens
3.5. Fracture Toughness of Specimens
4. Conclusions
- (1)
- The resistance curves and fracture toughness are relatively different for the specimens without side grooves, while they are very close for the specimens with side grooves. Therefore, the side grooves specimen should be selected when measuring the resistance curve of X90 pipeline steel.
- (2)
- The side grooves have an effect on the stress distribution, J-integral and stress triaxial constraint of the specimen. For the specimen without side grooves, the stress distribution, J-integral and stress triaxial constraint of the specimen reaches the maximum firstly in the thickness center and then begins to crack. However, for the specimen with side grooves, the stress distribution, J-integral and stress triaxial constraint of the specimen reaches the maximum firstly in the thickness edge and begins to crack, and the crack at the thickness center starts to crack later and propagates to both sides.
- (3)
- The deviation of the side grooves size can affect the determination of fracture toughness of the specimen. When the side grooves depth remains unchanged, the fracture toughness decreases with the decreasing of root radius and increases with the increasing of root radius. When the root radius remains unchanged, the fracture toughness increases with the decreasing of side grooves depth and decreases with the increasing of side grooves depth.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| W | height of specimen |
| S | length of specimen |
| B | thickness of specimen |
| a0 | length of original fatigue crack |
| BN | effective thickness of the specimen with side grooves |
| maximum fatigue crack prefabricated force when the crack growth is 1.3 mm | |
| maximum fatigue crack prefabricated force when the crack growth is 2.5%W | |
| Minimum of maximum fatigue crack prefabricated force | |
| g1(a0/W) | stress intensity factor coefficient |
| R | loading stress ratio |
| F | applied load |
| V | notch opening displacement |
| Vp | notch opening plastic displacement component |
| Ap | area plastic component |
| coefficient | |
| E | Young’s modulus |
| v | Poisson’s ratio |
| JL | experimental equivalent to the J-integral values |
| Jave | J-integral average value |
| JQ0.2BL | fracture toughness value J of the intersection of fitting curve and passivation line at 0.2 mm stable crack |
| α | fitting constant |
| β | fitting constant |
| Rm | tensile strength of material perpendicular to crack plane at test temperature |
| Δa | stable crack growth including blunting |
| εnom | nominal strain |
| σnom | nominal stress |
| ε | real strain |
| σ | real stress |
| Tz | stress triaxial constraints |
| σ11 | normal stresses along x direction |
| σ22 | normal stresses along y direction |
| σ33 | normal stresses along z direction |
Appendix A
References
- Van der Hoeven, M. World Energy Outlook 2012; International Energy Agency: Paris, France, 2012. [Google Scholar]
- Wang, X.X. Several hot issues of current research and development of line pipe. Welded Pipe Tube 2014, 37, 5–13. [Google Scholar]
- Feng, Y.R.; Ji, L.K.; Chen, H.Y.; Jiang, J.X.; Wang, X.; Ren, Y.; Zhang, D.H.; Niu, H.; Bai, M.Z.; Li, S.P. Research progress and prospect of key technologies for high-strain line pipe steel and pipes. Nat. Gas Ind. B 2021, 8, 146–153. [Google Scholar] [CrossRef]
- Feng, Y.R.; Zhuang, C.J. Some aspects on X80 line pipe application. Welded Pipe Tube 2006, 29, 6–10. [Google Scholar]
- Feng, Y.R.; Han, L.; Zhang, F.; Bai, Z.; Liu, W. Research progress and prospect of oil and gas well tubing string integrity technology. Nat. Gas Ind. 2014, 34, 73–81. [Google Scholar]
- Hoyos, J.J.; Masoumi, M.; Pereira, V.F.; Tschiptschin, A.P.; Paes, M.T.P.; Avila, J.A. Influence of hydrogen on the microstructure and fracture toughness of friction stir welded plates of API 5L X80 pipeline steel. Int. J. Hydrogen Energy 2019, 44, 23458–23471. [Google Scholar] [CrossRef]
- Chatzidouros, E.V.; Traidia, A.; Devarapalli, R.S.; Pantelis, D.I.; Steriotis, T.A.; Jouiad, M. Effect of hydrogen on fracture toughness properties of a pipeline steel under simulated sour service conditions. Int. J. Hydrogen Energy 2018, 43, 5747–5759. [Google Scholar] [CrossRef]
- Wu, S.W.; Zhang, Z. Long term ageing effect on fracture toughness of the GTAW welded joints for nuclear power main pipelines. Int. J. Press. Vessel. Pip. 2020, 188, 104250. [Google Scholar] [CrossRef]
- An, T.; Zhang, S.; Feng, M.; Luo, B.W.; Zheng, S.Q.; Chen, L.Q.; Zhang, L. Synergistic action of hydrogen gas and weld defects on fracture toughness of X80 pipeline steel. Int. J. Fatigue 2018, 120, 23–32. [Google Scholar] [CrossRef]
- Anandavijayan, S.; Mehmanparast, A.; Brennan, F.; Chahardehi, A. Material pre-straining effects on fracture toughness variation in offshore wind turbine foundations. Eng. Fract. Mech. 2021, 252, 107844. [Google Scholar] [CrossRef]
- Xiong, J.Z.; Yang, X.Q.; Lin, W.; Liu, K.X. Evaluation of inhomogeneity in tensile strength and fracture toughness of underwater wet friction taper plug welded joints for low-alloy pipeline steels. J. Manuf. Processes 2018, 32, 280–287. [Google Scholar] [CrossRef]
- Liu, L.G.; Xiao, H.; Li, Q.; Liu, Y.; Li, P.; Yang, Z.Q.; Yu, H. Evaluation of the fracture toughness of X70 pipeline steel with ferrite-bainite microstructure. Mater. Sci. Eng. A 2017, 688, 388–395. [Google Scholar]
- Han, P.H.; Cheng, P.; Yuan, S.; Bai, Y. Characterization of ductile fracture criterion for API X80 pipeline steel based on a phenomenological approach. Thin-Walled Struct. 2021, 164, 107254. [Google Scholar] [CrossRef]
- Yang, Y.H.; Shi, L.; Xu, Z.; Lu, H.S.; Chen, X.; Wang, X.; Wang, X. Fracture toughness of the materials in welded joint of X80 pipeline steel. Eng. Fract. Mech. 2015, 148, 337–349. [Google Scholar] [CrossRef]
- Luna, S.D.; Fernández-Sáez, J.; Pérez-Castellanos, J.L.; Navarro, C. An analysis of the static and dynamic fracture behaviour of a pipeline steel. Int. J. Press. Vessel. Pip. 2000, 77, 691–696. [Google Scholar] [CrossRef]
- Shin, S.Y.; Hwang, B.; Kim, S.; Lee, S. Fracture toughness analysis in transition temperature region of API X70 pipeline steels. Mater. Sci. Eng. A 2006, 429, 196–204. [Google Scholar] [CrossRef]
- Shin, S.Y.; Woo, K.J.; Hwang, B.; Kim, S.; Lee, S. Fracture-toughness analysis in transition-temperature region of three american petroleum institute X70 and X80 pipeline steels. Metall. Mater. Trans. A 2009, 40, 867–876. [Google Scholar] [CrossRef] [Green Version]
- Tkaczyk, T.; Nikbin, K. The effect of prestrain on ductile fracture toughness of reeled pipeline steels. J. Press. Vessel Technol. 2011, 133, 031701. [Google Scholar] [CrossRef]
- Said, G.; Aytekin, H. A new method for determining the fracture toughness of main pipeline steels. Fatigue Fract. Eng. Mater. Struct. 2013, 36, 640–649. [Google Scholar] [CrossRef]
- Nowak-Coventry, M.; Pisarski, H.; Moore, P. The effect of fatigue pre-cracking forces on fracture toughness. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 135–148. [Google Scholar] [CrossRef]
- Park, D.Y.; Amirkhiz, B.S.; Gravel, J.P.; Liang, J.; Zavadil, R.; Liu, P.; Duan, D.M. Forming mechanism of delamination cracks observed during tensile and fracture toughness testing of X70 pipeline steel. Int. J. Fract. 2018, 209, 223–229. [Google Scholar] [CrossRef]
- Chanda, S.; Ru, C.Q. Temperature effects on fracture toughness parameters for pipeline steels. Int. J. Steel Struct. 2018, 18, 1754–1760. [Google Scholar] [CrossRef]
- Guo, W.L.; Dong, H.; Yang, Z.; Lu, M.X.; Zhao, X.W.; Luo, J.H. Effects of thickness and delamination on fracture toughness of X 60 pipeline steel. Acta Metall. Sin. 2001, 37, 386–390. [Google Scholar]
- Guo, W.L.; Dong, H.; Lu, M.; Zhao, X. The coupled effects of thickness and delamination on cracking resistance of X70 pipeline steel. Int. J. Press. Vessel. Pip. 2002, 79, 403–412. [Google Scholar] [CrossRef]
- Yang, Z.; Huo, C.Y.; Zhao, X.W. Effects of thickness and delaminating on fracture of high strength and high toughness pipeline steel. Key Eng. Mater. 2006, 306, 393–398. [Google Scholar] [CrossRef]
- Dong, H.R.; Guo, W.L.; Yang, Z. Mechanism of delamination and its effects on fracture of surface crack bodies in ductile pipeline steel. Key Eng. Mater. 2005, 297–300, 1235–1240. [Google Scholar] [CrossRef]
- Xu, J.; Fan, Y. Effects of temperature and crack tip constraint on cleavage fracture toughness in the weld thermal simulated X80 pipeline steels. Adv. Mater. Res. 2011, 197–198, 1595–1598. [Google Scholar] [CrossRef]
- Xiao, G.C.; Jing, H.Y.; Xu, L.Y.; Zhao, L.; Ji, J.C. Prediction of temperature and prestraining effects on fracture toughness of high-strength structural steel by the local approach. Mater. Sci. Eng. A 2011, 528, 3044–3048. [Google Scholar] [CrossRef]
- Li, Y.Z.; Gong, B.M.; Mauro, C.; Deng, C.Y.; Wang, D.P. Experimental investigation of out-of-plane constraint effect on fracture toughness of the SE(T) specimens. Int. J. Mech. Sci. 2017, 128–129, 644–651. [Google Scholar] [CrossRef]
- ASTM E1820-13. Standard Test Method for Measurement of Fracture Toughnes; ASTM International: West Conshohocken, PA, USA, 2013. [Google Scholar]
- ISO Standard 12135:2016(E). Metallic Materials-Unified Method of Test for the Determination of Quasistatic Fracture Toughness; International Organization for Standardization: London, UK, 2016. [Google Scholar]
- Shih, C.F.; de Lorenzi, H.G.; Andrews, W.R. Elastic compliances and stress-intensity factors for side-grooved compact specimens. Int. J. Fract. 1977, 13, 544–548. [Google Scholar] [CrossRef]
- Andrews, W.R.; Shih, C.D. Thickness and Side-Groove Effects on J- and δ-Resistance Curves for A533-B Steel at 93 °C; ASTM International: West Conshohocken, PA, USA, 1979; pp. 426–450. [Google Scholar]
- Shivakumar, K.N.; Newman, J.C., Jr. Verification of effective thicknesses for side-grooved compact specimens. Eng. Fract. Mech. 1992, 43, 269–275. [Google Scholar] [CrossRef]
- Shen, G.; Tyson, W.R.; Gianetto, J.A.; Park, D.Y. Effect of side grooves on compliance, J-integral and constraint of a clamped SE(T) specimen. In Proceedings of the ASME 2010 Pressure Vessels and Piping Division/K-PVP Conference, Bellevue, WA, USA, 18–22 July 2010; pp. 81–89. [Google Scholar]
- Sarzosa, D.F.B.; Souza, R.F.D.; Ruggieri, C. J-CTOD relations in clamped SE(T) fracture specimens including 3-D stationary and growth analysis. Eng. Fract. Mech. 2015, 147, 331–354. [Google Scholar] [CrossRef]
- American Petroleum Institute. Specifications for Line Pipe: API Specifications L, 45th ed.; American Petroleum Institute: Washington, DC, USA, 2012. [Google Scholar]
- Begley, J.; ALandes, J.D. The J-Integral as a Fracture Criterion; American Society for Testing and Materials: West Conshohocken, PA, USA, 1972. [Google Scholar]
- Landes, J.D. The blunting line in elastic-plastic fracture. Fatigue Fract. Eng. Mater. Struct. 1995, 18, 1289–1297. [Google Scholar] [CrossRef]
- Li, X.Q.; Ding, Z.Y.; Liu, C.; Bao, S.Y.; Gao, Z.L. Evaluation and comparison of fracture toughness for metallic materials in different conditions by ASTM and ISO standards. Int. J. Press. Vessel. Pip. 2020, 187, 104189. [Google Scholar] [CrossRef]
- Guo, W.L. Three-dimensional analyses of plastic constraint for through-thickness cracked bodies. Eng. Fract. Mech. 1999, 62, 383–407. [Google Scholar] [CrossRef]
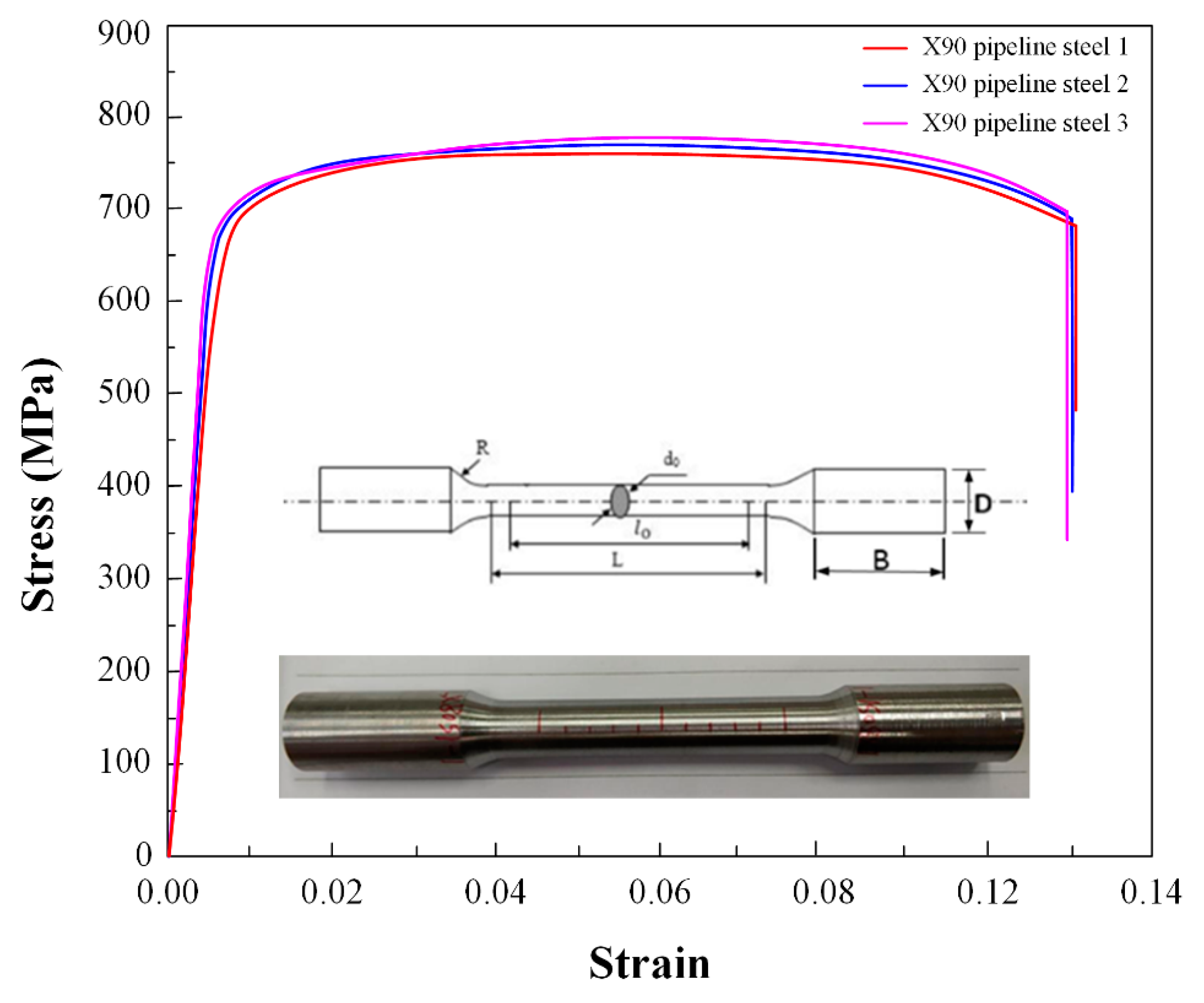
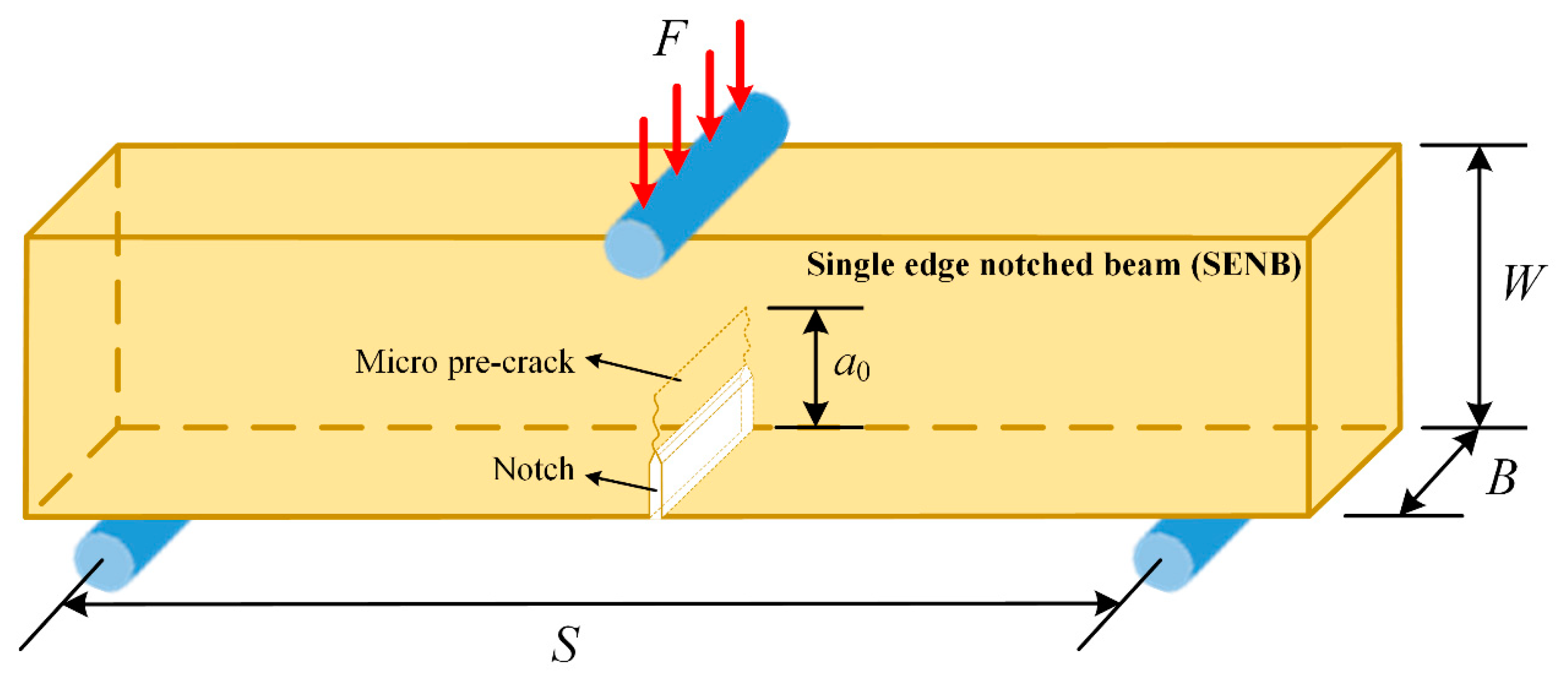
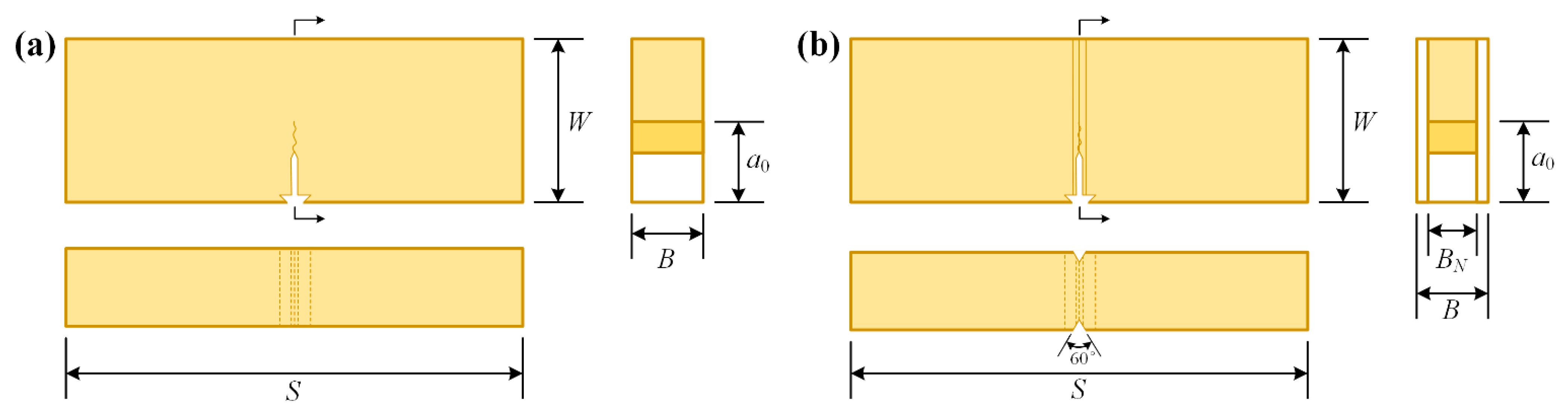

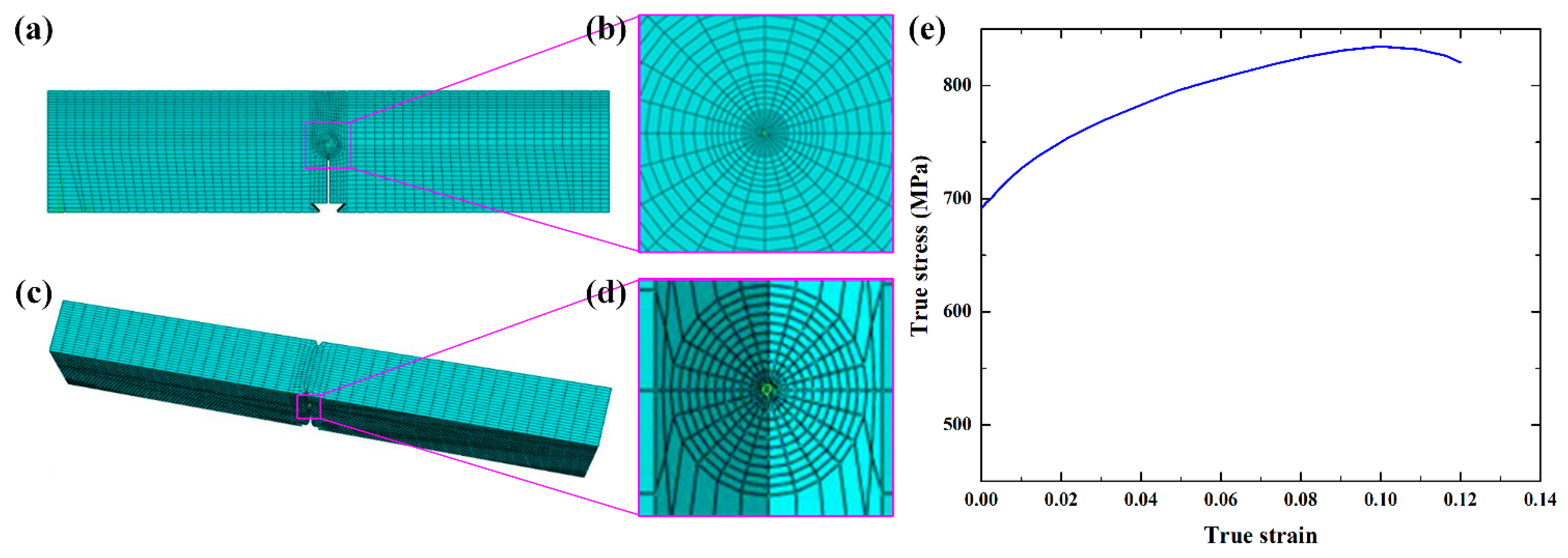
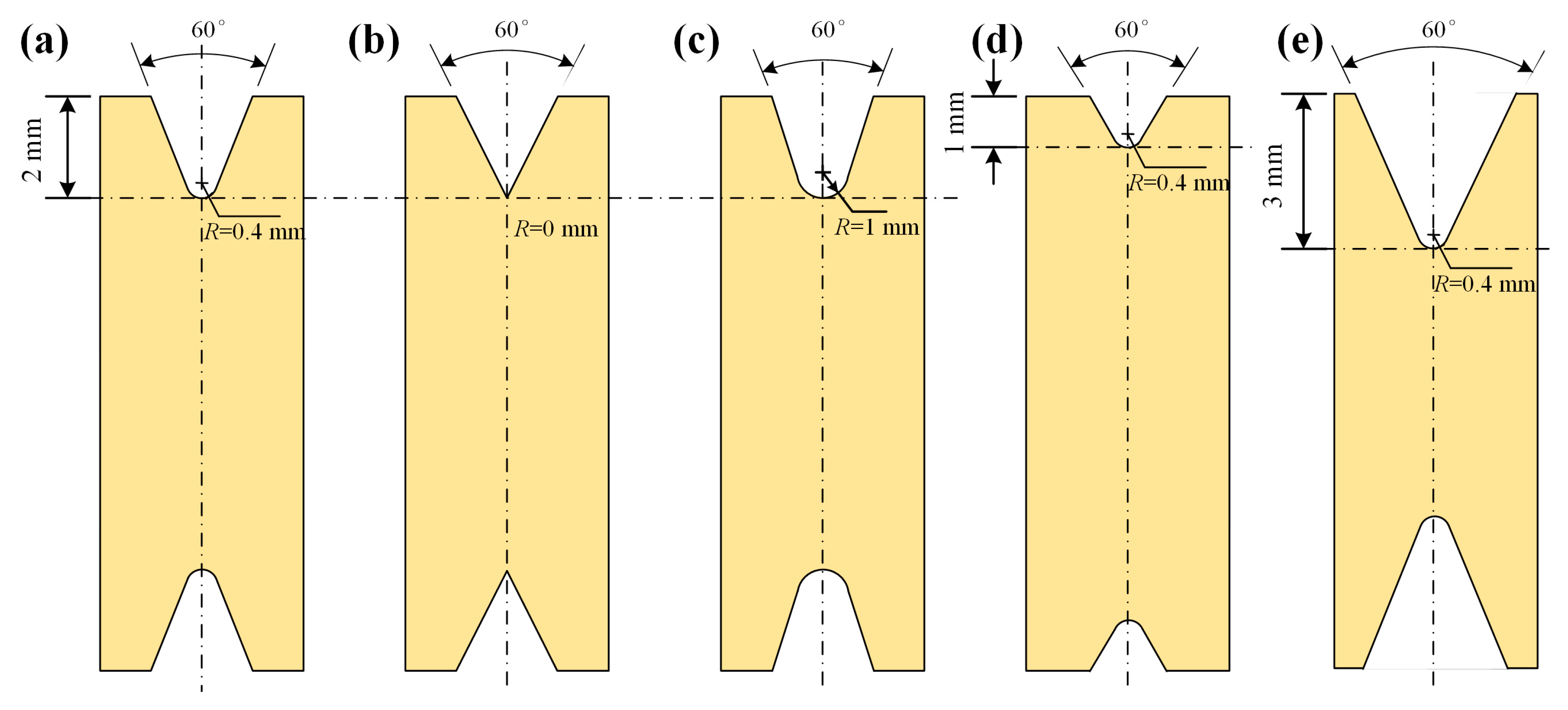
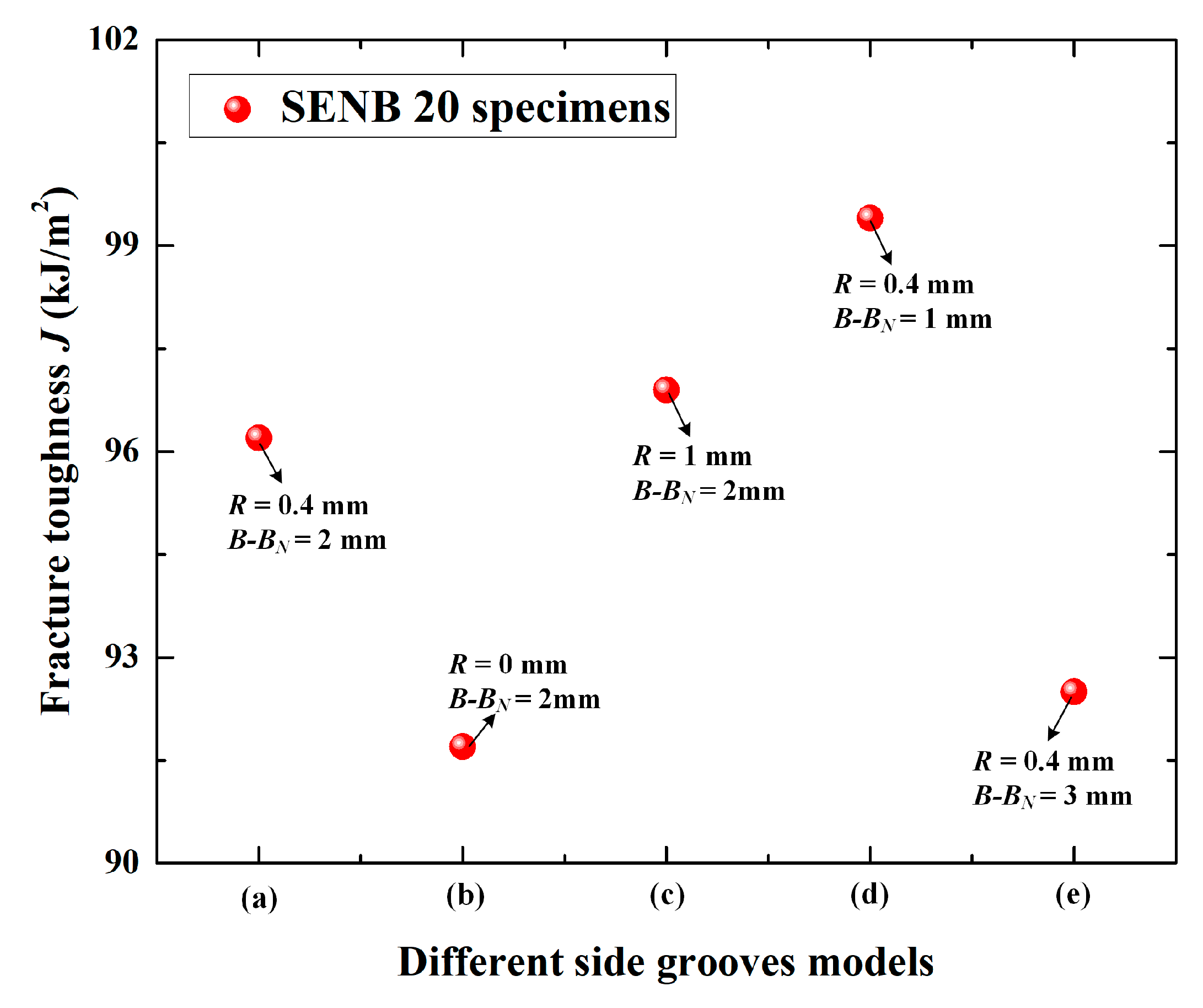
| Chemical Composition | C | Mn | Si | P | S | Nb | Cu | Ni | Cr | Fe |
|---|---|---|---|---|---|---|---|---|---|---|
| Mass fraction (%) | 0.046 | 1.77 | 0.22 | 0.011 | 0.001 | 0.059 | 0.15 | 0.20 | 0.03 | 97.3 |
| Parameters | Density (g/cm3) | Young’s Modulus (MPa) | Poisson Ratio | Yield Strength (MPa) | Tensile Strength (MPa) | Total Elongation (%) | Rt0.5/Rm1 |
|---|---|---|---|---|---|---|---|
| Mechanical properties | 7.84 | 206 | 0.3 | 692 | 783 | 13 | 0.88 |
| Specimen Types | No. | Length S (mm) | Height W (mm) | Thickness B (mm) | Effective Thickness with Side Grooves BN (mm) 1 |
|---|---|---|---|---|---|
| SENB 20 (without side grooves) | A-1 | 160 | 40.12 | 20.03 | -- |
| A-2 | 160 | 40.14 | 19.94 | -- | |
| A-3 | 160 | 40.05 | 19.88 | -- | |
| A-4 | 160 | 40.10 | 20.04 | -- | |
| A-5 | 160 | 40.12 | 20.11 | -- | |
| A-6 | 160 | 40.15 | 20.06 | -- | |
| SENB 20 (with side grooves) | B-1 | 160 | 40.01 | 20.03 | 16.02 |
| B-2 | 160 | 40.05 | 20.04 | 16.11 | |
| B-3 | 160 | 40.05 | 19.95 | 16.18 | |
| B-4 | 160 | 40.11 | 20.02 | 16.03 | |
| B-5 | 160 | 40.14 | 20.12 | 16.01 | |
| B-6 | 160 | 40.17 | 20.14 | 15.96 | |
| SENB 18 (without side grooves) | C-1 | 144 | 36.01 | 18.04 | -- |
| C-2 | 144 | 36.04 | 18.11 | -- | |
| C-3 | 144 | 36.05 | 18.12 | -- | |
| C-4 | 144 | 35.98 | 18.14 | -- | |
| C-5 | 144 | 36.12 | 18.14 | -- | |
| C-6 | 144 | 36.14 | 18.01 | -- | |
| SENB 18 (with side grooves) | D-1 | 144 | 36.06 | 17.96 | 14.51 |
| D-2 | 144 | 36.06 | 17.89 | 14.49 | |
| D-3 | 144 | 36.13 | 18.08 | 14.45 | |
| D-4 | 144 | 36.11 | 18.12 | 14.50 | |
| D-5 | 144 | 36.04 | 18.14 | 14.37 | |
| D-6 | 144 | 36.15 | 18.04 | 14.35 |
| Specimen Types | (kN) (Equation (1)) | (kN) (Equations (2) and (3)) | Minimum of Maximum Fatigue Crack Prefabricated Force Ff (kN) |
|---|---|---|---|
| SENB20 (without side grooves) | 22.4 | 10.5 | 10.5 |
| SENB20 (with side grooves) | 22.4 | 9.4 | 9.4 |
| SENB18 (without side grooves) | 20.2 | 9.0 | 9.0 |
| SENB18 (with side grooves) | 20.2 | 8.0 | 8.0 |
| Plastic Strain | 0 | 0.002 | 0.004 | 0.008 | 0.010 | 0.015 | 0.020 | 0.030 | 0.040 | 0.070 | 0.080 | 0.090 | 0.100 | 0.120 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Yield stress (MPa) | 692 | 701 | 707 | 719 | 728 | 737 | 754 | 769 | 789 | 709 | 827 | 834 | 831 | 828 |
| Specimen Types | No. | a0 (mm) | Δa (mm) | g1 (a/W) | F (kN) | Ap (J) | J (kJ·m−2) |
|---|---|---|---|---|---|---|---|
| SENB20 (without side grooves) | A-1 | 21.75 | 1.16 | 3.40 | 51.26 | 48.11 | 419 |
| A-2 | 21.66 | 1.04 | 3.34 | 51.28 | 44.67 | 392 | |
| A-3 | 21.54 | 0.82 | 3.24 | 51.04 | 37.80 | 330 | |
| A-4 | 21.63 | 0.70 | 3.22 | 51.12 | 33.21 | 288 | |
| A-5 | 21.72 | 0.47 | 3.19 | 50.85 | 22.91 | 197 | |
| A-6 | 21.71 | 0.18 | 3.12 | 50.42 | 8.59 | 75 | |
| SENB20 (with side grooves) | B-1 | 21.84 | 1.25 | 3.47 | 40.86 | 46.96 | 418 |
| B-2 | 21.93 | 1.08 | 3.43 | 41.03 | 43.52 | 379 | |
| B-3 | 21.95 | 0.84 | 3.36 | 40.82 | 33.21 | 289 | |
| B-4 | 21.76 | 0.66 | 3.25 | 40.65 | 29.78 | 258 | |
| B-5 | 21.81 | 0.43 | 3.21 | 40.55 | 19.47 | 171 | |
| B-6 | 21.86 | 0.21 | 3.15 | 40.34 | 9.28 | 81 | |
| SENB18 (without side grooves) | C-1 | 19.68 | 0.98 | 3.41 | 41.62 | 46.96 | 408 |
| C-2 | 19.62 | 0.84 | 3.35 | 41.63 | 41.24 | 360 | |
| C-3 | 19.71 | 0.63 | 3.31 | 41.98 | 34.36 | 298 | |
| C-4 | 19.73 | 0.57 | 3.29 | 41.71 | 32.07 | 281 | |
| C-5 | 19.59 | 0.34 | 3.18 | 41.47 | 20.62 | 182 | |
| C-6 | 19.60 | 0.17 | 3.13 | 41.12 | 9.16 | 80 | |
| SENB18 (with side grooves) | D-1 | 19.81 | 0.95 | 3.43 | 32.25 | 38.94 | 340 |
| D-2 | 19.77 | 0.75 | 3.37 | 32.01 | 29.78 | 258 | |
| D-3 | 19.74 | 0.64 | 3.32 | 32.32 | 28.63 | 247 | |
| D-4 | 19.68 | 0.51 | 3.25 | 32.04 | 24.05 | 209 | |
| D-5 | 19.72 | 0.36 | 3.22 | 31.87 | 18.32 | 160 | |
| D-6 | 19.83 | 0.19 | 3.21 | 31.64 | 8.93 | 78 |
| Specimen Types | Experiment Result JQ0.2BL (kJ·m−2) | Simulation Result J (kJ·m−2) | Error (%) |
|---|---|---|---|
| SENB20 (without side grooves) | 107 | 112.5 | 4.21 |
| SENB20 (with side grooves) | 102 | 96.2 | 5.69 |
| SENB18 (without side grooves) | 126 | 120.8 | 4.13 |
| SENB18 (with side grooves) | 108 | 104.1 | 3.61 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Hao, W.; Xie, J.; He, F.; Wang, F.; Huo, C. Stress Triaxial Constraint and Fracture Toughness Properties of X90 Pipeline Steel. Metals 2022, 12, 72. https://doi.org/10.3390/met12010072
Wang P, Hao W, Xie J, He F, Wang F, Huo C. Stress Triaxial Constraint and Fracture Toughness Properties of X90 Pipeline Steel. Metals. 2022; 12(1):72. https://doi.org/10.3390/met12010072
Chicago/Turabian StyleWang, Peng, Wenqian Hao, Jiamiao Xie, Fang He, Fenghui Wang, and Chunyong Huo. 2022. "Stress Triaxial Constraint and Fracture Toughness Properties of X90 Pipeline Steel" Metals 12, no. 1: 72. https://doi.org/10.3390/met12010072
APA StyleWang, P., Hao, W., Xie, J., He, F., Wang, F., & Huo, C. (2022). Stress Triaxial Constraint and Fracture Toughness Properties of X90 Pipeline Steel. Metals, 12(1), 72. https://doi.org/10.3390/met12010072






