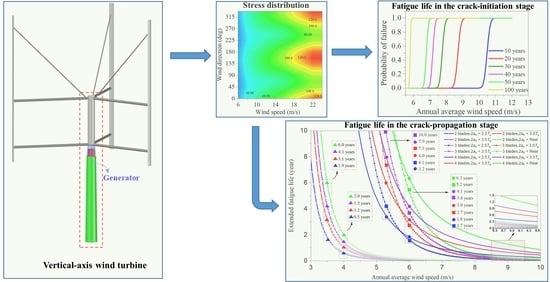
Effects of Blade Numbers on Wind-Induced Fatigue Lives of Straight-Bladed Vertical-Axis Wind-Turbine Tower Bases
Abstract
:1. Introduction
2. Methodology
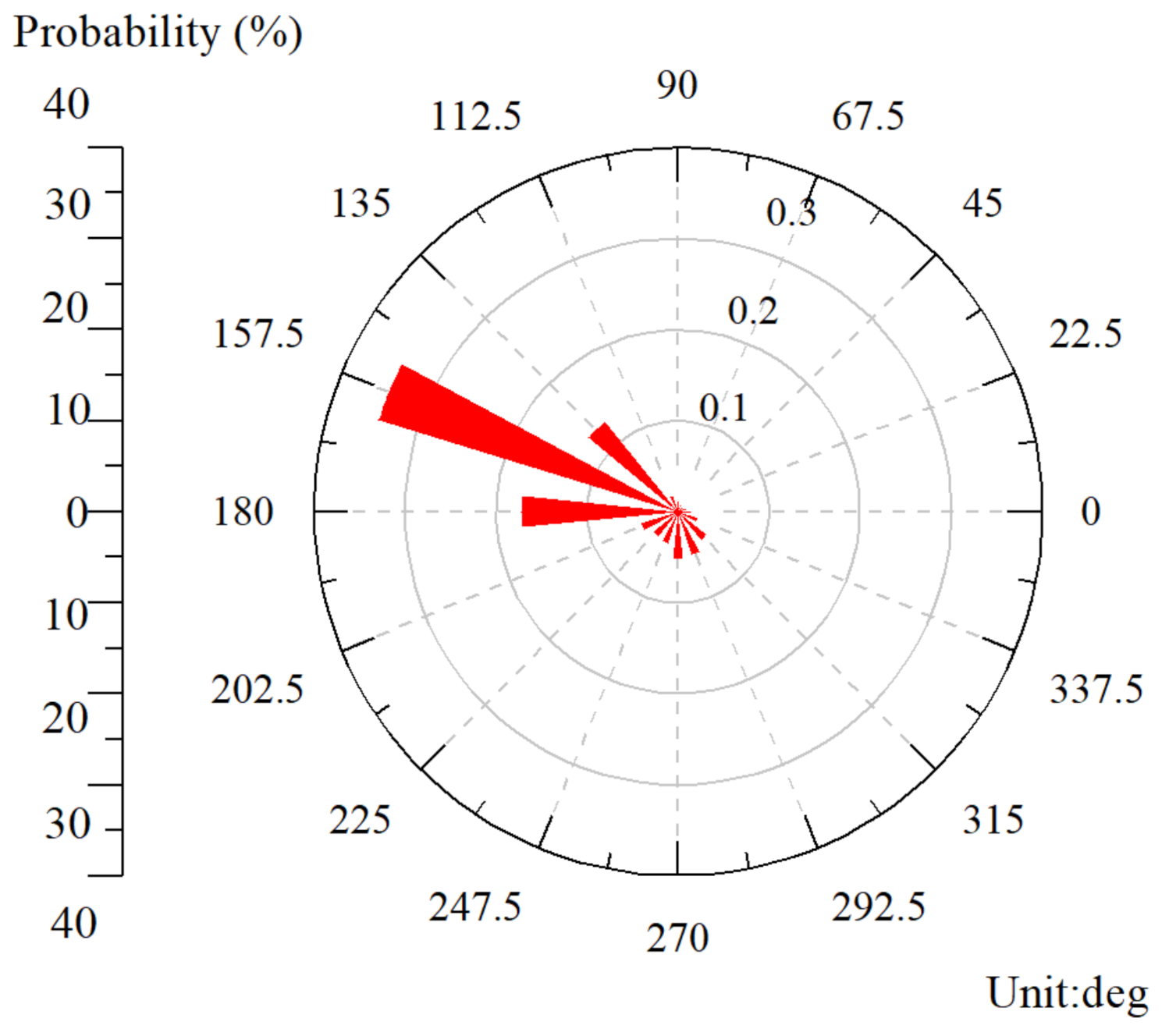
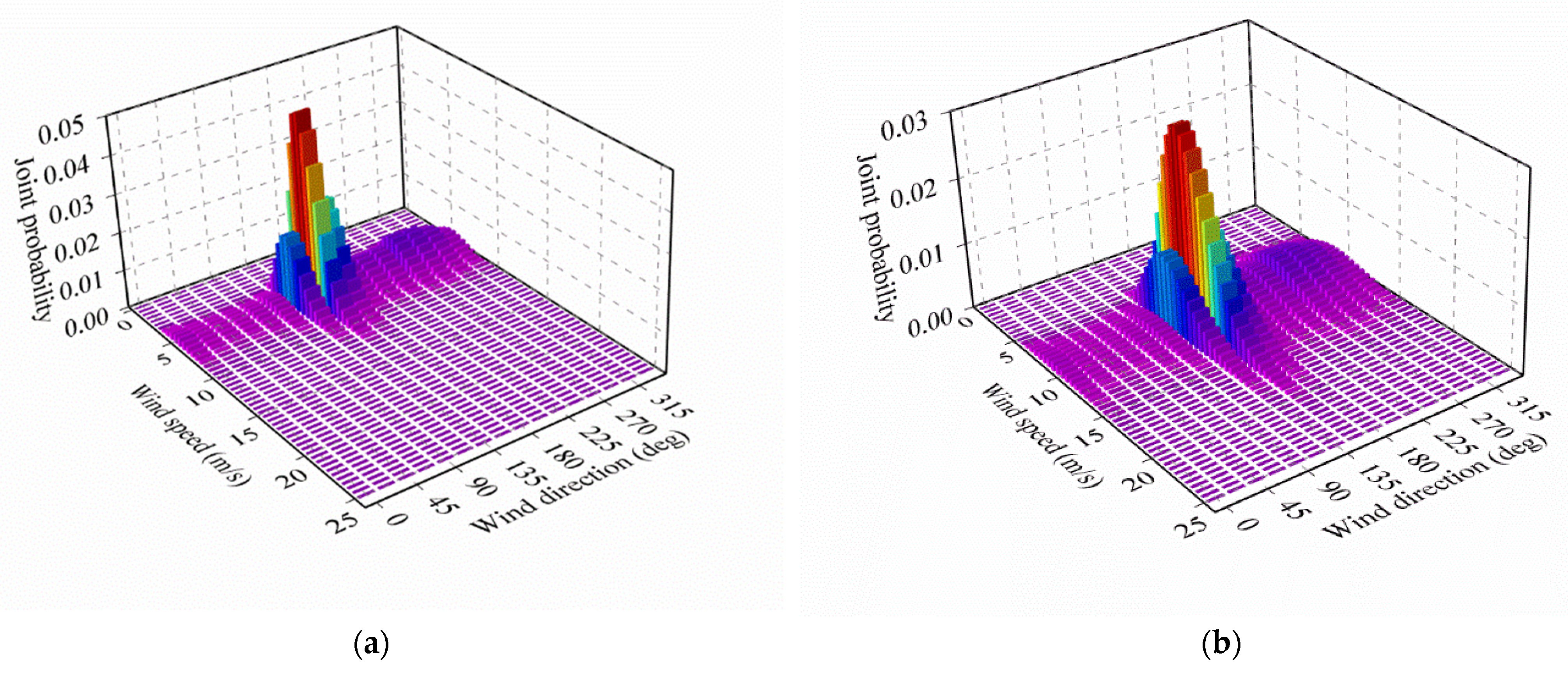
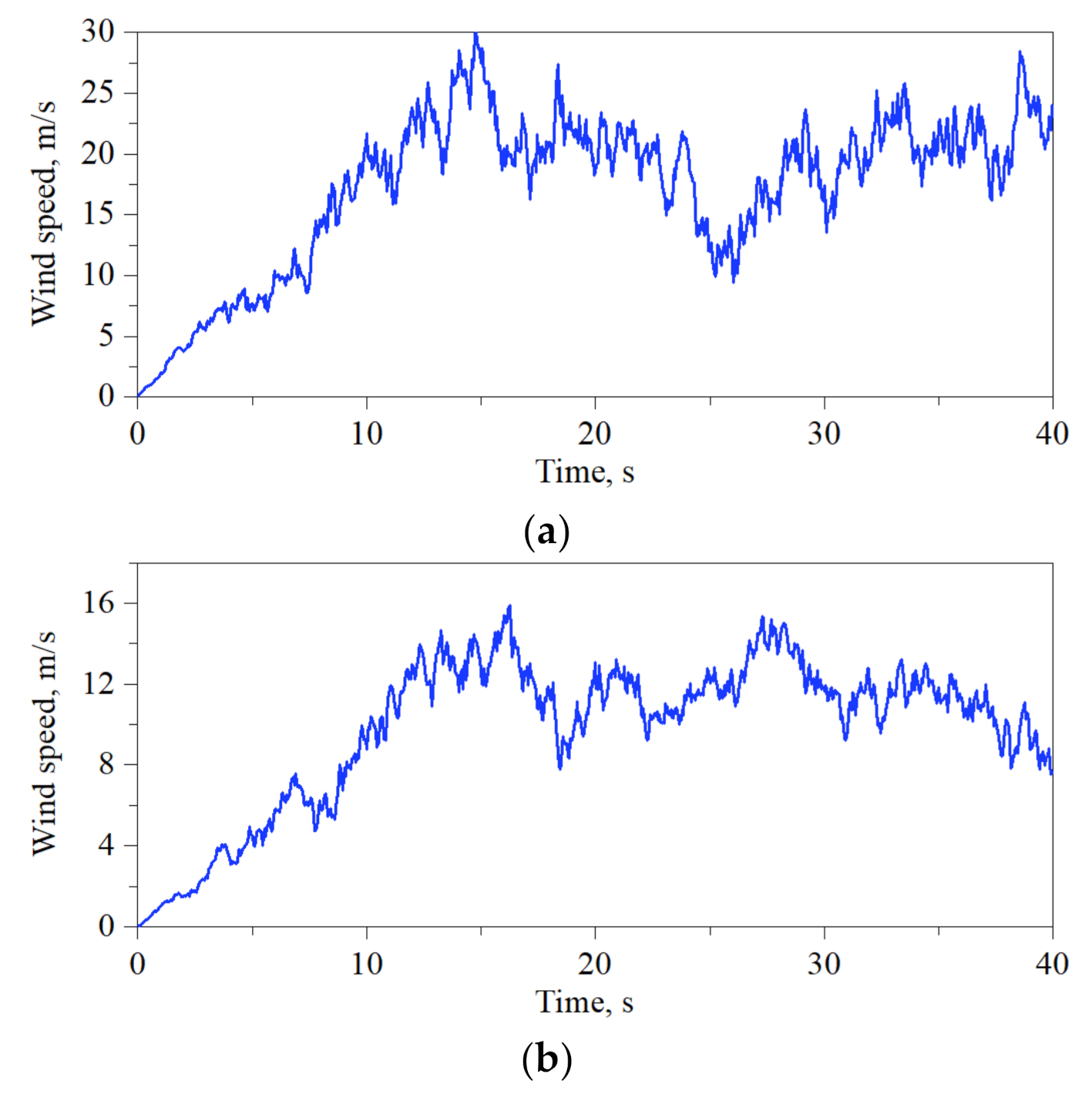
2.1. Wind-Field Simulation Method
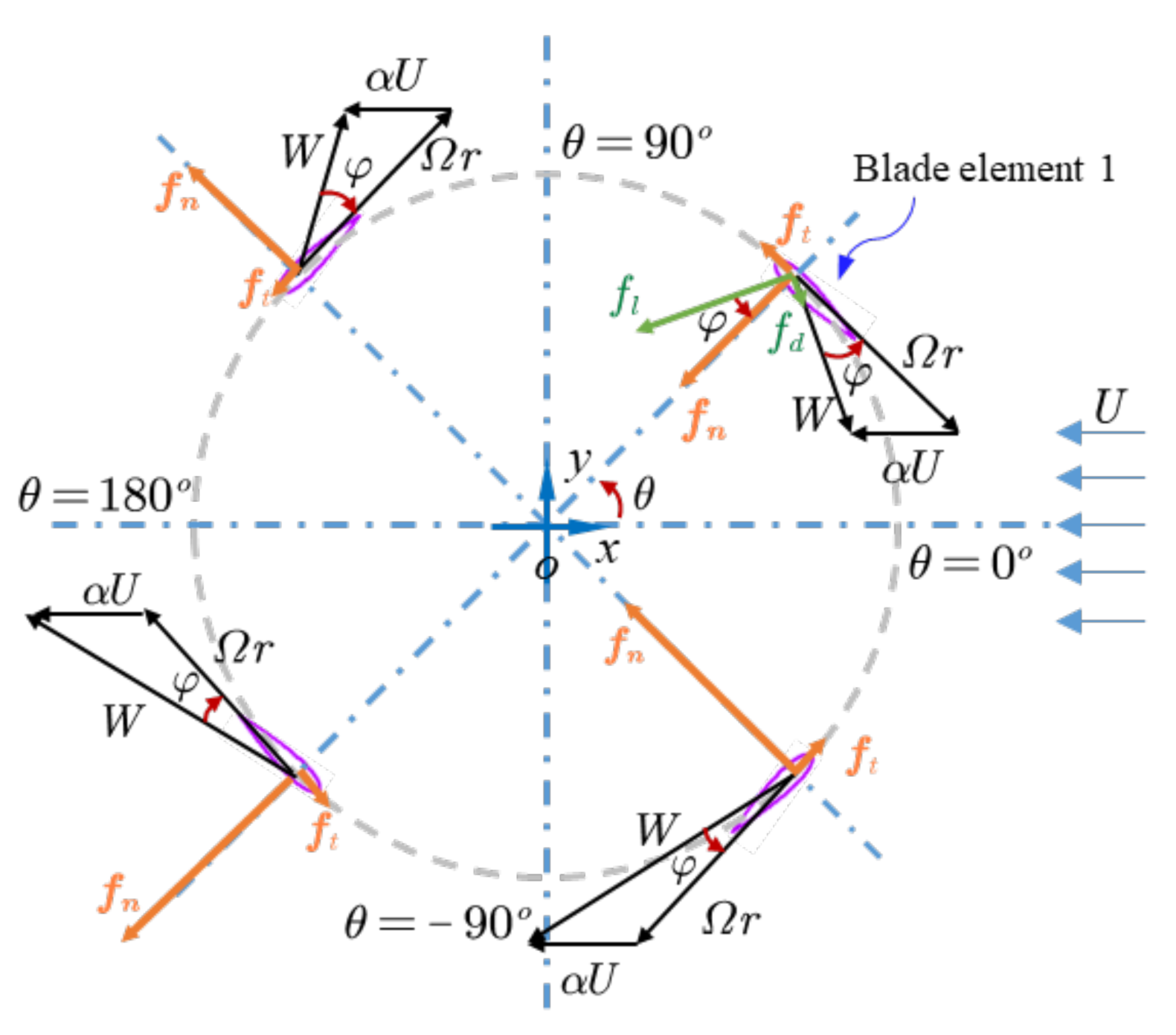
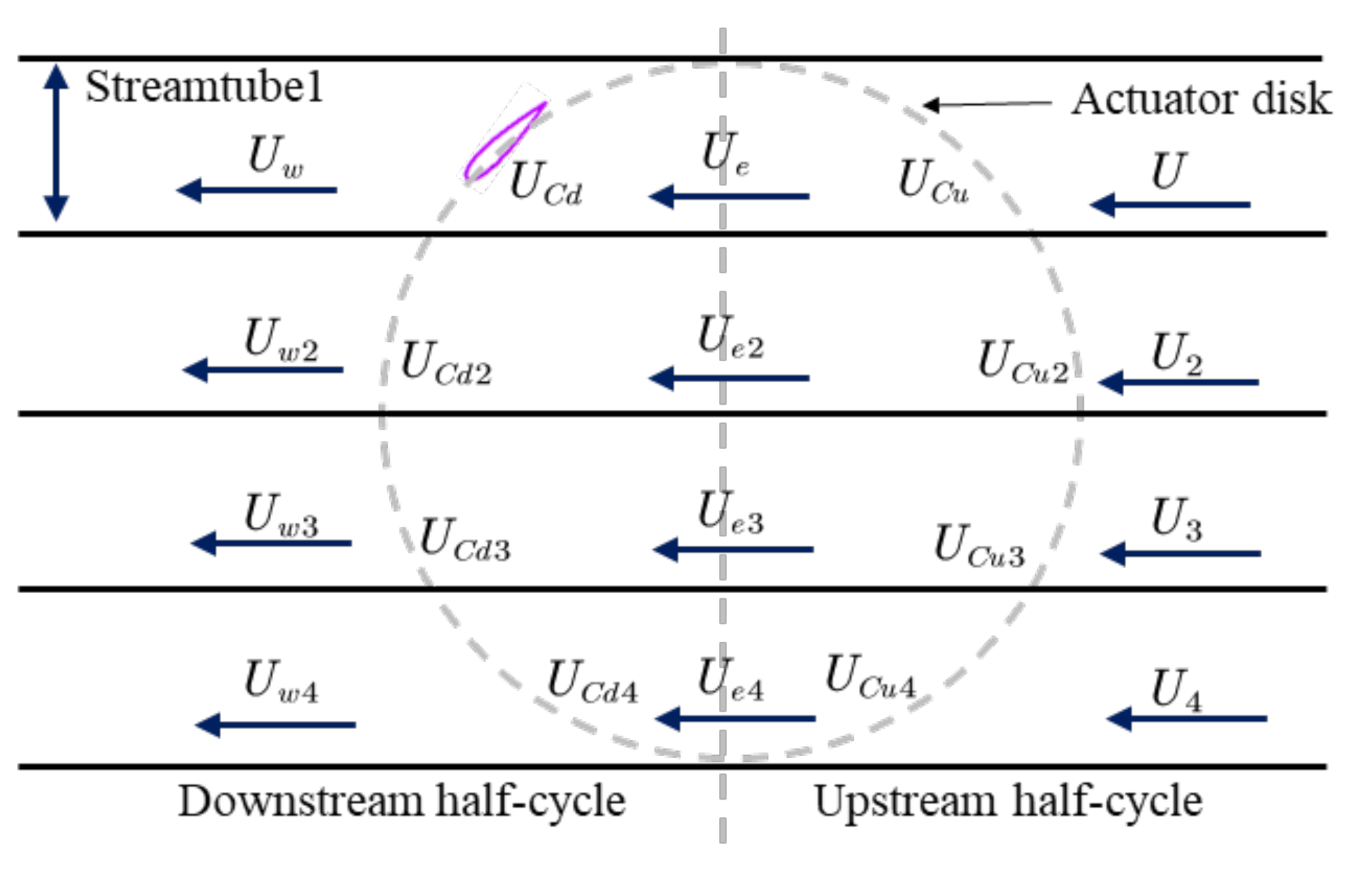
2.2. Aerodynamic Loading Calculation Method for VAWTs
3. VAWT Models
3.1. Design of Straight-Bladed VAWTs
3.2. Control Strategy for VAWTs
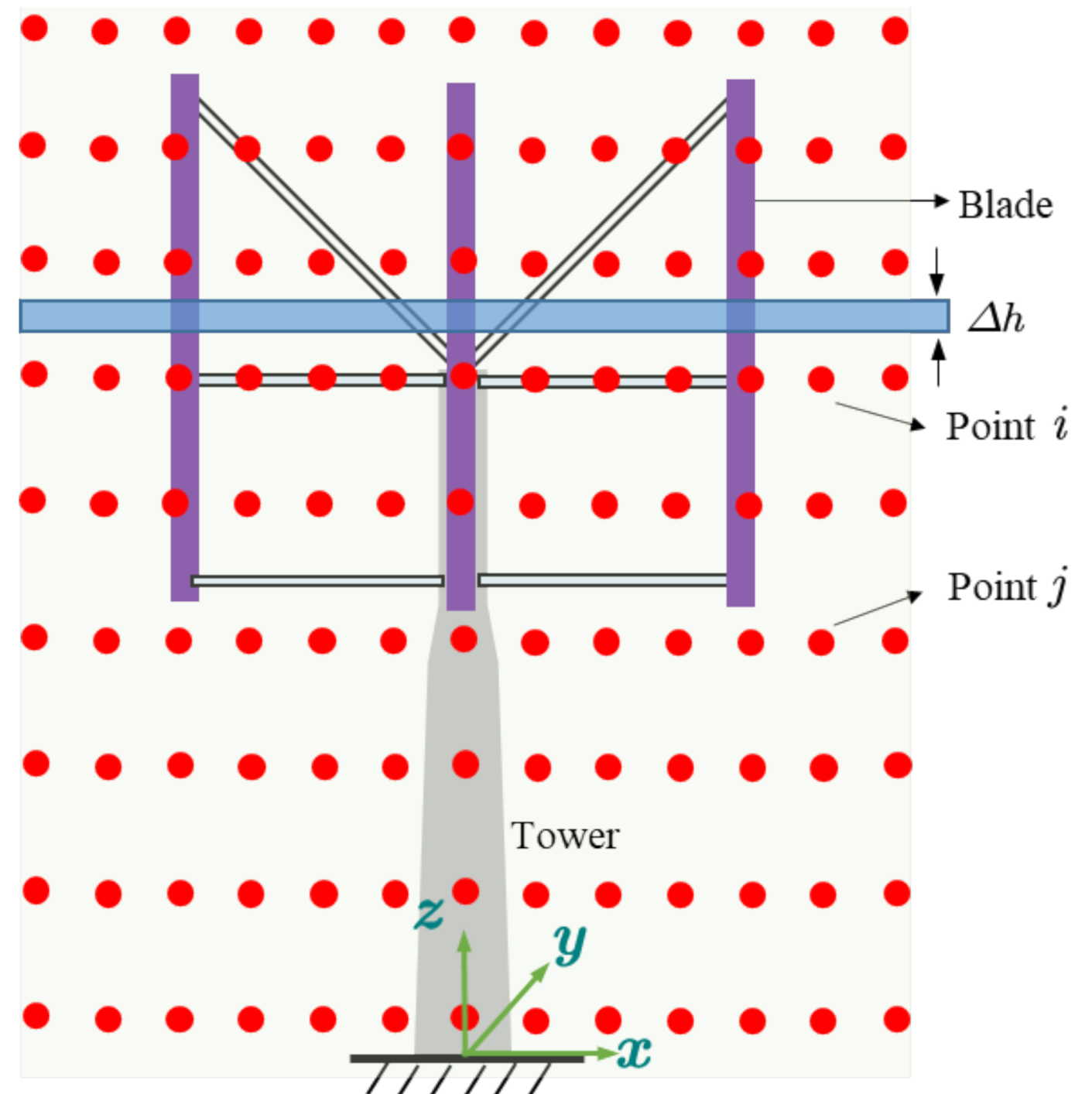
3.3. Numerical Models for VAWTs and Wind Field
4. Procedure for Fatigue-Life Assessment
4.1. Fatigue Life in Crack-Initiation Stage
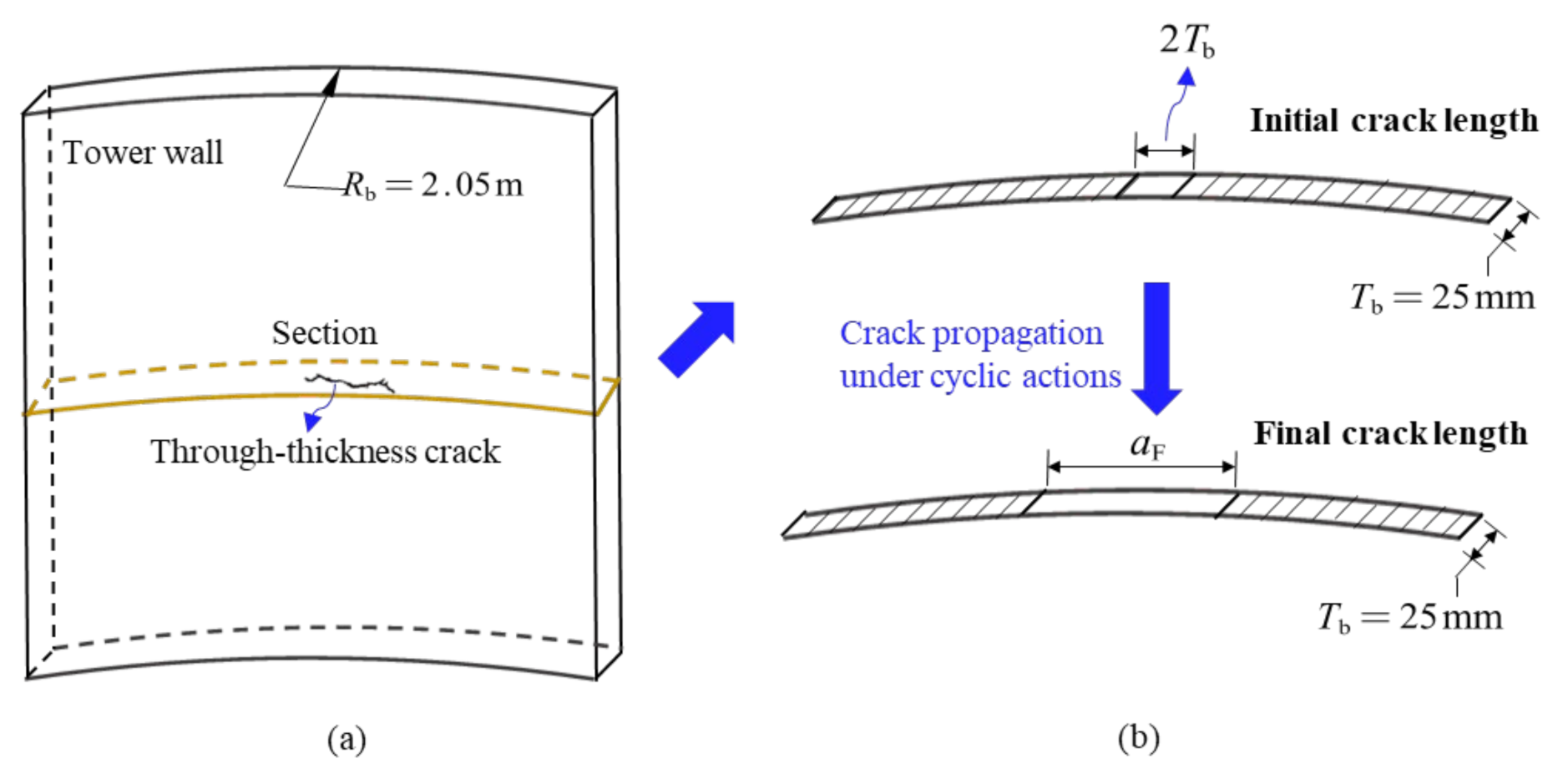
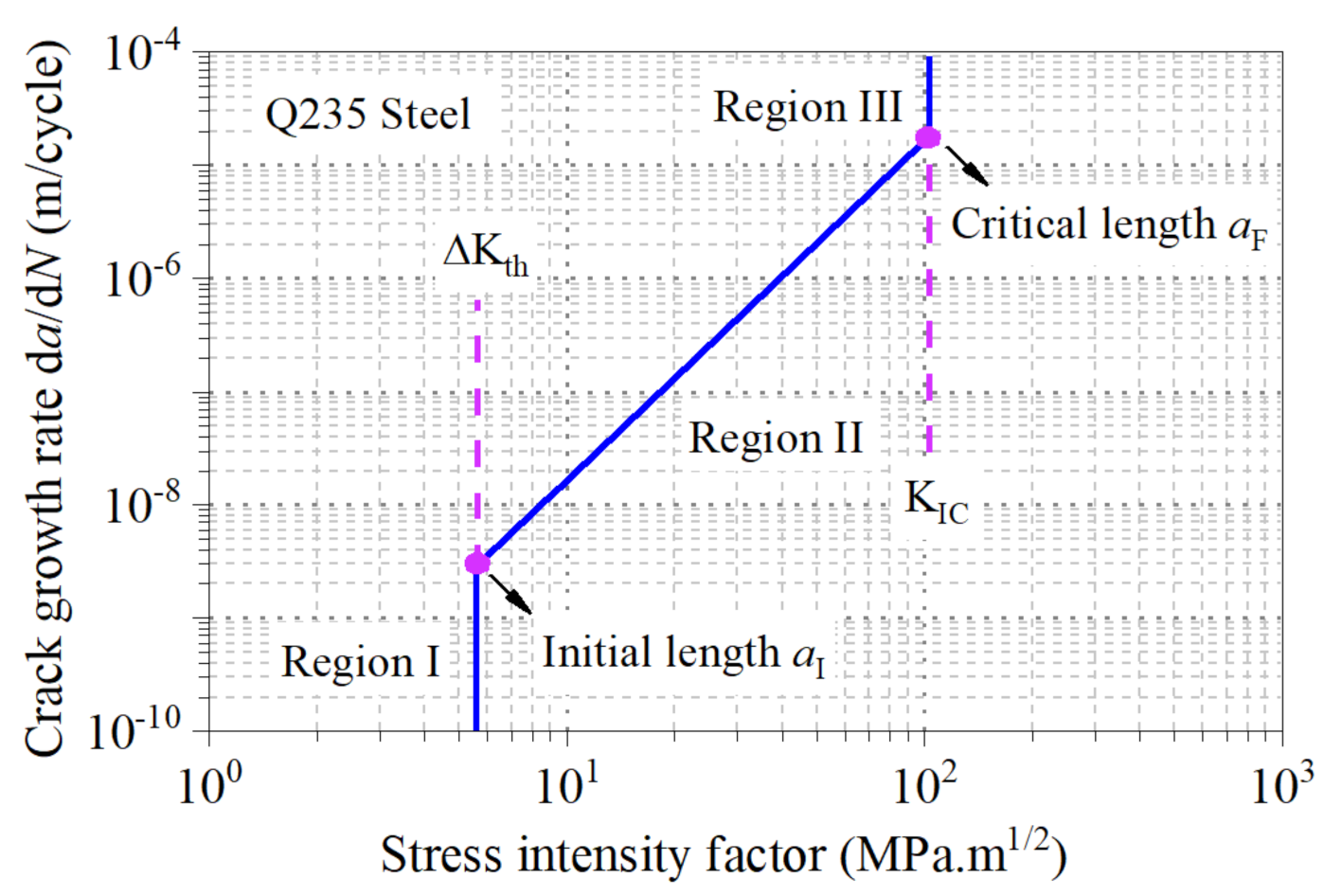
4.2. Fatigue Life in Crack-Propagation Stage
5. Results and Discussion
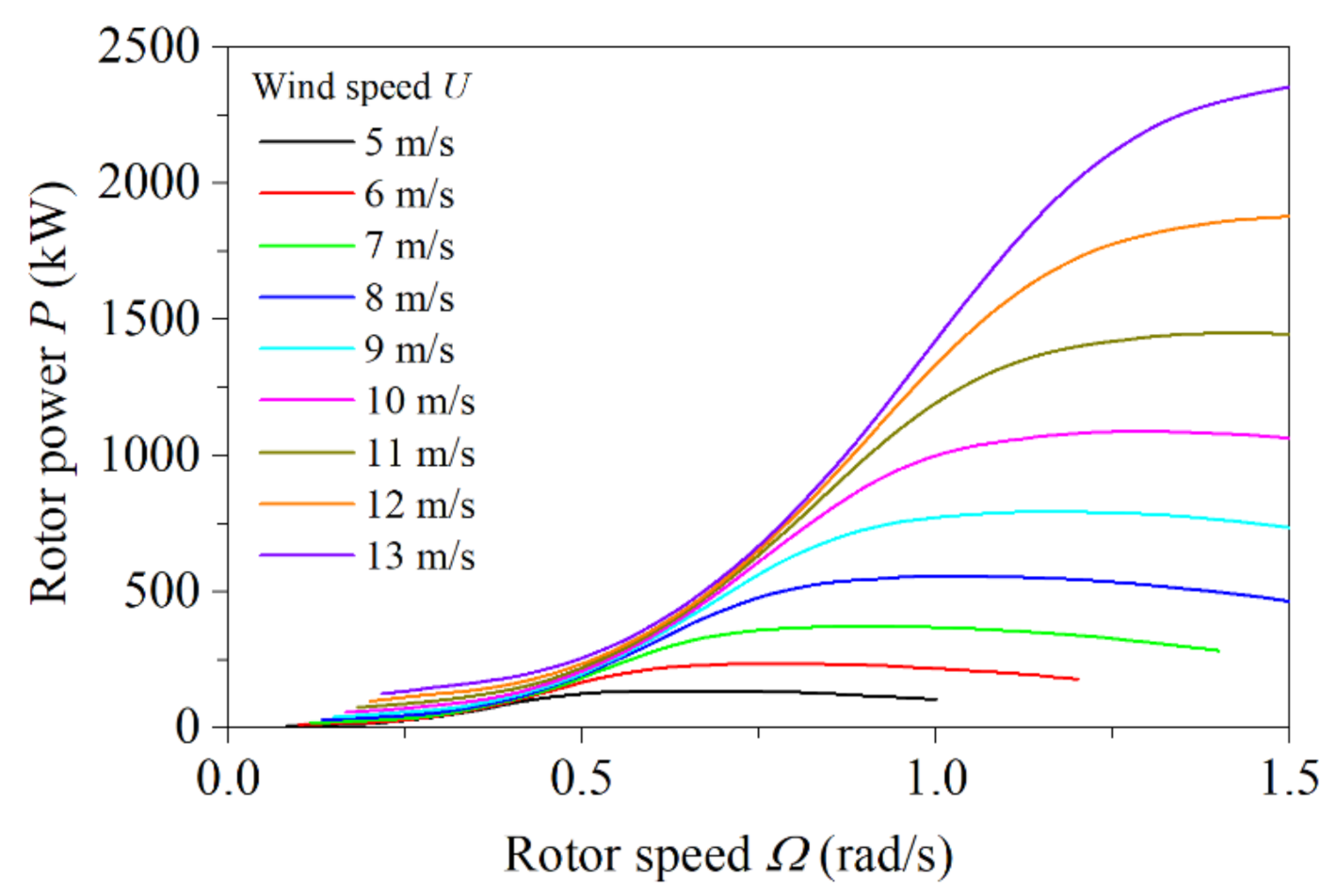
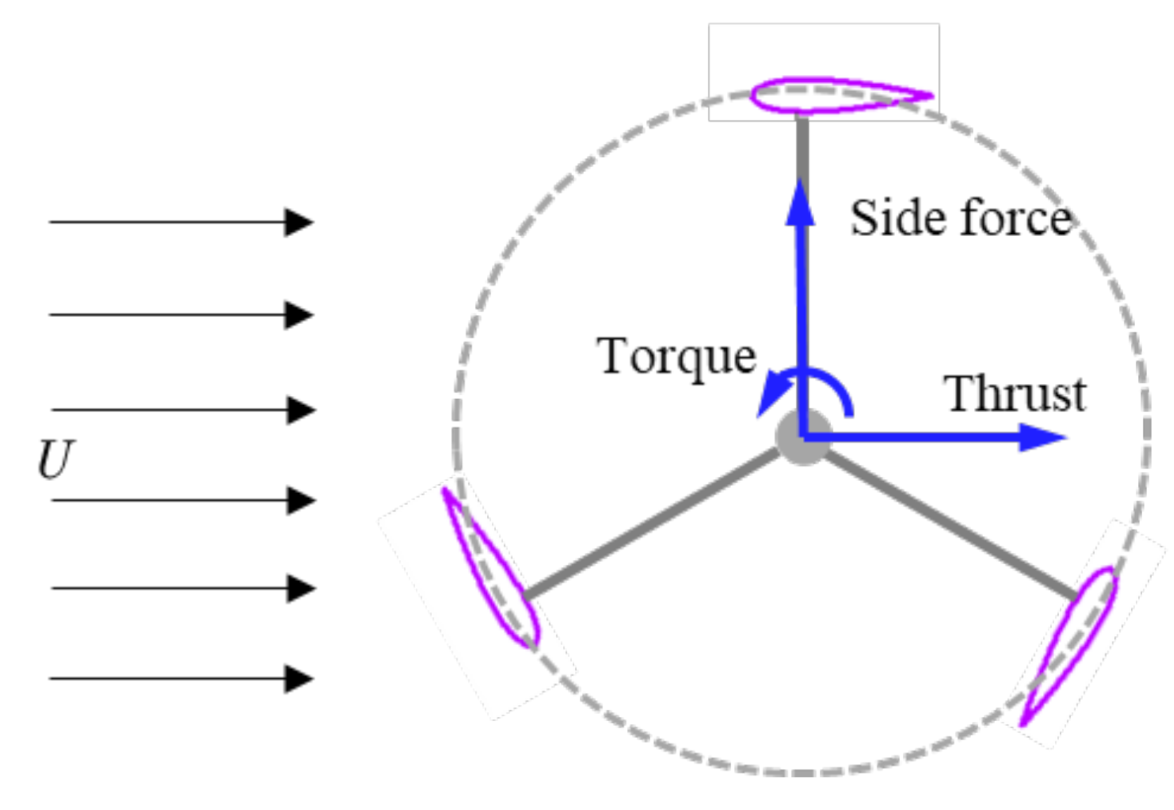
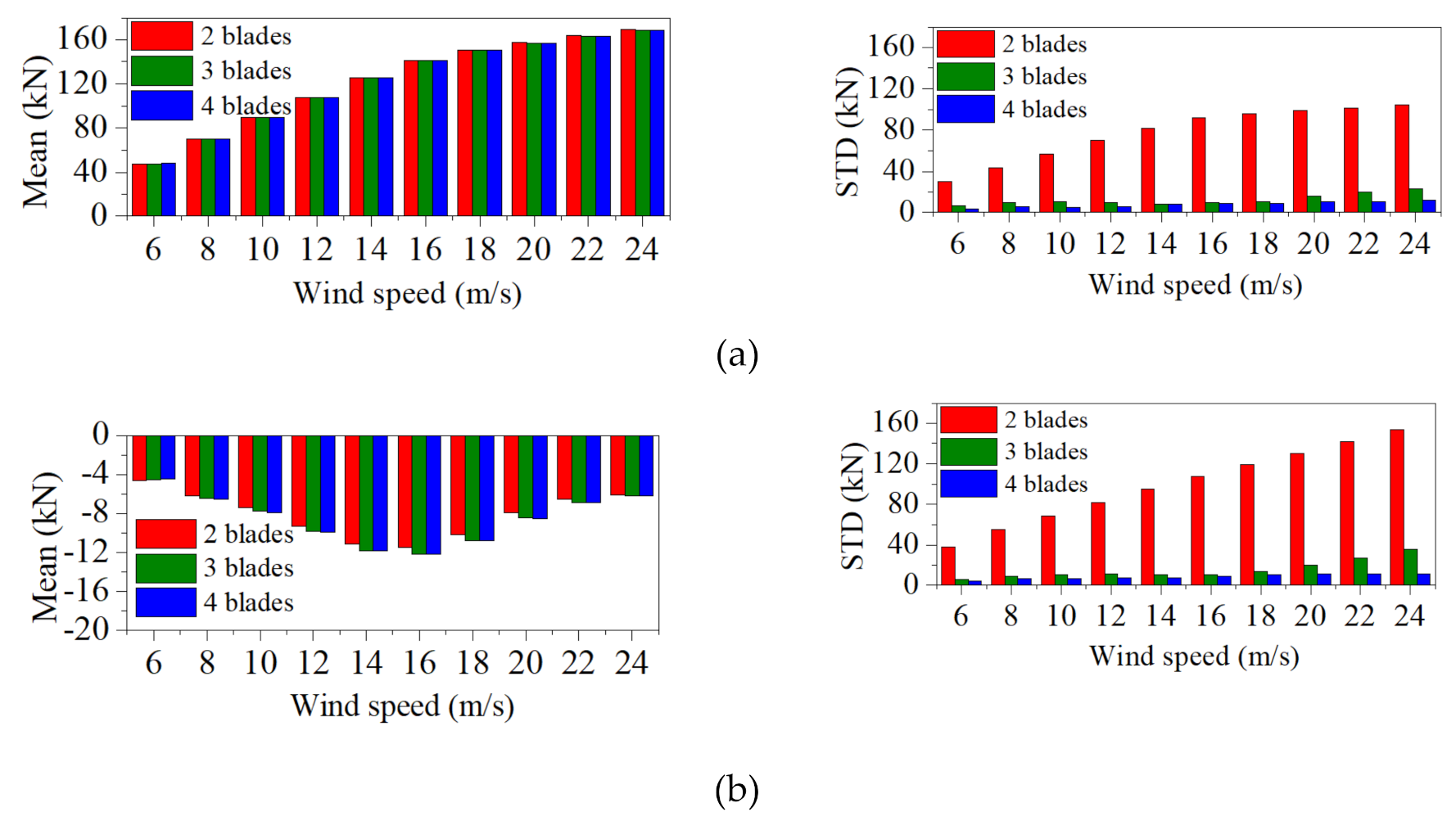
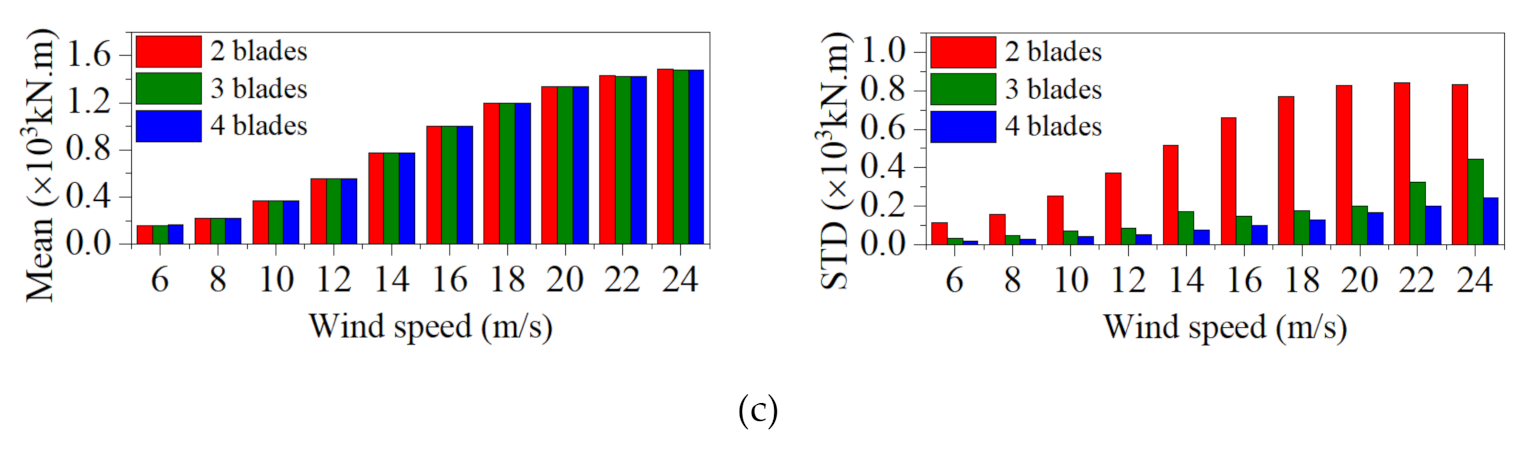
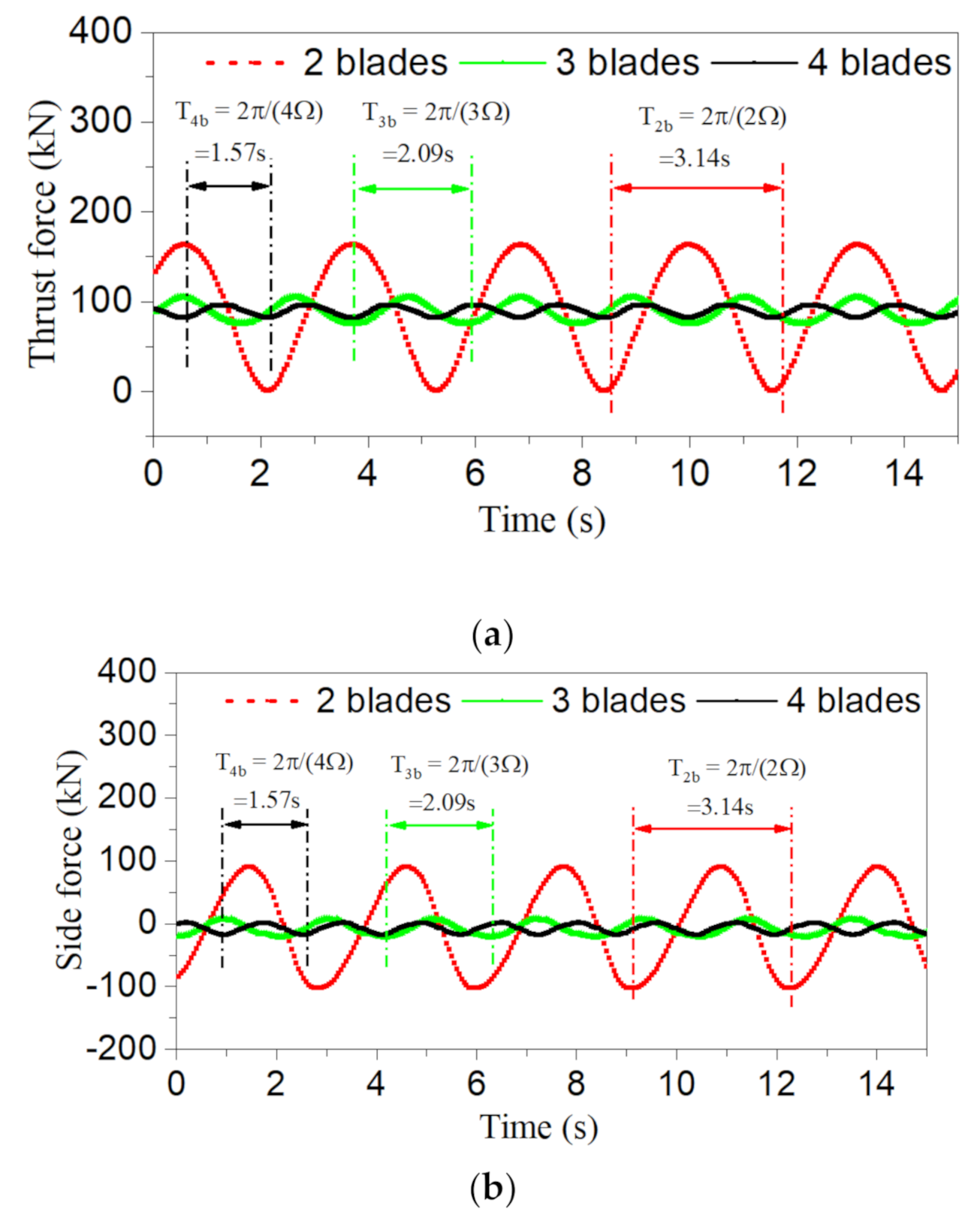
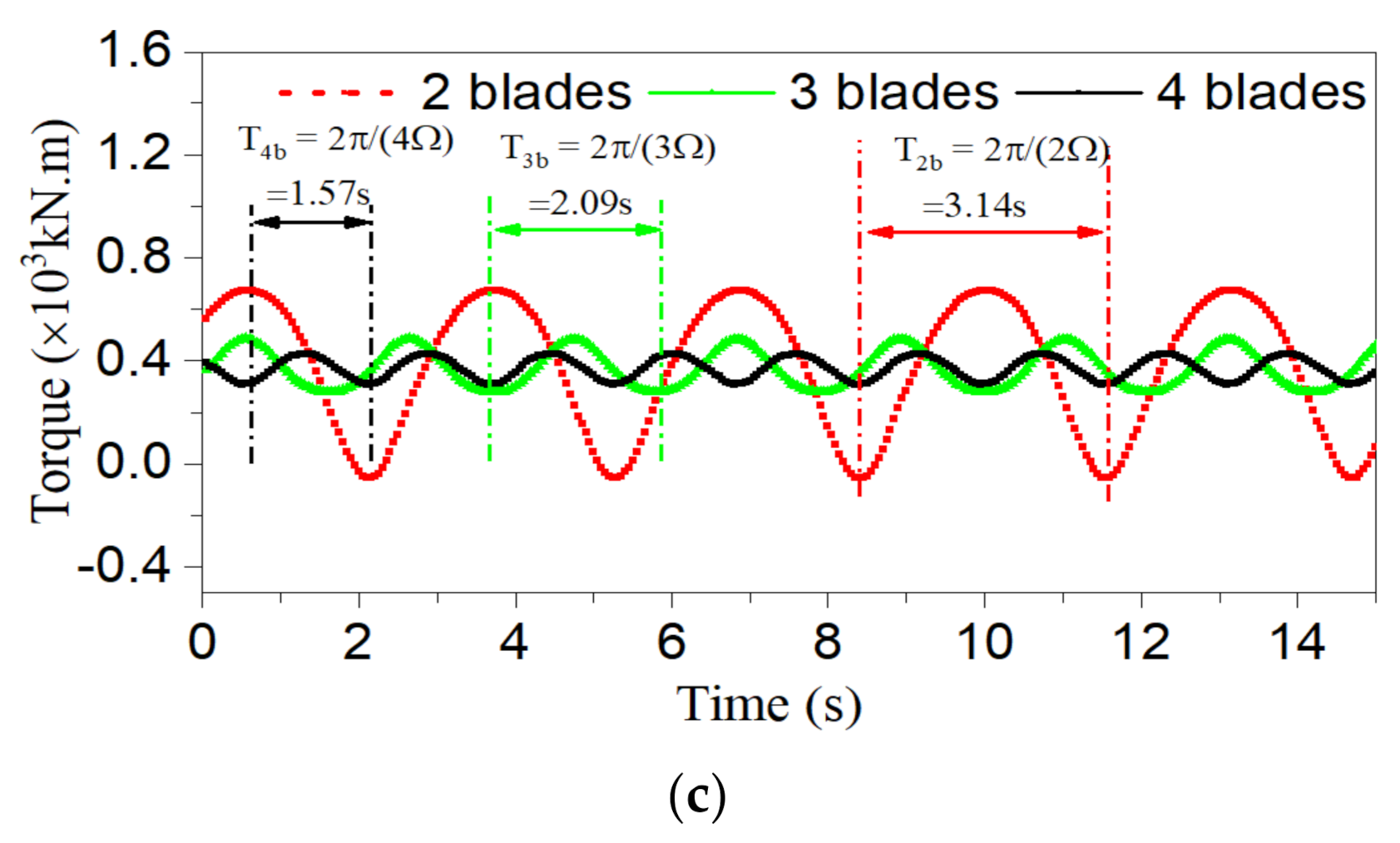
5.1. Aerodynamic-Loading Characteristics of Two-to-Four-Bladed VAWTs
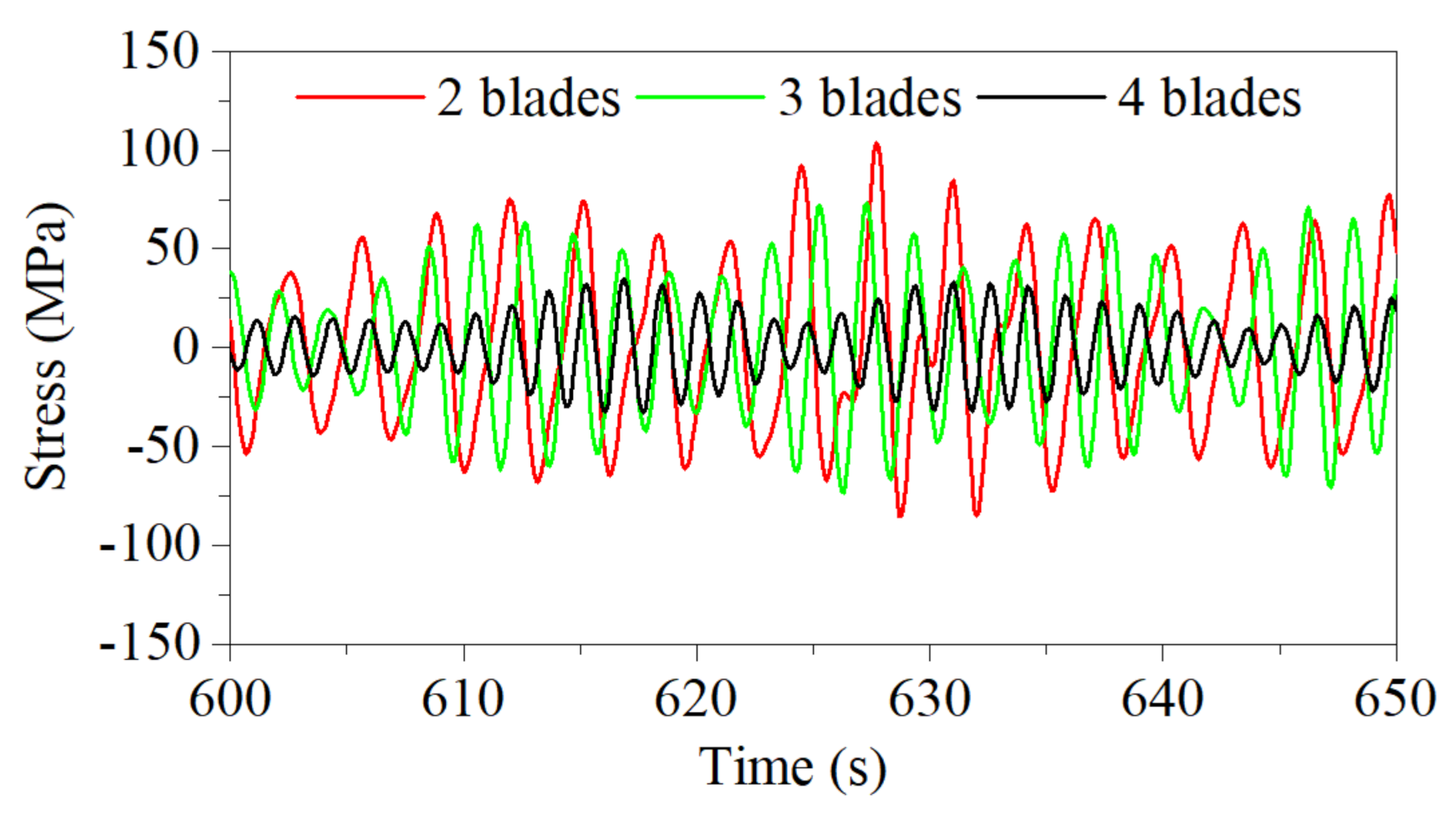
5.2. Stress Response at Location of Critical Fatigue Damage
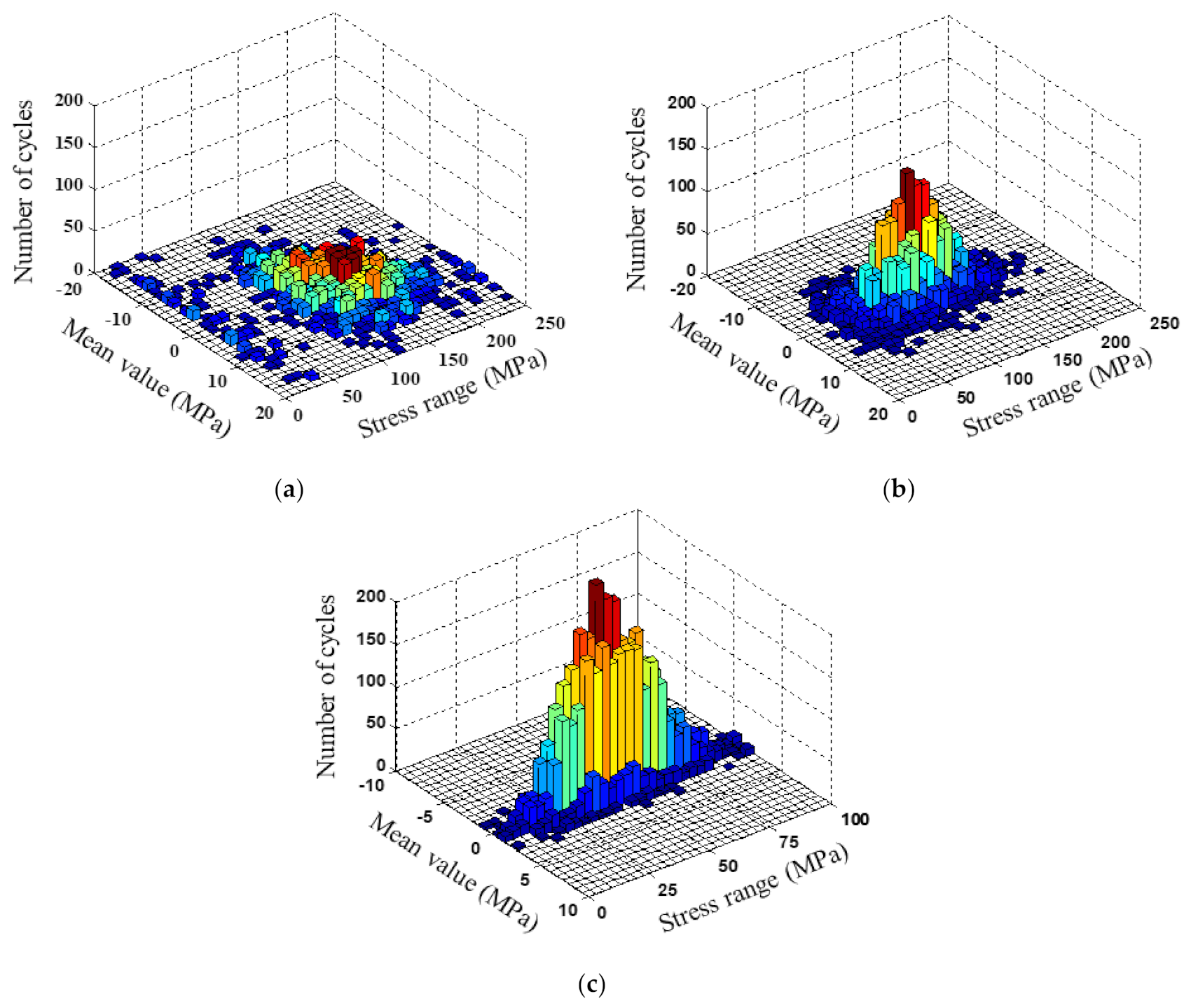
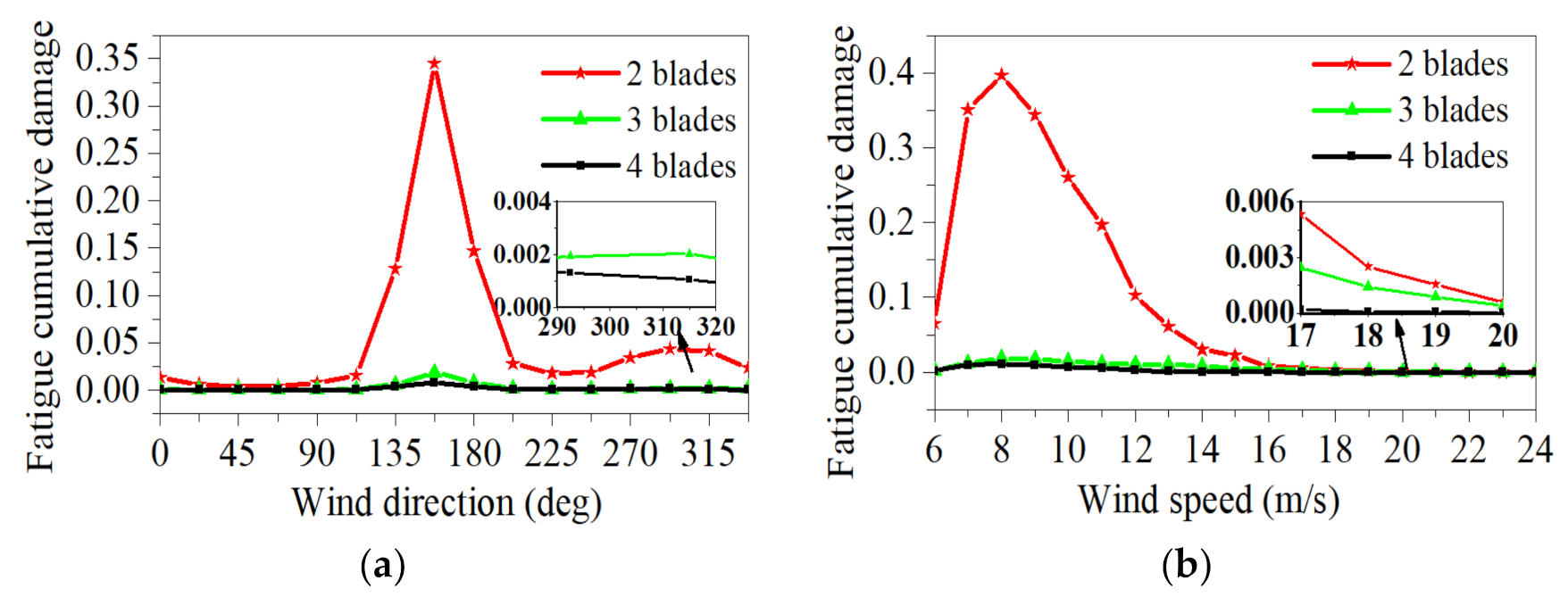
5.3. Fatigue-Life Evaluation in Crack-Initiation Stage
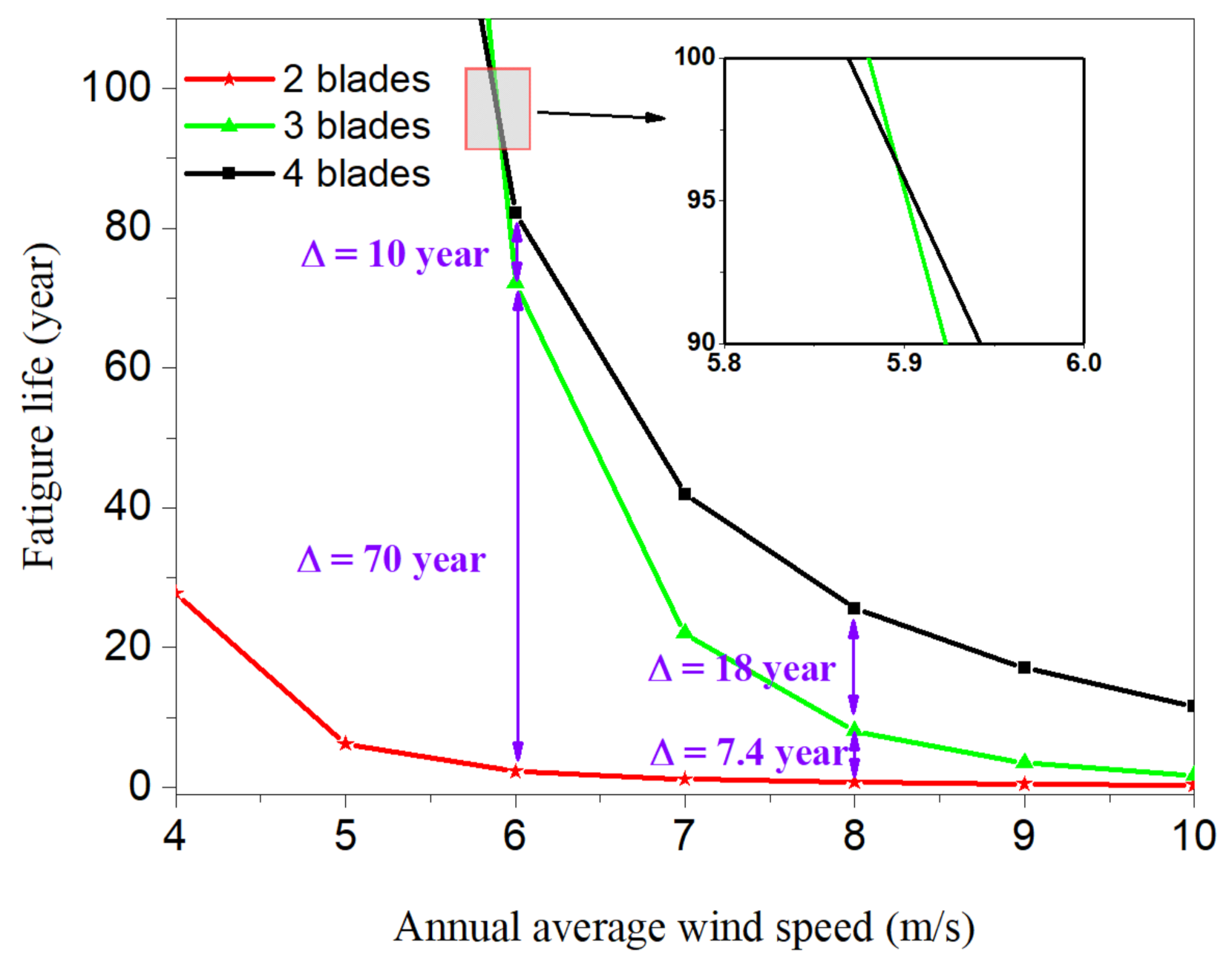
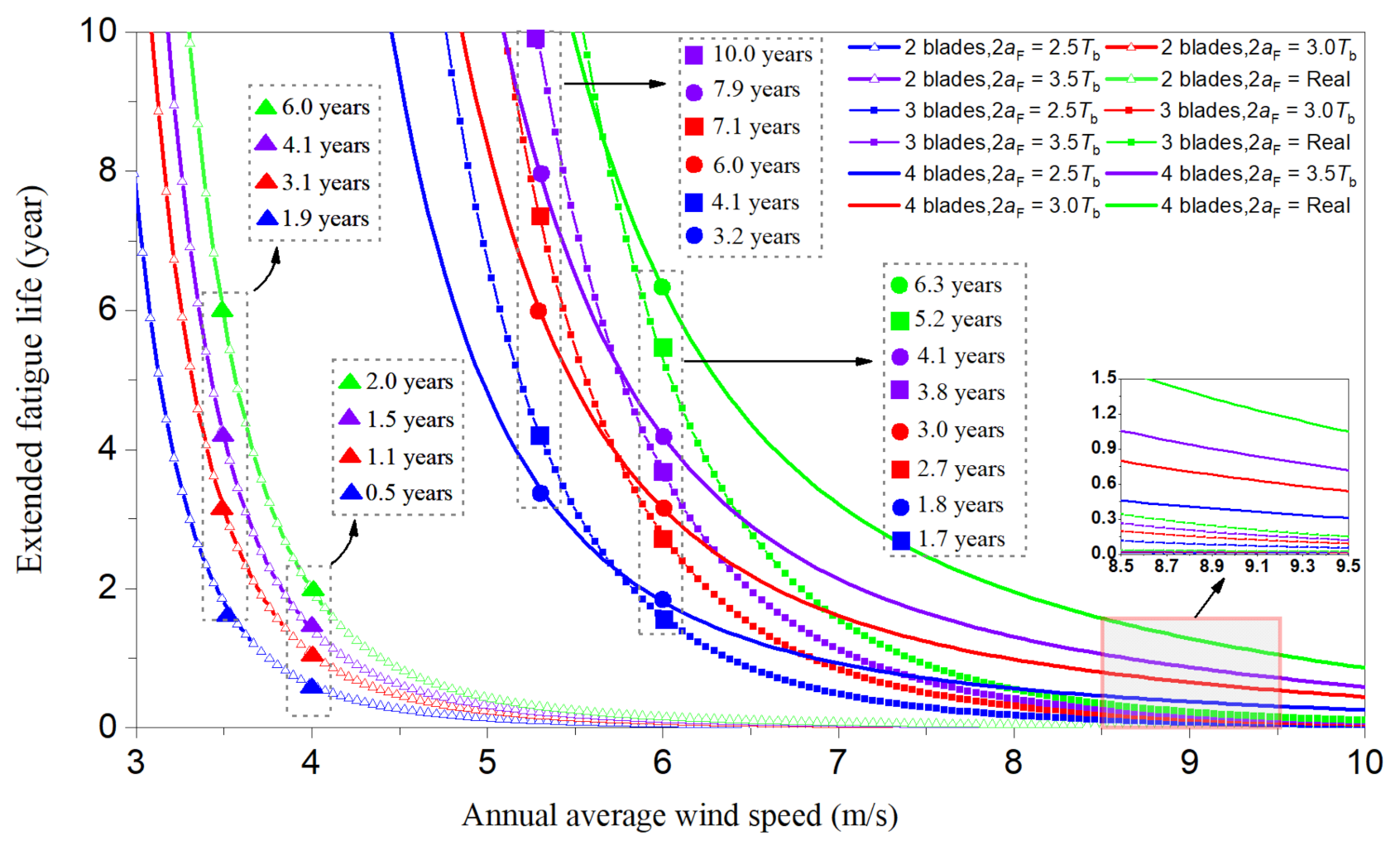
5.4. Fatigue-Life Evaluation in Crack-Propagation Stage
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviation
| [-] | Induced coefficient | |
| [-] | Induced coefficient at the upstream half-cycle | |
| [-] | Induced coefficient at the downstream half-cycle | |
| [m/s] | Turbulent wind speed component | |
| [m/s] | Mean wind speed component | |
| [-] | Correlation coefficient | |
| [Hz] | Frequency component of wind speed | |
| [m] | Spatial distance between field points | |
| [m] | Coherence parameter | |
| [m/s] | Wind speed at the reference height | |
| [m] | Reference height | |
| [m2/s ] | KAIMAL spectrum at point | |
| [m2/s] | KAIMAL spectrum at point | |
| [m2/s] | Cross-spectrum at points and | |
| [m2/s] | Cross-spectrum matrix | |
| [m2/s] | Lower triangular matrix | |
| [Hz] | Frequency interval | |
| [rad] | Phase angle | |
| [m] | Height | |
| [-] | Ground roughness index | |
| [m/s] | Annual average wind speed | |
| [deg] | Wind direction | |
| [rad/s] | Rotor rotation speed | |
| [m/s] | Induced wind speed | |
| [rad] | Azimuthal angle | |
| [m] | Rotor radius | |
| [-] | Blade number | |
| [m] | Chord length | |
| [m/s] | Wind speed seen by blades | |
| [m/s] | Wind speed seen by blades at the upstream half-cycle | |
| [m/s] | Wind speed seen by blades at the downstream half-cycle | |
| [rad] | Angle of attack | |
| [rad] | Angle of attack at the upstream half-cycle | |
| [rad] | Angle of attack at the downstream half-cycle | |
| [m/s] | Far-field wind speed | |
| [m/s] | Induced wind speed | |
| [m/s] | Wind speed at the middle of disk | |
| [-] | Normal force coefficient at the upstream half-cycle | |
| [-] | Normal force coefficient at the downstream half-cycle | |
| [-] | Tangential force coefficient at the upstream half-cycle | |
| [-] | Tangential force coefficient at the downstream half-cycle | |
| [-] | Power coefficient | |
| [MW] | Power of wind turbine | |
| [kg/m3] | Air density | |
| [m] | Blade length | |
| [-] | Rotor solidity | |
| [MPa] | Yield stress | |
| [-] | Tip speed ratio | |
| [-] | Reynolds number | |
| [MPa] | Effective stress range | |
| [-] | Occurrence probability | |
| [cycle] | Cycle number | |
| [-] | Material parameter | |
| [hr] | Simulation time | |
| [year] | Expected fatigue life under the special case | |
| [-] | Fatigue-damage index | |
| [cycle] | Cycle number during -hr | |
| [year] | Fatigue life | |
| [] | Coefficient of crack-growth rate | |
| [-] | Material constant | |
| [MPa ] | Stress intensity factor | |
| [-] | Dimensionless function of geometry and the relative crack length | |
| [mm] | Crack length | |
| [mm] | Initial crack length | |
| [mm] | Final crack length | |
| [m] | Tower-wall curve radius | |
| [mm] | Tower-wall thickness | |
| [cycle] | Cycle number corresponding to the initial crack length | |
| [cycle] | Cycle number corresponding to the final crack length | |
| [cycle] | Cycle number required for the crack-propagation stage | |
| [MPa] | Maximum tensile stress |
References
- Exajoules, C.; Emissions, C.D. Statistical Review of World Energy June 2020; BP: London, UK, 2006. [Google Scholar]
- GWEC. Global Wind Energy Council. Global Wind Report 2021; GWEC: Brussels, Belgium, 2019. [Google Scholar]
- Barnes, A.; Hughes, B. Determining the impact of VAWT farm configurations on power output. Renew. Energy 2019, 143, 1111–1120. [Google Scholar] [CrossRef]
- Zheng, H.D.; Zheng, X.Y.; Zhao, S.X. Arrangement of clustered straight-bladed wind turbines. Energy 2020, 200, 117563. [Google Scholar] [CrossRef]
- Jonkman, J.M.; Buhl, M.L., Jr. FAST User’s Guide; National Renewable Energy Laboratory: Golden, CO, USA, 2005 October; pp. 365–366. [Google Scholar]
- Garrad Hassan, G.L. Bladed User Manual Version 4.2; Garrad Hassan & Partners Ltd.: Bristol, UK, 2012. [Google Scholar]
- Orcina, L.T.C. OrcaFlex User Manual: OrcaFlex Version 10.2 c; Daltongate Ulverston: Cumbria, UK, 2018. [Google Scholar]
- Larsen, T.J.; Hansen, A.M. How 2 HAWC2, the User’s Manual; Risø National Laboratory: Roksilde, Denmark, 2007. [Google Scholar]
- Balduzzi, F.; Bianchini, A.; Maleci, R.; Ferrara, G.; Ferrari, L. Critical issues in the CFD simulation of Darrieus wind turbines. Renew. Energy 2016, 85, 419–435. [Google Scholar]
- Zanforlin, S.; Nishino, T. Fluid dynamic mechanisms of enhanced power generation by closely spaced vertical axis wind turbines. Renew. Energy 2016, 99, 1213–1226. [Google Scholar]
- Strickland, J.H.; Webster, B.T.; Nguyen, T. A vortex model of the Darrieus turbine: An analytical and experimental study. J. Fluids Eng. 1979, 101, 500–505. [Google Scholar] [CrossRef]
- Chen, N. Aerothermodynamics of Turbomachinery: Analysis and Design; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Hirsch, I.H.; Mandal, A.C. A cascade theory for the aerodynamic performance of Darrieus wind turbines. Wind. Eng. 1987, 11, 164–175. [Google Scholar]
- Madsen, H.A.; Paulsen, U.S.; Vitae, L. Analysis of VAWT aerodynamics and design using the Actuator Cylinder flow model. J. Phys. Conf. Ser. 2014, 555, 012065. [Google Scholar] [CrossRef] [Green Version]
- Paraschivoiu, I. Double-Multiple Streamtube Model for Darrieus in Turbines; NASA Lewis Research Center: Cleveland, OH, USA, 1981. [Google Scholar]
- Islam, M.; Ting, D.S.K.; Fartaj, A. Aerodynamic models for Darrieus-type straight-bladed vertical axis wind turbines. Renew. Sustain. Energy Rev. 2008, 12, 1087–1109. [Google Scholar] [CrossRef]
- Cheng, Z.; Madsen, H.A.; Gao, Z.; Moan, T. Effect of the number of blades on the dynamics of floating straight-bladed vertical axis wind turbines. Renew. Energy 2017, 101, 1285–1298. [Google Scholar] [CrossRef]
- Zheng, X.Y.; Zheng, H.D.; Lei, Y.; Chen, H. Nonlinear stochastic responses of a newly developed floating wind-solar-aquaculture system. Ocean. Eng. 2021, 241, 110055. [Google Scholar] [CrossRef]
- Zheng, H.D.; Zheng, X.Y.; Lei, Y.; Li, D.-A.; Xiang, C. Experimental validation on the dynamic response of a novel floater uniting a vertical-axis wind turbine with a steel fishing cage. Ocean. Eng. 2022, 243, 110257. [Google Scholar] [CrossRef]
- Liu, L.; Guo, Y.; Zhao, H.; Tang, Y. Motions of a 5 MW floating VAWT evaluated by numerical simulations and model tests. Ocean. Eng. 2017, 144, 21–34. [Google Scholar] [CrossRef]
- Möllerström, E.; Gipe, P.; Beurskens, J.; Ottermo, F. A historical review of vertical axis wind turbines rated 100 kW and above. Renew. Sustain. Energy Rev. 2019, 105, 1–13. [Google Scholar]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Nijssen, R.P.L. Fatigue Life Prediction and Strength Degradation of Wind Turbine Rotor Blade Composites; Contractor Report SAND2006-7810P; Sandia National Laboratories: Albuquerque, NM, USA, 2006. [Google Scholar]
- Harte, R.; Van Zijl, G.P. Structural stability of concrete wind turbines and solar chimney towers exposed to dynamic wind action. J. Wind. Eng. Ind. Aerodyn. 2007, 95, 1079–1096. [Google Scholar] [CrossRef]
- Paredes, J.A.; Barbat, A.H.; Oller, S. A compression–tension concrete damage model, applied to a wind turbine reinforced concrete tower. Eng. Struct. 2011, 33, 3559–3569. [Google Scholar] [CrossRef]
- Do, T.Q.; van de Lindt, J.W.; Mahmoud, H. Fatigue life fragilities and performance-based design of wind turbine tower base connections. J. Struct. Eng. 2015, 141, 04014183. [Google Scholar] [CrossRef]
- Huo, T.; Tong, L. An approach to wind-induced fatigue analysis of wind turbine tubular towers. J. Constr. Steel Res. 2020, 166, 105917. [Google Scholar] [CrossRef]
- Fu, B.; Zhao, J.; Li, B.; Yao, J.; Teifouet, A.R.M.; Sun, L.; Wang, Z. Fatigue reliability analysis of wind turbine tower under random wind load. Struct. Saf. 2020, 87, 101982. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. Wind Turbines-Part 1: Design Requirements, 3rd ed.; International Electrotechnical Commission: Geneva, Switzerland, 2006. [Google Scholar]
- Higham, N.J. Analysis of the Cholesky Decomposition of a Semi-Definite Matrix; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Goode, J.S.; van de Lindt, J.W. Development of a semiprescriptive selection procedure for reliability-based fatigue design of high-mast lighting structural supports. J. Perform. Constr. Facil. 2007, 21, 193–206. [Google Scholar] [CrossRef]
- Leishman, J.G.; Beddoes, T.S. A Semi-Empirical model for dynamic stall. J. Am. Helicopter Soc. 1989, 34, 3–17. [Google Scholar]
- Huse, E. Current Force on Individual Elements of Riser Arrays. In Proceedings of the Second International Offshore and Polar Engineering Conference, San Francisco, CA, USA, 14–19 June 1992. [Google Scholar]
- Borg, M.; Manuel, L.; Collu, M.; Liu, J. Long-term global performance analysis of a vertical-axis wind turbine supported on a semi-submersible floating platform. Int. Conf. Offshore Mech. Arct. Eng. 2015, 56574, V009T09A066. [Google Scholar]
- Cheng, Z.; Wang, K.; Gao, Z.; Moan, T. A comparative study on dynamic responses of spar-type floating horizontal and vertical axis wind turbines. Wind Energy 2017, 20, 305–323. [Google Scholar] [CrossRef] [Green Version]
- Higham, D.J.; Higham, N.J. MATLAB Guide; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2016. [Google Scholar]
- ASCE–American Wind Energy Association. Recommended Practice for Compliance of Large Land-Based Wind Turbine Support Structures; American Wind Energy Association: Reston, VA, USA; Washington, DC, USA, 2011. [Google Scholar]
- Zheng, X.; Zheng, H.; Lei, Y.; Li, Y.; Li, W. An offshore floating wind–solar–aquaculture system: Concept design and extreme response in survival conditions. Energies 2020, 13, 604. [Google Scholar] [CrossRef] [Green Version]
- Zheng, H.D.; Fan, J. Progressive collapse analysis of a truss transmission tower-line system subjected to downburst loading. J. Constr. Steel Res. 2022, 188, 107044. [Google Scholar] [CrossRef]
- Niesłony, A. Determination of fragments of multiaxial service loading strongly influencing the fatigue of machine components. Mech. Syst. Signal Processing 2009, 23, 2712–2721. [Google Scholar] [CrossRef]
- Schilling, C.G. Fatigue of Welded Steel Bridge Members under Variable-Amplitude Loadings; NCHRP Report; Transportation Research Board: Washington, DC, USA, 1978. [Google Scholar]
- Miner, M.A. Cumulative damage in fatigue. J. Appl. Mach. 1945, 12, A159–A164. [Google Scholar] [CrossRef]
- Chung, H.Y.; Manuel, L.; Frank, K.H. Optimal Inspection of Fracture-Critical Steel Trapezoidal Girders: A Summary; Center for Transportation Research, University of Texas at Austin: Austin, TX, USA, 2004. [Google Scholar]
- Paris, P.; Erdogan, F. A critical analysis of crack propagation laws. J. Fluids Eng. 1963, 85, 528–533. [Google Scholar] [CrossRef]
- BS7910. Guide to Methods for Assessing the Acceptability of Flaws in Metallic Structures; British Standards Institution (BSI): London, UK, 2005. [Google Scholar]
- Dowling, N.E. Mechanical Behavior of Materials: Engineering Methods for Deformation, Fracture, and Fatigue; Prentice Hall international: Hoboken, NJ, USA, 1993. [Google Scholar]
- DEA. Loads and Safety of Wind Turbine Construction (DS472); Danish Engineering Association: Copenhagen, Denmark, 2017. [Google Scholar]
- Thomsen, K.; Madsen, P.H.; Jørgensen, E. Status og Perspektiver for Forskning I Aeroelasticitet. Lastgrundlag og Sikkerhed. Lastgrundlag og sikkerhed-DTU; Forskningscenter Risø: Roskilde, Denmark, 1997. [Google Scholar]




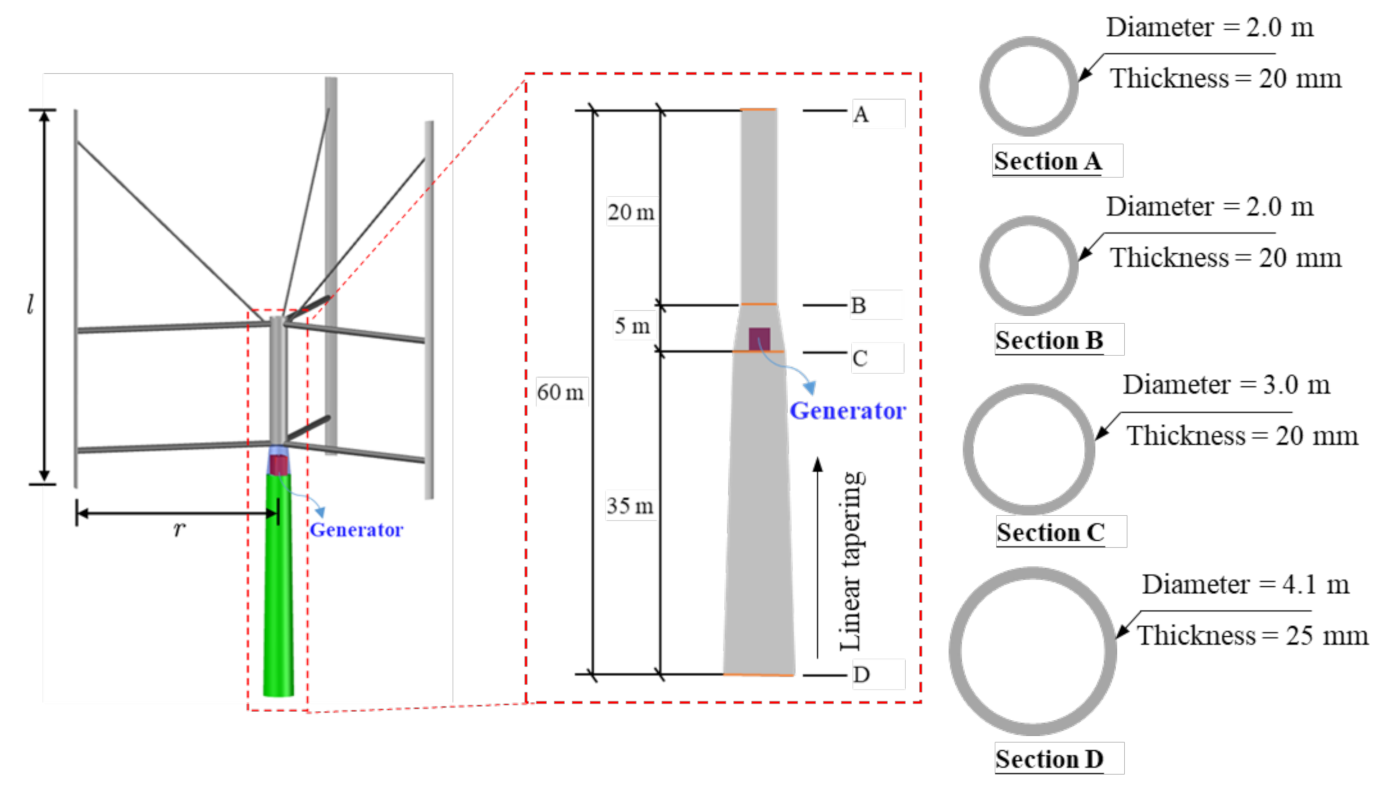
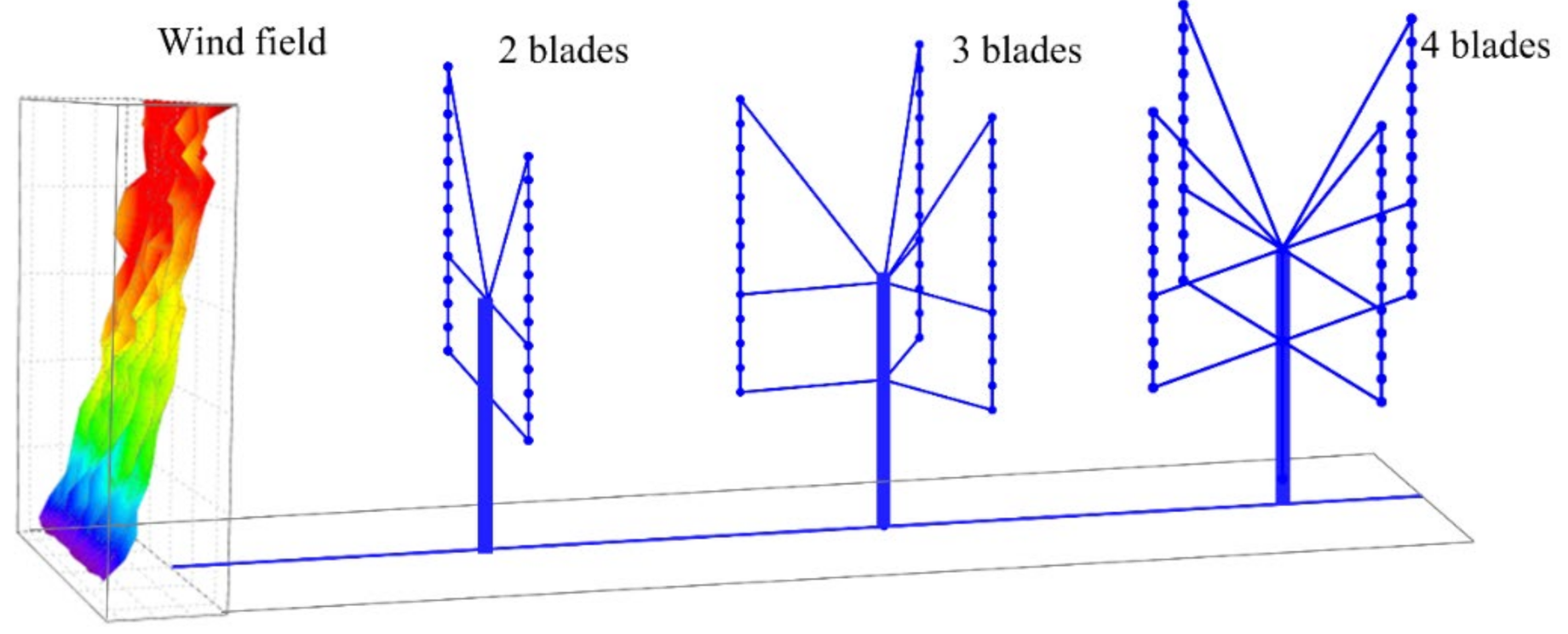


| Parameter | VAWTs | ||
|---|---|---|---|
| 2 Blades | 3 Blades | 4 Blades | |
| Rated Power, P (MW) | 1 | 1 | 1 |
| Blade Number | 2 | 3 | 4 |
| Rotor Radius, R (m) | 30 | 30 | 30 |
| Height, l (m) | 60 | 60 | 60 |
| Chord Length, C (m) | 3 | 2 | 1.5 |
| Tower Height (m) | 60 | 60 | 60 |
| Aerofoil Section | NACA 0018 | NACA 0018 | NACA 0018 |
| Cut-in, Rated, Cut-out Wind Speeds (m/s) | 5, 10, 24 | 5, 10, 24 | 5, 10, 24 |
| Rated Rotor Speed (rad/s) | 1 | 1 | 1 |
| Material Parameters | Value |
|---|---|
| 100 () | |
| 3 | |
| 235 MPa |
| Item | VAWT | ||
|---|---|---|---|
| Two Blades | Three Blades | Four Blades | |
| Cycle number | 3596 | 5079 | 6677 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, H.-D.; Zhang, B.; Wang, S.-B.; Zhou, G.-Z. Effects of Blade Numbers on Wind-Induced Fatigue Lives of Straight-Bladed Vertical-Axis Wind-Turbine Tower Bases. Metals 2022, 12, 321. https://doi.org/10.3390/met12020321
Zheng H-D, Zhang B, Wang S-B, Zhou G-Z. Effects of Blade Numbers on Wind-Induced Fatigue Lives of Straight-Bladed Vertical-Axis Wind-Turbine Tower Bases. Metals. 2022; 12(2):321. https://doi.org/10.3390/met12020321
Chicago/Turabian StyleZheng, Hua-Dong, Bo Zhang, Sheng-Bin Wang, and Guan-Zheng Zhou. 2022. "Effects of Blade Numbers on Wind-Induced Fatigue Lives of Straight-Bladed Vertical-Axis Wind-Turbine Tower Bases" Metals 12, no. 2: 321. https://doi.org/10.3390/met12020321
APA StyleZheng, H.-D., Zhang, B., Wang, S.-B., & Zhou, G.-Z. (2022). Effects of Blade Numbers on Wind-Induced Fatigue Lives of Straight-Bladed Vertical-Axis Wind-Turbine Tower Bases. Metals, 12(2), 321. https://doi.org/10.3390/met12020321