Nanocrystalline ZnSnN2 Prepared by Reactive Sputtering, Its Schottky Diodes and Heterojunction Solar Cells
Abstract
:1. Introduction
2. Materials and Methods
2.1. Preparation and Characterization of ZnSnN2
2.2. Preparation and Characterization of the Schottky Diodes and Heterojunctions
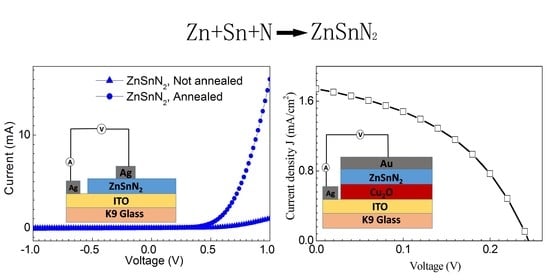
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Punya, A.; Paudel, T.R.; Lambrecht, W. Electronic and lattice dynamical properties of II-IV-N2 semiconductors. Phys. Status Solidi C 2011, 8, 2492–2499. [Google Scholar] [CrossRef]
- Laidouci, A.; Aissat, A.; Vilcot, J. Numerical study of solar cells based on ZnSnN2 structure. Sol. Energy 2020, 211, 237–243. [Google Scholar] [CrossRef]
- Chinnakutti, K.; Panneerselvam, V.; Salammal, S. Ba-acceptor doping in ZnSnN2 by reactive RF magnetron sputtering: (002) faceted Ba-ZnSnN2 films. J. Alloys Compd. 2021, 855, 157380. [Google Scholar] [CrossRef]
- Ye, F.; Chen, Q.Q.; Cai, X.M.; Xie, Y.Z.; Ma, X.F.; Vaithinathan, K.; Zhang, D.P.; Fan, P.; Roy, V. Improving the chemical potential of nitrogen to tune the electron density and mobility of ZnSnN2. J. Mater. Chem. C 2020, 8, 4314–4320. [Google Scholar] [CrossRef]
- Wang, Y.; Ohsawa, T.; Meng, X.; Alnjiman, F.; Pierson, J.; Ohashi, N. Suppressing the carrier concentration of zinc tin nitride thin films by excess zinc content and low temperature growth. Appl. Phys. Lett. 2019, 115, 232104. [Google Scholar] [CrossRef]
- Gogova, D.; Olsen, V.; Bazioti, C.; Lee, I.; Vines, L.; Kuznetsov, A. High electron mobility single-crystalline ZnSnN2 on ZnO (0001) substrates. CrystEngComm 2020, 22, 6268–6274. [Google Scholar] [CrossRef]
- Alnjiman, F.; Diliberto, S.; Ghanbaja, J.; Haye, E.; Kassavetis, S.; Patsalas, P.; Gendarme, C.; Bruyère, S.; Cleymand, F.; Miska, P.; et al. Chemical environment and functional properties of highly crystalline ZnSnN2 thin films deposited by reactive sputtering at room temperature. Sol. Energy Mater. Sol. Cells 2018, 182, 30–36. [Google Scholar] [CrossRef]
- Shing, A.; Tolstova, Y.; Lewis, N.; Atwater, H. Effects of surface condition on the work function and valence-band position of ZnSnN2. Appl. Phys. A-Mater. 2017, 123, 735. [Google Scholar] [CrossRef]
- Fioretti, A.; Stokes, A.; Young, M.; Gorman, B.; Toberer, E.; Tamboli, A.; Zakutayev, A. Effects of Hydrogen on Acceptor Activation in Ternary Nitride Semiconductors. Adv. Electron. Mater. 2017, 3, 1600544. [Google Scholar] [CrossRef]
- Chinnakutti, K.; Panneerselvam, V.; Salammal, S. Investigation on structural and optoelectronic properties of in-situ post growth annealed ZnSnN2 thin films. Mater. Sci. Semicond. Process. 2019, 89, 234–239. [Google Scholar] [CrossRef]
- Qin, R.; Cao, H.; Liang, L.; Xie, Y.; Zhuge, F.; Zhang, H.; Gao, J.; Javaid, K.; Liu, C.; Sun, W. Semiconducting ZnSnN2 thin films for Si/ZnSnN2 p-n junctions. Appl. Phys. Lett. 2016, 108, 142104. [Google Scholar] [CrossRef]
- Javaid, K.; Wu, W.; Wang, J.; Fang, J.; Zhang, H.; Gao, J.; Liang, L.; Cao, H. Band Offset Engineering in ZnSnN2-Based Heterojunction for Low-Cost Solar Cells. ACS Photonics 2018, 5, 2094–2099. [Google Scholar] [CrossRef]
- Wu, X.; Meng, F.; Chu, D.; Yao, M.; Guan, K.; Zhang, D.; Meng, J. Carrier Tuning in ZnSnN2 by Forming Amorphous and Microcrystalline Phases. Inorg. Chem. 2019, 58, 8480–8485. [Google Scholar] [CrossRef]
- Cai, X.; Wang, B.; Ye, F.; Vaithinathan, K.; Zeng, J.; Zhang, D.; Fan, P.; Roy, V. Tuning the photoluminescence, conduction mechanism and scattering mechanism of ZnSnN2. J. Alloys Compd. 2019, 779, 237–243. [Google Scholar] [CrossRef]
- Veal, T.; Feldberg, N.; Quackenbush, N.; Linhart, W.; Scanlon, D.; Piper, L.; Durbin, S. Band Gap Dependence on Cation Disorder in ZnSnN2 Solar Absorber. Adv. Energy Mater. 2015, 5, 1501462. [Google Scholar] [CrossRef] [Green Version]
- Kawamura, F.; Yamada, N.; Imai, M.; Taniguchi, T. Synthesis of ZnSnN2crystals via a high-pressure metathesis reaction. Cryst. Res. Technol. 2016, 51, 220–224. [Google Scholar] [CrossRef]
- Quayle, P.; Junno, G.; He, K.; Blanton, E.; Shan, J.; Kash, K. Vapor-liquid-solid synthesis of ZnSnN2. Phys. Status Solidi B 2017, 254, 1600718. [Google Scholar] [CrossRef]
- Chen, S.; Narang, P.; Atwater, H.A.; Wang, L. Phase Stability and Defect Physics of a Ternary ZnSnN2Semiconductor: First Principles Insights. Adv. Mater. 2014, 26, 311–315. [Google Scholar] [CrossRef]
- Pan, J.; Cordell, J.; Tucker, G.J.; Tamboli, A.; Zakutayev, A.; Lany, S. Interplay between composition, electronic structure, disorder, and doping due to dual sublattice mixing in non-equilibrium synthesis of ZnSnN2:O. Adv. Mater. 2019, 31, 1807406. [Google Scholar] [CrossRef]
- Cao, X.; Kawamura, F.; Ninomiya, Y.; Taniguchi, T.; Yamada, N. Conduction-band effective mass and bandgap of ZnSnN2 earth-abundant solar absorber. Sci. Rep. 2017, 7, 14987. [Google Scholar] [CrossRef]
- Jones, D.; Spear, W.; Lecomber, P. Transport properties of amorphous-germanium prepared by glow-discharge technique. J. Non-Cryst. Solids 1976, 20, 259–270. [Google Scholar] [CrossRef]
- Spear, W.; Willeke, G.; Le Comber, P. Electronic properties of microcrystalline silicon prepared in the glow discharge plasma. Physica 1983, 117–118, 908–913. [Google Scholar]
- Willeke, G.; Spear, W.; Jones, D.; Le Comber, P. Thermoelectric power, Hall effect and density-of-states measurements on glow-discharge microcrystalline silicon. Philos. Mag. B 1982, 46, 177–190. [Google Scholar] [CrossRef]
- Chinnakutti, K.; Panneerselvam, V.; Salammal, S. Tailoring optoelectronic properties of earth abundant ZnSnN2 by combinatorial RF magnetron sputtering. J. Alloys Compd. 2019, 772, 348–358. [Google Scholar] [CrossRef]
- Zatsepin, D.; Boukhvalov, D.; Kurmaev, E.; Zhidkov, I.; Kim, S.; Cui, L.; Gavrilov, N.; Cholakh, S. XPS and DFT study of Sn incorporation into ZnO and TiO2 host matrices by pulsed ion implantation. Phys. Status Solidi B 2015, 252, 1890–1896. [Google Scholar] [CrossRef] [Green Version]
- Ye, F.; Zeng, J.; Qiu, Y.; Cai, X.; Wang, B.; Wang, H.; Zhang, D.; Fan, P.; Roy, V. Deposition-rate controlled nitrogen-doping into cuprous oxide and its thermal stability. Thin Solid Films 2019, 674, 44–51. [Google Scholar] [CrossRef]
- Asahi, R.; Morikawa, T.; Ohwaki, T.; Aoki, K.; Taga, Y. Visible-Light Photocatalysis in Nitrogen-Doped Titanium Oxides. Science 2001, 293, 269–271. [Google Scholar] [CrossRef] [PubMed]
- Chand, S.; Kumar, J. Current-voltage characteristics and barrier parameters of Pd2Si/p-Si (111) Schottky diodes in a wide temperature range. Semicond. Sci. Technol. 1995, 10, 1680–1688. [Google Scholar] [CrossRef]
- Sze, S.; Ng, K. Physics of Semiconductor Devices, 3rd ed.; Wiley Interscience: Hoboken, NJ, USA, 2006; p. 159. [Google Scholar]
- Javaid, K.; Yu, J.; Wu, W.; Wang, J.; Zhang, H.; Gao, J.; Zhuge, F.; Liang, L.; Cao, H. Thin Film Solar Cell Based on ZnSnN2/SnO Heterojunction. Phys. Status Solidi RRL 2018, 12, 1700332. [Google Scholar] [CrossRef]
- Punya, A.; Lambrecht, W. Band offsets between ZnGeN2, GaN, ZnO, and ZnSnN2and their potential impact for solar cells. Phys. Rev. B 2013, 88, 075302-1–075302-6. [Google Scholar] [CrossRef] [Green Version]
- Cowley, A.M.; Sze, S.M. Surface States and Barrier Height of Metal-Semiconductor Systems. J. Appl. Phys. 1965, 36, 3212–3220. [Google Scholar] [CrossRef]
- Eglash, S.J.; Newman, N.; Pan, S.; Mo, D.; Shenai, K.; Spicer, W.; Collins, D.M. Engineered Schottky barrier diodes for themodification and control of Schottky barrier heights. J. Appl. Phys. 1987, 61, 5159–5169. [Google Scholar] [CrossRef]
- Shannon, J.M. Increasing the effective height of a Schottky barrier using low-energy ion implantation. Appl. Phys. Lett. 1974, 25, 75–77. [Google Scholar] [CrossRef]
- Turut, A.; Saglam, M.; Efeoglu, H.; Yalcin, N.; Yildirim, M.; Abay, B. Interpreting the nonideal reverse bias C-V characteristicsand importance of the dependence of Schottky barrier heighton applied voltage. Phys. B 1995, 205, 41–50. [Google Scholar] [CrossRef]
- Wronski, C.; Carlson, D. Surface states and barrier heights of metal-amorphous silicon Schottky barriers. Solid State Commun. 1977, 23, 421–424. [Google Scholar] [CrossRef]
- Chattopadhyay, P.; Raychaudhuri, B. Origin of the anomalous peak in the forward capacitance-voltage plot of a Schottky barrier diode. Solid State Electron. 1992, 35, 875–878. [Google Scholar]
- Chattopadhyay, P.; Raychaudhuri, B. Frequency dependence of forward capacitance-voltage characteristics of Schottky barrier diodes. Solid State Electron. 1993, 36, 605–610. [Google Scholar] [CrossRef]
- Vasudev, P.; Mattes, B.; Pietras, E.; Bube, R. Excess capacitance and non-ideal Schottky barriers on GaAs. Solid State Electron. 1976, 19, 557–559. [Google Scholar] [CrossRef]
- Szatkowski, J.; Sierański, K. Simple interface-layer model for the nonideal characteristics of the Schottky-barrier diode. Solid State Electron. 1992, 35, 1013–1015. [Google Scholar] [CrossRef]
- Buene, L.; Jacobsen, S.-T. Room Temperature Interdiffusion in Evaporated Au-Sn Films. Phys. Scr. 1978, 18, 397. [Google Scholar] [CrossRef]
- Chiu, F.-C. A review on conduction mechanism in dielectric films. Adv. Mater. Sci. Eng. 2014, 2014, 578168. [Google Scholar] [CrossRef] [Green Version]
- Hegedus, S.; Shafarman, W. Thin-film solar cells: Device measurements and analysis. Prog. Photovolt Res. Appl. 2004, 12, 155–176. [Google Scholar] [CrossRef]
- Chen, S.; Ishap, M.; Xiong, W.; Shah, U.; Farooq, U.; Luo, J.; Zheng, Z.; Su, Z.; Fan, P.; Zhang, X.; et al. Improved open-circuit voltage of Sb2Se3 thin film solar cells via interfacial sulfur diffusion-induced gradient bandgap engineering. Solar RRL 2021, 5, 2100419. [Google Scholar] [CrossRef]
- Carlson, D.E.; Wronski, C.R. Amorphous silicon solar cell. Appl. Phys. Lett. 1976, 28, 671–673. [Google Scholar] [CrossRef]
- Li, X.; Zhu, H.; Wang, K.; Cao, A.; Wei, J.; Li, C.; Jia, Y.; Li, Z.; Li, X.; Wu, D. Graphene-On-Silicon Schottky Junction Solar Cells. Adv. Mater. 2010, 22, 2743–2748. [Google Scholar] [CrossRef] [PubMed]
- Minami, T.; Nishi, Y.; Miyata, T. Efficiency enhancement using a Zn1-xGex-O thin film as an n-type window layer in Cu2O-based heterojunction solar cells. Appl. Phys. Express. 2016, 9, 052301-1–052301-4. [Google Scholar] [CrossRef]
- Zhang, Z.; Lin, J.; Sun, P.; Zeng, Q.; Deng, X.; Mo, Y.; Chen, J.; Zheng, Y.; Wang, W.; Li, G. Air-stable MXene/GaAs heterojunction solar cells with a high initial efficiency of 9.69%. J. Mater. Chem. A 2021, 9, 16160–16168. [Google Scholar] [CrossRef]
- Masuko, K.; Shigematsu, M.; Hashiguchi, T.; Fujishima, D.; Kai, M.; Yoshimura, N.; Yamaguchi, T.; Ichihashi, Y.; Mishima, T.; Matsubara, N.; et al. Achievement of More Than 25% Conversion Efficiency With Crystalline Silicon Heterojunction Solar Cell. IEEE J. Photovolt. 2014, 4, 1433–1435. [Google Scholar] [CrossRef]
- Virfeu, A.; Alnjiman, F.; Ghanbaja, J.; Borroto, A.; Gendarme, C.; Migot, S.; Kopprio, L.; Gall, S.L.; Longeaud, C.; Vilcot, J.-P. Approaching Theoretical Band Gap of ZnSnN2 Films via Bias Magnetron Cosputtering at Room Temperature. ACS Appl. Electron. Mater. 2021, 3, 3855–3866. [Google Scholar] [CrossRef]
- Quayle, P.C.; He, K.; Shan, J.; Kash, K. Synthesis, lattice structure, and band gap of ZnSnN2. MRS Commun. 2013, 3, 135–138. [Google Scholar] [CrossRef]
- Quayle, P.C.; Blanton, E.W.; Punya, A.; Junno, G.T.; He, K.; Han, L.; Zhao, H.; Shan, J.; Lambrecht, W.R.L.; Kash, K. Charge-neutral disorder and polytypes in heterovalent wurtzite-based ternary semiconductors: The importance of the octet rule. Phys. Rev. B 2015, 91, 205207. [Google Scholar] [CrossRef] [Green Version]
- Meyer, B.K.; Polity, A.; Reppin, D.; Becker, M.; Hering, P.; Klar, P.J.; Sander, T.; Reindl, C.; Benz, J.; Eickhoff, M.; et al. Binary copper oxide semiconductors: From materials towards devices, Phys. Status Solidi B 2012, 249, 1487–1509. [Google Scholar] [CrossRef]











| °C | μ (cm2V−1s−1) | n (cm−3) |
|---|---|---|
| 300 | 0.988 | 5.34 × 1017 |
| 350 | 5.54 | 8.37 × 1018 |
| 400 | 2.96 | 6.48 × 1018 |
| 450 | 1.22 | 8.11 × 1018 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, F.; Hong, R.-T.; Qiu, Y.-B.; Xie, Y.-Z.; Zhang, D.-P.; Fan, P.; Cai, X.-M. Nanocrystalline ZnSnN2 Prepared by Reactive Sputtering, Its Schottky Diodes and Heterojunction Solar Cells. Nanomaterials 2023, 13, 178. https://doi.org/10.3390/nano13010178
Ye F, Hong R-T, Qiu Y-B, Xie Y-Z, Zhang D-P, Fan P, Cai X-M. Nanocrystalline ZnSnN2 Prepared by Reactive Sputtering, Its Schottky Diodes and Heterojunction Solar Cells. Nanomaterials. 2023; 13(1):178. https://doi.org/10.3390/nano13010178
Chicago/Turabian StyleYe, Fan, Rui-Tuo Hong, Yi-Bin Qiu, Yi-Zhu Xie, Dong-Ping Zhang, Ping Fan, and Xing-Min Cai. 2023. "Nanocrystalline ZnSnN2 Prepared by Reactive Sputtering, Its Schottky Diodes and Heterojunction Solar Cells" Nanomaterials 13, no. 1: 178. https://doi.org/10.3390/nano13010178
APA StyleYe, F., Hong, R.-T., Qiu, Y.-B., Xie, Y.-Z., Zhang, D.-P., Fan, P., & Cai, X.-M. (2023). Nanocrystalline ZnSnN2 Prepared by Reactive Sputtering, Its Schottky Diodes and Heterojunction Solar Cells. Nanomaterials, 13(1), 178. https://doi.org/10.3390/nano13010178