Double Beta Decay: A Shell Model Approach
Abstract
:1. Introduction
2. Neutrinoless Double Beta Decay and Neutrino Physics
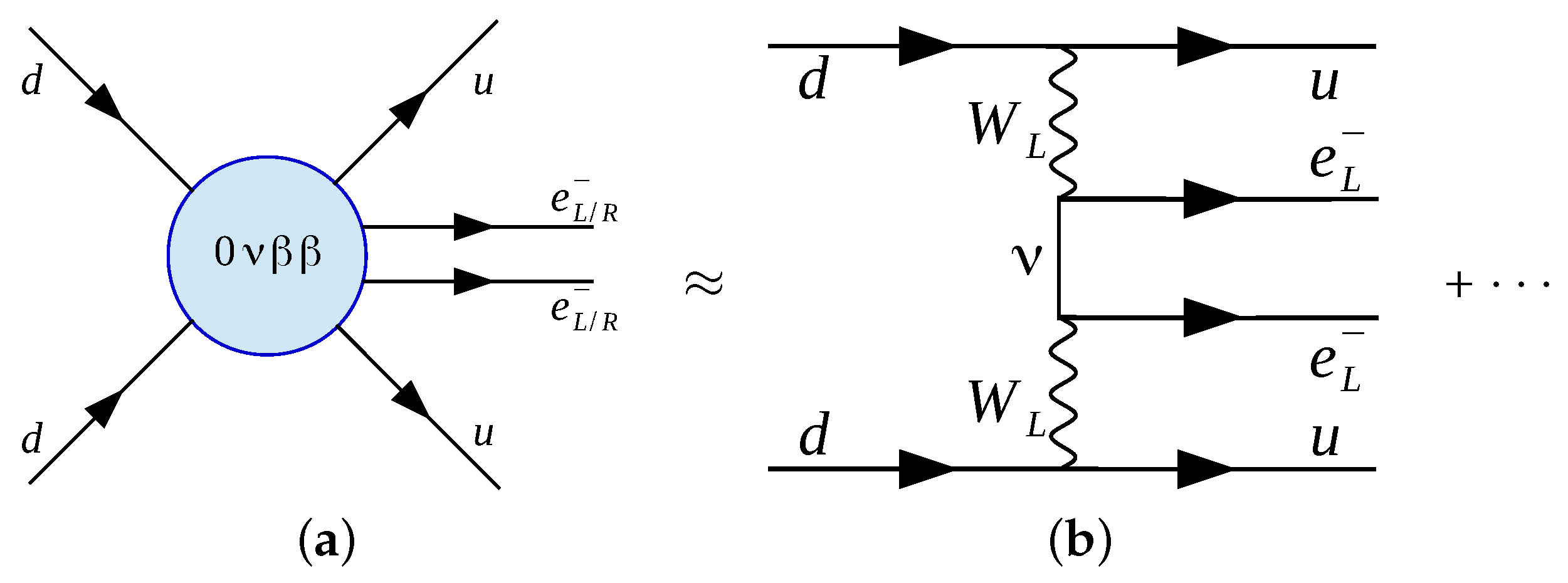
2.1. LNV Models Contributing to
2.2. EFT Approach to Decay
3. Neutrinoless Double Beta Decay Nuclear Matrix Elements
3.1. The Anatomy of the NMEs
3.2. The NME in Closure Approximation
4. Two-Neutrino Double Beta Decay
5. Conclusions
Funding
Conflicts of Interest
Abbreviations
| neutrinoless double beta decay | |
| two-neutrino double beta decay | |
| BSM | beyond the Standard Model |
| CMU | Central Michigan University |
| EFT | effective field theory |
| g.s. | ground state |
| s.p. | single particle |
| LNV | lepton number violation |
| NME | nuclear matrix element |
| PCAC | Partial Conservation of Axial Current |
| PMNS | Pontecorvo–Maki–Nakagawa–Sakata |
| PSF | phase space factor |
| QCD | Quantum Chromodynamics |
| QRPA | quasiparticle random phase approximation |
| SUSY | super symmetry |
| TBTD | two-body transition densities |
References
- Fukuda, Y. et al. [Super-Kamiokande Collaboration] Evidence for oscillation of atmospheric neutrinos. Phys. Rev. Lett. 1998, 81, 1562–1567. [Google Scholar] [CrossRef]
- Ahmad, Q.R. et al. [SNO Collaboration] Measurement of the rate of νe + d → p + p + e− interactions produced by 8B solar neutrinos at the Sudbury Neutrino Observatory. Phys. Rev. Lett. 2001, 87, 071301. [Google Scholar] [CrossRef]
- Kajita, T. Nobel Lecture: Discovery of atmospheric neutrino oscillations. Rev. Mod. Phys. 2016, 88, 03051. [Google Scholar] [CrossRef]
- McDonald, A.B. Nobel Lecture: The Sudbury Neutrino Observatory: Observation of flavor change for solar neutrinos. Rev. Mod. Phys. 2016, 88, 030502. [Google Scholar] [CrossRef]
- Schechter, J.; Valle, J.W.F. Neutrinoless doubl-β decay in SU(2) × U(1) theories. Phys. Rev. D 1982, 25, 2951–2954. [Google Scholar] [CrossRef]
- Nieves, J. Dirac and pseudo-Dirac neutrinos and neutrinoless double beta decay. Phys. Lett. B 1984, 147, 375–379. [Google Scholar] [CrossRef]
- Takasugi, E. Can the neutrinoless double beta decay take place in the case of Dirac neutrinos? Phys. Lett. B 1984, 149, 372–376. [Google Scholar] [CrossRef]
- Hirsch, M.; Kovalenko, S.; Schmidt, I. Extended black box theorem for lepton number and flavor violating processes. Phys. Lett. B 2006, 642, 106–110. [Google Scholar] [CrossRef]
- Pati, J.C.; Salam, A. Lepton number as the fourth “color”. Phys. Rev. D 1974, 10, 275–289. [Google Scholar] [CrossRef]
- Mohapatra, R.N.; Pati, J.C. “Natural” left-right symmetry. Phys. Rev. D 1975, 11, 2558–2561. [Google Scholar] [CrossRef]
- Senjanovic, G.; Mohapatra, R.N. Exact left-right symmetry and spontaneous violation of parity. Phys. Rev. D 1975, 12, 1502–1505. [Google Scholar] [CrossRef]
- Keung, W.-Y.; Senjanovic, G. Majorana neutrinos and the production of the right-handed charged gauge boson. Phys. Rev. Lett. 1983, 50, 1427–1430. [Google Scholar] [CrossRef]
- Barry, J.; Rodejohann, W. Lepton number and flavor violation in TeV-scale left-right symmetric theories with large left-right mixing. J. High Energy Phys. 2013, 2013, 153. [Google Scholar] [CrossRef]
- Khachatryan, V. et al. [CMS Collaboration] Search for heavy neutrinos and W bosons with right-handed couplings in proton-proton collisions at = 8 TeV. Eur. Phys. J. C 2014, 74, 3149. [Google Scholar] [CrossRef]
- Horoi, M.; Neacsu, A. Analysis of mechanisms that could contribute to neutrinoless double-beta decay. Phys. Rev. D 2016, 93, 113014. [Google Scholar] [CrossRef]
- Neacsu, A.; Horoi, M. Shell Model studies of competing mechanisms to the neutrinoless double-beta decay in 124Sn, 130Te, and 136Xe. Adv. High Energy Phys. 2016, 2016, 1903767. [Google Scholar] [CrossRef]
- Horoi, M.; Neacsu, A. Shell model study of using an effective field theory for disentangling several contributions to neutrinoless double-β decay. Phys. Rev. C 2018, 98, 035502. [Google Scholar] [CrossRef]
- Cirigliano, V.; Dekens, W.; de Vries, J.; Graesser, M.L.; Mereghetti, E. Neutrinoless double beta decay in chiral effective field theory: Lepton number violation at dimension seven. J. High Energy Phys. 2017, 2017, 82. [Google Scholar] [CrossRef]
- Cirigliano, V.; Dekens, W.; Graesser, M.; Mereghetti, E. Neutrinoless double beta decay and chiral SU(3). Phys. Lett. B 2017, 769, 460–464. [Google Scholar] [CrossRef]
- Berkowitz, E.; Brantley, D.; Bouchard, C.; Chang, C.C.; Clark, M.A.; Garron, N.; Joo, B.; Kurth, T.; Monahan, C.; Monge-Camacho, H.; et al. An accurate calculation of the nucleon axial charge with lattice QCD. arXiv 2017, arXiv:1704.01114. [Google Scholar] [CrossRef]
- Hirsch, M.; Klapdor-Kleingrothaus, H.V.; Kovalenko, S.G. On the SUSY accompanied neutrino exchange mechanism of neutrinoless double beta decay. Phys. Lett. B 1996, 372, 181–186. [Google Scholar] [CrossRef]
- Päs, H.; Hirsch, M.; Klapdor-Kleingrothaus, H.V.; Kovalenko, S.G. Towards a superformula for neutrinoless double beta decay. Phys. Lett. B 1999, 453, 194–198. [Google Scholar] [CrossRef]
- Päs, H.; Hirsch, M.; Klapdor-Kleingrothaus, H.V.; Kovalenko, S.G. A Superformula for neutrinoless double beta decay. II. The short range part. Phys. Lett. B 2001, 498, 35–39. [Google Scholar] [CrossRef]
- Deppisch, F.F.; Hirsch, M.; Päs, H. Neutrinoless double-beta decay and physics beyond the standard model. J. Phys. G Nucl. Part. Phys. 2012, 39, 124007. [Google Scholar] [CrossRef]
- Barabash, A.S. Precise half-life values for two-neutrino double-β decay: 2020 review. Universe 2020, 6, 159. [Google Scholar] [CrossRef]
- Barabash, A.S.; Hubert, P.; Nachab, A.; Konovalov, S.I.; Vanyushin, I.A.; Umatov, V. Search for β+ EC and ECEC processes in 112Sn and β−β− decay of 124Sn to the excited states of 124Te. Nucl. Phys. A 2008, 807, 269–289. [Google Scholar] [CrossRef]
- Neacsu, A.; Horoi, M. An effective method to accurately calculate the phase space factors for β−β− decay. Adv. High Energy Phys. 2016, 2016, 7486712. [Google Scholar] [CrossRef]
- Stoica, S.; Mirea, M. New calculations for phase space factors involved in double-β decay. Phys. Rev. C 2013, 88, 037303. [Google Scholar] [CrossRef]
- Arnold, R. et al. [NEMO-3 Collaboration] Measurement of the double-beta decay half-life and search for the neutrinoless double-beta decay of 48Ca with the NEMO-3 detector. Phys. Rev. D 2016, 93, 112008. [Google Scholar] [CrossRef]
- Agostini, M. et al. [GERDA Collaboration] Final results of GERDA on the search for neutrinoless Double-β decay. Phys. Rev. Lett. 2020, 125, 252502. [Google Scholar] [CrossRef]
- Waters, D. et al. [NEMO-3 and SuperNEMO Collaborations] Latest Results from NEMO-3 and Status of the SuperNEMO Experiment. Talk at the Neutrino 2016: XXVII Intern. Conf. on Neutrino Physics and Astrophysics, London, UK, 4–9 July 2016. Available online: http://neutrino2016.iopconfs.org/IOP/media/uploaded/EVIOP/event_948/10.25__5__waters.pdf (accessed on 1 September 2022).
- Adams, D.Q. et al. [CUORE Collaboration] Improved limit on neutrinoless double-beta decay in 130Te with CUORE. Phys. Rev. Lett. 2020, 124, 122501. [Google Scholar] [CrossRef] [PubMed]
- Gando, A. et al. [KamLAND-Zen Collaboration] Search for Majorana neutrinos near the inverted mass hierarchy region with KamLAND-Zen. Phys. Rev. Lett. 2016, 117, 082503. [Google Scholar] [CrossRef]
- Retamosa, J.; Caurier, E.; Nowacki, F. Neutrinoless double beta decay of 48Ca. Phys. Rev. C 1995, 51, 371–378. [Google Scholar] [CrossRef] [PubMed]
- Caurier, E.; Nowacki, F.; Poves, A.; Retamosa, J. Shell model studies of the double beta decays of 76Ge, 82Se, and 136Xe. Phys. Rev. Lett. 1996, 77, 1954–1957. [Google Scholar] [CrossRef]
- Horoi, M. Shell model analysis of competing contributions to the double-β decay of 48Ca. Phys. Rev. C 2013, 87, 014320. [Google Scholar] [CrossRef]
- Neacsu, A.; Stoica, S. Constraints on heavy neutrino and SUSY parameters derived from the study of neutrinoless double beta decay. Adv. High Energy Phys. 2014, 2014, 724315. [Google Scholar] [CrossRef]
- Caurier, E.; Menendez, J.; Nowacki, F.; Poves, A. Influence of pairing on the nuclear matrix elements of the neutrinoless ββ decays. Phys. Rev. Lett. 2008, 100, 052503. [Google Scholar] [CrossRef] [PubMed]
- Menendez, J.; Poves, A.; Caurier, E.; Nowacki, F. Disassembling the nuclear matrix elements of the neutrinoless ββ decay. Nucl. Phys. A 2009, 818, 139–151. [Google Scholar] [CrossRef]
- Caurier, E.; Martinez-Pinedo, G.; Nowacki, F.; Poves, A.; Zuker, A.P. The shell model as a unified view of nuclear structure. Rev. Mod. Phys. 2005, 77, 427–487. [Google Scholar] [CrossRef]
- Horoi, M.; Stoica, S. Shell model analysis of the neutrinoless double-β decay of 48Ca. Phys. Rev. C 2010, 81, 024321. [Google Scholar] [CrossRef] [Green Version]
- Neacsu, A.; Stoica, S.; Horoi, M. Fast, efficient calculations of the two-body matrix elements of the transition operators for neutrinoless double-β decay. Phys. Rev. C 2012, 86, 067304. [Google Scholar] [CrossRef]
- Sen’kov, R.A.; Horoi, M. Neutrinoless double-β decay of 48Ca in the shell model: Closure versus nonclosure approximation. Phys. Rev. C 2013, 88, 064312. [Google Scholar] [CrossRef]
- Horoi, M.; Brown, B.A. Shell-model analysis of the 136Xe double beta decay nuclear matrix elements. Phys. Rev. Lett. 2013, 110, 222502. [Google Scholar] [CrossRef] [PubMed]
- Sen’kov, R.A.; Horoi, M.; Brown, B.A. Neutrinoless double-β decay of 82Se in the shell model: Beyond the closure approximation. Phys. Rev. C 2014, 89, 054304. [Google Scholar] [CrossRef]
- Brown, B.A.; Horoi, M.; Sen’kov, R.A. Nuclear structure aspects of neutrinoless double-β decay. Phys. Rev. Lett. 2014, 113, 262501. [Google Scholar] [CrossRef] [PubMed]
- Neacsu, A.; Stoica, S. Study of nuclear effects in the computation of the 0νββ decay matrix elements. J. Phys. G Nucl. Part. Phys. 2014, 41, 015201. [Google Scholar] [CrossRef]
- Sen’kov, R.A.; Horoi, M. Accurate shell-model nuclear matrix elements for neutrinoless double-β decay. Phys. Rev. C 2014, 90, 051301(R). [Google Scholar] [CrossRef]
- Neacsu, A.; Horoi, M. Shell model studies of the 130Te neutrinoless double-β decay. Phys. Rev. C 2015, 91, 024309. [Google Scholar] [CrossRef]
- Horoi, M.; Neacsu, A. Shell model predictions for 124Sn double-β decay. Phys. Rev. C 2016, 93, 024308. [Google Scholar] [CrossRef]
- Horoi, M.; Stoica, S.; Brown, B.A. Shell-model calculations of two-neutrino double–β decay rates of 48Ca with the GXPF1A interaction. Phys. Rev. C 2007, 75, 034303. [Google Scholar] [CrossRef] [Green Version]
- Blennow, M.; Fernandez-Martinez, E.; Lopéz-Pavon, J.; Menendez, J. Neutrinoless double beta decay in seesaw models. J. High Energy Phys. 2010, 2010, 096. [Google Scholar] [CrossRef]
- Šimkovic, F.; Pantis, G.; Vergados, J.D.; Faessler, A. Additional nucleon current contributions to neutrinoless double–β decay. Phys. Rev. C 1999, 60, 055502. [Google Scholar] [CrossRef]
- Suhonen, J.; Civitarese, O. Effects of orbital occupancies and spin-orbit partners on 0νββ-decay rates. Nucl. Phys. A 2010, 847, 207–232. [Google Scholar] [CrossRef]
- Faessler, A.; Meroni, A.; Petcov, S.T.; Šimkovic, F.; Vergados, J. Uncovering multiple CP-nonconserving mechanisms of (ββ)0ν decay. Phys. Rev. D 2011, 83, 113003. [Google Scholar] [CrossRef]
- Mustonen, M.T.; Engel, J. Large-scale calculations of the double-β decay of 76Ge, 130Te, 136Xe, and 150Nd in the deformed self-consistent Skyrme quasiparticle random-phase approximation. Phys. Rev. C 2013, 87, 064302. [Google Scholar] [CrossRef]
- Faessler, A.; Gonzalez, M.; Kovalenko, S.; Šimkovic, F. Arbitrary mass Majorana neutrinos in neutrinoless double beta decay. Phys. Rev. D 2014, 90, 096010. [Google Scholar] [CrossRef]
- Barea, J.; Iachello, F. Neutrinoless double-β decay in the microscopic interacting boson model. Phys. Rev. C 2009, 79, 044301. [Google Scholar] [CrossRef]
- Barea, J.; Kotila, J.; Iachello, F. Limits on neutrino masses from neutrinoless double-β decay. Phys. Rev. Lett. 2012, 109, 042501. [Google Scholar] [CrossRef]
- Barea, J.; Kotila, J.; Iachello, F. Nuclear matrix elements for double-β decay. Phys. Rev. C 2013, 87, 014315. [Google Scholar] [CrossRef]
- Barea, J.; Kotila, J.; Iachello, F. 0νββ and 2νββ nuclear matrix elements in the interacting boson model with isospin restoration. Phys. Rev. C 2015, 91, 034304. [Google Scholar] [CrossRef] [Green Version]
- Rath, P.K.; Chandra, R.; Chaturvedi, K.; Lohani, P.; Raina, P.K.; Hirsch, J.G. Neutrinoless ββ decay transition matrix elements within mechanisms involving light Majorana neutrinos, classical Majorons, and sterile neutrinos. Phys. Rev. C 2013, 88, 064322. [Google Scholar] [CrossRef]
- Rodriguez, T.R.; Martinez-Pinedo, G. Energy density functional study of nuclear matrix elements for neutrinoless ββ decay. Phys. Rev. Lett. 2010, 105, 252503. [Google Scholar] [CrossRef] [PubMed]
- Song, L.S.; Yao, J.M.; Ring, P.; Meng, J. Relativistic description of nuclear matrix elements in neutrinoless double-β decay. Phys. Rev. C 2014, 90, 054309. [Google Scholar] [CrossRef]
- Faessler, A.; Rodin, V.; Šimkovic, F. Nuclear matrix elements for neutrinoless double-beta decay and double-electron capture. J. Phys. G Nucl. Part. Phys. 2012, 39, 124006. [Google Scholar] [CrossRef]
- Vogel, P. Nuclear structure and double beta decay. J. Phys. G Nucl. Part. Phys. 2012, 39, 124002. [Google Scholar] [CrossRef]
- Holt, J.D.; Engel, J. Effective double-β-decay operator for 76Ge and 82Se. Phys. Rev. C 2013, 87, 064315. [Google Scholar] [CrossRef]
- Jiao, C.F.; Horoi, M.; Neacsu, A. Neutrinoless double-β decay of 14Sn, 130Te, and 136Xe in the Hamiltonian-based generator-coordinate method. Phys. Rev. C 2018, 98, 064324. [Google Scholar] [CrossRef]
- Brown, B.A.; Fang, D.L.; Horoi, M. Evaluation of the theoretical nuclear matrix elements for ββ decay of 76Ge. Phys. Rev. C 2015, 92, 041301(R). [Google Scholar] [CrossRef]
- Sen’kov, R.A.; Horoi, M. Shell-model calculation of neutrinoless double-β decay of 76Ge. Phys. Rev. C 2016, 93, 044334. [Google Scholar] [CrossRef]
- Doi, M.; Kotani, T.; Takasugi, E. Double-beta decay and Majorana neutrino. Prog. Theor. Phys. Suppl. 1985, 83, 1–175. [Google Scholar] [CrossRef] [Green Version]
- Doi, M.; Kotani, T.; Nishiura, H.; Takasugi, E. Double beta decay. Progr. Theor. Exp. Phys. 1983, 69, 602–635. [Google Scholar] [CrossRef]
- Rodejohann, W. Neutrinoless double-beta decay and neutrino physics. J. Phys. G Nucl. Part. Phys. 2012, 39, 124008. [Google Scholar] [CrossRef]
- Mohapatra, R.N.; Pati, J.C. Left-right gauge symmetry and the “isoconjugate” model of CP violation. Phys. Rev. D 1975, 11, 566–571. [Google Scholar] [CrossRef]
- Hirsch, M.; Klapdor-Kleingrothaus, H.V.; Kovalenko, S.G. Supersymmetry and neutrinoless double β decay. Phys. Rev. D 1996, 53, 1329–1348. [Google Scholar] [CrossRef]
- Kolb, S.; Hirsch, M.; Klapdor-Kleingrothaus, H.V. Squark mixing and its consequences for minimal supersymmetric standard model couplings. Phys. Rev. D 1997, 56, 4161–4165. [Google Scholar] [CrossRef]
- Faessler, A.; Gutsche, T.; Kovalenko, S.; Šimkovic, F. Pion dominance in R-parity violating supersymmetry induced neutrinoless double beta decay. Phys. Rev. D 2008, 77, 113012. [Google Scholar] [CrossRef]
- Suhonen, J.; Civitarese, O. Weak-interaction and nuclear-structure aspects of nuclear double beta decay. Phys. Rep. 1998, 300, 123–214. [Google Scholar] [CrossRef]
- Kotila, J.; Iachello, F. Phase-space factors for double-β decay. Phys. Rev. C 2012, 85, 034316. [Google Scholar] [CrossRef]
- Vergados, J.D.; Ejiri, H.; Šimkovic, F. Theory of neutrinoless double-beta decay. Rep. Prog. Phys. 2012, 75, 106301. [Google Scholar] [CrossRef]
- Bhupal Dev, P.S.; Goswami, S.; Mitra, M. TeV-scale left-right symmetry and large mixing effects in neutrinoless double beta decay. Phys. Rev. D 2015, 91, 113004. [Google Scholar] [CrossRef] [Green Version]
- Tomoda, T. 0+ → 2+ neutrinoless ββ decay of 76Ge. Nucl. Phys. A 1988, 484, 635–646. [Google Scholar] [CrossRef]
- Fang, D.-L.; Faessler, A. Nuclear matrix elements for the 0νββ(0+ → 2+) decay of 76Ge within the two-nucleon mechanism. Phys. Rev. C 2021, 103, 045501. [Google Scholar] [CrossRef]
- Fang, D.-L.; Faessler, A. 0νββ to the first 2+ state with two-nucleon mechanism for L-R symmetric model. arXiv 2022, arXiv:2208.08595. [Google Scholar] [CrossRef]
- Štefanik, D.; Dvornicky, R.; Šimkovic, F.; Vogel, P. Reexamining the light neutrino exchange mechanism of the 0νββ decay with left- and right-handed leptonic and hadronic currents. Phys. Rev. C 2015, 92, 055502. [Google Scholar] [CrossRef]
- Muto, K.; Bender, E.; Klapdor, H.V. Nuclear structure effects on the neutrinoless double beta decay. Z. Phys. A 1989, 334, 187–194. [Google Scholar] [CrossRef]
- Faessler, A.; Šimkovic, F. Double beta decay. J. Phys. G Nucl. Part. Phys. 1998, 24, 2139–2178. [Google Scholar] [CrossRef]
- Avignone, F.T., III; Elliott, S.R.; Engel, J. Double beta decay, Majorana neutrinos, and neutrino mass. Rev. Mod. Phys. 2008, 80, 481. [Google Scholar] [CrossRef]
- Deppisch, F.F.; Harz, J.; Huang, W.-C.; Hirsch, M.; Päs, H. Falsifying high-scale baryogenesis with neutrinoless double beta decay and lepton flavor violation. Phys. Rev. D 2015, 92, 036005. [Google Scholar] [CrossRef]
- Ahmed, F.; Neacsu, A.; Horoi, M. Interference between light and heavy neutrinos for 0νββ decay in the left–right symmetric model. Phys. Lett. B 2017, 769, 299–304. [Google Scholar] [CrossRef]
- Ahmed, F.; Horoi, M. Interference effects for 0νββ decay in the left-right symmetric model. Phys. Rev. C 2020, 101, 035504. [Google Scholar] [CrossRef] [Green Version]
- Nuclear Structure Resources. Available online: https://people.nscl.msu.edu/~brown/resources/resources.html (accessed on 1 September 2022).
- Tomoda, T. Double beta decay. Rep. Prog. Phys. 1991, 54, 53–126. [Google Scholar] [CrossRef]
- Belley, A.; Payne, C.G.; Stroberg, S.R.; Miyagi, T.; Holt, J.D. Ab initio neutrinoless double-Bbta decay matrix elements for 48Ca, 76Ge, and 82Se. Phys. Rev. Lett. 2021, 126, 042502. [Google Scholar] [CrossRef]
- Coraggio, L.; Gargano, A.; Itaco, N.; Mancino, R.; Nowacki, F. Calculation of the neutrinoless double-β decay matrix element within the realistic shell model. Phys. Rev. C 2020, 101, 044315. [Google Scholar] [CrossRef]
- Kwiatkowski, A.A.; Brunner, T.; Holt, J.D.; Chaudhuri, A.; Chowdhury, U.; Eibach, M.; Engel, J.; Gallant, A.T.; Grossheim, A.; Horoi, M.; et al. New determination of double-β-decay properties in 48Ca: High-precision Qββ-value measurement and improved nuclear matrix element calculations. Phys. Rev. C 2014, 89, 045502. [Google Scholar] [CrossRef]
- Honma, M.; Otsuka, T.; Brown, B.A.; Mizusaki, T. New effective interaction for pf-shell nuclei and its implications for the stability of the N = Z = 28 closed core. Phys. Rev. C 2004, 69, 034335. [Google Scholar] [CrossRef]
- Honma, M.; Otsuka, T.; Mizusaki, T.; Hjorth-Jensen, M. New effective interaction for f5pg9-shell nuclei. Phys. Rev. C 2009, 80, 064323. [Google Scholar] [CrossRef]
- Qi, C.; Xu, Z.X. Monopole-optimized effective interaction for tin isotopes. Phys. Rev. C 2010, 86, 044323. [Google Scholar] [CrossRef]
- Poves, A.; Sánchez-Solano, J.; Caurier, E.; Nowacki, F. Shell model study of the isobaric chains A = 50, A = 51 and A = 52. Nucl. Phys. A 2001, 694, 157–198. [Google Scholar] [CrossRef]
- Caurier, E.; Nowacki, F.; Poves, A.; Sieja, K. Collectivity in the light xenon isotopes: A shell model study. Phys. Rev. C 2010, 82, 064304. [Google Scholar] [CrossRef]
- Caurier, E.; Poves, A.; Zuker, A.P. A full 0ℏω description of the 2νββ decay of 48Ca. Phys. Lett. B 1990, 252, 13–17. [Google Scholar] [CrossRef]
- Engel, J.; Haxton, H.; Vogel, P. Effective summation over intermediate states in double-beta decay. Phys. Rev. C 1992, 46, 2153(R). [Google Scholar] [CrossRef] [Green Version]

| Ca | Ge | Se | Sn | Te | Xe | |
|---|---|---|---|---|---|---|
| [28] | 4.268 | 2.039 | 2.998 | 2.291 | 2.528 | 2.458 |
| 1480 | ||||||
| 19 | > | 22 | ||||
| > | [29] | 800 [30] | [31] | > [26] | 40 [32] | 1100 [33] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Horoi, M. Double Beta Decay: A Shell Model Approach. Physics 2022, 4, 1135-1149. https://doi.org/10.3390/physics4040074
Horoi M. Double Beta Decay: A Shell Model Approach. Physics. 2022; 4(4):1135-1149. https://doi.org/10.3390/physics4040074
Chicago/Turabian StyleHoroi, Mihai. 2022. "Double Beta Decay: A Shell Model Approach" Physics 4, no. 4: 1135-1149. https://doi.org/10.3390/physics4040074
APA StyleHoroi, M. (2022). Double Beta Decay: A Shell Model Approach. Physics, 4(4), 1135-1149. https://doi.org/10.3390/physics4040074





