Influence of Magnetic Field on Characteristics of Corona Discharge in Wire-Cylinder Electrodes Configuration

Abstract

The behavior of corona discharge was investigated in wire–cylinder electrodes under the effect of a crossed magnetic field. Townsend’s formula was used commonly with a modified empirical formula to evaluate the different parameters of corona discharge in positive and negative discharge. By using a least-squares fitting, the dimensional constants A, K, and the exponent n displayed a significant dependence on the applied magnetic field. An improvement of pre-breakdown has been achieved by using a crossed magnetic field. For both polarities, while the magnetic field is present, breakdown voltage V_B and corona inception voltage V₀ increased, whereas the corona current decreases. In addition, the corona inception voltage was greater in positive corona in the absence of a magnetic field, while the opposite occurred regarding the crossed magnetic field. Furthermore, the breakdown streamer demonstrated significant triggering in the negative corona by applying the magnetic field.

1. Introduction

The characteristics of positive and negative corona discharge have been studied in a wide variety of electrostatic processes. These studies were carried out in different geometrical configurations and various operating conditions to sustain a stable corona discharge for increased optimization of current–voltage characteristics [1,2,3,4,5,6]. Corona discharge of the wire-cylinder system occurs when a high potential difference is applied between the wire and cylinder electrodes in the air at atmospheric pressure. The ionization of air molecules around the wire electrode induces a corona discharge due to electron avalanche. The electron distribution in the negative corona discharge is expected to be different from that in the positive corona due to the difference in the generation mechanisms. The ionization process produces a series of successive generations of electron avalanche progress toward the wire as the electrons are accelerated toward its surface. The positive ions created in the wake of electron avalanches drift out the ionization region and move along the conduction region to the outer cylinder, while the electrons are neutralized in contact with the positive surface of the wire. Furthermore, in negative corona discharge, the recombination mechanisms with positive ions can be ignored. Therefore, the electron production only competes with the electron attachment phenomena which lead to the formation of negative ions. Corona discharge usually happens when a non-uniform electric field is produced from different geometrical electrodes such as point-to-plane, point-to-grade, wire-to-plane, bipolar wires-to-plane, multipoint-to-plane, wire-cylinder, and blade-plane electrodes. An intensive electric field is formed at the high-voltage electrode and causes gas ionization and partial breakdown. Every created ion as shown in Figure 1 is enclosed by the produced electric field resulting from the displacement of such ions in a zone called the drift region. In the drift region, the ions of the same polarity sweep away towards the other electrode. Figure 1 represents the positive corona discharge in the coaxial wire–cylinder electrode system. Many collisions are supposed to take place in the drift region between the free electrons with electrically neutral air molecules resulting in a momentum transfer from the ionic space charge to the air bulk. Plasma is created around the active electrode when emitted electrons from a high-voltage electrode ionize the ambient air in the inter-electrode gap [2,4].

The current–voltage characteristics of corona for both positive and negative discharge have been extensively analyzed in several studies under different operating conditions and various electrode geometries. With a point-to-plane geometry, a new general formula in characterizing the relationship of corona current-voltage was derived by Meng et al. [1]. It was demonstrated that the proposed formula is applicable not only for both negative and positive coronas in point-to-plane geometries but also for both polarities in point-to-ring geometry. By applying the general formula proposed by Meng et al. [1], an experimental investigation was carried out by Kaci et al. [2] for positive and negative corona discharge in blade-to-plane electrodes. The current-voltage characteristics, breakdown voltage, and the Warburg current distribution were measured. The current-voltage characteristics of both polarities in a blade-to-plane electrode configuration were found. In the wire cylinder reactor, Zheng et al. [3] presented an experimental measurement and numerical analysis of the current-voltage characteristics of DC corona discharges in an air gap between the electrodes. The measured results were fitted by different empirical formulae and analyzed by using a fluid model. In the more general configuration of electrodes, the behavior of DC corona discharge in the air with the wire-to-plane geometry was analyzed by Ait Said et al. [4]. The formulae $\mathrm{I}=\mathrm{AV}\left(\mathrm{V}-{\mathrm{V}}_0\right)$ and $\mathrm{I}=\mathrm{K}{\left(\mathrm{V}-{\mathrm{V}}_0\right)}^{\mathrm{n}}$ were used to determine different corona parameters for the two polarities of the corona discharge. By using the curve fitting, it was shown that the geometric factors K and A and the exponent n are strongly affected by the number of discharging wires. On the other hand, the influence of the magnetic field on current-voltage characteristics has been analyzed in many experimental and theoretical studies. In the magnetically enhanced corona discharge, Junfeng et al. [5] showed that corona currents are enhanced when a longitudinal magnetic field was applied towards the direction of the free electrons in the air gap between the electrodes. The corona currents were enhanced because of the Larmor movements of free electrons in the ionization region. It was assumed that the increase in discharge currents is attributed to only the enhanced ionization process in the small ionization region and is not relevant to the lengthening trajectory of free electrons in the wide drift inter-electrode region. In the case of a transverse magnetic field, an improvement in pre-breakdown characteristics has been investigated experimentally by Karim [6] when the magnetic field was applied perpendicularly to the electric field between the wire-cylinder electrodes. The influence of the transverse magnetic field has the effect of increasing the corona onset voltage and decreasing the corona current. In addition, Stariskovskiy et al. [7] proposed a numerical simulation for the development of streamer discharge using and external longitudinal magnetic field. The self-focusing effect of a streamer discharge in such external longitudinal magnetic field was observed for both positive and negative pulse polarities.

The current-voltage characteristics of corona discharge have been described in several empirical formulas. Although the phenomenon of corona discharge is considered as a complex process, the DC steady corona current-voltage relationship in wire-cylinders electrode system can be characterized by the Townsend relationship [8], which is provided as follows:

$$\mathrm{I}=\mathrm{AV}\left(\mathrm{V}-{\mathrm{V}}_0\right)$$

(1)

where I is the corona current, V is the applied voltage, V₀ is the corona inception voltage, and A is a dimensional constant depending on the inter-electrode distance, including charge carrier mobility in the drift region and other geometrical factors. Another empirical formula was proposed by Ferreira et al. [9] for small distances of inter-electrode gap separations, which is expressed as follows:

$$\mathrm{I}=\mathrm{K}{\left(\mathrm{V}-{\mathrm{V}}_0\right)}^2$$

(2)

where K is a dimensional constant. Meng et al. [1] suggested another kind of relationship for point-to-plane electrode system, which is expressed as follows.

$$\mathrm{I}=\mathrm{K}{\left(\mathrm{V}-{\mathrm{V}}_0\right)}^n$$

(3)

It was demonstrated that the exponent n falls into a limited scope of 1.5–2.0. This formula has been used widely in many proposal studies in describing corona current-voltage characteristics because it well explained the struggles met by other existing formulae and represented corona characteristics with suitable accuracy. Equation (3) can be rewritten as follows:

$${\log }_{10}\left(\mathrm{I}\right)={\mathrm{n}\log }_{10}\left(\mathrm{V}-{\mathrm{V}}_0\right)+\mathrm{C}$$

(4)

where K = 10^C, and the current-voltage characteristics of the corona discharge can be described by Equations (1) and (2), where the parameters A, K, V₀, and n depend on the electrode’s geometry, the charge carrier’s mobility. and the physical parameters of the gas, such as the pressure, temperature, and humidity [6]. The present study is concerned with an investigation of a corona discharge for both positive and negative polarity under the influence of transverse magnetic field in a wire-cylinder electrode system. The main goal of the study is based on the application of the magnetic field B perpendicularly along the axis of the inter-electrode gap. The radius of cylinder R and the radius of the wire r₀ are fixed during the current-voltage measurements. The correlations of corona parameters such as the dimensional constants A, K, exponent n, and corona inception voltage V₀ will be analyzed separately at different values of a crossed magnetic field B by applying the general relationships of Townsend (Equation (1)) and the empirical formula proposed by Meng et al. [1] (Equation (3)).

2. Materials and Methods

The schematic diagram of the experimental setup is shown in Figure 2. The system apparatus consists of a wire-cylinder arrangement. A 350 mm long tube electrode of 50 mm inner diameter and a 400 mm long wire electrode with 8 mm diameter were employed for corona measurements. The electrodes were made of aluminum and placed horizontally. The wire probe was inserted and precisely fitted at the center of the cylindrical tube using a two rubber stoppers at both sides. Fitting holes are made into the two rubber stoppers by using a sophisticated machine to ensure stability and homogeneity of the produced corona discharge plasma. A high voltage DC power supply with (maximum 25 kV and maximum 285 microamperes, Leybold, LN 30909729) was used to provide the system with high voltage. Both positive dc and negative dc voltages are applied to the wire electrode, while the tube electrode is grounded. A multimeter (CHAUVIN ARNOUX, C.A 401) was connected to measure the corona currents for both polarities. For the present study, a coil magnet was made to produce a magnetic field intensity up to 100 mT. The magnetic field was applied perpendicularly along the axis of the inter-electrode gap.

The magnet coil was surrounded the cylinder tube and insulated by a Teflon tube of 6 cm diameter. The alignment of the magnetic field was organized in such a manner as to provide a uniform and homogenous distribution of the crossed magnetic field along the gap between the electrodes. Analysis software was performed to determine corona parameters with their approximated errors. All measurements were carried out in the low field region and in the air at a room temperature of 300 K, atmospheric pressure of 1 atm, and relative humidity (RH) at 62.2%.

3. Results and Discussions

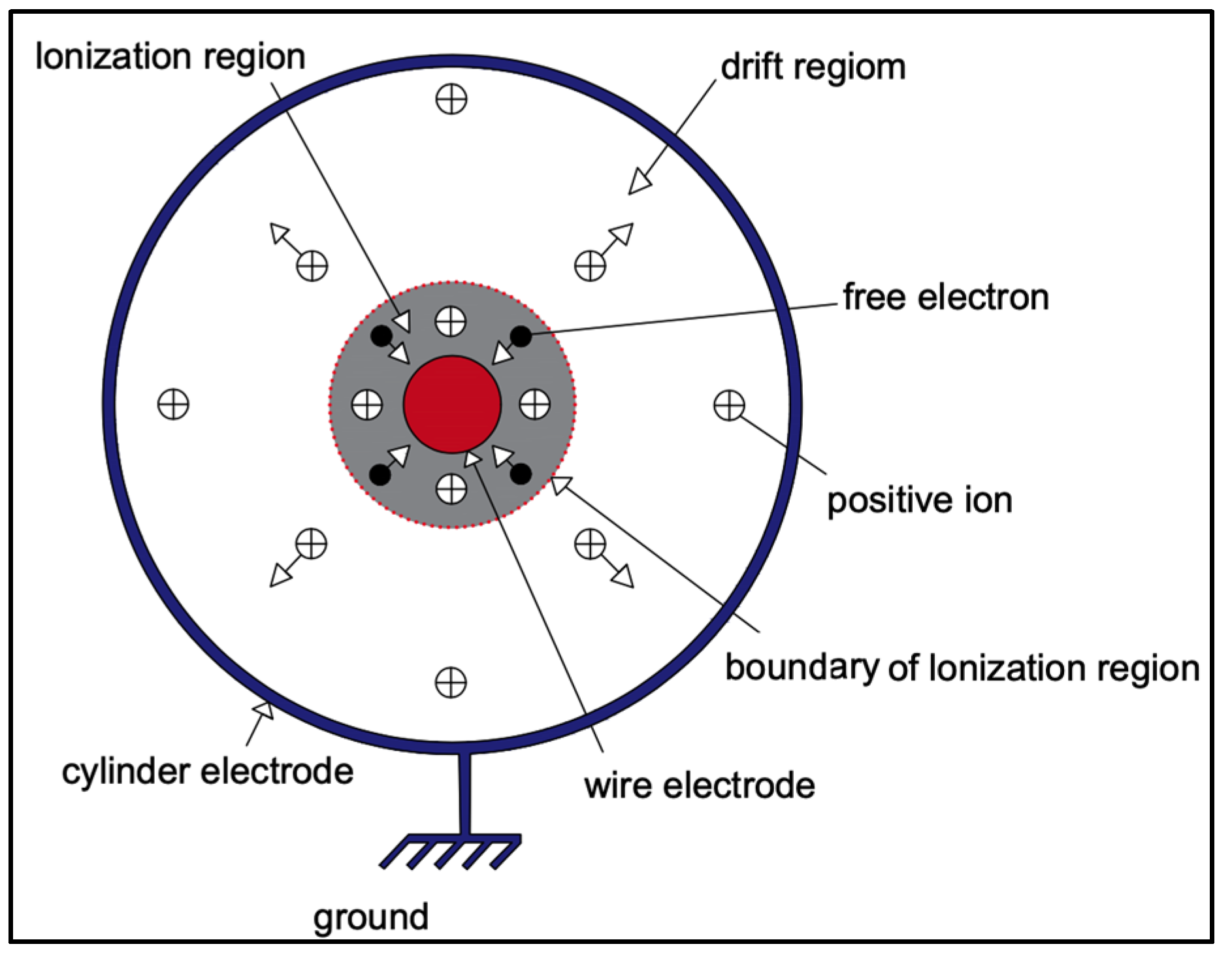
3.1. Current-Voltage Characteristics

The experimental current-voltage data at different values of a crossed magnetic field B are shown in Figure 3 and Figure 4 for positive and negative corona discharge, respectively. The influence of the transverse magnetic field was demonstrated as a pronounced downward shifting of current-voltage characteristics for both discharge polarities. On the other hand, the maximum corona currents decreased by increasing the crossed magnetic field. The reduction in corona currents was more significant in negative discharge compared to that in positive discharge.

The variation of corona currents versus applied magnetic field at a fixed value of applied voltage is shown in Figure 5 and Figure 6 for both discharge polarities. The effect of the crossed magnetic field was considered in both discharge polarities but it was more considerable in negative corona discharge. The results demonstrated that the breakdown streamer was triggered in the negative corona at a higher voltage with the crossed magnetic field than that in the positive corona. Thus, the transverse mode of the magnetic field made a significant contribution in the breakdown streamer in both positive and negative corona discharges. This was because of the distribution of space charges due to the breakdown streamer with a crossed magnetic field in the ionization region. On the other hand, the breakdown takes place due to positive and negative streamers that were initiated from the ionization region in the vicinity of wire electrodes under positive and negative corona, respectively [6,7].

Current-voltage characteristics confirmed that the influence of transverse magnetic field for negative corona was greater than positive corona, which could be attributed to the fact that the mass of electrons is smaller than the mass of ions while the electrons have a larger mean free path compared to ions. Thus, a greater deflection of free electrons in the drift region is supposed to take place than compared to ions. The small mass with the larger mean free path of electrons results in larger bending under the effect of a transverse magnetic field [10].

The transverse magnetic field could be considered as a barrier of restriking the movement of free electrons in both the ionization region and drift region. Therefore, the barrier of crossed magnetic field embarrasses the progression of the charge carrier in such regions in the absence of applied voltage. Accordingly, a significant increase was observed in the corona inception voltage with a reduction in corona currents at both corona discharge polarities.

3.2. Corona Inception Voltage

It was demonstrated that it is impossible to measure an accurate corona inception voltage during an abrupt corona inception current. The corona inception voltage for positive and negative corona discharges is highly close to the steady corona current at about 0.1 μA from Trichel pulse inception as the corona current is shifting back and forth uncertainly depending on an aperiodic nature of the discharge. The influence of geometrical configuration on current-voltage characteristics referred to an order of 0.1 μA as a threshold point of the corona inception current [1]. However, the estimated inception voltage could be deduced from experimental measurements of corona inception current into the range of 0.1–1.0 μA. In the present study, the corona inception voltage was measured at an initial rise of corona current for both discharge polarities whether with or without the crossed magnetic field. 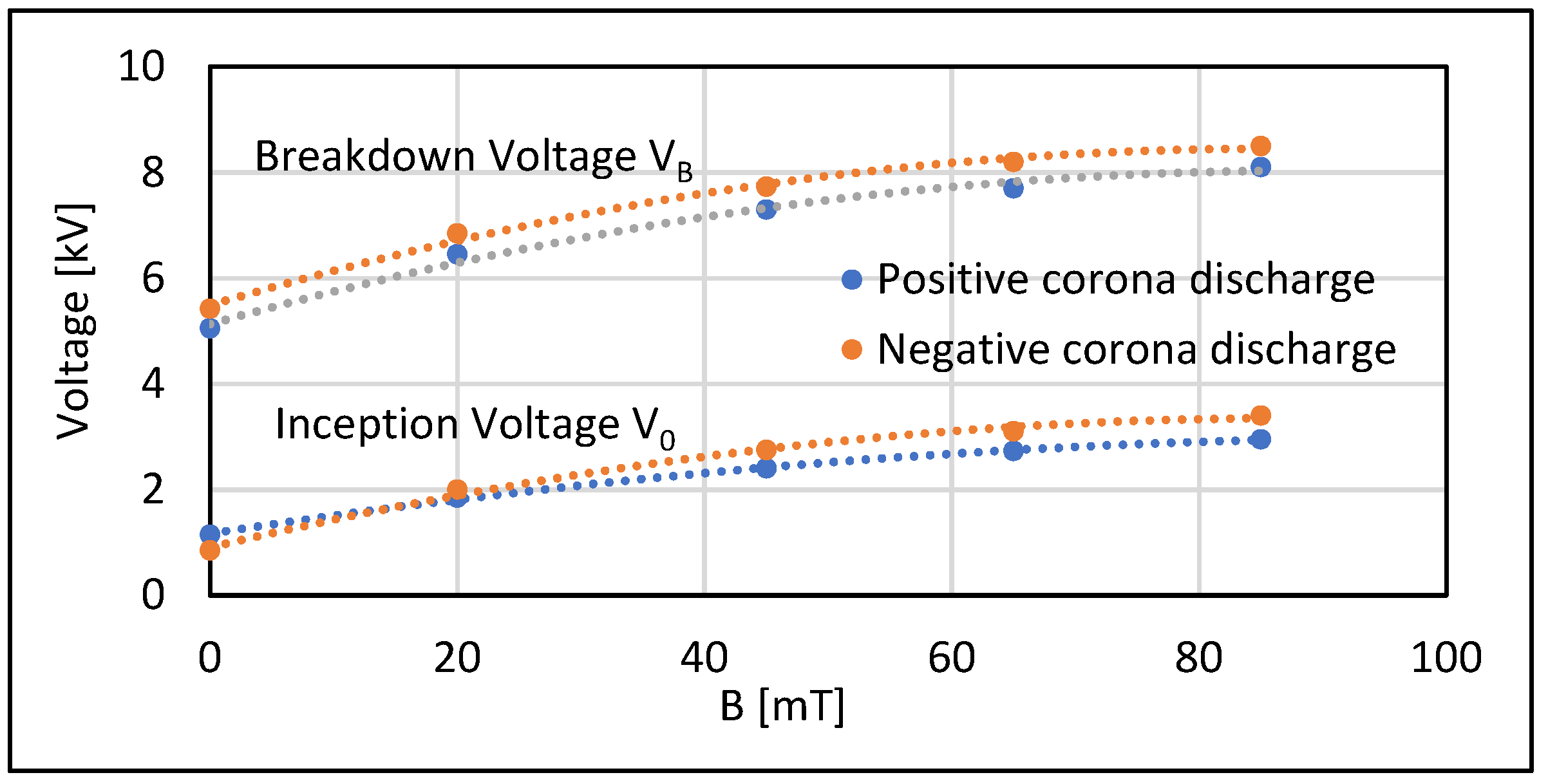The variation of the measured corona inception voltages and breakdown voltages against the cross magnetic field is shown in Figure 7.

In the presence of the crossed magnetic field, an observable increase was shown in the corona inception voltage and breakdown voltage at a different range of applied voltage for both positive and negative coronas. In the absence of a crossed magnetic field, Figure 7 shows that the inception voltage of the positive corona is greater than the negative corona while the opposite occurs when applying a crossed magnetic field. It was also observed that the voltage required for breakdown is smaller in the positive corona than the negative corona whether with the presence or absence of crossed magnetic fields.

The small radius of the wire electrode provides a large inter-electrode gap separation between the wire and cylinder electrodes; therefore, the breakdown discharge needs more potential difference to reach the threshold point of corona inception voltage. A higher corona inception voltage was observed for positive corona in the absence of a crossed magnetic field. This can be attributed to the large cross-section area of the cylinder compared to the wire electrode, which in turn needs less potential to sustain the breakdown of negative corona discharge [11,12]. The contribution of a transverse magnetic field was obvious in the improvement of pre-breakdown characteristics, which are attributed to the fact that the crossed magnetic field accelerates the motion of the electrons released by ions falling on the cathode in the curvature path. The electrons in a strong magnetic field are inclined completely, and the anode is incapable in attracting such electrons anymore. Therefore, the electrons are supposed to be recaptured by the cathode, which results in a reduction in the ionization mean free path λ of electrons, the primary ionization coefficient α, and the secondary ionization coefficient γ. Accordingly, lower corona currents were observed as the crossed magnetic field increased [13,14]. Using a least-squares fitting routine, a linear dependence of corona inception voltage V₀ versus the crossed magnetic field B is clearly shown in Figure 8 on a log₁₀ scale for both discharge polarities. A plot of log₁₀ scale is usually used to transfer a nonlinear dependence between two variables into a linear relationship to find a suitable value of such dependence [1,5]. For this purpose, the data of V₀ in Figure 7 were used on log₁₀ scale to determine a value of an exponent that represents the relationship between the corona inception voltage and the transverse magnetic field.

Figure 8 represents a linear relationship of V₀ with crossed magnetic field B for both discharge polarities. From the curve fitting, the following relationships of corona inception voltage were obtained for positive and negative corona discharges, respectively.

$${\mathrm{V}}_0^{+}\left[\mathrm{kV}\right]=0.698{(\mathrm{B}\left[\mathrm{mT}\right])}^{0.325}$$

(5)

$${\mathrm{V}}_0^{-}\left[\mathrm{kV}\right]=0.669{(\mathrm{B}\left[\mathrm{mT}\right])}^{0.367}$$

(6)

Equations (5) and (6) confirmed that the corona inception voltage increased for both discharge polarities as the transverse magnetic field increases.

Table 1. The experimental and the calculated values of V₀ at different B for positive and negative corona discharge.

B (mT)	0	20	45	65	85
${\mathrm{V}}_0^{+}\left(\mathrm{Exp}.\right)$	1.15 ± 0.0011	1.85 ± 0.0011	2.4 ± 0.0011	2.73 ± 0.0011	2.95 ± 0.0011
${\mathrm{V}}_0^{+}\left(\mathrm{Cal},\right)$		1.853 ± 0.01	2.412 ± 0.015	2.732 ± 0.021	2.966 ± 0.032
${\mathrm{V}}_0^{-}\left(\mathrm{Exp}.\right)$	0.85 ± 0.0011	2.00 ± 0.0011	2.75 ± 0.0011	3.1 ± 0.0011	3.4 ± 0.0011
${\mathrm{V}}_0^{-}\left(\mathrm{Cal},\right)$		2.012 ± 0.012	2.709 ± 0.018	3.1001 ± 0.023	3.421 ± 0.036

includes the experimental values of corona inception voltage V0 whether with and without a crossed magnetic field. Furthermore, in the presence of a transverse magnetic field, the analysis software calculated the values of V0 using Equations (5) and (6) with their approximated errors and compared them with those measured experimentally for both corona polarities as shown in Table 1.

3.3. The Geometrical Factor A versus the Crossed Magnetic Field B

For a geometrical configuration system consisting of wire and cylinder electrodes, the current-voltage characteristics have been analytically found by the Townsend relationship with acceptable accuracy, as referred to in Equation (10). The most reliable and widely accepted method of applying the Townsend relationship is an experimental analysis of acquired current-voltage data by using the least-squares fittings technique [15]. The analysis of the present study was employed to modify the generalized criterion relation of Townsend and the empirical formula proposed by Meng et al [1] under the influence of a crossed magnetic field for the majority of the experimental data arrays of the positive and negative corona. Equation (1) can be rewritten as follows:

$$\mathrm{I}/\mathrm{V}=\mathrm{A}\left(\mathrm{V}-{\mathrm{V}}_0\right)$$

(7)

where the geometrical factor A in the case of wire cylinder electrodes is given by the following [16]:

$$\mathrm{A}=\frac{8{\mathsf{\pi }\mathsf{\epsilon }}_0\mathsf{\mu }}{{\mathrm{R}}^2\ln \left(\frac{\mathrm{R}}{{\mathrm{r}}_0}\right)}$$

(8)

where ε₀ is the permittivity of the medium, μ is the mobility of the charge carriers, and R and r0 are the radius of the cylinder tube and wire electrode, respectively. Equation (8) indicates that factor A depends on the gas properties and the geometrical configuration of the electrodes. From Equation (7), geometrical factor A can be easily determined from the curve fitting of the current/voltage ratio I/V versus the voltage difference (V − V0). A linear dependence of I/V versus (V − V0) was found as shown in Figure 9 and Figure 10 for positive and negative corona, respectively.

The geometrical factor A represented the slope of the straight lines using the least-squares fitting method for both discharge polarities at the different crossed magnetic fields. The extracted values of A from Figure 9 and Figure 10 were plotted against the transverse magnetic field B for both discharge polarities. It has been found that factor A decreases as the transverse magnetic field B increases in a non-linear dependence manner as shown in Figure 11. By using the log₁₀ scale, a linear dependence between A and B was found, as shown in Figure 12.

From the curve fitting, a relationship was obtained individually for each discharge polarity that represents the variation of the geometrical factor A versus the crossed magnetic field B as follows.

$${\mathrm{A}}^{+}\left[\mathsf{\mu }\mathrm{A}/{\mathrm{kV}}^2\right]=0.109{(\mathrm{B}\left[\mathrm{mT}\right])}^{-0.33}$$

(9)

$${\mathrm{A}}^{-}\left[\mathsf{\mu }\mathrm{A}/{\mathrm{kV}}^2\right]=0.176{(\mathrm{B}\left[\mathrm{mT}\right])}^{-0.33}$$

(10)

The mobility of the charge carriers μ was calculated using Equation (8), where $\frac{{\mathrm{A}}^{-}}{{\mathrm{A}}^{+}}=\frac{{\mathsf{\mu }}^{-}}{{\mathsf{\mu }}^{+}}$ for the same geometrical configuration of electrodes. This ratio was 1.54 for the present study, which confirms that the mobility of the negative charge carriers is always higher than those of the positive charge carriers. It has been mentioned in several studies that there is a small difference of about 10% between the mobilities μ⁺ and μ⁻. It was noted that the values of A for the negative corona are always higher than those of the positive corona for the same value of the crossed magnetic field, which could be attributed to the fact that, during the negative corona discharge, one component of the negative charge in the drift region is formed by electrons of which its mobility is higher than those of ions [17,18]. The extracted values of A from Figure 9 and Figure 10 were compared with those calculated by Equations (9) and (10), as shown in

Table 2. The extracted and the calculated values of A and the mobility of charge carries μ at different magnetic field B for positive and negative corona discharge.

B (mT)	${\mathbf{A}}_{\mathbf{E}\mathbf{x}\mathbf{t}\mathbf{r}\mathbf{a}\mathbf{c}\mathbf{t}\mathbf{e}\mathbf{d}}^{+}$	${\mathbf{A}}_{\mathbf{C}\mathbf{a}\mathbf{l}\mathbf{c}\mathbf{u}\mathbf{l}\mathbf{a}\mathbf{t}\mathbf{e}\mathbf{d}}^{+}$	${\mathbf{A}}_{\mathbf{E}\mathbf{x}\mathbf{t}\mathbf{r}\mathbf{a}\mathbf{c}\mathbf{t}\mathbf{e}\mathbf{d}}^{-}$	${\mathbf{A}}_{\mathbf{C}\mathbf{a}\mathbf{l}\mathbf{c}\mathbf{u}\mathbf{l}\mathbf{a}\mathbf{t}\mathbf{e}\mathbf{d}}^{-}$	${\mathsf{\mu }}_{\mathbf{C}\mathbf{a}\mathbf{l}\mathbf{c}\mathbf{u}\mathbf{l}\mathbf{a}\mathbf{t}\mathbf{e}\mathbf{d}}^{+}$	${\mathsf{\mu }}_{\mathbf{C}\mathbf{a}\mathbf{l}\mathbf{c}\mathbf{u}\mathbf{l}\mathbf{a}\mathbf{t}\mathbf{e}\mathbf{d}}^{-}$	A/A+
0	0.0498 ± 0.002		0.0779 ± 0.014		0.2565 ± 0.017	0.4012 ± 0.019	1.5643 ± 0.006
20	0.0398 ± 0.001	0.0403 ± 0.003	0.0638 ± 0.016	0.0647 ± 0.015	0.2050 ± 0.021	0.3286 ± 0.027	1.6030 ± 0.002
45	0.0316 ± 0.003	0.0308 ± 0.004	0.0511 ± 0.028	0.0494 ± 0.022	0.1627 ± 0.028	0.2632 ± 0.032	1.6171 ± 0.001
65	0.0275 ± 0.005	0.0273 ± 0.004	0.0432 ± 0.034	0.0437 ± 0.029	0.1416 ± 0.025	0.2225 ± 0.028	1.5709 ± 0.002
85	0.0244 ± 0.003	0.0249 ± 0.004	0.0394 ± 0.045	0.0399 ± 0.048	0.1257 ± 0.031	0.2029 ± 0.033	1.6148 ± 0.004

with their approximated errors at various transverse magnetic fields B and for both positive and negative polarities.

According to Equations (8)–(10), the current against the different voltage mobility of charge carriers for positive and negative corona discharges can be provided as follows.

$${\mathsf{\mu }}^{+}\left[{\mathrm{cm}}^2/\mathrm{V}·\mathrm{s}\right]=0.561\mathrm{B}{\left(\left[\mathrm{mT}\right]\right)}^{-0.33}$$

(11)

$${\mathsf{\mu }}^{-}\left[{\mathrm{cm}}^2/\mathrm{V}·\mathrm{s}\right]=0.906\mathrm{B}{\left(\left[\mathrm{mT}\right]\right)}^{-0.33}$$

(12)

It was confirmed from Equations (11) and (12) that the mobility of both positive and negative charge carriers decreased as the transverse magnetic field increases. However, the experimental results declared that the influence of the transverse magnetic field restricts the mobility of charge carriers, which in turn results in a decrease in their velocity in the draft region (v = μE), and this reduces the electrical wind produced by corona discharge [19,20].

3.4. The Geometrical Factor K versus the Crossed Magnetic Field B

The effect of a crossed magnetic field on the current-voltage characteristics of the wire-cylinder electrodes system was also subjected to analysis using the empirical formula proposed by Meng et al. [1] shown in Equation (3). By performing the analysis process of acquired current-voltage data, exponent n and geometrical factor K can be easily determined for both positive and negative corona discharges using Equation (4). A linear dependence of corona current against the difference voltage (V − V₀) on the log₁₀ scale is presented in Figure 13 and Figure 14 for positive and negative coronas, respectively. The experimental results of the exponent n and the geometrical factor K are shown in

Table 3. The extracted values of the exponent n and the geometrical factor K for both discharge polarities.

B (mT)	n+	n−	K+ (μA/kV2)	K− (μA/kV2)
0	1.7004 ± 0.014	1.8351 ± 0.011	0.1615 ± 0.025	0.1372 ± 0.024
20	1.6665 ± 0.016	1.7852 ± 0.017	0.1437 ± 0.023	0.1289 ± 0.026
45	1.5554 ± 0.021	1.7491 ± 0.024	0.1393 ± 0.028	0.1120 ± 0.03
65	1.5321 ± 0.03	1.7513 ± 0.031	0.1373 ± 0.03	0.1033 ± 0.032
85	1.5168 ± 0.031	1.7149 ± 0.033	0.1355 ± 0.032	0.0958 ± 0.034

with their approximated errors.

It was noted that the exponent n for both corona discharge polarities decreased as the cross magnetic field increased. Moreover, the extracted values of exponent n were relatively higher in negative corona than those determined in positive corona. The geometrical factor K decreased slightly as the transverse magnetic field increased, and there were little differences between their values in both corona discharge polarities, but the negative corona was higher than positive corona discharge. The extracted values of K from Figure 13 and Figure 14 were plotted against the crossed magnetic field on the log₁₀ scale for both discharge polarities, as shown in Figure 15.

By using a least-squares fitting method, the following expression regarding geometrical factor K for positive and negative corona discharges was obtained, respectively.

$${\mathrm{K}}^{+}\left[\mathsf{\mu }\mathrm{A}/{\mathrm{kV}}^2\right]=0.162\mathrm{B}{\left(\left[\mathrm{mT}\right]\right)}^{-0.04}$$

(13)

$${\mathrm{K}}^{-}\left[\mathsf{\mu }\mathrm{A}/{\mathrm{kV}}^2\right]=0.237\mathrm{B}{\left(\left[\mathrm{mT}\right]\right)}^{-0.2}$$

(14)

It is clear from Equations (13) and (14) that geometrical factor K is affected appreciably by the transverse magnetic field in negative corona more than positive corona where the magnetic field has less influence. Similarly, the following expressions were obtained for the exponent n as referred to by Figure 16 for positive and negative discharges, respectively.

$${\mathrm{n}}^{+}=2.023\mathrm{B}{\left(\left[\mathrm{mT}\right]\right)}^{-0.066}$$

(15)

$${\mathrm{n}}^{-}=1.918\mathrm{B}{\left(\left[\mathrm{mT}\right]\right)}^{-0.024}$$

(16)

According to the experimental investigations performed in the present study concerning all corona parameters, a more specific relationship of the current-voltage characteristics under the influence of a transverse magnetic field for both discharge polarities in wire-cylinder electrodes system could be introduced. These relationships present a modification of the formulae proposed by Townsend and Meng et al. [1]. Therefore, Equation (1) can be rewritten depending on the experimental results of the present study for positive and negative coronas, respectively, as follows.

$${\mathrm{I}}_{\mathrm{Eq}\_1}^{+}\left[\mathsf{\mu }\mathrm{A}\right]=0.109\mathrm{V}\left[\mathrm{kV}\right]{(\mathrm{B}\left[\mathrm{mT}\right])}^{-0.33}(\mathrm{V}\left[\mathrm{kV}\right]-0.698\left(\mathrm{B}\left[\mathrm{mT}\right]{)}^{0.325}\right)$$

(17)

$${\mathrm{I}}_{\mathrm{Eq}\_1}^{-}\left[\mathsf{\mu }\mathrm{A}\right]=0.176\mathrm{V}\left[\mathrm{kV}\right]{(\mathrm{B}\left[\mathrm{mT}\right])}^{-0.33}(\mathrm{V}\left[\mathrm{kV}\right]-0.669{(\mathrm{B}\left[\mathrm{mT}\right])}^{0.367})$$

(18)

Similarly, the modification of Equation (3) produced the following expressions.

$${\mathrm{I}}_{\mathrm{Eq}\_3}^{+}\left[\mathsf{\mu }\mathrm{A}\right]=0.162{(\mathrm{B}\left[\mathrm{mT}\right])}^{-0.04}(\mathrm{V}\left[\mathrm{kV}\right]-0.698{(\mathrm{B}\left[\mathrm{mT}\right]{)}^{0.325})}^{2.023{(\mathrm{B}\left[\mathrm{mT}\right])}^{-0.066}}$$

(19)

$${\mathrm{I}}_{\mathrm{Eq}\_3}^{-}\left[\mathsf{\mu }\mathrm{A}\right]=0.237 {(\mathrm{B}\left[\mathrm{mT}\right])}^{-0.2}(\mathrm{V}\left[\mathrm{kV}\right]-0.669{(\mathrm{B}\left[\mathrm{kV}\right]{)}^{0.367})}^{1.918{(\mathrm{B}\left[\mathrm{mT}\right])}^{-0.024}}$$

(20)

The above equations represent modified empirical formulae describing current-voltage characteristics of corona discharge under the influence of the transverse magnetic field of a wire-cylinder electrode system in the air at atmospheric pressure and room temperature 300 K. It is believed from experimental investigations of this study that the characteristics of wire-cylinder corona discharge under the effect of a crossed magnetic field for both discharge polarities met with certain complications in agreement completely with the Townsend formula (Equation (1)) and Meng et al. [1] relationship (Equation (3)). Despite several theoretical and experimental investigations on corona discharge, there have been discrepancies in describing current-voltage characteristics in different electrode configurations.

In this study, the investigations showed that the transverse magnetic field has almost the same contribution on the potential scope for determining corona inception voltage V₀, where the proportional exponents of the magnetic field were 0.325 and 0.367 with constant coefficients 0.698 and 0.669 for positive and negative corona discharge, respectively. The estimated inception voltages were chosen once the corona current arose in both discharge polarities and the resulting corona inception voltages followed a nonlinear trend with a crossed magnetic field as shown in Figure 7. The dependence of geometrical factor A in the Townsend formula (Equation (1)) on the crossed magnetic field showed an equal correlation exponent of −0.33 with a coefficient of small differences such as 0.109 and 0.176 for positive and negative coronas, respectively.

The linear dependence of corona currents I and voltage difference (V − V₀) on the log₁₀ scale provided the values of the exponent n for both discharge polarities as shown in Figure 13 and Figure 14. Exponent n was deduced in the range 1.5168–1.7004 for positive corona and 1.7149–1.8351 for negative corona, where the correlation between the magnetic field B and exponent n was inversely proportional. For the modified relationships referred to by Equations (19) and (20), exponent n was pivotal for describing an accurate characteristic of corona discharge. A plot of exponent n versus B on the log₁₀ scale provided little difference in the variation in n to B, as shown in Figure 16, where n was proportional to the magnetic field by exponent −0.066 and coefficient 2.023 for positive corona while for negative corona, the exponent was −0.024 with coefficient 1.918. The geometrical factor K mentioned in Equation (3) showed a significant difference in dealing with the transverse magnetic field between the positive and negative corona discharges, as shown in Figure 15. The log₁₀ scale presents a proportionality between K and B observed at exponents −0.04 and −0.2 with coefficients 0.162 and 0.237 for positive and negative coronas, respectively.

Finally, it is reasonable to make a simple comparison between the experimental results of the present study with those proposed in Equations (1) and (3), as shown in Figure 17. It is believed that the influence of the transverse magnetic field has a different scope of dependence between the corona parameters to present a good crossmatching of current-voltage characteristics of this study with what has been proposed in Equations (1) and (3). There was a difficulty in meeting the corona characteristics of the three studies in an acceptable agreement despite fixing most conditions of the wire-cylinder electrode system such as the radius of the wire and cylinder, working pressure, temperature, and humidity of the ambient environment.

The agreement of the present study was more acceptable with Equation (1) in positive corona, while in negative corona, the compatibility of the present study was almost the same with both Equations (1) and (3). In negative corona, the current-voltage curves were found to converge more with an increasing magnetic field, and this convergence was observed at B = 85 mT. However, the increase in the transverse magnetic field is accompanied by a decrease in exponent n, which in turn excludes the agreement between the present study with Equation (3). It is believed that the contribution of the transverse magnetic field in wire-cylinder coronas for both discharge polarities enhanced some properties such as per-breakdown, but in general it restricts the operating conditions in such a manner that decreased the corona current through a reduction in the electric field.

4. Conclusions

In this study, the influence of the transverse magnetic field on current-voltage characteristics of wire-cylinder corona discharge has been investigated and compared with the previous empirical formula. The measurements have been carried out in air at an atmospheric pressure in which the crossed magnetic field was applied in four different values 20, 45, 65 and 85 mT. The corona discharge for both polarities has taken place in the lower field regions, where the maximum applied voltage reaches 10.5 kV, whereas the maximum corona current was at 7.3 μA. A significant downward trend of current-voltage characteristics of both discharge polarities was observed as the transverse magnetic field increased, where the reduction in corona current was more observable in the negative corona. The trigger breakdown streamer was found clearly at high applied voltages despite the breakdown that happened with or without the transverse magnetic field. It is believed that the pre-breakdowns for both corona polarities were enhanced with a crossed magnetic field due to the decrease in the electric field in the ionization region. Notable increases in corona inception voltage and breakdown voltage were observed in the presence of a crossed magnetic field at both discharge polarities. The corona inception voltage was greater in the positive corona in the absence of magnetic files while the opposite took place with a crossed magnetic field. The ratio $\frac{{\mathrm{A}}^{-}}{{\mathrm{A}}^{+}}=\frac{{\mathsf{\mu }}^{-}}{{\mathsf{\mu }}^{+}}>1$ confirmed that the mobility of electrons in the drift region is higher than ions for which the corona discharge is lower in negative polarity. By using least-squares curve fitting, all corona parameters such as the geometrical factors A and K, corona inception voltage V₀, and exponent n were determined on a log₁₀ scale with or without a crossed magnetic field. Finally, a comparison was performed between the experimental investigations of the present study with two well-known and widely used empirical formulae. It is believed that the effect of the transverse magnetic field met with a different scope of difficulties in having an acceptable compatibility between all corona parameters, although all conditions of the operating system were fixed.