Investigating Practical Impacts of Using Single-Antenna and Dual-Antenna GNSS/INS Sensors in UAS-Lidar Applications
Abstract
:1. Introduction
- provide the theoretical foundations behind different heading determination techniques used by GNSS/INS sensors;
- detail the practical considerations for implementing these heading determination techniques during UAS-lidar field operations (e.g., INS initialization procedures and mission planning considerations);
- compare the precisions of heading orientation estimates reported by a single-antenna and a dual-antenna GNSS/INS sensor at different UAS flying speeds; and
- assess the positional precisions of UAS-lidar point clouds generated from a single-antenna and a dual-antenna GNSS/INS sensor.
2. Materials and Methods
2.1. Equipment/Sensor
2.2. GNSS/INS Heading Determination Techniques
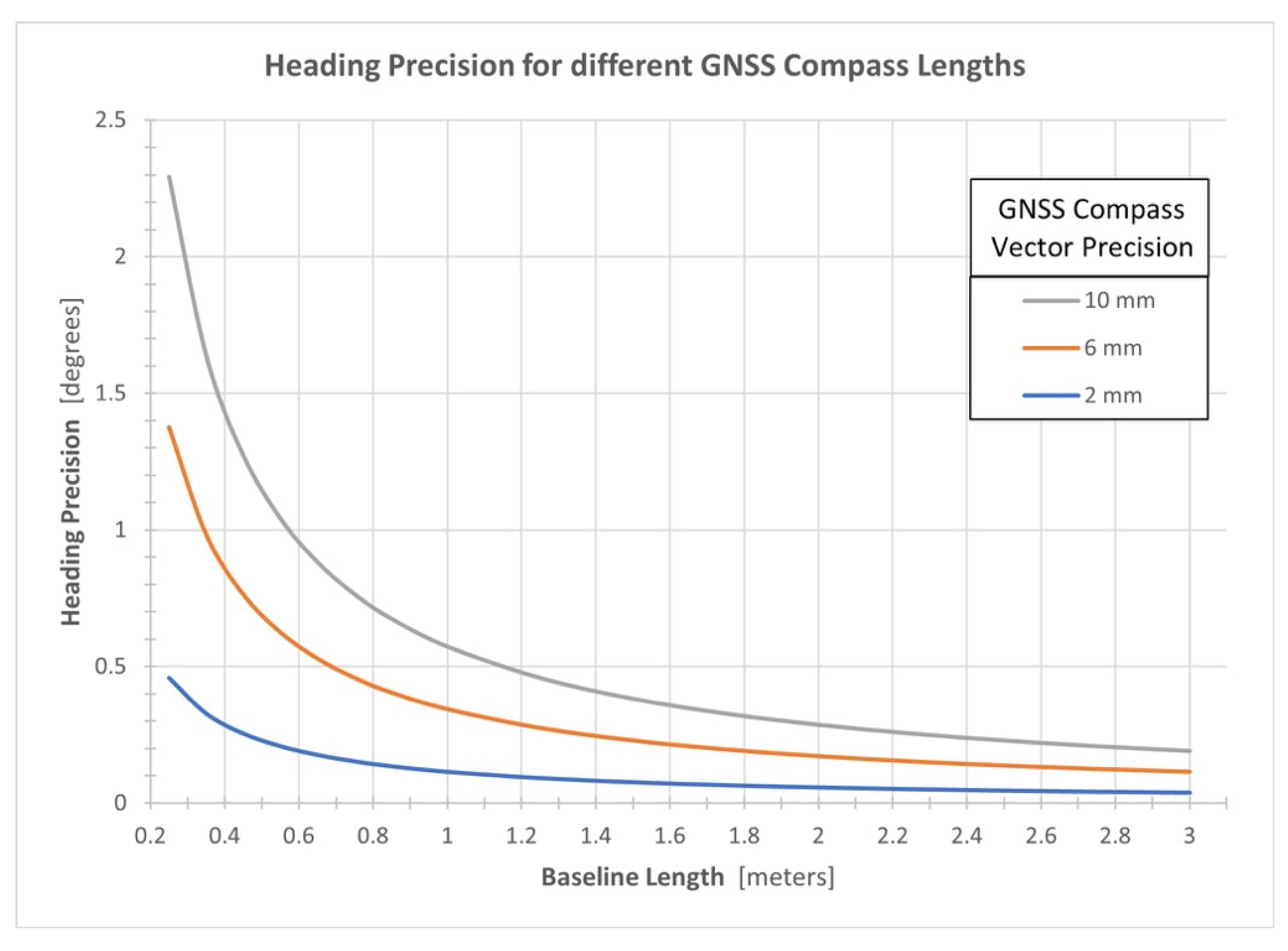
2.3. Effects of Heading Precision on the Positional Precision of a UAS-Lidar Point Cloud
2.4. Single-Antenna versus Dual-Antenna GNSS/INS Heading Precision Experiment
2.5. Summary
3. Results
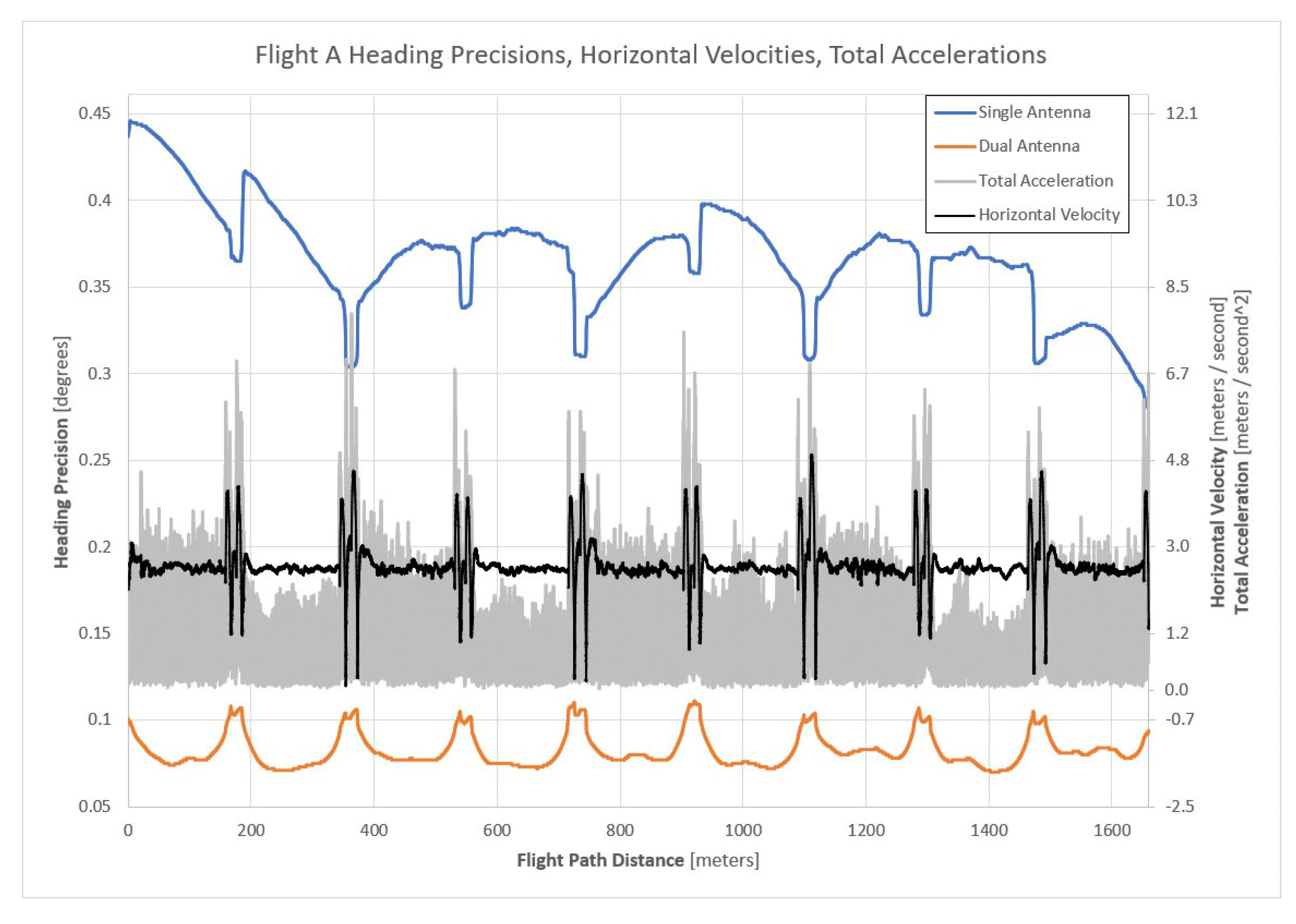
3.1. Analysis of Heading Precision Estimates for Flight A
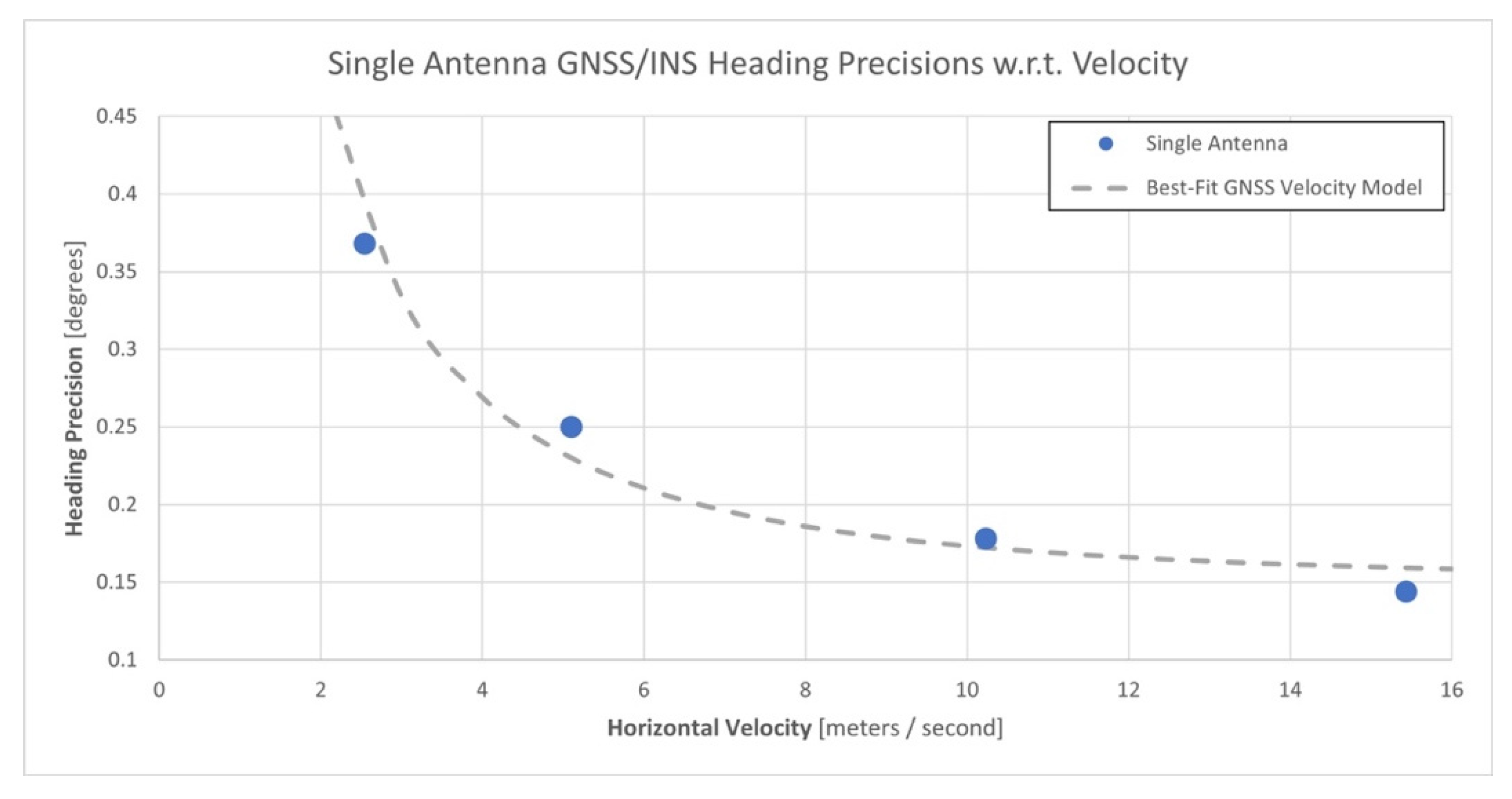
3.2. Analysis of Heading Precision Estimates for All Flights
3.3. Analysis of the Remaining Trajectory Precision Estimates for All Flights
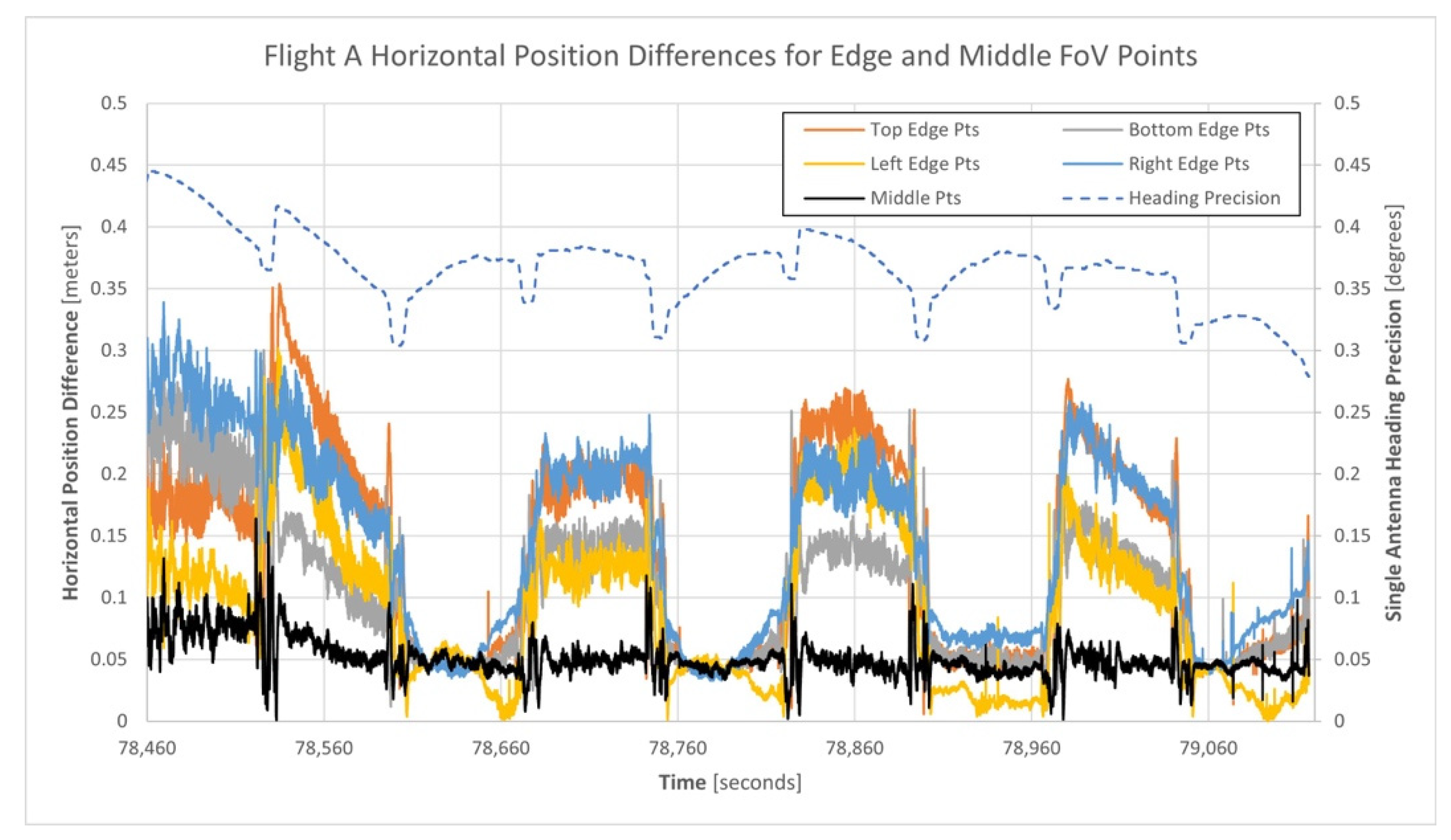
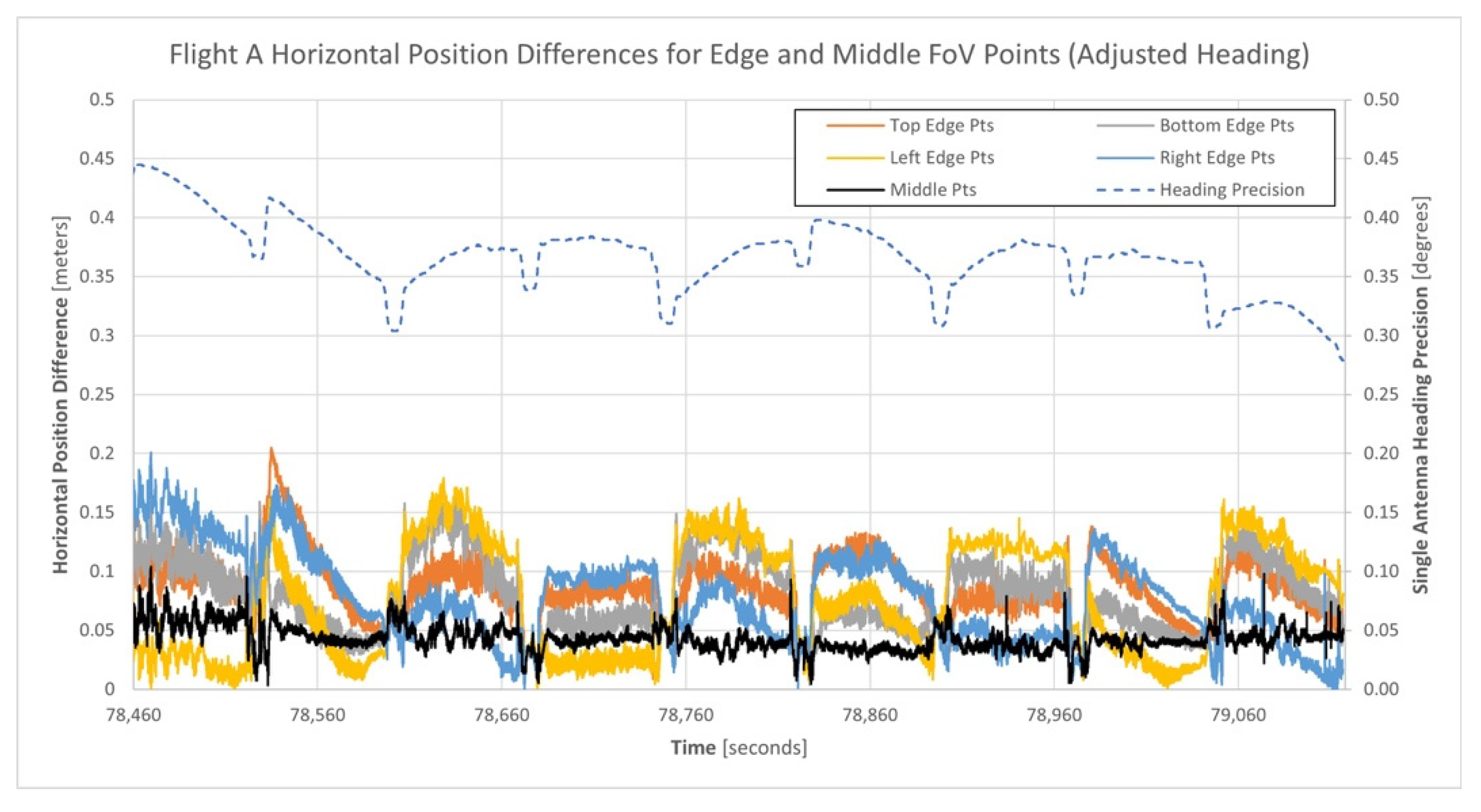
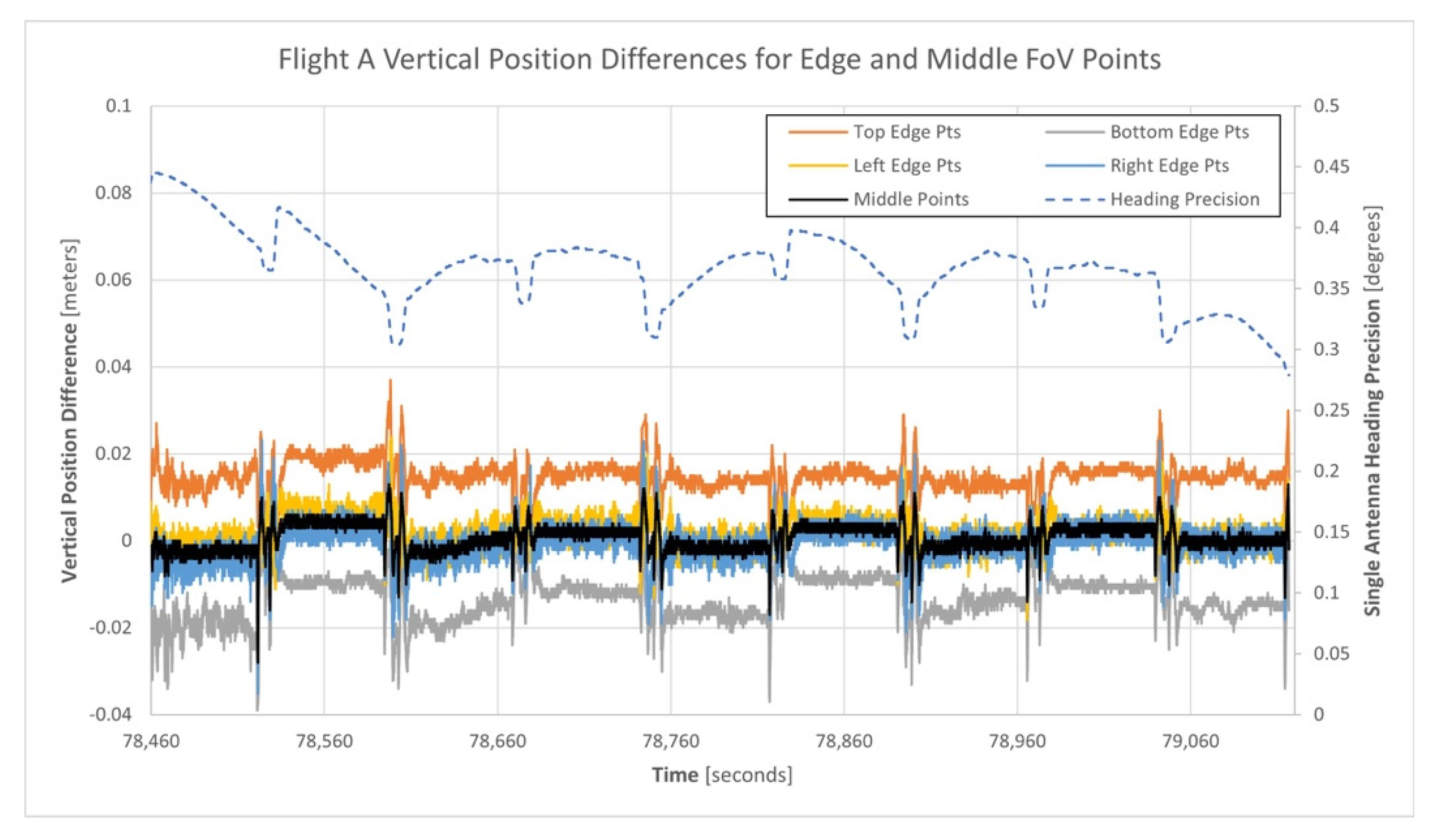
3.4. Analysis of the Point Cloud Horizontal and Vertical Positional Precision for Flight A
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jones, E.; Sofonia, J.; Canales, C.; Hrabar, S.; Kendoul, F. Advances and applications for automated drones in underground mining operations. In Proceedings of the Ninth International Conference on Deep and High Stress Mining; Joughin, W., Ed.; The Southern African Institute of Mining and Metallurgy: Johannesburg, South Africa, 2019; pp. 323–334. [Google Scholar]
- Adler, B. System Design and Real-Time Guidance of an Unmanned Aerial Vehicle for Autonomous Exploration of Outdoor Environments. Ph.D. Thesis, The University of Hamburg, Hamburg, Germany, 2014. [Google Scholar]
- Eling, C.; Wieland, M.; Hess, C.; Klingbeil, L.; Kuhlmann, H. Development and Evaluation of a UAV Based Mapping System for Remote Sensing and Surveying Applications. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 233. [Google Scholar] [CrossRef] [Green Version]
- Stocker, C.; Nex, F.; Koeva, M.; Gerke, M. Quality Assessment of Combined IMU/GNSS Data for Direct Georeferencing in the Context of UAV-based Mapping. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 355. [Google Scholar] [CrossRef] [Green Version]
- Mian, O.; Lutes, J.; Lipa, G.; Hutton, J.; Gavelle, E.; Borghini, S. Direct Georeferencing on Small Unmanned Aerial Platforms for Improved Reliability and Accuracy of Mapping without the need for Ground Control Points. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 397. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Shen, X. Direct georeferencing of airborne LiDAR data in national coordinates. ISPRS J. Photogramm. Remote Sens. 2013, 84, 43–51. [Google Scholar] [CrossRef]
- U.S. Department of Defense. Global Positioning System Standard Positioning Service Performance Standard, 5th ed.; National Coordination Office for Space-Based Positioning, Navigation, and Timing: Washington, DC, USA, 2020.
- Gaglione, S. How does a GNSS receiver estimate velocity? Inside GNSS Mag. 2015, 38–41. Available online: https://insidegnss.com/wp-content/uploads/2018/01/marapr15-SOLUTIONS.pdf (accessed on 1 May 2021).
- Noureldin, A.; Karamat, T.; Georgy, J. Fundamentals of Inertial Navigation, Satellite-Based Positioning and Their Integration; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Park, K.; Chung, D.; Chung, H.; Lee, J. Dead Reckoning Navigation of Mobile Robot Using an Indirect Kalman Filter. In Proceedings of the 1996 IEEE/SCIE/RSJ International Conference on Multisensor Fusion and Integration for Intelligent Systems, Washington, DC, USA, 8–11 December 1996; pp. 132–138. [Google Scholar]
- VectorNav. Inertial Navigation Primer; VectorNav Technologies LLC: Dallas, TX, USA, 2020; Available online: https://www.vectornav.com/resources/inertial-navigation-primer (accessed on 1 May 2021).
- Gade, K. The Seven Ways to Find Heading. J. Navig. 2016, 69, 955–970. [Google Scholar] [CrossRef] [Green Version]
- Applanix. POS MV V5 Installation and Operation Guide; Applanix Corporation: Richmond Hill, ON, Canada, 2017; Available online: https://www.applanix.com (accessed on 1 May 2021).
- Pilarska, M.; Ostrowski, W.; Bakula, K.; Gorski, K.; Kurczynski, Z. The potential of light laser scanners developed for unmanned aerial vehicles—The review and accuracy. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLII-2/W2, 87–95. [Google Scholar] [CrossRef] [Green Version]
- Jozkow, G.; Wieczorek, P.; Karpina, M.; Walicka, A.; Borkowski, A. Performance evaluation of sUAS equipped with Velodyne HDL-32E LiDAR sensor. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, XLII-2/W6, 171–177. [Google Scholar] [CrossRef] [Green Version]
- Applanix. APX-18 UAV–Single Board Dual Antenna GNSS-Inertial Solution; Applanix Corporation: Richmond Hill, ON, Canada, 2019; Available online: https://www.applanix.com/downloads/products/specs/APX18_UAV.pdf (accessed on 1 May 2021).
- Scherzinger, B.; Hutton, J. Applanix IN-Fusion Technology Explained; Applanix Corporation: Richmond Hill, ON, Canada, 2021; Available online: https://www.applanix.com/pdf/Applanix_IN-Fusion.pdf (accessed on 1 May 2021).
- Renaudin, V.; Afzal, M.; Lachapelle, G. Complete Triaxis Magnetometer Calibration in the Magnetic Domain. J. Sens. 2010, 2010, 967245. [Google Scholar] [CrossRef] [Green Version]
- Godha, S. Performance Evaluation of Low Cost MEMS-Based IMU Integrated with GPS for Land Vehicle Navigation Application. Master’s Thesis, The University of Calgary, Calgary, AB, Canada, 2006. [Google Scholar]
- Chen, W.; Qin, H.; Zhang, Y.; Jin, T. Accuracy assessment of single and double difference models for the single epoch GPS compass. Adv. Space Res. 2012, 49, 725–738. [Google Scholar] [CrossRef]
- Shin, E. Estimation Techniques for Low-Cost Inertial Navigation. Ph.D. Thesis, The University of Calgary, Calgary, AB, Canada, 2005. [Google Scholar]
- Glennie, C. Rigorous 3D error analysis of kinematic scanning LIDAR systems. J. Appl. Geod. 2007, 1, 147–157. [Google Scholar] [CrossRef]
- Habib, A.; Al-Durgham, M.; Kersting, A.; Quackenbush, P. Error budget of lidar systems and quality control of the derived point cloud. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XXXVII, 203–209. [Google Scholar]
- Rodarmel, C.; Lee, M.; Gilbert, J.; Wikinson, B.; Theiss, H.; Dolloff, J.; O’Neill, C. The Universal Lidar Error Model. Photogramm. Eng. Remote Sens. 2015, 81, 543–556. [Google Scholar] [CrossRef]
- Harre, I. A Standardised Algorithm for the Determination of Position Errors by the Example of GPS with and without ‘Selective Availability’. Int. Hydrogr. Rev. 2001, 2, 29–36. [Google Scholar]
- Brazeal, R.; Wilkinson, B.; Stamnes, G. Development of an open-source lidar and imagery-based mobile mapping system. HardwareX 2021. under review. [Google Scholar]
- Applanix. APX-15 User Manual; Applanix Corporation: Richmond Hill, ON, Canada, 2015; Available online: https://www.applanix.com (accessed on 1 May 2021).
- ASPRS. ASPRS Positional Accuracy Standards for Digital Geospatial Data. Photogramm. Eng. Remote Sens. 2015, 81, A1–A26. [Google Scholar] [CrossRef]










| Characteristic | GNSS | INS |
|---|---|---|
| Accuracy of navigation solution | High long-term accuracy but noisy in short-term | High short-term accuracy but deteriorates with time |
| Initial conditions | Not required | Required |
| Orientation information | Typically not available 1 | Available |
| Sensitive to gravity | No | Yes |
| Self-contained | No | Yes |
| Jamming immunity | No | Yes |
| Output data rate | Low | High |
| SPS 1 | RTK | PP-RTX 2 | Post-Processed | |
|---|---|---|---|---|
| Position (m) | 1.5–3.0 | 0.02–0.05 | 0.03–0.06 | 0.02–0.05 |
| Velocity (m/s) | 0.05 | 0.02 | 0.015 | 0.015 |
| Roll and Pitch (deg) | 0.04 | 0.03 | 0.025 | 0.025 |
| True Heading (deg) | 0.15 | 0.10 | 0.08 | 0.080 |
| Flight Name | Horizontal Velocity | Duration 1 | Wind Direction (from) | Wind Speeds |
|---|---|---|---|---|
| A | 2.5 m/s | 657 s | S | 2–3 m/s |
| B | 5 m/s | 351 s | S–SW | 1–2 m/s |
| C | 10 m/s | 227 s | S | 2–3 m/s |
| D | 15 m/s | 178 s | S | 2–3 m/s |
| Flight | Mean Horizontal Velocity * | Single-Antenna Heading Precisions | Dual-Antenna Heading Precisions | Improvement in Heading Precision | ||||
|---|---|---|---|---|---|---|---|---|
| Min. | Max. | Mean * | Min. | Max. | Mean | |||
| A | 2.5 m/s | 0.28° | 0.45° | 0.369° | 0.07° | 0.11° | 0.082° | 4.5× |
| B | 5.1 m/s | 0.21° | 0.35° | 0.251° | 0.07° | 0.11° | 0.086° | 2.9× |
| C | 10.2 m/s | 0.16° | 0.20° | 0.175° | 0.08° | 0.12° | 0.093° | 1.9× |
| D | 15.4 m/s | 0.12° | 0.16° | 0.141° | 0.08° | 0.11° | 0.094° | 1.5× |
| Flight | Hor. Velocity | Trajectory Estimates | Single-Antenna Precisions | Dual-Antenna Precisions | Δ | ||||
|---|---|---|---|---|---|---|---|---|---|
| Min. | Max. | Mean | Min. | Max. | Mean | ||||
| A | 2.5 m/s | North | 0.019 m | 0.025 m | 0.020 m | 0.019 m | 0.023 m | 0.020 m | 0.000 m |
| East | 0.019 m | 0.024 m | 0.020 m | 0.018 m | 0.022 m | 0.019 m | 0.001 m | ||
| Height | 0.036 m | 0.036 m | 0.036 m | 0.036 m | 0.036 m | 0.036 m | 0.000 m | ||
| Roll | 0.03° | 0.07° | 0.038° | 0.03° | 0.06° | 0.037° | 0.001° | ||
| Pitch | 0.03° | 0.07° | 0.039° | 0.03° | 0.06° | 0.037° | 0.002° | ||
| Heading | 0.28° | 0.45° | 0.369° | 0.07° | 0.11° | 0.082° | 0.287° | ||
| B | 5 m/s | North | 0.019 m | 0.024 m | 0.020 m | 0.019 m | 0.023 m | 0.020 m | 0.000 m |
| East | 0.019 m | 0.022 m | 0.020 m | 0.018 m | 0.022 m | 0.020 m | 0.000 m | ||
| Height | 0.036 m | 0.036 m | 0.036 m | 0.036 m | 0.036 m | 0.036 m | 0.000 m | ||
| Roll | 0.03° | 0.07° | 0.039° | 0.03° | 0.06° | 0.038° | 0.001° | ||
| Pitch | 0.03° | 0.07° | 0.041° | 0.03° | 0.06° | 0.039° | 0.003° | ||
| Heading | 0.21° | 0.35° | 0.251° | 0.07° | 0.11° | 0.086° | 0.165° | ||
| C | 10 m/s | North | 0.019 m | 0.022 m | 0.021 m | 0.019 m | 0.022 m | 0.021 m | 0.000 m |
| East | 0.019 m | 0.024 m | 0.021 m | 0.019 m | 0.022 m | 0.021 m | 0.000 m | ||
| Height | 0.036 m | 0.037 m | 0.036 m | 0.036 m | 0.037 m | 0.036 m | 0.000 m | ||
| Roll | 0.03° | 0.08° | 0.045° | 0.03° | 0.08° | 0.042° | 0.003° | ||
| Pitch | 0.03° | 0.07° | 0.041° | 0.03° | 0.07° | 0.041° | 0.000° | ||
| Heading | 0.16° | 0.20° | 0.175° | 0.08° | 0.12° | 0.093° | 0.082° | ||
| D | 15 m/s | North | 0.020 m | 0.022 m | 0.021 m | 0.020 m | 0.022 m | 0.021 m | 0.000 m |
| East | 0.020 m | 0.024 m | 0.022 m | 0.020 m | 0.023 m | 0.021 m | 0.001 m | ||
| Height | 0.035 m | 0.038 m | 0.036 m | 0.035 m | 0.038 m | 0.036 m | 0.000 m | ||
| Roll | 0.03° | 0.09° | 0.051° | 0.03° | 0.08° | 0.048° | 0.003° | ||
| Pitch | 0.03° | 0.07° | 0.046° | 0.03° | 0.07° | 0.045° | 0.001° | ||
| Heading | 0.12° | 0.16° | 0.141° | 0.08° | 0.11° | 0.094° | 0.047° | ||
| Region Name | Minimum Hor. Angle | Maximum Hor. Angle | Minimum Vert. Angle | Maximum Vert. Angle |
|---|---|---|---|---|
| Top Edge Points | −4.4° * | 4.4° * | 18.7° | 19.2° |
| Bottom Edge Points | −4.4° * | 4.4° * | −19.2° | −18.7° |
| Left Edge Points | 18.7° | 19.2° | −4.4° * | 4.4° * |
| Right Edge Points | −19.2° | −18.7° | −4.4° * | 4.4° * |
| Middle Points | −0.25° | 0.25° | −0.25° | 0.25° |
| Region | Horizontal Position Differences | Mean Lidar Range | No. of Points | ||
|---|---|---|---|---|---|
| Minimum | Maximum | Mean | |||
| Top Edge Points | 0.006 m | 0.354 m | 0.137 m | 68.2 m | 263,266 |
| Bottom Edge Points | 0.012 m | 0.300 m | 0.105 m | 68.8 m | 258,259 |
| Left Edge Points | 0.000 m | 0.302 m | 0.092 m | 68.1 m | 285,623 |
| Right Edge Points | 0.033 m | 0.339 m | 0.145 m | 68.2 m | 286,220 |
| Middle Points | 0.001 m | 0.164 m | 0.051 m | 64.6 m | 297,850 |
| Region | Horizontal Position Differences | ||
|---|---|---|---|
| Minimum | Maximum | Mean | |
| Top Edge Points | 0.009 m | 0.205 m | 0.087 m |
| Bottom Edge Points | 0.004 m | 0.168 m | 0.080 m |
| Left Edge Points | 0.001 m | 0.179 m | 0.075 m |
| Right Edge Points | 0.001 m | 0.201 m | 0.078 m |
| Middle Points | 0.004 m | 0.104 m | 0.043 m |
| Region | Vertical Position Differences | ||
|---|---|---|---|
| Minimum | Maximum | Mean | |
| Top Edge Points | −0.004 m | 0.037 m | 0.015 m |
| Bottom Edge Points | −0.039 m | 0.005 m | −0.013 m |
| Left Edge Points | −0.034 m | 0.025 m | 0.002 m |
| Right Edge Points | −0.035 m | 0.023 m | −0.001 m |
| Middle Points | −0.028m | 0.013 m | 0.001 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brazeal, R.G.; Wilkinson, B.E.; Benjamin, A.R. Investigating Practical Impacts of Using Single-Antenna and Dual-Antenna GNSS/INS Sensors in UAS-Lidar Applications. Sensors 2021, 21, 5382. https://doi.org/10.3390/s21165382
Brazeal RG, Wilkinson BE, Benjamin AR. Investigating Practical Impacts of Using Single-Antenna and Dual-Antenna GNSS/INS Sensors in UAS-Lidar Applications. Sensors. 2021; 21(16):5382. https://doi.org/10.3390/s21165382
Chicago/Turabian StyleBrazeal, Ryan G., Benjamin E. Wilkinson, and Adam R. Benjamin. 2021. "Investigating Practical Impacts of Using Single-Antenna and Dual-Antenna GNSS/INS Sensors in UAS-Lidar Applications" Sensors 21, no. 16: 5382. https://doi.org/10.3390/s21165382
APA StyleBrazeal, R. G., Wilkinson, B. E., & Benjamin, A. R. (2021). Investigating Practical Impacts of Using Single-Antenna and Dual-Antenna GNSS/INS Sensors in UAS-Lidar Applications. Sensors, 21(16), 5382. https://doi.org/10.3390/s21165382






