DAN-SuperPoint: Self-Supervised Feature Point Detection Algorithm with Dual Attention Network
Abstract
:1. Introduction
2. Related Work
2.1. Local Feature Learning
2.2. The Combination of Feature Extraction and Attention Mechanism
3. Method
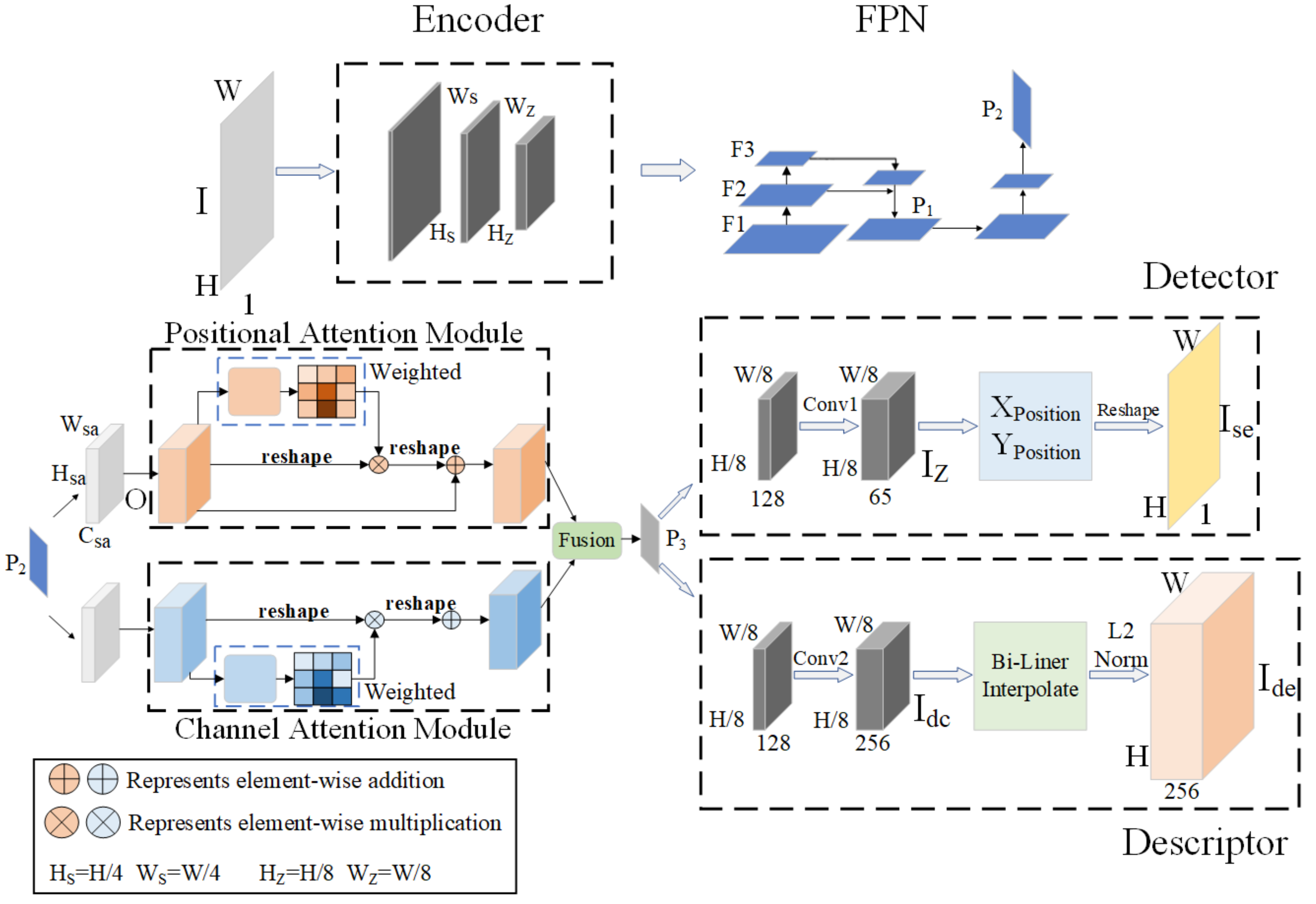
3.1. Network Structure
3.2. Dual Attention Network Weights
3.3. Loss Functions
3.3.1. Detector Head Loss
3.3.2. Descriptor Head Loss
4. Experiments and Analysis
4.1. Feature Point Detection and Matching
4.2. KITTI Dataset Test
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the 7th IEEE International Conference on Computer Vision, Corfu, Greece, 20–27 September 1999; pp. 1150–1157. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF, 2011. In Proceedings of the International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Rosten, E.; Porter, R.; Drummond, T. Faster and Better: A Machine Learning Approach to Corner Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 32, 105–119. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mair, E.; Hager, G.D.; Burschka, D.; Suppa, M.; Hirzinger, G. Adaptive and Generic Corner Detection Based on the Accelerated Segment Test. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2010; pp. 183–196. [Google Scholar] [CrossRef]
- Salti, S.; Lanza, A.; Di Stefano, L. Keypoints from symmetries by wave propagation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2898–2905. [Google Scholar]
- Yi, K.M.; Trulls, E.; Lepetit, V.; Fua, P. LIFT: Learned Invariant Feature Transform. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2016; pp. 467–483. [Google Scholar] [CrossRef] [Green Version]
- Verdie, Y.; Yi, K.; Fua, P.; Lepetit, V. Tilde: A temporally invariant learned detector. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5279–5288. [Google Scholar]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superpoint: Self-supervised interest point detection and description. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 224–236. [Google Scholar]
- Tang, J.; Folkesson, J.; Jensfelt, P. Geometric Correspondence Network for Camera Motion Estimation. IEEE Robot. Autom. Lett. 2018, 3, 1010–1017. [Google Scholar] [CrossRef]
- Tang, J.; Ericson, L.; Folkesson, J.; Jensfelt, P. GCNv2: Efficient Correspondence Prediction for Real-Time SLAM. IEEE Robot. Autom. Lett. 2019, 4, 3505–3512. [Google Scholar] [CrossRef] [Green Version]
- Lin, T.-Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3146–3154. [Google Scholar]
- Mur-Artal, R.; Tardos, J.D. ORB-SLAM2: An Open-Source SLAM System for Monocular, Stereo, and RGB-D Cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef] [Green Version]
- Tian, Y.; Fan, B.; Wu, F. L2-Net: Deep Learning of Discriminative Patch Descriptor in Euclidean Space. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6128–6136. [Google Scholar] [CrossRef]
- Balntas, V.; Johns, E.; Tang, L.; Mikolajczyk, K. PN-Net: Conjoined triple deep network for learning local image descriptors. arXiv 2016, arXiv:1601.05030. [Google Scholar]
- Savinov, N.; Seki, A.; Ladicky, L.; Sattler, T.; Pollefeys, M. Quad-networks: Unsupervised learning to rank for interest point detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1822–1830. [Google Scholar]
- Ono, Y.; Trulls, E.; Fua, P.; Yi, K.M. LF-Net: Learning local features from images. Adv. Neural Inf. Process. Syst. 2018, 31, 6234–6244. [Google Scholar]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A.J. Deep image homography estimation. arXiv 2016, arXiv:1606.03798. [Google Scholar]
- Li, G.; Yu, L.; Fei, S. A deep-learning real-time visual SLAM system based on multi-task feature extraction network and self-supervised feature points. Measurement 2020, 168, 108403. [Google Scholar] [CrossRef]
- Christiansen, P.H.; Kragh, M.F.; Brodskiy, Y.; Karstoft, H.J. Unsuperpoint: End-to-end unsupervised interest point detector and descriptor. arXiv 2019, arXiv:1907.04011. [Google Scholar]
- Jau, Y.-Y.; Zhu, R.; Su, H.; Chandraker, M. Deep Keypoint-Based Camera Pose Estimation with Geometric Constraints. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NE, USA, 25–29 October 2020; pp. 4950–4957. [Google Scholar]
- Luo, Z.; Zhou, L.; Bai, X.; Chen, H.; Zhang, J.; Yao, Y.; Li, S.; Fang, T.; Quan, L. Aslfeat: Learning local features of accurate shape and localization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 6589–6598. [Google Scholar]
- Dusmanu, M.; Rocco, I.; Pajdla, T.; Pollefeys, M.; Sivic, J.; Torii, A.; Sattler, T. D2-net: A trainable CNN for joint description and detection of local features. In Proceedings of the IEEE/cvf Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8092–8101. [Google Scholar]
- Revaud, J.; Weinzaepfel, P.; De Souza, C.; Pion, N.; Csurka, G.; Cabon, Y.; Humenberger, M.J. R2D2: Repeatable and reliable detector and descriptor. arXiv 2019, arXiv:1906.06195. [Google Scholar]
- Barroso-Laguna, A.; Riba, E.; Ponsa, D.; Mikolajczyk, K. Key. net: Keypoint detection by handcrafted and learned CNN filters. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Long Beach, CA, USA, 15–20 June 2019; pp. 5836–5844. [Google Scholar]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7794–7803. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I.J.A. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Sun, J.; Shen, Z.; Wang, Y.; Bao, H.; Zhou, X. LoFTR: Detector-free local feature matching with transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 8922–8931. [Google Scholar]
- Wang, Z.; Li, X.; Li, Z. Local Representation is Not Enough: Soft Point-Wise Transformer for Descriptor and Detector of Local Features. IJCAI 2021, 2, 1150–1156. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, X.; Huang, L.; Huang, C.; Wei, Y.; Liu, W. Ccnet: Criss-cross attention for semantic segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Long Beach, CA, USA, 15–20 June 2019; pp. 603–612. [Google Scholar]
- Huang, L.; Yuan, Y.; Guo, J.; Zhang, C.; Chen, X.; Wang, J.J. Interlaced sparse self-attention for semantic segmentation. arXiv 2019, arXiv:1907.12273. [Google Scholar]
- Simonyan, K.; Zisserman, A.J. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Lin, T.-Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Honolulu, HI, USA, 21–26 July 2017; pp. 2980–2988. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G. Pytorch: Tensors and dynamic neural networks in python with strong gpu acceleration. PyTorch Tensors Dyn. Neural Netw. 2017, 6, 3. [Google Scholar]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2014; pp. 740–755. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The KITTI vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar] [CrossRef]
- Balntas, V.; Lenc, K.; Vedaldi, A.; Mikolajczyk, K. HPatches: A benchmark and evaluation of handcrafted and learned local descriptors. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5173–5182. [Google Scholar]
- Xiong, Y.-J.; Ma, S.; Gao, Y.; Fang, Z.J.J. PC-SuperPoint: Interest point detection and descriptor extraction using pyramid convolution and circle loss. J. Electron. Imaging 2021, 30, 033024. [Google Scholar] [CrossRef]







| HomoGraphy Estimation | Repeatability | Time (ms) | |||
|---|---|---|---|---|---|
| Epsilon = 1 | 3 | 5 | |||
| Superpoint | 0.331 | 0.684 | 0.829 | 0.581 | 103 |
| LIFT | 0.284 | 0.598 | 0.717 | 0.449 | |
| SIFT | 0.424 | 0.676 | 0.759 | 0.495 | 80 |
| ORB | 0.150 | 0.395 | 0.538 | 0.641 | 125 |
| BRISK | 0.300 | 0.653 | 0.746 | 0.566 | |
| Ours | 0.505 | 0.729 | 0.788 | 0.586 | 170 |
| Dataset | Ours | SuperPoint | ORB | SIFT | FAST | PC-SuperPoint |
|---|---|---|---|---|---|---|
| 01 | 88.082 | 85.587 | 875.248 | 199.891 | 326.547 | 63.743 |
| 02 | 58.625 | 25.647 | 214.623 | 43.423 | 78.519 | 34.829 |
| 03 | 0.493 | 2.481 | 42.648 | 12.341 | 2.438 | 7.257 |
| 04 | 0.573 | 2.573 | 6.775 | 2.286 | 2.382 | 1.967 |
| 05 | 5.380 | 6.415 | 96.519 | 41.629 | 23.065 | 21.698 |
| 06 | 11.837 | 7.696 | 17.509 | 7.270 | 2.883 | 9.577 |
| 07 | 10.911 | 9.100 | 25.138 | 9.346 | 8.592 | 8.072 |
| 08 | 12.529 | 16.729 | 325.808 | 79.576 | 16.878 | 33.347 |
| 09 | 5.562 | 16.785 | 31.988 | 16.006 | 31.190 | 14.703 |
| 10 | 4.677 | 22.755 | 28.935 | 9.474 | 11.387 | 11.057 |
| Dataset | Ours | SuperPoint | ORB | SIFT | FAST |
|---|---|---|---|---|---|
| 01 | 0.317 | 0.357 | 1.869 | 0.861 | 0.906 |
| 02 | 0.275 | 0.1455 | 0.808 | 0.157 | 0.260 |
| 03 | 0.102 | 0.073 | 0.180 | 0.111 | 0.090 |
| 04 | 0.061 | 0.056 | 0.172 | 0.085 | 0.057 |
| 05 | 0.057 | 0.059 | 0.469 | 0.135 | 0.120 |
| 06 | 0.125 | 0.084 | 0.163 | 0.072 | 0.058 |
| 07 | 0.083 | 0.093 | 0.168 | 0.092 | 0.082 |
| 08 | 0.109 | 0.122 | 0.796 | 0.243 | 0.148 |
| 09 | 0.120 | 0.139 | 0.183 | 0.153 | 0.153 |
| 10 | 0.145 | 0.168 | 0.136 | 0.092 | 0.145 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Cao, J.; Hao, Q.; Zhao, X.; Ning, Y.; Li, D. DAN-SuperPoint: Self-Supervised Feature Point Detection Algorithm with Dual Attention Network. Sensors 2022, 22, 1940. https://doi.org/10.3390/s22051940
Li Z, Cao J, Hao Q, Zhao X, Ning Y, Li D. DAN-SuperPoint: Self-Supervised Feature Point Detection Algorithm with Dual Attention Network. Sensors. 2022; 22(5):1940. https://doi.org/10.3390/s22051940
Chicago/Turabian StyleLi, Zhaoyang, Jie Cao, Qun Hao, Xue Zhao, Yaqian Ning, and Dongxing Li. 2022. "DAN-SuperPoint: Self-Supervised Feature Point Detection Algorithm with Dual Attention Network" Sensors 22, no. 5: 1940. https://doi.org/10.3390/s22051940
APA StyleLi, Z., Cao, J., Hao, Q., Zhao, X., Ning, Y., & Li, D. (2022). DAN-SuperPoint: Self-Supervised Feature Point Detection Algorithm with Dual Attention Network. Sensors, 22(5), 1940. https://doi.org/10.3390/s22051940








