A Hybrid Multi-Target Path Planning Algorithm for Unmanned Cruise Ship in an Unknown Obstacle Environment
Abstract
:1. Introduction
2. Related Works
2.1. Multi-Target Path Planning
2.2. Unknown Obstacles Environment
3. Preliminaries and Problem Formulation
3.1. Map Construction
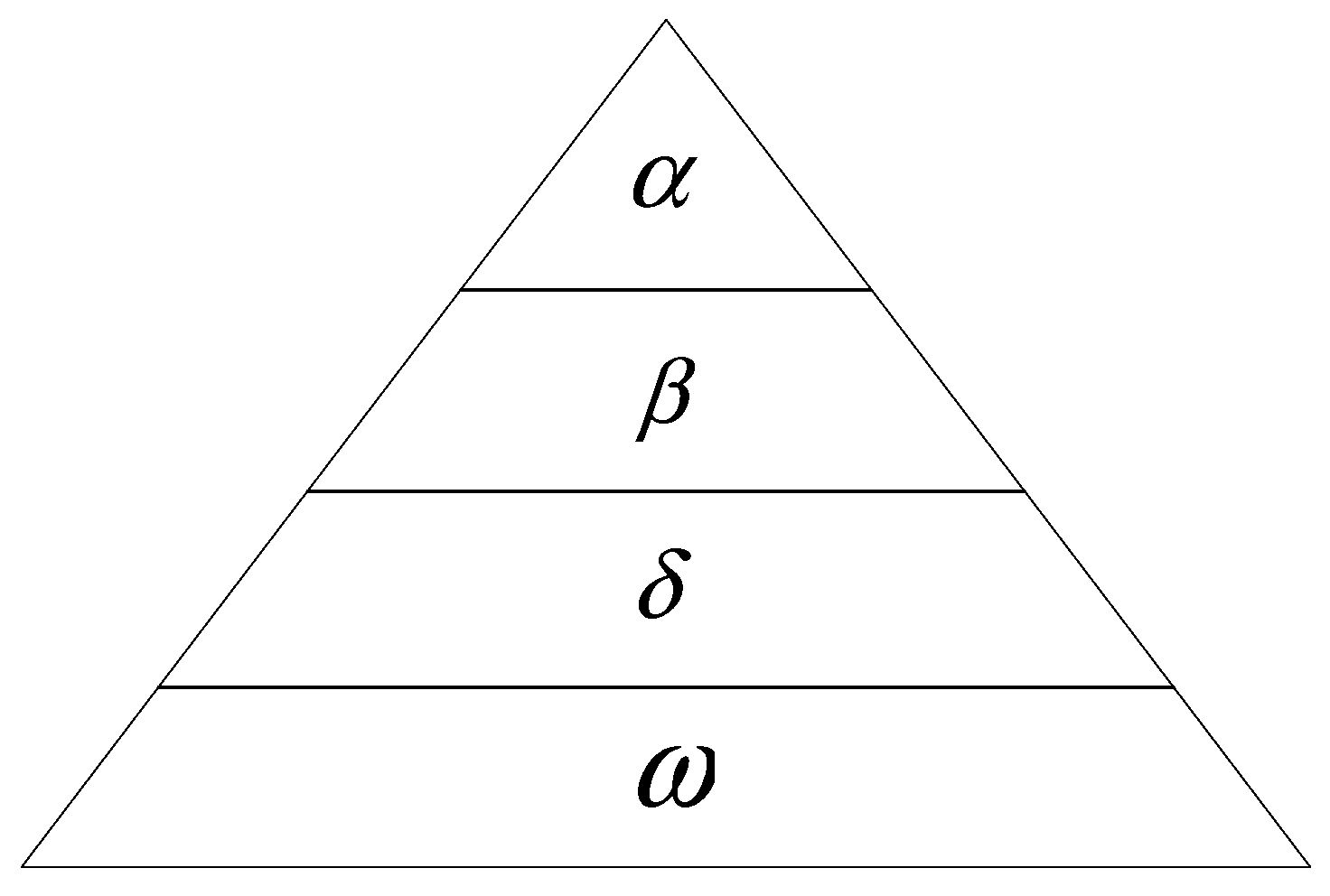
3.2. GWO Algorithm
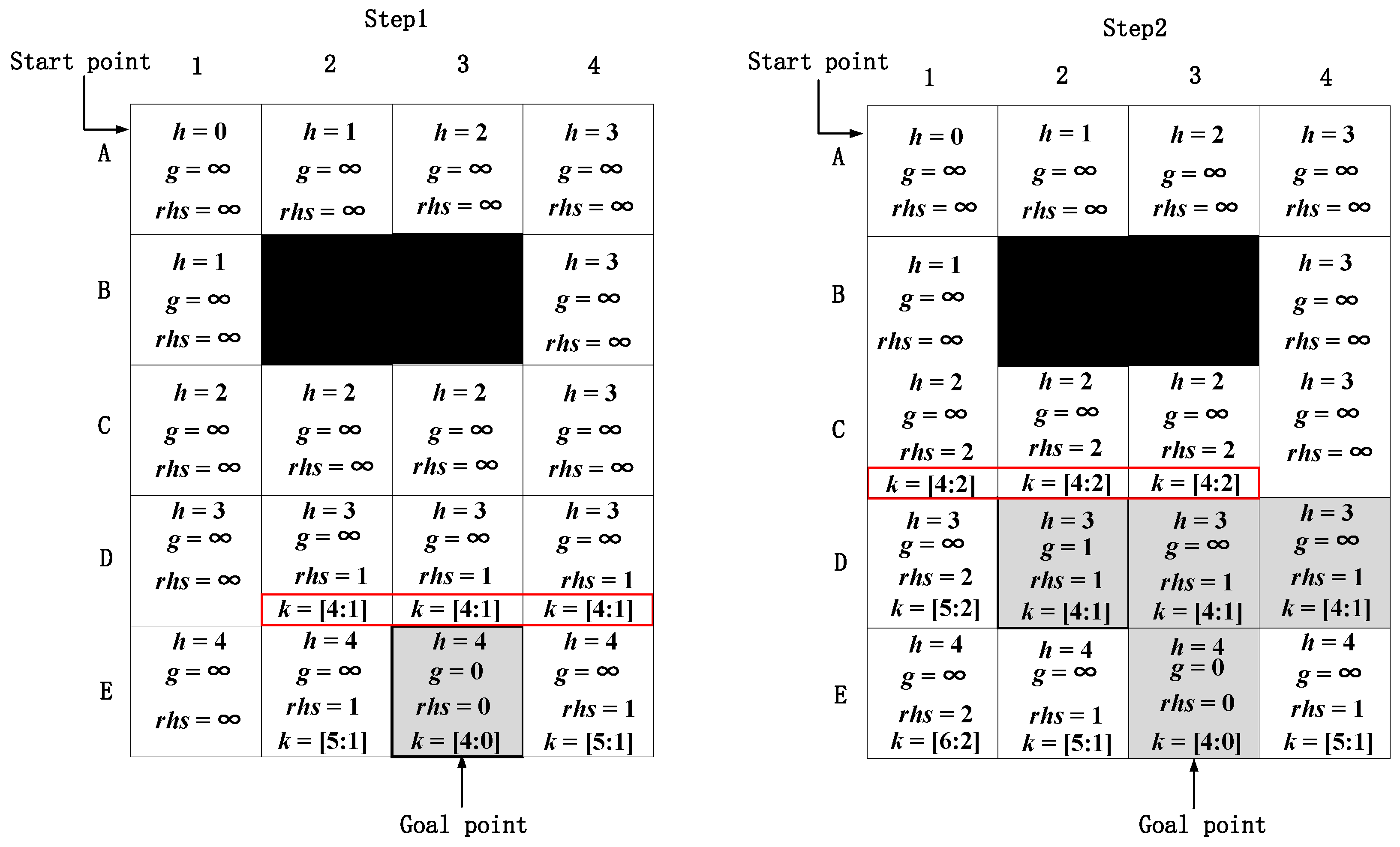
3.3. D* Lite Algorithm
3.4. Problem Formulation
4. Traversal Multi-Target Path Planning
4.1. Improved GWO
4.1.1. Multi-Target Encoding Construction
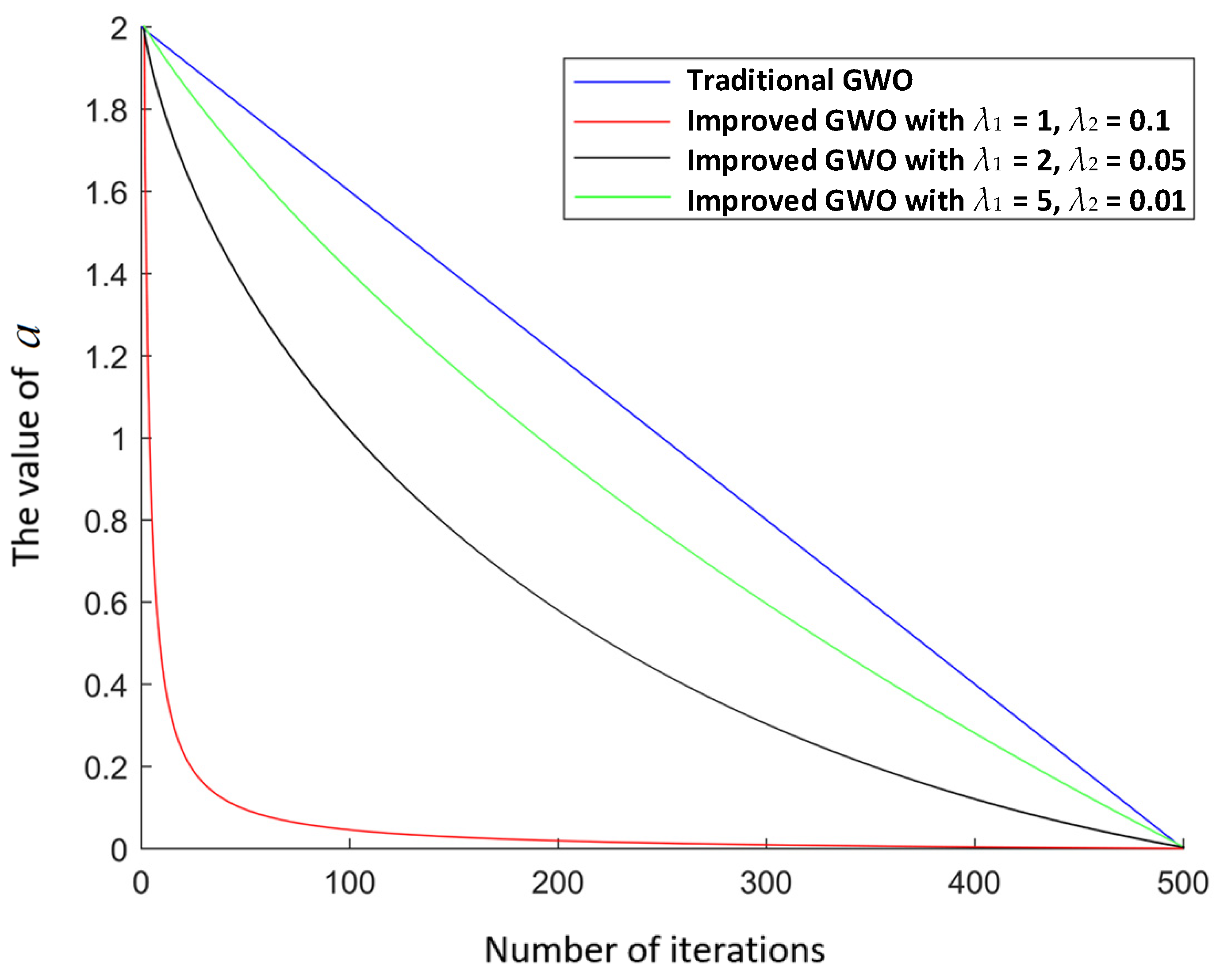
4.1.2. Convergence Factor Improvement
| Algorithm: The Improved GWO Algorithm. | |
| Step 1 | Initialize parameters |
| Step 2 | Construct matrix X using Equation (11) |
| Step 3 | Construct matrix P and calculate |
| Step 4 | Construct fitness function f using Equations (12) and (13) |
| Step 5 | Calculate and update the target sequence using Equations (2)–(6) and (10)–(14), respectively |
| Step 6 | if number of iterations < n |
| Step 7 | Repeat Steps 5–7 |
| Step 8 | else Output the target sequence |
4.2. Improved D* Lite Algorithm
4.2.1. Heuristic Function Improvement
4.2.2. Path Smoothing
| Algorithm: Path smoothing. | |
| Step 1 | Label each point on the planning path from one to n |
| Step 2 | Connect points 1 and 2 and check whether the connection passes through the obstacles |
| Step 3 | Check until the connection between points 1 and k (k < n) passes through the obstacle |
| Step 4 | Connect point 1 and (k − 1) and replace the previous path from point 1 to (k − 1) |
| Step 5 | Use point (k − 1) as a new start point and repeat the above steps until the target is reached |
| Algorithm: Improved D* Lite algorithm. | |
| Step 1 | Parameter initialization |
| Step 2 | Expand adjacent nodes from sgoal |
| Step 3 | Compare current k(s) values and select the node with the smallest k(s) as the next expanded node |
| Step 4 | Expand the nodes constantly until reach sstart |
| Step 5 | Calculate the values of rhs(s) and move to the node with the smallest rhs(s) |
| Step 6 | If the surrounding environment has changed |
| Step 7 | update adjacent nodes and return to Step 2 |
| Step 8 | else the current node is the new start node s’start |
| Step 9 | If node s’start is node sgoal |
| Step 10 | Perform path smoothing |
| Step 11 | else return to Step 2 |
| Step 12 | Complete path planning between every two target points |
4.3. Algorithm Overview
| Algorithm: The proposed multi-target hybrid path planning algorithm. | |
| Step 1 | Parameter initialization |
| Step 2 | Introduce improved convergence factor |
| Step 3 | Calculate fitness function |
| Step 4 | Determine target sequence of α, β, δ, and ω |
| Step 5 | If the maximum number of iterations is reached |
| Step 6 | Output the target sequence |
| Step 7 | else Update adjacent nodes and return to Step 2 |
| Step 8 | Perform path planning between two target points by the improved D* Lite algorithm |
| Step 9 | If the surrounding environment has not changed |
| Step 10 | If the new start point s’start is the target point |
| Step 11 | If it is the final target point |
| Step 12 | return to the start point |
| Step 13 | else return to Step 8 |
| Step 14 | else return to Step 8 |
| Step 15 | else return to Step 8 |
| Step 16 | Perform path smoothing |
| Step 17 | Complete multi-target path planning |
5. Simulation Experiments
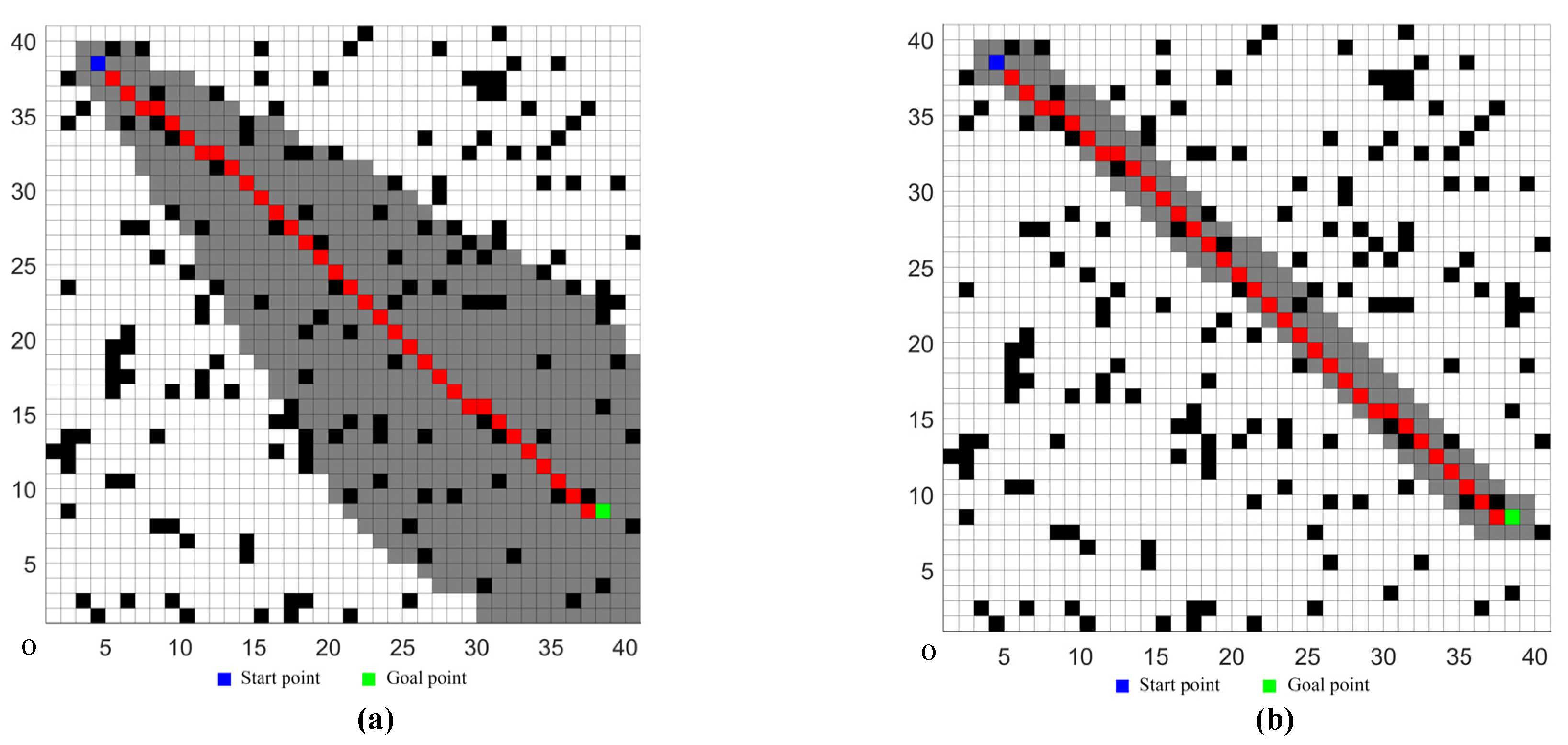
5.1. Simulations in Ordinary Environments
5.2. Simulations in Complex Environments
5.3. Performance Testing of the Proposed Algorithm
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Felski, A.; Zwolak, K. The ocean-going autonomous ship—Challenges and threats. J. Mar. Sci. Eng. 2020, 8, 41. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Zhang, G.; Hu, X.; Xiao, J. Unmanned aerial vehicle route planning method based on a star algorithm. In Proceedings of the 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, China, 31 May–2 June 2018; pp. 1510–1514. [Google Scholar] [CrossRef]
- Jose, S.; Antony, A. Mobile robot remote path planning and motion control in a maze environment. In Proceedings of the 2016 IEEE International Conference on Engineering and Technology (ICETECH), Coimbatore, India, 17–18 March 2016; pp. 207–209. [Google Scholar] [CrossRef]
- Akram, V.; Dagdeviren, O. Breadth-First Search-Based Single-Phase algorithms for bridge detection in wireless sensor networks. Sensors 2013, 13, 8786–8813. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dawid, W.; Pokonieczny, K. Methodology of using terrain passability maps for planning the movement of troops and navigation of unmanned ground vehicles. Sensors 2021, 21, 4682. [Google Scholar] [CrossRef]
- Xu, Z.; Deng, D.; Shimada, K. Autonomous UAV exploration of dynamic environments via incremental sampling and probabilistic roadmap. IEEE Robot. Autom. Lett. 2021, 6, 2729–2736. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, D.; Chen, G.; Ren, Y.; Du, D. A hybrid path planning method based on articulated vehicle model. Comput. Mater. Contin. 2020, 65, 1781–1793. [Google Scholar] [CrossRef]
- Gil, J.M.; Han, Y.H. A target coverage scheduling scheme based on genetic algorithms in directional sensor networks. Sensors 2011, 11, 1888–1906. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Çil, Z.A.; Mete, S.; Serin, F. Robotic disassembly line balancing problem: A mathematical model and ant colony optimization approach. Appl. Math. Model. 2020, 86, 335–348. [Google Scholar] [CrossRef]
- Dabiri, N.; Tarokh, M.J.; Alinaghian, M. New mathematical model for the bi-objective inventory routing problem with a step cost function: A multi-objective particle swarm optimization solution approach. Appl. Math. Model. 2017, 49, 302–318. [Google Scholar] [CrossRef]
- Yoo, Y.J. Hyperparameter optimization of deep neural network using univariate dynamic encoding algorithm for searches. Knowl.-Based Syst. 2019, 178, 74–83. [Google Scholar] [CrossRef]
- Lin, N.; Tang, J.; Li, X.; Zhao, L. A Novel Improved Bat Algorithm in UAV Path Planning. Comput. Mater. Contin. 2019, 61, 323–344. [Google Scholar] [CrossRef]
- Bai, X.; Yan, W.; Cao, M. Clustering-based algorithms for multivehicle task assignment in a time-invariant drift field. IEEE Robot. Autom. Lett. 2017, 2, 2166–2173. [Google Scholar] [CrossRef] [Green Version]
- Yao, P.; Xie, Z.; Ren, P. Optimal UAV route planning for coverage search of stationary target in river. IEEE Trans. Control. Syst. Technol. 2017, 27, 822–829. [Google Scholar] [CrossRef]
- Yu, J.; Deng, W.; Zhao, Z.; Wang, X.; Xu, J.; Wang, L.; Sun, Q.; Shen, Z. A hybrid path planning method for an unmanned cruise ship in water quality sampling. IEEE Access 2019, 7, 87127–87140. [Google Scholar] [CrossRef]
- Khaksar, W.; Vivekananthen, S.; Saharia, K.S.M.; Yousefi, M.; Ismail, F.B. A review on mobile robots motion path planning in unknown environments. In Proceedings of the 2015 IEEE International Symposium on Robotics and Intelligent Sensors (IRIS), Langkawi, Malaysia, 18–20 October 2015; pp. 295–300. [Google Scholar] [CrossRef]
- Abubakr, O.A.; Jaradat, M.A.K.; Hafez, M.A. A reduced cascaded fuzzy logic controller for dynamic window weights optimization. In Proceedings of the 2018 11th International Symposium on Mechatronics and its Applications (ISMA), Sharjah, United Arab Emirates, 4–6 March 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Gan, R.; Guo, Q.; Chang, H.; Yi, Y. Improved ant colony optimization algorithm for the traveling salesman problems. J. Syst. Eng. Electron. 2010, 21, 329–333. [Google Scholar] [CrossRef]
- Pan, G.; Li, K.; Ouyang, A.; Li, K. Hybrid immune algorithm based on greedy algorithm and delete-cross operator for solving TSP. Soft Comput. 2016, 20, 555–566. [Google Scholar] [CrossRef]
- Yujie, L.; Yu, P.; Yixin, S.; Huajun, Z.; Danhong, Z.; Yong, S. Ship path planning based on improved particle swarm optimization. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018; pp. 226–230. [Google Scholar] [CrossRef]
- Jang, D.-S.; Chae, H.-J.; Choi, H.-L. Optimal control-based UAV path planning with dynamically-constrained TSP with neighborhoods. In Proceedings of the 17th International Conference on Control, Automation and Systems (ICCAS), Jeju, Korea, 18–21 October 2017; pp. 373–378. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Sopto, D.S.; Ayon, S.I.; Akhand, M.A.H.; Siddique, N. Modified grey wolf optimization to solve traveling salesman problem. In Proceedings of the 2018 International Conference on Innovation in Engineering and Technology (ICIET), Dhaka, Bangladesh, 27–28 December 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Xu, R.; Cao, M.; Huang, M.X.; Zhu, Y.H. Research on the Quasi-TSP problem based on the improved grey wolf optimization algorithm: A case study of tourism. Geogr. Geo-Inf. Sci. 2018, 34, 14–21. (In Chinese) [Google Scholar]
- Hossain, M.A.; Ferdous, I. Autonomous robot path planning in dynamic environment using a new optimization technique inspired by bacterial foraging technique. Robot. Auton. Syst. 2015, 64, 137–141. [Google Scholar] [CrossRef]
- Hosseininejad, S.; Dadkhah, C. Mobile robot path planning in dynamic environment based on cuckoo optimization algorithm. Int. J. Adv. Robot. Syst. 2019, 16, 1–13. [Google Scholar] [CrossRef]
- Faridi, A.Q.; Sharma, S.; Shukla, A.; Tiwari, R.; Dhar, J. Multi-robot multi-target dynamic path planning using artificial bee colony and evolutionary programming in unknown environment. Intell. Serv. Robot. 2018, 11, 171–186. [Google Scholar] [CrossRef]
- Ma, Y.; Hu, M.; Yan, X. Multi-objective path planning for unmanned surface vehicle with currents effects. ISA Trans. 2018, 75, 137–156. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Yan, X.; Liu, C.; Guodong, L.I. Dynamic path planning for mobile robot based on improved genetic algorithm. Chin. J. Electron. 2020, 19, 245–248. (In Chinese) [Google Scholar]
- Huang, L.; Zhou, F.T. Mobile robot path planning based on path optimization D* lite algorithm. J. Control. Decis. 2020, 35, 112–119. (In Chinese) [Google Scholar]
- Al-Mutib, K.; AlSulaiman, M.; Emaduddin, M.; Ramdane, H.; Mattar, E. D* lite based real-time multi-agent path planning in dynamic environments. In Proceedings of the 2011 Third International Conference on Computational Intelligence, Modelling & Simulation, Langkawi, Malaysia, 20–22 September 2011; pp. 170–174. [Google Scholar] [CrossRef] [Green Version]
- Barillas, F.; Fernández-Villaverde, J. A generalization of the endogenous grid method. J. Econ. Dyn. Control. 2007, 31, 2698–2712. [Google Scholar] [CrossRef]
- Koenig, S.; Likhachev, M.; Furcy, D. Lifelong planning A*. Artif. Intell. 2004, 155, 93–146. [Google Scholar] [CrossRef] [Green Version]
- Koenig, S.; Likhachev, M. Fast replanning for navigation in unknown terrain. IEEE Trans. Robot. 2005, 21, 354–363. [Google Scholar] [CrossRef]
- Rehman, A.; Mubeen, S.; Safdar, R.; Sadiq, N. Properties of k-beta function with several variables. Open Math. 2015, 13, 308–320. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Yang, F. Task assignment strategy for multi-robot based on improved Grey Wolf Optimizer. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 6319–6335. [Google Scholar] [CrossRef]
- Jun, L.; Zhibing, S. Research on Path Planning Based on Improved D* Lite Genetic Algorithm. Mach. Tool Hydraul. 2019, 47, 39–42. (In Chinese) [Google Scholar]
- Wang, J.; Garratt, M.; Anavatti, S. Dynamic path planning algorithm for autonomous vehicles in cluttered environments. In Proceedings of the 2016 IEEE International Conference on Mechatronics and Automation, Harbin, China, 7–10 August 2016; pp. 1006–1011. [Google Scholar] [CrossRef]
- Asghari, S.; Navimipour, N.J. Cloud service composition using an inverted ant colony optimization algorithm. Int. J. Bio. Inspired Comput. 2019, 13, 257–268. [Google Scholar] [CrossRef]
- Drezner, Z.; Drezner, T.D. Biologically Inspired Parent Selection in Genetic Algorithms. Ann. Oper. Res. 2020, 287, 161–183. [Google Scholar] [CrossRef]
- Qu, Y.; Cai, Z. Identification of singular samples in near infrared spectrum of starch water content prediction by using Monte Carlo cross validation combined with T test. IOP Conf. Ser. Earth Environ. Sci. 2018, 186. [Google Scholar] [CrossRef] [Green Version]
- Long, W.; Jiao, J.; Liang, X.; Tang, M. An exploration-enhanced grey wolf optimizer to solve high-dimensional numerical optimization. Eng. Appl. Artif. Intell. 2018, 68, 63–80. [Google Scholar] [CrossRef]






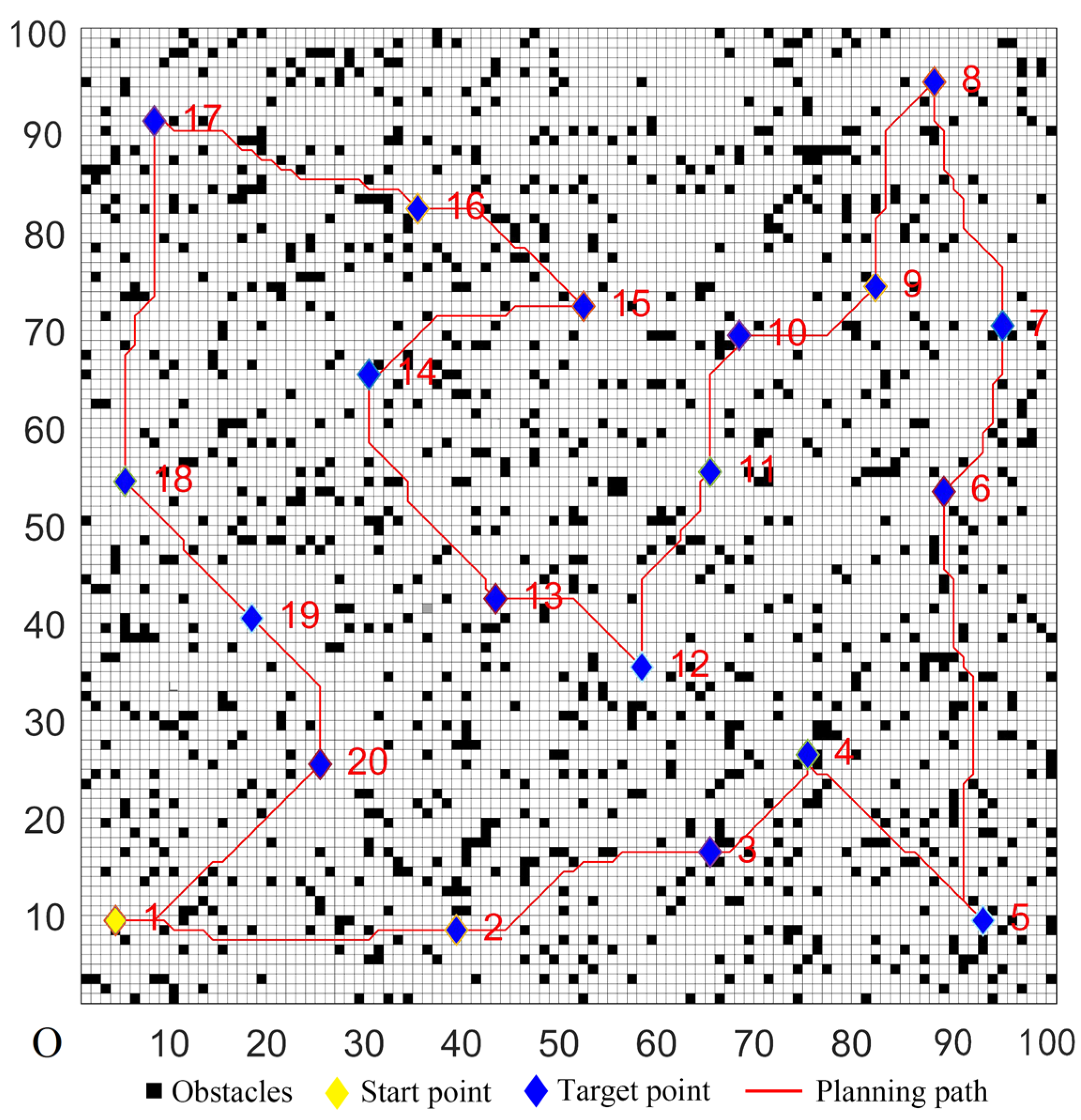

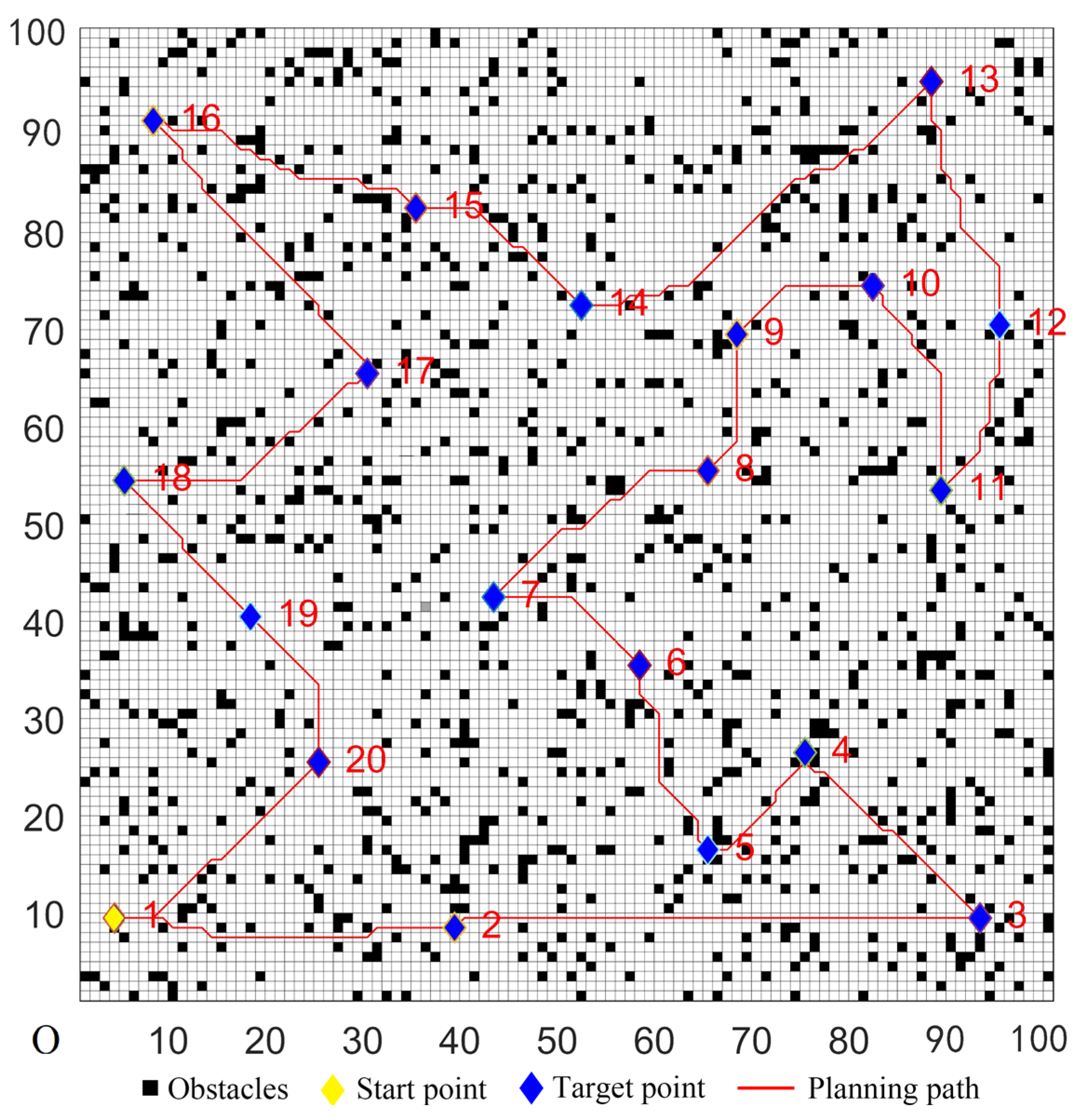
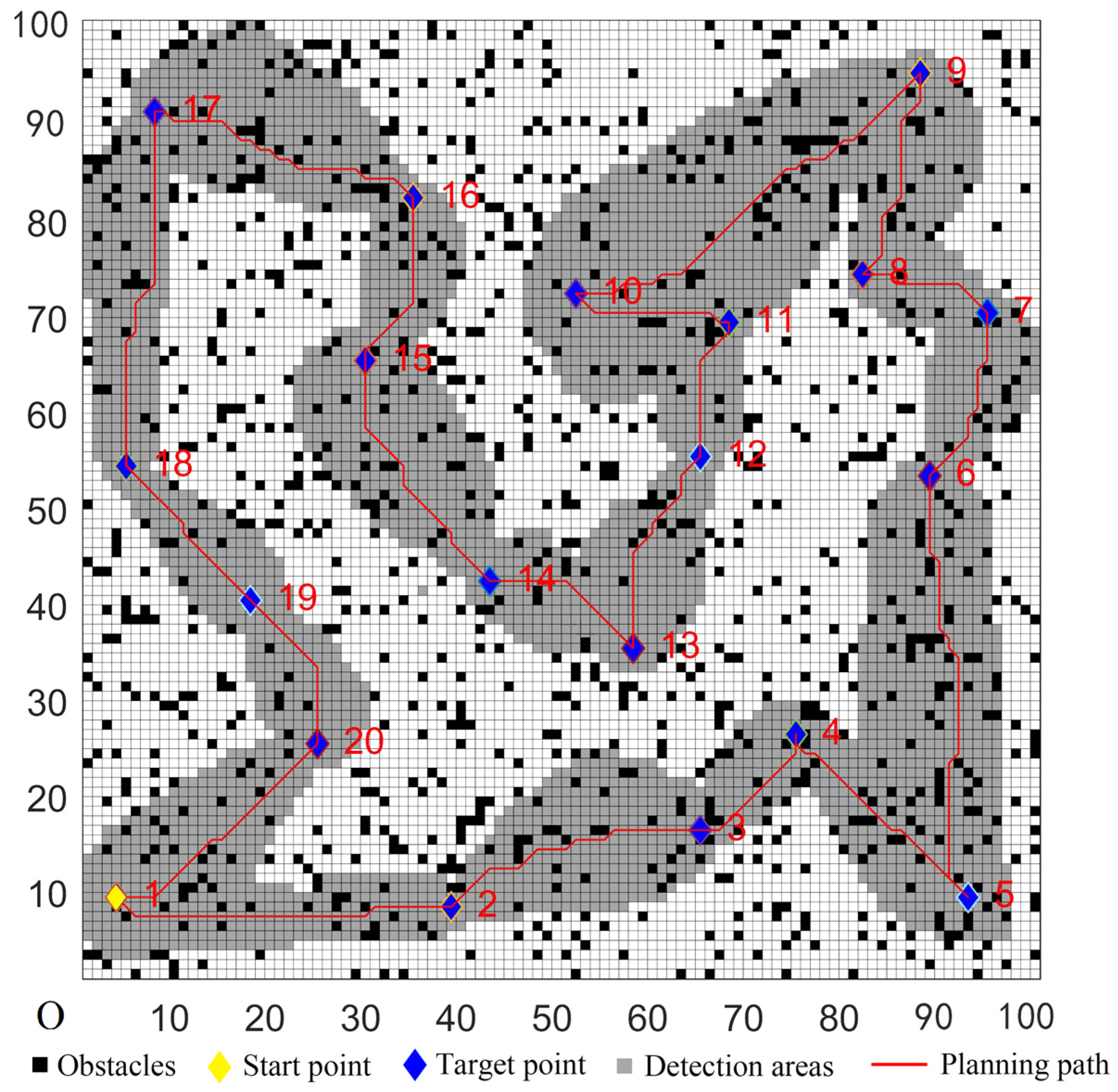
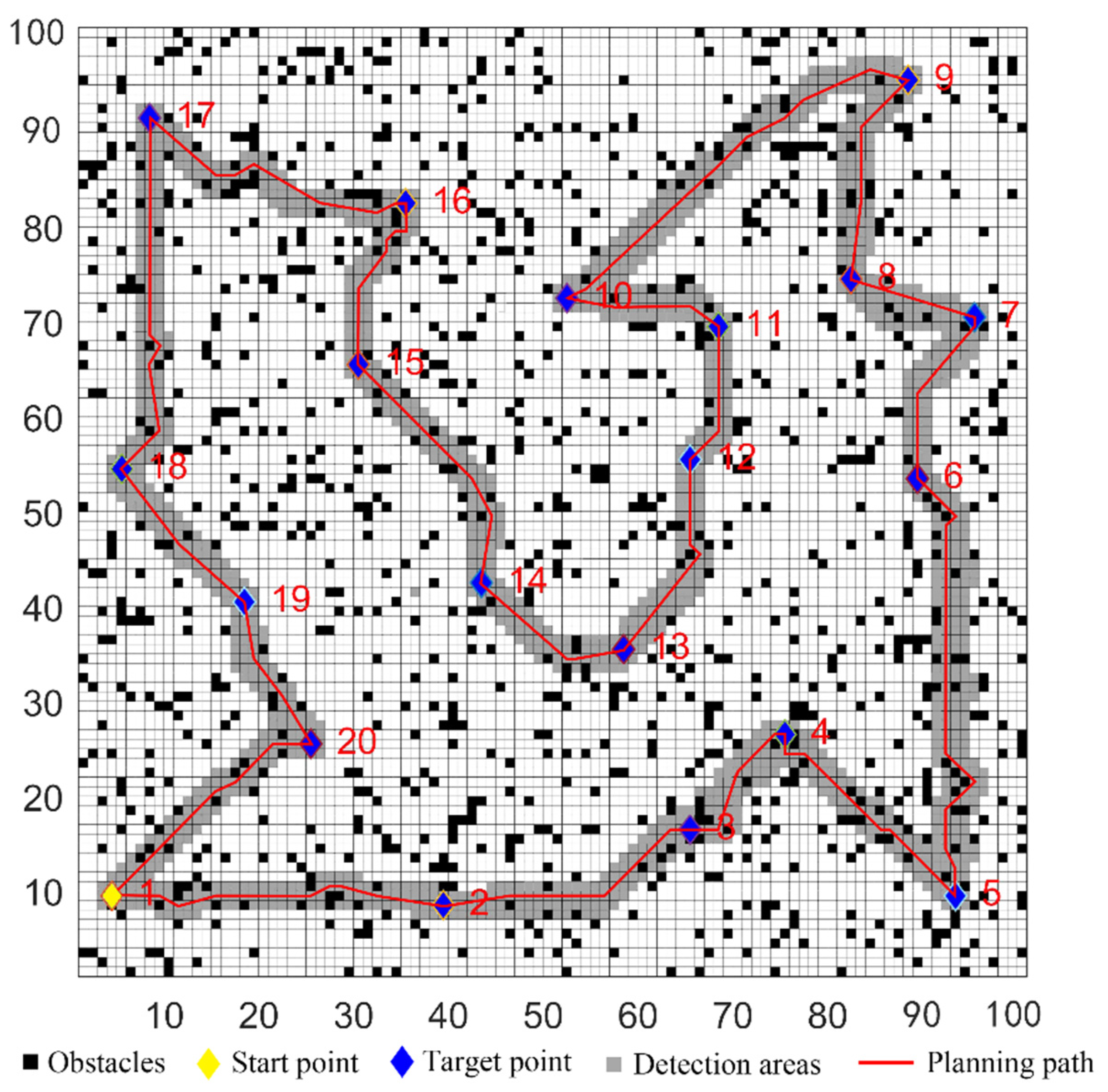

| Case | Target Coordinate |
|---|---|
| 1 | (4, 46), (8, 28), (6, 19), (14, 10), (17, 22), (26, 29), (29, 11), (41, 4), (39, 26), (37, 41) |
| 2 | (37, 26), (38, 3), (26, 9), (11, 8), (2, 18), (3, 24), (6, 27), (16, 28), (25, 32), (36, 30) |
| 3 | (17, 23), (31, 22), (8, 9), (11, 11), (19, 18), (5, 14), (38, 17), (26, 18), (14, 33), (35, 37) |
| 4 | (26, 24), (13, 31), (6, 9), (15, 7), (12, 28), (33, 24), (6, 4), (36, 33), (16, 37), (6, 13) |
| Symbol | Definition | Numerical Value |
|---|---|---|
| nw | Number of grey wolves | 20 |
| tmax | Maximum number of iterations | 200 |
| μ1, μ2 | Position adjustment factors | 0.01, 0.1 |
| λ1, λ2 | Speed adjustment factors | 1, 0.1 |
| U | Priority list | ∅ |
| ks | Initial value of km | 0 |
| rhs(s) | Path cost of node s | ∞ |
| rhs(sgoal) | Path cost of node sgoal | 0 |
| g(s) | Actual path cost of node s | ∞ |
| Performance Indicator | Statistics | Algorithm 1 | Algorithm 2 | Algorithm 3 | Algorithm 4 | Proposed Algorithm |
|---|---|---|---|---|---|---|
| Planning time (s) | Best | 21.562 | 10.185 | 9.667 | 12.927 | 9.746 |
| Mean | 30.112 | 10.671 | 10.470 | 13.823 | 10.356 | |
| Worst | 37.608 | 11.145 | 11.293 | 14.773 | 11.106 | |
| Std. Dev. | 5.134 | 0.626 | 1.015 | 1.035 | 0.483 | |
| t-test | 2.1233 × 10−10 (+) | 0.779 | 4.7421 × 10−5 (+) | 5.7973 × 10−6 (+) | --- | |
| Planning length (m) | Best | 1677.354 | 1769.300 | 1695.650 | 1698.624 | 1669.643 |
| Mean | 1693.280 | 1812.457 | 1728.564 | 1708.821 | 1678.002 | |
| Worst | 1720.697 | 1855.835 | 1760.541 | 1721.100 | 1691.8235 | |
| Std. Dev. | 12.171 | 30.153 | 15.851 | 7.511 | 5.981 | |
| t-test | 0.000067 (+) | 8.5439 × 10−6 (+) | 6.8328 × 10−9 (+) | 5.8455 × 10−8 (+) | --- | |
| Number of inflection points | Best | 54.000 | 53.000 | 48.000 | 38.000 | 35.000 |
| Mean | 56.360 | 62.560 | 51.540 | 42.020 | 36.740 | |
| Worst | 59.000 | 79.000 | 56.000 | 44.000 | 38.000 | |
| Std. Dev. | 1.764 | 7.919 | 2.566 | 1.937 | 0.906 | |
| t-test | 4.7190 × 10−13 (+) | 6.9541 × 10−7 (+) | 2.7559 × 10−10 (+) | 3.3352 × 10−9 (+) | --- |
| Case | Performance Indicator | Algorithm 1 | Algorithm 2 | Algorithm 3 | Algorithm 4 | Proposed Algorithm |
|---|---|---|---|---|---|---|
| 1 | Planning time (s) | 29.583 | 11.176 | 10.740 | 13.823 | 10.338 |
| Planning length (m) | 1695.393 | 1816.817 | 1731.559 | 1708.821 | 1679.052 | |
| Number of inflection points | 56 | 61 | 52 | 39 | 35 | |
| 2 | Planning time (s) | 25.235 | 10.861 | 9.198 | 11.043 | 8.977 |
| Planning length (m) | 1468.860 | 1647.985 | 1502.314 | 1532.208 | 1443.670 | |
| Number of inflection points | 36 | 54 | 40 | 32 | 26 | |
| 3 | Planning time (s) | 26.402 | 12.400 | 11.271 | 13.043 | 9.853 |
| Planning length (m) | 1566.704 | 1691.964 | 1629.008 | 1630.361 | 1542.882 | |
| Number of inflection points | 51 | 70 | 49 | 42 | 34 | |
| 4 | Planning time (s) | 21.743 | 8.671 | 8.231 | 11.562 | 8.174 |
| Planning length (m) | 1230.362 | 1339.065 | 1276.521 | 1298.388 | 1210.675 | |
| Number of inflection points | 32 | 44 | 39 | 29 | 26 |
| Case | Target Coordinates |
|---|---|
| 1 | (4, 9), (39, 8), (65, 16), (75, 26), (93, 9), (89, 53), (95, 70), (82, 74), (88, 95), (52, 72), (68, 69), (65, 55), (58, 35), (43, 42), (30, 42), (35, 82), (8, 91), (5, 54), (18, 40), (25, 25) |
| 2 | (3, 19), (4, 38), (8, 28), (13, 10), (14, 75), (17, 22), (22, 32), (25, 50), (28, 11), (30, 30), (38, 25), (38, 51), (39, 5), (39, 64), (53, 76), (58, 40), (63, 60), (70, 13), (75, 77), (76, 42) |
| 3 | (17, 54), (56, 82), (21, 25), (26, 28), (31, 10), (30, 72), (36, 15), (36, 36), (40, 92), (45, 34), (98, 72), (56, 23), (53, 54), (49, 29), (60, 61), (67, 20), (69, 77), (74, 37), (23, 58), (93, 61) |
| 4 | (56, 3), (46, 34), (12, 67), (6, 28), (61, 45), (90, 12), (46, 87), (61, 63), (64, 72), (87, 34), (58, 52), (46, 43), (33, 51), (39, 39), (65, 61), (87, 70), (19, 87), (4, 35), (7, 5), (50, 94) |
| Performance Indicator | Statistics | Algorithm 1 | Algorithm 2 | Algorithm 3 | Algorithm 4 | Proposed Algorithm |
|---|---|---|---|---|---|---|
| Planning time (s) | Best | 69.319 | 22.216 | 21.037 | 29.200 | 20.742 |
| Mean | 76.248 | 25.635 | 23.714 | 31.234 | 22.891 | |
| Worst | 82.667 | 27.531 | 24.311 | 35.334 | 23.921 | |
| Std. Dev. | 4.387 | 1.532 | 1.472 | 1.989 | 1.121 | |
| t-test | 5.1372 × 10−25 (+) | 0.000084 (+) | 0.000454 (+) | 6.8413 × 10−8 (+) | --- | |
| Planning length (m) | Best | 4945.233 | 5186.258 | 5166.254 | 4998.402 | 4804.200 |
| Mean | 5034.751 | 5262.745 | 5219.564 | 5048.473 | 4841.964 | |
| Worst | 5141.769 | 5402.847 | 5287.889 | 5109.630 | 4897.646 | |
| Std. Dev. | 52.138 | 103.700 | 64.732 | 47.351 | 33.136 | |
| t-test | 1.8643 × 10−8 (+) | 1.931 × 10−7 (+) | 2.6843 × 10−12 (+) | 4.2784 × 10−6 (+) | --- | |
| Numbers of inflection points | Best | 103.000 | 136.000 | 106.000 | 92.000 | 74.000 |
| Mean | 115.460 | 150.200 | 126.780 | 104.760 | 80.640 | |
| Worst | 130.000 | 184.000 | 154.000 | 117.000 | 93.000 | |
| Std. Dev. | 12.568 | 20.183 | 23.976 | 10.806 | 8.585 | |
| t-test | 3.3506 × 10−19 (+) | 1.746 × 10−11 (+) | 8.1961 × 10−21 (+) | 7.1776 × 10−15 (+) | --- |
| Case | Performance Indicator | Algorithm 1 | Algorithm 2 | Algorithm 3 | Algorithm 4 | Proposed Algorithm |
|---|---|---|---|---|---|---|
| 1 | Planning time (s) | 78.278 | 25.680 | 23.714 | 31.564 | 22.891 |
| Planning length (m) | 5012.741 | 5292.691 | 5263.574 | 5054.457 | 4830.673 | |
| Numbers of inflection points | 107 | 150 | 106 | 104 | 79 | |
| 2 | Planning time (s) | 66.327 | 24.010 | 23.207 | 25.347 | 22.355 |
| Planning length (m) | 4051.769 | 4511.827 | 4309.645 | 4109.230 | 3989.236 | |
| Numbers of inflection points | 114 | 146 | 102 | 99 | 76 | |
| 3 | Planning time (s) | 64.283 | 25.738 | 25.211 | 28.576 | 24.336 |
| Planning length (m) | 4366.763 | 4685.202 | 4554.248 | 4568.221 | 4279.043 | |
| Numbers of inflection points | 99 | 133 | 110 | 101 | 84 | |
| 4 | Planning time (s) | 92.273 | 28.472 | 27.393 | 36.371 | 26.284 |
| Planning length (m) | 5264.147 | 5668.923 | 5554.954 | 5461.986 | 5093.817 | |
| Numbers of inflection points | 134 | 180 | 156 | 143 | 122 |
| Function Type | Function Name | Function Formula | Dimension | Search Range | fmin |
|---|---|---|---|---|---|
| Unimodal function | Sphere | 30 | [−100, 100] | 0 | |
| Schwefel’s 2.21 | 30 | [−100, 100] | 0 | ||
| Multimodal function | Rastrigin | 30 | [−5.12, 5.12] | 0 | |
| Alpine | 30 | [−10, 10] | 0 |
| Test Function | Statistics | Ant Colony Optimization | Genetic Algorithm | Chaos Multi-Population Particle Swarm Optimization | Grey Wolf Optimization | Proposed Algorithm |
|---|---|---|---|---|---|---|
| f1 | Mean | 4.62 × 10−16 | 5.01 × 10−22 | 2.58 × 10−43 | 1.21 × 10−69 | 3.23 × 10−93 |
| Std. Dev. | 3.49 × 10−16 | 1.87 × 10−22 | 2.12 × 10−43 | 7.38 × 10−69 | 4.66 × 10−93 | |
| f2 | Mean | 9.28 × 10−20 | 9.31 × 10−42 | 9.35 × 10−77 | 3.66 × 10−135 | 7.57 × 10−191 |
| Std. Dev. | 5.72 × 10−20 | 7.63 × 10−42 | 6.27 × 10−77 | 2.98 × 10−135 | 8.43 × 10−191 | |
| f3 | Mean | 1.24 × 10−2 | 5.78 × 10−4 | 6.95 × 10−9 | 1.71 × 10−15 | 0 |
| Std. Dev. | 9.36 × 10−2 | 2.33 × 10−4 | 3.25 × 10−9 | 0.62 × 10−15 | 0 | |
| f4 | Mean | 5.32 × 10−7 | 4.23 × 10−9 | 1.09 × 10−24 | 9.54 × 10−34 | 1.95 × 10−49 |
| Std. Dev. | 7.14 × 10−7 | 2.11 × 10−9 | 1.87 × 10−24 | 6.03 × 10−34 | 5.82 × 10−49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Liu, G.; Xu, J.; Zhao, Z.; Chen, Z.; Yang, M.; Wang, X.; Bai, Y. A Hybrid Multi-Target Path Planning Algorithm for Unmanned Cruise Ship in an Unknown Obstacle Environment. Sensors 2022, 22, 2429. https://doi.org/10.3390/s22072429
Yu J, Liu G, Xu J, Zhao Z, Chen Z, Yang M, Wang X, Bai Y. A Hybrid Multi-Target Path Planning Algorithm for Unmanned Cruise Ship in an Unknown Obstacle Environment. Sensors. 2022; 22(7):2429. https://doi.org/10.3390/s22072429
Chicago/Turabian StyleYu, Jiabin, Guandong Liu, Jiping Xu, Zhiyao Zhao, Zhihao Chen, Meng Yang, Xiaoyi Wang, and Yuting Bai. 2022. "A Hybrid Multi-Target Path Planning Algorithm for Unmanned Cruise Ship in an Unknown Obstacle Environment" Sensors 22, no. 7: 2429. https://doi.org/10.3390/s22072429
APA StyleYu, J., Liu, G., Xu, J., Zhao, Z., Chen, Z., Yang, M., Wang, X., & Bai, Y. (2022). A Hybrid Multi-Target Path Planning Algorithm for Unmanned Cruise Ship in an Unknown Obstacle Environment. Sensors, 22(7), 2429. https://doi.org/10.3390/s22072429






