Acoustic Multi-Parameter Early Warning Method for Transformer DC Bias State
Abstract
:1. Introduction
2. Analysis on Vibration Law of Transformer in Operation State
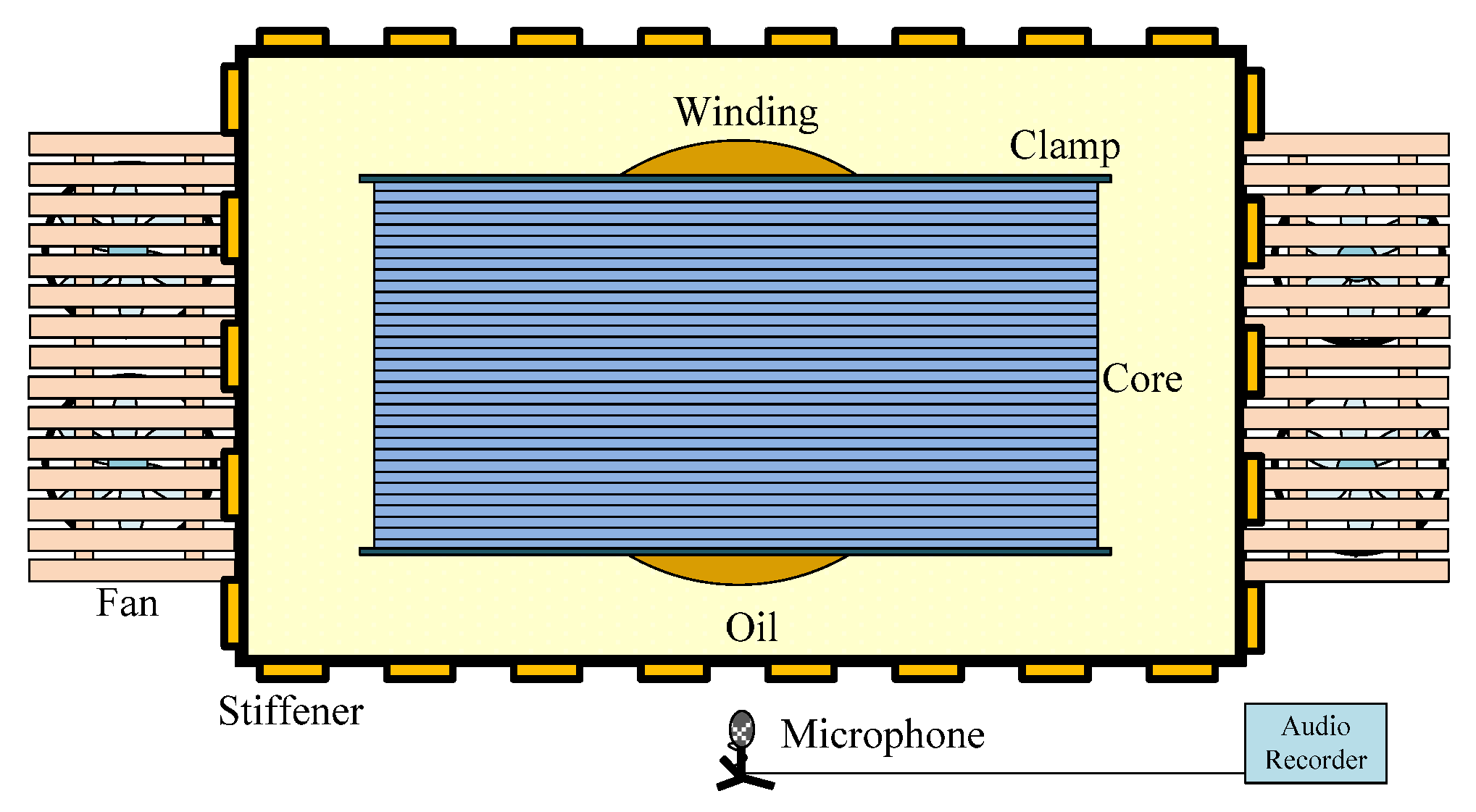
3. Acoustic Signal Acquisition Experiment of Transformer in DC Bias State
3.1. DC Bias Experiment of 500 kV Transformer
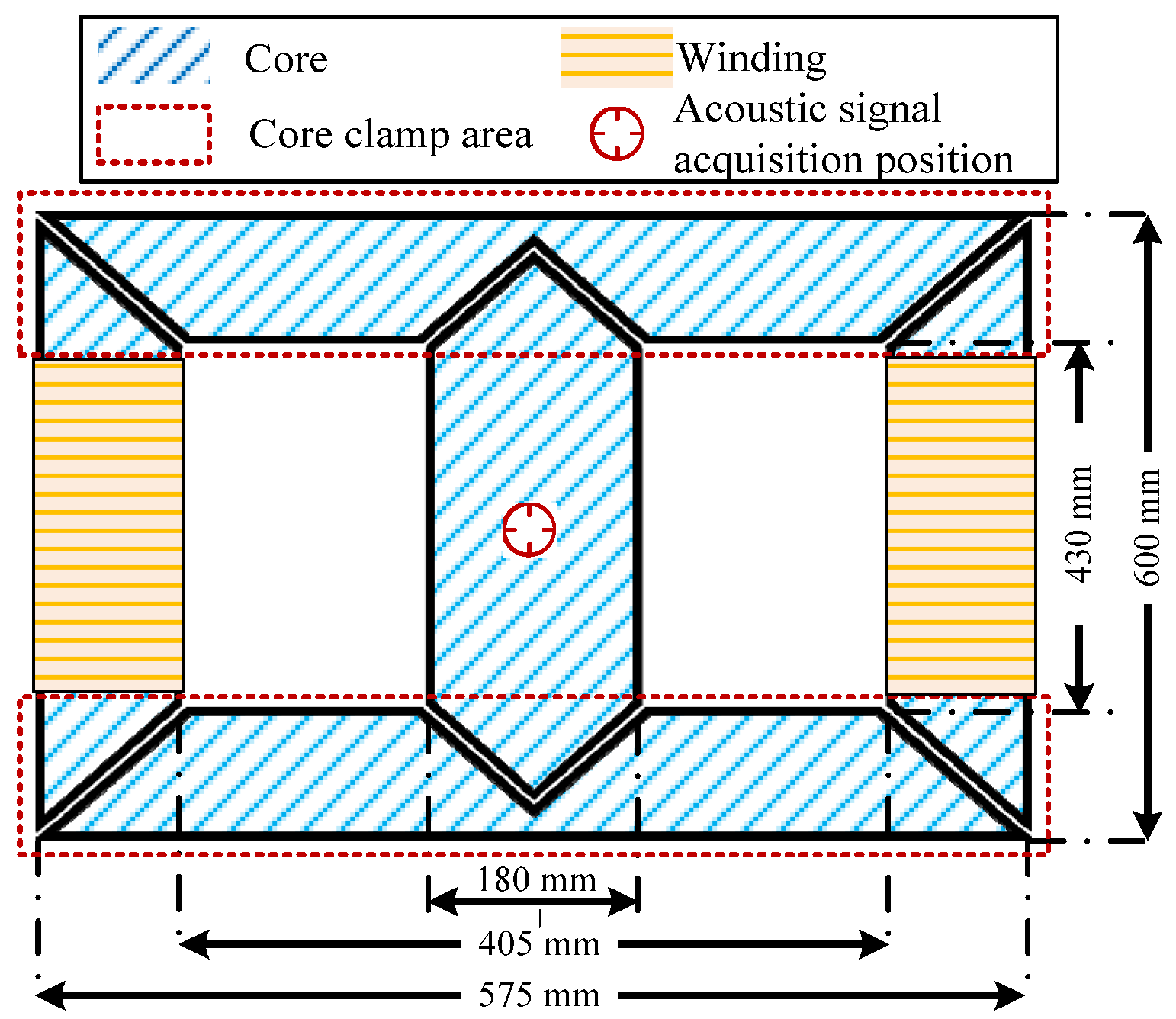
3.2. DC Bias Experiment of Core Model
4. Comparative Analysis of DC Bias Acoustic Signals
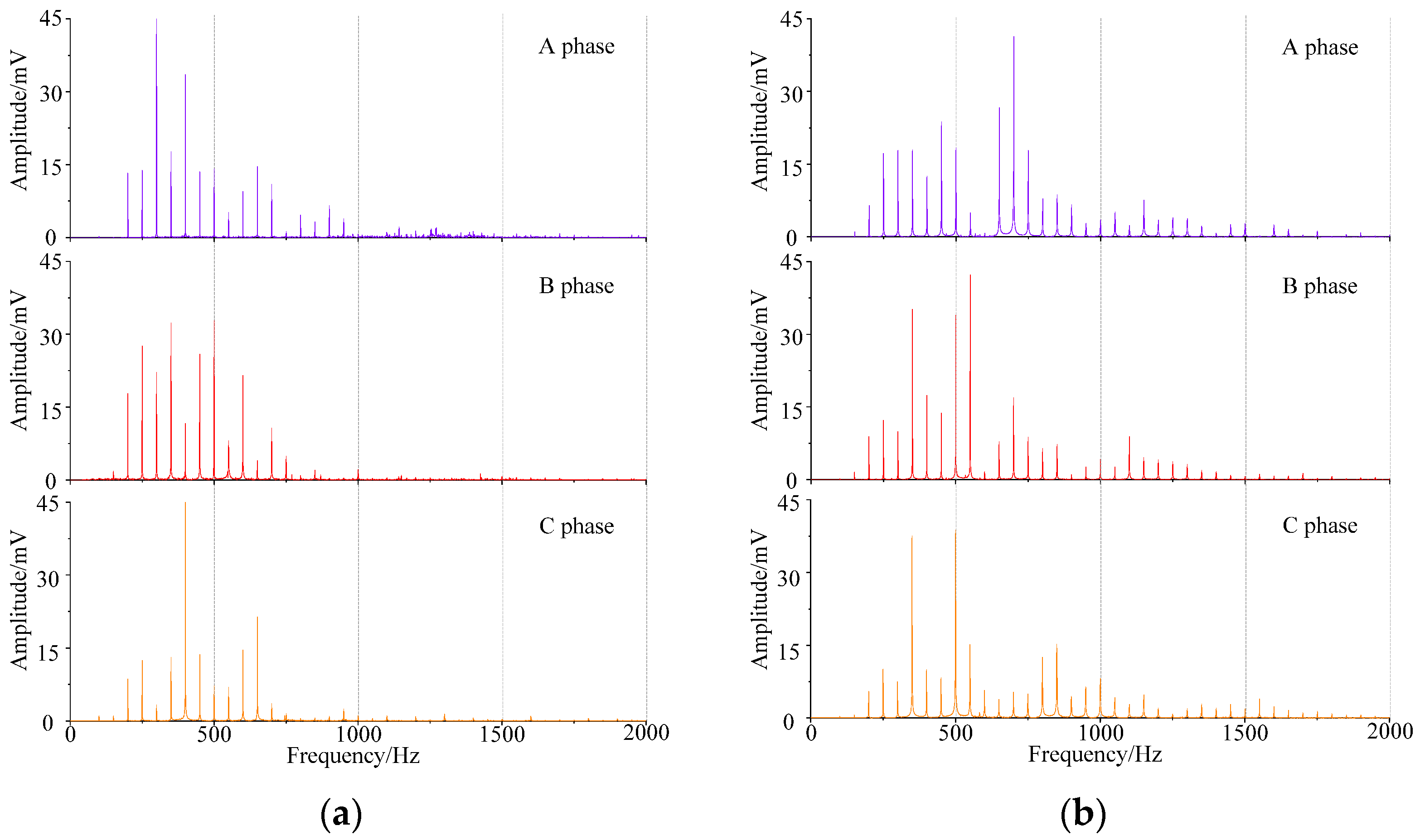
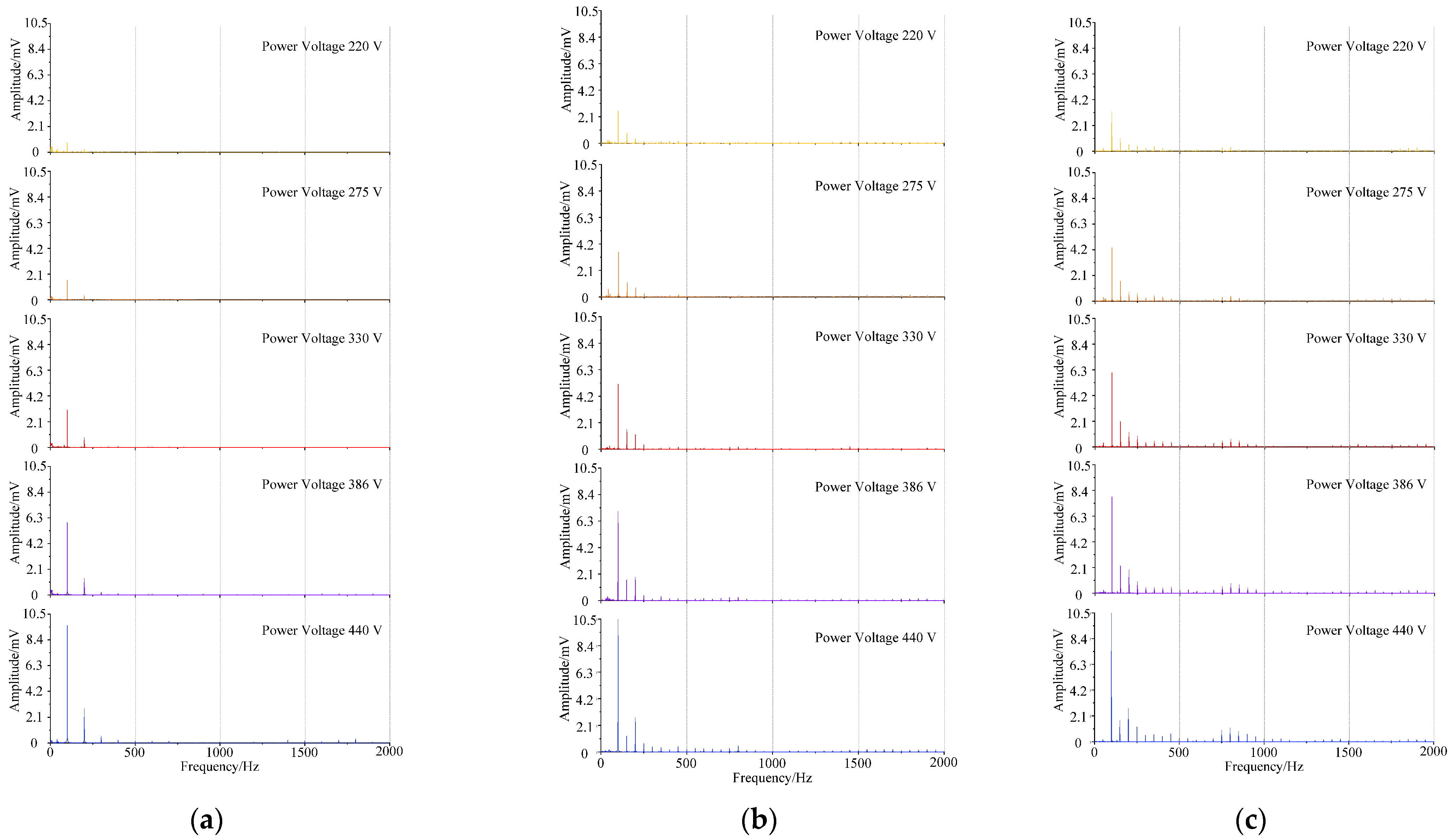
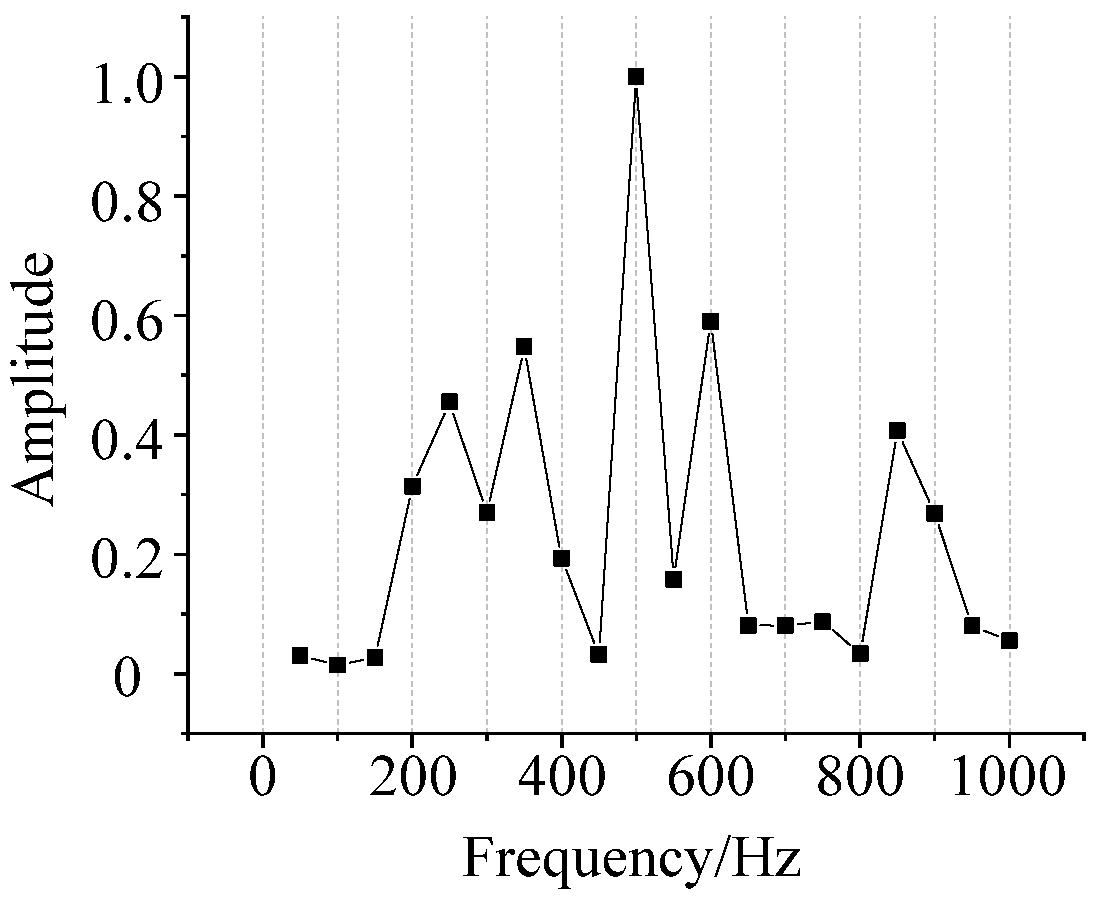
4.1. Acoustic Signal Frequency Spectrum Analysis
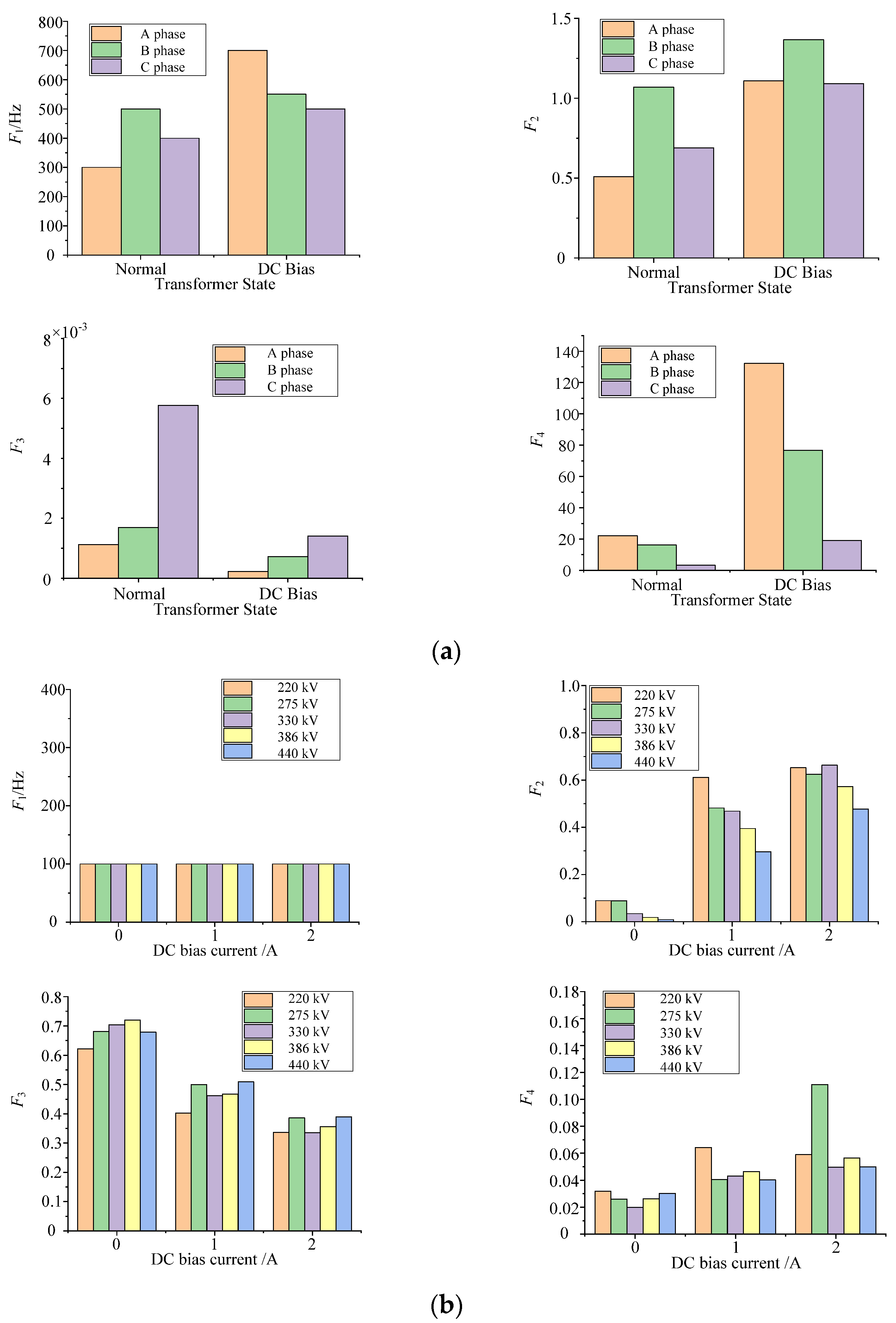
4.2. Frequency Domain Parameters Comparative Analysis
- (1)
- Dominant frequency F1,
- (2)
- Ratio between odd and even harmonics F2,
- (3)
- Ratio of fundamental frequency F3,
- (4)
- Total harmonic distortion F4,where Xf is the amplitude of frequency component at frequency f; fmax is the upper limit of statistical frequency. Because the energy of transformer acoustic signal is mainly distributed in the range of 0–2000 Hz, fmax is generally 2000 Hz. The calculation results are shown in Figure 6.
5. Determination of Acoustic Parameters Warning Threshold for DC Bias
5.1. Acoustic Signal Acquisition of 162 Normal Transformers
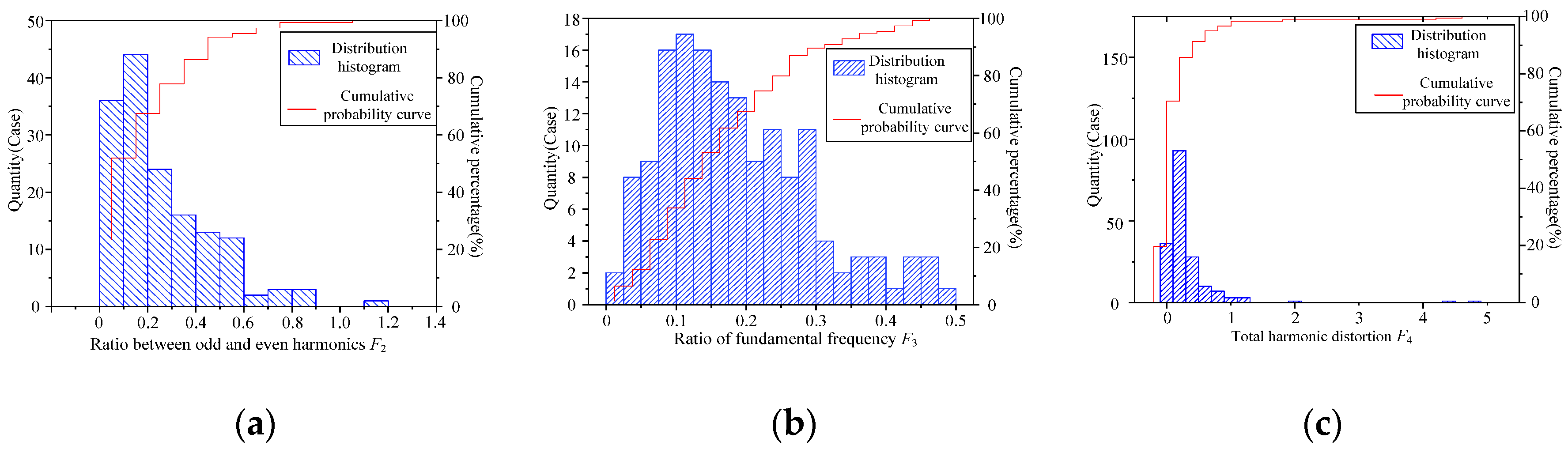
5.2. Acoustic Parameter Distribution
- (1)
- The 50 Hz odd/even frequency multiplication ratio F2:
- (2)
- Fundamental frequency proportion F3:
- (3)
- High/low-frequency ratio F4:
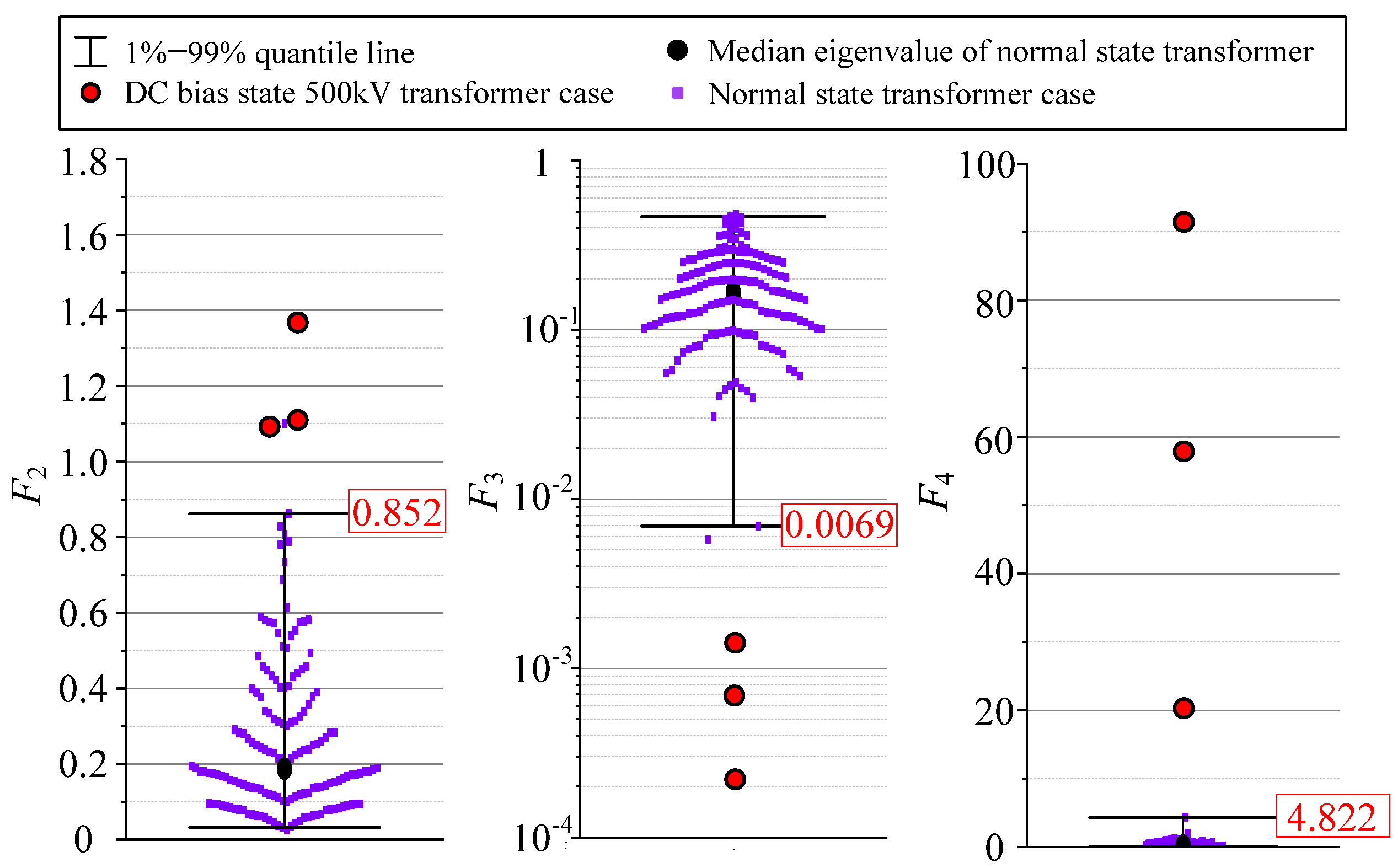
5.3. Early Warning Threshold and Example Verification
6. Conclusions
- (1)
- The dominant frequency F1 variation law of acoustic signal in the laboratory core model is different from that in the 500 kV real transformer. This is because the DC bias state of the real transformer is more serious, and the acoustic signal of the real transformer will be affected by the frequency response function of the acoustic transmission medium.
- (2)
- Under ideal laboratory conditions, the core model and DC bias state acoustic signal of field transformer can only compare their acoustical parameters with state changes, but cannot compare the values with each other. Therefore, the data of the laboratory model cannot be used to delineate the parameters warning threshold.
- (3)
- The numerical distribution of F2, F3, and F4 parameters of a large number of transformer acoustic samples in the normal state has strong aggregation. The comparison results of real cases illustrate that the warning threshold given in this paper based on three-item parameter data statistics enables stable identification of DC bias state.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Takasu, N.; Oshi, T.; Miyawaki, F.; Saito, S.; Fujiwara, Y. An experimental analysis of DC excitation of transformers by geomagnetically induced currents. IEEE Trans. Power Deliv. 1994, 9, 1173–1182. [Google Scholar] [CrossRef]
- Ding, D.W.; Zhao, D.B.; Zhang, X.H.; Lan, X.S.; Li, C.X.; Cui, B. Investigation of vibration impacts on HVAC transformer from HVDC system under monopole operation. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 1386–1392. [Google Scholar] [CrossRef]
- He, Y.D.; Zhou, Q.; Lin, S.; Zhao, L.P. Validity Evaluation Method Based on Data Driving for On-Line Monitoring Data of Transformer under DC-Bias. Sensors 2020, 20, 4321. [Google Scholar] [CrossRef] [PubMed]
- Rusakov, V.; Raikher, Y. Magnetorelaxometry in the Presence of a DC Bias Field of Ferromagnetic Nanoparticles Bearing a Viscoelastic Corona. Sensors 2018, 18, 1661. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Asif, M.; Lee, H.Y.; Park, K.H.; Lee, B.W. Accurate Evaluation of Steady-State Sheath Voltage and Current in HVDC Cable Using Electromagnetic Transient Simulation. Energies 2020, 12, 4161. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.H.; Zhou, G.; Wei, Z.N. Influence of High Voltage DC Transmission on Measuring Accuracy of Current Transformers. IEEE Access 2018, 6, 72629–72634. [Google Scholar] [CrossRef]
- Xiang, W.L.; Lin, W.X.; Xu, L.; Wen, J.Y. I Enhanced Independent Pole Control of Hybrid MMC-HVdc System. IEEE Trans. Power Deliv. 2018, 32, 861–872. [Google Scholar] [CrossRef] [Green Version]
- Wu, W.; Lin, W.X.; Xu, L.; Wen, J.Y. Calculation and Analysis of DC Magnetic Bias Current of Urban Main Transformer under the Action of Stray Current. Mob. Inf. Syst. 2021, 2021, 4806136. [Google Scholar] [CrossRef]
- Shao, S.; Chen, L.L.; Shan, Z.Y.; Gao, F.; Chen, H.; Sha, D.S.; Dragicevic, T. Modeling and Advanced Control of Dual-Active-Bridge DC-DC Converters: A Review. IEEE Trans. Power Electron. 2021, 2021, 4806136. [Google Scholar] [CrossRef]
- Ben, T.; Yang, Q.X.; Yan, R.G.; Zhu, L.H. Magnetically Controlled Saturable Reactor Core Vibration Under Practical Working Conditions. IEEE Trans. Magn. 2017, 53, 8202904. [Google Scholar]
- Rajagopal, K.; Jafari, S.; Kacar, S.; Karthikeyan, A.; Akgul, A. Fractional Order Simple Chaotic Oscillator with Saturable Reactors and Its Engineering Applications. Inf. Technol. Control 2019, 48, 115–128. [Google Scholar] [CrossRef] [Green Version]
- Garcia-Perez, A.; Romero-Troncoso, R.J.; Cabal-Yepez, E.; Osornio-Rios, R.A.; Lucio-Martinez, J.A. Application of high-resolution spectral analysis for identifying faults in induction motors by means of sound. J. Vib. Control 2012, 18, 1585–1594. [Google Scholar] [CrossRef]
- Saimurugan, M.; Ramprasad, R. A dual sensor signal fusion approach for detection of faults in rotating machines. J. Vib. Control 2018, 24, 2621–2630. [Google Scholar] [CrossRef]
- Zou, L.; Guo, Y.K.; Liu, H.; Zhao, T. A Method of Abnormal States Detection Based on Adaptive Extraction of Transformer Vibro-Acoustic Signals. Energies 2018, 10, 2076. [Google Scholar] [CrossRef] [Green Version]
- Hussain, A.; Lee, S.J.; Choi, M.S.; Brikci, F. An expert system for acoustic diagnosis of power circuit breakers and on-load tap changers. Expert Syst. Appl. 2015, 42, 9426–9433. [Google Scholar] [CrossRef]
- Zhang, H.; Ye, G.R.; Zhang, Z.C. Acoustic Radiation of a Cylindrical Piezoelectric Power Transformer. J. Vib. Control 2013, 80, 061019. [Google Scholar] [CrossRef]
- Wang, F.H.; Geng, C.; Su, L. A Parameter identification and prediction of Jiles-Atherton model for DC-biased transformer using improved shuffled frog leaping algorithm and least square support vector machine. IET Electr. Power Appl. 2015, 9, 660–669. [Google Scholar] [CrossRef]
- Majer, K. Vibrations of Transformer Cores Operating with Submagnetizing of DC Flux. Int. J. Appl. Electromagn. Mech. 2016, 51, S173–S182. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, B.; Chen, X. Research on Dynamic Magnetic Flux Measurement Under DC-Biased Magnetization by the Type-c Transducer. IEEE Trans. Magn. 2015, 51, 6101304. [Google Scholar]
- Zhang, B.; Yan, N.; Du, J.M.; Han, F.X.; Wang, H. A Novel Approach to Investigate the Core Vibration in Power Transformers. IEEE Trans. Magn. 2018, 54, 8400804. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Li, Q.; Zhang, D.H.; Bai, B.D.; Xie, D.X.; Koh, C.S. Magnetostriction of Silicon Steel Sheets Under Different Magnetization Conditions. IEEE Trans. Magn. 2016, 52, 6100204. [Google Scholar] [CrossRef]
- Kunicki, M.; Wotzka, D. A Classification Method for Select Defects in Power Transformers Based on the Acoustic Signals. Sensors 2019, 19, 5212. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huerta, R.J.R.; Granados, L.D.; Garcia, P.A.; Camarena, M.D.; Amezquita, S.J.P.; Valtierra, R.M. Short-Circuited Turn Fault Diagnosis in Transformers by Using Vibration Signals, Statistical Time Features, and Support Vector Machines on FPGA. Sensors 2021, 21, 3598. [Google Scholar] [CrossRef] [PubMed]
- Secic, A.; Krpan, M.; Kuzle, I. Vibro-acoustic methods in the condition assessment of power transformers: A survey. IEEE Access 2019, 7, 83915–83931. [Google Scholar] [CrossRef]
- Hong, K.X.; Huang, H.; Fu, Y.Q.; Zhou, J.P. A vibration measurement system for health monitoring of power transformers. Measurement 2016, 93, 135–147. [Google Scholar] [CrossRef]
- Bartoletti, C.; Desiderio, M.; Di Carlo, D.; Fazio, G.; Muzi, F.; Sacerdoti, G.; Salvatori, F. Vibro-acoustic techniques to diagnose power transformers. IEEE Trans. Power Deliv. 2004, 19, 221–229. [Google Scholar] [CrossRef]
- García, B.; Burgos, J.C.; Alonso, Á.M. Transformer tank vibration modeling as a method of detecting winding deformations-part I: Theoretical foundatio. IEEE Trans. Power Deliv. 2006, 21, 157–163. [Google Scholar] [CrossRef]
- García, B.; Burgos, J.C.; Alonso, Á.M. Transformer tank vibration modeling as a method of detecting winding deformations-part II: Experimental verification. IEEE Trans. Power Deliv. 2006, 21, 164–169. [Google Scholar] [CrossRef]
- Zhang, F.; Ji, S.C.; Shi, Y.H.; Zhan, C.; Zhu, L.Y. Investigation on vibration source and transmission characteristics in power transformers. Appl. Acoust. 2019, 151, 99–112. [Google Scholar] [CrossRef]
- Wang, S.H.; Lv, F.C.; Liu, Y.P. Multi-Frequency Acoustic Signal Under Short-Circuit Transient and Its Application on the Condition Monitoring of Transformer Winding. IEEE Trans. Power Deliv. 2019, 34, 1666–1673. [Google Scholar]
- Michael, E.K.; Cullity, B.D. The magnetostriction of iron under tensile and compressive stress. Intern. J. Magn. 1971, 1, 323–325. [Google Scholar]
- Gao, P.; Wang, F.H.; Su, L.; Jiang, Y.M. Analysis on vibration characteristics of power transformer under DC bias. Power Syst. Technol. 2014, 38, 1536–1541. [Google Scholar]




| Status | Voltage | DC Bias | Magnetic Flux Density of Core Center Pillar |
|---|---|---|---|
| Normal | 193 V | 0 A | 0.7 T |
| 276 V | 0 A | 1.0 T | |
| 330 V | 0 A | 1.2 T | |
| 386 V | 0 A | 1.4 T | |
| 440 V | 0 A | 1.6 T | |
| DC bias | 193 V | 0.5 A | - |
| 276 V | 0.5 A | - | |
| 330 V | 0.5 A | - | |
| 386 V | 0.5 A | - | |
| 440 V | 0.5 A | - | |
| 193 V | 1.0 A | - | |
| 276 V | 1.0 A | - | |
| 330 V | 1.0 A | - | |
| 386 V | 1.0 A | - | |
| 440 V | 1.0 A | - |
| Parameters | Parameter Values | ||
|---|---|---|---|
| Value of 500 kV Transformer | Value of Core Model | Value of Core Model (Calculated with Frequency Spectrum Conversion Model) | |
| F1 | >300 Hz | 100 Hz | 500 Hz |
| F2 | >0.5 | 0~0.65 | 0.972 |
| F3 | <0.0058 | 0.336~0.720 | 0.0054 |
| F4 | >3.31 | 0.019~0.111 | 3526.836 |
| Substation Name | Voltage Level/kV | Quantity/Set | Substation Name | Voltage Level/kV | Quantity/Set |
|---|---|---|---|---|---|
| Xingtai | 1000 | 6 | Baoding | 1000 | 6 |
| Xinji | 500 | 12 | Qingyuan | 500 | 12 |
| Pengcun | 500 | 12 | Shibei | 500 | 9 |
| Lianzhou | 500 | 9 | Xinan | 500 | 9 |
| Linhe | 500 | 9 | Cangxi | 500 | 9 |
| Ciyun | 500 | 9 | Xingxi | 500 | 6 |
| Zongzhou | 500 | 6 | Wuyi | 500 | 6 |
| Huanghua | 500 | 6 | Guishan | 500 | 6 |
| Guangyuan | 500 | 6 | Yishui | 500 | 6 |
| Yingzhou | 500 | 6 | Yuanshi | 500 | 6 |
| Xuanhuihe | 500 | 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Wang, B. Acoustic Multi-Parameter Early Warning Method for Transformer DC Bias State. Sensors 2022, 22, 2906. https://doi.org/10.3390/s22082906
Zhou Y, Wang B. Acoustic Multi-Parameter Early Warning Method for Transformer DC Bias State. Sensors. 2022; 22(8):2906. https://doi.org/10.3390/s22082906
Chicago/Turabian StyleZhou, Yuhao, and Bowen Wang. 2022. "Acoustic Multi-Parameter Early Warning Method for Transformer DC Bias State" Sensors 22, no. 8: 2906. https://doi.org/10.3390/s22082906
APA StyleZhou, Y., & Wang, B. (2022). Acoustic Multi-Parameter Early Warning Method for Transformer DC Bias State. Sensors, 22(8), 2906. https://doi.org/10.3390/s22082906





