The Concept of Using the Decision-Robustness Function in Integrated Navigation Systems
Abstract
:1. Introduction
- a new concept of using the decision-robustness function in maritime navigation;
- a new technique for selecting the best navigation system based on the concept of the decision-robustness function;
- new possibilities of using the function in one-man-bridge systems or in autonomous vehicle algorithms;
- increasing the range of available methods in the automation of navigation processes thanks to the new concept of the decision function.
- the adaptation of the decision-robustness function to the needs of maritime navigation;
- the possibility of using the decision-robustness function to solve typical navigation tasks.
2. Related Work
3. Description of Mathematical Model
3.1. Robust Estimation Task and Its Solution
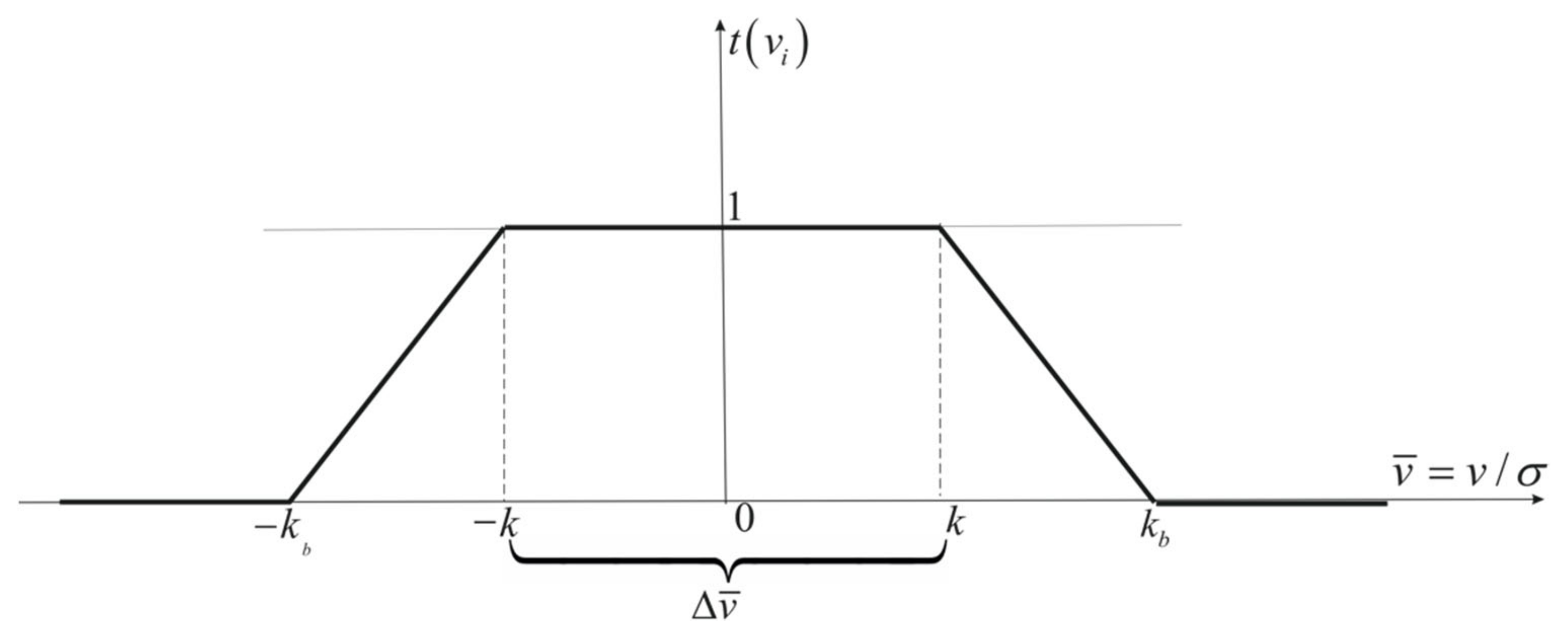
3.2. Decision Function as an a Priori Object
3.3. Attenuation Function as an a Posteriori Object
4. Experimental Results
4.1. Computer Application
4.2. Practical Use of the Decision-Robustness Function in Maritime Navigation
4.2.1. Determination of Fix Position #1
4.2.2. Determination of Fix Position #3
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alexander, L.; Ryan, J.F.; Casey, M.J. Integrated Navigation System: Not a Sum of Its Parts. In Proceedings of the Canadian Hydrographic Conference, Ottawa, ON, Canada, 25–27 May 2004; p. 297. [Google Scholar]
- IMO. Recommendation on Performance Standards for Integrated Bridge Systems (IBS); IMO Resolution MSC.64(67), Annex 1, 4; IMO: London, UK, 1996. [Google Scholar]
- IMO. Adoption of New and Amended Performance Standards; IMO Resolution MSC.64(67); IMO: London, UK, 1996. [Google Scholar]
- IMO. Adoption of the Revised Performance Standards for Integrated Navigation Systems (INS); IMO Resolution MSC.252(83); IMO: London, UK, 2007. [Google Scholar]
- Czaplewski, K. Global Positioning System: Political Support, Directions of Development, and Expectations. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2015, 9, 229–232. [Google Scholar] [CrossRef]
- Wąż, M. Navigation Based on Characteristic Points from Radar Images. Sci. J. Marit. Univ. Szczec. 2010, 20, 140–145. [Google Scholar]
- Naus, K.; Wąż, M.; Szymak, P.; Gucma, L.; Gucma, M. Assessment of ship position estimation accuracy based on radar navigation mark echoes identified in an Electronic Navigational Chart. Measurement 2021, 169, 108630. [Google Scholar] [CrossRef]
- Hein, G.W. Status, perspectives and trends of satellite navigation. Satell. Navig. 2020, 1, 22. [Google Scholar] [CrossRef] [PubMed]
- Zrinjski, M.; Barković, D.; Matika, K. Razvoj i modernizacija GNSS-a. Geod. List 2019, 73, 45–65. [Google Scholar]
- DeLaPena, C.A. Military Communications & Positioning, Navigation, and Timing Overview with GPS Update. In Proceedings of the 26th National Space-Based Positioning, Navigation & Timing Advisory Board Meeting, Annapolis, MD, USA, 4–5 May 2022. [Google Scholar]
- Zhang, J.; Cui, X.; Xu, H.; Lu, M. A Two-Stage Interference Suppression Scheme Based on Antenna Array for GNSS Jamming and Spoofing. Sensors 2019, 19, 3870. [Google Scholar] [CrossRef]
- Kwon, K.-C.; Shim, D.-S. Performance Analysis of Direct GPS Spoofing Detection Method with AHRS/Accelerometer. Sensors 2020, 20, 954. [Google Scholar] [CrossRef]
- Narins, M.; Enge, P.; Peterson, B.; Lo, S.; Chen, Y.-H.; Akos, D.; Lombardi, M. The Need for a Robust, Precise Time and Frequency Alternative to GNSS. In Proceedings of the 25th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2012), Nashville, TN, USA, 20–24 September 2012; pp. 2057–2062. [Google Scholar]
- Han, S.; Gong, Z.; Meng, W.; Li, C.; Gu, X. Future Alternative Positioning, Navigation, and Timing Techniques: A Survey. IEEE Wirel. Commun. 2016, 23, 154–160. [Google Scholar] [CrossRef]
- Yang, Y.; Song, L.; Xu, T. Robust estimator for correlated observations based on bifactor equivalent weights. J. Geod. 2002, 76, 353–358. [Google Scholar] [CrossRef]
- Czaplewski, K. Positioning with Interactive Navigational Structures Implementation. Monograph. Annu. Navig. 2004, 7, 119. [Google Scholar]
- Czaplewski, K.; Wąż, M.; Zienkiewicz, M.H. A Novel Approach of Using Selected Unconventional Geodesic Methods of Estimation on VTS Areas. Mar. Geod. 2019, 42, 447–468. [Google Scholar] [CrossRef]
- Wilk, A.; Koc, W.; Specht, C.; Judek, S.; Karwowski, K.; Chrostowski, P.; Czaplewski, K.; Dabrowski, P.S.; Grulkowski, S.; Licow, R.; et al. Digital Filtering of Railway Track Coordinates in Mobile Multi–Receiver GNSS Measurements. Sensors 2020, 20, 5018. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, C.; Zhang, D. Data Fusion Based on Adaptive Interacting Multiple Model for GPS/INS Integrated Navigation System. Appl. Sci. 2018, 8, 1682. [Google Scholar] [CrossRef]
- Jiang, C.; Zhang, S.-B.; Zhang, Q.Z. Adaptive Estimation of Multiple Fading Factors for GPS/INS Integrated Navigation Systems. Sensors 2017, 17, 1254. [Google Scholar] [CrossRef]
- Vidmar, P.; Perkovič, M.; Gucma, L.; Łazuga, K. Risk Assessment of Moored and Passing Ships. Appl. Sci. 2020, 10, 6825. [Google Scholar] [CrossRef]
- Czaplewski, K.; Świerczyński, S. A Method of Increasing the Accuracy of Radar Distance Measurement in VTS Systems for Vessels with Very Large Dimensions. Remote Sens. 2021, 13, 3066. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Legat, K.; Wieser, M. Image-based navigation. In Navigation; Springer: Vienna, Austria, 2013. [Google Scholar]
- Groves, P.D. The PNT boom, future trends in integrated navigation. Inside GNSS 2013, 8, 44–49. [Google Scholar]
- Veth, M.J. Navigation using images, a survey of techniques. J. Inst. Navig. 2011, 58, 127–139. [Google Scholar] [CrossRef]
- Naus, K.; Wąż, M. Precision in Determining Ship Position using the Method of Comparing an Omnidirectional Map to a Visual Shoreline Image. J. Navig. 2016, 69, 391–413. [Google Scholar] [CrossRef]
- Naus, K.; Szymak, P.; Piskur, P.; Niedziela, M.; Nowak, A. Methodology for the Correction of the Spatial Orientation Angles of the Unmanned Aerial Vehicle Using Real Time GNSS, a Shoreline Image and an Electronic Navigational Chart. Energies 2021, 14, 2810. [Google Scholar] [CrossRef]
- Yang, Y.; Cheng, M.; Shum, C.; Tapley, B.D. Robust estimation of systematic errors of satellite laser range. J. Geod. 1999, 73, 345–349. [Google Scholar] [CrossRef]
- Wisniewski, Z. Concept of Adjustment Methods in Navigation; Polish Naval Academy: Gdynia, Poland, 2002. (In Polish) [Google Scholar]
- Wiśniewski, Z. Adjustment Methods in Navigation and Hydrography; Polish Naval Academy: Gdynia, Poland, 2003. (In Polish) [Google Scholar]
- Duchnowski, R. Robust estimation of variance coefficient (VR-estimation) for dependent observations. Geod. Kartogr. 2000, 49, 131–143. [Google Scholar]
- Wiśniewski, Z. The most effective estimator of variance coefficient in geodetic observation systems. Geod. Kartogr. 1999, 48, 105–131. [Google Scholar]
- Gucma, S. Inżynieria Ruchu Morskiego; Wydawnictwo Okrętownictwo i Żegluga: Gdańsk, Poland, 2001. (In Polish) [Google Scholar]
- Gucma, S. Nawigacja Pilotażowa; Wydawnictwo Fundacji Promocji Przemysłu Okrętowego i Gospodarki Morskiej: Gdańsk, Poland, 2004. (In Polish) [Google Scholar]
- UKHO. Sailing Directions-Nord Sea (West Pilot), 12th ed.; UKHO: London, UK, 2021. [Google Scholar]
- UKHO. Available online: https://www.admiralty.co.uk/ (accessed on 20 May 2022).
- Huber, P.J. Robust Statistics; John Wiley & Sons: New York, NY, USA, 1981. [Google Scholar]
- Hampel, F.R.; Ronchetti, E.M.; Rousseeuw, P.J.; Stahel, W.A. Robust Statistics. The Approach Based on Influence Functions; John Wiley & Sons: New York, NY, USA, 1986. [Google Scholar]
- Krarup, K.; Kubik, K. The Danish Method: Experience and Philosophy; Series A, Issue 98; Deutsche Geodätische Kommission bei der Bayerischen Akademie Wissen: München, Germany, 1983; pp. 131–134. [Google Scholar]
- Weintrit, A. Clarification, Systematization and General Classification of Electronic Chart Systems and Electronic Navigational Charts Used in Marine Navigation. Part 1-Electronic Chart Systems. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2018, 12, 471–482. [Google Scholar] [CrossRef]







| Ship’s Positions | X (m) | Y (m) |
|---|---|---|
| #1 | 6,044,630.76 | 358,462.92 |
| #2 | 6,048,890.43 | 359,497.90 |
| #3 | 6,051,460.48 | 361,197.74 |
| #4 | 6,053,586.87 | 363,475.51 |
| #5 | 6,054,839.70 | 365,398.69 |
| Ship’s Positions | GNSS | Radar |
|---|---|---|
| #1 | ||
| #2 | ||
| #3 | ||
| #4 | ||
| #5 |
| Ship’s Positions | X (m) | Y (m) |
|---|---|---|
| #2 | 6,048,733.2 | 359,533.2 |
| #4 | 6,053,600.4 | 363,533.4 |
| #5 | 6,054,855.5 | 365,474.5 |
| Radar Echo | X (m) | Y (m) |
|---|---|---|
| #R1 | 6,052,469.34 | 358,694.38 |
| #R2 | 6,045,676.69 | 341,307.40 |
| #R3 | 6,059,266.78 | 376,133.21 |
| #R4 | 6,047,000.12 | 377,600.23 |
| #R5 | 6,041,466.54 | 359,666.50 |
| Ship’s Positions | ||
|---|---|---|
| #1 | #R1 | 7842.00 |
| #R2 | 17,187.00 | |
| #R3 | 22,945.00 | |
| #R4 | 19,283.00 | |
| #R5 | 3600.00 | |
| #3 | #R1 | 2700.00 |
| #R2 | 20,714.00 | |
| #R3 | 16,852.00 | |
| #R4 | 16,998.00 | |
| #R5 | 10,300.00 | |
| Step of Iteration | Parameters of the Attenuation Function | Values of the Attenuation Function for Individual Observations | Values of Standardised Corrections for Individual Observations | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.2 | 1 | 0.135 | 0.515 | 0.699 | 0.782 | 0.063 | 1.528 | 1.158 | 1.893 | 0.835 | 4.931 |
| 2 | 0.4 | 2 | 1 | 1 | 1 | 1 | 0.032 | 1.007 | 0.289 | 0.263 | 0.254 | 3.800 |
| 3 | 0.6 | 3 | 1 | 1 | 1 | 1 | 0.03 | 0.951 | 0.270 | 0.250 | 0.244 | 3.690 |
| 4 | 0.8 | 5 | 1 | 1 | 1 | 1 | 0.00002 | 0.023 | 0.039 | 0.040 | 0.068 | 0.086 |
| Step of Iteration | Parameters of the Attenuation Function | Values of the Attenuation Function for Individual Observations | Values of Standardised Corrections for Individual Observations | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.2 | 1 | 0.444 | 0.636 | 0.356 | 0.663 | 0.163 | 2.356 | 2.505 | 2.717 | 2.041 | 5.915 |
| 2 | 0.2 | 2 | 0.975 | 0.950 | 0.902 | 1 | 0.047 | 0.945 | 0.663 | 1.094 | 0.508 | 3.915 |
| 3 | 0.6 | 3 | 1 | 1 | 1 | 1 | 0.015 | 0.367 | 0.246 | 0.334 | 0.137 | 2.277 |
| 4 | 4.5 | 0.005 | 1 | 1 | 1 | 1 | 0.011 | 0.301 | 0.203 | 0.246 | 0.096 | 2.008 |
| Ship’s Positions | X (m) | Y (m) |
|---|---|---|
| #1 | 6,044,630.6 | 358,462.8 |
| #2 | 6,048,733.2 | 359,533.2 |
| #3 | 6,051,464.1 | 361,198.1 |
| #4 | 6,053,600.4 | 363,533.4 |
| #5 | 6,054,855.5 | 365,474.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czaplewski, K.; Czaplewski, B. The Concept of Using the Decision-Robustness Function in Integrated Navigation Systems. Sensors 2022, 22, 6157. https://doi.org/10.3390/s22166157
Czaplewski K, Czaplewski B. The Concept of Using the Decision-Robustness Function in Integrated Navigation Systems. Sensors. 2022; 22(16):6157. https://doi.org/10.3390/s22166157
Chicago/Turabian StyleCzaplewski, Krzysztof, and Bartosz Czaplewski. 2022. "The Concept of Using the Decision-Robustness Function in Integrated Navigation Systems" Sensors 22, no. 16: 6157. https://doi.org/10.3390/s22166157
APA StyleCzaplewski, K., & Czaplewski, B. (2022). The Concept of Using the Decision-Robustness Function in Integrated Navigation Systems. Sensors, 22(16), 6157. https://doi.org/10.3390/s22166157







