Radar-Based Detection of Respiration Rate with Adaptive Harmonic Quefrency Selection
Abstract
:1. Introduction
2. Methods
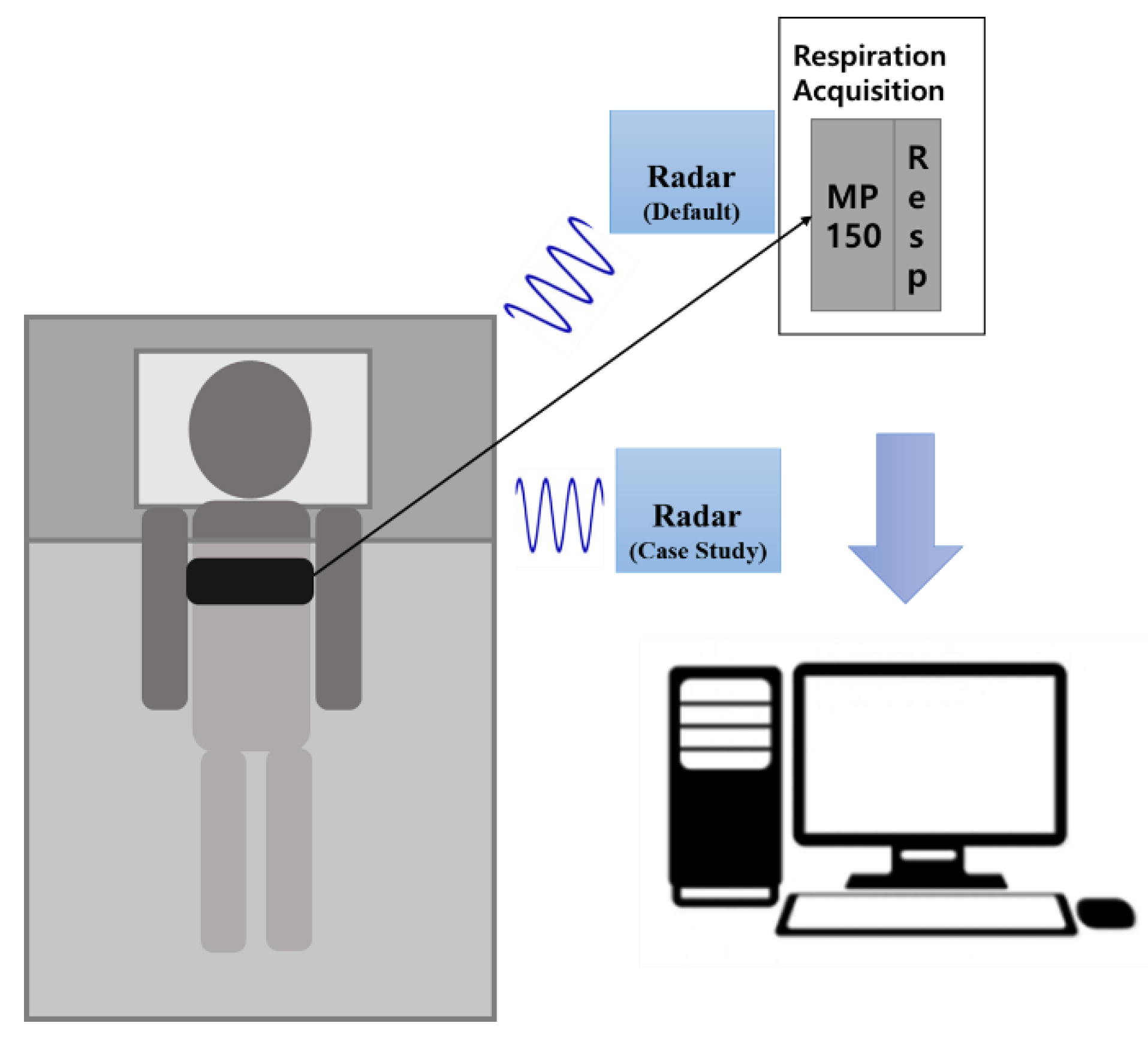
2.1. Experiment
2.1.1. Experiment Overview
2.1.2. Case Studies
2.2. Adaptive Harmonic Quefrency Selection
2.3. Evaluation
2.3.1. Ground Truth
2.3.2. Evaluation of the Respiration Rate Comparison
2.3.3. Statistical Evaluation
3. Results
3.1. Visual Inspection
3.2. Radar-Based Respiration Rate Detection
3.3. Comparison of Respiration Rates
3.4. Radar Comparison
3.5. Respiration Rate Detection Over Long Periods
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Al-Khalidi, F.Q.; Saatchi, R.; Burke, D.; Elphick, H.; Tan, S. Respiration rate monitoring methods: A review. Pediatric Pulmonol. 2011, 46, 523–529. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miwa, H.; Sakai, K. Development of heart rate and respiration rate measurement system using body-sound. In Proceedings of the 2009 9th International Conference on Information Technology and Applications in Biomedicine, Larnaka, Cyprus, 4–7 November 2009; pp. 1–4. [Google Scholar]
- Folke, M.; Cernerud, L.; Ekström, M.; Hök, B. Critical review of non-invasive respiratory monitoring in medical care. Med Biol. Eng. Comput. 2003, 41, 377–383. [Google Scholar] [CrossRef] [PubMed]
- Nam, Y.; Kim, Y.; Lee, J. Sleep monitoring based on a tri-axial accelerometer and a pressure sensor. Sensors 2016, 16, 750. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, C.; Peng, Z.; Huang, T.; Fan, T.; Wang, F.; Horng, T.; Muñoz-Ferreras, J.; Gómez-García, R.; Ran, L.; Lin, J. A review on recent progress of portable short-range noncontact microwave radar systems. IEEE Trans. Microw. Theory Tech. 2017, 65, 1692–1706. [Google Scholar] [CrossRef]
- Ren, L.; Wang, H.; Naishadham, K.; Liu, Q.; Fathy, A.E. Non-invasive detection of cardiac and respiratory rates from stepped frequency continuous wave radar measurements using the state space method. In Proceedings of the 2015 IEEE MTT-S International Microwave Symposium, Phoenix, AZ, USA, 17–22 May 2015; pp. 1–4. [Google Scholar]
- Zakrzewski, M.; Raittinen, H.; Vanhala, J. Comparison of center estimation algorithms for heart and respiration monitoring with microwave Doppler radar. IEEE Sens. J. 2011, 12, 627–634. [Google Scholar] [CrossRef]
- Norton, M.P.; Karczub, D.G. Fundamentals of Noise and Vibration Analysis for Engineers; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Heo, H.; Sung, D.; Lee, K. Note onset detection based on harmonic cepstrum regularity. In Proceedings of the 2013 IEEE International Conference on Multimedia and Expo. (ICME), San Jose, CA, USA, 15–19 July 2013; pp. 1–6. [Google Scholar]
- Skowronski, M.D.; Shrivastav, R.; Hunter, E.J. Cepstral peak sensitivity: A theoretic analysis and comparison of several implementations. J. Voice 2015, 29, 670–681. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Konstantin-Hansen, H.; Herlufsen, H. Envelope and cepstrum analyses for machinery fault identification. Sound Vib. 2010, 44, 10. [Google Scholar]
- Respiration Recording, Biopac. Available online: https://www.biopac.com/knowledge-base/respiration-recording (accessed on 28 January 2020).
- Bland, J.M.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Hanneman, S.K. Design, analysis, and interpretation of method-comparison studies. AACN Adv. Crit. Care 2008, 19, 223–234. [Google Scholar]
- Kim, T.H. Differential diagnosis and treatment of dyspnea. Korean J. Med. 2009, 76, 425–430. [Google Scholar]
- Sarkar, S.; Amelung, P.J. Evaluation of the dyspneic patient in the office. Prim. Care Clin. Off. Pract. 2006, 33, 643–657. [Google Scholar] [CrossRef] [PubMed]
- Depaso, W.J.; Winterbauer, R.H.; Lusk, A.A.; Dreis, D.P.; Springmeyer, S.C. Chronic dyspnea unexplained by history, physical examination, chest roentgenogram, and spirometry: Analysis of a seven-year experience. Chest 1991, 100, 1293–1299. [Google Scholar] [CrossRef] [PubMed]
- Novak, P.; Novak, V. Time/frequency mapping of the heart rate, blood pressure and respiratory signals. Med. Biol. Eng. Comput. 1993, 31, 103–110. [Google Scholar] [CrossRef] [PubMed]








| No. | Respiration Rate Comparison | Bland–Altman | |||
|---|---|---|---|---|---|
| Belt (Mean ± SD) | Radar (Mean ± SD) | Diff | Mean Difference | 95% Limits of Agreement | |
| 1 | 18 ± 0.2 | 18 ± 0.3 | 0 | −0.1 | 1.30 (0.5 to −0.8) |
| 2 | 18 ± 0.3 | 18 ± 0.3 | 0 | −0.1 | 1.30 (0.5 to −0.8) |
| 3 | 19 ± 0.3 | 19 ± 0.1 | 0 | −0.1 | 1.30 (0.5 to −0.8) |
| 4 | 20 ± 0.4 | 20 ± 0.3 | 0 | 0.1 | 2.36 (1.3 to −1.1) |
| 5 | 20 ± 0.7 | 19 ± 0.3 | 1 | −0.6 | 2.42 (0.6 to −1.8) |
| 6 | 16 ± 0.2 | 15 ± 0.1 | 1 | −1.3 | 2.30 (−0.1 to −2.4) |
| 7 | 18 ± 0.3 | 16 ± 0.2 | 2 | −1.4 | 1.98 (−0.4 to −2.4) |
| 8 | 20 ± 0.5 | 18 ± 0.2 | 2 | −1.5 | 3.14 (0.0 to −3.1) |
| 9 | 21 ± 0.4 | 20 ± 0.5 | 1 | −1.4 | 1.98 (−0.4 to −2.4) |
| 10 | 19 ± 0.3 | 18 ± 0.5 | 1 | −1.2 | 2.86 (0.3 to −2.6) |
| 11 | 18 ± 0.5 | 16 ± 0.4 | 2 | −2.1 | 3.24 (−0.4 to −3.7) |
| 12 | 20 ± 0.5 | 20 ± 0.6 | 0 | −0.2 | 3.26 (1.4 to −1.9) |
| 13 | 19 ± 1.0 | 18 ± 1.0 | 1 | −1.1 | 4.70 (1.3 to −3.4) |
| 14 | 20 ± 0.6 | 19 ± 0.4 | 1 | −0.9 | 3.06 (0.7 to −2.4) |
| 15 | 20 ± 0.7 | 22 ± 0.9 | 2 | 1.8 | 2.86 (3.3 to 0.4) |
| 16 | 20 ± 0.6 | 20 ± 0.8 | 0 | 0.2 | 3.72 (2.0 to −1.7) |
| No. | Respiration Rate Comparison | Bland–Altman | ||||||
|---|---|---|---|---|---|---|---|---|
| Peak Counting | FFT | Peak Counting | FFT | |||||
| Mean ± SD | Diff | Mean ± SD | Diff | M.D. | 2SD | M.D. | 2SD | |
| 1 | 19 ± 0.4 | 1 | 19 ± 0.3 | 1 | 0.7 | 1.94 (1.6 to −0.3) | 0.9 | 1.30 (1.5 to 0.2) |
| 2 | 19 ± 0.2 | 1 | 19 ± 0.3 | 1 | 1.1 | 0.96 (1.5 to 0.6) | 0.9 | 1.30 (1.5 to 0.2) |
| 3 | 19 ± 0.3 | 0 | 20 ± 0.3 | 1 | 0.2 | 1.54 (0.9 to −0.6) | 0.5 | 2.02 (1.5 to −0.5) |
| 4 | 21 ± 0.5 | 1 | 19 ± 1.0 | 1 | 1 | 3.40 (2.7 to −0.7) | −0.9 | 4.90 (1.5 to −3.4) |
| 5 | 22 ± 0.4 | 2 | 18 ± 2.9 | 2 | 2.4 | 3.66 (4.2 to 0.5) | −1.7 | 9.58 (3.1 to −6.5) |
| 6 | 22 ± 0.6 | 6 | 17 ± 0.1 | 1 | 5.7 | 2.38 (6.8 to 4.5) | 0.3 | 1.94 (1.3 to −0.6) |
| 7 | 22 ± 0.7 | 4 | 18 ± 0.2 | 0 | 4.5 | 3.94 (6.4 to 2.5) | 0.1 | 2.74 (1.5 to −1.3) |
| 8 | 19 ± 0.3 | 1 | 15 ± 2.6 | 5 | −0.7 | 2.76 (0.7 to −2.0) | −4.9 | 11.12 (0.6 to −10.5) |
| 9 | 21 ± 0.4 | 0 | 17 ± 1.4 | 4 | −0.4 | 1.98 (0.6 to −1.4) | −4.1 | 5.96 (−1.1 to −7.0) |
| 10 | 19 ± 0.8 | 0 | 17 ± 1.7 | 2 | 0.2 | 3.54 (2.0 to −1.5) | −2.1 | 7.90 (1.9~−6.0) |
| 11 | 19 ± 0.8 | 1 | 17 ± 0.8 | 1 | 0.5 | 2.02 (1.5 to −0.5) | −0.8 | 3.98 (1.2 to −2.8) |
| 12 | 22 ± 0.4 | 2 | 21 ± 1.4 | 1 | 1.9 | 2.58 (3.2 to 0.6) | 0.8 | 5.58 (3.6 to −2.0) |
| 13 | 22 ± 0.3 | 3 | 16 ± 2.8 | 3 | 3.2 | 5.58 (6.0 to 0.4) | −3.2 | 13.18 (3.3 to −9.8) |
| 14 | 22 ± 0.6 | 2 | 16 ± 2.3 | 4 | 1.9 | 2.74 (3.3 to 0.5) | −4.2 | 8.22 (−0.1 to −8.3) |
| 15 | 23 ± 0.3 | 3 | 18 ± 1.2 | 2 | 2.6 | 3.90 (4.6 to 0.7) | −1.9 | 6.56 (1.3 to −5.2) |
| 16 | 22 ± 1.0 | 2 | 16 ± 2.5 | 4 | 2.5 | 4.18 (4.6 to 0.4) | −3.6 | 10.08 (1.4 to −8.7) |
| No. | G.T. | Respiration Rate Comparison | Bland–Altman | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Radar 1 | Radar 2 | Radar 1 | Radar 2 | ||||||
| Mean ± SD | Mean ± SD | Diff | Mean ± SD | Diff | M.D. | 2SD | M.D. | 2SD | |
| 1 | 18 ± 0.2 | 18 ± 0.3 | 0 | 18 ± 0.3 | 0 | 0.2 | 1.54 (0.9 to −0.6) | 0.5 | 2.02 (1.5 to −0.5) |
| 2 | 18 ± 0.3 | 18 ± 0.4 | 0 | 18 ± 0.3 | 0 | 0 | 2.40 (1.2 to −1.2) | 0.1 | 1.90 (1.1 to −0.8) |
| 3 | 19 ± 0.2 | 19 ± 0.2 | 0 | 19 ± 0.1 | 0 | 0.2 | 2.08 (1.2 to −0.9) | 0.2 | 2.20 (1.3 to −0.9) |
| 4 | 20 ± 0.3 | 19 ± 0.3 | 1 | 20 ± 0.4 | 0 | −0.3 | 2.30 (0.9 to −1.4) | −0.1 | 1.68 (0.8 to −0.9) |
| 5 | 18 ± 0.6 | 18 ± 0.7 | 0 | 19 ± 0.3 | 1 | 0.3 | 2.38 (1.5 to −0.8) | 0.8 | 2.20 (1.9 to −0.3) |
| 6 | 15 ± 0.2 | 15 ± 0.3 | 0 | 15 ± 0.3 | 0 | −0.1 | 0.96 (0.4 to −0.5) | 0.3 | 1.94 (1.3 to −0.6) |
| 7 | 18 ± 0.2 | 18 ± 0.2 | 0 | 19 ± 0.3 | 1 | −0.3 | 1.84 (0.6 to −1.2) | 0.3 | 1.84 (1.2 to −0.6) |
| 8 | 18 ± 0.2 | 18 ± 0.1 | 0 | 18 ± 0.3 | 0 | −0.5 | 2.02 (0.5 to −1.5) | −0.1 | 2.74 (1.3 to −1.5) |
| 9 | 19 ± 0.3 | 19 ± 0.4 | 0 | 19 ± 0.3 | 0 | 0.3 | 1.84 (1.2 to −0.6) | 0.1 | 1.30 (0.8 to −0.5) |
| 10 | 18 ± 0.7 | 18 ± 0.5 | 0 | 18 ± 0.6 | 0 | 0.1 | 2.36 (1.3 to −1.1) | 0.3 | 3.38 (2.0 to −1.3) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Yoo, S.K. Radar-Based Detection of Respiration Rate with Adaptive Harmonic Quefrency Selection. Sensors 2020, 20, 1607. https://doi.org/10.3390/s20061607
Lee J, Yoo SK. Radar-Based Detection of Respiration Rate with Adaptive Harmonic Quefrency Selection. Sensors. 2020; 20(6):1607. https://doi.org/10.3390/s20061607
Chicago/Turabian StyleLee, JeeEun, and Sun K. Yoo. 2020. "Radar-Based Detection of Respiration Rate with Adaptive Harmonic Quefrency Selection" Sensors 20, no. 6: 1607. https://doi.org/10.3390/s20061607





