Secrecy Performance Analysis of Wireless Powered Sensor Networks Under Saturation Nonlinear Energy Harvesting and Activation Threshold
Abstract
:1. Introduction
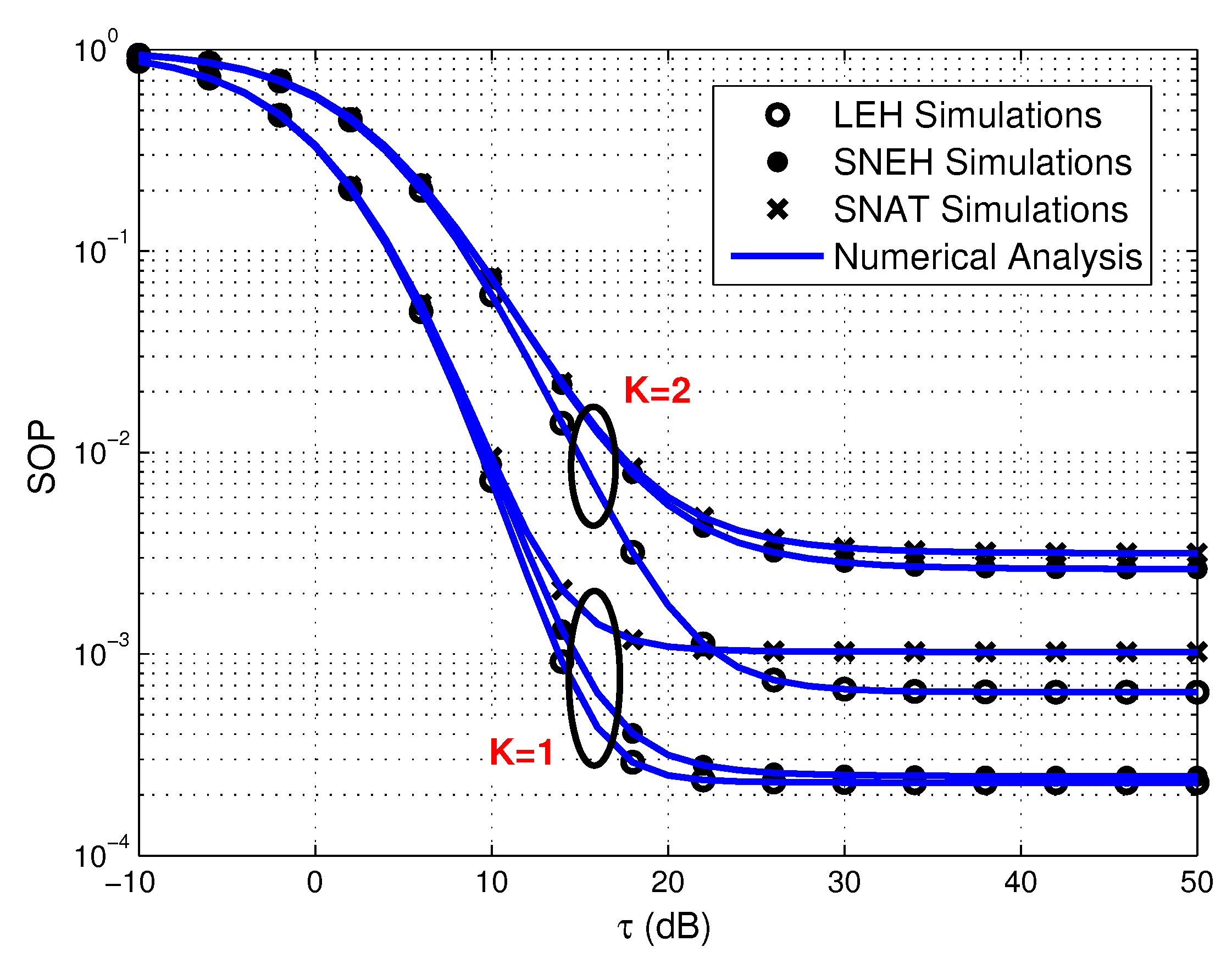
- We explore the PLS in the multiuser WPSNs with GMS scheme, where the Kth-best source sensor is chosen by the main channel for improving the security. Furthermore, we obtain the exact closed expressions for SOP of the system under linear energy harvesting (LEH), saturation nonlinear energy harvesting (SNEH) and saturation nonlinear energy harvesting with activation threshold (SNAT), respectively.
- With the help of the SOP expressions, we further discuss the impact of various key parameters on secrecy performance of the multiuser WPSNs, including the number of source sensor, the EH efficiency factor, the generalized selection coefficient, the saturation threshold, the activation threshold, the transmit power of PB and the time-switching coefficient. To get a deeper insight, we further investigate the maximization problem of SEE and compare the SEE under three different EH modes.
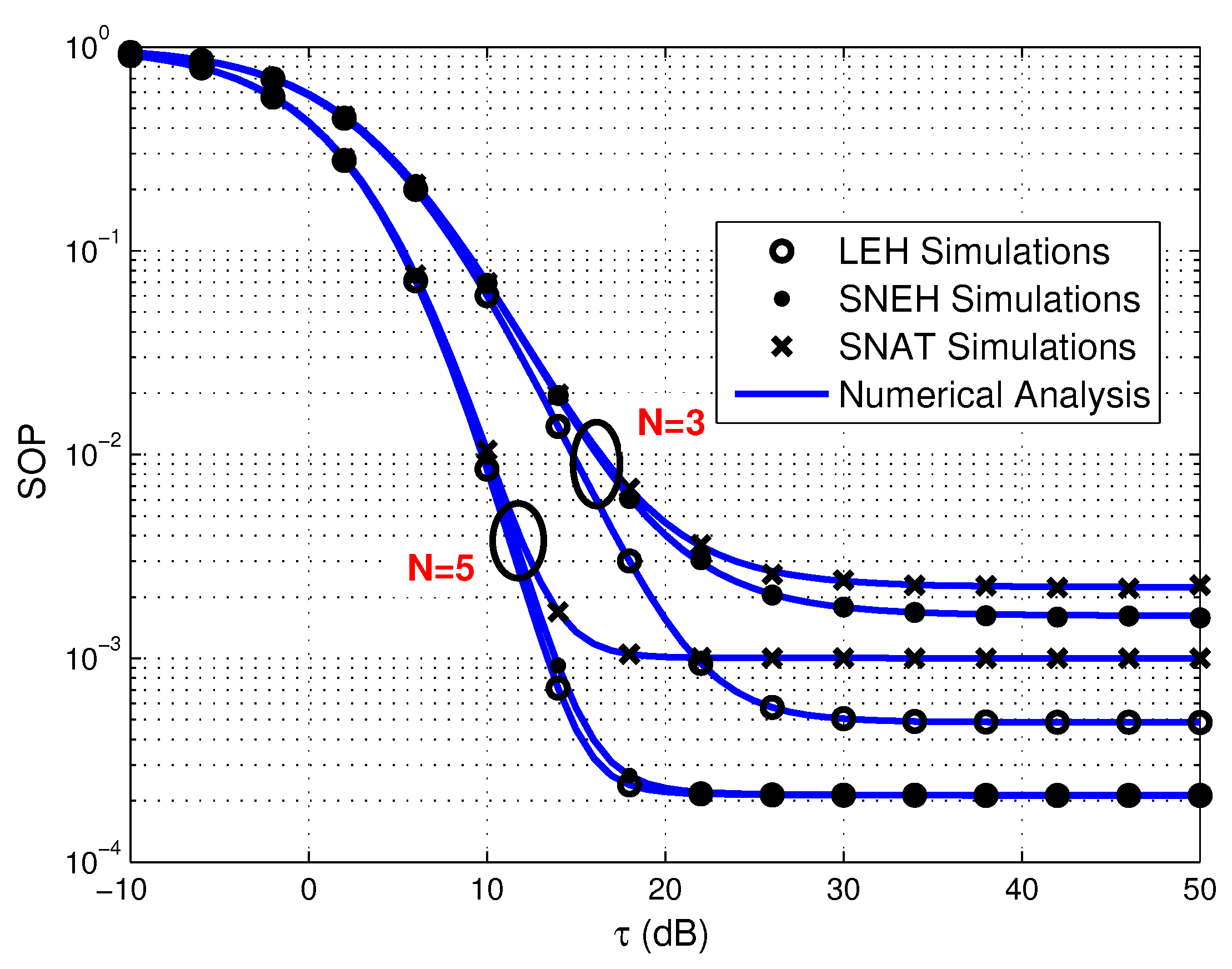
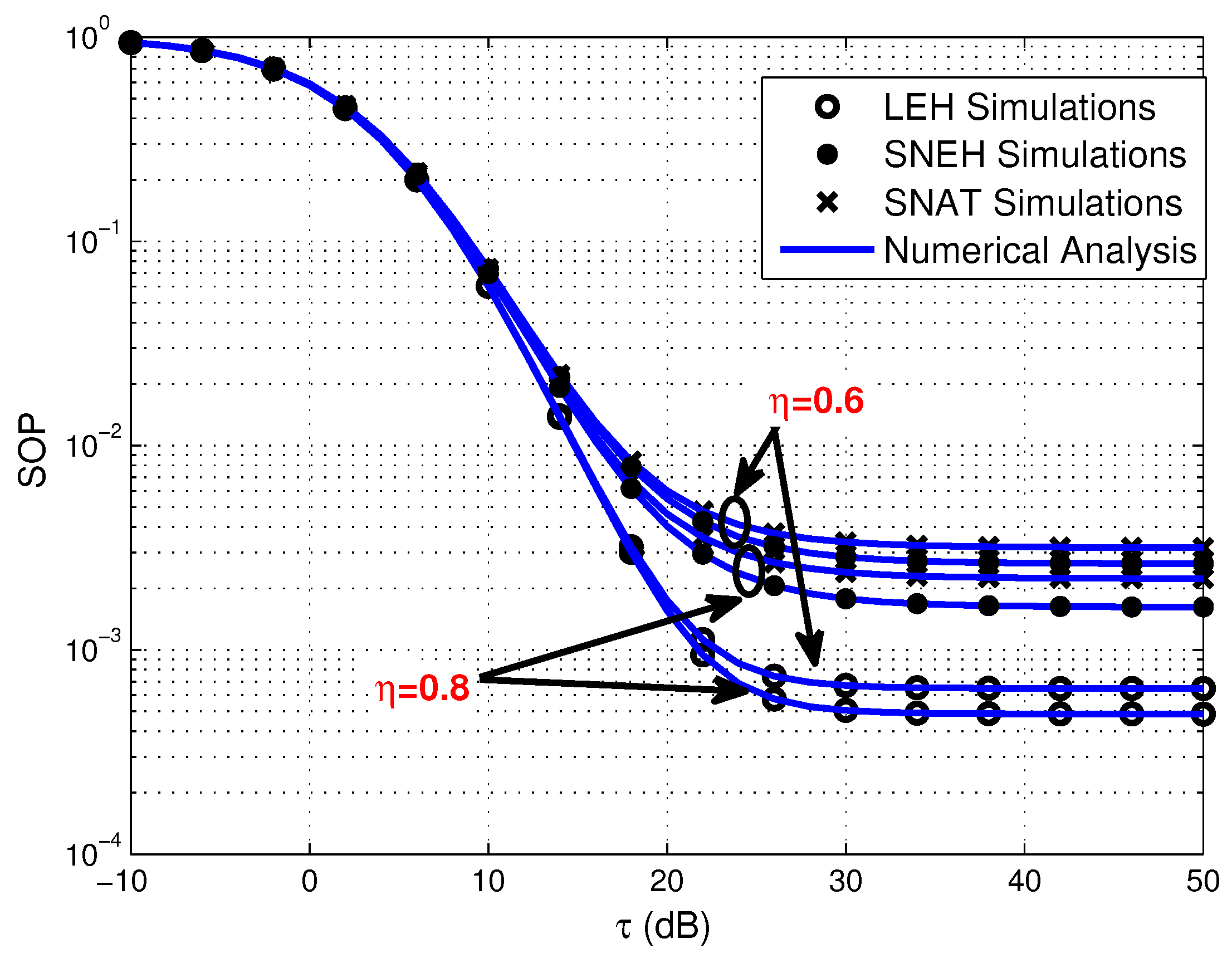
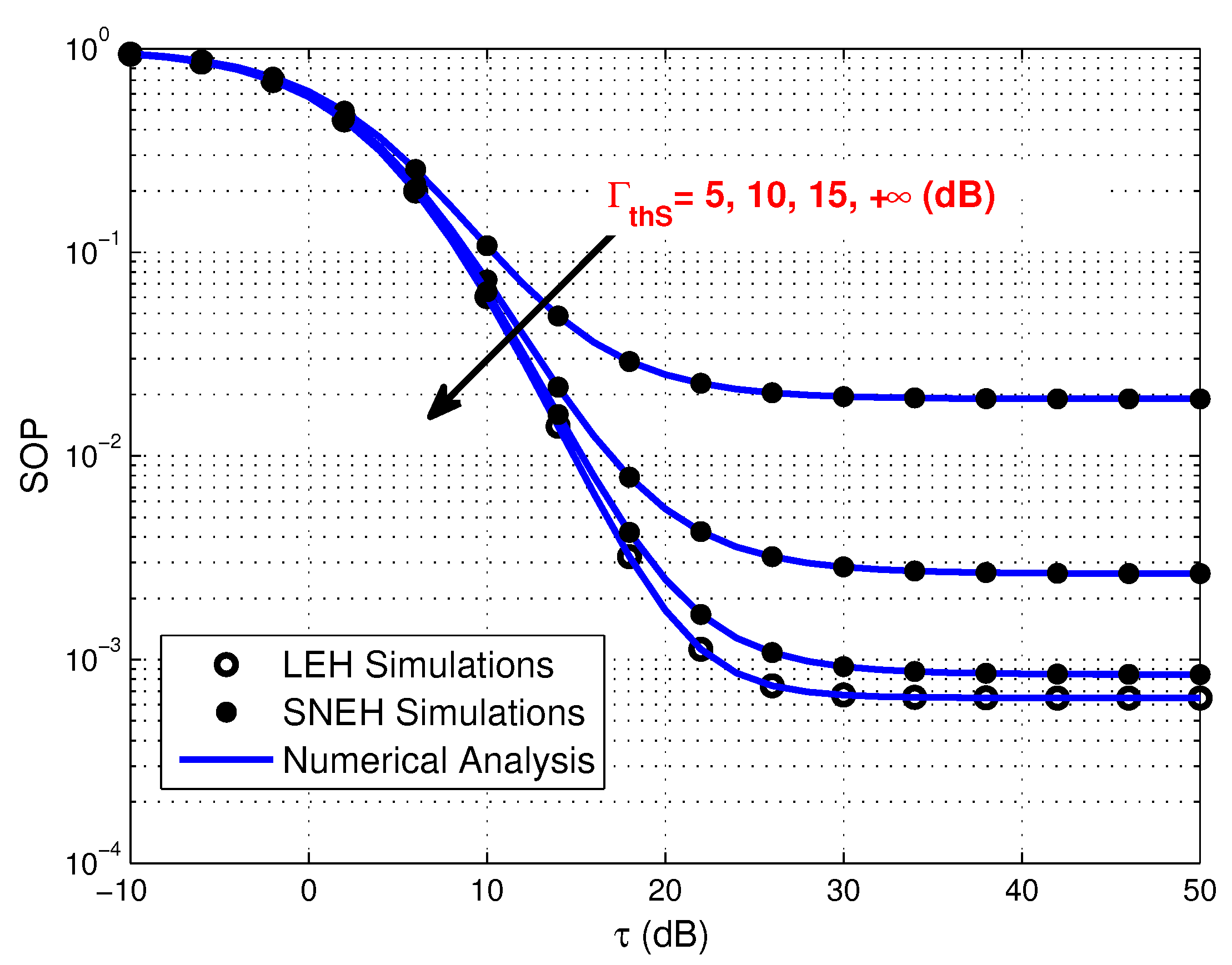
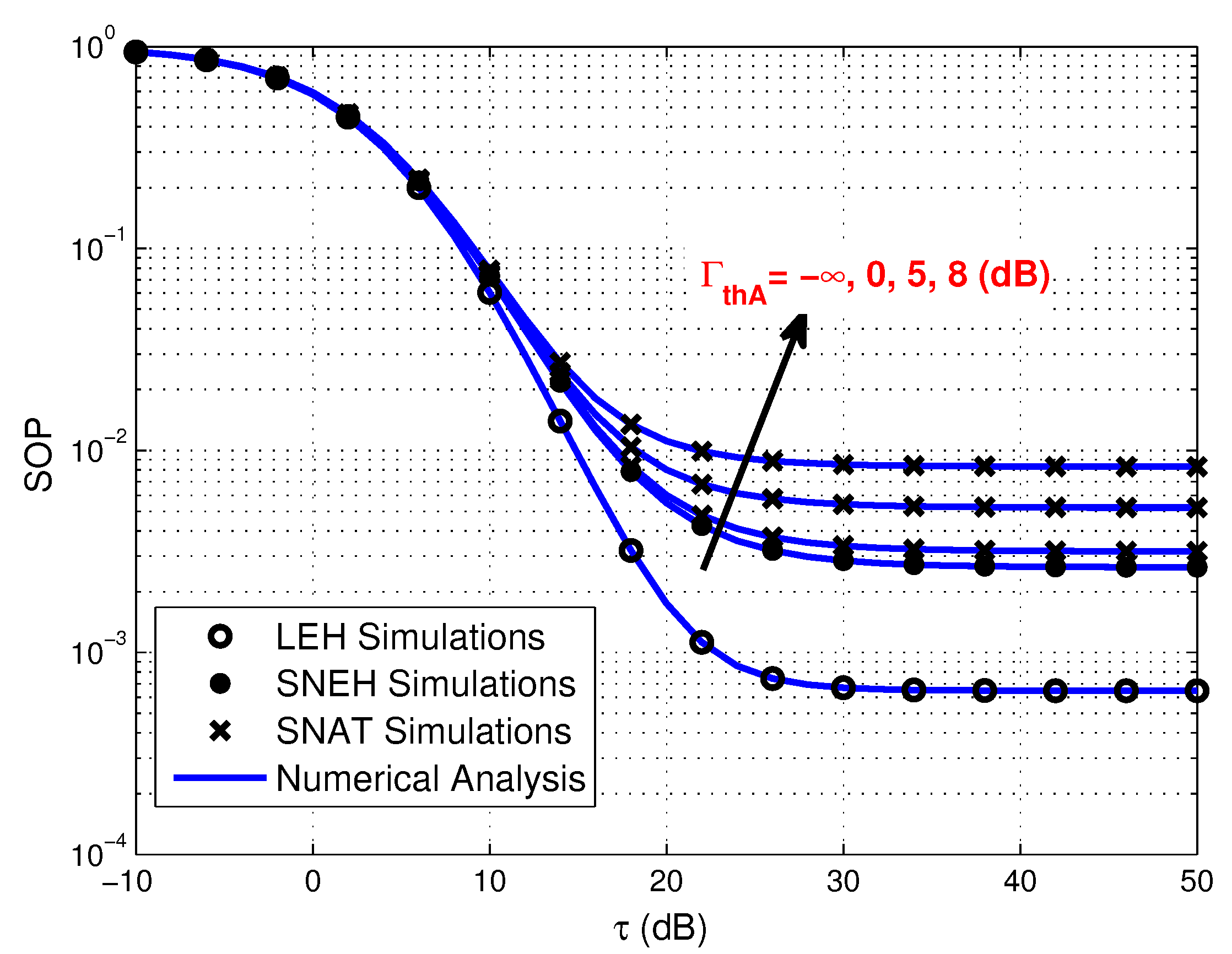
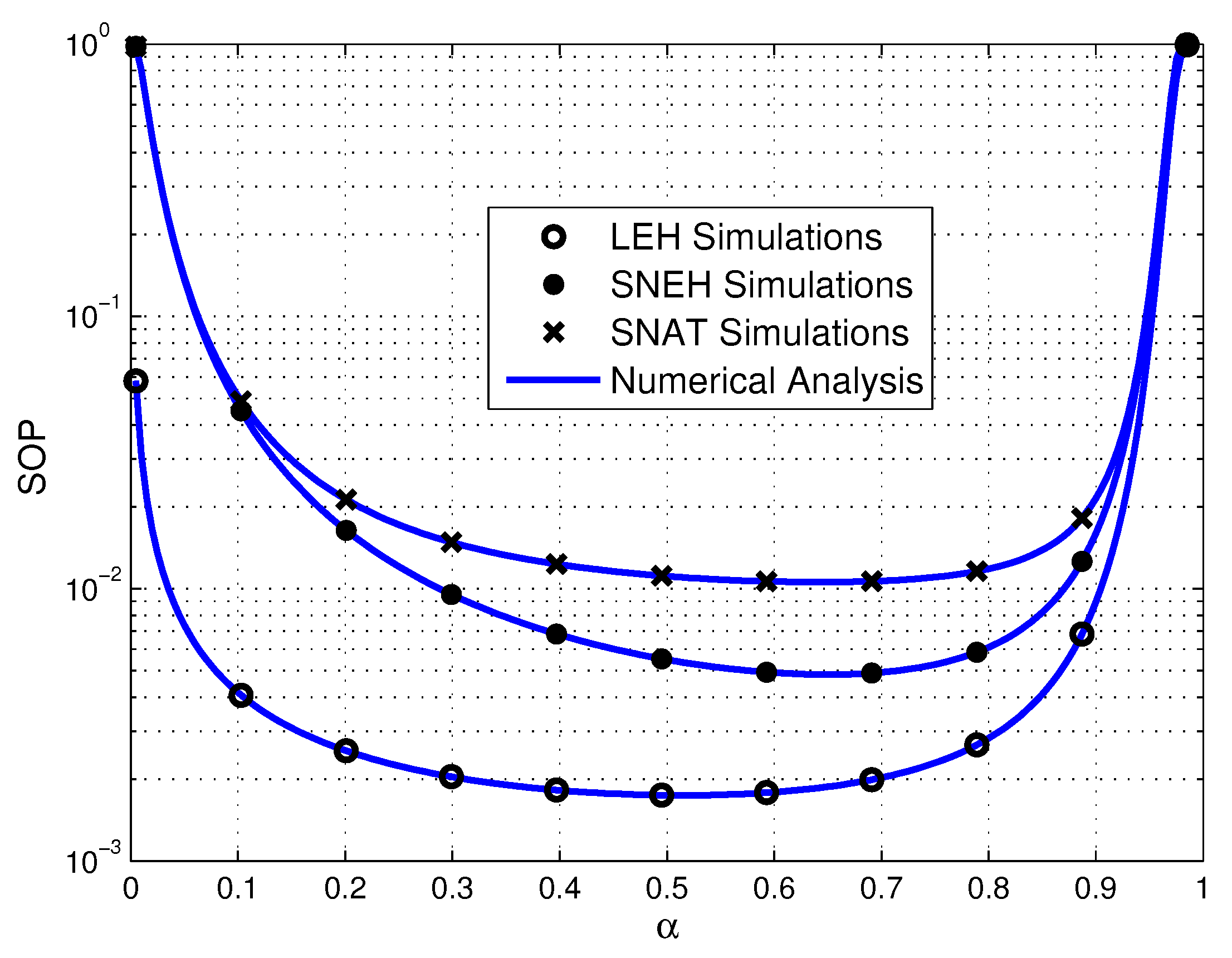
- Simulation results demonstrate that increasing the number of source sensors, enhancing the EH efficiency and strengthening the transmit power of PB all favorable to improve secrecy performance of the multiuser WPSNs. Meanwhile, the smaller generalized selection coefficient is beneficial for SOP in three EH modes. Furthermore, the SOP of SNEH is better when the saturation threshold is higher and LEH is an ideal situation for SNEH when the saturation threshold is large enough. The SOP of SNAT is better when the activation threshold is lower and SNEH is a special situation for SNAT when the activation threshold is low enough. In addition, for providing secure and efficient communication, the time-switching factor should be optimized seriously. Finally, the activation threshold has an important impact on the SEE of the considered system, which is worth considering carefully.
2. System Model and Signal Analysis
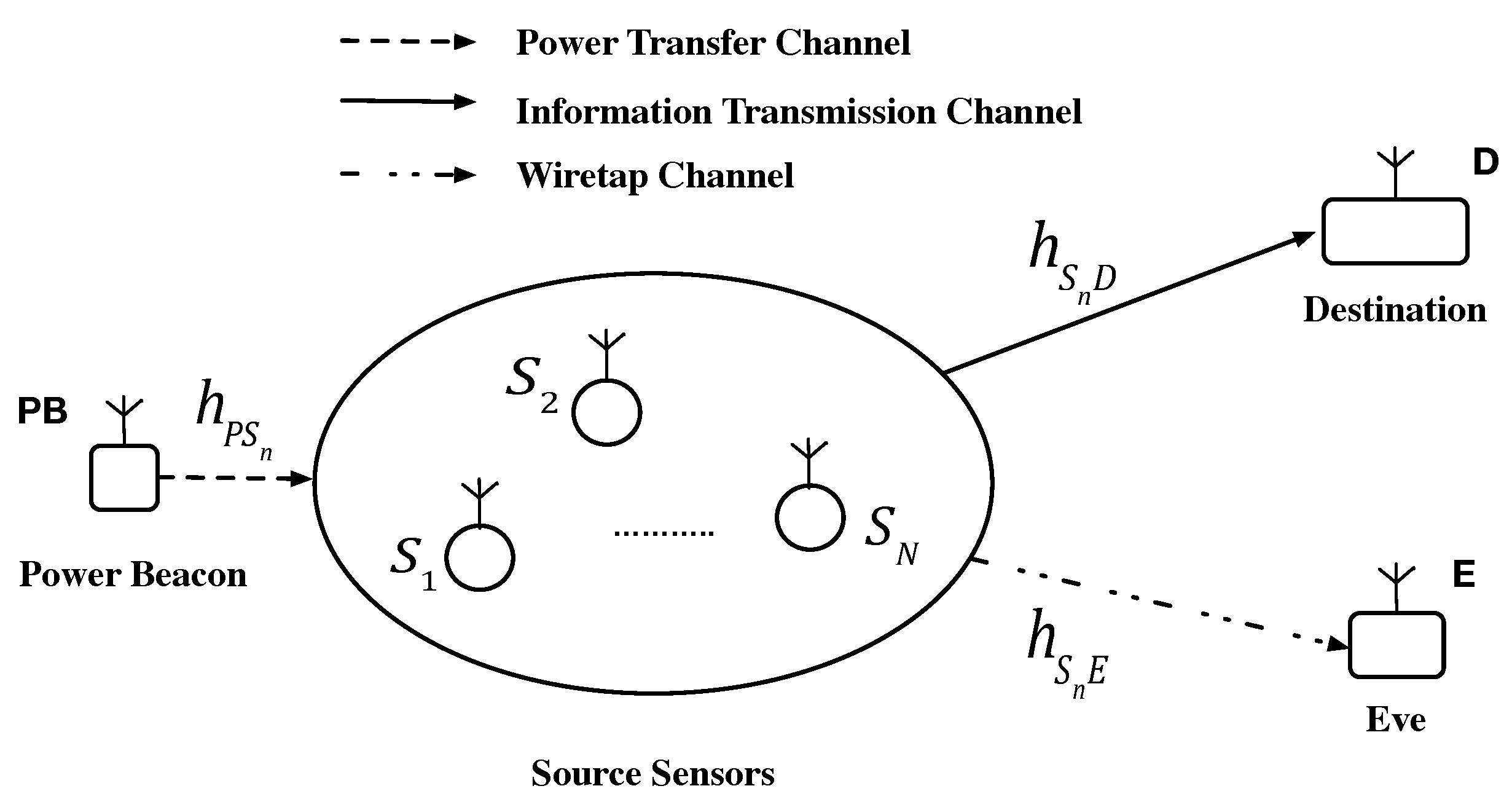
2.1. System Model
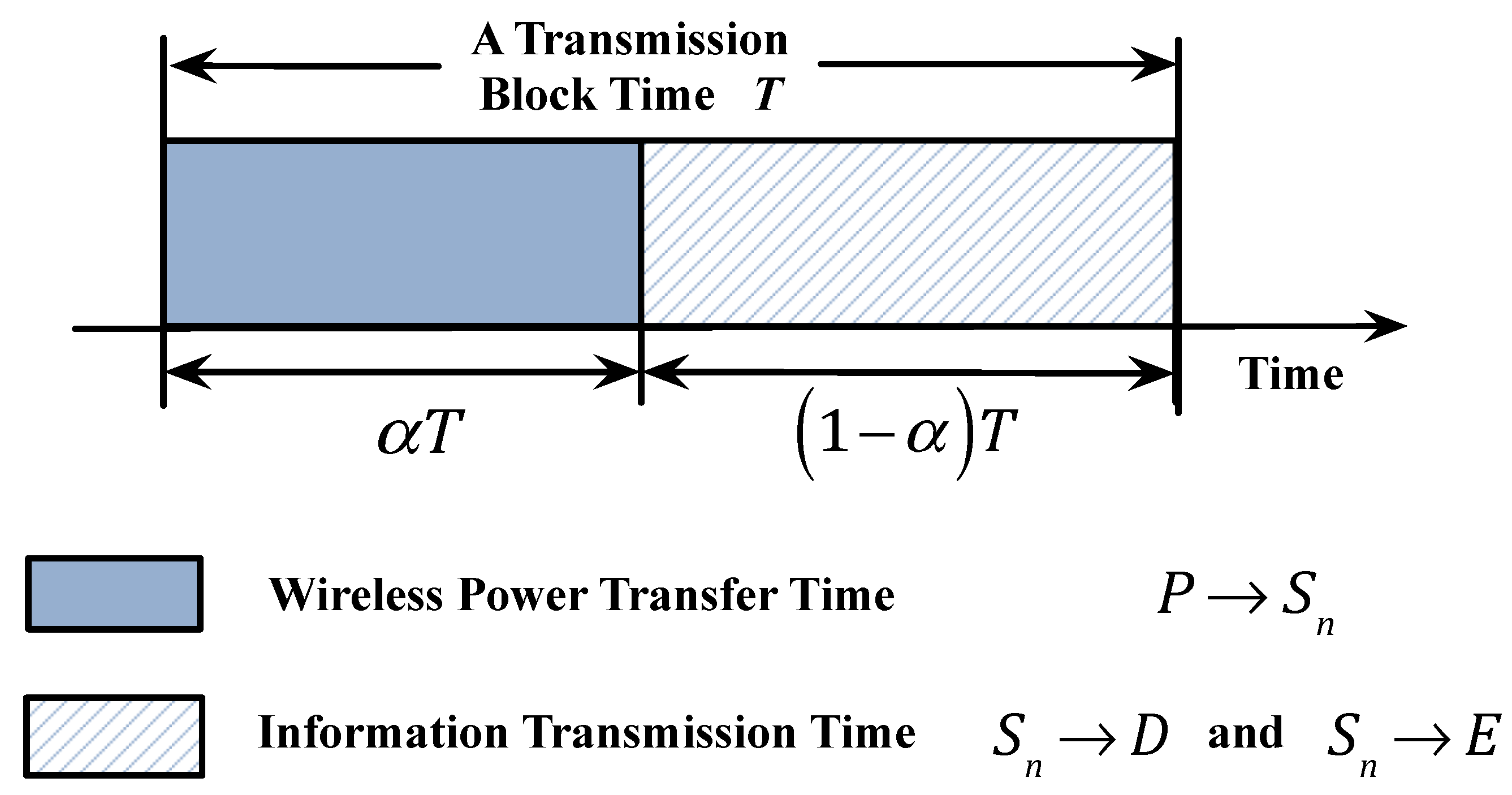
2.2. Wireless Power Transfer and Signal Analysis
2.3. Generalized Multiuser Scheduling
2.4. Energy Harvesting Mode
2.4.1. Linear Energy Harvesting Mode
2.4.2. Saturation Nonlinear Energy Harvesting Mode
2.4.3. Saturation Nonlinear Energy Harvesting with Activation Threshold
3. Secrecy Performance Analysis
3.1. Preliminaries
3.2. Secrecy Outage Probability Analysis
3.2.1. Derivation for LEH Mode
3.2.2. Derivation for SNEH Mode
3.2.3. Derivation for SNAT Mode
3.3. Secure Energy Efficiency Maximization
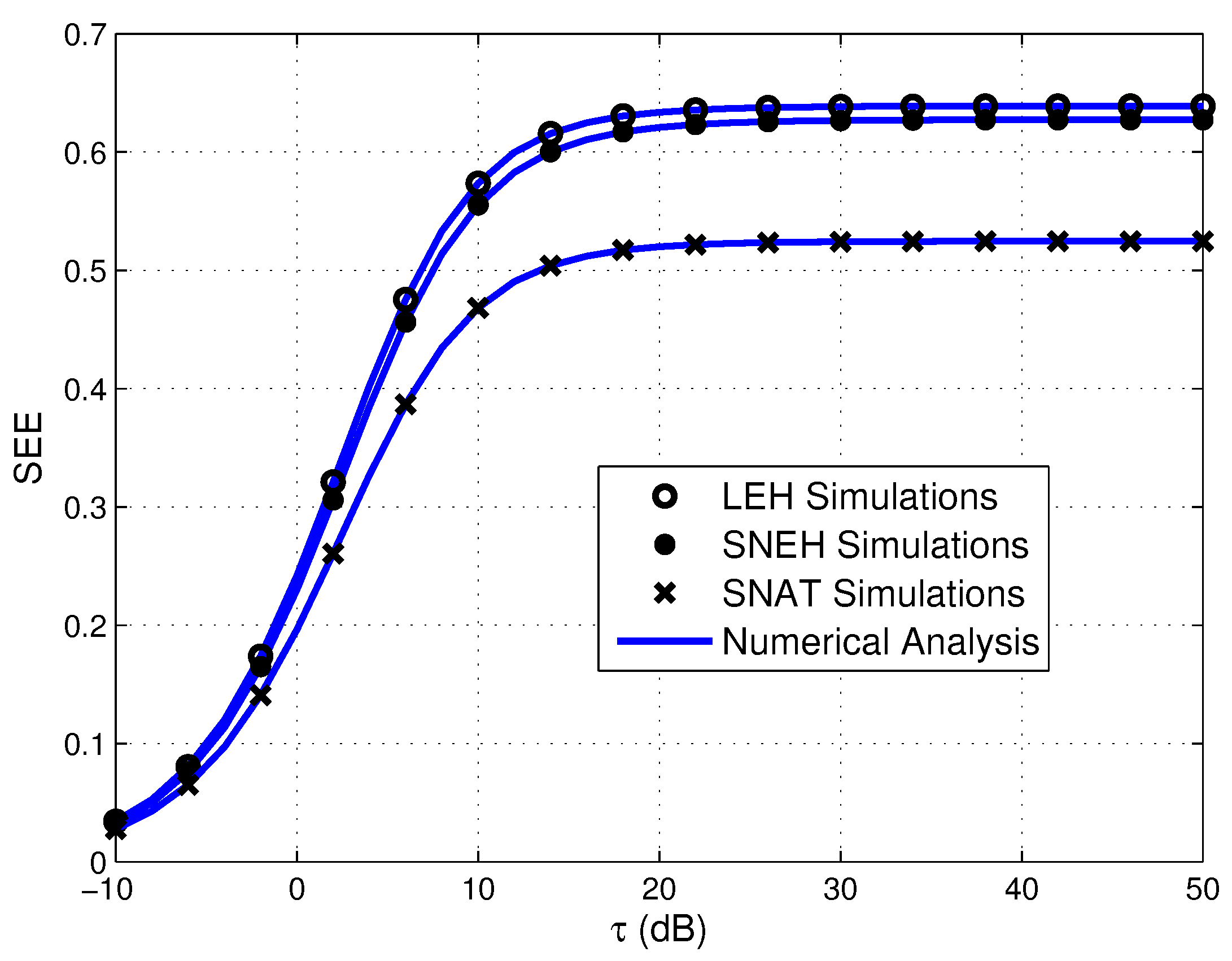
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Akpakwu, G.A.; Silva, B.J.; Hancke, G.P.; Abu-Mahfouz, A.M. A survey on 5G networks for the Internet of Things: Communication technologies and challenges. IEEE Access 2018, 6, 3619–3647. [Google Scholar] [CrossRef]
- Agiwal, M.; Roy, A.; Saxena, N. Next generation 5G wireless networks: A comprehensive survey. IEEE Commun. Surv. Tutor. 2016, 18, 1617–1655. [Google Scholar] [CrossRef]
- Atzori, L.; Iera, A.; Morabito, G. The internet of things: A survey. Comput. Netw. 2010, 54, 2787–2805. [Google Scholar] [CrossRef]
- Li, Q.; Feng, G.; Leung, V. Optimal Transmission Policies for Relay Communication Networks with Ambient Energy Harvesting Relays. IEEE J. Sel. Areas Commun. 2016, 34, 3754–3768. [Google Scholar]
- Sudevalayam, S.; Kulkarni, P. Energy Harvesting Sensor Nodes: Survey and Implications. IEEE Commun. Surv. Tutor. 2011, 13, 443–461. [Google Scholar] [CrossRef] [Green Version]
- Rajesh, R.; Sharma, V.; Viswanath, P. Capacity of guassian channels with energy harvesting and processing cost. IEEE Trans. Inf. Theory 2014, 60, 2563–2575. [Google Scholar] [CrossRef]
- Alevizos, P.N.; Bletsas, A. Sensitive and nonlinear far-field RF energy harvesting in wireless communications. IEEE Trans. Wirel. Commun. 2018, 17, 3670–3685. [Google Scholar] [CrossRef] [Green Version]
- Bi, S.; Ho, C.K.; Zhang, R. Wireless powered communication: Opportunities and challenges. IEEE Commun. Mag. 2015, 53, 117–125. [Google Scholar] [CrossRef] [Green Version]
- Bi, S.; Zeng, Y.G.; Zhang, R. Wireless powered communication networks: An overview. IEEE Trans. Wirel. Commun. 2016, 23, 10–18. [Google Scholar] [CrossRef] [Green Version]
- Tabassum, H.; Hossain, E.; Ogundipe, A.; Kim, D.I. Wireless powered cellular networks: Key challenges and solution techniques. IEEE Commun. Mag. 2015, 53, 63–71. [Google Scholar] [CrossRef]
- Niyato, D.; Kim, D.I.; Miso, M.; Han, Z. Wireless powered comunication networks: Research direction and technological approaches. IEEE Wirel. Commun. 2017, 24, 88–97. [Google Scholar] [CrossRef]
- Ramezani, P.; Jamalipour, A. Toward the evolution of wireless powered communication networks for the future internet of things. IEEE Netw. 2017, 31, 62–69. [Google Scholar] [CrossRef]
- Chen, H.; Zhai, C.; Li, Y.; Vucetic, B. Cooperative strategies for wireless-powered communications: An overview. IEEE Wirel. Commun. 2018, 25, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Ortega, Y.R.; Upadhyay, P.K.; da Costa, D.B.; Bithas, P.S.; Kanatas, A.G.; Dias, U.S.; de Sousa Junior, R.T. Joint effect of jamming and noise on the secrecy outage performance of wiretap channels with feedback delay and multiple antennas. IEEE Trans. Emerg. Telecommun. Technol. 2017. [Google Scholar] [CrossRef]
- Bloch, M.; Barros, J. Physical-Layer Security: From Information Theory to Security Engineering; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Rodriguez, L.J.; Tran, N.H.; Duong, T.Q.; Le-Ngoc, T.; Elkashlan, M.; Shetty, S. Physical layer security in wireless cooperative relay networks: State of the art and beyond. IEEE Commun. Mag. 2015, 53, 32–39. [Google Scholar] [CrossRef]
- Hamamreh, J.M.; Furqan, H.M.; Arslan, H. Classifications and applications of physical layer security techniques for confidentiality: A comprehensive survey. IEEE Commun. Surv. Tutor. 2019, 21, 1773–1828. [Google Scholar] [CrossRef]
- Lei, H.; Dai, Z.; Park, K.; Lei, W.; Pan, G.; Alouini, M. Secrecy outage analysis of mixed RF-FSO downlink SWIPT systems. IEEE Trans. Commun. 2018, 66, 6384–6395. [Google Scholar] [CrossRef] [Green Version]
- Lei, H.; Xu, M.; Ansari, I.S.; Pan, G.; Qaraqe, K.A.; Alouini, M. On secure underlay MIMO cognitive radio networks with energy harvesting and transmit antenna selection. IEEE Trans. Green Commun. Netw. 2017, 1, 192–203. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.; Lim, J.-T.; Choi, H.-H. Impact of Outdated CSI on the Secrecy Performance of Wireless-Powered Untrusted Relay Networks. IEEE Trans. Inf. Forensics Secur. 2019, 15, 1423–1433. [Google Scholar] [CrossRef]
- Sun, X.; Yang, W.; Cai, Y.; Xiang, Z.; Tang, X. Secure transmissions in millimeter wave SWIPT UAV-based relay networks. IEEE Wirel. Commun Lett. 2019, 8, 785–788. [Google Scholar] [CrossRef]
- Ng, D.; Lo, E.; Schober, R. Robust beamforming for secure communication in systems with wireless information and power transfer. IEEE Trans. Wirel. Commun. 2014, 13, 4599–4615. [Google Scholar] [CrossRef] [Green Version]
- Pan, G.; Tang, C.; Li, T.; Chen, Y. Secrecy performance analysis for SIMO simultaneous wireless information and power transfer systems. IEEE Trans. Commun. 2015, 63, 3423–3433. [Google Scholar] [CrossRef]
- Shi, Q.; Xu, W.; Wu, J.; Song, E.; Wang, Y. Secure beamforming for MIMO broadcast with wireless information and power transfer. IEEE Trans. Wirel. Commun. 2015, 14, 2841–2853. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Zhou, X.; Durrani, S.; Popovski, P. Secure communication with a wireless powered friendly jammer. IEEE Trans. Wirel. Commun. 2016, 15, 401–415. [Google Scholar] [CrossRef] [Green Version]
- Moon, J.; Lee, H.; Song, C.; Lee, I. Secrecy performance optimization for wireless powered communication networks with an energy harvesting jammer. IEEE Trans. Commun. 2017, 65, 764–774. [Google Scholar] [CrossRef]
- Shafie, A.E.; Niyato, D.; Al-Dhahir, N. Security of an ordered-based distributive jamming scheme. IEEE Wirel. Commun Lett. 2017, 21, 72–75. [Google Scholar] [CrossRef]
- Li, B.; Fei, Z.; Chen, H. Robust artificial noise-aided secure beamforming in wireless powered non-regenerative relay networks. IEEE Access 2016, 4, 7921–7929. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, X.; Feng, S. Joint power splitting and secure beamforming design in the multiple non-regenerative wireless-powered relay networks. IEEE Commun. Lett. 2015, 19, 1540–1543. [Google Scholar] [CrossRef] [Green Version]
- Xing, H.; Wong, K.K.; Nalllanathan, A.; Zhang, R. Wireless powered cooperative jamming for secrecy multi-AF relaying networks. IEEE Trans. Wirel. Commun. 2016, 15, 7971–7984. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, N.P.; Duong, T.Q.; Ngo, H.Q.; Hadzi-Velkov, Z.; Shu, L. Secure 5G wireless communications: A joint relay selection and wireless power transfer approach. IEEE Access 2016, 4, 3349–3359. [Google Scholar] [CrossRef]
- Vo, V.N.; Nguyen, T.G.; So-In, C.; Baig, Z.A.; Sanguanpong, S. Secrecy outage performance analysis for energy harvesting sensor networks with a jammer using relay selection strategy. IEEE Access 2018, 6, 23406–23419. [Google Scholar]
- Wang, Y.; Yang, W.; Shang, X.; Hu, J.; Huang, Y.; Cai, Y. Energy-efficient secure transmission for wireless powered internet of things with multiple power beacons. IEEE Access 2018, 6, 75086–75098. [Google Scholar] [CrossRef]
- Yang, M.; Guo, D.; Huang, Y.; Duong, T.Q.; Zhang, B. Secure multiuser scheduling in downlink dual-hop regenerative relay networks over Nakagami-m fading channels. IEEE Trans. Wirel. Commun. 2016, 15, 8009–8024. [Google Scholar] [CrossRef] [Green Version]
- Yang, M.; Guo, D.; Huang, Y.; Duong, T.Q.; Zhang, B. Physical layer security with threshold-based multiuser scheduling in multi-antenna wireless networks. IEEE Trans. Commun. 2016, 64, 5189–5202. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Pan, G.; Xie, Y. Secrecy analysis of wireless-powered multi-antenna relaying system with nonlinear energy harvests and imperfect CSI. IEEE Trans. Green Commun. Netw. 2018, 2, 460–470. [Google Scholar] [CrossRef]
- Wang, D.; Negra, R. Design of a dual-band rectifier for wireless power transmission. In Proceedings of the 2013 IEEE Wireless Power Transfer (WPT), Perugia, Italy, 15–16 May 2013. [Google Scholar]
- Le, T.; Mayaram, K.; Fiez, T. Efficient far-field radio frequency energy harvesting for passively powered sensor networks. IEEE J. Solid-State Circuits 2008, 43, 1287–1302. [Google Scholar] [CrossRef]
- Boshkovska, E.; Ng, D.W.K.; Dai, L.; Schober, R. Power-efficient and secure WPCNs with hardware impairments and non-linear EH circuit. IEEE Trans. Commun. 2018, 66, 2642–2657. [Google Scholar] [CrossRef]
- Clerckx, B.; Zhang, R.; Schober, R.; Ng, D.W.K.; Kim, D.I.; Poor, H.V. Fundamentals of wireless information and power transfer: From RF energy harvester models to signal and system designs. IEEE J. Sel. Areas Commun. 2019, 37, 4–33. [Google Scholar] [CrossRef] [Green Version]
- Niu, H.; Guo, D.; Huang, Y.; Zhang, B. Robust energy efficiency optimization for secure MIMO SWIPT systems with non-linear EH models. IEEE Commun. Lett. 2017, 21, 2610–2613. [Google Scholar] [CrossRef]
- Fan, L.; Lei, X.; Yang, N.; Duong, T.Q.; Karagiannidis, G.K. Secrecy cooperative nerworks with outdated relay selection over correlated fading channels. IEEE Trans. Veh. Technol. 2017, 68, 7599–7603. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Hadley, L.; Ding, Z.; Dai, X. Improving secrecy performance of a wirelessly powered network. IEEE Trans. Commun. 2017, 65, 4996–5008. [Google Scholar] [CrossRef] [Green Version]
- Mekikis, P.-V.; Antonopoulos, A.; Kartsakli, E.; Lalos, A.S.; Alonso, L.; Verikoukis, C. Information Exchange in Randomly Deployed Dense WSNs with Wireless Energy Harvesting Capabilities. IEEE Trans. Wirel. Commun. 2016, 15, 3008–3018. [Google Scholar] [CrossRef] [Green Version]
- Paing, T.; Shin, J.; Zane, R.; Popovic, Z. Resistor emulation approach to low-power RF energy harvesting. IEEE Trans. Power Electron. 2008, 23, 1494–1501. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, R.; Ho, C.K. Wireless information and power transfer: Architecture design and rate-energy tradeoff. IEEE Trans. Commun. 2013, 63, 4754–4767. [Google Scholar] [CrossRef] [Green Version]
- Shinohara, N. Wireless Power Transfer via Radiowaves; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Pham, B.L.; Pham, A.-V. Triple bands antenna and high efficiency rectifier design for RF energy harvesting at 900, 1900 and 2400 MHz. In Proceedings of the 2013 IEEE MTT-S International Microwave Symposium Digest (MTT), Seattle, WA, USA, 2–7 June 2013; pp. 1–3. [Google Scholar]
- Kang, X.; Liang, Y.; Yang, J. A new spectrum sharing paradigm for wireless-powered IoT devices. IEEE Trans. Wirel. Commun. 2018, 17, 6335–6347. [Google Scholar] [CrossRef]
- Huang, Y.; Al-Qahtani, F.S.; Duong, T.Q.; Wang, J. Secure transmission in MIMO wiretap channels using general-order transmit antenna selection with outdated CSI. IEEE Trans. Commun. 2015, 63, 2959–2971. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Yin, H.; Huang, Y.; Wang, Y. Impact of correlated fading channels on cognitive relay networks with generalized relay selection. IEEE Access 2017, 6, 6040–6047. [Google Scholar] [CrossRef]
- Dong, Y.; Hossain, M.J.; Cheng, J. Performance of wireless powered amplify and forward relaying over Nakagamim fading channels with nonlinear energy harvester. IEEE Wirel. Commun. Lett. 2016, 20, 672–675. [Google Scholar] [CrossRef]
- Boshkovska, E.; Ng, D.W.K.; Zlatanov, N.; Schober, R. Practical non-linear energy harvesting model and resource allocation for SWIPT systems. IEEE Wirel. Commun. Lett. 2015, 19, 20822–22085. [Google Scholar] [CrossRef] [Green Version]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 7th ed.; Academic: New York, NY, USA, 2007. [Google Scholar]
- Do, N.T.; Costa, D.B.D.; Duong, T.Q.; Ng, V.; Bao, Q.; An, B. Exploiting direct links in multiuser multirelay SWIPT cooperative networks with opportunistic scheduling. IEEE Trans. Wirel. Commun. 2017, 16, 5410–5427. [Google Scholar] [CrossRef] [Green Version]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, X.; Yin, H.; Wang, Y.; Li, M.; Wang, Y. Secrecy Performance Analysis of Wireless Powered Sensor Networks Under Saturation Nonlinear Energy Harvesting and Activation Threshold. Sensors 2020, 20, 1632. https://doi.org/10.3390/s20061632
Shang X, Yin H, Wang Y, Li M, Wang Y. Secrecy Performance Analysis of Wireless Powered Sensor Networks Under Saturation Nonlinear Energy Harvesting and Activation Threshold. Sensors. 2020; 20(6):1632. https://doi.org/10.3390/s20061632
Chicago/Turabian StyleShang, Xiaohui, Hao Yin, Yida Wang, Mu Li, and Yong Wang. 2020. "Secrecy Performance Analysis of Wireless Powered Sensor Networks Under Saturation Nonlinear Energy Harvesting and Activation Threshold" Sensors 20, no. 6: 1632. https://doi.org/10.3390/s20061632




