Time Series Forecasting of Univariate Agrometeorological Data: A Comparative Performance Evaluation via One-Step and Multi-Step Ahead Forecasting Strategies
Abstract
:1. Introduction
- Quantitative assessment of n-step ahead forecasting capabilities of statistical and machine-learning-based Time Series Forecasting Algorithms (TSFAs) using univariate agrometeorological datasets.
- Application of recursive approximation, walk forward validation and fixed forecast horizon in evaluating model performance.
- Validate the forecast proficiency of TSFAs over fixed temporal partitioning of the dataset while evaluating the average performance of models over entire dataset.
2. Materials and Methods
2.1. Test Site and Dataset Description
2.2. Background
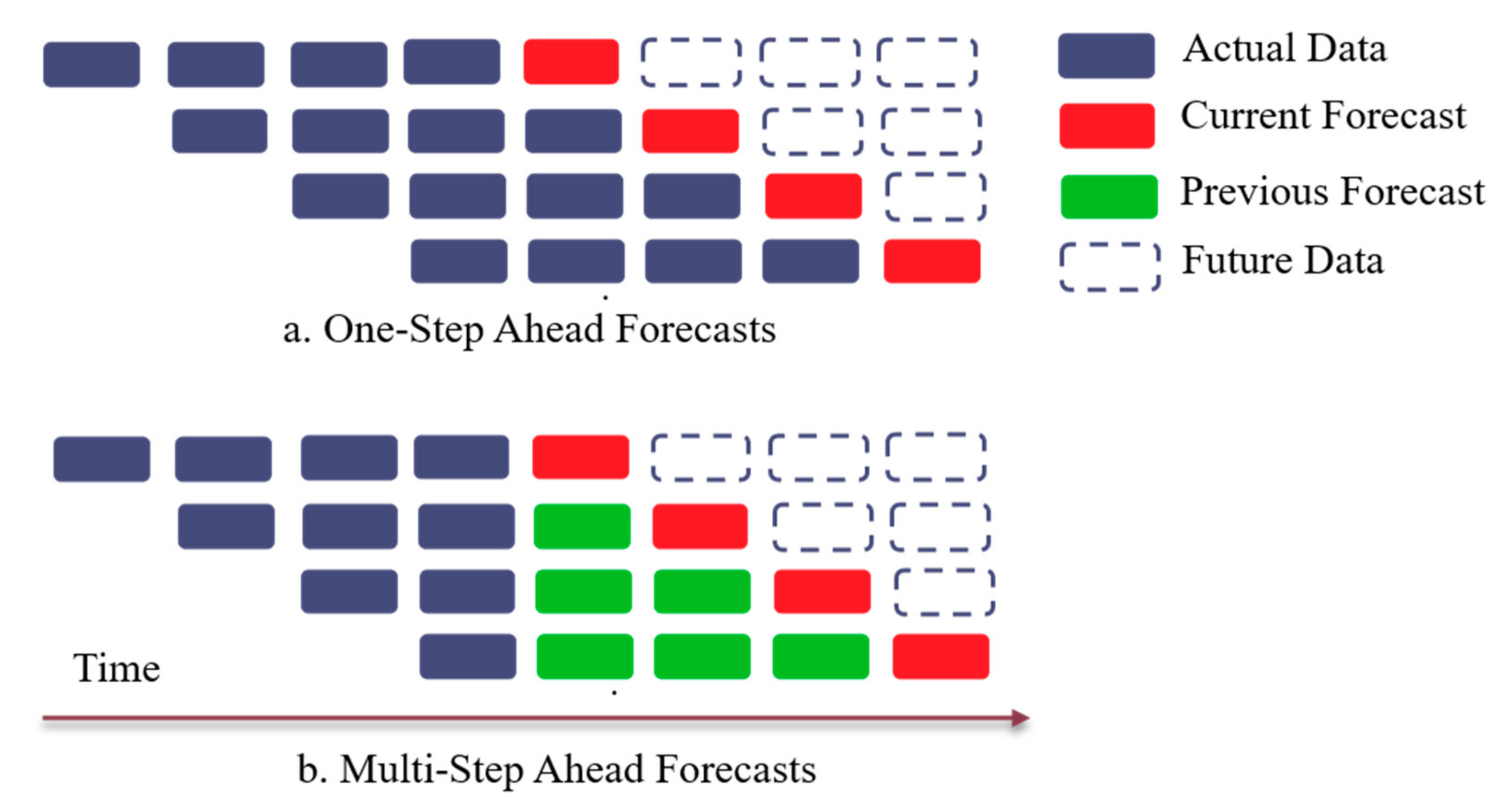
2.2.1. One-Step vs. Multi-Step Ahead Forecasting
2.2.2. Walk Forward Validation and Data Bifurcation
2.3. Time Series Forecasting Algorithms (TSFAs) Modelling
2.3.1. Seasonal Auto-Regressive Integrated Moving Average (SARIMA)
2.3.2. Support Vector Regression (SVR)
2.3.3. Multilayer Perceptron (MLP)
2.3.4. Simple Recurrent Neural Networks (RNN)
2.3.5. Long-Short Term Memory (LSTM)
2.4. Accuracy Measures for Model Evaluation
2.5. Intuition for Walk-Forward Validation and Representative Train-Test Split
3. Results and Discussions
3.1. Univariate Timeseries and Seasonal and Trend Decomposition Using Loess (STL) Decomposition
3.2. Forecast Generation Using Time Series Forecasting Algorithms (TSFAs)
3.2.1. Seasonal Autoregressive Integrated Moving Average (SARIMA)
3.2.2. Support Vector Regression (SVR)
3.2.3. Multilayer Perceptron (MLP)
3.2.4. Recurrent Neural Networks (RNN)
3.2.5. Long-Short Term Memory (LSTM)
3.3. Performance Evaluation of TSFAs over One-Step and Multi-Step Ahead Forecast Horizon
3.4. Assessing Impact of Data Bifurcation on Forecasting Capability of TSFAs
3.5. Visualization for Absolute Performance of TSFAs Using Baseline Naïve and Seasonal Naïve Methods
4. Conclusions and Future Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Allen, P. Economic forecasting in agriculture. Int. J. Forecast. 1994, 10, 81–135. [Google Scholar] [CrossRef]
- Kim, K.-J. Financial time series forecasting using support vector machines. Neurocomputing 2003, 55, 307–319. [Google Scholar] [CrossRef]
- De Gooijer, J.G.; Hyndman, R.J. 25 years of time series forecasting. Int. J. Forecast. 2006, 22, 443–473. [Google Scholar] [CrossRef] [Green Version]
- Maçaira, P.M.; Thomé, A.M.T.; Oliveira, F.L.C.; Ferrer, A.L.C. Time series analysis with explanatory variables: A systematic literature review. Environ. Model. Softw. 2018, 107, 199–209. [Google Scholar] [CrossRef]
- Kang, Y.; Hyndman, R.J.; Li, F. Efficient Generation of Time Series with Diverse and Controllable Characteristics (No. 15/18); Department of Econometrics and Business Statistics, Monash University: Clayton, Australia, 2018. [Google Scholar]
- Mehdizadeh, S. Estimation of daily reference evapotranspiration (ETo) using artificial intelligence methods: Offering a new approach for lagged ETo data-based modeling. J. Hydrol. 2018, 559, 794–812. [Google Scholar] [CrossRef]
- Sanikhani, H.; Deo, R.C.; Samui, P.; Kisi, O.; Mert, C.; Mirabbasi, R.; Gavili, S.; Yaseen, Z.M. Survey of different data-intelligent modeling strategies for forecasting air temperature using geographic information as model predictors. Comput. Electron. Agric. 2018, 152, 242–260. [Google Scholar] [CrossRef]
- Antonopoulos, V.Z.; Papamichail, D.M.; Aschonitis, V.G.; Antonopoulos, A.V. Solar radiation estimation methods using ANN and empirical models. Comput. Electron. Agric. 2019, 160, 160–167. [Google Scholar] [CrossRef]
- Zeynoddin, M.; Ebtehaj, I.; Bonakdari, H. Development of a linear based stochastic model for daily soil temperature prediction: One step forward to sustainable agriculture. Comput. Electron. Agric. 2020, 176, 105636. [Google Scholar] [CrossRef]
- Le Borgne, Y.-A.; Santini, S.; Bontempi, G. Adaptive model selection for time series prediction in wireless sensor networks. Signal. Process. 2007, 87, 3010–3020. [Google Scholar] [CrossRef]
- Ojha, T.; Misra, S.; Raghuwanshi, N.S. Wireless sensor networks for agriculture: The state-of-the-art in practice and future challenges. Comput. Electron. Agric. 2015, 118, 66–84. [Google Scholar] [CrossRef]
- Bhandari, S.; Bergmann, N.; Jurdak, R.; Kusy, B. Time Series Data Analysis of Wireless Sensor Network Measurements of Temperature. Sensors 2017, 17, 1221. [Google Scholar] [CrossRef] [Green Version]
- Gilbert, E.P.K.; Kaliaperumal, B.; Rajsingh, E.B.; Lydia, M. Trust based data prediction, aggregation and reconstruction using compressed sensing for clustered wireless sensor networks. Comput. Electr. Eng. 2018, 72, 894–909. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. Statistical and Machine Learning forecasting methods: Concerns and ways forward. PLoS ONE 2018, 13, e0194889. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mehdizadeh, S. Assessing the potential of data-driven models for estimation of long-term monthly temperatures. Comput. Electron. Agric. 2018, 144, 114–125. [Google Scholar] [CrossRef]
- Shiri, J.; Marti, P.; Karimi, S.; Landeras, G. Data splitting strategies for improving data driven models for reference evapotranspiration estimation among similar stations. Comput. Electron. Agric. 2019, 162, 70–81. [Google Scholar] [CrossRef]
- Hinich, M.J. Testing for Gaussianity and Linearity of a Stationary Time Series. J. Time Ser. Anal. 1982, 3, 169–176. [Google Scholar] [CrossRef]
- Hansen, P.R.; Timmermann, A. Choice of Sample Split in Out-of-Sample Forecast Evaluation. 2012. Available online: http://hdl.handle.net/1814/21454 (accessed on 8 January 2021).
- Baillie, R.T.; Bollerslev, T.; Mikkelsen, H.O. Fractionally integrated generalized autoregressive conditional heteroskedasticity. J. Econ. 1996, 74, 3–30. [Google Scholar] [CrossRef]
- Sorjamaa, A.; Hao, J.; Reyhani, N.; Ji, Y.; Lendasse, A. Methodology for long-term prediction of time series. Neurocomputing 2007, 70, 2861–2869. [Google Scholar] [CrossRef] [Green Version]
- Weigend, A.S. Time Series Prediction: Forecasting the Future and Understanding the Past; Routledge: Abingdon, UK, 2018. [Google Scholar]
- Kohzadi, N.; Boyd, M.S.; Kermanshahi, B.; Kaastra, I. A comparison of artificial neural network and time series models for forecasting commodity prices. Neurocomputing 1996, 10, 169–181. [Google Scholar] [CrossRef]
- Fushiki, T. Estimation of prediction error by using K-fold cross-validation. Stat. Comput. 2011, 21, 137–146. [Google Scholar] [CrossRef]
- Lim, B.; Zohren, S. Time-series forecasting with deep learning: A survey. arXiv 2004, arXiv:2004.13408. [Google Scholar]
- Dabrowski, J.J.; Zhang, Y.; Rahman, A. ForecastNet: A Time-Variant Deep Feed-Forward Neural Network Architecture for Multi-step-Ahead Time-Series Forecasting. In International Conference on Neural Information Processing; Springer: Cham, Switzerland, 2020; pp. 579–591. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. arXiv 2020, arXiv:1706.03762. [Google Scholar]
- Hewage, P.; Trovati, M.; Pereira, E.; Behera, A. Deep learning-based effective fine-grained weather forecasting model. Pattern Anal. Appl. 2021, 24, 343–366. [Google Scholar] [CrossRef]
- Powers, J.G.; Klemp, J.B.; Skamarock, W.C.; Davis, C.A.; Dudhia, J.; Gill, D.O.; Coen, J.L.; Gochis, D.J.; Ahmadov, R.; Peckham, S.E.; et al. The Weather Research and Forecasting Model: Overview, System Efforts, and Future Directions. Bull. Am. Meteorol. Soc. 2017, 98, 1717–1737. [Google Scholar] [CrossRef]
- Ferreira, L.B.; da Cunha, F.F. Multi-step ahead forecasting of daily reference evapotranspiration using deep learning. Comput. Electron. Agric. 2020, 178, 105728. [Google Scholar] [CrossRef]
- Hu, J.; Zheng, W. Multistage attention network for multivariate time series prediction. Neurocomputing 2020, 383, 122–137. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Chang, X.; Zhang, C. Connecting the dots: Multivariate time series forecasting with graph neural networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery Data Mining, Virtual Event, CA, USA, 23–27 August 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 753–763. [Google Scholar]
- Song, C.; Lin, Y.; Guo, S.; Wan, H. Spatial-Temporal Synchronous Graph Convolutional Networks: A New Framework for Spatial-Temporal Network Data Forecasting. Proc. Conf. AAAI Artif. Intell. 2020, 34, 914–921. [Google Scholar] [CrossRef]
- Moody, J.E.; Saffell, M. Reinforcement Learning for Trading. Available online: https://papers.nips.cc/paper/1998/file/4e6cd95227cb0c280e99a195be5f6615-Paper.pdf (accessed on 18 March 2021).
- Carta, S.; Ferreira, A.; Podda, A.S.; Recupero, D.R.; Sanna, A. Multi-DQN: An ensemble of Deep Q-learning agents for stock market forecasting. Expert Syst. Appl. 2021, 164, 113820. [Google Scholar] [CrossRef]
- Luo, Z.; Guo, W.; Liu, Q.; Zhang, Z. A hybrid model for financial time-series forecasting based on mixed methodologies. Expert Syst. 2021, 38, 12633. [Google Scholar] [CrossRef]
- Li, Z.; Han, J.; Song, Y. On the forecasting of high-frequency financial time series based on ARIMA model improved by deep learning. J. Forecast. 2020, 39, 1081–1097. [Google Scholar] [CrossRef]
- Cappelli, C.; Cerqueti, R.; D’Urso, P.; Di Iorio, F. Multiple breaks detection in financial interval-valued time series. Expert Syst. Appl. 2021, 164, 113775. [Google Scholar] [CrossRef]
- Niu, T.; Wang, J.; Lu, H.; Yang, W.; Du, P. Developing a deep learning framework with two-stage feature selection for multivariate financial time series forecasting. Expert Syst. Appl. 2020, 148, 113237. [Google Scholar] [CrossRef]
- Singh, A.; Ganapathysubramanian, B.; Singh, A.K.; Sarkar, S. Machine learning for high-throughput stress phenotyping in plants. Trends Plant Sci. 2016, 21, 110–124. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Antonopoulos, V.Z.; Antonopoulos, A.V. Daily reference evapotranspiration estimates by artificial neural networks technique and empirical equations using limited input climate variables. Comput. Electron. Agric. 2017, 132, 86–96. [Google Scholar] [CrossRef]
- Kar, S.; Tanaka, R.; Korbu, L.B.; Kholová, J.; Iwata, H.; Durbha, S.S.; Adinarayana, J.; Vadez, V. Automated discretization of ‘transpiration restriction to increasing VPD’ features from outdoors high-throughput phenotyping data. Plant Methods 2020, 16, 1–20. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef] [Green Version]
- Peddinti, S.R.; Kambhammettu, B.V.N.P.; Rodda, S.R.; Thumaty, K.C.; Suradhaniwar, S. Dynamics of Ecosystem Water Use Efficiency in Citrus Orchards of Central India Using Eddy Covariance and Landsat Measurements. Ecosystems 2019, 23, 511–528. [Google Scholar] [CrossRef]
- Taieb, S.B.; Hyndman, R.J. Recursive and Direct Multi-Step Forecasting: The Best of Both Worlds; Department of Econometrics and Business Statistics, Monash University: Clayton, Australia, 2012; Volume 19. [Google Scholar]
- Chevillon, G.; Hendry, D.F. Non-parametric direct multi-step estimation for forecasting economic processes. Int. J. Forecast. 2005, 21, 201–218. [Google Scholar] [CrossRef] [Green Version]
- Cai, M.; Pipattanasomporn, M.; Rahman, S. Day-ahead building-level load forecasts using deep learning vs. traditional time-series techniques. Appl. Energy 2019, 236, 1078–1088. [Google Scholar] [CrossRef]
- Taieb, S.B.; Atiya, A.F. A bias and variance analysis for multistep-ahead time series forecasting. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 62–76. [Google Scholar] [CrossRef]
- Fan, J.; Yao, Q. Nonlinear Time Series: Nonparametric and Parametric Methods; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Ben Taieb, S.; Bontempi, G.; Atiya, A.F.; Sorjamaa, A. A review and comparison of strategies for multi-step ahead time series forecasting based on the NN5 forecasting competition. Expert Syst. Appl. 2012, 39, 7067–7083. [Google Scholar] [CrossRef] [Green Version]
- Akanbi, A.; Masinde, M. A Distributed Stream Processing Middleware Framework for Real-Time Analysis of Heterogeneous Data on Big Data Platform: Case of Environmental Monitoring. Sensors 2020, 20, 3166. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Hyndman, R.J.; Athanasopoulos, G.; Bergmeir, C.; Caceres, G.; Chhay, L.; O’Hara-Wild, M.; Petropoulos, F.; Razbash, S.; Wang, E.; Yasmeen, F.; et al. Forecast: Forecasting Functions for Time Series and Linear Models. 2018. Available online: https://researchportal.bath.ac.uk/en/publications/forecast-forecasting-functions-for-time-series-and-linear-models (accessed on 8 January 2021).
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1997, 9, 155–161. [Google Scholar]
- Koskela, T.; Lehtokangas, M.; Saarinen, J.; Kaski, K. Time series prediction with multilayer perceptron, FIR and Elman neural networks. In Proceedings of the 1996 World Congress on Neural Networks, Bochum, Germany, 16–19 July 1996; INNS Press: San Diego, CA, USA, 1996; pp. 491–496. [Google Scholar]
- Connor, J.T.; Martin, R.D.; Atlas, L.E. Recurrent neural networks and robust time series prediction. IEEE Trans. Neural Netw. 1994, 5, 240–254. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Vargha, A.; Delaney, H.D. The Kruskal-Wallis test and stochastic homogeneity. J. Educ. Behav. Stat. 1998, 23, 170–192. [Google Scholar] [CrossRef]
- Terpilowski, M. Scikit-posthocs: Pairwise multiple comparison tests in Python. J. Open Source Softw. 2019, 4, 1169. [Google Scholar] [CrossRef]
- Bennett, K.P.; Campbell, C. Support vector machines: Hype or hallelujah? ACM SIGKDD Explor. Newslett. 2000, 2, 1–13. [Google Scholar] [CrossRef]
- Gers, F.A.; Eck, D.; Schmidhuber, J. Applying LSTM to time series predictable through time-window approaches. In Neural Nets WIRN Vietri-01; Springer: London, UK, 2002; pp. 193–200. [Google Scholar]
- Ahmed, N.K.; Atiya, A.F.; El Gayar, N.; El-Shishiny, H. An Empirical Comparison of Machine Learning Models for Time Series Forecasting. Econ. Rev. 2010, 29, 594–621. [Google Scholar] [CrossRef]
- Hyndman, R.J. A brief history of forecasting competitions. Int. J. Forecast. 2020, 36, 7–14. [Google Scholar] [CrossRef]
- Bao, Y.; Xiong, T.; Hu, Z. Multi-step-ahead time series prediction using multiple-output support vector regression. Neurocomputing 2014, 129, 482–493. [Google Scholar] [CrossRef] [Green Version]






















| Temperature Partitions for KW and Nemenyi Tests | ||||
| Temp_0 | Temp_1 | Temp_2 | Temp_3 | |
| Temp_0 | 1 | 0.022 | 0 | 0 |
| Temp_1 | 0.022 | 1 | 0 | 0 |
| Temp_2 | 0 | 0 | 1 | 0.943 |
| Temp_3 | 0 | 0 | 0.943 | 1 |
| Humidity Partitions for KW and Nemenyi Tests | ||||
| Hud_0 | Hud_1 | Hud_2 | Hud_3 | |
| Hud_0 | 1 | 0 | 0.654 | 0.086 |
| Hud_1 | 0 | 1 | 0.003 | 0 |
| Hud_2 | 0.654 | 0.003 | 1 | 0.002 |
| Hud_3 | 0.086 | 0 | 0.002 | 1 |
| Mean and SD for Data Partitions | ||||
|---|---|---|---|---|
| Humidity | Temperature | |||
| Mean | SD | Mean | SD | |
| Day 1–7 (P1) | 48.05 | 18.73 | 22.24 | 6.70 |
| Day 8–14 (P2) | 42.17 | 13.07 | 23.65 | 5.33 |
| Day 15–21 (P3) | 45.78 | 15.46 | 26.01 | 5.68 |
| Day 22–28 (P4) | 51.47 | 20.80 | 26.21 | 4.99 |
| Total 1–28 (Mean, SD) | 46.88 | 17.61 | 24.52 | 5.94 |
| One-Step Ahead Forecasting | Multi-Step Ahead Forecasting | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Temperature | Humidity | Temperature | Humidity | |||||||||||||||||
| Day | SARIMA | SVR | MLP | RNN | LSTM | SARIMA | SVR | MLP | RNN | LSTM | SARIMA | SVR | MLP | RNN | LSTM | SARIMA | SVR | MLP | RNN | LSTM |
| 3 | 0.37 | 1.88 | 2.14 | 0.76 | 2.06 | 1.58 | 2.66 | 7.12 | 2.84 | 4.22 | 3.20 | 3.46 | 4.97 | 7.59 | 5.40 | 10.90 | 24.49 | 14.24 | 8.65 | 15.48 |
| 4 | 0.40 | 0.45 | 1.28 | 0.74 | 0.87 | 2.11 | 2.39 | 4.85 | 2.94 | 2.05 | 2.58 | 2.21 | 1.74 | 5.95 | 5.90 | 7.24 | 20.94 | 10.74 | 13.64 | 10.78 |
| 5 | 0.41 | 0.47 | 0.72 | 0.63 | 0.50 | 1.81 | 1.91 | 3.30 | 2.68 | 2.44 | 1.55 | 2.72 | 1.44 | 9.49 | 6.63 | 5.88 | 6.41 | 17.26 | 11.56 | 16.02 |
| 6 | 0.36 | 0.44 | 1.71 | 0.54 | 0.50 | 1.61 | 1.80 | 4.35 | 1.77 | 1.65 | 4.03 | 3.86 | 2.71 | 9.39 | 3.50 | 12.17 | 8.49 | 24.06 | 18.57 | 10.22 |
| 7 | 0.36 | 0.34 | 0.74 | 0.58 | 0.51 | 1.57 | 1.70 | 3.70 | 2.06 | 1.62 | 2.32 | 2.27 | 2.86 | 3.90 | 4.40 | 13.43 | 13.38 | 25.82 | 13.26 | 19.74 |
| 8 | 0.59 | 0.57 | 0.88 | 0.84 | 0.72 | 2.14 | 2.33 | 2.79 | 2.57 | 2.13 | 2.30 | 1.84 | 2.23 | 6.01 | 5.55 | 17.14 | 14.93 | 11.05 | 8.73 | 8.81 |
| 9 | 0.45 | 0.45 | 0.72 | 0.74 | 0.53 | 2.30 | 2.33 | 3.43 | 3.16 | 2.52 | 3.04 | 1.31 | 2.22 | 6.22 | 3.18 | 11.03 | 11.29 | 5.49 | 16.20 | 10.81 |
| 10 | 0.41 | 0.45 | 0.81 | 0.64 | 0.51 | 2.00 | 2.25 | 3.33 | 2.46 | 2.10 | 3.09 | 3.55 | 3.90 | 4.21 | 4.22 | 8.57 | 7.63 | 12.93 | 14.16 | 12.14 |
| 11 | 0.39 | 0.39 | 0.59 | 0.55 | 0.52 | 1.69 | 1.87 | 2.79 | 1.78 | 1.91 | 2.31 | 1.40 | 3.43 | 9.79 | 4.22 | 15.58 | 15.31 | 17.93 | 21.20 | 13.40 |
| 12 | 0.63 | 0.61 | 0.87 | 0.74 | 0.65 | 2.60 | 2.60 | 2.56 | 2.65 | 2.66 | 3.04 | 2.49 | 3.14 | 5.45 | 3.84 | 14.19 | 10.85 | 31.26 | 7.26 | 15.34 |
| 13 | 0.51 | 0.48 | 1.14 | 0.65 | 0.59 | 2.03 | 2.17 | 2.87 | 2.51 | 2.12 | 3.43 | 3.14 | 7.51 | 5.58 | 2.81 | 10.22 | 9.56 | 14.49 | 27.70 | 8.09 |
| 14 | 0.44 | 0.41 | 1.01 | 0.52 | 0.61 | 1.68 | 1.67 | 2.56 | 1.68 | 1.89 | 2.27 | 1.68 | 3.53 | 8.20 | 2.98 | 10.61 | 8.00 | 7.38 | 13.84 | 11.58 |
| 15 | 0.41 | 0.41 | 0.68 | 0.57 | 0.60 | 1.73 | 1.83 | 2.60 | 1.85 | 1.91 | 2.62 | 2.62 | 2.01 | 3.01 | 5.66 | 11.18 | 7.52 | 16.45 | 7.68 | 8.62 |
| 16 | 0.32 | 0.31 | 0.52 | 0.36 | 0.39 | 1.33 | 1.31 | 1.80 | 1.27 | 1.36 | 2.63 | 2.41 | 2.99 | 9.14 | 4.67 | 10.03 | 10.44 | 24.42 | 21.69 | 11.78 |
| 17 | 0.42 | 0.38 | 1.30 | 0.55 | 0.67 | 1.52 | 1.45 | 1.85 | 1.49 | 1.74 | 1.54 | 1.38 | 1.56 | 4.98 | 4.26 | 7.27 | 6.53 | 18.90 | 16.58 | 13.28 |
| 18 | 0.39 | 0.37 | 0.55 | 0.48 | 0.61 | 1.74 | 1.66 | 1.79 | 1.80 | 1.82 | 2.59 | 2.30 | 15.33 | 10.23 | 4.09 | 9.41 | 8.95 | 13.65 | 9.95 | 16.62 |
| 19 | 0.40 | 0.35 | 0.57 | 0.44 | 0.60 | 1.81 | 1.71 | 1.78 | 1.87 | 1.90 | 1.43 | 1.30 | 11.35 | 3.20 | 4.42 | 4.27 | 6.51 | 18.86 | 18.70 | 9.36 |
| 20 | 0.46 | 0.42 | 0.50 | 0.47 | 0.56 | 1.94 | 1.87 | 2.02 | 1.94 | 2.12 | 1.85 | 1.94 | 0.95 | 7.93 | 7.80 | 7.35 | 7.19 | 11.73 | 19.97 | 5.17 |
| 21 | 0.42 | 0.42 | 0.50 | 0.43 | 0.63 | 1.59 | 1.56 | 1.89 | 1.58 | 1.45 | 3.61 | 3.36 | 10.98 | 5.02 | 1.99 | 11.81 | 9.49 | 20.73 | 12.01 | 7.58 |
| 22 | 0.32 | 0.30 | 0.52 | 0.43 | 0.40 | 1.77 | 1.76 | 2.07 | 1.81 | 1.85 | 2.28 | 1.85 | 5.93 | 9.54 | 3.77 | 12.23 | 11.50 | 35.42 | 15.93 | 11.61 |
| 23 | 0.38 | 0.33 | 0.92 | 0.38 | 0.46 | 1.76 | 1.76 | 2.10 | 1.91 | 1.86 | 1.55 | 1.46 | 5.77 | 6.98 | 5.01 | 11.38 | 12.87 | 13.92 | 19.73 | 18.82 |
| 24 | 0.37 | 0.32 | 0.54 | 0.40 | 0.48 | 1.84 | 1.76 | 1.79 | 1.87 | 1.80 | 0.93 | 1.44 | 4.50 | 9.93 | 3.52 | 9.00 | 10.35 | 11.21 | 22.66 | 17.86 |
| 25 | 0.37 | 0.35 | 0.71 | 0.36 | 0.49 | 2.20 | 2.16 | 2.21 | 2.20 | 2.05 | 1.61 | 1.56 | 2.88 | 6.93 | 5.85 | 10.92 | 7.03 | 20.23 | 10.22 | 5.08 |
| 26 | 0.30 | 0.29 | 0.56 | 0.30 | 0.68 | 1.55 | 1.52 | 2.01 | 1.62 | 1.77 | 2.37 | 2.17 | 4.66 | 5.44 | 3.82 | 8.38 | 6.19 | 27.25 | 7.36 | 6.90 |
| 27 | 0.38 | 0.38 | 0.58 | 0.37 | 0.50 | 2.51 | 2.62 | 3.55 | 2.64 | 3.55 | 3.53 | 3.40 | 12.76 | 6.61 | 3.18 | 26.34 | 23.15 | 11.77 | 13.37 | 12.56 |
| 28 | 0.38 | 0.35 | 0.57 | 0.38 | 0.60 | 2.22 | 2.27 | 2.56 | 2.36 | 2.69 | 1.93 | 1.73 | 5.69 | 3.35 | 4.57 | 17.57 | 14.97 | 33.68 | 12.50 | 14.98 |
| Average | 0.41 | 0.46 | 0.83 | 0.53 | 0.62 | 1.87 | 1.96 | 2.83 | 2.13 | 2.12 | 2.45 | 2.26 | 4.89 | 6.58 | 4.43 | 11.31 | 11.31 | 18.11 | 14.74 | 12.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suradhaniwar, S.; Kar, S.; Durbha, S.S.; Jagarlapudi, A. Time Series Forecasting of Univariate Agrometeorological Data: A Comparative Performance Evaluation via One-Step and Multi-Step Ahead Forecasting Strategies. Sensors 2021, 21, 2430. https://doi.org/10.3390/s21072430
Suradhaniwar S, Kar S, Durbha SS, Jagarlapudi A. Time Series Forecasting of Univariate Agrometeorological Data: A Comparative Performance Evaluation via One-Step and Multi-Step Ahead Forecasting Strategies. Sensors. 2021; 21(7):2430. https://doi.org/10.3390/s21072430
Chicago/Turabian StyleSuradhaniwar, Saurabh, Soumyashree Kar, Surya S. Durbha, and Adinarayana Jagarlapudi. 2021. "Time Series Forecasting of Univariate Agrometeorological Data: A Comparative Performance Evaluation via One-Step and Multi-Step Ahead Forecasting Strategies" Sensors 21, no. 7: 2430. https://doi.org/10.3390/s21072430
APA StyleSuradhaniwar, S., Kar, S., Durbha, S. S., & Jagarlapudi, A. (2021). Time Series Forecasting of Univariate Agrometeorological Data: A Comparative Performance Evaluation via One-Step and Multi-Step Ahead Forecasting Strategies. Sensors, 21(7), 2430. https://doi.org/10.3390/s21072430






