A Synchronous Prediction Model Based on Multi-Channel CNN with Moving Window for Coal and Electricity Consumption in Cement Calcination Process
Abstract
:1. Introduction
2. Related Work
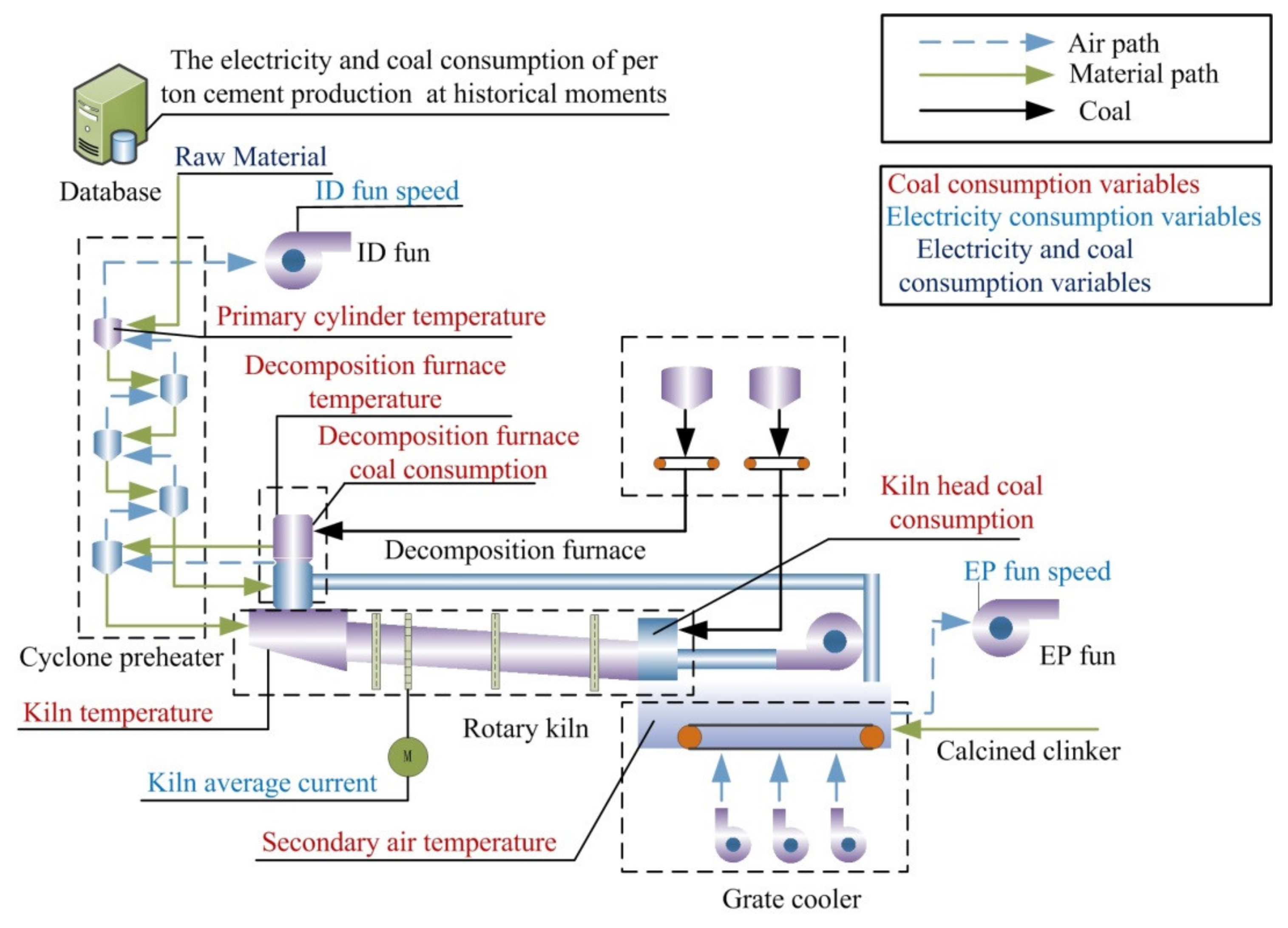
3. Process Analysis and Variable Selection of Cement Industry
4. The Establishment of the MWMC-CNN Model
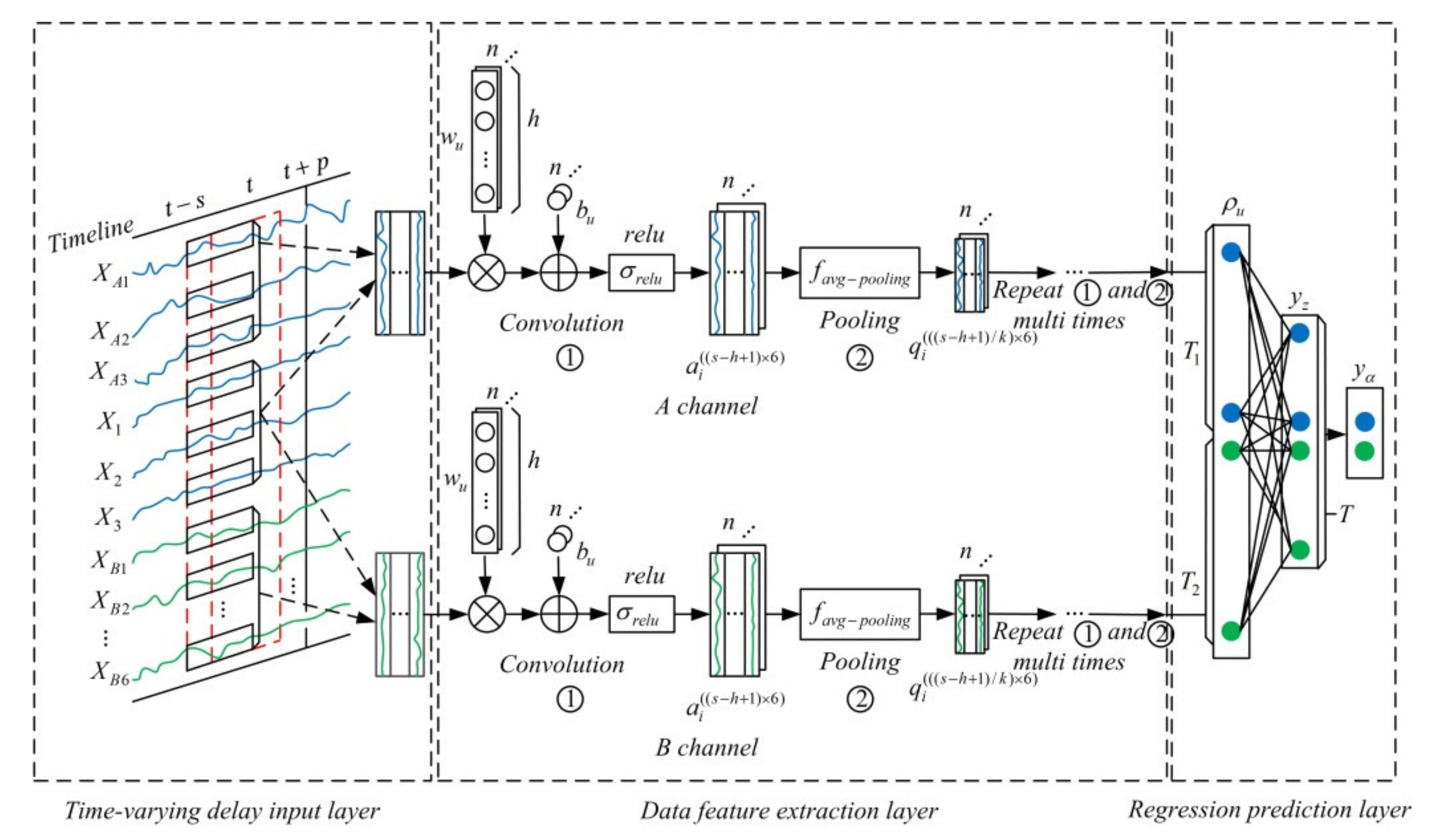
4.1. The Structure of the MWMC-CNN Model
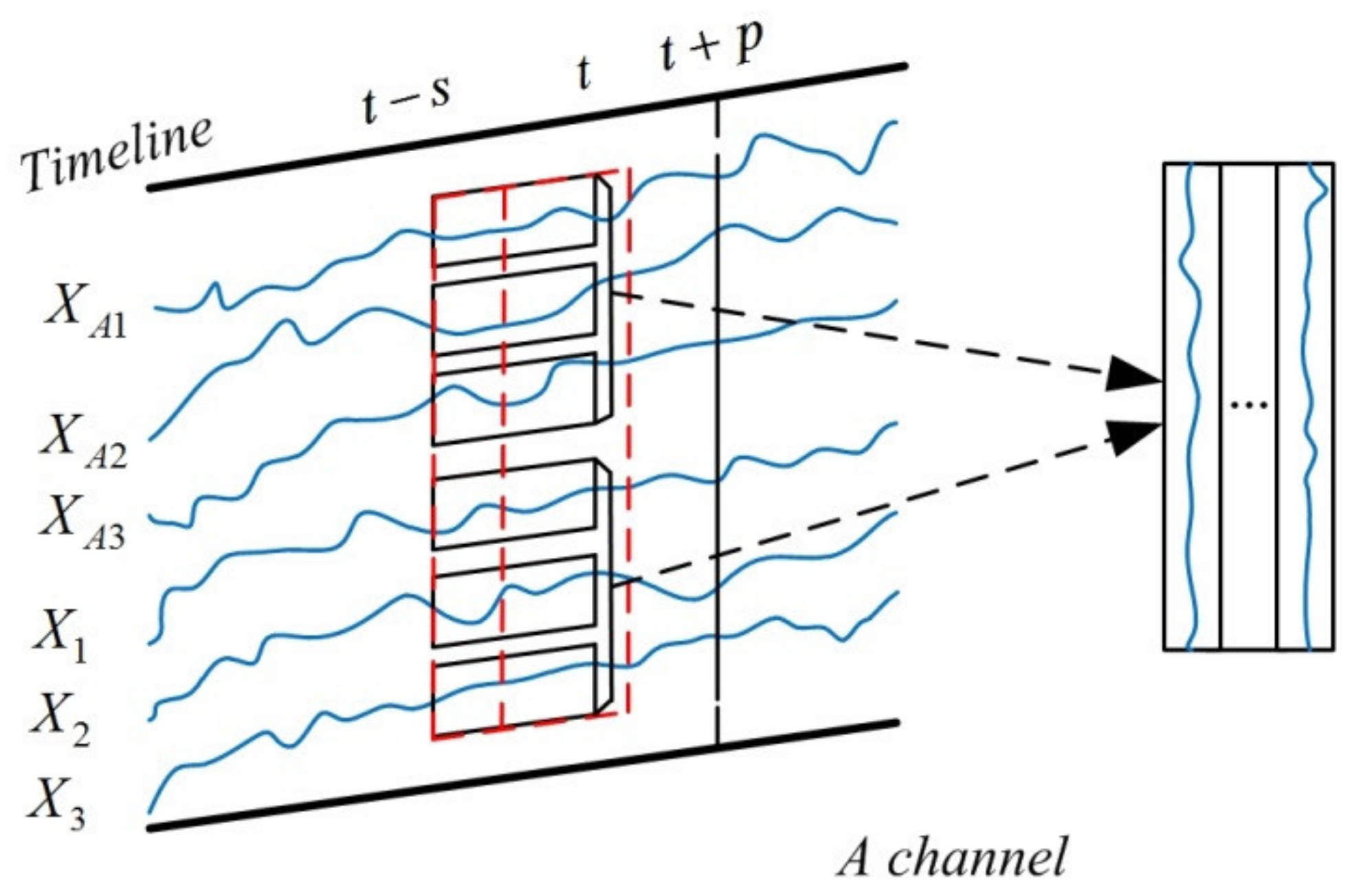
4.1.1. The Time-Varying Delay Input Layer Structure of MWMC-CNN
4.1.2. The Structure of the MWMC-CNN Data Feature Extraction Layer
4.1.3. The Regression Prediction Layer of MWMC-CNN
4.1.4. Parameter Adjustment Algorithm of MWMC-CNN
4.2. Research on MWMC-CNN Algorithm
| Algorithm 1 Energy consumption prediction algorithm of MWMC-CNN |
| Input A: ID fan speed (), EP fan speed (), kiln average current (), the amount of raw material (), the ECPC at historical moments (), and the CCPC at historical moments () Input B: Primary cylinder temperature (), decomposition furnace coal consumption (), decomposition furnace temperature (), kiln temperature (),secondary air temperature (), kiln head coal consumption (), the amount of raw material (), the ECPC at historical moments (), and the CCPC at historical moments (). Output: The ECPC at future moments (), the CCPC at future moments (). (Step 1) Initialization: (Step 1.1) Normalization: (Step 1.2) Moving Window Processing: (Step 2) Convolution and pooling: (Step 2.1) Convolution and activation: A channel: B channel: (Step 2.2) Pooling: A channel: B channel: Repeat Step 2.1–2.2 several times in each channel. (Step 3) Full connection and output: (Step 3.1) Full connection: (Step 3.2) Output: |
| Algorithm 2 Parameter adjustment algorithm of MWMC-CNN |
| The parameter update process of Adam algorithm for every element. Objective function: Parameter Initialization: (Learning rate) , (Exponential decay rates of moment estimates) (Constant) (Initialize 1st moment vector) (Initialize 2nd moment vector) (Initialize time step) while not converged do: (Randomly select L sets of data) (Calculate the gradient of ) (Calculate the gradient of ) (Update biased 1st moment estimate of ) (Update biased 1st moment estimate of ) (Update biased 2nd moment estimate of ) (Update biased 2nd moment estimate of ) (Compute bias-corrected 1st moment estimate of ) (Compute bias-corrected 1st moment estimate of ) (Compute bias-corrected 2nd moment estimate of ) (Compute bias-corrected 2nd moment estimate of ) (Calculate parameter update value of ) (Calculate parameter update value of ) (Update parameter ) (Update parameter ) end while return , |
5. Results
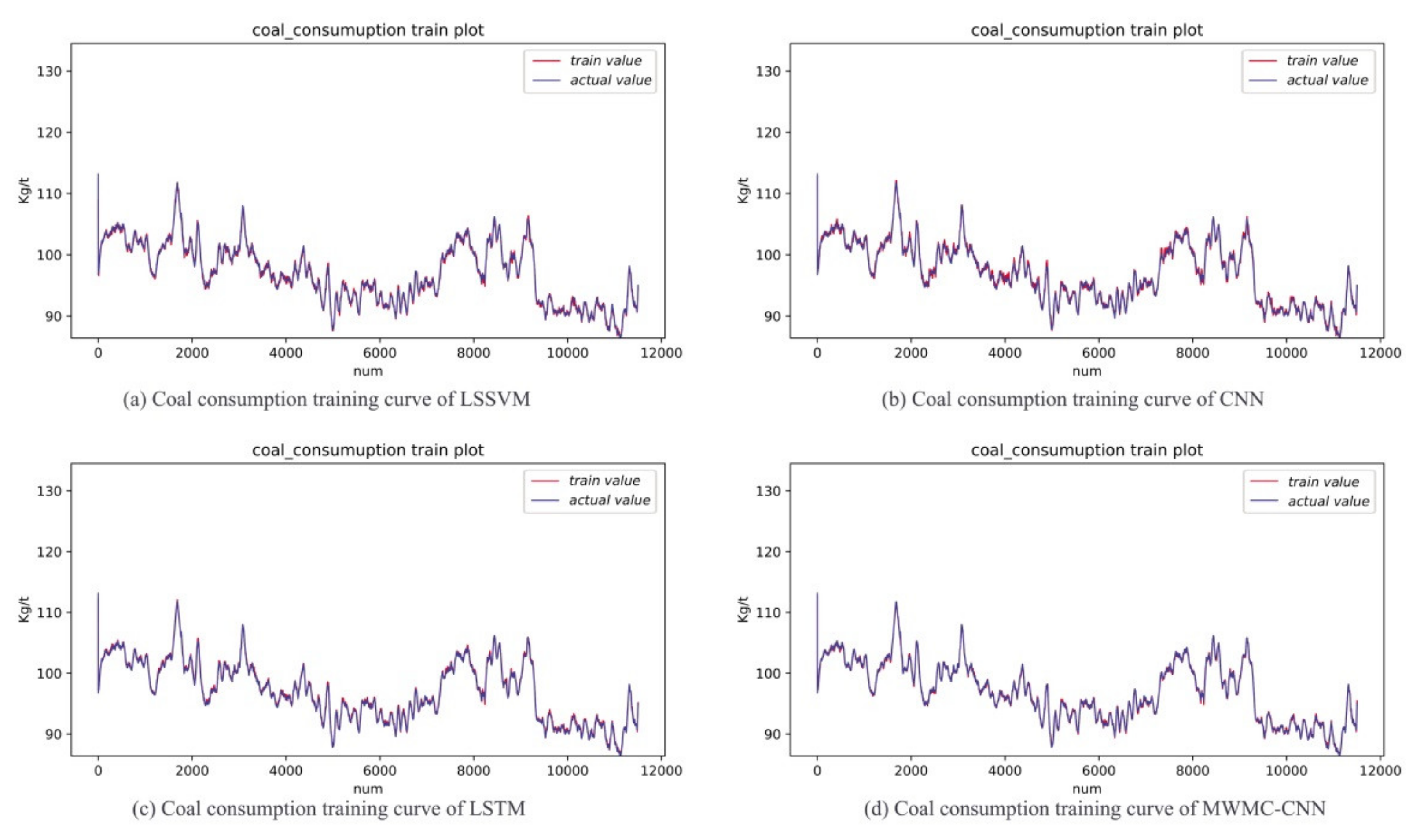
5.1. Parameter and Structure Adjustment Experiment of MWMC-CNN
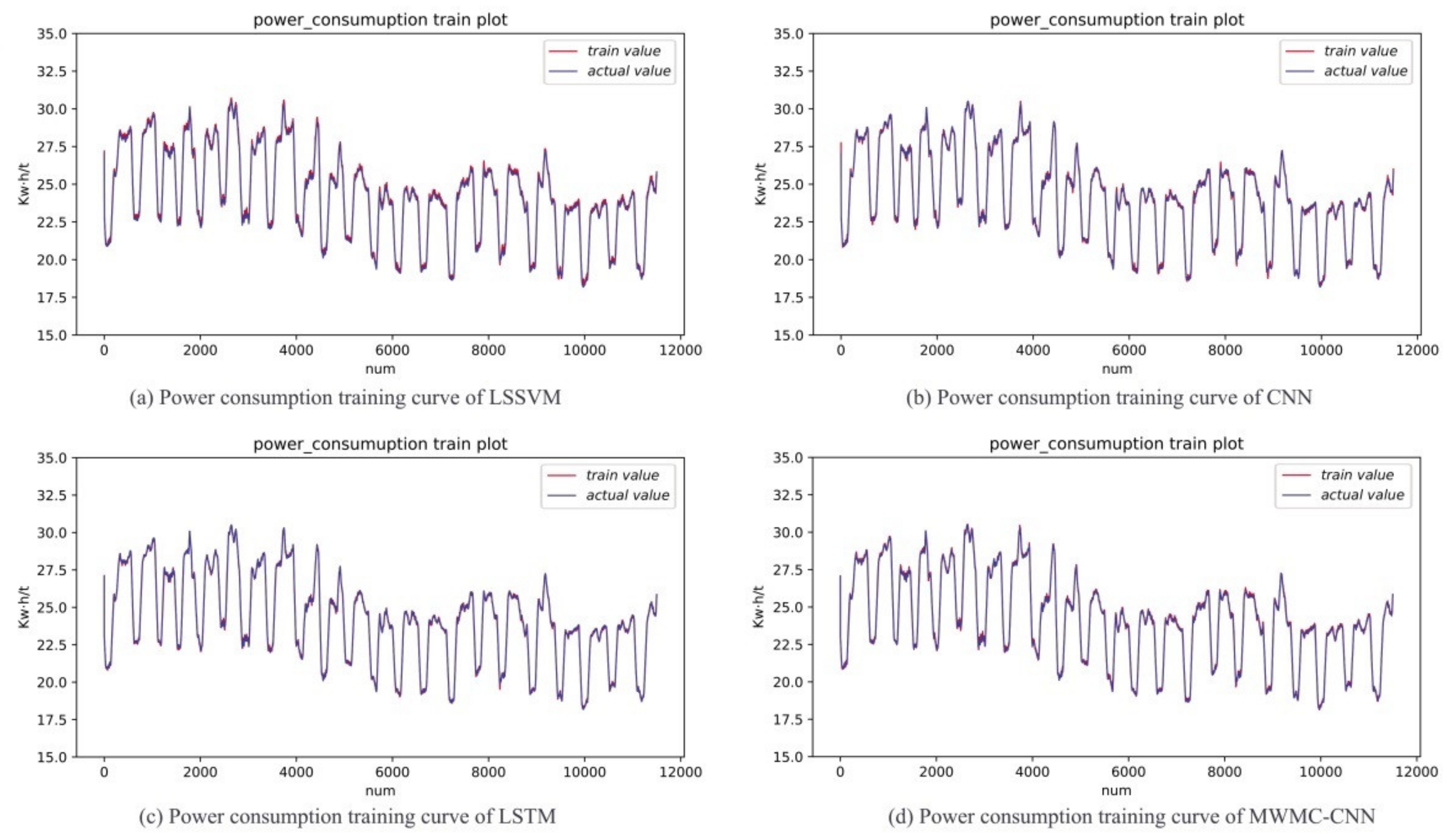
5.2. Experiments Comparison of MWMC-CNN and Other Models
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, C.; Yu, B.; Chen, J.; Wei, Y. Green transition pathways for cement industry in China. Resour. Conserv. Recycl. 2021, 166, 1–16. [Google Scholar] [CrossRef]
- Shen, W.; Liu, Y.; Yan, B.; Wang, J.; He, P.; Zhou, C.; Huo, X.; Zhang, W.; Xu, G.; Ding, Q. Cement industry of China: Driving force, environment impact and sustainable development. Renew. Sustain. Energy Rev. 2017, 75, 618–628. [Google Scholar] [CrossRef]
- Jin, X.; Qi, F.; Wu, Q.; Mu, Y.; Jia, H.; Yu, X.; Li, Z. Integrated optimal scheduling and predictive control for energy management of an urban complex considering building thermal dynamics. Int. J. Electr. Power Energy Syst. 2020, 123, 106273. [Google Scholar] [CrossRef]
- Banik, R.; Das, P.; Ray, S.; Biswas, A. Prediction of electrical energy consumption based on machine learning technique. Electr. Eng. 2021, 103, 909–920. [Google Scholar] [CrossRef]
- Ma, M.D.; Wong, D.S.H.; Jang, S.S.; Tseng, S.T. Fault Detection Based on Statistical Multivariate Analysis and Microarray Visualization. IEEE Trans. Ind. Inform. 2010, 6, 18–24. [Google Scholar]
- Ceperic, E.; Ceperic, V.; Baric, A. A Strategy for Short-Term Load Forecasting by Support Vector Regression Machines. IEEE Trans. Power Syst. 2013, 28, 4356–4364. [Google Scholar] [CrossRef]
- Gao, C.H.; Jian, L.; Luo, S.H. Modeling of the Thermal State Change of Blast Furnace Hearth with Support Vector Machines. IEEE Trans. Ind. Elect. 2012, 59, 1134–1145. [Google Scholar] [CrossRef]
- Fan, G.F.; Wei, X.; Li, Y.T.; Hong, W.C. Forecasting electricity consumption using a novel hybrid model. Sustain. Cities Soc. 2020, 62, 102320. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, N.; Wang, H.J. Power Consumption Prediction Modeling of Cement Manufacturing Based on the Improved Multiple Non-linear Regression Algorithm. Appl. Mech. Mater. 2014, 687–691, 5185–5189. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, X.H.; Zhang, Q.; Huang, C.Y. Empirical mode decomposition based hybrid ensemble model for electrical energy consumption forecasting of the cement grinding process. Measurement 2019, 138, 314–324. [Google Scholar] [CrossRef]
- Cao, K.; Hu, T.; Li, Z.; Zhao, G.; Qian, X. Deep multi-task learning model for time series prediction in wireless communication. Phys. Commun. 2021, 44, 101251. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, Y.; Wang, D.; De, G.; Li, Y.; Liu, X.; Wang, Y. A novel combined multi-task learning and Gaussian process regression model for the prediction of multi-timescale and multi-component of solar radiation. J. Clean. Prod. 2021, 284, 124710. [Google Scholar] [CrossRef]
- Yan, S.; Yan, X. Joint monitoring of multiple quality-related indicators in nonlinear processes based on multi-task learning. Measurement 2020, 165, 108158. [Google Scholar] [CrossRef]
- Sun, Z.; Liang, D.; Zhuang, Z.; Chen, L.; Ming, X. Multi-task processing oriented production layout based on evolutionary programming mechanism. Appl. Soft Comput. J. 2021, 98, 106896. [Google Scholar] [CrossRef]
- Lavanya, M.; Shanthi, B.; Saravanan, S. Multi objective task scheduling algorithm based on SLA and processing time suitable for cloud environment. Comput. Commun. 2020, 151, 183–195. [Google Scholar] [CrossRef]
- Hamer, A.M.; Simms, D.M.; Waine, T.W. Replacing huming interpretation of agricultural land in Afghanistan with a deep convolutional neural network. Int. J. Remote Sens. 2021, 42, 3017–3038. [Google Scholar] [CrossRef]
- Youcef, D.; Gautam, S.; Jerry, C.L. Fast and Accurate Convolution Neural Network for Detecting Manufacturing Data. IEEE Trans. Ind. Inform. 2021, 17, 2947–2955. [Google Scholar]
- Bianco, V.; Manca, O.; Nardini, S. Electricity consumption forecasting in Italy using linear regression models. Energy 2009, 34, 1413–1421. [Google Scholar] [CrossRef]
- Catalina, T.; Iordache, V.; Caracaleanu, B. Multiple regression model for fast prediction of the heating energy demand. Energy Build. 2013, 57, 302–312. [Google Scholar] [CrossRef]
- Dudek, G. Pattern-based local linear regression models for short-term load forecasting. Electr. Power Syst. Res. 2016, 130, 139–147. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.C.; Kaufman, L.; Smola, A.; Vapnik, V. Support Vector Regression Machines. Adv. Neural Inf. Process. Syst. NIPS 1996, 9, 155–161. [Google Scholar]
- Wang, S.; Yu, L.; Tang, L.; Wang, S.Y. A novel seasonal decomposition based least squares support vector regression ensemble learning approach for hydropower consumption forecasting in China. Energy 2011, 36, 6542–6554. [Google Scholar] [CrossRef]
- Assouline, D.; Mohajeri, N.; Scartezzini, J.L. Quantifying rooftop photovoltaic solar energy potential: A machine learning approach. Solar Energy 2017, 141, 278–296. [Google Scholar] [CrossRef]
- Zhou, J.Y.; Shi, J.; Li, G. Fine tuning support vector machines for short-term wind speed forecasting. Energy Convers. Manag. 2011, 52, 1990–1998. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Samet, H.; Marzbani, F. A new hybrid Modified Firefly Algorithm and Support Vector Regression model for accurate Short Term Load Forecasting. Expert Syst. Appl. 2014, 41, 6047–6056. [Google Scholar] [CrossRef]
- Yin, S.; Ding, S.X.; Xie, X.C.; Luo, H. A Review on Basic Data-Driven Approaches for Industrial Process Monitoring. IEEE Trans. Indusrial Electron. 2014, 61, 6418–6428. [Google Scholar] [CrossRef]
- Fachini, F.; Fuly, B.I.L. A comparison of machine learning regression models for critical bus voltage and load mapping with regards to max reactive power in PV buses. Electr. Power Syst. Res. 2021, 191, 106883. [Google Scholar] [CrossRef]
- Gong, M.; Wang, J.; Bai, Y.; Li, B.; Zhang, L. Heat load prediction of residential buildings based on discrete wavelet transform and tree-based ensemble learning. J. Build. Eng. 2020, 32, 101455. [Google Scholar] [CrossRef]
- Lu, S.; Li, Q.; Bai, L.; Wang, R. Performance predictions of ground source heat pump system based random forest and back propagation neural network models. Energy Convers. Manag. 2019, 197, 111864. [Google Scholar] [CrossRef]
- Qiu, T.; Zhang, M.; LIU, X.; Liu, J.; Chen, C.; Zhao, W. A Directed Edge Weight Prediction Model Using Dectsion Tree Ensembles in Industrial Internet of Things. IEEE Trans. Ind. Inform. 2021, 17, 2160–2168. [Google Scholar] [CrossRef]
- Kumar, A.; Jaiswal, A. A Deep Swarm-Optimized Model for Laveraging Industrial Data Analystic in Cognitive Manufacturing. IEEE Trans. Ind. Inform. 2021, 17, 2938–2946. [Google Scholar] [CrossRef]
- Marugan, A.P.; Marquez, F.P.G.; Perez, J.M.P.; Ruiz-Hernandez, D. A survey artificial neural network in wind energy systems. Appl. Energy 2018, 228, 1822–1836. [Google Scholar] [CrossRef] [Green Version]
- Debnath, K.B.; Mourshed, M. Forecasting methods in energy planning models. Renew. Sustain. Energy Rev. 2018, 88, 297–325. [Google Scholar] [CrossRef] [Green Version]
- Azadeh, A.; Ghaderi, S.F.; Sohrabkhani, S. Annual electricity consumption forecasting by neural network in high energy consuming industrial sectors. Energy Convers. Manag. 2008, 49, 2272–2278. [Google Scholar] [CrossRef]
- Zeng, Y.R.; Zeng, Y.; Choi, B.; Lin, W. Multifactor-influenced energy consumption forecasting using enhanced back-propagation neural network. Energy 2017, 127, 381–396. [Google Scholar] [CrossRef]
- Rodrigues, F.; Cardeira, C.; Calado, J.M.F. The daily and hourly energy consumption and load forecasting using artificial neural network method: A case study using a set of 93 households in Portugal. Energy Procedia 2014, 62, 220–229. [Google Scholar] [CrossRef] [Green Version]
- Panapakidis, I.P.; Dagoumas, A.S. Day-ahead electricity price forecasting via the application of artificial neural network based models. Appl. Energy 2016, 172, 132–151. [Google Scholar] [CrossRef]
- Szoplik, J. Forecasting of natural gas consumption with artificial neural networks. Energy 2015, 85, 208–220. [Google Scholar] [CrossRef]
- Zhang, C.; Lim, P.; Qin, A.K.; Tan, C.K. Multiobjective Deep Belief Networks Ensemble for Remaining Useful Life Estimation in Prognostics. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2306–2318. [Google Scholar] [CrossRef] [PubMed]
- Anagnostis, A.; Papageorgiou, E.; Bochtis, D. Application of Artificial Neural Networks for Natural Gas Consumption Forecasting. Sustainability 2020, 12, 6409. [Google Scholar] [CrossRef]
- Kim, T.-Y.; Cho, S.-B. Predicting residential energy consumption using CNN-LSTM neural networks. Energy 2019, 182, 72–81. [Google Scholar] [CrossRef]
- Hwang, J.; Suh, D.; Otto, M.O. Forecasting Electricity Consumption in Commercial Buildings Using a Machine Learning Approach. Energies 2020, 13, 5885. [Google Scholar] [CrossRef]
- Son, N.; Yang, S.; Na, J. Deep Neural Network and Long Short-Term Memory for electric Power Load Forecasting. Appl. Sci. 2020, 10, 6489. [Google Scholar] [CrossRef]
- Atef, S.; Eltawil, A.B. Assessment of stacked unidirectional and bidirectional long short-term memory networks for electricity load forecasting. Electr. Power Syst. Res. 2020, 187, 106489. [Google Scholar] [CrossRef]
- Gu, J.X.; Wang, Z.H.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.B.; Wang, Z.D.; Liu, X.H.; Zeng, N.; Liu, Y.; Alsaadi, F.E. A survey of deep neural network architectures and their applications. Neurocomputing 2017, 234, 11–26. [Google Scholar] [CrossRef]
- Zhang, Q.C.; Yang, L.T.; Chen, Z.K.; Li, P. A survey on deep learning for big data. Inf. Fusion 2018, 42, 146–157. [Google Scholar] [CrossRef]
- Wang, J.J.; Ma, Y.L.; Zhang, L.B.; Gao, R.X.; Wu, D.Z. Deep learning for smart manufacturing: Methods and applications. J. Manuf. Syst. 2018, 48, 144–156. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.W.; Lin, X.T. Big data deep learning: Challenges and perspectives. IEEE Access 2014, 2, 514–525. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Chen, Z.K.; Yang, L.T.R.; Zhang, Q.C.; Deen, M.J. Deep Convolutional Computation Model for Feature Learning on Big Data in Internet of Things. IEEE Trans. Ind. Inform. 2018, 14, 790–798. [Google Scholar] [CrossRef]
- Cha, Y.J.; Choi, W.; Buyukozturk, O. Deep Learning-Based Crack Damage Detection Using Convolutional Neural Networks. Comput. Aided Civ. Infrastruct. Eng. 2017, 32, 361–378. [Google Scholar] [CrossRef]
- Zhang, W.; Li, C.H.; Peng, G.L.; Chen, Y.H.; Zhang, Z.J. A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load. Mech. Syst. Signal Process. 2018, 100, 439–453. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, R.Q.; Wang, J.J.; Mao, K.Z. Learning to Monitor Machine Health with Convolutional Bi-Directional LSTM Networks. Sensors 2017, 17, 273. [Google Scholar] [CrossRef] [PubMed]
- Jing, L.Y.; Zhao, M.; Li, P.; Xu, X.Q. A convolutional neural network based feature learning and fault diagnosis method for the condition monitoring of gearbox. Measurement 2017, 111, 1–10. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations, ICLR, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]





| Model | Parameter | Prediction Error | ||
|---|---|---|---|---|
| RMSE | MRE | MAE | ||
| LSSVM | p = 0.03 g = 0.01 | 0.0172 | 0.0340 | 0.0132 |
| CNN | 4-1 | 0.0168 | 0.0284 | 0.0126 |
| LSTM | 48-48 | 0.0142 | 0.0227 | 0.0101 |
| MWMC-CNN | 10-1 | 0.0108 | 0.0175 | 0.0079 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, X.; Huang, G.; Hao, X.; Yang, Y.; Li, Z. A Synchronous Prediction Model Based on Multi-Channel CNN with Moving Window for Coal and Electricity Consumption in Cement Calcination Process. Sensors 2021, 21, 4284. https://doi.org/10.3390/s21134284
Shi X, Huang G, Hao X, Yang Y, Li Z. A Synchronous Prediction Model Based on Multi-Channel CNN with Moving Window for Coal and Electricity Consumption in Cement Calcination Process. Sensors. 2021; 21(13):4284. https://doi.org/10.3390/s21134284
Chicago/Turabian StyleShi, Xin, Gaolu Huang, Xiaochen Hao, Yue Yang, and Ze Li. 2021. "A Synchronous Prediction Model Based on Multi-Channel CNN with Moving Window for Coal and Electricity Consumption in Cement Calcination Process" Sensors 21, no. 13: 4284. https://doi.org/10.3390/s21134284
APA StyleShi, X., Huang, G., Hao, X., Yang, Y., & Li, Z. (2021). A Synchronous Prediction Model Based on Multi-Channel CNN with Moving Window for Coal and Electricity Consumption in Cement Calcination Process. Sensors, 21(13), 4284. https://doi.org/10.3390/s21134284





