4th Order LC-Based Sigma Delta Modulators
Abstract
:1. Introduction
- The Industrial, Scientific and Medical(ISM) radio bands are reserved internationally to be used for industrial, scientific, and medical purposes other than communications [3]. In general, communications equipment operating in these bands must tolerate any interference generated by ISM equipment, and users have no regulatory protection from ISM device operation.
- Advanced Research and Global Observation Satellite (ARGOS) is a global satellite-based location and data-collection system dedicated to studying and protecting Earth’s environment [4]. It allows any mobile object equipped with a compatible transmitter to be located across the world.
- National Environmental Data System—“Sistema Nacional de Dados Ambientais” (SINDA) is the Brazilian data collection system, which has been built to collect environmental data such as temperature, pressure, and ultraviolet (UV) radiations from all Brazilian territory and provide this information to end users as hydroelectric power plants.
- The Medical Implant Communication Service (MICS) is used for diagnostic and therapeutic purposes in implanted medical devices in the human body. For example, MICS devices include implanted cardiac pacemakers and defibrillators as well as a neuromuscular stimulator that help restore sensation, mobility, and other functions to limbs and organs.
- Private Mobile Radio 446 (PMR446) is a part of the radio frequency range which is open and without licensing, used for business and personal use in most countries of the European Union.
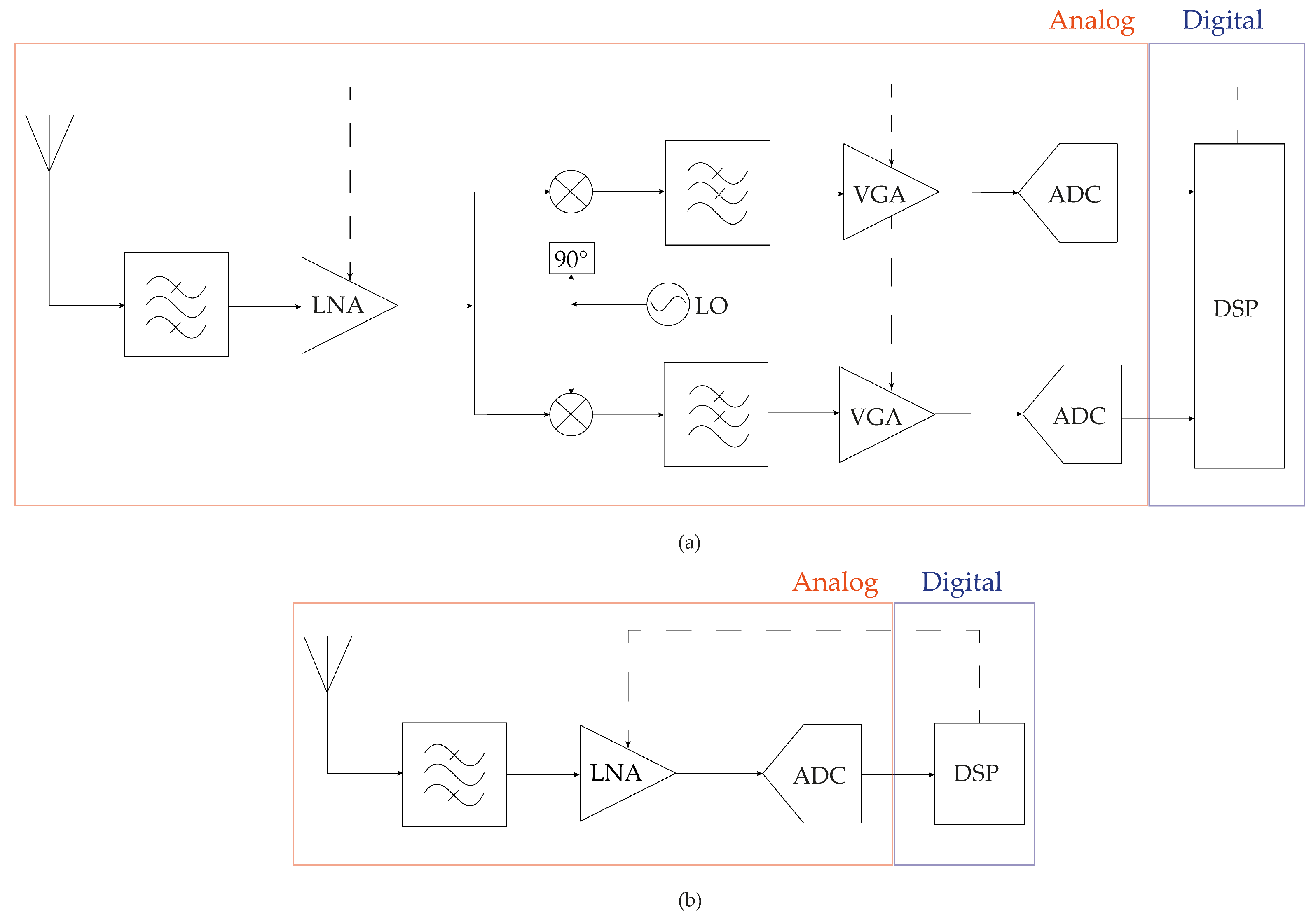
2. Materials and Methods
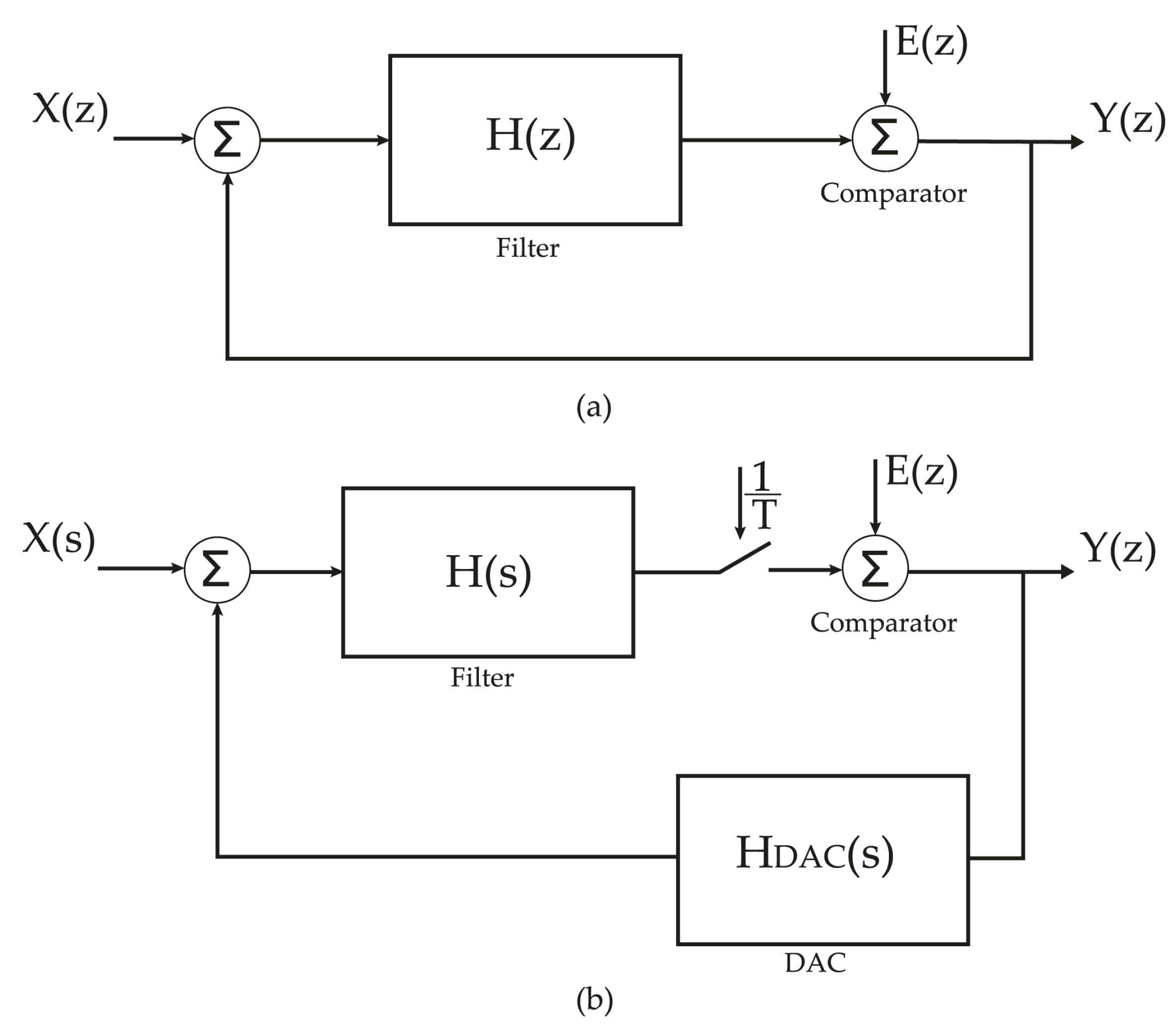
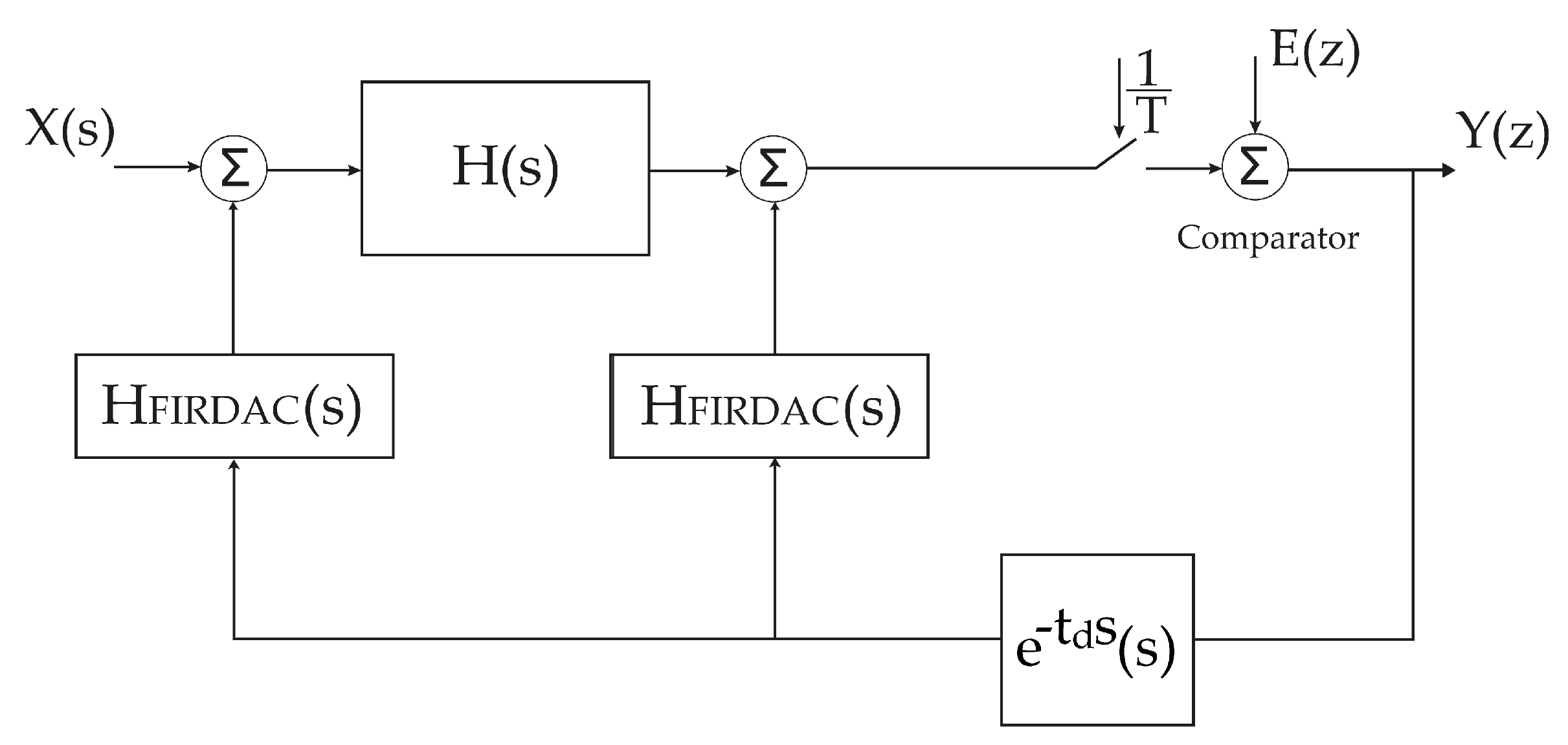
DT to CT Equivalence
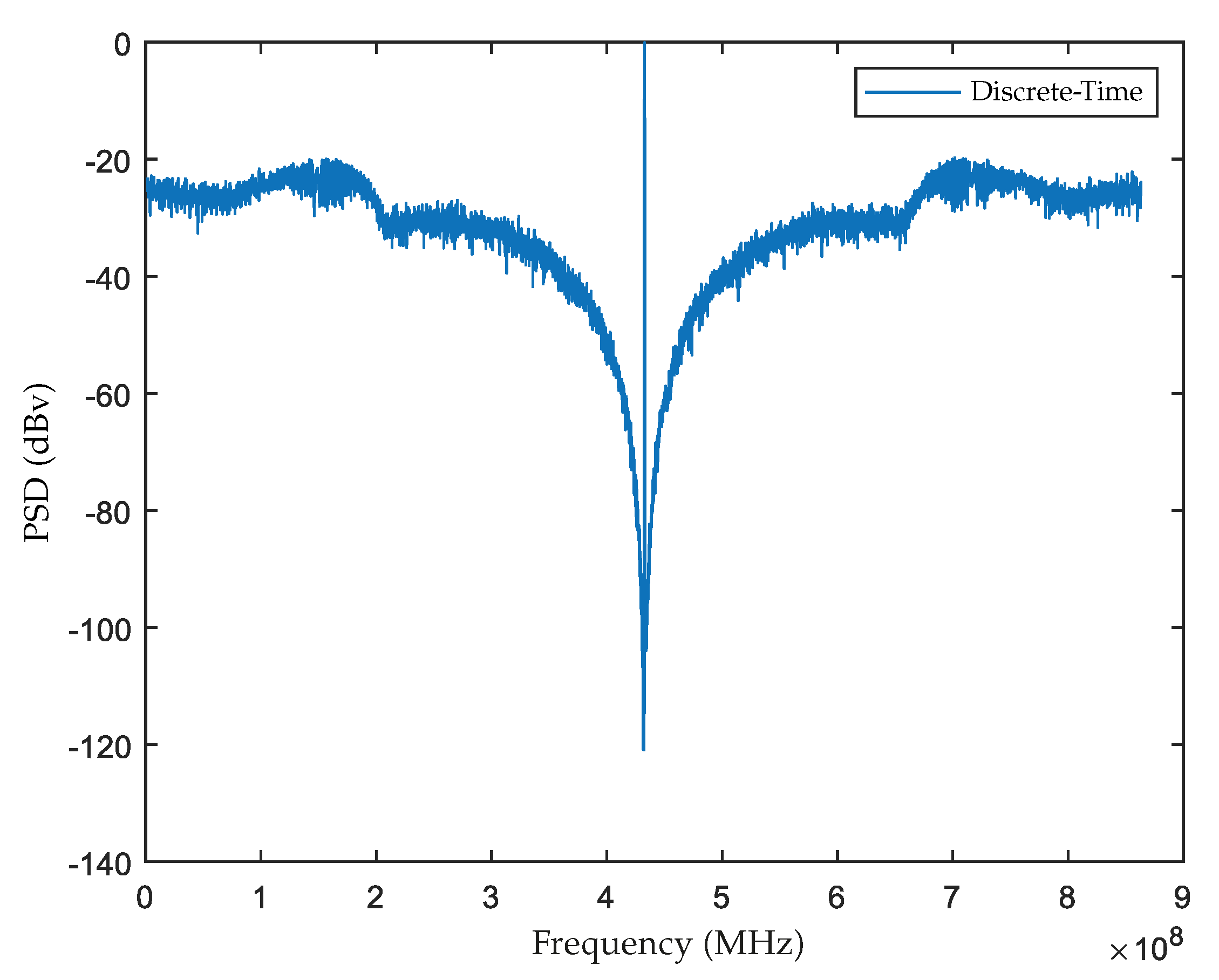
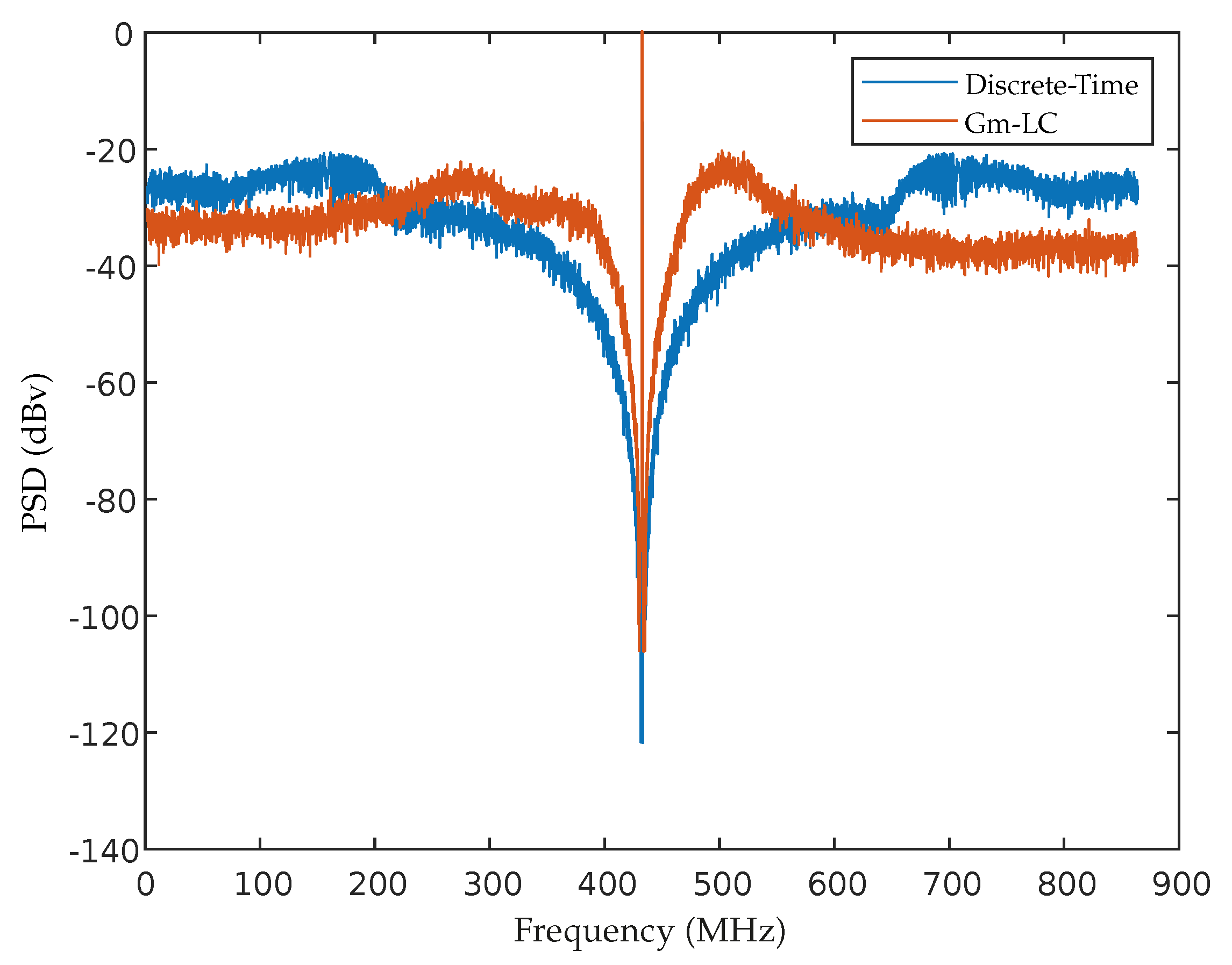
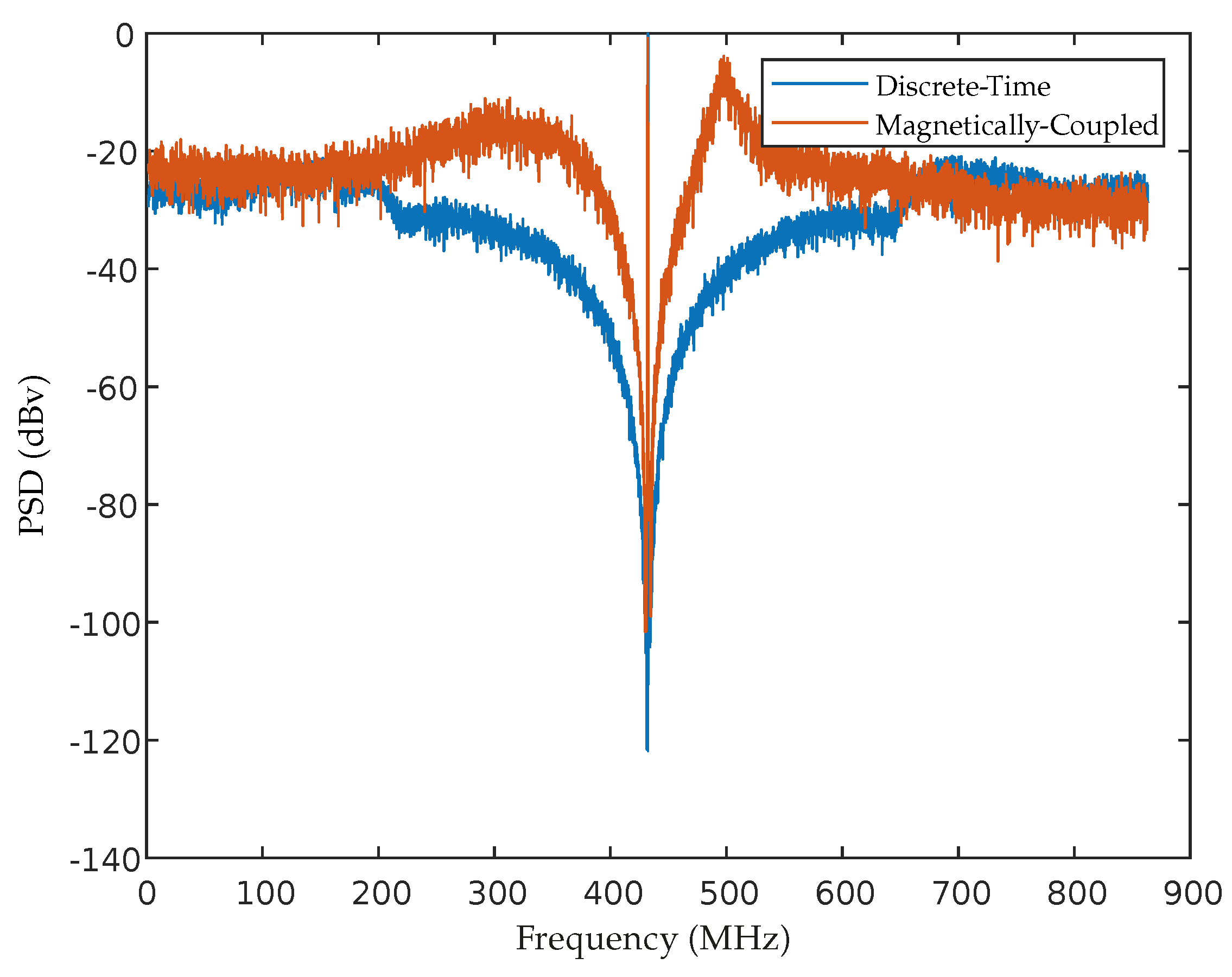
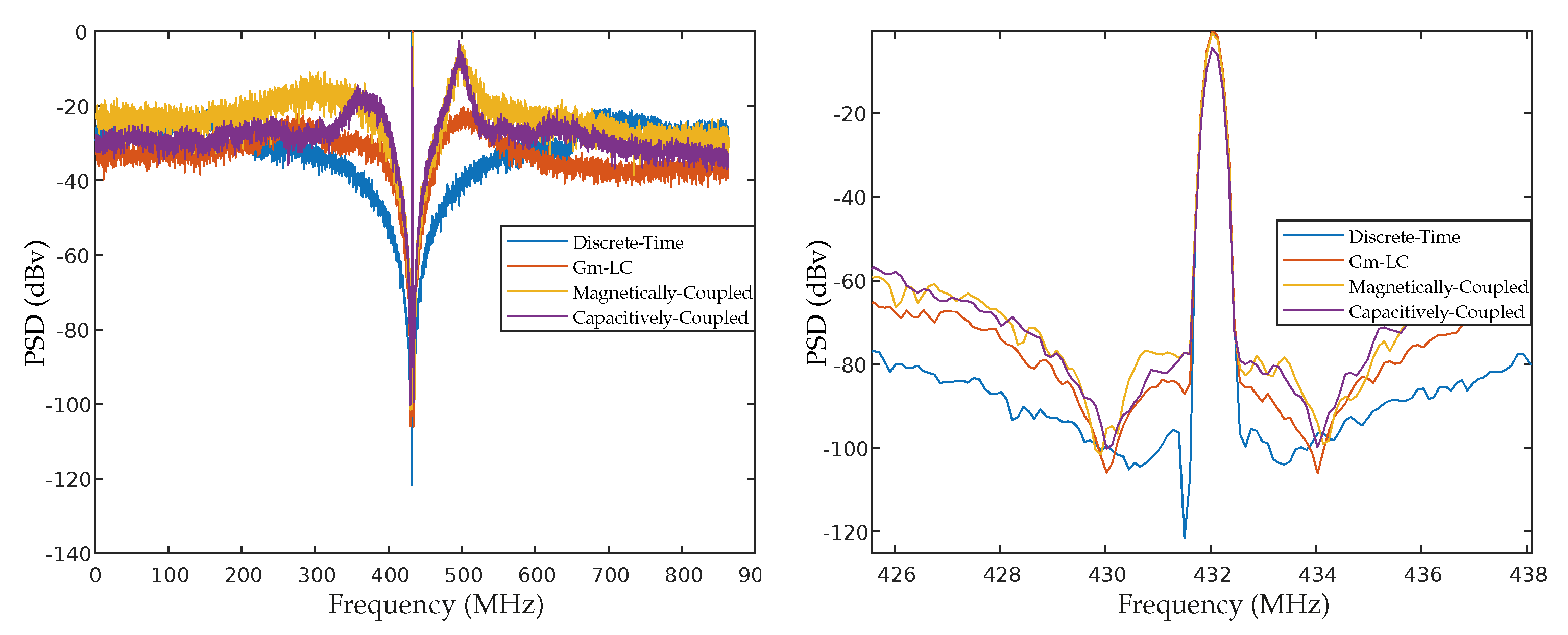
3. Results
3.1. 4th Order Gm-LC M
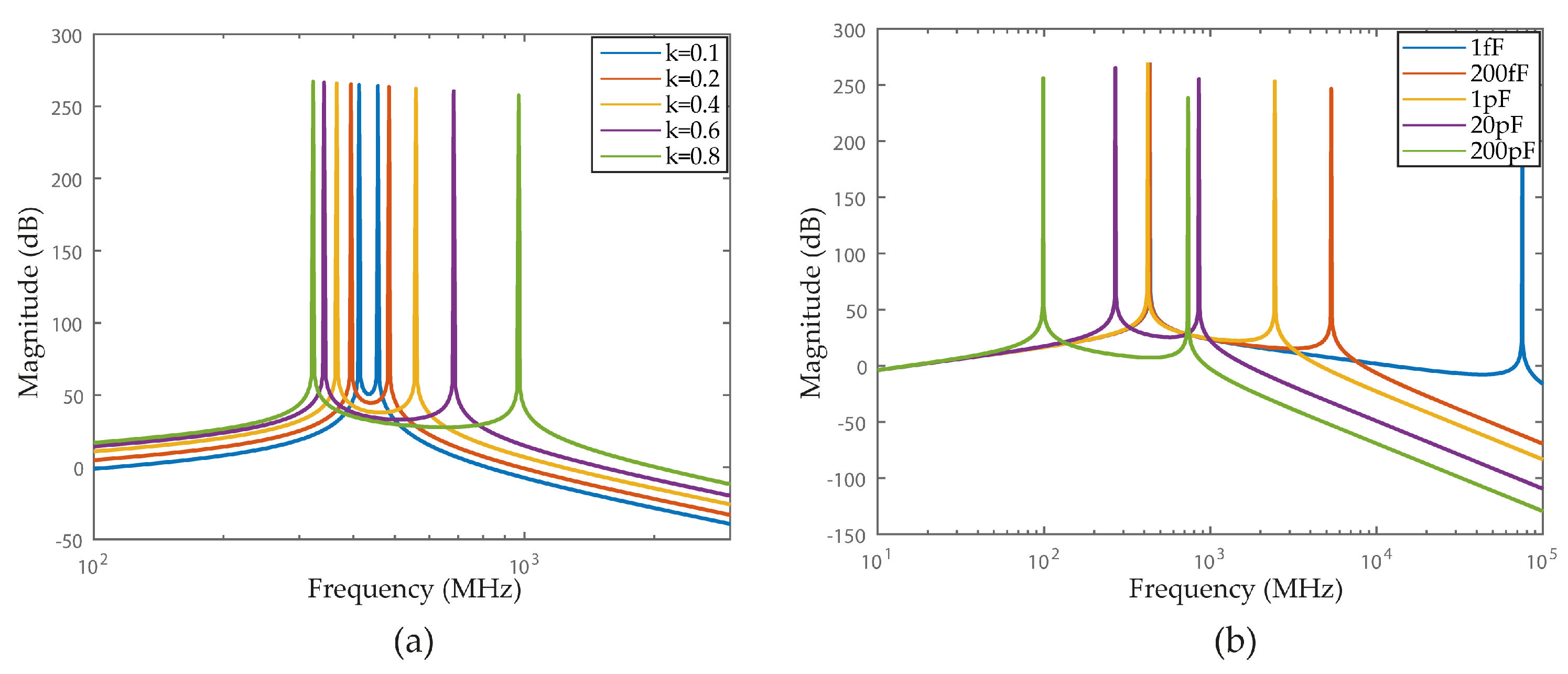
3.2. 4th Order Magnetically Coupled M
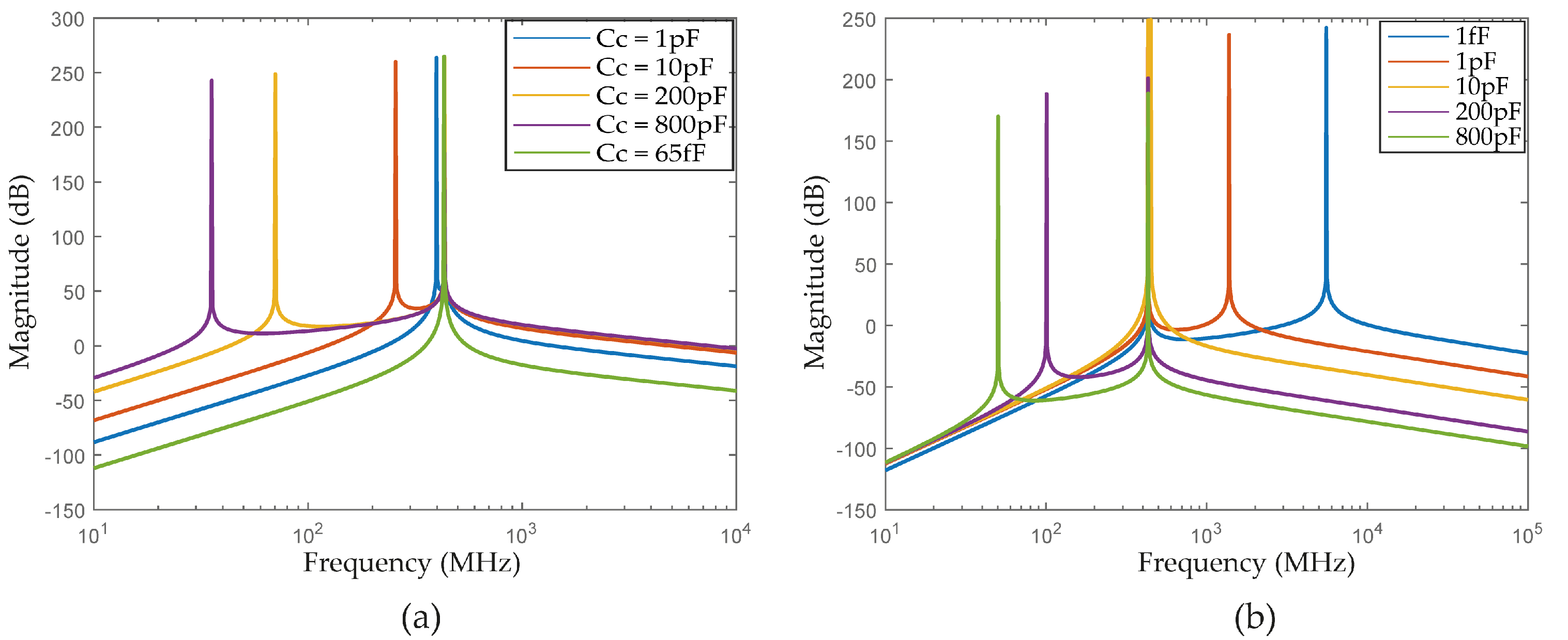
3.3. 4th Order Capacitively Coupled M
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Koch, P.; Prasad, R. The universal handset. IEEE Spectr. 2009, 46, 36–41. [Google Scholar] [CrossRef]
- Belfort, D.R.; Catunda, S.Y.; Aboushady, H. 4th order capacitively-coupled LC-based ΣΔ modulator. Microelectron. J. 2017, 62, 99–107. [Google Scholar] [CrossRef]
- Karl, H.; Willig, A. Protocols and Architectures for Wireless Sensor Networks; John Wiley & Sons: Hoboken, NJ, USA, 2007; ISBN 978-0-470-09510-2. [Google Scholar]
- Richharia, M.; Westbrook, L.D. Satellite Systems for Personal Applications: Concepts and Technology; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 978-1-119-95610-5. [Google Scholar]
- Kenington, P.B.; Astier, L. Power consumption of A/D converters for software radio applications. IEEE Transactions on Vehicular Technology. Analog. Integr. Circ. Signal Process. 2000, 49, 643–650. [Google Scholar] [CrossRef]
- Norsworthy, S.R.; Schreier, R.; Temes, G.C. Delta-Sigma Data Converters Theory, Design, and Simulation; IEEE Press: New York, NY, USA, 1996; ISBN 978-0-780-31045-2. [Google Scholar]
- Beilleau, N.; Aboushady, H.; Montaudon, F.; Cathelin, A. A 1.3 V 26 mW 3.2 Gs/s undersampled LC bandpass ΣΔ ADC for an SDR ISM-band receiver in 130 nm CMOS. In Proceedings of the IEEE Radio Frequency Integrated Circuits Symposium, Boston, MA, USA, 7–9 June 2009; pp. 383–386. [Google Scholar]
- Gupta, S.; Gangopadhyay, D.; Lakdawala, H.; Rudell, J.C.; Allstot, D.J. A QPLL-timed direct-RF sampling band-pass ΣΔ ADC with a 1.2 GHz tuning range in 0.13 µm CMOS. In Proceedings of the IEEE Radio Frequency Integrated Circuits Symposium, Baltimore, MD, USA, 5–7 June 2011; pp. 1–4. [Google Scholar]
- Passian, A.; Imam, N. Nanosystems, Edge Computing, and the Next Generation Computing Systems. Sensors 2019, 19, 4048. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ashry, A.; Aboushady, A. A 3.6 GS/s, 15mW, 50dB SNDR, 28MHz bandwidth RF ΣΔ ADC with a FoM of 1 pJ/bit in 130 nm CMOS. In Proceedings of the IEEE Custom Integrated Circuits Conference (CICC 2011), San Jose, CA, USA, 19–21 September 2011; pp. 1–4. [Google Scholar]
- Beilleau, N.; Kammoun, A.; Aboushady, H. Systematic Design Method for LC Bandpasss SD Modulators with Feedback FIRDACs. In Proceedings of the IEEE International Symposium on Circuits and Systems, Kos, Greece, 21–24 May 2006. [Google Scholar]
- Beilleau, N.; Aboushady, H.; Louerat, M.M. Using finite impulse response feedback DACs to design SD modulators based on LC filters. In Proceedings of the 48th Midwest Symposium on Circuits and Systems, Covington, GA, USA, 7–10 August 2005; pp. 696–699. [Google Scholar]
- Ashry, A.; Aboushady, H. A generalized approach to design CT ΣΔ Ms based on FIR DAC. In Proceedings of the International Symposium on Circuits and Systems, Paris, France, 30 May–2 June 2010; pp. 21–24. [Google Scholar]
- Leuciuc, A. A linear MOS transconductor using source degeneration and adaptive biasing. IEEE Trans. Circ. Syst. II Analog. Digit. Signal Process. 2001, 48, 937–943. [Google Scholar] [CrossRef]
- Sanchez-Sinencio, E.; Silva-Martinez, J. CMOS transconductance amplifiers, architectures and active filters: A tutorial. IEEE Proc.-Circ. Devices Syst. 2000, 147, 3–12. [Google Scholar] [CrossRef] [Green Version]
- Tiebout, M. A Fully Integrated 1.3GHz VCO for GSM in 0.25 um Standard CMOS with a Phasenoise of -142 dBc/Hz at 3 MHz Offset. In Proceedings of the 30th European Microwave Conference, Paris, France, 2–5 October 2000; pp. 1–4. [Google Scholar]
- Mohieldin, A.; Sanchez-Sinencio, E.; Silva-Martinez, J. A 2.7 V, 1.8 GHz, 4th order tunable LC bandpass filter with +/-0.25 dB passband ripple. In Proceedings of the 28th European Solid-State Circuits Conference, Florence, Italy, 24–26 September 2002; pp. 343–346. [Google Scholar]
- Aboushady, H.; Louerat, M.M. Systematic approach for discrete time to continuous-time transformation of ΣD modulators. Proceedings of IEEE International Symposium on Circuits and Systems, Phoenix-Scottsdale, AZ, USA, 26–29 May 2002; pp. 229–232. [Google Scholar]
- Aboushady, H. Design for Reuse of Current-Mode Continuous-Time SD Analog-to-Digital Converters. Ph.D. Thesis, University of Paris VI, Paris, France, 2002. [Google Scholar]
- Shoaei, O.; Snelgrove, W. Optimal (bandpass) continuous-time ΣΔ modulator. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS’94), London, UK, 30 May–2 June 1994; Volume 5, pp. 489–492. [Google Scholar]
- Schreier, R. Delta SigmaToolbox. MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/19-delta-sigma-toolbox (accessed on 10 October 2022).
- Kuhn, W.B.; Stephenson, F.W.; Elshabini-Riad, A. Dynamic range of high-Q OTA-C and enhanced-Q LC RF bandpass filters. In Proceedings of the 37th Midwest Symposium on Circuits and Systems, Lafayette, LA, USA, 3–5 August 1994; pp. 767–771. [Google Scholar]
- Li, D.; Tsividis, Y. Active LC filters on silicon. IEEE Proc.-Circ. Devices Syst. 2000, 147, 49–56. [Google Scholar] [CrossRef]
- Ashry, A.; Aboushady, A. A 4th order 3.6 GS/s RF/spl sigma//spl delta/ADC with a FoM of 1 pJ/bit. IEEE Trans. Circ. Syst. 2013, 60, 2606–2617. [Google Scholar] [CrossRef]
- Chae, H.; Flynn, M.P. A 69 dB SNDR, 25 MHz BW, 800 MS/s Continuous-Time Bandpass ΔΣ Modulator Using a Duty-Cycle-Controlled DAC for Low Power and Reconfigurability. IEEE J. Solid-State Circ. 2016, 51, 649–659. [Google Scholar] [CrossRef]
- Sayed, A.; Badran, T.; Louërat, M.; Aboushady, H. A 1.5-to-3.0 GHz Tunable RF Sigma-Delta ADC With a Fixed Set of Coefficients and a Programmable Loop Delay. IEEE Trans. Circ. Syst. II Express Briefs 2020, 67, 1559–1563. [Google Scholar] [CrossRef]
- Davoudzadeh, N.; Tafazzoli, M.; Sayeh, M.R. Optical delta sigma modulator system design: The best approach for THz A/D conversion. In Proceedings of the Global Symposium on Millimeter-Waves (GSMM 2015), Montreal, QC, Canada, 25–27 May 2015; pp. 1–3. [Google Scholar]
- Lin, W.; Zhang, Y.; Gao, G.; Liu, H.; Yuan, X. FAST telescope optical transmission system based on Delta-Sigma Modulation. In Proceedings of the International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB), Paris, France, 27–29 October 2020; pp. 1–5. [Google Scholar]



| Ref. | Frequency Range (MHz) | Channel Bandwidth (kHz) | Application |
|---|---|---|---|
| ARGOS | 401.635–401.665 | 30 | Active RC |
| SINDA | 401.605–401.635 | 30 | Satellite |
| MICS | 401.0–406.0 | 300 | Medical |
| ISM-433 | 433.050–434.790 | 1840 | any |
| PMR-466 | 446.0–446.2 | 12.5 | Voice |
| KDR-444 | 444.6–444.975 | 16 | Voice |
| FIRDACs | Coefficient 0 | Coefficient 1 | Coefficient 2 | Coefficient 3 |
|---|---|---|---|---|
| FIRDACm | −0.27 | −0.27 | −0.21 | −0.21 |
| FIRDACc | −0.52 | 0.00 | 0.19 | 0.00 |
| FIRDACs | Coefficient 0 | Coefficient 1 | Coefficient 2 | Coefficient 3 |
|---|---|---|---|---|
| FIRDACm | −1.0 | 1.19 | −0.85 | 0.94 |
| FIRDACc | −0.61 | 0.15 | 0.13 | 0.00 |
| FIRDACs | Coefficient 0 | Coefficient 1 | Coefficient 2 | Coefficient 3 |
|---|---|---|---|---|
| FIRDACm | −0.82 | 1.19 | −0.60 | 0.97 |
| FIRDACc | −0.90 | 0.72 | −0.15 | 0.00 |
| Ref. | [This Work] | [Ashry] [24] 2013 | [Chae] [25] 2016 | [Belfort] [2] 2017 | [Sayed] [26] 2020 |
|---|---|---|---|---|---|
| Architecture | Gm-LC | Magnetic Coupling | Capacitive Coupling | Gm-LC | Active RC | Capacitive Coupling | LC based |
| Order | 4 | 4 | 6 | 4 | 2 |
| Tuning range (GHz) | – | – | 0.180–0.20 | 0.40–0.44 | 1.50–3.00 |
| Sampling Frequency, (GHz) | 1.72 | 0.36 | 0.80 | 0.58 | 6.00–12.00 |
| Center Frequency, (GHz) | 0.432 | 0.90 | 0.40–0.44 | 0.40–0.44 | 1.50–3.00 |
| 4 | 4 | 4–4/3 | 4/3 | 1/4 | |
| Bandwidth, BW (MHz) | 4.00 | 28.13 | 25.55 | 4.50 | 47.00–93.00 |
| SNR (dB) | 51.39|48.48|46.50 | 50.00 | 69.00 | 50.00 | 37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lima, E.C.d.O.; Soares, A.W.A.; Belfort, D.R. 4th Order LC-Based Sigma Delta Modulators. Sensors 2022, 22, 8915. https://doi.org/10.3390/s22228915
Lima ECdO, Soares AWA, Belfort DR. 4th Order LC-Based Sigma Delta Modulators. Sensors. 2022; 22(22):8915. https://doi.org/10.3390/s22228915
Chicago/Turabian StyleLima, Evelyn Cristina de Oliveira, Antonio Wallace Antunes Soares, and Diomadson Rodrigues Belfort. 2022. "4th Order LC-Based Sigma Delta Modulators" Sensors 22, no. 22: 8915. https://doi.org/10.3390/s22228915
APA StyleLima, E. C. d. O., Soares, A. W. A., & Belfort, D. R. (2022). 4th Order LC-Based Sigma Delta Modulators. Sensors, 22(22), 8915. https://doi.org/10.3390/s22228915






