Automatic Post-Stroke Severity Assessment Using Novel Unsupervised Consensus Learning for Wearable and Camera-Based Sensor Datasets
Abstract
:1. Introduction
- The function of the affected hand in post-stroke patients (level of severity) was investigated using unsupervised learning.
- The general movements categorized as activities of daily living, such as holding a cup and drinking, eating apples, answering the phone, etc., were utilized.
- For the first time, position data in the frequency domain was used in addition to the acceleration data.
- The novel labeling method for each cluster using trunk displacement is one of the main contributions made by this study.
- In the study, the proposed method investigated not only wearable datasets but also camera-based datasets.
2. Related-Work
2.1. Wearable Sensors
2.2. Camera-Based Sensors
3. Clustering Analysis
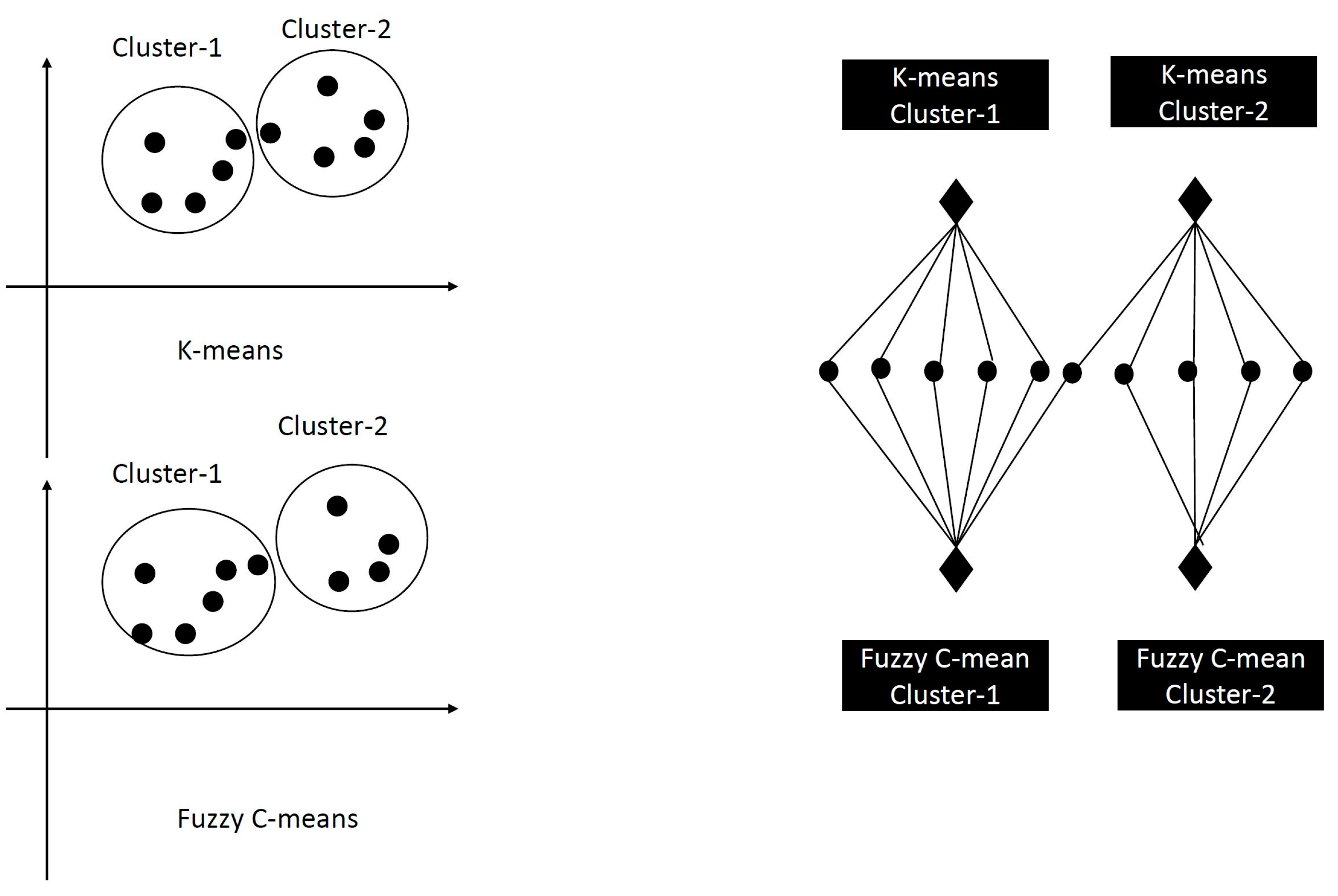
3.1. K-Means Clustering
3.2. Fuzzy C-Means Clustering
3.3. SOM Clustering
3.4. Hierarchical Clustering
3.5. Spectral Clustering:
3.6. Gaussian Mixture Models Clustering:
3.7. DBScan Clustering:
- Core points: A point x in D is a core point if it has at least MinPts points in its eps-neighborhood, including itself.
- Border points: A point y in D is a border point if it is not a core point but has at least one core point within its eps-neighborhood.
- Noise points: A point z in D is a noise point if it is neither a core nor a border point.
3.8. OPTICS Clustering:
4. The Consensus Solvers
4.1. Meta-Clustering Algorithm (MCLA) Consensus Solver
4.2. HyperGraph Partitioning Algorithm (HGPA) Consensus Solver
4.3. Cluster-based Similarity Partitioning Algorithm (CSPA) Consensus Solver
4.4. Hybrid Bipartite Graph Formulation (HBGF) Consensus Solver
5. The Proposed Post-Stroke Severity Assessment Model using Modified NMF-Consensus Solver (PSA-MNMF)
5.1. The Modified Nonnegative Matric Factorization (MNMF) Consensus Solver
5.2. Exhaustive Search
5.3. THE PSA-MNMF Consensus Clustering Algorithm
| Algorithm 1: PSA-MNMF |
| Input: Dataset A={a1,…., an}, a set of partitions B of data points B = {b1,b2, ….., bt} such that each partition B consists of a set of clustering Dt= {d1t, d2t, …., dkt} that uses a selected clustering methodology. Output: The set H of B heterogeneous clusterings that included the 10 best and highest F-scores (or performance metrics α) and appeared in all 100 runs when using the exhaustive search method. Initialization: Calculate the X-cluster= {The results of each clustering Initialize H= {}. Define the connectivity matric CM as follows: Define a matrix Nixk such that in each row only “1” can exist and the rest of the values should be zeros. Calculate the NNT. If i belongs to k, the results will equal 1, otherwise they will equal zero. Define L as L = NTN. Begin , where NTN=1 Step 5: The exhaustive method finds the best performance metric from among the top 10 recorded combinations. Step 4: Steps 1-4 are repeated 100 times. Step 6: The final consensus clustering solution assigns each data point in the input data set to a consensus cluster. Step 7: The algorithm returns H and performance metrics α (including F-score, accuracy, precision, and recall) End |
6. Data, Materials, and Methods
7. Data Preprocessing
7.1. Wearable Sensors (Dataset 1)
7.2. Camera-Based Sensors (Dataset-2)
7.3. Trunk Displacement Measurement
7.4. Data Labeling
8. Experimental Analysis and Results
8.1. The Averaged Normalized Mutual Information (ANMI)
8.1.1. Performance Evaluation: Wearable Sensors (Dataset-1)
8.1.2. Performance Evaluation: Camera-Based Data (Dataset 2)
9. Discussion
10. Conclusions and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Oubre, B.; Daneault, J.-F.; Jung, H.-T.; Whritenour, K.; Miranda, J.G.V.; Park, J.; Ryu, T.; Kim, Y.; Lee, S.I. Estimating Upper-Limb Impairment Level in Stroke Survivors Using Wearable Inertial Sensors and a Minimally-Burdensome Motor Task. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 601–611. [Google Scholar] [CrossRef] [PubMed]
- Singer, B.; Garcia-Vega, J. The Fugl-Meyer Upper Extremity Scale. J. Physiother. 2016, 63, 53. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, S.I.; Adans-Dester, C.P.; Grimaldi, M.; Dowling, A.V.; Horak, P.C.; Black-Schaffer, R.M.; Bonato, P.; Gwin, J.T. Enabling Stroke Rehabilitation in Home and Community Settings: A Wearable Sensor-Based Approach for Upper-Limb Motor Training. IEEE J. Transl. Eng. Health Med. 2018, 6, 2100411. [Google Scholar] [CrossRef] [PubMed]
- Psychometric Comparisons of 2 Versions of the Fugl-Meyer Motor Scale and 2 Versions of the Stroke Rehabilitation Assessment of Movement. Available online: https://journals.sagepub.com/doi/epdf/10.1177/1545968308315999 (accessed on 22 January 2023).
- Lee, S.; Lee, Y.-S.; Kim, J. Automated Evaluation of Upper-Limb Motor Function Impairment Using Fugl-Meyer Assessment. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 26, 125–134. [Google Scholar] [CrossRef]
- Tanaka, K.; Yano, H. Errors of Visual Judgement in Precision Measurements. Ergonomics 1984, 27, 767–780. [Google Scholar] [CrossRef]
- van Beers, R.J.; Haggard, P.; Wolpert, D.M. The Role of Execution Noise in Movement Variability. J. Neurophysiol. 2004, 91, 1050–1063. [Google Scholar] [CrossRef]
- Harbourne, R.T.; Stergiou, N. Movement Variability and the Use of Nonlinear Tools: Principles to Guide Physical Therapist Practice. Phys. Ther. 2009, 89, 267–282. [Google Scholar] [CrossRef] [Green Version]
- Razfar, N.; Kashef, R.; Mohammadi, F. A Comprehensive Overview on IoT-Based Smart Stroke Rehabilitation Using the Advances of Wearable Technology. In Proceedings of the 2021 IEEE 23rd Int Conf on High Performance Computing & Communications; Cloud & Big Data Systems & Application (HPCC/DSS/SmartCity/DependSys), Haikou, China, 20–22 December 2021; pp. 1359–1366. [Google Scholar]
- Sacco, R.L.; Adams, R.; Albers, G.; Alberts, M.J.; Benavente, O.; Furie, K.; Goldstein, L.B.; Gorelick, P.; Halperin, J.; Harbaugh, R. Guidelines for Prevention of Stroke in Patients with Ischemic Stroke or Transient Ischemic Attack: A Statement for Healthcare Professionals from the American Heart Association/American Stroke Association Council on Stroke: Co-Sponsored by the Council on Cardiovascular Radiology and Intervention: The American Academy of Neurology Affirms the Value of This Guideline. Stroke 2006, 37, 577–617. [Google Scholar] [CrossRef]
- Billinger, S.A.; Arena, R.; Bernhardt, J.; Eng, J.J.; Franklin, B.A.; Johnson, C.M.; MacKay-Lyons, M.; Macko, R.F.; Mead, G.E.; Roth, E.J. Physical Activity and Exercise Recommendations for Stroke Survivors: A Statement for Healthcare Professionals from the American Heart Association/American Stroke Association. Stroke 2014, 45, 2532–2553. [Google Scholar] [CrossRef] [Green Version]
- Simbaña, E.D.O.; Baeza, P.S.-H.; Huete, A.J.; Balaguer, C. Review of Automated Systems for Upper Limbs Functional Assessment in Neurorehabilitation. IEEE Access 2019, 7, 32352–32367. [Google Scholar] [CrossRef]
- Zhou, H.; Hu, H. Human Motion Tracking for Rehabilitation—A Survey. Biomed. Signal Process. Control 2008, 3, 1–18. [Google Scholar] [CrossRef]
- Paulich, M.; Schepers, M.; Rudigkeit, N.; Bellusci, G. Xsens MTw Awinda: Miniature Wireless Inertial-Magnetic Motion Tracker for Highly Accurate 3D Kinematic Applications; Xsens: Enschede, The Netherlands, 2018. [Google Scholar]
- Chae, S.H.; Kim, Y.; Lee, K.-S.; Park, H.-S. Development and Clinical Evaluation of a Web-Based Upper Limb Home Rehabilitation System Using a Smartwatch and Machine Learning Model for Chronic Stroke Survivors: Prospective Comparative Study. JMIR mHealth uHealth 2020, 8, e17216. [Google Scholar] [CrossRef]
- Panwar, M.; Biswas, D.; Bajaj, H.; Jöbges, M.; Turk, R.; Maharatna, K.; Acharyya, A. Rehab-Net: Deep Learning Framework for Arm Movement Classification Using Wearable Sensors for Stroke Rehabilitation. IEEE Trans. Biomed. Eng. 2019, 66, 3026–3037. [Google Scholar] [CrossRef]
- Liu, X.; Rajan, S.; Ramasarma, N.; Bonato, P.; Lee, S.I. The Use of a Finger-Worn Accelerometer for Monitoring of Hand Use in Ambulatory Settings. IEEE J. Biomed. Health Inform. 2019, 23, 599–606. [Google Scholar] [CrossRef]
- Kaku, A.; Parnandi, A.; Venkatesan, A.; Pandit, N.; Schambra, H.; Fernandez-Granda, C. Towards Data-Driven Stroke Rehabilitation via Wearable Sensors and Deep Learning. In Proceedings of the 5th Machine Learning for Healthcare Conference, PMLR, City, Country, 18 September 2020; pp. 143–171. [Google Scholar]
- Sapienza, S.; Adans-Dester, C.; O’Brien, A.; Vergara-Diaz, G.; Lee, S.; Patel, S.; Black-Schaffer, R.; Zafonte, R.; Bonato, P.; Meagher, C.; et al. Using a Minimum Set of Wearable Sensors to Assess Quality of Movement in Stroke Survivors. In Proceedings of the 2017 IEEE/ACM International Conference on Connected Health: Applications, Systems and Engineering Technologies (CHASE), Philadelphia, PA, USA, 17–19 July 2017; pp. 284–285. [Google Scholar]
- Adans-Dester, C.; Hankov, N.; O’Brien, A.; Vergara-Diaz, G.; Black-Schaffer, R.; Zafonte, R.; Dy, J.; Lee, S.I.; Bonato, P. Enabling Precision Rehabilitation Interventions Using Wearable Sensors and Machine Learning to Track Motor Recovery. NPJ Digit. Med. 2020, 3, 121. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Xiong, D.; Guo, L.; Wang, J. A Remote Quantitative Fugl-Meyer Assessment Framework for Stroke Patients Based on Wearable Sensor Networks. Comput. Methods Programs Biomed. 2016, 128, 100–110. [Google Scholar] [CrossRef] [PubMed]
- Lucas, A.; Hermiz, J.; Labuzetta, J.; Arabadzhi, Y.; Karanjia, N.; Gilja, V. Use of Accelerometry for Long Term Monitoring of Stroke Patients. IEEE J. Transl. Eng. Health Med. 2019, 7, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Guan, Y.; Shi, J.Q.; Du, X.-L.; Eyre, J. Designing Compact Features for Remote Stroke Rehabilitation Monitoring Using Wearable Accelerometers. CCF Trans. Pervasive Comput. Interact. 2022, 5, 206–225. [Google Scholar] [CrossRef]
- Meng, L.; Zhang, A.; Chen, C.; Wang, X.; Jiang, X.; Tao, L.; Fan, J.; Wu, X.; Dai, C.; Zhang, Y. Exploration of Human Activity Recognition Using a Single Sensor for Stroke Survivors and Able-Bodied People. Sensors 2021, 21, 799. [Google Scholar] [CrossRef]
- Jiang, Y.; Qin, Y.; Kim, I.; Wang, Y. Towards an IoT-Based Upper Limb Rehabilitation Assessment System. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju, Repulic of Korea, 11–15 July 2017; pp. 2414–2417. [Google Scholar]
- van Meulen, F.B.; Reenalda, J.; Buurke, J.H.; Veltink, P.H. Assessment of Daily-Life Reaching Performance after Stroke. Ann. Biomed. Eng. 2015, 43, 478–486. [Google Scholar] [CrossRef]
- Li, H.-T.; Huang, J.-J.; Pan, C.-W.; Chi, H.-I.; Pan, M.-C. Inertial Sensing Based Assessment Methods to Quantify the Effectiveness of Post-Stroke Rehabilitation. Sensors 2015, 15, 16196–16209. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Patel, S.; Hughes, R.; Hester, T.; Stein, J.; Akay, M.; Dy, J.G.; Bonato, P. A Novel Approach to Monitor Rehabilitation Outcomes in Stroke Survivors Using Wearable Technology. Proc. IEEE 2010, 98, 450–461. [Google Scholar] [CrossRef]
- Del Din, S.; Patel, S.; Cobelli, C.; Bonato, P. Estimating Fugl-Meyer Clinical Scores in Stroke Survivors Using Wearable Sensors. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 5839–5842. [Google Scholar]
- Chaeibakhsh, S.; Phillips, E.; Buchanan, A.; Wade, E. Upper Extremity Post-Stroke Motion Quality Estimation with Decision Trees and Bagging Forests. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 4585–4588. [Google Scholar]
- Wang, J.; Yu, L.; Wang, J.; Guo, L.; Gu, X.; Fang, Q. Automated Fugl-Meyer Assessment Using SVR Model. In Proceedings of the 2014 IEEE International Symposium on Bioelectronics and Bioinformatics (IEEE ISBB 2014), Chung Li, Taiwan, 11–14 April 2014; pp. 1–4. [Google Scholar]
- Lee, S.I.; Jung, H.-T.; Park, J.; Jeong, J.; Ryu, T.; Kim, Y.; dos Santos, V.S.; Miranda, J.G.V.; Daneault, J.-F. Towards the Ambulatory Assessment of Movement Quality in Stroke Survivors Using a Wrist-Worn Inertial Sensor. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 2825–2828. [Google Scholar]
- Kim, W.-S.; Cho, S.; Baek, D.; Bang, H.; Paik, N.-J. Upper Extremity Functional Evaluation by Fugl-Meyer Assessment Scoring Using Depth-Sensing Camera in Hemiplegic Stroke Patients. PLoS ONE 2016, 11, e0158640. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Otten, P.; Kim, J.; Son, S.H. A Framework to Automate Assessment of Upper-Limb Motor Function Impairment: A Feasibility Study. Sensors 2015, 15, 20097–20114. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, S.-H.; Song, M.; Kim, J. Towards Clinically Relevant Automatic Assessment of Upper-Limb Motor Function Impairment. In Proceedings of the 2016 IEEE-EMBS International Conference on Biomedical and Health Informatics (BHI), Las Vegas, NV, USA, 24–27 February 2016; pp. 148–151. [Google Scholar]
- Olesh, E.V.; Yakovenko, S.; Gritsenko, V. Automated Assessment of Upper Extremity Movement Impairment Due to Stroke. PLoS ONE 2014, 9, e104487. [Google Scholar] [CrossRef] [PubMed]
- Zhi, T.; Meng, C.; Fu, L. Design of Intelligent Rehabilitation Evaluation Scale for Stroke Patients Based on Genetic Algorithm and Extreme Learning Machine. J. Sens. 2022, 2022, 9323152. [Google Scholar] [CrossRef]
- Bochniewicz, E.M.; Emmer, G.; McLeod, A.; Barth, J.; Dromerick, A.W.; Lum, P. Measuring Functional Arm Movement after Stroke Using a Single Wrist-Worn Sensor and Machine Learning. J. Stroke Cerebrovasc. Dis. 2017, 26, 2880–2887. [Google Scholar] [CrossRef]
- Lee, T.K.M.; Leo, K.-H.; Sanei, S.; Chew, E.; Zhao, L. Triaxial Rehabilitative Data Analysis Incorporating Matching Pursuit. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos, Greece, 28 August–2 September 2017; pp. 434–438. [Google Scholar]
- Park, E.; Lee, K.; Han, T.; Nam, H.S. Automatic Grading of Stroke Symptoms for Rapid Assessment Using Optimized Machine Learning and 4-Limb Kinematics: Clinical Validation Study. J. Med. Internet Res. 2020, 22, e20641. [Google Scholar] [CrossRef]
- Bisio, I.; Garibotto, C.; Lavagetto, F.; Sciarrone, A. When EHealth Meets IoT: A Smart Wireless System for Post-Stroke Home Rehabilitation. IEEE Wirel. Commun. 2019, 26, 24–29. [Google Scholar] [CrossRef]
- Mannini, A.; Trojaniello, D.; Cereatti, A.; Sabatini, A.M. A Machine Learning Framework for Gait Classification Using Inertial Sensors: Application to Elderly, Post-Stroke and Huntington’s Disease Patients. Sensors 2016, 16, 134. [Google Scholar] [CrossRef] [Green Version]
- Butt, A.H.; Zambrana, C.; Idelsohn-Zielonka, S.; Claramunt-Molet, M.; Ugartemendia-Etxarri, A.; Rovini, E.; Moschetti, A.; Molleja, C.; Martin, C.; Salleras, E.O.; et al. Assessment of Purposeful Movements for Post-Stroke Patients in Activites of Daily Living with Wearable Sensor Device. In Proceedings of the 2019 IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB), Siena, Italy, 9–11 July 2019; pp. 1–8. [Google Scholar]
- Bobin, M.; Amroun, H.; Boukalle, M.; Anastassova, M.; Ammi, M. Smart Cup to Monitor Stroke Patients Activities during Everyday Life. In Proceedings of the 2018 IEEE International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData), Halifax, NS, Canada, 30 July–3 August 2018; pp. 189–195. [Google Scholar]
- Woytowicz, E.J.; Rietschel, J.C.; Goodman, R.N.; Conroy, S.S.; Sorkin, J.D.; Whitall, J.; McCombe Waller, S. Determining Levels of Upper Extremity Movement Impairment by Applying a Cluster Analysis to the Fugl-Meyer Assessment of the Upper Extremity in Chronic Stroke. Arch. Phys. Med. Rehabil. 2017, 98, 456–462. [Google Scholar] [CrossRef] [Green Version]
- Jiang, F.; Jiang, Y.; Zhi, H.; Dong, Y.; Li, H.; Ma, S.; Wang, Y.; Dong, Q.; Shen, H.; Wang, Y. Artificial Intelligence in Healthcare: Past, Present and Future. Stroke Vasc. Neurol. 2017, 2. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boukhennoufa, I.; Zhai, X.; Utti, V.; Jackson, J.; McDonald-Maier, K.D. Wearable Sensors and Machine Learning in Post-Stroke Rehabilitation Assessment: A Systematic Review. Biomed. Signal Process. Control 2022, 71, 103197. [Google Scholar] [CrossRef]
- O’Brien, M.K.; Shawen, N.; Mummidisetty, C.K.; Kaur, S.; Bo, X.; Poellabauer, C.; Kording, K.; Jayaraman, A. Activity Recognition for Persons with Stroke Using Mobile Phone Technology: Toward Improved Performance in a Home Setting. J. Med. Internet Res. 2017, 19, e7385. [Google Scholar] [CrossRef] [PubMed]
- Massé, F.; Gonzenbach, R.R.; Arami, A.; Paraschiv-Ionescu, A.; Luft, A.R.; Aminian, K. Improving Activity Recognition Using a Wearable Barometric Pressure Sensor in Mobility-Impaired Stroke Patients. J. Neuroeng. Rehabil. 2015, 12, 72. [Google Scholar] [CrossRef] [Green Version]
- Miller, A.; Quinn, L.; Duff, S.V.; Wade, E. Comparison of Machine Learning Approaches for Classifying Upper Extremity Tasks in Individuals Post-Stroke. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2020, 2020, 4330–4336. [Google Scholar] [CrossRef] [PubMed]
- Hsu, W.-C.; Sugiarto, T.; Lin, Y.-J.; Yang, F.-C.; Lin, Z.-Y.; Sun, C.-T.; Hsu, C.-L.; Chou, K.-N. Multiple-Wearable-Sensor-Based Gait Classification and Analysis in Patients with Neurological Disorders. Sensors 2018, 18, 3397. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.-C.; Chen, S.-F.; Lin, C.-H.; Shih, C.-J.; Lin, A.-C.; Yuan, W.; Li, Y.-C.; Kuo, T.-Y. Detection and Classification of Stroke Gaits by Deep Neural Networks Employing Inertial Measurement Units. Sensors 2021, 21, 1864. [Google Scholar] [CrossRef]
- Derungs, A.; Schuster-Amft, C.; Amft, O. Wearable Motion Sensors and Digital Biomarkers in Stroke Rehabilitation. Curr. Dir. Biomed. Eng. 2020, 6, 229–232. [Google Scholar] [CrossRef]
- Balestra, N.; Sharma, G.; Riek, L.M.; Busza, A. Automatic Identification of Upper Extremity Rehabilitation Exercise Type and Dose Using Body-Worn Sensors and Machine Learning: A Pilot Study. DIB 2021, 5, 158–166. [Google Scholar] [CrossRef]
- Yang, G.; Deng, J.; Pang, G.; Zhang, H.; Li, J.; Deng, B.; Pang, Z.; Xu, J.; Jiang, M.; Liljeberg, P.; et al. An IoT-Enabled Stroke Rehabilitation System Based on Smart Wearable Armband and Machine Learning. IEEE J. Transl. Eng. Health Med. 2018, 6, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Capela, N.A.; Lemaire, E.D.; Baddour, N. Feature Selection for Wearable Smartphone-Based Human Activity Recognition with Able Bodied, Elderly, and Stroke Patients. PLoS ONE 2015, 10, e0124414. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tran, T.; Chang, L.-C.; Almubark, I.; Bochniewicz, E.M.; Shu, L.; Lum, P.; Dromerick, A. Robust Classification of Functional and Nonfunctional Arm Movement after Stroke Using a Single Wrist-Worn Sensor Device. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018. [Google Scholar] [CrossRef]
- Chen, P.-W.; Baune, N.; Zwir, I.; Wang, J.; Swamidass, V.; Wong, A. Measuring Activities of Daily Living in Stroke Patients with Motion Machine Learning Algorithms: A Pilot Study. Int. J. Environ. Res. Public Health 2021, 18, 1634. [Google Scholar] [CrossRef] [PubMed]
- Boukhennoufa, I.; Zhai, X.; McDonald-Maier, K.D.; Utti, V.; Jackson, J. Improving the Activity Recognition Using GMAF and Transfer Learning in Post-Stroke Rehabilitation Assessment. In Proceedings of the 2021 IEEE 19th World Symposium on Applied Machine Intelligence and Informatics (SAMI), Herl’any, Slovakia, 21–23 January 2021; pp. 000391–000398. [Google Scholar]
- Hosseini, Z.-S.; Peyrovi, H.; Gohari, M. The Effect of Early Passive Range of Motion Exercise on Motor Function of People with Stroke: A Randomized Controlled Trial. J. Caring Sci. 2019, 8, 39–44. [Google Scholar] [CrossRef]
- Taub, E.; Crago, J.E.; Uswatte, G. Constraint-Induced Movement Therapy: A New Approach to Treatment in Physical Rehabilitation. Rehabil. Psychol. 1998, 43, 152–170. [Google Scholar] [CrossRef]
- Stinear, C.M.; Lang, C.E.; Zeiler, S.; Byblow, W.D. Advances and Challenges in Stroke Rehabilitation. Lancet Neurol. 2020, 19, 348–360. [Google Scholar] [CrossRef]
- Lun, R.; Zhao, W. A Survey of Applications and Human Motion Recognition with Microsoft Kinect. Int. J. Patt. Recogn. Artif. Intell. 2015, 29, 1555008. [Google Scholar] [CrossRef] [Green Version]
- Gu, Y.; Do, H.; Ou, Y.; Sheng, W. Human Gesture Recognition through a Kinect Sensor. In Proceedings of the 2012 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guangzhou, China, 11–14 December 2012; pp. 1379–1384. [Google Scholar]
- Mohamed, A.A.; Awad, M.I.; Maged, S.A.; Gaber, M.M. Automated Upper Limb Motor Functions Assessment System Using One-Class Support Vector Machine. In Proceedings of the 2021 16th International Conference on Computer Engineering and Systems (ICCES), Cairo, Egypt, 15–16 December 2021; pp. 1–6. [Google Scholar]
- Seo, N.J.; Crocher, V.; Spaho, E.; Ewert, C.R.; Fathi, M.F.; Hur, P.; Lum, S.A.; Humanitzki, E.M.; Kelly, A.L.; Ramakrishnan, V. Capturing Upper Limb Gross Motor Categories Using the Kinect® Sensor. Am. J. Occup. Ther. 2019, 73, 7304205090p1–7304205090p10. [Google Scholar] [CrossRef]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Springer Science & Business Media: New York, NY, USA, 2013; ISBN 978-1-4757-0450-1. [Google Scholar]
- Kuruba Manjunath, Y.S.; Kashef, R.F. Distributed Clustering Using Multi-Tier Hierarchical Overlay Super-Peer Peer-to-Peer Network Architecture for Efficient Customer Segmentation. Electron. Commer. Res. Appl. 2021, 47, 101040. [Google Scholar] [CrossRef]
- Close, L.; Kashef, R. Combining Artificial Immune System and Clustering Analysis: A Stock Market Anomaly Detection Model. JILSA 2020, 12, 83–108. [Google Scholar] [CrossRef]
- Li, M.; Kashef, R.; Ibrahim, A. Multi-Level Clustering-Based Outlier’s Detection (MCOD) Using Self-Organizing Maps. Big Data Cogn. Comput. 2020, 4, 24. [Google Scholar] [CrossRef]
- Ariza Colpas, P.; Vicario, E.; De-La-Hoz-Franco, E.; Pineres-Melo, M.; Oviedo-Carrascal, A.; Patara, F. Unsupervised Human Activity Recognition Using the Clustering Approach: A Review. Sensors 2020, 20, 2702. [Google Scholar] [CrossRef] [PubMed]
- Jia, H.; Ding, S.; Xu, X.; Nie, R. The Latest Research Progress on Spectral Clustering. Neural Comput. Appl. 2014, 24, 1477–1486. [Google Scholar] [CrossRef]
- Patel, E.; Kushwaha, D.S. Clustering Cloud Workloads: K-Means vs Gaussian Mixture Model. Procedia Comput. Sci. 2020, 171, 158–167. [Google Scholar] [CrossRef]
- Li, G.; Wang, Z.; Zhang, Q.; Sun, J. Offline and Online Objective Reduction via Gaussian Mixture Model Clustering. IEEE Trans. Evol. Comput. 2022, 27, 341–354. [Google Scholar] [CrossRef]
- Kashef, R.; Warraich, M. Homogeneous vs. Heterogeneous Distributed Data Clustering: A Taxonomy. In Data Management and Analysis: Case Studies in Education, Healthcare and Beyond; Alhajj, R., Moshirpour, M., Far, B., Eds.; Studies in Big Data; Springer International Publishing: Cham, Switzerland, 2020; pp. 51–66. ISBN 978-3-030-32587-9. [Google Scholar]
- OPTICS: Ordering Points to Identify the Clustering Structure: ACM SIGMOD Record: Vol 28, No 2. Available online: https://dl-acm-org.ezproxy.lib.torontomu.ca/doi/10.1145/304181.304187 (accessed on 28 February 2023).
- Ghosh, J.; Acharya, A. Cluster Ensembles. WIREs Data Min. Knowl. Discov. 2011, 1, 305–315. [Google Scholar] [CrossRef]
- Fern, X.Z.; Brodley, C.E. Solving Cluster Ensemble Problems by Bipartite Graph Partitioning. In Proceedings of the Twenty-First International Conference on Machine Learning, Banff, AB, Canada, 4 July 2004; Association for Computing Machinery: New York, NY, USA, 2004; p. 36. [Google Scholar]
- Li, T.; Ding, C.; Jordan, M.I. Solving Consensus and Semi-Supervised Clustering Problems Using Nonnegative Matrix Factorization. In Proceedings of the Seventh IEEE International Conference on Data Mining (ICDM 2007), Omaha, NE, USA, 28–31 October 2007; pp. 577–582. [Google Scholar]
- Averta, G.; Barontini, F.; Catrambone, V.; Haddadin, S.; Handjaras, G.; Held, J.P.O.; Hu, T.; Jakubowitz, E.; Kanzler, C.M.; Kühn, J.; et al. U-Limb: A Multi-Modal, Multi-Center Database on Arm Motion Control in Healthy and Post-Stroke Conditions. GigaScience 2021, 10, giab043. [Google Scholar] [CrossRef]
- Schwarz, A.; Bhagubai, M.M.C.; Wolterink, G.; Held, J.P.O.; Luft, A.R.; Veltink, P.H. Assessment of Upper Limb Movement Impairments after Stroke Using Wearable Inertial Sensing. Sensors 2020, 20, E4770. [Google Scholar] [CrossRef]
- Schwarz, A.; Bhagubai, M.M.C.; Nies, S.H.G.; Held, J.P.O.; Veltink, P.H.; Buurke, J.H.; Luft, A.R. Characterization of Stroke-Related Upper Limb Motor Impairments across Various Upper Limb Activities by Use of Kinematic Core Set Measures. J. NeuroEng. Rehabil. 2022, 19, 2. [Google Scholar] [CrossRef]
- Rey, V.F.; Hevesi, P.; Kovalenko, O.; Lukowicz, P. Let There Be IMU Data: Generating Training Data for Wearable, Motion Sensor Based Activity Recognition from Monocular RGB Videos. In Proceedings of the Adjunct Proceedings of the 2019 ACM International Joint Conference on Pervasive and Ubiquitous Computing and Proceedings of the 2019 ACM International Symposium on Wearable Computers, London, UK, 9 September 2019; ACM: London, UK, 2019; pp. 699–708. [Google Scholar]
- Schwarz, A.; Veerbeek, J.M.; Held, J.P.O.; Buurke, J.H.; Luft, A.R. Measures of Interjoint Coordination Post-Stroke Across Different Upper Limb Movement Tasks. Front. Bioeng. Biotechnol. 2021, 8, 620805. [Google Scholar] [CrossRef]
- Subramanian, S.K.; Yamanaka, J.; Chilingaryan, G.; Levin, M.F. Validity of Movement Pattern Kinematics as Measures of Arm Motor Impairment Poststroke. Stroke 2010, 41, 2303–2308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brouwer, N.P.; Yeung, T.; Bobbert, M.F.; Besier, T.F. 3D Trunk Orientation Measured Using Inertial Measurement Units during Anatomical and Dynamic Sports Motions. Scand. J. Med. Sci. Sport. 2021, 31, 358–370. [Google Scholar] [CrossRef] [PubMed]
- Cai, S.; Li, G.; Zhang, X.; Huang, S.; Zheng, H.; Ma, K.; Xie, L. Detecting Compensatory Movements of Stroke Survivors Using Pressure Distribution Data and Machine Learning Algorithms. J. Neuroeng. Rehabil. 2019, 16, 131. [Google Scholar] [CrossRef] [PubMed]
- Jayasinghe, S.A.L.; Wang, R.; Gebara, R.; Biswas, S.; Ranganathan, R. Compensatory Trunk Movements in Naturalistic Reaching and Manipulation Tasks in Chronic Stroke Survivors. J. Appl. Biomech. 2021, 37, 215–223. [Google Scholar] [CrossRef] [PubMed]
- Levin, M.F.; Liebermann, D.G.; Parmet, Y.; Berman, S. Compensatory Versus Noncompensatory Shoulder Movements Used for Reaching in Stroke. Neurorehabil. Neural Repair. 2016, 30, 635–646. [Google Scholar] [CrossRef] [Green Version]
- Lo Presti, D.; Zaltieri, M.; Bravi, M.; Morrone, M.; Caponero, M.A.; Schena, E.; Sterzi, S.; Massaroni, C. A Wearable System Composed of FBG-Based Soft Sensors for Trunk Compensatory Movements Detection in Post-Stroke Hemiplegic Patients. Sensors 2022, 22, 1386. [Google Scholar] [CrossRef]
- He, Z.; Xu, X.; Deng, S. K-ANMI: A Mutual Information Based Clustering Algorithm for Categorical Data. Inf. Fusion 2008, 9, 223–233. [Google Scholar] [CrossRef] [Green Version]
- Sano, T.; Migita, T.; Takahashi, N. A Damped Newton Algorithm for Nonnegative Matrix Factorization Based on Alpha-Divergence. In Proceedings of the 2019 6th International Conference on Systems and Informatics (ICSAI), Shanghai, China, 2–4 November 2019; pp. 463–468. [Google Scholar]
- Csiszar, I.; Shields, P. Information Theory and Statistics: A Tutorial. Found. Trends Commun. Inf. Theory 2004, 1, 417–528. [Google Scholar] [CrossRef] [Green Version]







| References | Assessment Tests | Sensors | Result Types | Features | Machine Learning | Purpose |
|---|---|---|---|---|---|---|
| Meulen et al. (2015) [26] | Compared with FMA | 17 IMUs (Xsens system attached to the body) | Correlation | - Hand position relative to the trunk as well as pelvic region - Quantitative analysis of arm and trunk (Distance) | NA | To assess arm movements and compare them with FMA scores |
| Li et al. (2015) [27] | Compared with Wolf Motor Function Test | 2 IMUs attached to the arm and wrist | Correlation | Acceleration and gyroscope | NA | To evaluate motion quality before and after rehabilitation tasks |
| Del Din et al. (2011) [29] | Compared with FMA | Accelerometers to hand, forearm, upper finger, thumb, and sternum. | Prediction | Acceleration | Random Forest | To estimate FMA scores |
| Yu et al. (2016) [21] | Compared with FMA | 2 Accelerometers and 7 flex sensors | Prediction | Amp, Mean, RMS, JERK, ApEn 1 | ELM and SVM to map the result to FMA | To predict FMA scores |
| Chaeibakhsh et al. (2016) [30] | Compared with FMA | 5 APDM Opal motion monitoring sensors (APDM Inc., OR, USA). on the sternum, bilateral, dorsal wrists, and bilateral upper arms proximal to the elbow. | Prediction | -Accelerometer and gyroscope sensor, RMSE value, entropy, and dominant frequency | Decision tree and Bootstrap Aggregation Forest | To estimate FMA scores |
| Wang et al. (2014) [31] | Compared with FMA | 2 Accelerometer attached to elbow and shoulder | Estimation | Acceleration | a Support Vector Regression | To estimate the FMA scores of shoulder and elbow movements |
| Oubre et al. (2020) [1] | Compared with FMA | 9 IMUs (MTw Awinda, Xsens, Netherlands) on the wrist, Sternum | Estimation | Mean velocity Time duration travel distance | DBScan and Regression Model | To estimate FMA scores |
| Lee et al. (2018) [32] | Compared with Functional ability Scale | 9 IMUs (MTw Awinda, Xsens, Netherlands) attached to the wrist | Correlation | Velocity | K-means Cluster | - Utilizes kinematic characteristics of voluntary limb movements. -Focuses on the quality of movement in stroke survivors |
| Patel et al. (2010) [28] | Compared with FAS | Accelerometers attached to the hand, forearm, and upper arm | Prediction | Acceleration | Random Forest | To estimate FAS score |
| Adans-Dester et al. (2020) [20] | FMA and FAS | IMU | Upper limb | Displacement, velocity, acceleration, and jerk | Random Forest | Different ADL tasks to evaluate the FAS and FMA scoring |
| References | Assessments Test | Sensors | Results Type | Features | Machine Learning | Purpose |
|---|---|---|---|---|---|---|
| Kim et al. (2016) [33] | FMA | Kinect camera data | Correlation | Positions, angles, and the distance between two joints (for instance, hand-shoulder, hand-head and elbow-head) | Artificial Neural Network (ANN) | To develop the FMA tool by utilizing a Kinect camera and to classify the 6 FMA upper extremity tasks |
| Mohamed et al.(2021) [65] | FMA | Kinect V1 and Myo armband | N/A | EMG and position data | SVM | Predicting FMA Scores |
| Soe et al. (2019) [66] | Mallet Clinical Rating Scale | Kinect V1 | N/A | Velocity | Rule-based classification | Classifying the Mallet clinical rating scale |
| Lee et al. (2017) [5] | FMA | Kinect, force and resistor sensing hand | Correlation | Acceleration data | Rule-based classifier | Classifying FMA tasks |
| Otten et al. (2015) [34] | FMA | -The Kinect camera pressure sensor (FSR 400 series, Interlink Electronics, Westlake Village, CA, USA) - Glove sensors (a Shimmer inertial measurement unit; IMU, Shimmer, Dublin) - A glove sensor (DG5-VHand glove 3.0, DGTech, Bazzano, Italy) | Prediction | Kinematic features such as finger flexion and extension, joint angle, and supination and pronation of the hand | SVM-Linear SVM-Kernel BNN | To predict 24 out of 33 FMA tasks as 0, 1, or 2 scores. |
| Lee et al. (2016) [35] | FMA | Kinect v2 and force-sensing | Prediction | Joint motion (abduction and adduction, flexion extension, etc.) | Fuzzy-logic classification | To classify movements for FMA prediction purposes. The healthy subjects were used. |
| Olesh et al. (2014) [36] | Arm movements from FMA and Action Research Arm Test | The low-cost motion capture device is called the impulse motion capture system. | Estimation | Joint Angle | Principle Components Analysis (PCA) | Comparing quantitative scores derived from the qualitative clinical scores generated by clinicians |
| Step 1 | Step 2 | Step 3 |
|---|---|---|
| Reaching distally and grasping a glass | Drinking for 3 s | Placing it back in the initial position |
| Reaching distally and grasping a phone | Moving it to the subject’s ear for 3 s | Placing it back in the initial position |
| Reaching distally and grasping a small cup | Drinking for 3 s | Placing it back in the initial position |
| Reaching distally and grasping an apple | Pretending to bite | Placing it back in the initial position |
| Characteristics | Mean (SD)/Count (Camera Sensor) | Mean (SD)/Count (Wearable Sensor) |
|---|---|---|
| Age | 46.77 ± 15.25 | 61.00 ±10.69 |
| Sex | 6 female; 12 male | 5 female; 15 male |
| FMMA-UE | 17.75 ± 2.05 | 46.00 ± 10.16 |
| Affected Hand | 12 right; 8 left | 11 right; 9 left |
| k = 2 | Fuzzy | K-Means | SOM | Gaussian Mixture | DBSCAN | Hierarchical | Spectral | OPTICS | PSA-MNMF |
|---|---|---|---|---|---|---|---|---|---|
| Accuracy | 60.4% ± 0.0001 | 60.7% ± 0.003 | 60.7% ± 0.036 | 58.8% ± 0.0001 | 29.4% ± 0.0001 | 71.5% ± 0.0002 | 59.2% ± 0.001 | 65.5% ± 0.0001 | 75% ± 0.0001 |
| P | 65.8% ± 0.0002 | 65.9% ± 0.003 | 66.3% ± 0.024 | 65.6% ± 0.0001 | 16.2% ± 0.0001 | 69.1% ± 0.0002 | 65.9% ± 0.004 | 55.1% ± 0.0001 | 73.9% ± 0.0001 |
| R | 60.4% ± 0.0001 | 60.7% ± 0.003 | 60.7% ± 0.036 | 58.8% ± 0.0001 | 29.4% ± 0.0001 | 71.5% ± 0.0002 | 59.2% ± 0.001 | 65.5% ± 0.0001 | 75% ± 0.0001 |
| F = score | 61.8% ± 0.0001 | 62.1% ± 0.003 | 61.9% ± 0.034 | 60.4% ± 0.0001 | 14.6% ± 0.0001 | 68.7% ± 0.0001 | 60.7% ± 0.001 | 57% ± 0.0001 | 74% ± 0.0001 |
| k = 2 | Fuzzy | K-Means | SOM | Gaussian Mixture | DBSCAN | Hierarchical | Spectral | OPTICS | PSA-MNMF |
|---|---|---|---|---|---|---|---|---|---|
| Accuracy | 52.2% ± 0.0001 | 52.2% ± 0.0002 | 58.6% ± 0.039 | 57.1% ± 0.0001 | 65% ± 0.0001 | 43.4% ± 0.0001 | 59.7% ± 0.041 | 65% ± 0.0001 | 69.6% ± 0.002 |
| P | 70.1% ± 0.0001 | 70.1% ± 0.0001 | 68.7% ± 0.008 | 67.4% ± 0.0001 | 67% ± 0.0001 | 69% ± 0.0001 | 69.1% ± 0.005 | 48.2% ± 0.0001 | 70.4% ± 0.001 |
| R | 52.2% ± 0.0002 | 52.2% ± 0.0001 | 58.6% ± 0.039 | 57.1% ± 0.0001 | 65% ± 0.0001 | 43.4% ± 0.0001 | 59.7% ± 0.041 | 65% ± 0.0001 | 69.6% ± 0.001 |
| F = score | 52.2% ± 0.0001 | 52.1% ± 0.0001 | 59.7% ± 0.041 | 58.4% ± 0.0001 | 67% ± 0.0001 | 38.4% ± 0.0001 | 60.9% ± 0.042 | 54.6% ± 0.0001 | 68.6% ± 0.001 |
| k = 2 | Fuzzy | K-Means | SOM | Gaussian Mixture | DBSCAN | Hierarchical | Spectral | OPTICS | PSA-MNMF |
|---|---|---|---|---|---|---|---|---|---|
| Accuracy | 58.1% ± 0.011 | 54.4% ± 0.002 | 61.5% ± 0.033 | 55.5% ± 0.0001 | 35.2% ± 0.0001 | 73.3% ± 0.0001 | 61.2% ± 0.004 | 42.5% ± 0.0001 | 74.3% ± 0.001 |
| P | 70.1% ± 0.001 | 70.1% ± 0.004 | 70.4% ± 0.011 | 65.7% ± 0.0001 | 49.6% ± 0.0001 | 75.3% ± 0.0001 | 70.9% ± 0.003 | 47.8% ± 0.0001 | 76.4% ± 0.002 |
| R | 58% ± 0.011 | 54.4% ± 0.002 | 61.5% ± 0.033 | 55.5% ± 0.0001 | 35.2% ± 0.0001 | 73.3% ± 0.0001 | 61.2% ± 0.004 | 42.5% ± 0.0001 | 74.3% ± 0.0019 |
| F = score | 59% ± 0.013 | 54.8% ± 0.003 | 62.7% ± 0.035 | 56.9% ± 0.0001 | 32.2% ± 0.0001 | 73.7% ± 0.0001 | 62.5% ± 0.005 | 44.5% ± 0.0001 | 74.1% ± 0.001 |
| k = 3 | Fuzzy | K-Means | SOM | Gaussian Mixture | DBSCAN | Hierarchical | Spectral | OPTICS | PSA-MNMF |
|---|---|---|---|---|---|---|---|---|---|
| Accuracy | 48.1% ± 0.016 | 46.9% ± 0.005 | 47.8% ± 0.036 | 44.9% ± 0.0001 | 13.1% ±0.0001 | 44.9% ± 0.0001 | 48.8% ± 0.009 | 57.5% ± 0.0001 | 72.1% ± 0.002 |
| P | 60% ± 0.016 | 61.3% ± 0.004 | 57.5% ± 0.026 | 61.3% ± 0.0001 | 16.9% ± 0.0001 | 63.9% ± 0.0001 | 56% ± 0.003 | 48.5% ± 0.0001 | 79.8% ± 0.001 |
| R | 48.1% ± 0.016 | 46.9% ± 0.005 | 47.8% ± 0.036 | 44.9% ± 0.0001 | 13.1% ± 0.0001 | 44.9% ± 0.0001 | 48.8% ± 0.009 | 57.5% ± 0.0001 | 72.1% ± 0.002 |
| F = score | 51.1% ± 0.012 | 50% ± 0.005 | 50.3% ± 0.034 | 47.1% ± 0.0001 | 14.1% ± 0.0001 | 46.4% ± 0.0001 | 51.3% ± 0.008 | 44.3% ± 0.0001 | 72.3% ± 0.001 |
| k = 3 | Fuzzy | K-Means | SOM | Gaussian Mixture | DBSCAN | Hierarchical | Spectral | OPTICS | PSA-MNMF |
|---|---|---|---|---|---|---|---|---|---|
| Accuracy | 46.2% ± 0.0001 | 46.5% ± 0.007 | 45% ± 0.026 | 48% ± 0.0001 | 22.1% ± 0.0001 | 43.6% ± 0.0001 | 38% ± 0.0002 | 51.5% ± 0.0001 | 67.30% ± 0.007 |
| P | 67.4% ± 0.0001 | 67.7% ± 0.004 | 56.6% ± 0.072 | 50% ± 0.0001 | 65.8% ± 0.0001 | 69.5% ± 0.0001 | 68.6% ± 0.0002 | 38.1% ± 0.0001 | 70.30% ± 0.03 |
| R | 46.2% ± 0.0001 | 46.5% ± 0.007 | 45% ± 0.026 | 48% ± 0.0001 | 22.1% ± 0.0001 | 43.6% ± 0.0001 | 38% ± 0.0002 | 51.5% ± 0.0001 | 67.3% ± 0.007 |
| F = score | 47.3% ± 0.0001 | 47.5% ± 0.008 | 45.7% ± 0.03 | 48.6% ± 0.0001 | 12.8% ± 0.0001 | 43% ± 0.0001 | 34.3% ± 0.0002 | 41.9% ± 0.0001 | 66% ± 0.007 |
| k = 3 | Fuzzy | K-Means | SOM | Gaussian Mixture | DBSCAN | Hierarchical | Spectral | OPTICS | PSA-MNMF |
|---|---|---|---|---|---|---|---|---|---|
| Accuracy | 46.2% ± 0.0001 | 46.2% ± 0.005 | 46.6% ± 0.03 | 48.7% ± 0.003 | 22.6% ± 0.0001 | 46.9% ± 0.0001 | 40.3% ± 0.0001 | 46.5% ± 0.0001 | 67.9% ± 0.04 |
| P | 67.7% ± 0.0001 | 68.8% ± 0.007 | 57.5% ± 0.062 | 53.6% ± 0.006 | 27.2% ± 0.0001 | 70.3% ± 0.0002 | 67.5% ± 0.0002 | 35% ± 0.0001 | 70.80% ± 0.053 |
| R | 46.2% ± 0.0001 | 46.2% ± 0.005 | 46.6% ± 0.03 | 48.7% ± 0.003 | 22.6% ± 0.0001 | 46.9% ± 0.0002 | 40.3% ± 0.0001 | 46.5% ± 0.0001 | 67.9% ± 0.01 |
| F = score | 46.4% ± 0.0001 | 46% ± 0.007 | 47.3% ± 0.033 | 49.8% ± 0.003 | 14.8%± 0.0001 | 45.4% ± 0.0001 | 37.6% ± 0.0001 | 39.2% ± 0.0001 | 66.20% ± 0.03 |
| k = 2 | Fuzzy | K-Means | SOM | Gaussian Mixture | DBSCAN | Hierarchical | Spectral | OPTICS | PSA-MNMF |
|---|---|---|---|---|---|---|---|---|---|
| Accuracy | 50.6% ± 0.021 | 49.1% ± 0.001 | 47.6% ± 0.065 | 56.9% ± 0.001 | 35.9% ± 0.0001 | 40.8% ± 0.0001 | 48.5% ± 0.0001 | 45.2% ± 0.0002 | 60.1%± 0.001 |
| P | 50.7% ± 0.022 | 49.1% ± 0.001 | 47.6% ± 0.067 | 57% ± 0.001 | 35.7% ± 0.0001 | 40.8% ± 0.0002 | 48.5% ± 0.0001 | 25.9% ± 0.0010 | 65.6%± 0.003 |
| R | 50.6% ± 0.021 | 49.1% ± 0.001 | 47.6% ± 0.065 | 56.9% ± 0.001 | 35.9% ± 0.0001 | 40.8% ± 0.0001 | 48.5% ± 0.0002 | 45.2% ± 0.0001 | 60.1%± 0.001 |
| F = score | 50.1% ± 0.017 | 48.9% ± 0.001 | 47.3% ± 0.065 | 56.7% ± 0.001 | 35.7% ± 0.0001 | 40.7% ± 0.0001 | 48.4% ± 0.0002 | 31.4% ± 0.0002 | 59.8%± 0.001 |
| k = 2 | Fuzzy | K-Means | SOM | Gaussian Mixture | DBSCAN | Hierarchical | Spectral | OPTICS | PSA-MNMF |
|---|---|---|---|---|---|---|---|---|---|
| Accuracy | 39% ± 0.0001 | 38.9% ± 0.003 | 38.4% ± 0.035 | 36.2% ± 0.0001 | 46.2% ± 0.0001 | 30.5% ± 0.0001 | 49.4% ± 0.0001 | 48.1% ± 0.0001 | 55.3% ± 0.0008 |
| P | 38.4% ± 0.0001 | 38.4% ± 0.003 | 38.1% ± 0.034 | 36.2% ± 0.0002 | 45% ± 0.0001 | 26.6% ± 0.0002 | 24.8% ± 0.0001 | 24.4% ± 0.0002 | 64.1% ± 0.0007 |
| R | 39% ± 0.0001 | 38.9% ± 0.003 | 38.4% ± 0.035 | 36.2% ± 0.0001 | 46.2% ± 0.0001 | 30.5% ± 0.0001 | 49.4% ± 0.0001 | 48.1% ± 0.0001 | 55.4% ± 0.0008 |
| F = score | 38.2% ± 0.0001 | 38.2% ± 0.003 | 38% ± 0.033 | 36.2% ± 0.0001 | 43.1% ± 0.0001 | 27.5% ± 0.0001 | 33% ± 0.0001 | 32.4% ± 0.0001 | 55.5% ± 0.0008 |
| k = 2 | Fuzzy | K-Means | SOM | Gaussian Mixture | DBSCAN | Hierarchical | Spectral | OPTICS | PSA-MNMF |
|---|---|---|---|---|---|---|---|---|---|
| Accuracy | 38.7% ± 0.0001 | 39% ± 0.002 | 37.9% ± 0.046 | 37.5% ± 0.0001 | 47.4% ± 0.0001 | 31.5% ± 0.0002 | 49.4% ± 0.0001 | 56.1% ± 0.0001 | 56.6% ± 0.009 |
| P | 38.2% ± 0.0001 | 38.5% ± 0.002 | 37.6% ± 0.046 | 37.5% ± 0.0002 | 47.1% ± 0.0002 | 28.4% ± 0.0001 | 24.8% ± 0.0002 | 51.9% ± 0.0001 | 57.1% ± 0.0019 |
| R | 38.7% ± 0.0002 | 39% ± 0.002 | 37.9% ± 0.046 | 37.5% ± 0.0001 | 47.4% ± 0.0002 | 31.5% ± 0.0001 | 49.4% ± 0.0001 | 56.1% ± 0.0001 | 56.6% ± 0.001 |
| F = score | 38% ± 0.0001 | 38.3% ± 0.002 | 37.5% ± 0.046 | 37.5% ± 0.0001 | 46.3% ± 0.0002 | 29% ± 0.0002 | 33% ± 0.0002 | 47.4% ± 0.0001 | 55.7% ± 0.002 |
| k = 3 | Fuzzy | K-Means | SOM | Gaussian Mixture | DBSCAN | Hierarchical | Spectral | OPTICS | PSA-MNMF |
|---|---|---|---|---|---|---|---|---|---|
| Accuracy | 50.6% ± 0.019 | 49.1% ± 0.001 | 47.7% ± 0.051 | 56.8% ± 0.002 | 35.9% ± 0.0 | 40.8% ± 0.0 | 48.5% ± 0.013 | 45.2% ± 0.0 | 59.41% ± 0.004 |
| P | 50.6% ± 0.02 | 49.1% ± 0.001 | 47.7% ± 0.052 | 56.9% ± 0.002 | 35.7% ± 0.0 | 40.8% ± 0.0 | 48.5% ± 0.021 | 25.9% ± 0.0 | 75.3% ± 0.0001 |
| R | 50.6% ± 0.019 | 49.1% ± 0.001 | 47.7% ± 0.051 | 56.8% ± 0.002 | 35.9% ± 0.0 | 40.8% ± 0.0 | 48.5% ± 0.013 | 45.2% ± 0.0 | 59.41% ± 0.004 |
| F-score | 50.1% ± 0.016 | 49% ± 0.001 | 47.5% ± 0.05 | 56.6% ± 0.001 | 35.7% ± 0.0 | 40.7% ± 0.0 | 48.4% ± 0.016 | 31.4% ± 0.0 | 58.4% ± 0.0001 |
| K = 3 | Fuzzy | K-Means | SOM | Gaussian Mixture | DBSCAN | Hierarchical | Spectral | OPTICS | PSA-MNMF |
|---|---|---|---|---|---|---|---|---|---|
| Accuracy | 27% ± 0.009 | 26.4% ± 0.01 | 29.1% ± 0.043 | 26.6% ± 0.022 | 23.8% ± 0.0001 | 30.3% ± 0.0001 | 48.9% ± 0.0001 | 14% ± 0.0001 | 54.4% ± 0.0001 |
| P | 51% ± 0.007 | 51.1% ± 0.004 | 47.4% ± 0.06 | 50.8% ± 0.009 | 24.3% ± 0.0001 | 58.5% ± 0.0001 | 24.8% ± 0.0001 | 39.9% ± 0.0001 | 68.1% ± 0.0001 |
| R | 27% ± 0.009 | 26.4% ± 0.01 | 29.1% ± 0.043 | 26.6% ± 0.022 | 23.8% ± 0.0001 | 30.3% ± 0.0001 | 48.9% ± 0.0001 | 14% ± 0.0001 | 54.4% ± 0.0002 |
| F-score | 33.9% ± 0.008 | 33.2% ± 0.007 | 35.8% ± 0.047 | 33.7% ± 0.018 | 24.1% ± 0.0001 | 32.3% ± 0.0001 | 32.9% ± 0.0001 | 17% ± 0.0001 | 55% ± 0.0002 |
| k = 3 | Fuzzy | K-Means | SOM | Gaussian Mixture | DBSCAN | Hierarchical | Spectral | OPTICS | PSA-MNMF |
|---|---|---|---|---|---|---|---|---|---|
| Accuracy | 27.9% ± 0.017 | 26% ± 0.016 | 28.7% ± 0.04 | 33.1% ± 0.002 | 32% ± 0.0001 | 30% ± 0.0001 | 48.6% ± 0.0001 | 43.4% ± 0.0001 | 54.2% ± 0.009 |
| P | 49.4% ± 0.015 | 50.6% ± 0.009 | 47.7% ± 0.052 | 46.8% ± 0.004 | 25.6% ± 0.0001 | 58.7% ± 0.0001 | 24.6% ± 0.0001 | 33.3% ± 0.0001 | 70.9% ± 0.015 |
| R | 27.9% ± 0.017 | 26% ± 0.016 | 28.7% ± 0.04 | 33.1% ± 0.002 | 32% ± 0.0001 | 30% ± 0.0001 | 48.6% ± 0.0001 | 43.4% ± 0.0001 | 54.4% ± 0.07 |
| F = score | 34.4% ± 0.014 | 32.8% ± 0.013 | 35.7% ± 0.043 | 38.4% ± 0.003 | 28.5% ± 0.0001 | 32.4% ± 0.0001 | 32.6% ± 0.0001 | 31.5% ± 0.0001 | 54.1% ± 0.002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Razfar, N.; Kashef, R.; Mohammadi, F. Automatic Post-Stroke Severity Assessment Using Novel Unsupervised Consensus Learning for Wearable and Camera-Based Sensor Datasets. Sensors 2023, 23, 5513. https://doi.org/10.3390/s23125513
Razfar N, Kashef R, Mohammadi F. Automatic Post-Stroke Severity Assessment Using Novel Unsupervised Consensus Learning for Wearable and Camera-Based Sensor Datasets. Sensors. 2023; 23(12):5513. https://doi.org/10.3390/s23125513
Chicago/Turabian StyleRazfar, Najmeh, Rasha Kashef, and Farah Mohammadi. 2023. "Automatic Post-Stroke Severity Assessment Using Novel Unsupervised Consensus Learning for Wearable and Camera-Based Sensor Datasets" Sensors 23, no. 12: 5513. https://doi.org/10.3390/s23125513
APA StyleRazfar, N., Kashef, R., & Mohammadi, F. (2023). Automatic Post-Stroke Severity Assessment Using Novel Unsupervised Consensus Learning for Wearable and Camera-Based Sensor Datasets. Sensors, 23(12), 5513. https://doi.org/10.3390/s23125513






