Microsphere-Based Microsensor for Miniature Motors’ Vibration Measurement
Abstract
:1. Introduction
- (1)
- We combine a stretched single-mode optical fiber with a microsphere, with a diameter that is 5 μm, to fabricate a microsensor with a size in the micrometer scale.
- (2)
- The microsensor we propose overcomes difficulties encountered via conventional sensors in measuring the vibration of miniature motor shafts with diameters less than 1 mm or even microns within a confined space.
- (3)
- By exploiting the microsphere’s focusing properties (PNJ phenomenon), it becomes possible to accurately concentrate a sub-micron-sized light spot onto the surface of the measured rotating shaft. This, in turn, amplifies the reflected light intensity from the axial and radial positions of the miniature motor and enhances the signal-to-noise ratio of the measured signal, ultimately leading to improved measurement accuracy.
- (4)
- Only one light source is used to realize the measurement of the radial vibration and the axial vibration of the miniature motor simultaneously, and the measurement structure is compact.
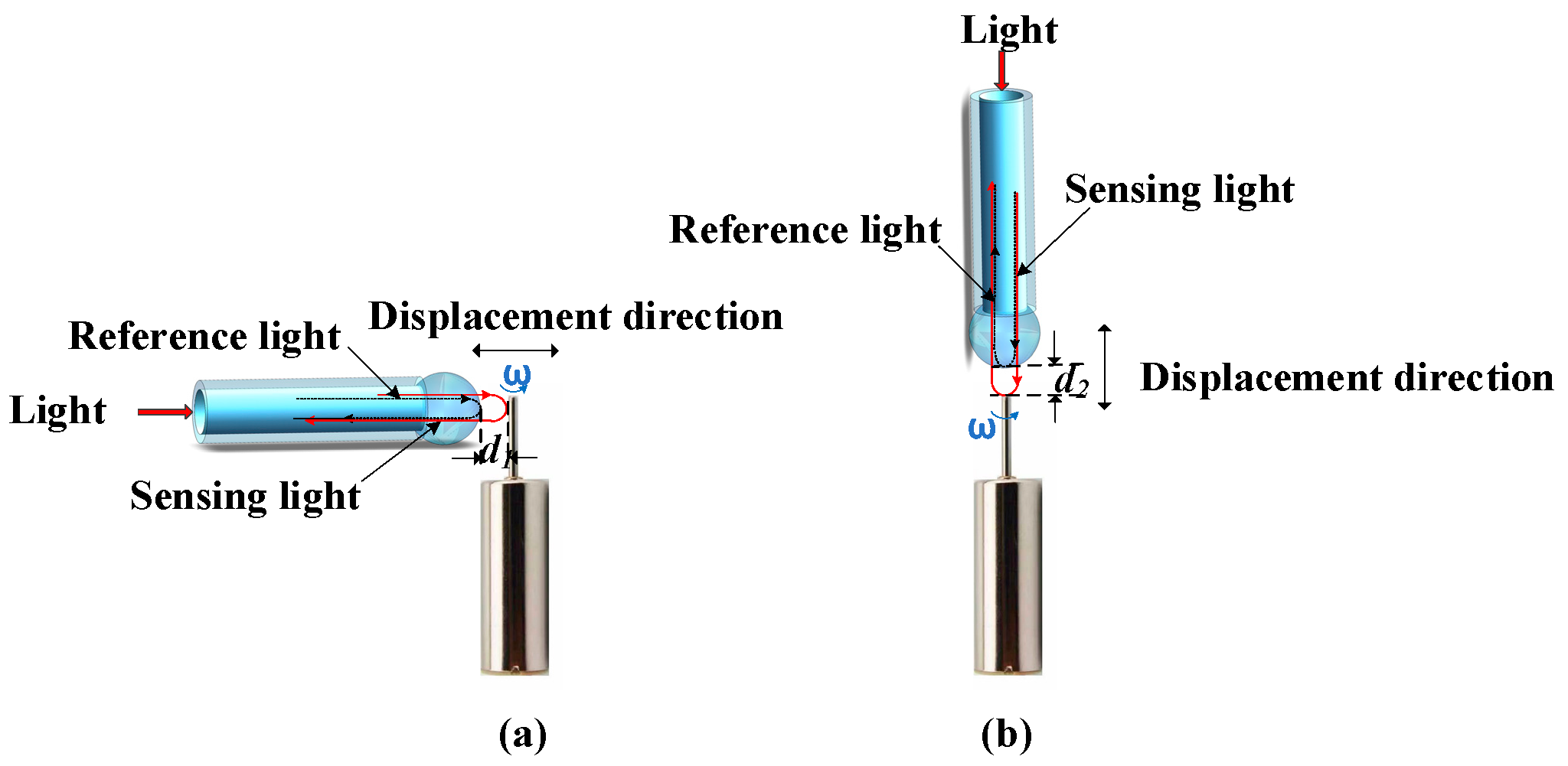
2. Theory of PNJ and Fabry–Perot Interference
2.1. Principle of the PNJ Generated by a Dielectric Microsphere
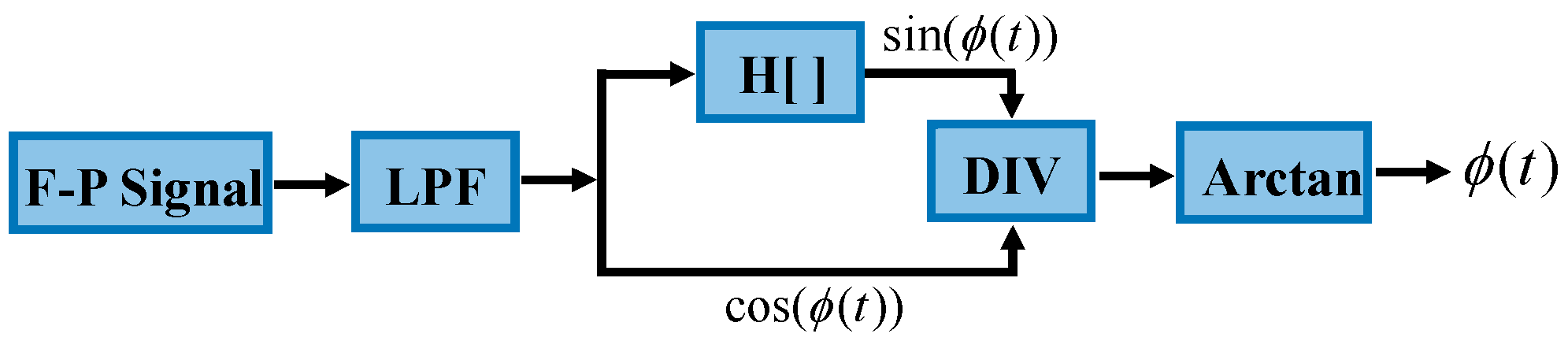
2.2. Phase Demodulation Principle of Fabry–Perot Interference Signal
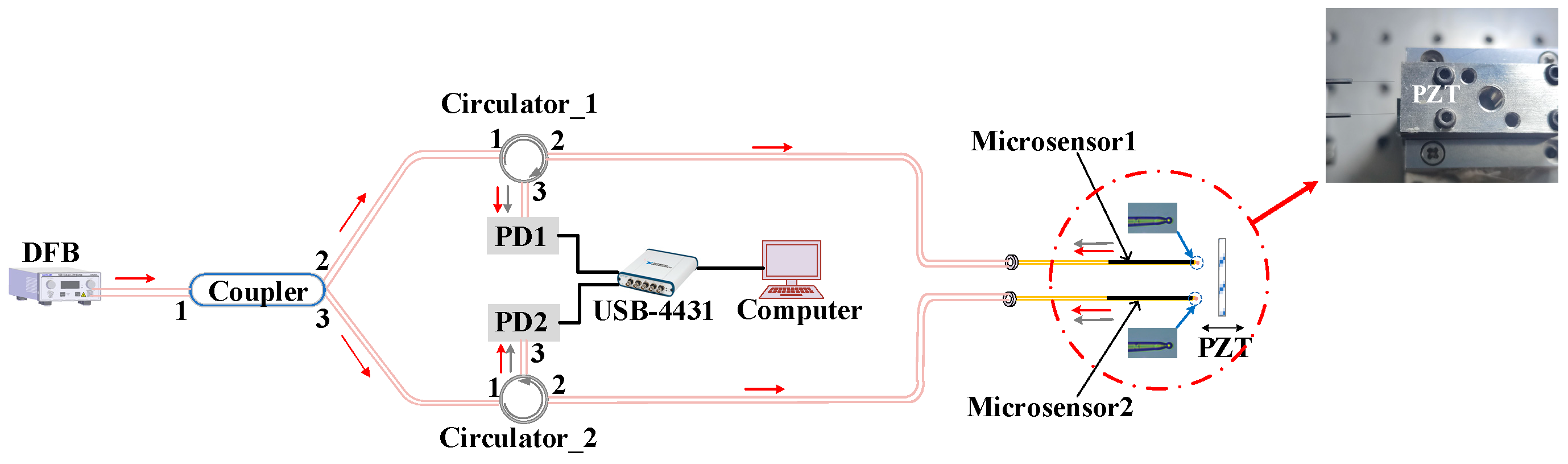
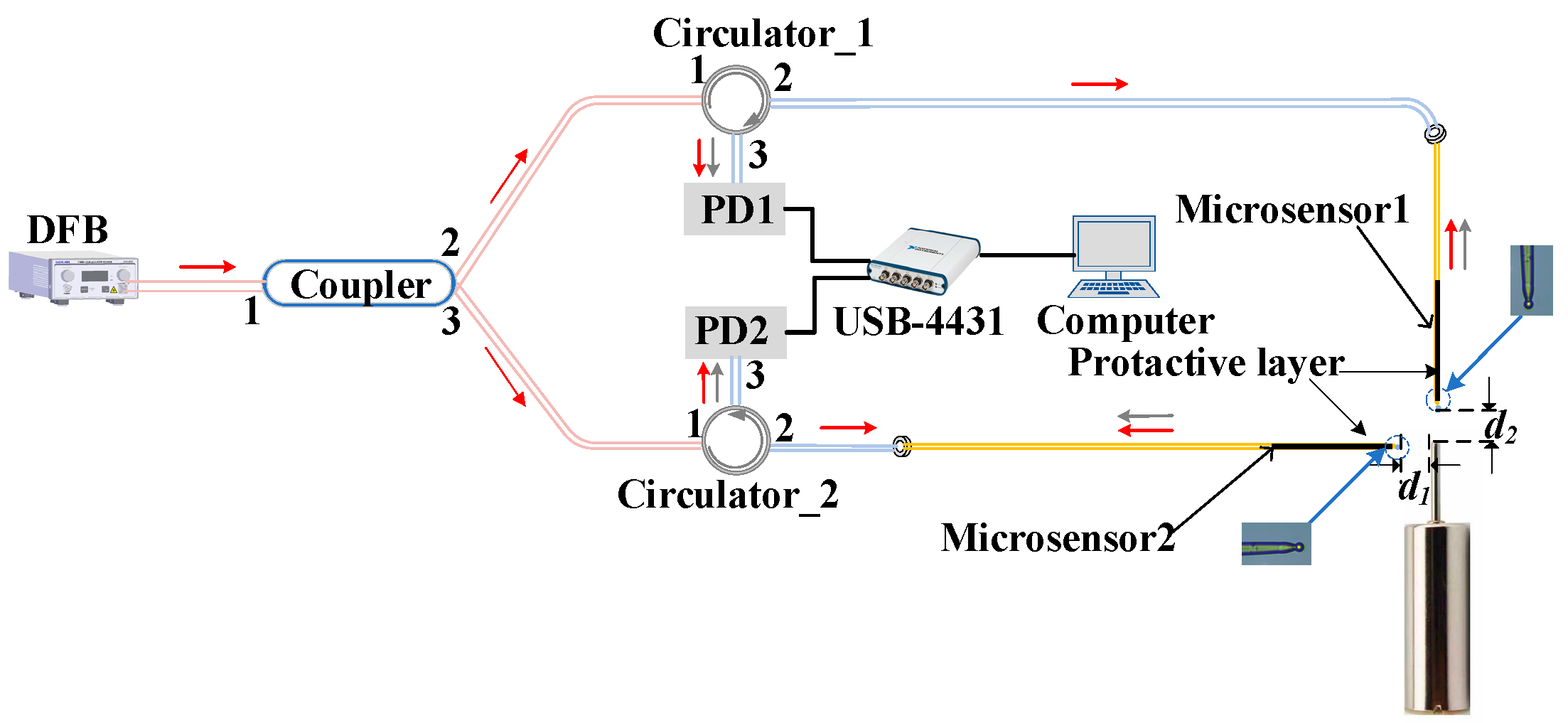
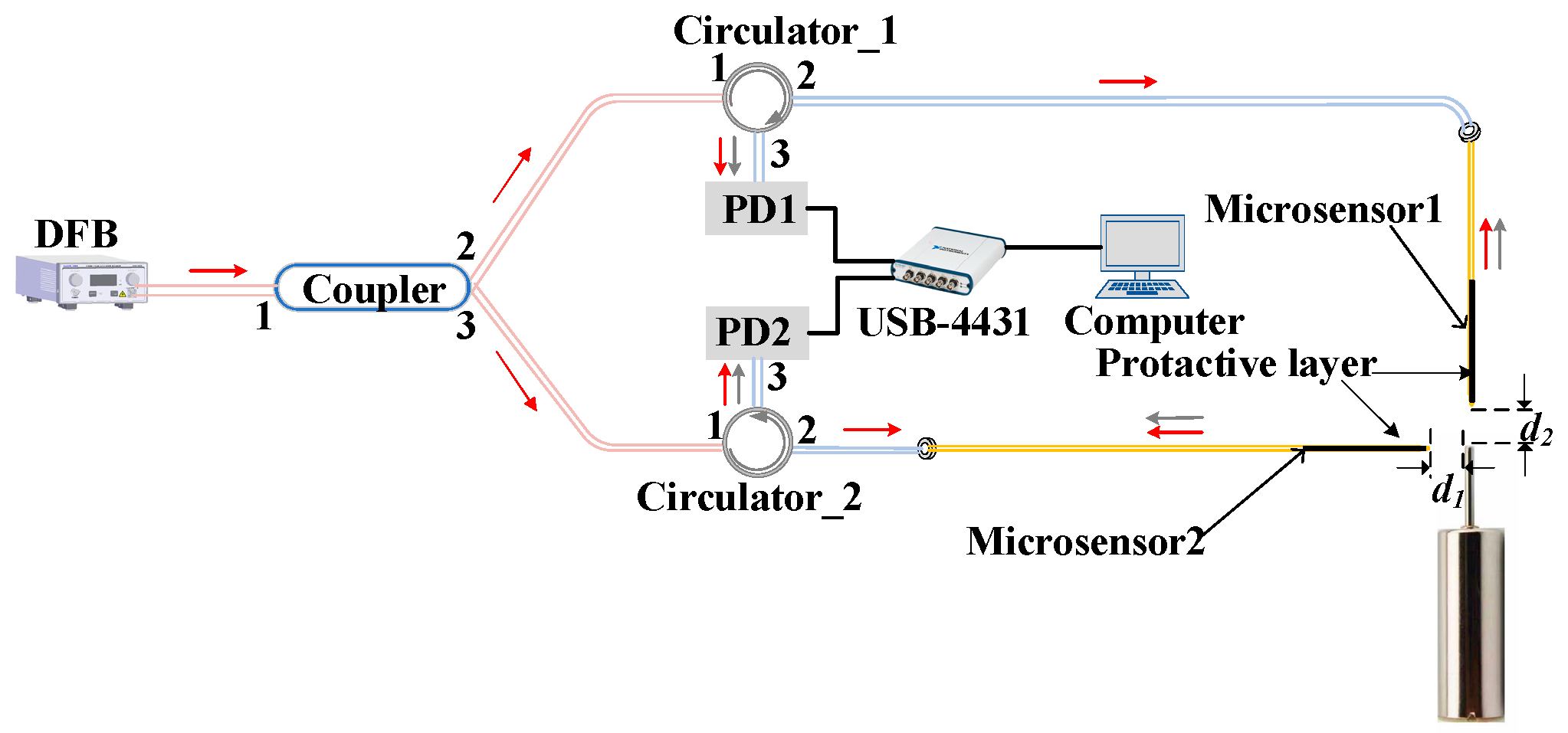
3. Experiments and Results
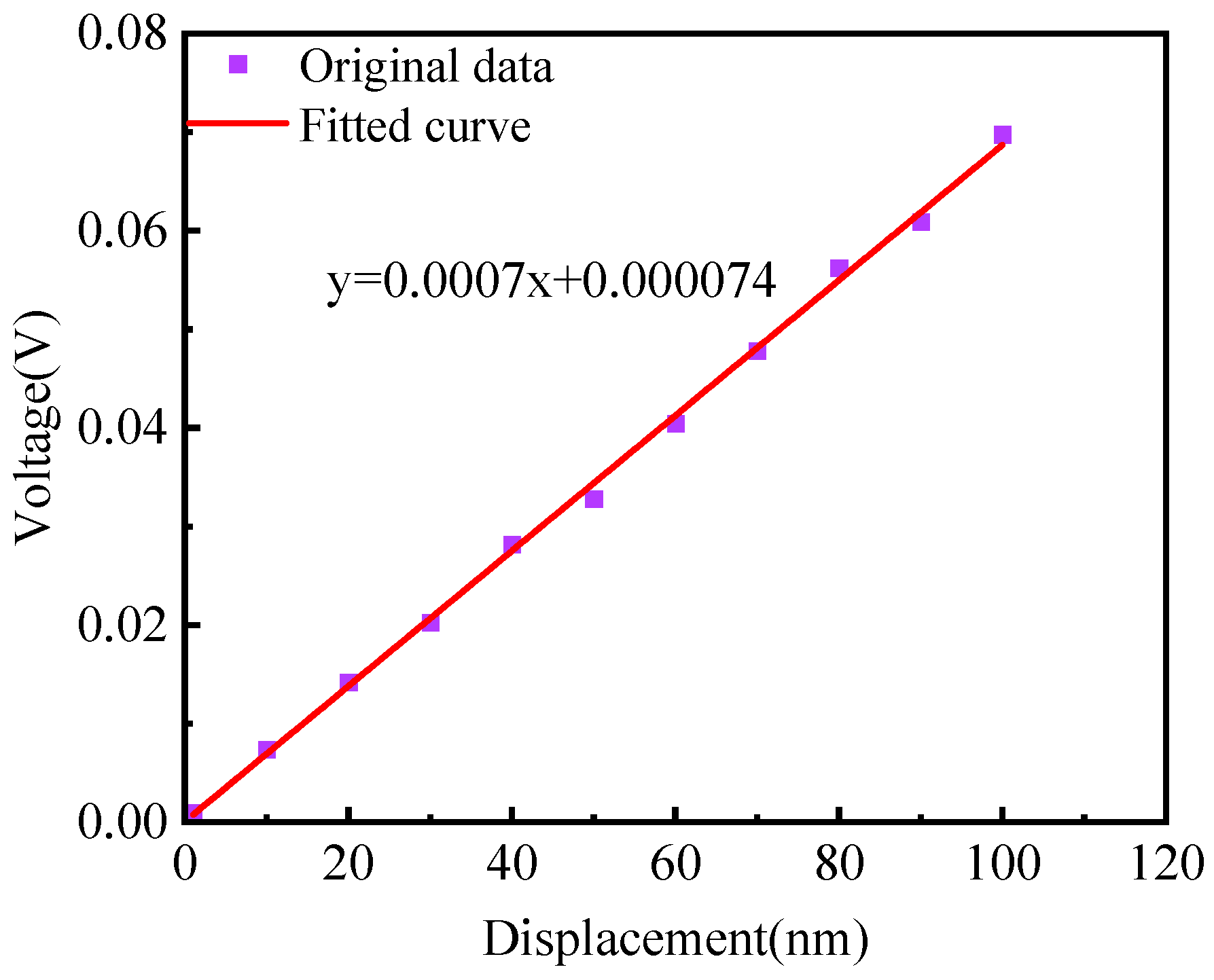
3.1. The Calibration Experiment and Results
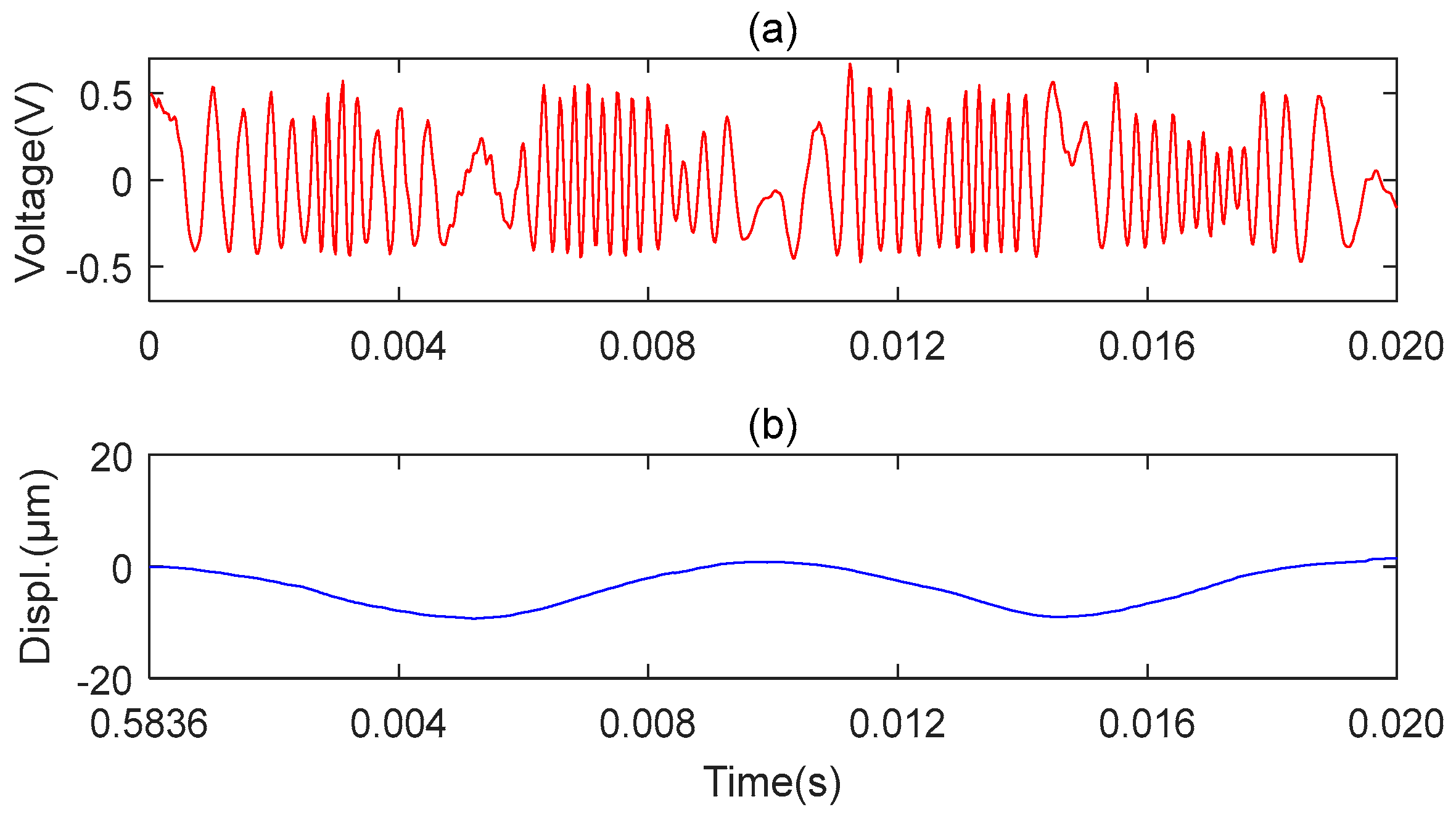
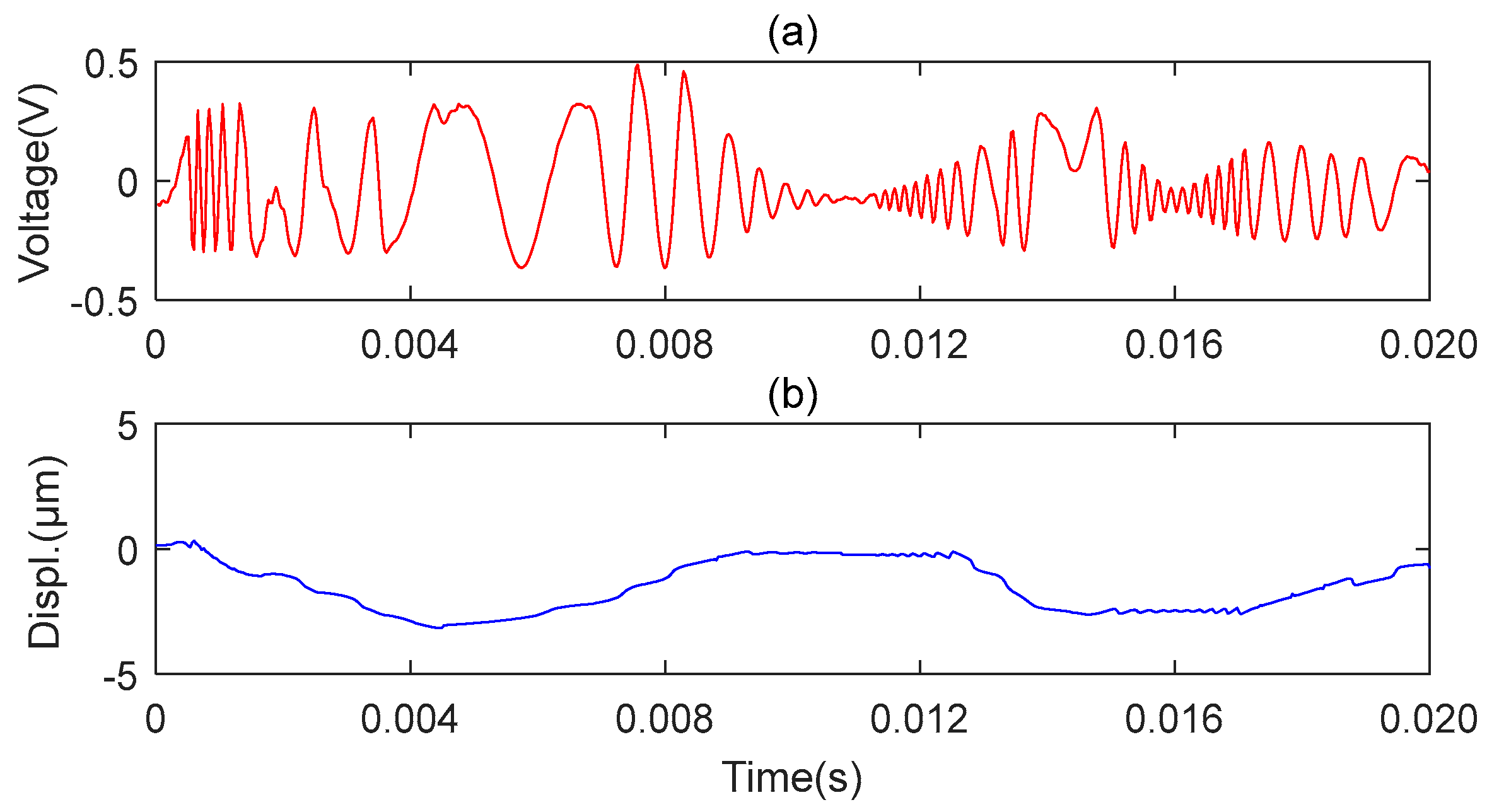
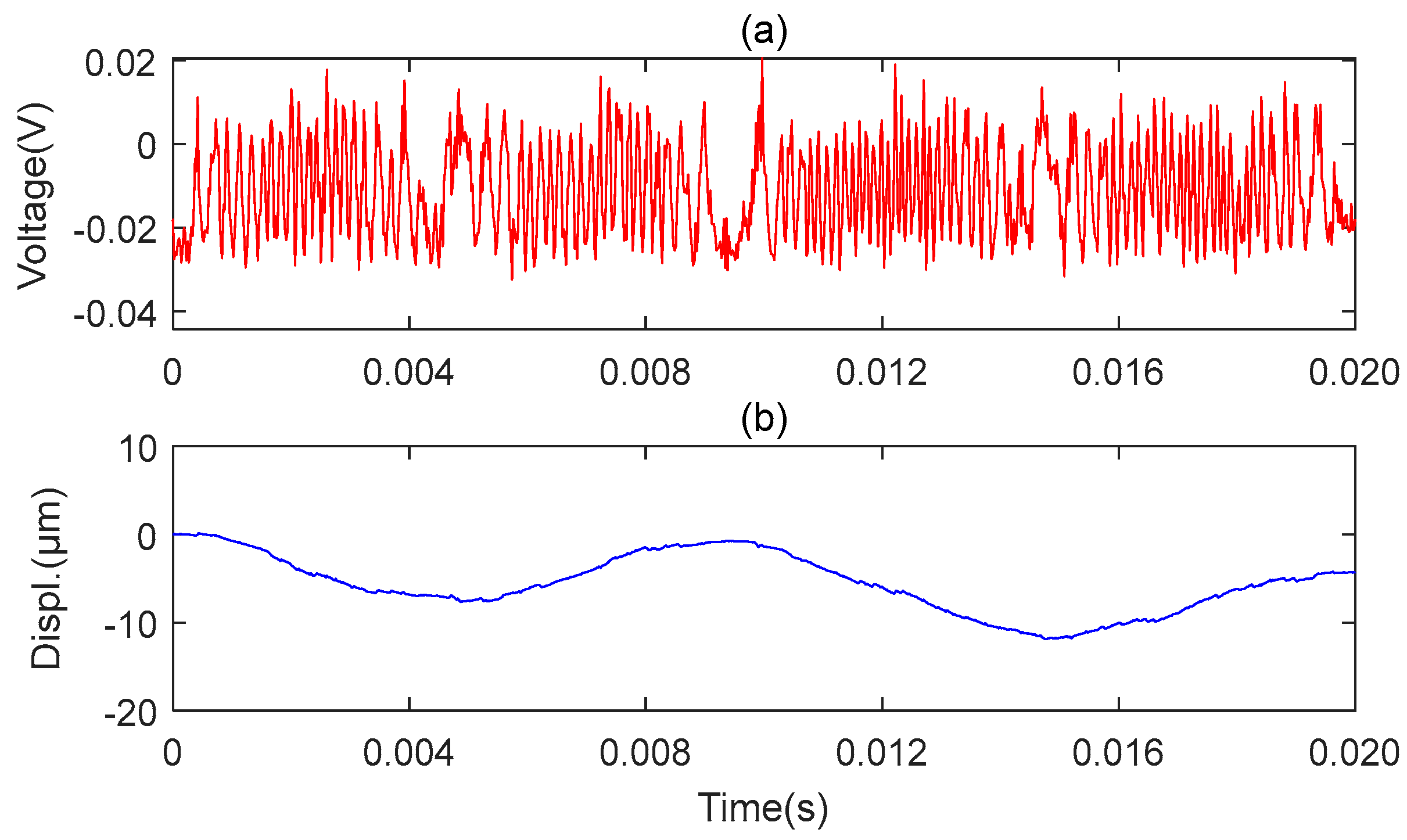
3.2. Experiments and Results of the MMS Vibration Measurement
3.3. Experiments and Results of Sensitivity Measurement
3.4. The Comparative Experiment and Results
4. Discussion
- (1)
- Clean the Surface: Ensure that the MMS surface is clean and free from dust, grease, or other contaminants. Using a cleaner or solvent can help remove any residues that might interfere with measurements.
- (2)
- Smooth the Surface: Inspect the MMS surface for smoothness, ensuring there are no dents, protrusions, or irregularities. Irregular surfaces can introduce measurement errors.
- (3)
- Rust Removal: If there is rust on the shaft surface, it should be removed to ensure accurate measurements. Sandpaper, a wire brush, or other tools can be used to eliminate rust.
- (4)
- Surface Treatment: For high-precision measurements, consider surface treatment such as grinding or polishing to ensure the surface is smooth and uniform. Surface condition is crucial for accurate vibration measurements.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MMS | Miniature motor shaft |
| PNJ | Photonic nanojet |
| LVDT | Linear variable differential transformer |
| LSMI | Laser self-mixing interference |
| DHI | Digital holographic interference |
| FWHM | Full width at half maximum |
| WD | Working distance |
| IDL | Intensity decay length |
| F-P | Fabry–Perot |
| MHT | Multiple Hilbert |
| PZT | Piezoelectric |
| DFB | Distributed feedback laser |
| DC | Direct current |
References
- Li, J.W.; Sun, Z.J.; Yan, H.; Chen, J.Y. Design of a Magnetically Anchored Laparoscope Using Miniature Ultrasonic Motors. Micromachines 2022, 13, 855. [Google Scholar] [CrossRef]
- Liu, C.S.; Lin, P.D.; Tsai, M.C. A Miniature Spindle Motor with Fluid Dynamic Bearings for Portable Storage Device Applications. Microsyst. Technol. 2009, 15, 1001–1007. [Google Scholar] [CrossRef]
- Xie, Z.P.; Zhao, R.C.; Zheng, J.M.; Lang, Y.C. Failure Probability Modeling of Miniature DC Motors and Its Application in Fault Diagnosis. Shock. Vib. 2021, 2021, 9958412. [Google Scholar] [CrossRef]
- Tanabe, M.; Xie, S.; Tagawa, N.; Moriya, T.; Furukawa, Y. Development of a Mechanical Scanning-Type Intravascular Ultrasound System Using a Miniature Ultrasound Motor. Jpn. J. Appl. Phys. 2007, 46, 4805. [Google Scholar] [CrossRef]
- Miyoshi, K.; Mashimo, T. Miniature Direct-Drive Two-Link Using a Micro-Flat Ultrasonic Motor. Adv. Robot. 2018, 32, 1102–1110. [Google Scholar] [CrossRef]
- Lin, Y.; Xu, H. Development of Single-Channel Shaft Vibration Meter for Rotating Machinery. Instrum. Tech. Sens. 2009, 7, 1–26. [Google Scholar]
- Lin, J.; Bissonnette, M.R. A New Capacitive Proximity Probe Immune to Electrical Runout. Proc. Can. Mach. Vib. Assoc. 1997, 10, 1–5. [Google Scholar]
- Chen, C.B.; Ye, G.L. Development of Small-Strain Triaxial Apparatus Using LVDT Sensors and Its Application to Soft Clay Test. Rock Soil Mech. 2018, 39, 2304–2310. [Google Scholar] [CrossRef]
- Atashkhooei, R.; Urresty, J.C.; Royo, S.; Riba, J.R.; Romeral, L. Runout Tracking in Electric Motors Using Self-Mixing Interferometry. IEEE-ASME Trans. Mechatron. 2014, 19, 184–190. [Google Scholar] [CrossRef]
- Tatar, K.; Gren, P.; Lycksam, H. Digital Holographic Interferometry for Simultaneous Orthogonal Radial Vibration Measurements along Rotating Shafts. Appl. Opt. 2008, 47, 3269–3274. [Google Scholar] [CrossRef]
- Huber, E.; Frost, M. Light Scattering by Small Particles. Aqua 1998, 47, 87–94. [Google Scholar]
- Luk’yanchuk, B.S.; Paniagua-Dominguez, R.; Minin, I.; Minin, O.; Wang, Z.B. Refractive Index Less Than Two: Photonic Nanojets Yesterday, Today and Tomorrow Invited. Opt. Mater. Express 2017, 7, 1820–1847. [Google Scholar] [CrossRef]
- Darafsheh, A. Photonic nanojets and their applications. J. Phys. Photonics 2021, 3, 022001. [Google Scholar] [CrossRef]
- Li, H.; Song, W.Y.; Zhao, Y.; Cao, Q.; Wen, A.H. Optical Trapping, Sensing, and Imaging by Photonic Nanojets. Photonics 2021, 8, 434. [Google Scholar] [CrossRef]
- Bouaziz, D.; Chabrol, G.; Guessoum, A.; Demagh, N.E.; Lecler, S. Photonic Jet-Shaped Optical Fiber Tips Versus Lensed Fibers. Photonics 2021, 8, 373. [Google Scholar] [CrossRef]
- Wang, X.F.; Guo, X.Y.; Wang, Y.; Jiang, C.L.; Jiang, J.G.; Zhang, Z.H. All-Fiber Differential Interferometer for Nanometric Displacement Measurement. Opt. Commun. 2020, 475, 126283. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhu, T.; Hou, Y.S.; Chiang, K.S. All-Fiber Vibration Sensor Based on a Fabry-Perot Interferometer and a Microstructure Beam. J. Opt. Soc. Am. B-Opt. Phys. 2013, 30, 1211–1215. [Google Scholar] [CrossRef]
- Zhang, H.Z.; Jiang, Q. Highly Sensitive Air Pressure Sensor Based on Fabry-Perot Interference. IEEE Sens. J. 2022, 22, 6637–6643. [Google Scholar] [CrossRef]
- Fu, X.H.; Wang, D.; Liu, L.X.; Liu, F.; Wen, J.; Fu, G.W.; Bi, W.H. A Double-Cladding Fiber Curvature Sensor Based on the Extrinsic Fabry-Perot Interferometer. Optoelectron. Lett. 2019, 15, 6–10. [Google Scholar] [CrossRef]
- Gao, H.C.; Jiang, Y.; Zhang, L.C.; Jiang, L. Five-Step Phase-Shifting White-Light Interferometry for the Measurement of Fiber Optic Extrinsic Fabry-Perot Interferometers. Appl. Opt. 2018, 57, 1168–1173. [Google Scholar] [CrossRef]
- Liang, H.W.; Sun, Y.; Huang, Z.; Jiang, C.L.; Zhang, Z.H.; Kan, L.L. Reconstruction of Fabry-Perot Cavity Interferometer Nanometer Micro-Displacement Based on Hilbert Transform. Chin. Opt. Lett. 2021, 19, 091202. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Li, C.W.; Huang, Z. Vibration Measurement Based on Multiple Hilbert Transform for Self-Mixing Interferometry. Opt. Commun. 2019, 436, 192–196. [Google Scholar] [CrossRef]
- Tamez, J.P.; Bhardwaj, M.C.; Bhalla, A.; Guo, R.Y. Simulation and Experimental Studies on Tri-Phasic PZT Piezoelectric Transducer. Ferroelectrics 2014, 473, 45–54. [Google Scholar] [CrossRef]
- Sun, J.J.; Ren, J.Y.; Sun, H.X. A Novel Design of an Inner Rotor for Optimizing the Air-Gap Magnetic Field of Hollow-Cup Motors. Machines 2022, 10, 314. [Google Scholar] [CrossRef]







| Amplitude (μm) | Maximum Absolute Error (nm) | Average Absolute Error (nm) | Maximum Relative Error (%) |
|---|---|---|---|
| 3.1 | 75 | 68 | 1.21% |
| 6.2 | 99 | 90 | 0.80% |
| 7 | 132 | 123 | 0.94% |
| 8 | 155 | 138 | 0.97% |
| Amplitude (μm) | Maximum Absolute Error (nm) | Average Absolute Error (nm) | Maximum Relative Error (%) |
|---|---|---|---|
| 3.1 | 78 | 69 | 1.26% |
| 6.2 | 95 | 88 | 0.77% |
| 7 | 144 | 132 | 1.01% |
| 8 | 165 | 156 | 1.03% |
| Frequency (Hz) | PZT Amplitude (μm) | PDV_100 Amplitude (μm) | Maximum Absolute Error (nm) |
|---|---|---|---|
| 5 | 2 | 1.970 | 30 |
| 5 | 4 | 3.957 | 43 |
| 5 | 6 | 5.960 | 40 |
| 5 | 8 | 7.953 | 47 |
| 5 | 10 | 9.956 | 44 |
| Parameter | Numerical Values |
|---|---|
| Resolution ratio | 1 nm |
| Linearity | ±1.5% |
| Working temperature | −40~100 °C |
| Sensing distance | <1 cm |
| Frequency response | 0.5 Hz~100 kHz |
| Dynamic range | 10 nm~500 μm |
| Relative error | <2% |
| Sensitivity | 0.7 mV/nm |
| Repeatability | ±1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, K.; Jiang, C.; Ban, Q.; Dai, P.; Fan, Y.; Yang, S.; Zhang, Y.; Wang, J.; Wang, Y.; Chen, X.; et al. Microsphere-Based Microsensor for Miniature Motors’ Vibration Measurement. Sensors 2023, 23, 9196. https://doi.org/10.3390/s23229196
Xu K, Jiang C, Ban Q, Dai P, Fan Y, Yang S, Zhang Y, Wang J, Wang Y, Chen X, et al. Microsphere-Based Microsensor for Miniature Motors’ Vibration Measurement. Sensors. 2023; 23(22):9196. https://doi.org/10.3390/s23229196
Chicago/Turabian StyleXu, Kaichuan, Chunlei Jiang, Qilu Ban, Pan Dai, Yaqiang Fan, Shijie Yang, Yue Zhang, Jiacheng Wang, Yu Wang, Xiangfei Chen, and et al. 2023. "Microsphere-Based Microsensor for Miniature Motors’ Vibration Measurement" Sensors 23, no. 22: 9196. https://doi.org/10.3390/s23229196
APA StyleXu, K., Jiang, C., Ban, Q., Dai, P., Fan, Y., Yang, S., Zhang, Y., Wang, J., Wang, Y., Chen, X., Zeng, J., & Wang, F. (2023). Microsphere-Based Microsensor for Miniature Motors’ Vibration Measurement. Sensors, 23(22), 9196. https://doi.org/10.3390/s23229196





